9.2 用样本估计总体
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高一数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
必修第二册同步拔高,难度2颗星!
模块导图
知识剖析
总体取值规律的估计
① 频率直方图
(1) 画频率直方图的步骤
求极差--决定组距与组数--将数据分组--列频率分布表--画频率分布直方图.
(2) 小长方形的面积=频率
(3) 在直方图中,各小长方形的面积之和等于\(1\).
总体百分位数的估计
① 第p百分位数的概念
一般地,一组数据的第\(p\)百分位数是这样一个值,它使得这组数据中至少有\(p\%\)的数据小于或等于这个值,且至少有\((100-p)\%\)的数据大于或等于这个值.
② 计算一组n个数据的第p百分位数
第一步:按从小到大排列原始数据;
第二步:计算\(i=n×p\%\);
第三步:若\(i\)不是整数,而大于\(i\)的比邻整数为\(j\),则第\(p\)百分位数为第j项数据;若\(i\)是整数,则第\(p\)百分位数为第\(i\)项与第\((i+1)\)项数据的平均数.
③ 四分位数的概念
四分位数:包含第\(25\)百分位数,第\(50\)百分位数,第\(75\)百分位数.
中位数相当于第\(50\)百分位数,第\(25\)百分位数也称为第一四分位数或下四分位数,第75百分位数也称为第三四分位数或上四分位数.
总体集中趋势的估计
一般来说,对一个单峰的频率分布直方图来说,如果直方图的形状是对称的,那么平均数和中位数应该大体上差不多;如果直方图在右边“拖尾”,那么平均数大于中位数;如果直方图在左边“拖尾”,那么平均数小于中位数.
一般地,对数值型数据(如用水量,身高,收入,产量等)集中趋势的描述,可以用平均数、中位数;而对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
总体离散程度的估计
① 方差,标准差的概念
(1)假设一组数据是\(x_1\),\(x_2\),…,\(x_n\),用\(\bar{x}\)表示这组数据的平均数,我们称
这组数据的方差,为了计算方便也可以用 \(\dfrac{1}{n} \sum_{i=1}^n x_i^2-\bar{x}^2\);
标准差是 \(S=\sqrt{\dfrac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2}\).
② 方差,标准差的意义
方差越大,表明数据波动越大,越不稳定;方差越小,表明数据波动越小,越稳定.
经典例题
【题型一】常见统计数据
【典题1】 某地一年之内\(12\)个月的月降水量从小到大分别为:\(46\),\(51\), \(48\),\(53\),\(56\), \(53\),\(56\),\(64\),\(58\),\(56\),\(66\),\(71\),则该地区的月降水量\(20\%\)分位数和\(75\%\)分位数为( )
A.\(51\),\(58\) \(\qquad \qquad \qquad \qquad\) B.\(51\),\(61\) \(\qquad \qquad \qquad \qquad\) C.\(52\),\(58\) \(\qquad \qquad \qquad \qquad\) D.\(52\),\(61\)
【解析】该组数据从小到大排列为:\(46\),\(48\),\(51\),\(53\),\(53\),\(56\),\(56\),\(56\),\(58\),\(64\),\(66\),\(71\),
因为\(20\%×12=2.4\),计算结果不是整数,
所以\(20\%\)分位数为第\(3\)项数据,即\(51\);
因为\(75\%×12=9\),计算结果是整数,
所以\(75\%\)分位数为第\(9\)项和第\(10\)项数据的平均数,即\(\dfrac{58+64}{2}=61\).
【点拨】计算一组\(n\)个数据的第\(p\)百分位数的步骤:
第一步:按从小到大排列原始数据;
第二步:计算\(i=n×p\%\);
第三步:若\(i\)不是整数,而大于\(i\)的比邻整数为\(j\),则第\(p\)百分位数为第j项数据;若\(i\)是整数,则第\(p\)百分位数为第\(i\)项与第\((i+1)\)项数据的平均数.
【典题2】 甲、乙两人在相同条件下各打靶\(10\)次,每次打靶的成绩情况如图所示:下列说法错误的是( )

A.从平均数和方差相结合看,甲波动比较大,乙相对比较稳定
B.从折线统计图上两人射击命中环数走势看,甲更有潜力
C.从平均数和命中\(9\)环及\(9\)环以上的次数相结合看,甲成绩较好
D.从平均数和中位数相结合看,乙成绩较好
【解析】由图可知,甲打靶的成绩为\(2\),\(4\),\(6\),\(8\),\(7\),\(7\),8,\(9\),\(9\),\(10\),
所以甲的平均数为\(\overline{x_{\text {甲 }}}=7\),
甲方差\(S_{\text {甲 }}^2=\dfrac{1}{10}[(2-7)^2+(4-7)^2+(6-7)^2+2 \times(7-7)^2+2 \times(8-7)^2\)\(+2 \times(9-7)^2+(10-7)^2]=5.4\);
乙打靶的成绩分别为\(9\),\(5\),\(7\),\(8\),\(7\),\(6\),\(8\),\(6\),\(7\),\(7\),
乙的平均数为 \(\overline{x_乙}=7\),
乙方差 \(S_{\text {乙 }}^2=\dfrac{1}{10}\left[(9-7)^2+(5-7)^2+4 \times(7-7)^2+2 \times(8-7)^2+2 \times(6-7)^2\right]=1.2\);
所以\(S_{\text {甲 }}^2>S_{\text {乙 }}^2 \text { , }\),从平均数和方差相结合看,甲波动比较大,乙波动比较小,故\(A\)正确,
(不求方差,看图也可知道甲的波动比乙的要打些)
从折线统计图看,在后半部分,甲呈上升趋势,而乙呈下降趋势,甲更有潜力,故\(B\)正确,
甲打靶的成绩为\(2\),\(4\),\(6\),\(7\),\(7\),\(8\),\(8\),\(9\),\(9\),\(10\),中位数为\(7.5\),
乙打靶的成绩为\(5\),\(6\),\(6\),\(7\),\(7\),\(7\),\(7\),\(8\),\(8\),\(9\),中位数为\(7\),
甲\(9\)环以及\(9\)环以上的次数为\(3\)次,乙\(9\)环以及\(9\)环以上的次数为\(1\)次,
而二人的平均数相同,故甲成绩更好点,故\(C\)正确,
甲乙的平均数相同,而甲的中位数大于乙的中位数,故甲的成绩比较好,故\(D\)错误,
故选:\(D\).
【典题3】 已知\(x_1\),\(x_2\),…,\(x_n\)的平均数为\(10\),标准差为\(2\),则\(2x_1-1\),\(2x_2-1\),…,\(2x_n-1\)的平均数和标准差分别为\(\underline{\quad \quad}\) .
【解析】\(\because x_1\),\(x_2\),…,\(x_n\)的平均数为\(10\),标准差为\(2\),
\(\therefore 2x_1-1\),\(2x_2-1\),…,\(2x_n-1\)的平均数为:\(2×10-1=19\),标准差为: \(\sqrt{2^2 \times 2^2}=4\).
【点拨】若原有的数据\(x_1\),\(x_2\),…,\(x_n\)平均数为\(m\),方差为\(n\),在原数据基础上进行线性变化\(y_n=ax_n+b\),则新的平均数为\(am+b\),新的方差为\(a^2 n\).
【典题4】 为了解本市居民的生活成本,甲、乙、内三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),甲、乙、丙所调查数据的标准差分别为\(s_1\),\(s_2\),\(s_3\),则它们的大小关系为( )

A.\(s_1>s_2>s_3\) \(\qquad \qquad\) B.\(s_1>s_3>s_2\) \(\qquad \qquad\) C.\(s_3>s_2>s_1\) \(\qquad \qquad\) D.\(s_3>s_1>s_2\)
【解析】根据三个频率分步直方图知,
甲数据的两端数字较多,绝大部分数字都处在两端数据偏离平均数远,最分散,其方差、标准差最大;
丙数据是单峰的每一个小长方形的差别比较小,数字分布均匀,数据不如第一组偏离平均数大,方差比第一组中数据中的方差、标准差小,
而乙数据绝大部分数字都在平均数左右,数据最集中,故其方差、标准差最小,
总上可知\(s_1>s_3>s_2\),
故选:\(B\).
【点拨】根据方差的意义就可以判断方差的大小. 数据波动越大,方差越大;数据波动越小,方差越小.
【典题5】在发生某公共卫生事件期间,有专业机构认为该事件在一段事时间内没有发生大规模群体感染的标志是“连续\(10\)日,每天新增疑似病例不超过\(7\)人”.过去\(10\)日,甲、乙、丙、丁四地新增疑似病例数据信息如下:
甲地:中位数为\(2\),众数为\(3\);
乙地:总体平均数为\(2\),总体方差为\(3\);
丙地:总体平均数为\(1\),总体方差大于\(0\);
丁地:总体平均数为\(3\),中位数为\(4\).
则甲、乙、丙、丁四地中,一定没有发生大规模群体感染的是\(\underline{\quad \quad}\)地
【解析】(要每天军不超过\(7\)人方能确定没发生大规模群体感染,即\(10\)个数不出现极端数值)
根据题意,依次分析选项:
对于甲地:中位数为\(2\),众数为\(3\),则从小排到大的数据形式是\(a,b,c,d,2,2,3,3,3,e\);
有可能出现超过\(7\)人的情况,如数据\(0,0,1,1,2,2,3,3,3,8\),
出现了每天新增疑似病例超过\(7\)人的情况,可能发生大规模群体感染;
② 对于丙地,若要满足题意,则总和是\(10\),且不能\(10\)个数都是\(1\),
对于数据\(8,1,1,0,0,0,0,0,0,0\),总体平均数为\(1\),总体方差大于\(0\),
而出现了每天新增疑似病例超过\(7\)人的情况,可能发生大规模群体感染;
③ 对于丁地,平均数与中位数不能限制极端值的出现,则有可能出现超过\(7\)人的情况,可能发生大规模群体感染,比如\(0,0,0,0,4,4,4,4,4,10\);
④ (甲丙丁都排除了,那如何证明乙地是一定没有发生大规模群体感染?用反证法)
对于乙地,假设过去\(10\)天新增疑似病例数据存在一个数据\(x\),\(x≥8\),
而总体平均数为\(2\),则总体方差\(S^2>\dfrac{1}{10}(x-2)^2 \geq 3.6\),故不成立,
故假设不成立,故符合没有发生大规模群体感染的标志,一定没有发生大规模群体感染;
故答案为:乙.
【点拨】
(1)先明确众数、平均数、众数对极端数值的出现影响较小,了解满足各项的要求的数据形
式,再通过举反例进行排除.
(2)当证明含“一定”“唯一”“至多”“至少”等字眼的命题或从正面较难求解的,可尝试间接证明方法--反证法.
【典题6】 (多选) 气象意义上从春季进入夏季的标志为“当且仅当连续\(5\)天每天日平均温度不低于\(22^{\circ} C\)”.现有甲、乙、丙三地连续\(5\)天日平均温度的记录数据(数据均为正整数,单位\(^{\circ} C\))且满足以下条件:
甲地:\(5\)个数据的中位数是\(24\),众数是\(22\);
乙地:\(5\)个数据的中位数是\(27\),平均数是\(24\);
丙地:\(5\)个数据有\(1\)个是\(30\),平均数是\(24\),方差是\(9.6\).
根据以上数据,下列统计结论正确的是( )
A.甲地进入了夏季
B.乙地进入了夏季
C.不能确定丙地进入了夏季
D.恰有\(2\)地确定进入了夏季
【解析】甲地:\(5\)个数据由小到大排,
则\(22,22,24,a,b\),其中\(24<a<b\),满足进入夏季的标志;
乙地:将\(5\)个数据由小到大排,则\(a,b,27,c,d\),其中\(a≤b≤27≤c≤d\),
则\(27+c+d≥81\),而\(a+b+27+c+d=120\),
故\(a+b≤39\),其中必有一个小于\(22\),故不满足一定进入夏季的标志;
丙地:设\(5\)个数据为\(a,b,c,d,30\),且\(a,b,c,d\in Z\),
由方差公式可知:
\((a-24)^2+(b-24)^2+(c-24)^2+(d-24)^2+(30-24)^2=9.6 \times 5=48\),
则 \((a-24)^2+(b-24)^2+(c-24)^2+(d-24)^2=12=9+1+1+1\),
不妨设\(|a-24|=3\),\(|b-24|=|c-24|=|d-24|=1\),
则\(b,c,d\)均大于\(22\),但\(a\)不确定是否大于\(22\),故不能确定丙地进入夏天.
故选:\(AC\).
巩固练习
1. (★)以下数据为参加数学竞赛决赛的\(15\)人的成绩:(单位:分)
\(78,70,72,86,88,79,80,81,94,84,56,98,83,90,91\).
则这\(15\)人成绩的第\(80\)百分位数是\(\underline{\quad \quad}\).
2.(★) 已知甲、乙两组数据(已按从小到大的顺序排列):
甲组:\(27、28、39、40、m、50\);
乙组:\(24、n、34、43、48、52\).
若这两组数据的\(30\)百分位数、\(80\)百分位数分别相等,则\(\dfrac{m}{n}\)等于 \(\underline{\quad \quad}\) .
3. (★)某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )

A.\(100\) \(\qquad \qquad \qquad \qquad\) B.\(110\) \(\qquad \qquad \qquad \qquad\) C.\(115\) \(\qquad \qquad \qquad \qquad\) D.\(120\)
4. (★★) 在某次测量中得到\(E\)的样本数据如下:\(80,82,82,84,84\),\(84,84,86,86,86,86\).若\(F\)的样本数据恰好是\(E\)的样本数据都减去\(2\)后得到的数据,则关于\(E\),\(F\)两样本数据特征的下列说法中,正确的是( )
A.\(E\),\(F\)样本数据的众数为\(84\) \(\qquad \qquad \qquad \qquad\) B.\(E\),\(F\)样本数据的方差相同
C.\(E\),\(F\)样本数据的平均数相同 \(\qquad \qquad \qquad \qquad\) D.\(E\),\(F\)样本数据的中位数相同
5. (★★)下列命题中不正确的是( )
A.一组数据\(1,2,3,3,4,5\)的众数大于中位数
B.数据\(6,5,4,3,3,3,2,2,2,1\)的\(85\%\)分位数为\(5\)
C.若甲组数据的方差为\(5\),乙组数据为\(5\),\(6\),\(9\),\(10\),\(5\),则这两组数据中较稳定的是乙
D.为调查学生每天平均阅读时间,某中学从在校学生中,利用分层抽样的方法抽取初中生\(20\)人,高中生\(10\)人.经调查,这\(20\)名初中生每天平均阅读时间为\(60\)分钟,这\(10\)名高中生每天平均阅读时间为\(90\)分钟,那么被抽中的\(30\)名学生每天平均阅读时间为\(70\)分钟
6.(★★) 已知数据\(x_1\),\(x_2\),\(x_3\),…, \(\text { , } x_{100}\)是杭州市\(100\)个普通职工的2016年10月份的收入(均不超过\(2\)万元),设这\(100\)个数据的中位数为\(x\),平均数为\(y\),方差为\(z\),如果再加上马云2016年10月份的收入\(x_{101}\)(约\(100\)亿元),则相对于\(x\)、\(y\)、\(z\),这\(101\)个月收入数据( )
A.平均数可能不变,中位数可能不变,方差可能不变
B.平均数大大增大,中位数可能不变,方差也不变
C.平均数大大增大,中位数一定变大,方差可能不变
D.平均数大大增大,中位数可能不变,方差变大
7. (★★) 设样本\(x_1\),\(x_2\),…,\(x_{10}\)数据的平均值和方差分别为\(2\)和\(5\),若\(y_i=x_i+a\)(\(a\)为非零实数,\(i=1,2,…,10\)),则\(y_1\),\(y_2\),…,\(y_{10}\)的均值和方差分别为( )
A.\(2\),\(5\) \(\qquad \qquad\) B.\(2+a\),\(5\) \(\qquad \qquad\) C.\(2+a\),\(5+a\) \(\qquad \qquad\) D.\(2\),\(5+a\)
8. (★★★)(多选) 在全球新型冠状病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续\(7\)天每天新增感染人数不超过\(5\)人”,根据连续\(7\)天的新增病例数计算,下列各项中,一定符合上述指标的是( )
A.平均数\(\bar{x} \leq 3\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) B.标准差\(S≤2\)
C.平均数\(\bar{x} \leq 3\)且极差小于或等于\(2\) \(\qquad \qquad\) D.众数等于\(1\)且极差小于或等于\(4\)
9. (★★★) (多选)甲同学投掷骰子\(5\)次,并请乙同学将向上的点数记录下来,计算出平均数和方差.由于记录遗失,乙同学只记得这五个点数的平均数为\(2\),方差在区间\([1.2,2.4]\)内,则这五个点数( )
A.众数可能为\(1\) \(\qquad\) B.中位数可能为\(3\) \(\qquad\) C.一定不会出现\(6\) \(\qquad\) D.出现\(2\)的次数不超过两次
参考答案
-
【答案】\(90.5\)
【解析】该组数据从小到大排列为:
\(56,70,72,78,79,80,81,83,84\),\(86,88,90,91,94,98\).
且\(15×80\%=12\),
所以这\(15\)人成绩的第\(80\)百分位数是 \(\dfrac{1}{2}(90+91)=90.5\).
故答案为:\(90.5\). -
【答案】 \(\dfrac{12}{7}\)
【解析】因为\(6×30\%=1.8\),\(6×80\%=4.8\),
所以乙组的\(30\)百分位数为\(n=28\),甲组的\(80\)百分位数为\(m=48\),
则 \(\dfrac{m}{n}=\dfrac{48}{28}=\dfrac{12}{7}\). -
【答案】\(C\)
【解析】根据频率分布折线图,得;折线的最高点对应的值是\(115\),
据此估计此次考试成绩的众数是\(115\).故选:\(C\). -
【答案】\(B\)
【解析】\(\because\)在某次测量中得到\(E\)的样本数据如下:\(80,82,82,84,84,84,84,86,86,86,86\).
若\(F\)的样本数据恰好是\(E\)的样本数据都减去\(2\)后得到的数据,
\(\therefore E\)样本数据的众数是\(84\)和\(86\),\(F\)样本数据的众数是\(82\)和\(84\),故\(A\)错误;
\(E\),\(F\)样本数据的方差相同,故\(B\)正确;
\(E\)样本数据的平均数比\(F\)样本数据的平均数大\(2\),故\(C\)错误;
\(E\)样本数据的中位数比\(F\)样本数据的中位数大\(2\),故\(D\)错误.
故选:\(B\). -
【答案】\(A\)
【解析】选项\(A:1,2,3,3,4,5\)的众数为\(3\),中位数为 \(\dfrac{3+3}{2}=3\),
故相等,所以\(A\)错误,
选项\(B\):将数据从小到大排列为:\(1,2,2,2,3,3,3,4,5,6\),
则它们的\(85\%\)分位数为\(10×85\%=8.5\),即为\(5\),故\(B\)正确,
选项\(C\):乙组数据的平均值为 \(\dfrac{5+6+9+10+5}{5}=7\),
所以方差为 \(\dfrac{1}{5}\left[(5-7)^2+(6-7)^2+(9-7)^2+(10-7)^2+(5-7)^2\right]=4.4<5\)
所以这两组数据中较稳定的是乙,故\(C\)正确,
选项\(D\):被抽中的\(30\)名学生每天平均阅读时间为 \(\dfrac{20 \times 60+10 \times 90}{30}=70\),故\(D\)正确,
故选:\(A\). -
【答案】\(B\)
【解析】\(\because\)数据\(x_1,x_2,x_3,…,x_n\)是上海普通职工\(n(n≥3,n∈N^*)\)个人的年收入,
而\(x_{n+1}\)为世界首富的年收入
则\(x_{n+1}\)会远大于\(x_1, x_2, x_3, \ldots, x_n\),
故这\(n+1\)个数据中,年收入平均数大大增大,
但中位数可能不变,也可能稍微变大,
但由于数据的集中程序也受到\(x_{n+1}\)比较大的影响,而更加离散,则方差变大
故选\(B\) -
【答案】\(B\)
【解析】根据题意,样本\(x_1\),\(x_2\),…,\(x_{10}\)数据的平均值和方差分别为\(2\)和\(5\),
则有\(\bar{x}=\dfrac{1}{10}\left(x_1+x_2+\ldots+x_{10}\right)=2\),
\(S_x^2=\dfrac{1}{10}\left[\left(x_1-2\right)^2+\left(x_2-2\right)^2+\ldots+\left(x_{10}-2\right)^2\right]=5\),
对于\(y_i=x_i+a\);
则有 \(\bar{y}=\dfrac{1}{10}\left(x_1+a+x_2+a+\ldots+x_{10}+a\right)=\left(x_1+x_2+\ldots+x_{10}+10 a\right)=2+a\),
\(S_y^2=\dfrac{1}{10}\left[\left(y_1-2-a\right)^2+\left(y_2-2-a\right)^2+\ldots+\left(y_{10}-2-a\right)^2\right]=5\),
故选:\(B\). -
【答案】\(CD\)
【解析】\(A\)错,举反例:\(0,0,0,0,2,6,6\),其平均数 \(\bar{x}=2 \leq 3\),不符合指标,
\(B\)错,举反例:\(0,3,3,3,3,3,6\),平均数\(x=3\),且标准差 \(S=\sqrt{\dfrac{18}{7}} \leq 2\),不符合指标,
\(C\)对,若极差等于\(0\)或\(1\),在\(\bar{x} \leq 3\)的条件下,显然符合指标;若极差等于\(2\)且\(\bar{x} \leq 3\),
则每天新增感染人数的最小值与最大值有下列可能:(1)\(0\),\(2\),(2)\(1\),\(3\),(3)\(2\),\(4\),符合指标,
\(D\)对,若众数等于\(1\)且极差小于或等于\(4\),则最大值不超过\(5\),符合指标.
故选:\(CD\). -
【答案】\(ACD\)
【解析】对于\(A\),向上的点数为\(1,1,1,2,5\)时,众数为\(1\),平均数为\(2\),
方差为\(\dfrac{1}{5}\left[(1-2)^2+(1-2)^2+(1-2)^2+(2-2)^2+(5-2)^2\right]=1.2 \in[1.2,2.4]\),故\(A\)正确;
若中位数为\(3\),设五次数据从小到大为:\(a_1,a_2,a_3,a_4,a_5\),则\(a_3=3\),
\(\therefore a_1+a_2+a_4+a_5=2×5-3=7\),
\(a_1+a_2≥2\),\(a_4+a_5≤5\),矛盾,故\(B\)错误;
若出现了\(6\),则其它四次和为\(4\),即数据为\(1,1,1,1,6\),
方差为 \(\dfrac{1}{5}\left[(1-2)^2+(1-2)^2+(1-2)^2+(1-2)^2+(6-2)^2\right]=4 \notin[1.2,2.4]\),矛盾,故\(C\)正确;
若出现\(3\)次\(2\),则其它\(2\)次和为\(4\),这两次为\(1\),\(4\),
方差为 \(\dfrac{1}{5}\left[(1-2)^2+(2-2)^2+(2-2)^2+(2-2)^2+(4-2)^2\right]=0.4 \notin[1.2,2.4]\),矛盾,故\(D\)正确.
故选:\(ACD\).
【题型二】频率直方图的运用
【典题1】 某校从参加高一年级期末考试的学生中抽出\(60\)名学生,将其成绩(均为整数)分成六段\([40,50)\),\([50,60)\),\([60,70)\),\([70,80)\),\([80,90)\),\([90,100]\)后,画出如图所示部分频率分布直方图.观察图形,回答下列问题:

(1) 求第四小组的频率,并补全这个频率分布直方图;
(2) 估计这次考试成绩的中位数(结果取整数值);
(3) 估计这次考试的众数、平均分、方差.
【解析】(1) 因为各组的频率和等于\(1\),
故第四组的频率: \(f_4=1-(0.025+0.015 \times 2+0.01+0.005) \times 10=0.3\),
直方图如右所示.

(2) 成绩在\([40,70)\)的频率为\((0.01+0.015+0.015)×10=0.4\),
成绩在\([40,80)\)的频率为:\(0.4+0.03×10=0.7\),
\(\therefore\)中位数在\([70,80)\)内,
设中位数为\(x\),
\(\because\)中位数要平分直方图的面积,
\(\therefore 0.4+0.03(x-70)=0.5\),解得\(x≈ 73\).
即中位数为\(73\).
(3) 频率最大的是\([70,80]\)组,则众数是\(75\);
利用组中值估算抽样学生的平均分为:
\(45f_1+55f_2+65f_3+75f_4+85f_5+95f_6\)
\(=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71\)
估计这次考试的平均分是\(71\)(分).
方差 \(S^2=(45-71)^2 \times 0.1+(55-71)^2 \times 0.15+(65-71)^2 \times 0.15+(75-71)^2 \times 0.3\) \(+(85-71)^2 \times 0.25+(95-71)^2 \times 0.05=194\).
【点拨】
① 利用频率之和为\(1\),得到所有矩形面积之和为\(1\);
② 在频率直方图中
众数=最高那组的组中值;
平均数=每组的组中值×每组的面积之和;
方差\(=(每组的组中值-平均数)^2×\)每组的概率之和;
中位数:设中位数为\(m\),则直线\(x=m\)能够把所有矩形的面积平分,即在直线\(x=m\)左边的矩形面积为\(0.5\).
巩固练习
1.(★) 为了了解某种进口茶叶的质量(单位:克),从中抽取若干包进行检查,获得样本的频率分布直方图如图所示.若已知样本中质量在\([155.5,160.5)\)内的茶叶有\(10\)包,则样本容量为( )

A.\(150\) \(\qquad \qquad \qquad \qquad\) B.\(100\) \(\qquad \qquad \qquad \qquad\) C.\(70\) \(\qquad \qquad \qquad \qquad\) D.\(50\)
2.(★★) 某市高三数学抽样考试中,对\(90\)分以上(含\(90\)分)的成绩进行统计,其频率分布图如图所示,若\(130~140\)分数段的人数为\(90\)人,则\(90~100\)分数段的人数为( )
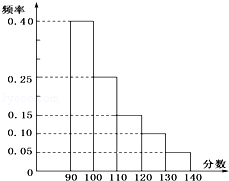
A.\(740\) \(\qquad \qquad \qquad \qquad\) B.\(180\) \(\qquad \qquad \qquad \qquad\) C.\(720\) \(\qquad \qquad \qquad \qquad\) D.\(540\)
3.(★★) 某市要对辖区内的中学教师的年龄进行调查,现从中随机抽出\(200\)名教师,已知抽到的教师年龄都在\([25,50)\)岁之间,根据调查结果得出教师的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市辖区内中学教师的年龄的中位数大约是( )

A.\(37.1\)岁 \(\qquad \qquad \qquad \qquad\) B.\(38.1\)岁 \(\qquad \qquad \qquad \qquad\) C.\(38.7\)岁 \(\qquad \qquad \qquad \qquad\) D.\(43.1\)岁
4.(★★) (多选) 为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:

则下列结论正确的是( )
A.估计该地农户家庭年收入不低于\(8.5\)万元的农户比例为\(30\%\)
B.估计该地农户家庭年收入的第三四分位数为\(9\)万元
C.估计该地农户家庭年收入的平均值不超过\(6.5\)万元
D.估计该地农户家庭年收入的中位数为\(8\)万元
5.(★★) (多选) 要坚持健康第一的教育理念,加强学校体育工作,推动青少年文化学习和体育锻炼协调发展.某学校对高一和高二年级每周在校体育锻炼时长进行了统计,得到数据(单位:小时)如表:
高一年级在校体育锻炼时长
关于高一和高二年级在校体育锻炼时长,下列说法正确的是( )

A.高一年级时长的众数比高二年级的大
B.高一年级时长的平均数比高二年级的小
C.高一年级时长的中位数比高二年级的大
D.高一年级时长的方差比高二年级的大

6.(★★) 为对考生的月考成绩进行分析,某地区随机抽查了\(10000\)名考生的成绩,根据所得数据画了如下的样本频率分布直方图.
(1)求成绩在\([600,650)\)的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析成绩与班级、学校等方面的关系,必须按成绩再从这\(10000\)人中用分层抽样方法抽出\(20\)人作进一步分析,则成绩在\([550,600)\)的这段应抽多少人?

7.(★★) 某学校\(1800\)名学生在一次百米测试中,成绩全部介于\(13\)秒与\(18\)秒之间,抽取其中\(50\)个样本,将测试结果按如下方式分成五组:第一组\([13,14]\),第二组\([14,15)\),第五组\([17,18]\),如图是按上述分组方法得到的频率分布直方图.
(1)若成绩小于\(15\)秒认为良好,求该样本在这次百米测试中成绩良好的人数;
(2)请估计学校\(1800\)名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数、中位数、平均数和方差.

参考答案
- 【答案】\(D\)
【解析】\(\because\)样本中质量在\([155.5,160.5)\)内的茶叶有\(10\)包,
由频率分布直方图得质量在\([155.5,160.5)\)内的频率为\(0.04×5=0.2\),
\(\therefore\)样本容量 \(n=\dfrac{10}{0.2}=50\).故选:\(D\). - 【答案】\(C\)
【解析】根据频率分布直方图得\(130~140\)分数段的人数为\(90\)人,对应的频率是\(0.05\),
\(\therefore\)样本容量是 \(\dfrac{90}{0.05}=1800\);\(\therefore 90~100\)分数段的人数\(1800×0.40=720\).
故选:\(C\). - 【答案】\(B\)
【解析】根据频率和等于\(1\)得年龄在\([30,35)\)岁之间的频率为
\(1-(0.01+0.08+0.05+0.02)×5=0.2\)
\(\because 0.01×5+0.2=0.25<0.5,0.25+0.08×5=0.65>0.5\),
\(\therefore\)令\(0.25+0.08×x=0.5\),解得\(x=3.125\);
\(\therefore\)该市辖区内中学教师的年龄的中位数大约\(35+3.125≈38.1\)岁.
故选:\(B\). - 【答案】\(AB\)
【解析】对于\(A\),该地农户家庭年收入不低于\(8.5\)万元的农户比例为\((0.1×2+0.04+0.02×3)×1=0.3=30\%\),故\(A\)正确;
对于\(B\),该地农户家庭年收入的第三四分位数为\(m\)万元,
则\(0.02+0.04+0.1+0.14+0.20×2+0.10×(m﹣8.5)=0.75\),
解得\(m=9.0\),故\(B\)正确;
对于\(C\),该地农户家庭所收入的平均值为:
\(3×0.02+4×0.04+5×0.10+6×0.14+7×0.2+8×0.2+9×0.1+10×0.1\)\(+11×0.04+12×0.02+13×0.02+14×0.02=7.68\),故\(C\)错误;
对于\(D\),设该地农户家庭年收入的中位数为\(x\)万元,
则\(0.02+0.04+0.10+0.14+0.2=0.5\),即\(x=7.5\),
则中位数为\(7.5\),故\(D\)错误.
故选:\(AB\). - 【答案】\(BD\)
【解析】对于高一年级,由表可进行下列计算:
时长众数为\(3.5\),时长平均数为\(2.5×0.25+3.5×0.3+4.5×0.2+5.5×0.25=3.95\),
时长中位数为 \(3+\dfrac{0.55-0.5}{0.3}=\dfrac{19}{6}\)
时长方差为 \((2.5-3.95)^2 \times 0.25+(3.5-3.95)^2 \times 0.30+(4.5-3.95)^2 \times 0.20\)\(+(5.5-3.95)^2 \times 0.25=1.2475\);
对于高二年级,由频率分布直方图可进行下列计算:
时长众数为\(4.5\),时长平均数为\(2.5×0.15+3.5×0.25+4.5×0.35+5.5×0.25=4.2\),
时长中位数为 \(4+\dfrac{0.75-0.5}{0.35}=\dfrac{33}{7}\),
时长方差为 \((2.5-4.2)^2 \times 0.15+(3.5-4.2)^2 \times 0.25+(4.5-4.2)^2 \times 0.35\)
\(+(5.5-4.2)^2 \times 0.25=0.5693\).
由上可知:\(3.5<4.5\),\(3.95<4.2\), \(\dfrac{19}{6}<\dfrac{33}{7}\),\(1.2475>0.5693\),
故选:\(BD\). - 【答案】(1)\(0.15\) (2) \(540\) (3) \(5\)
【解析】(1)根据频率分布直方图,得;
成绩在\([600,650)\)的频率为\(0.003×(650﹣600)=0.15\);.
(2)因为\(0.002×(450﹣400)=0.1\),\(0.004×(500﹣450)=0.2\),
\(0.005×(550﹣500)=0.25\),且\(0.1+0.2+0.25=0.55>0.5\),
所以,样本数据的中位数为 \(500+\dfrac{0.5-(0.1+0.2)}{0.005}=500+40=540\)(分);
(3)成绩在\([550,600)\)的频率为\(0.005×(600﹣550)=0.25\),
所以\(10000\)名考生中成绩在\([550,600)\)的人数为\(0.25×10000=2500\)(人),
再从\(10000\)人用分层抽样方法抽出\(20\)人,
则成绩在\([550,600)\)的这段应抽取 \(20 \times \dfrac{2500}{10000}=5\)人. - 【答案】(1) \(11\) (2) \(576\) (3) \(15.74\)
【解析】(1)样本在这次百米测试中成绩良好的人数是:
\(1×0.06×50+1×0.16×50=3+9=11\)(人);
(2)学校\(1800\)名学生中,成绩属于第四组的人数\(1×0.32×1800=576\)(人);
(3)由图可知众数落在第三组\([15,16)\),是 \(\dfrac{15+16}{2}=15.5\),
因为数据落在第一、二组的频率\(=1×0.06+1×0.16=0.22<0.5\)
数据落在第一、二、三组的频率\(=1×0.06+1×0.16+1×0.38=0.6>0.5\),
所以中位数一定落在第三组\([15,16)\)中,
假设中位数是\(x\),所以\(1×0.06+1×0.16+(x﹣15)×0.38=0.5\),
解得中位数 .


 浙公网安备 33010602011771号
浙公网安备 33010602011771号