8.2 一元线性回归模型及其应用
基础知识
一元线性回归模型
用\(x\)表示父亲身高，\(Y\)表示儿子身高，\(e\)表示随机误差，假定随机误差\(e\)的均值为\(0\)，方差为与父亲身高无关的定值\(\sigma ^2\)，则它们之间的关系可以表示为
我们称它为\(Y\)关于\(x\)的一元线性回归模型.
其中\(Y\)称为因变量或响应变量，\(x\)称为自变量或解释变量，\(a\)称为截距参数，\(b\)称为斜率参数.
线性回归方程
对于变量\(x\)和变量\(y\)，设经过随机抽样获得的成对样本数据为\((x_1 ，y_1 )\) ，\((x_2 ，y_2 )\)，… ，\((x_n ，y_n)\)，其中\(x_1\) ，\(x_2\)，… ，\(x_n\)和\(y_1\) ，\(y_2\) ，… ，\(y_n\)的均值分别为\(\bar{x}\)和\(\bar{y}\)，其中
我们将\(\hat{y}=\hat{b} x+\hat{a}\)称为\(Y\)关于\(x\)的经验回归方程，其图形称为经验回归直线，这种求经验回归方程的方法叫做最小二乘法.
注 线性回归直线经过定点\((\bar{x} ，\bar{y})\) .
残差分析
通过观测得到的数据称为观测值，通过经验回归方程得到的\(y\) ̂称为预测量，观测值减去预测值称为残差，残差是随机误差的估计结果，通过对残差的分析可以判断模型刻画数据的效果，以及判定原始数据是否存在可疑数据，这方面的工作称为残差分析.
通过观察残差图可以直观判断模型是否满足一元线性回归模型中对随机误差的假设，那残差应是均值为\(0\)，方差为\(\sigma ^2\)的随机变量的观测值.
比较模型的拟合效果
(i) 残差平方和
残差平方和\(Q=\sum_{i=1}^n\left(y_i-\hat{y}\right)^2\)越小，拟合效果越好.
(ii) 相关指数\(R^2\)
\(R^2\)越大，残差平方和\(\sum_{i=1}^n\left(y_i-\hat{y}\right)^2\)越小，模型拟合效果越好.
基本方法
【题型1】 一元线性回归模型
【典题1】 (多选) \(5G\)技术的运营不仅提高了网络传输速度，更拓宽了网络资源的服务范围．目前，我国加速了\(5G\)技术的融合与创新，前景美好！某手机商城统计了\(5\)个月的\(5G\)手机销量，如表所示:
| 月份 | 2020年6月 | 2020年7月 | 2020年8月 | 2020年9月 | 2020年10月 |
|---|---|---|---|---|---|
| 月份编号\(x\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
| 销量\(y/\)部 | \(52\) | \(95\) | \(a\) | \(185\) | \(227\) |
若\(y\)与\(x\)线性相关，由上表数据求得线性回归方程为\(\hat{y}=44x+10\)，则下列说法正确的是( )
A．\(5G\)手机的销量逐月增加，平均每个月增加约\(10\)台
B．\(a=151\)
C．\(y\)与\(x\)正相关
D．预计\(12\)月份该手机商城的\(5G\)手机销量约为\(318\)部
解析 线性回归方程为\(\hat{y}=44x+10\)，\(5G\)手机的销量逐月增加，平均每个月增加约\(44\)台，
所以\(A\)不正确；
根据表中数据，可得\(\bar{x}=\dfrac{1+2+3+4+5}{5}=3\)，\(\therefore \bar{y}=44×3+10=142\)．
于是，\(52+95+a+185+227=142\times 5=710\)，即\(a=151\)，故\(B\)正确；
由回归方程中\(x\)的系数大于\(0\)，可知\(y\)与\(x\)正相关，且相关系数\(r>0\)，故\(C\)正确；
\(12\)月份时，\(x=7\)，\(\hat{y}=44\times 7+5=318\)部，故\(D\)正确．
故选:\(BCD\)．
【典题2】 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量\(x\)(吨)与相应的生产能耗\(y\)(吨标准煤)的几组对照数据：
| \(x\) | \(3\) | \(4\) | \(5\) | \(6\) |
|---|---|---|---|---|
| \(y\) | \(2.5\) | \(3\) | \(4\) | \(4.5\) |
(1)请画出上表数据的散点图；
(2)请根据上表提供的数据，用最小二乘法求出\(y\)关于\(x\)的线性回归方程\(\hat{y}=\hat{b}x+\hat{a}\)；
(3)已知该厂技改前\(100\)吨甲产品的生产能耗为\(90\)吨标准煤．试根据(2)求出的线性回归方程，预测生产\(100\)吨甲产品的生产能耗比技改前降低了多少吨标准煤？
(参考数值：\(3\times 2.5+4\times 3+5\times 4+6\times 4.5=66.5\))
解析 (1)散点图，如图所示．
(2)由题意，得\(\sum_{i=1}^4 x_i y_i=3 \times 2.5+4 \times 3+5 \times 4+6 \times 4.5=66.5\)，
\(\bar{x}=\dfrac{3+4+5+6}{4}=4.5\)， \(\bar{y}=\dfrac{2.5+3+4+4.5}{4}=3.5\)，
\(\sum_{i=1}^4 x_i^2=3^2+4^2+5^2+6^2=86\)，
则 \(\hat{b}=\dfrac{66.5-4 \times 4.5 \times 3.5}{86-4 \times 4.5^2}=\dfrac{66.5-63}{86-81}=0.7\)，
\(\hat{a}=\bar{y}-\hat{b}=\bar{x}=3.5-0.7 \times 4.5=0.35\)，
故线性回归方程为\(y=0.7x+0.35\).
(3)根据线性回归方程的预测，现在生产\(100\)吨产品消耗的标准煤的数量为\(0.7\times 100+0.35=70.35\)，
故消耗能源减少了\(90-70.35=19.65\)(吨)．
【巩固练习】
1.已知\(x\)，\(y\)的取值如下表：
| \(x\) | \(0\) | \(1\) | \(3\) | \(4\) |
|---|---|---|---|---|
| \(y\) | \(2.2\) | \(4.3\) | \(4.8\) | \(6.7\) |
从散点图可以看出\(y\)与\(x\)线性相关，且回归方程为\(\hat{y}=0.95x+a\)，则\(a=\)( )
A．\(3.25\) \(\qquad \qquad \qquad \qquad\) B．\(2.6\) \(\qquad \qquad \qquad \qquad\) C．\(2.2\) \(\qquad \qquad \qquad \qquad\) D．\(0\)
2.为了解儿子身高与其父亲身高的关系，随机抽取\(5\)对父子的身高数据如下：
| 父亲身高\(x(cm)\) | \(174\) | \(176\) | \(176\) | \(176\) | \(178\) |
|---|---|---|---|---|---|
| 儿子身高\(y(cm)\) | \(175\) | \(175\) | \(176\) | \(177\) | \(177\) |
则\(y\)对\(x\)的线性回归方程为( )
A．\(y=x-1\) \(\qquad \qquad \qquad\) B．\(y=x+1\) \(\qquad \qquad \qquad\) C． \(y=\dfrac{1}{2} x+88\) \(\qquad \qquad \qquad\) D．\(y=176\)
3.某商店老板为了研究每天营业时间与营业额的关系，统计了\(4\)天的营业情况如表:
| 营业时间\(x\)(小时) | \(8\) | \(9\) | \(10\) | \(11\) |
|---|---|---|---|---|
| 营业额\(y\)(元) | \(720\) | \(800\) | \(882\) | \(966\) |
经统计得到营业额\(y\)(元)与当天营业时间\(x\)(小时)之间具有线性关系，其回归直线方程为\(\hat{y}=82x+\hat{a}\)，则当营业时间为\(14\)小时，营业额大约为( )
A．\(1205\)元 \(\qquad \qquad \qquad \qquad\) B．\(1207\)元 \(\qquad \qquad \qquad \qquad\) C．\(1209\)元 \(\qquad \qquad \qquad \qquad\) D．\(1211\)元
4.假设关于某设备的使用年限\(x\)和所支出的维修费用\(y\)(万元)有如下的统计资料：
| 使用年限\(x\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
|---|---|---|---|---|---|
| 维修费用\(y\) | \(2.2\) | \(3.8\) | \(5.5\) | \(6.5\) | \(7.0\) |
若由资料知\(y\)对\(x\)成线性相关关系．试求：
(1)线性回归方程\(\hat{y}=\hat{b}x+\hat{a}\)的回归系数\(\hat{b}与\hat{a}\)；
(2)估计使用年限为\(10\)年时，维修费用是多少？
5.某商场经营一批进价是\(30\)元/台的小商品，在市场试验中发现，此商品的销售单价\(x\)(\(x\)取整数)元与日销售量\(y\)台之间有如下关系：
| \(x\) | \(35\) | \(40\) | \(45\) | \(50\) |
|---|---|---|---|---|
| \(y\) | \(56\) | \(41\) | \(28\) | \(11\) |
(1)\(y\)与\(x\)是否具有线性相关关系？如果具有线性相关关系，求出回归直线方程．(方程的斜率精确到个位)
(2)设经营此商品的日销售利润为\(P\)元，根据(1)写出\(P\)关于\(x\)的函数关系式，并预测当销售单价\(x\)为多少元时，才能获得最大日销售利润．
参考答案
-
答案 \(B\)
解析 线性回归方程一定经过样本取值的平均数点\((\bar{x}，\bar{y})\)，
由取值表可计算\(\bar{x}=\dfrac{0+1+3+4}{4}=2\)， \(\bar{y}=\dfrac{2.2+4.3+4.8+6.7}{4}=\dfrac{9}{2}\)，
知回归方程为\(\hat{y}=0.95x+a\)，
又经过点\(\left(2， \dfrac{9}{2}\right)\)，代入得\(a=2.6\). -
答案 \(C\)
解析 法一：由线性回归直线方程过样本中心\((176，176)\)，排除\(A\)，\(B\)答案，
结合选项可得\(C\)为正确答案．
法二：将表中的五组数值分别代入选项验证，可知\(y=88+\dfrac{1}{2} x\)最适合． -
答案 \(D\)
解析 \(\bar{x}=\dfrac{1}{4}(8+9+10+11)=\dfrac{19}{2}\)， \(\bar{y}=\dfrac{1}{4}(720+800+882+966)=842\)，
则 \(\widehat{a}=842-82 \times \dfrac{19}{2}=63\)，
当\(x=14\)时，\(\hat{y}=82\times 14+63=1211\)．
故选:\(D\)． -
答案 (1) \(\hat{b}=1.23\)，\(\hat{a}=0.08\); (2) \(12.38\)
解析 列表：
| $i$ | $1$ | $2$ | $3$ | $4$ | $5$ |
| $x_i$ | $2$ | $3$ | $4$ | $5$ | $6$ |
| $y_i$ | $2.2$ | $3.8$ | $5.5$ | $6.5$ | $7.0$ |
| $x_i y_i$ | $4.4$ | $11.4$ | $22.0$ | $32.5$ | $42.0$ |
| $x_i^2$ | $4$ | $9$ | $16$ | $25$ | $36$ |
| $\bar{x}=4$，$\bar{y}=5$， $\sum_{i=1}^5 x_i^2=90$， $\sum_{i=1}^5 x_i y_i=112.3$ | |||||
于是有\(\hat{b}=\dfrac{112.3-5 \times 4 \times 5}{90-5 \times 4^2}=\dfrac{12.3}{10}=1.23\)，\(\hat{a}=\bar{y}-\hat{b}\bar{x}=5-1.23\times 4=0.08\).
(2)回归直线方程是\(\hat{y}=1.23x+0.08\)，
当\(x=10\)(年)时，\(y=1.23\times 10+0.08=12.38\)(万元)，
即估计使用\(10\)年时维修费用是\(12.38\)万元．
- 答案 (1)两个变量线性相关， \(y=-3x+161.5\); (2) \(12.38\)
解析 (1)散点图如图所示，从图中可以看出这些点大致分布在一条直线附近，因此两个变量线性相关．
设回归直线为\(\hat{y}=\hat{b}x+\hat{a}\)，由题知\(\bar{x}=42.5\)，\(\bar{y}=34\)，
则求得 \(\hat{b}=\dfrac{\sum_{i=1}^4\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^4\left(x_i-\bar{x}\right)^2}=\dfrac{-370}{125} \approx-3\)，
\(\hat{a}=\bar{y}-\hat{b}\bar{x}=34-(-3)\times 42.5=161.5\)．
\(\therefore y=-3x+161.5\)．
(2)依题意有
\(P=(-3x+161.5)(x-30)=-3x^2+251.5x-4845\)
\(=-3\left(x-\dfrac{251.5}{6}\right)^2+\dfrac{251.5^2}{12}-4845\)．
\(\therefore\)当 \(x=\dfrac{251.5}{6} \approx 42\)时，\(P\)有最大值，约为\(426\)．
即预测销售单价为\(42\)元时，能获得最大日销售利润．
【题型2】 拟合效果
【典题1】 对于一组具有线性相关关系的数据\((x_i，y_i)\)\((i=1，2，3，…，n)\)，根据最小二乘法求得回归直线方程为\(\hat{y}=\hat{b}x+\hat{a}\)，则以下说法正确的是( )
A．预报变量\(y\)的值由解释变量\(x\)唯一确定
B．在回归分析中，\(R^2=0.80\)的模型比\(R^2=0.98\)的模型拟合效果好
C．所有的样本点均落在回归直线\(\hat{y}=\hat{b}x+\hat{a}\)上
D．残差图中，残差点分布水平带状区域的宽度越窄，则回归方程的预报精确度越高
解析 选项\(A\)，预报变量由解释变量进行估计，即选项\(A\)错误；
选项\(B\)，相关系数\(R^2\)越大，说明拟合效果越好，即选项\(B\)错误；
选项\(C\)，可能所有的样本点都不在回归直线上，即选项\(C\)错误；
选项\(D\)，在残差图中，残差点分布水平带状区域的宽度越窄，则回归方程的预报精确度越高，即选项\(D\)正确．
故选:\(D\)．
【典题2】 在一段时间内，某种商品的价格\(x\)(元)和需求量\(y\)(件)之间的一组数据为：
| \(x\)(元) | \(14\) | \(16\) | \(18\) | \(20\) | \(22\) |
|---|---|---|---|---|---|
| \(y\)(件) | \(12\) | \(10\) | \(7\) | \(5\) | \(3\) |
且知\(x\)与\(y\)具有线性相关关系，求出\(y\)对\(x\)的回归直线方程，并说明拟合效果的好坏．
解析 \(\bar{x}=\dfrac{1}{5} \times(14+16+18+20+22)=18\)， \(\bar{y}=\dfrac{1}{5} \times(12+10+7+5+3)=7.4\)，
\(\sum_{i=1}^5 x_i^2=14^2+16^2+18^2+20^2+22^2=1660\)，
\(\sum_{i=1}^5 x_i y_i=14 \times 12+16 \times 10+18 \times 7+20 \times 5+22 \times 3=620\)，
\(\therefore \hat{b}=\dfrac{\sum_{i=1}^5 x_i y_i-5 \bar{x} \bar{y}}{\sum_{i=1}^5 x_i^2-5 \bar{x}^2}=\dfrac{620-5 \times 18 \times 7.4}{1660-5 \times 18^2}=\dfrac{-46}{40}=-1.15\)．
\(\therefore \hat{a}=7.4+1.15 \times 18=28.1\)，
\(\therefore\)回归直线方程为\(\hat{y}=-1.15x+28.1\)．
列出残差表为：
| $y_i-\widehat{y_i}$ | $0$ | $0.3$ | $-0.4$ | $-0.1$ | $0.2$ |
| $y_i-\bar{y}$ | $4.6$ | $2.6$ | $-0.4$ | $-2.4$ | $-4.4$ |
\(\therefore \sum_{i=1}^5\left(y_i-\widehat{y}_i\right)^2=0.3\)，\(\sum_{i=1}^5\left(y_i-\bar{y}\right)^2=53.2\)，
\(R^2=1-\dfrac{\sum_{i=1}^5\left(y_i-\hat{y}_i\right)^2}{\sum_{i=1}^5\left(y_i-\bar{y}\right)^2} \approx 0.994\)．
故\(R^2≈0.994\)说明拟合效果较好．
【典题3】 近年来，共享单车进驻城市，绿色出行引领时尚．某公司计划对未开通共享单车的\(A\)县城进行车辆投放，为了确定车辆投放量，对过去在其他县城的投放量情况以及年使用人次进行了统计，得到了投放量\(x\)(单位:千辆)与年使用人次\(y\)(单位:千次)的数据如表所示，根据数据绘制投放量\(x\)与年使用人次\(y\)的散点图如图所示．
| \(x\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) |
|---|---|---|---|---|---|---|---|
| \(y\) | \(6\) | \(11\) | \(21\) | \(34\) | \(66\) | \(101\) | \(691\) |
(1)观察散点图，可知两个变量不具有线性相关关系，拟用对数函数模型\(y=a+b\lg x\)或指数函数模型\(y=c\cdot d^x (c>0，d>0)\)对两个变量的关系进行拟合，请问哪个模型更适宜作为投放量\(x\)与年使用人次\(y\)的回归方程类型(给出判断即可，不必说明理由)，并求出\(y\)关于\(x\)的回归方程；
(2)已知每辆单车的购入成本为\(200\)元，年调度费以及维修等的使用成本为每人次\(0.2\)元，按用户每使用一次，收费\(1\)元计算，若投入\(8000\)辆单车，则几年后可实现盈利？
参考数据:
| \(\bar{y}\) | \(\bar{v}\) | \(\sum_{i=1}^7 x_i y_i\) | \(\sum_{i=1}^7 x_i v_i\) | \(10^{0.54}\) |
|---|---|---|---|---|
| \(62.14\) | \(1.54\) | \(2535\) | \(50.12\) | \(3.47\) |
其中\(v_i=\lg y_i\)， \(\bar{v}=\dfrac{1}{7} \sum_{i=1}^7 v_i\)．
参考公式:对于一组数据\((u_1，v_1)\)，\((u_2，v_2)\)，…，\((u_n，v_n)\)，其回归直线\(\hat{v}=\hat{a}+\hat{\beta} u\)的斜率和截距的最小二乘估计公式分别为 \(\hat{\beta}=\dfrac{\sum_{i=1}^n u_i v_i-n \overline{u v}}{\sum_{i=1}^n u_i^2-n \bar{u}^2}\)， \(\hat{a}=\bar{v}-\hat{\beta} \bar{u}\)．
解析 (1)由散点图判断，\(y=c\cdot d^x\)适宜作为投放量\(x\)与年使用人次\(y\)的回归方程类型．
由\(y=c\cdot d^x\)，两边同时取常用对数得\(\lg y=\lg (c⋅d^k )=\lg c+x\lg d\)．
设\(\lg y=v\)，则\(v=\lg c+x\lg d\)．
因为\(\bar{x}=4\)，\(\bar{v}=1.54\)， \(\sum_{i=1}^7 x_i^2=140\)， \(\sum_{i=1}^7 x_i v_i=50.12\)，
所以\(\lg d=\dfrac{\sum_{i=1}^7 x_i v_i-7 \overline{x v}}{\sum_{i=1}^7 x_i^2-7 \bar{x}^2}=\dfrac{50.12-7 \times 4 \times 1.54}{140-7 \times 4^2}=\dfrac{7}{28}=0.25\)．
把\((4，1.54)\)代入\(\bar{v}=\operatorname{lgc}+\bar{x} \lg d\)，得\(\lg c=0.54\)，
所以 \(\widehat{v}=0.54+0.25 x\)，所以\(\lg \hat{y}=0.54+0.25x\)，
则\(\hat{y}=10^{0.54+0.25 x}=3.47 \times 10^{0.25 x}\)，
故\(y\)关于\(x\)的回归方程为\(\hat{y}=3.47\times 10^{0.25x}\)．
(2)投入\(8\)千辆单车，则年使用人次为 \(3.47 \times 10^{0.25 \times 8}=347^{-}\)千人次，
每年的收益为\(347\times (1-0.2)=277.6\)(千元)，
总投资\(8000\times 200=1600000=1600\)千元，
假设需要\(n\)年开始盈利，则\(n\times 277.6>1600\)，即\(n>5.76\)，
故需要\(6\)年才能开始盈利．
【巩固练习】
1.在两个变量\(y\)与\(x\)的回归模型中，分别选择了\(4\)个不同的模型．通过计算得\(R^2\)的值如下，其中拟合效果最好的模型是( )
A．模型\(1\)的\(R^2\)为\(0.98\) \(\qquad \qquad \qquad\) B．模型\(2\)的\(R^2\)为\(0.80\) \(\qquad\)
C．模型\(3\)的\(R^2\)为\(0.50\) \(\qquad \qquad \qquad\) D．模型\(4\)的\(R^2\)为\(0.25\)
2.某种产品的广告支出费用\(x\)(单位:万元)与销售量\(y\)(单位:万件)之间的对应数据如表所示:
| 广告支出费用\(x\) | \(2.2\) | \(2.6\) | \(4.0\) | \(5.3\) | \(5.9\) |
|---|---|---|---|---|---|
| 销售量\(y\) | \(3.8\) | \(5.4\) | \(7.0\) | \(11.6\) | \(12.2\) |
根据表中的数据可得回归直线方程\(\hat{y}=2.2x-1.08\)，\(R^2≈0.96\)，以下说法正确的是( )
A．第三个样本点对应的残差\(\widehat{e_3}=-1\)，回归模型的拟合效果一般
B．第三个样本点对应的残差 \(\widehat{e_3}=1\)，回归模型的拟合效果较好
C．销售量\(y\)的多少有\(96\%\)是由广告支出费用引起的
D．销售量\(y\)的多少有\(4\%\)是由广告支出费用引起的
3.如图，已知\(5\)个数据\(A\)，B，\(C\)，\(D\)，\(E\)，去掉\(D(3，10)\)后，下列说法错误的是( )
A．样本相关系数\(r\)变大 \(\qquad \qquad \qquad \qquad\) B．残差平方和变大
C．\(R^2\)变大 \(\qquad \qquad \qquad \qquad\) D．解释变量\(x\)与响应变量\(y\)的相关程度变强
4.2020年春季，新冠肺炎疫情在全球范围内相继爆发，因为政治制度、文化背景等因素的不同，各个国家疫情防控的效果具有明显差异．如图是西方某国在\(60\)天内感染新冠肺炎的累计病例人数\(y\)(万人)与时间\(t\)(天)的散点图，则下列最适宜作为此模型的回归方程的类型是( )
A．\(y=a+bx\) \(\qquad \qquad\) B．\(y=a+b\sqrt{x}\) \(\qquad \qquad\) C．\(y=a+be^x\) \(\qquad \qquad\) D．\(y=a+b\ln x\)
5.（多选）已知由样本数据\((x_i，y_i)(i=1，2，3，…，8)\)组成的一个样本，得到回归直线方程为\(\hat{y}=2x-0.4\)且\(\bar{x}=2\)，去除两个歧义点\((-2，7)\)和\((2，-7)\)后，得到新的回归直线的斜率为\(3\)．则下列说法正确的是( )
A．相关变量\(x\)，\(y\)具有正相关关系
B．去除歧义点后的回归直线方程为\(\hat{y}=3x-3.2\)
C．去除歧义点后，随\(x\)值增加相关变量\(y\)值增加速度变小
D．去除歧义点后，样本\((4，8.9)\)的残差为\(0.1\)(附: \(\widehat{e_i}=y_i-\widehat{y_i}\))
6.（多选）2020年的“金九银十”变成“铜九铁十”，全国各地房价“跳水”严重，但某地二手房交易却“逆市”而行．下图是该地某小区2019年12月至2020年12月间，当月在售二手房均价(单位:万元/平方米)的散点图．(图中月份代码1～13分别对应2019年12月～2020年12月)
根据散点图选择\(y=a+b\sqrt{x}\)和\(y=c+d\ln x\)两个模型进行拟合，经过数据处理得到的两个回归方程分别为\(\hat{y}=0.9369+0.0285\sqrt{x}\)和\(\hat{y}=0.9554+0.0306\ln x\)，并得到以下一些统计量的值:
| $\hat{y}=0.9369+0.0285\sqrt{x}$ | $\hat{y}=0.9554+0.0306\ln x$ | |
| $R^2$ | $0.923$ | $0.973$ |
注:\(\bar{x}\)是样本数据中\(x\)的平均数，\(\bar{y}\)是样本数据中\(y\)的平均数，则下列说法正确的是( )
A．当月在售二手房均价\(y\)与月份代码\(x\)呈负相关关系
B．由\(\hat{y}=0.9369+0.0285\sqrt{x}\)预测2021年3月在售二手房均价约为\(1.0509\)万元/平方米
C．曲线\(\hat{y}=0.9369+0.0285\sqrt{x}\)与\(\hat{y}=0.9554+0.0306\ln x\)都经过点\((\bar{x}，\bar{y})\)
D．模型\(\hat{y}=0.9554+0.0306\ln x\)回归曲线的拟合效果比模型\(\hat{y}=0.9369+0.0285\sqrt{x}\)的好
7.若对于变量\(y\)与\(x\)的\(10\)组统计数据的回归模型中，\(R^2=0.95\)，又知残差平方和为\(120.53\)，那么 \(\sum_{i=1}^{10}\left(y_i-\bar{y}\right)^2\)的值为\(\underline{\quad \quad}\)．
8.下表为收集到的一组数据：
| \(x\) | \(21\) | \(23\) | \(25\) | \(27\) | \(29\) | \(32\) | \(35\) |
|---|---|---|---|---|---|---|---|
| \(y\) | \(7\) | \(11\) | \(21\) | \(24\) | \(66\) | \(115\) | \(325\) |
(1)作出\(x\)与\(y\)的散点图，并猜测\(x\)与\(y\)之间的关系；
(2)建立\(x\)与\(y\)的关系，预报回归模型并计算残差；
(3)利用所得模型，预报时\(y\)的值．
9.某地1～10岁男童年龄\(x_i\)(岁)与身高的中位数\(y_i (cm)\)\((i=1，2，…，10)\)如表:
| \(x\)(岁) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|
| \(y(cm)\) | \(76.5\) | \(88.5\) | \(96.8\) | \(104.1\) | \(111.3\) |
| \(x\)(岁) | \(6\) | \(7\) | \(8\) | \(9\) | \(10\) |
| \(y(cm)\) | \(117.7\) | \(124.0\) | \(130.0\) | \(135.4\) | \(140.2\) |
对上表的数据作初步处理，得到下面的散点图及一些统计量的值．
| $\bar{x}$ | $\bar{y}$ | $\sum_{i=1}^{10}\left(x_i-\bar{x}\right)^2$ | $\sum_{i=1}^{10}\left(y_i-\bar{y}\right)^2$ | $\sum_{i=1}^{10}\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)$ |
| $5.5$ | $112.45$ | $82.50$ | $3947.71$ | $566.85$ |
(1)求\(y\)关于\(x\)的线性回归方程(回归方程系数精确到\(0.01\))；
(2)某同学认为，\(y=px^2+qx+r\)更适宜作为\(y\)关于\(x\)的回归方程类型，他求得的回归方程是\(y=-0.30x^2+10.17x+68.07\)．经调查，该地\(11\)岁男童身高的中位数为\(145.3cm\)．与(1)中的线性回归方程比较，哪个回归方程的拟合效果更好？
附:回归方程\(\hat{y}=\hat{b}x+\hat{a}\)中的斜率和截距的最小二乘估计公式分别为: \(\widehat{b}=\dfrac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}\)，\(\hat{a}=\bar{y}-\hat{b}\bar{x}\)．
10.某公司为了确定下一年度投入某种产品的宣传费，需要了解年宣传费\(x\)(单位:万元)，对年销售量\(y\)(单位:\(t\))和年利润\(z\)(万元)的影响，为此，该公司对近\(7\)年宣传费\(x_i\)和年销售量\(y_i=(i=1，2，…，7)\)的数据进行了初步处理，得到了如图所示的散点图和表中的统计量的值．
| \(\bar{x}\) | \(\bar{y}\) | \(\bar{k}\) | \(\sum_{i=1}^7\left(x_i-\bar{x}\right)^2\) |
|---|---|---|---|
| \(17.40\) | \(82.30\) | \(3.6\) | \(140\) |
| \(\sum_{i=1}^7\left(k_i-\bar{k}\right)^2\) | \(\sum_{i=1}^7\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)\) | \(\sum_{i=1}^7\left(x_i-\bar{x}\right)\left(k_i-\bar{k}\right)\) | |
| \(9.7\) | \(2935.1\) | \(35.0\) |
其中\(k_i=\ln y_i\)，\(\bar{k}=\dfrac{1}{7} \sum_{i=1}^7 k_i\)．
(1)根据散点图判断，\(y=bx+a\)与\(y=c_1 e^{c_2 x}\)哪一个更适宜作为年销售量\(y\)关于年宣传费\(x\)的回归方程类型？(给出判断即可，不必说明理由)
(2)根据(1)的判断结果及表中数据，建立\(y\)关于\(x\)的回归方程；
(3)已知这种产品年利润\(z\)与\(x\)，\(y\)的关系为\(z=e^{-2.5} y-0.1 x+10\)，当年宣传费为\(28\)万元时，年销售量及年利润的预报值分别是多少？
附:①对于一组具有有线性相关关系的数据 \(\left(\mu_i， v_i\right)\)\((i=1，2，3，…，n)\)，其回归直线\(v=\beta u+\alpha\)的斜率和截距的最小二乘估计分别为\(\hat{\beta}=\dfrac{\sum_{i=1}^n\left(u_i-\bar{u}\right)\left(v_i-\bar{v}\right)}{\sum_{i=1}^n\left(u_i-\bar{u}\right)^2}\)， \(\hat{\alpha}=\bar{v}-\hat{\beta} \bar{u}\)．
②
| \(e^{-2.5}\) | \(e^{0.75}\) | \(e\) | \(e^3\) | \(e^7\) |
|---|---|---|---|---|
| \(0.08\) | \(2.11\) | \(2.72\) | \(20.09\) | \(1096.63\) |
参考答案
-
答案 \(A\)
解析 \(R^2\)越接近于\(1\)，则该模型的拟合效果就越好，精度越高，故选\(A\)． -
答案 \(C\)
解析 由题意得， \(\widehat{e_3}=7-(2.2 \times 4-1.08)=-0.72\)，
由于\(R^2≈0.96\)，\(\therefore\)该回归方程的拟合效果比较好，故\(A\)，\(B\)错误；
在线性回归模型中，\(R^2\)表示解释变量对于预报变量的贡献率，\(R^2≈0.96\)，
则销售量\(y\)的多少有\(96\%\)是由广告支出费用引起的，\(C\)正确，\(D\)错误．
故选:\(C\)． -
答案 \(B\)
解析 由散点图可知，去掉\(D\)后，\(x\)与\(y\)的相关性越强，且为正相关，
所以\(r\)变大，\(R^2\)变大，残差平方和变小．故选：\(B\)． -
答案 \(C\)
解析 函数图像随着自变量的变大，函数值增长速度越来越快，属于指数型函数的特征，
只有选项\(C\)为指数型函数．
故选:\(C\)． -
答案 \(ABD\)
解析 由\(\bar{x}=2\)，代入\(\hat{y}=2x-0.4\)，得\(\bar{y}=2\times 2-0.4=3.6\)，
\(\therefore\)去除两个歧义点\((-2，7)\)和\((2，-7)\)后，
得到新的 \(\bar{x}=\dfrac{2 \times 8}{6}=\dfrac{8}{3}\)， \(\bar{y}=\dfrac{3.6 \times 8}{6}=4.8\)，
又得到新的回归直线的斜率为\(3\)，
\(\therefore\)新的线性回归方程的\(\hat{a}=4.8-3 \times \dfrac{8}{3}=-3.2\)，
则去除两个歧义点后的线性回归方程为\(\hat{y}=3x-3.2\)，故\(B\)正确；
又由斜率\(3>0\)，相关变量\(x\)，\(y\)具有正相关关系，故\(A\)正确；
且去除歧义点后，随\(x\)值增加相关变量\(y\)值增加速度变大，故\(C\)错误；
当\(x=4\)时，\(\hat{y}=3\times 4-3.2=8.8\)，
则去除歧义点后，样本\((4，8.9)\)的残差为\(8.9-8.8=0.1\)，故\(D\)正确．
故选:\(ABD\)． -
答案 \(BD\)
解析 由散点图可知，\(y\)随\(x\)的增加而增加，故\(A\)错误；
2021年3月，此时\(x=16\)，代入\(\hat{y}=0.9369+0.0285\sqrt{x}\)，求得\(1.0509\)，故\(B\)正确；
曲线\(\hat{y}=0.9369+0.0285\sqrt{x}\)经过点 \((\sqrt{\bar{x}}， \bar{y})\)，
曲线\(\hat{y}=0.9554+0.0306\ln x\)经过点\((\ln \bar{x}，\bar{y})\)，故\(C\)错误；
因为\(0.973>0.923\)，
所以模型\(\hat{y}=0.9554+0.0306\ln x\)回归曲线的拟合效果比模型\(\hat{y}=0.9369+0.0285\sqrt{x}\)的好，故\(D\)正确．
故选:\(BD\)． -
答案 \(2410.6\)
解析 依题意有 \(0.95=1-\dfrac{120.53}{\sum_{i=1}^{10}\left(y_i-\bar{y}\right)^2}\)，所以 \(\sum_{i=1}^{10}\left(y_i-\bar{y}\right)^2=2410.6\)． -
答案 (1) 略；(2)\(\hat{y}=e^{0.272x-3.849}\)；(3) \(1 131\)
解析 (1)作出散点图如图，从散点图可以看出\(x\)与\(y\)不具有线性相关关系，根据已有知识可以发现样本点分布在某一条指数函数曲线 \(y=c_1 e^{c_2 x}\)的周围，其中\(C_1\)，\(C_2\)为待定的参数．
(2)对两边取对数把指数关系变为线性关系，令\(z=\ln y\)，则有变换后的样本点应分布在直线\(z=bx+a\)，\(a=\ln c_1\)，\(b=c_2\)的周围，这样就可以利用线性回归模型来建立\(y\)与\(x\)之间的非线性回归方程了，数据可以转化为：
| \(x\) | \(21\) | \(23\) | \(25\) | \(27\) | \(29\) | \(32\) | \(35\) |
|---|---|---|---|---|---|---|---|
| \(z\) | \(1.946\) | \(2.398\) | \(3.045\) | \(3.178\) | \(4.190\) | \(4.745\) | \(5.784\) |
求得回归直线方程为\(\hat{z}=0.272 x-3.849\)，
\(\therefore \hat{y}=e^{0.272 x-3.849}\) ．
残差
| \(y_i\) | \(7\) | \(11\) | \(21\) | \(24\) | \(66\) | \(115\) | \(325\) |
|---|---|---|---|---|---|---|---|
| \(\hat{y_i}\) | \(6.443\) | \(11.101\) | \(19.125\) | \(32.950\) | \(56.770\) | \(128.381\) | \(290.325\) |
| \(\hat{e}_i\) | \(0.557\) | \(-0.101\) | \(1.875\) | \(-8.950\) | \(9.23\) | \(-13.381\) | \(34.675\) |
(3)当\(x=40\)时， \(y==e^{0.272 x-3.849} \approx 1131\)．
-
答案 (1)\(y=6.87x+74.67\)；(2)\(y=-0.30x^2+10.17x+68.07\)模拟合效果更好
解析 (1)由题意，\(\bar{x}=5.5\)，\(\bar{y}=112.45\)， \(\widehat{b}=\dfrac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}=\dfrac{566.85}{82.50} \approx 6.87\)，
\(\hat{a}=\bar{y}-\hat{b}\bar{x}=112.45-6.87\times 5.5≈74.67\)；
\(\therefore y\)关于\(x\)的线性回归方程\(y=6.87x+74.67\)；
(2)某同学认为，\(y=px^2+qx+r\)更适宜作为\(y\)关于\(x\)的回归方程类型，他求得的回归方程是\(y=-0.30x^2+10.17x+68.07\)．
当\(x=11\)时，代入回归方程是\(y=-0.30x^2+10.17x+68.07\)．可得\(y=142.74\)；
当\(x=11\)时，代入回归方程是\(y=6.87x+74.67\)；可得\(y=150.24\)；
由\(11\)岁男童身高的中位数为\(145.3cm\)．
可得回归方程是\(y=6.87x+74.67\)计算的误差比较大．
故回归方程是\(y=-0.30x^2+10.17x+68.07\)模拟合效果更好． -
答案 (1) \(y=c_1 e^{c_2 x}\)；(2)\(y=e^{\frac{1}{4} x-\frac{3}{4}}\)；(3)年销售量及年利润的预报值分别是\(519.73t\)和\(48.78\)万元．
解析 (1)根据散点图判断，\(y=c_1 e^{c_2 x}\)适宜作为年销售量\(y\)关于年宣传费\(x\)的回归方程类型；
(2)由\(y=c_1 e^{c_2 x}\)，得\(\ln y=c_2 x+\ln c_1\)，
令\(\ln y=k\)， \(c_2=\beta\)， \(\ln c_1=\alpha\)，
由图表中的数据可知 \(\hat{\beta}=\dfrac{35}{140}=\dfrac{1}{4}\)， \(\hat{\alpha}=-\dfrac{3}{4}\)，
\(\therefore \hat{k}=\frac{1}{4} x-\frac{3}{4}\)，
\(\therefore y\)关于\(x\)的回归方程为\(y=e^{\dfrac{1}{4} x-\dfrac{3}{4}}\)，
(3)当\(x=28\)时，由回归方程得: \(\hat{y}=1096.63 \div 2.11 \approx 519.73\)，
\(\hat{Z}=0.08 \times 519.73-2.8+10=48.78\)，
即当年宣传费为\(28\)万元时，年销售量及年利润的预报值分别是\(519.73t\)和\(48.78\)万元．
分层练习
【A组---基础题】
1.设某大学的女生体重\(y\)(单位：\(kg\))与身高\(x\)(单位：)具有线性相关关系，根据一组样本数据\((i=1，2，…，n)\)，用最小二乘法建立的回归方程为\(\hat{y}=0.85x-85.71\)，则下列结论中不正确的是( )
A．\(y\)与\(x\)具有正的线性相关关系
B．回归直线过样本点的中心\((\bar{x}，\bar{y})\)
C．若该大学某女生身高增加\(1 cm\)，则其体重约增加\(0.85 kg\)
D．若该大学某女生身高为\(170 cm\)，则可断定其体重必为\(58.79 kg\)
2.某产品的广告费用\(x\)与销售额\(y\)的统计数据如下表：
| 广告费用\(x/\)万元 | \(4\) | \(2\) | \(3\) | \(5\) |
|---|---|---|---|---|
| 销售额\(y/\)万元 | \(49\) | \(26\) | \(39\) | \(54\) |
根据上表可得回归方程\(\hat{y}=\hat{b}x+\hat{a}\)中的\(\hat{b}\)为\(9.4\)，据此模型预报广告费用为\(6\)万元时销售额为( )
A．\(63.6\)万元 \(\qquad \qquad\) B．\(65.5\)万元 \(\qquad \qquad\) C．\(67.7\)万元 \(\qquad \qquad\) D．\(72.0\)万元
3.某服装品牌市场部门为了研究销售情况，统计了一段时间内该品牌不同服装的单价\(x\)(元)和销售额\(y\)(元)的数据，整理得到下面的散点图:
已知销售额\(y=\)单价\(x\times\)销量\(z\)，根据散点图，下面四个回归方程类型中最适宜作为服装销量\(z\)与单价\(x\)的回归方程类型的是( )
A．\(z=a+bx\) \(\qquad \qquad\) B． \(z=a+\dfrac{b}{x}\) \(\qquad \qquad\) C．\(z=a+bx^2\) \(\qquad \qquad\)D．\(z=a+be^x\)
4.某校课外学习小组为研究某作物种子的发芽率\(y\)和温度\(x\)(单位:\(°C\))的关系，由实验数据得到右面的散点图．由此散点图，最适宜作为发芽率\(y\)和温度\(x\)的回归方程类型的是( )
A．\(y=a+bx\)\(\qquad \qquad\) B．\(y=a+b\ln x\) \(\qquad \qquad\) C．\(y=a+be^x\) \(\qquad \qquad\) D．\(y=a+bx^2\)
5.（多选）下列说法正确的是( )
A．在做回归分析时，残差图中残差点分布的带状区域的宽度越窄表示回归效果越差
B．某地气象局预报:6月9日本地降水概率为\(90\%\)，结果这天没下雨，这表明天气预报并不科学
C．回归分析模型中，残差平方和越小，说明模型的拟合效果越好
D．在回归直线方程\(\hat{y}=0.1x+10\)中，当解释变量每增加\(1\)个单位时，预报变量多增加\(0.1\)个单位
6.某考察团对全国\(10\)个城市进行职工人均工资水平\(x\)(千元)与居民人均消费水平\(y\)(千元)统计调查，\(y\)与\(x\)具有相关关系，回归方程为\(\hat{y}=0.66x+1.562\).若某城市居民人均工资为\(9 000\)元，则其居民人均消费水平为\(\underline{\quad \quad}\) 千元．
7.已知样本点\((x_i，y_i)\)\((i=1，2，3，…，n)\)的回归直线方程为\(\hat{y}=2x+a\)，若样本点\((r，1)\)与\((1，s)\)的残差相同，则\(s\)与\(r\)的关系式为\(\underline{\quad \quad}\) .(附:对于样本点\((x_i，y_i)\)的残差\(\hat{e}_i=y_i-\widehat{y_i}\))
8.下列说法:①分类变量\(A\)与\(B\)的随机变量\(K^2\)越大，说明“\(A\)与\(B\)有关系”的可信度越大，②以模型\(y=c e^{k x}\)去拟合一组数据时，为了求出回归方程，设\(z=\ln y\)，将其变换后得到线性方程\(z=0.3x+4\)，则\(c\)，\(k\)的值分别是\(e^4\)和\(0.3\)，③在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高，④若变量\(x\)和\(y\)满足关系\(y=-0.1x+1\)，且变量\(y\)与\(z\)正相关，则\(x\)与\(z\)也正相关，正确的个数是\(\underline{\quad \quad}\) ．
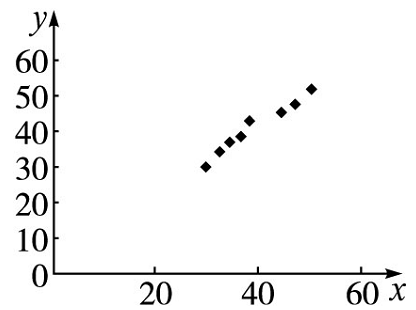
9.某运动员训练次数与运动成绩之间的数据关系如下：
| 次数\((x)\) | \(30\) | \(33\) | \(35\) | \(37\) | \(39\) | \(44\) | \(46\) | \(50\) |
|---|---|---|---|---|---|---|---|---|
| 成绩\((y)\) | \(30\) | \(34\) | \(37\) | \(39\) | \(42\) | \(46\) | \(48\) | \(51\) |
(1)作出散点图；
(2)求出线性回归方程；
(3)作出残差图，并说明模型的拟合效果；
(4)计算\(R^2\)，并说明其含义．
10.中国茶文化博大精深，茶水的口感与茶叶类型以及水温有关．经验表明，若某种绿茶用\(85^{\circ} \mathrm{C}\)的水泡制，等到茶水温度降至\(60^{\circ} \mathrm{C}\)时饮用，则口感最佳．某研究小组通过测量(室温恒为\(20^{\circ} \mathrm{C}\))，到下面的表格及散点图:
| 泡制时间\(x/min\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|---|---|
| 水温\(y/^{\circ} \mathrm{C}\) | \(85\) | \(79\) | \(74\) | \(71\) | \(65\) |
(1)小组成员根据散点图并考虑茶水温度降到室温(即\(20^{\circ} \mathrm{C}\))就不能再降的事实，决定选择函数模型\(y=kc^x+20(x≥0)\)来表示\(x\)和\(y\)的关系．
①令\(z=\ln (y-20)\)，求出\(z\)关于\(x\)的线性回归方程；
②利用①的结论，求出\(y=kc^x+20(x≥0)\)中的\(k\)与\(c\)的值．
(2)你认为该品种绿茶用\(85^{\circ} \mathrm{C}\)的水泡制多久后饮用，口感最佳？
参考数据:\(\ln 65≈4.2\)，\(\ln 59≈4.1\)，\(\ln 54≈4.0\)，\(\ln 51≈3.9\)，\(\ln 45≈3.8\)，\(\log _{0.9} 0.6 \approx 4.8\)， \(e^{-0.1} \approx 0.9\)， \(e^{4.2} \approx 66.7\)， \(\dfrac{400}{667} \approx 0.6\)．
参考公式:线性回归方程\(\hat{y}=\hat{b}x+\hat{a}\)中， \(\widehat{b}=\dfrac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}\)，\(\hat{a}=\bar{y}-\hat{b}\bar{x}\)．
参考答案
-
答案 \(D\)
解析 \(D\)选项中，若该大学某女生身高为\(170 cm\)，
则可断定其体重约为\(0.85\times 170-85.71=58.79(kg)\)．故\(D\)不正确． -
答案 \(B\)
解析 \(\because \hat{a}=\bar{y}-\hat{b} \bar{x}=\dfrac{49+26+39+54}{4}-9.4 \times \dfrac{4+2+3+5}{4}=9.1\)，
\(\therefore\)回归方程为\(\hat{y}=9.4x+9.1\)．
令\(x=6\)，得\(\hat{y}=9.4\times 6+9.1=65.5\)(万元)． -
答案 \(B\)
解析 由散点图知，销售额\(y\)与单价\(x\)呈线性关系，不妨设\(y=m+nx\)，
所以\(Z=\dfrac{y}{x}=\dfrac{m+n x}{x}=\dfrac{m}{x}+n\)，与选项\(B\)中的回归方程类型一致．
故选:\(B\)． -
答案 \(B\)
解析 由图知，散点图分布在一个对数函数的图象附近，因此最适合作为发芽率\(y\)和温度\(x\)的回归方程类型的是\(y=a+b\ln x\)．故选\(B\)． -
答案 \(CD\)
解析 对于\(A\)，可用残差图判断模型的拟合效果，残差点比较均匀地落在水平的带状区域中，说明这样的模型比较合适．带状区域的宽度越窄，说明模型的拟合精度越高．故\(A\)错误；
对于\(B\)，6月9日本地降水概率为\(90\%\)，只是表明下雨的可能性是\(90\%\)，有可能这天不下雨，不能说明天气预报并不科学，故\(B\)错误；
在回归分析模型中，残差平方和越小，说明模型的拟合效果越好，故\(C\)正确；
在回归直线方程\(\hat{y}=0.1x+10\)中，当解释变量\(x\)每增加\(1\)个单位时，预报变量\(y\)增加\(0.1\)个单位，故\(D\)正确．
故选:\(CD\)． -
答案 \(7.502\)
解析 当\(x=9\)千元时，\(y=0.66\times 9+1.562=7.502\). -
答案 \(s=3-2r\)
解析 \(\because\)回归直线方程为\(\hat{y}=2x+a\)，样本点\((r，1)\)与\((1，s)\)的残差相同，
\(\therefore 1-(2r+a)=s-(2+a)\)，即\(s=3-2r\)．
故答案为:\(s=3-2r\)． -
答案 \(3\)
解析 对于①，根据独立性原理知，分类变量\(A\)与\(B\)的随机变量\(K^2\)越大，说明“\(A\)与\(B\)有关系”的可信度越大，①正确；
对于②，根据回归模型和对数的运算性质知，以模型\(y=c e^{k x}\)去拟合一组数据时，为了求出回归方程，
设\(z=\ln y\)，将其变换后得到线性方程\(z=0.3x+4\)，则\(c\)，\(k\)的值分别是\(e^4\)和\(0.3\)，所以②正确；
对于③，利用残差分析模型拟合效果时，在残差图中，残差点分布的带状区域的宽度越狭窄，
其模型拟合的精度越高，所以③正确；
对于④，若变量\(x\)和\(y\)满足关系\(y=-0.1x+1\)，且变量\(y\)与\(z\)正相关，则\(x\)与\(z\)是负相关，所以④错误．
综上知，正确命题的序号是①②③，共\(3\)个．
故答案为:\(3\)． -
答案 (1)略 ；(2)\(\hat{y}=1.0415x-0.003875\) ；(3) 略；(4) \(R^2≈0.985 5\)，说明了该运动员的成绩的差异有\(98.55\%\)是由训练次数引起的．
解析 (1)作出该运动员训练次数\((x)\)与成绩\((y)\)之间的散点图，如图所示，由散点图可知，它们之间具有线性相关关系．
(2) \(\bar{x}=39.25\)，\(\bar{y}=40.875\)，\(\sum_{i=1}^8 x_i^2=12656\)，\(\sum_{i=1}^8 y_i^2=13731\)，\(\sum_{i=1}^8 x_i y_i=13180\)，
\(\therefore \hat{b}=\dfrac{\sum_{i=1}^8\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^8\left(x_i-\bar{x}\right)^2}=\dfrac{\sum_{i=1}^8 x_i y_i-8 \bar{x} \bar{y}}{\sum_{i=1}^8 x_i^2-8 \bar{x}^2} \approx 1.0415\)，
\(\hat{a}=\bar{y}-\hat{b}\bar{x}=-0.003875\)，
\(\therefore\)线性回归方程为\(\hat{y}=1.0415x-0.003875\)．
(3)作残差图如图所示，
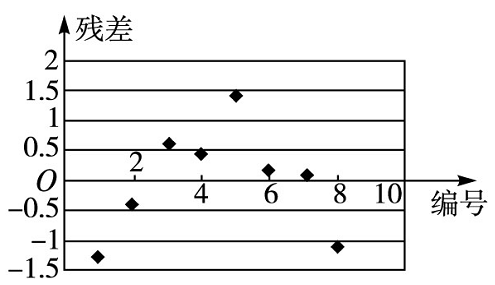
由图可知，残差点比较均匀地分布在水平带状区域中，说明选用的模型比较合适．
(4)计算得相关指数\(R^2≈0.985 5\)，说明了该运动员的成绩的差异有\(98.55\%\)是由训练次数引起的． -
答案 (1) ① \(\hat{z}=-0.1 x+4.2\) ② \(c=e^{-0.1} \approx 0.9\)， \(k=e^{4.2} \approx 66.7\)；(2) \(4.8\min\)
解析 (1)①由已知得出\(x\)与\(z\)的关系，如下表:
| 泡制时间\(x/min\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|---|---|
| \(z\) | \(4.2\) | \(4.1\) | \(4.0\) | \(3.9\) | \(3.8\) |
设线性回归方程\(\hat{z}=\hat{b} x+\hat{a}\)，
由题意，得\(\bar{x}=2\)，\(\bar{z}=4\)，
\(\therefore \sum_{i=1}^5\left(x_i-\bar{x}\right)\left(z_i-\bar{z}\right)=(-2) \times 0.2+(-1) \times 0.1+1 \times(-0.1)+2 \times(-0.2)=-1\)，
\(\sum_{i=1}^5\left(x_i-\bar{x}\right)^2=(-2)^2+(-1)^2+1^2+2^2=10\)，
则 \(\widehat{b}=\dfrac{\sum_{i=1}^5\left(x_i-\bar{x}\right)\left(z_i-\bar{z}\right)}{\sum_{i=1}^5\left(x_i-\bar{x}\right)^2}=\dfrac{-1}{10}=-0.1\)，
\(\hat{a}=\bar{z}-\hat{b} \bar{x}= 4+0.1 \times 2=4.2\)，
则\(z\)关于\(x\)的线性回归方程为\(\hat{z}=-0.1 x+4.2\)；
②由\(y=kc^x+20(x≥0)\)，得\(y-20=kc^x (x≥0)\)，
两边取对数得，\(\ln (y-20)=\ln k+x\ln c\)，
利用①的结论得:\(\ln c=-0.1\)，\(\ln k=4.2\)，
\(\therefore c=e^{-0.1} \approx 0.9\)， \(k=e^{4.2} \approx 66.7\)；
(2)由(1)得， \(y=66.7 \times 0.9^x+20(x \geq 0)\)，
令\(y=60\)，得 \(x \approx \log _{0.9} 0.6 \approx 4.8\)．
\(\therefore\)该品种绿茶用\(85^{\circ} \mathrm{C}\)的水泡制\(4.8\min\)后饮用，口感最佳．
【B组---提高题】
1.在彩色显影中，由经验知形成染料光学密度\(y\)与析出银的光学密度\(x\)由公式\(y=A e^{\frac{b}{x}}(b<0)\)表示，现测得试验数据如下：
| \(x_i\) | \(0.05\) | \(0.06\) | \(0.25\) | \(0.31\) | \(0.07\) | \(0.10\) |
|---|---|---|---|---|---|---|
| \(y_i\) | \(0.10\) | \(0.14\) | \(1.00\) | \(1.12\) | \(0.23\) | \(0.37\) |
| \(x_i\) | \(0.38\) | \(0.43\) | \(0.14\) | \(0.20\) | \(0.47\) | |
| \(y_i\) | \(1.19\) | \(1.25\) | \(0.59\) | \(0.79\) | \(1.29\) |
则\(y\)对\(x\)的回归方程是\(\underline{\quad \quad}\)．
2.近年来，随着我国汽车消费水平的提高，二手车流通行业得到迅猛发展．某汽车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计，得到频率分布直方图如图1．
(1)记“在2017年成交的二手车中随机选取一辆，该车的使用年限在\((8，16]\)”为事件\(A\)，试估计\(A\)的概率；
(2)根据该汽车交易市场的历史资料，得到散点图如图\(2\)，其中\(x\)(单位:年)表示二手车的使用时间，\(y\)(单位:万元)表示相应的二手车的平均交易价格．
由散点图看出，可采用\(y=e^{a+b x}\)作为二手车平均交易价格\(y\)关于其使用年限\(x\)的回归方程，相关数据如下表(表中\(Y_i=\ln y_i\)， \(\bar{Y}=\dfrac{1}{10} \sum_{i=1}^{10} Y_i\)):
| \(\bar{x}\) | \(\bar{y}\) | \(\bar{Y}\) | \(\sum_{i=1}^{10} x_i y_i\) | \(\sum_{i=1}^{10} x_i Y_i\) | \(\sum_{i=1}^{10} x_i^2\) |
|---|---|---|---|---|---|
| \(5.5\) | \(8.7\) | \(1.9\) | \(301.4\) | \(79.75\) | \(385\) |
①根据回归方程类型及表中数据，建立\(y\)关于\(x\)的回归方程；
②该汽车交易市场对使用\(8\)年以内(含\(8\)年)的二手车收取成交价格\(4\%\)的佣金，对使用时间\(8\)年以上(不含\(8\)年)的二手车收取成交价格\(10\%\)的佣金．在图\(1\)对使用时间的分组中，以各组的区间中点值代表该组的各个值．若以2017年的数据作为决策依据，计算该汽车交易市场对成交的每辆车收取的平均佣金．
附注:①对于一组数据\((u_1，v_1)\)，\((u_2，v_2)\)，…，\((u_n，v_n)\)，其回归直线 \(v=\alpha+\beta u\)的斜率和截距的最小二乘估计分别为\(\hat{\beta}=\dfrac{\sum_{i=1}^n u_i v_i-n \overline{u v}}{\sum_{i=1}^n u_i^2-n \bar{u}^2}\)， \(\hat{\alpha}=\bar{v}-\hat{\beta} \bar{u}\)；
②参考数据: \(e^{2.95} \approx 19.1\)， \(e^{1.75} \approx 5.75\)， \(e^{0.55} \approx 1.73\)， \(e^{-0.65} \approx 0.52\)， \(e^{-1.85} \approx 0.16\)．
参考答案
- 答案 \(\hat{y}=1.73 e^{-\frac{0.15}{x}}\)
解析 由题给的经验公式\(y=A e^{\frac{b}{x}}\)，两边取自然对数，便得\(\ln y=\ln A+\dfrac{b}{x}\)．与线性回归直线方程相对照，只要取\(u=\dfrac{1}{x}\)，\(v=\ln y\)，\(a=\ln A\)，就有\(v=a+bu\)，这是\(v\)对\(u\)的线性回归方程．对此我们已经掌握了一套相关性检验，求\(a\)与回归系数\(b\)的方法．题目所给数据经变量置换\(u=\dfrac{1}{x}\)，\(v=\ln y\)变成如下表所示的数据：
| \(u_i\) | \(20.000\) | \(16.667\) | \(4.000\) | \(3.226\) | \(14.286\) | \(10.000\) |
|---|---|---|---|---|---|---|
| \(v_i\) | \(-2.303\) | \(-1.966\) | \(0\) | \(0.113\) | \(-1.470\) | \(-0.994\) |
| \(u_i\) | \(2.632\) | \(2.326\) | \(7.143\) | \(5.000\) | \(2.128\) | |
| \(v_i\) | \(0.174\) | \(0.223\) | \(-0.528\) | \(-0.236\) | \(0.255\) |
\(|r|≈0.998>0.75\)，
故\(v\)与\(u\)之间具有很强的线性相关关系 ，求回归直线方程是有意义的．
由表中数据可得\(\hat{b} \approx-0.15\)， \(\hat{a} \approx 0.55\)，即\(\hat{v}=0.55-0.15 u\)．
把\(u\)与\(v\)换回原来的变量\(x\)与\(y\)，即\(u=\dfrac{1}{x}\)，\(v=\ln y\)，
故\(\ln \hat{y}=0.55-\dfrac{0.15}{x}\)，
即\(\hat{y}=e^{0.55-\frac{0.15}{x}}=e^{0.55} e^{-\frac{0.15}{x}} \approx 1.73 e^{-\frac{0.15}{x}}\)．
这就是\(y\)对\(x\)的回归曲线方程．
- 答案 (1)\(0.40\)；(2) ① \(\hat{y}=e^{3.55-0.3 x_0}\)②\(0.29\)万元
解析 (1)由频率分布直方图得，该汽车交易市场2017年成交的二手车使用时间
在\((8，12]\)的频率为\(0.07\times 4=0.28\)，在\((12，16]\)的频率为\(0.03\times 4=0.12\)，
所以\(P(A)=0.28+0.12=0.40\)；
(2)①由\(y=e^{a+b x}\)得\(\ln y=a+bx\)，即\(Y\)关于\(x\)的线性回归方程为\(\hat{Y}=a+bx\)；
因为 \(\hat{b}=\dfrac{\sum_{i=1}^{10} x_i Y_i-10 \bar{x} \cdot \bar{Y}}{\sum_{i=1}^{10} x_i^2-10 \bar{x}^2}=\dfrac{79.75-10 \times 5.5 \times 1.9}{385-10 \times 5.5^2}=-0.3\)，
\(\hat{a}=\bar{Y}-\hat{b} \cdot \bar{x}=1.9-(-0.3) \times 5.5=3.55\)，
所以\(Y\)关于\(x\)的线性回归方程为\(\hat{Y}=3.55-0.3x\)，
即\(y\)关于\(x\)的回归方程为 \(\hat{y}=e^{3.55-0.3 x}\)；
②根据①中的回归方程\(\hat{y}=e^{3.55-0.3 x}\)和图\(1\)，对成交的二手车可预测:
使用时间在\((0，4]\)的平均成交价格为 \(e^{3.55-0.3 \times 2}=e^{2.95} \approx 19.1\)，对应的频率为\(0.2\)；
使用时间在\((4，8]\)的平均成交价格为 \(e^{3.55-0.3 \times 6}=e^{1.75} \approx 5.75\)，对应的频率为\(0.36\)；
使用时间在\((8，12]\)的平均成交价格为 \(e^{3.55-0.3 \times 10}=e^{0.55} \approx 1.73\)，对应的频率为\(0.28\)；
使用时间在\((12，16]\)的平均成交价格为 \(e^{3.55-0.3 \times 14}=e^{-0.65} \approx 0.52\)，对应的频率为\(0.12\)；
使用时间在\((16，20]\)的平均成交价格为 \(e^{3.55-0.3 \times 18}=e^{-1.85} \approx 0.16\)，对应的频率为\(0.04\).
所以该汽车交易市场对于成交的每辆车可获得的平均佣金为
\((0.2\times 19.1+0.36\times 5.75)\times 4\%+(0.28\times 1.73+0.12\times 0.52+0.04\times 0.16)\times 10\%\)\(=0.29092≈0.29\)万元.
【C组---拓展题】
1.某同学使用某品牌暖水瓶，其内胆规格如图所示．若水瓶内胆壁厚不计，且内胆如图分为①②③④四个部分，它们分别为一个半球、一个大圆柱、一个圆台和一个小圆柱体若其中圆台部分的体积为\(52πcm^3\)，且水瓶灌满水后盖上瓶寒时水溢出 \(\dfrac{10 \pi}{3} \mathrm{~cm}^3\)．记盖上瓶塞后，水瓶的最大盛水量为\(V\)，
(1)求\(V\)；
(2)该同学发现:该品牌暖水瓶盛不同体积的热水时，保温效果不同．为了研究保温效果最好时暖水瓶的盛水体积，做以下实验:把盛有最大盛水量\(V\)的水的暖水瓶倒出不同体积的水，并记录水瓶内不同体积水在不同时刻的水温，发现水温\(y\)(单位:\(^{\circ} \mathrm{C}\))与时刻\(t\)满足线性回归方程\(y=ct+d\)，通过计算得到如表:
| 倒出体积\(xcm^3\) | \(0\) | \(30\) | \(60\) | \(90\) | \(120\) |
|---|---|---|---|---|---|
| 拟合结果 | \(y=c_1 t+d\) | \(y=c_2 t+d\) | \(y=c_3 t+d\) | \(y=c_4 t+d\) | \(y=c_5 t+d\) |
| 倒出体积\(xcm^3\) | \(150\) | \(180\) | \(210\) | … | \(450\) |
| 拟合结果 | \(y=c_6 t+d\) | \(y=c_7 t+d\) | \(y=c_8 t+d\) | … | \(y=c_{16}t+d\) |
注:表中倒出体积\(x\)(单位:\(cm^3\))是指从最大盛水量中倒出的那部分水的体积．其中:
| \(C_1\) | \(C_2\) | \(C_3\) | \(C_4\) | \(C_5\) | \(C_6\) | \(C_7\) |
|---|---|---|---|---|---|---|
| \(-1.4\) | \(-1.3\) | \(-1.2\) | \(-1\) | \(-1.1\) | \(-0.9\) | \(-0.8\) |
令\(w=|c|\)，\(|w_i=c_i |\)，\(x_i=30(i-1)\)，\(i=1\)，\(2\)，…，\(16\)．对于数据\((x_i，w_i)\)\((i=1，2，…，7)\)，可求得回归直线为\(L_1: w=\beta x+\alpha\)，对于数据\((x_i，w_i)\)\((i=8，9，…，16)\)，可求得回归直线为\(L_2:w=0.0009x+0.7\)．
(i)指出\(|c|\)的实际意义，并求出回归直线\(L_1\)的方程(参考数据:\(\dfrac{9}{2800} \approx 0.0032\)；)
(ⅱ)若\(L_1\)与\(L_2\)的交点横坐标即为最佳倒出体积，请问保温瓶约盛多少体积水时(盛水体积保留整数，且\(π\)取\(3.14\))保温效果最佳？
附:对于一组数据\((u_1，v_1)\)，\((u_2，v_2)\)，…，\((u_n，v_n)\)，其回归直线 \(v=\beta u+\alpha\)中的斜率和截距的最小二乘估计分别为 \(\beta=\dfrac{\sum_{i=1}^n\left(u_i-\bar{u}\right)\left(v_i-\bar{v}\right)}{\sum_{i=1}^n\left(u_i-\bar{u}\right)^2}\)， \(\hat{\alpha}=\bar{v}-\hat{\beta} \cdot \bar{u}\)．
参考答案
- 答案 (1) \(640πcm^3\) ；(2) (i) \(\omega=-0.0032 x+1.388\)，(ⅱ) \(1841.8cm^3\)
解析 (1)依题意得，半球的半径为\(r=5cm\)，
体积为 \(V_1=\dfrac{1}{2} \times \dfrac{4}{3} \times 125 \pi=\dfrac{250}{3} \pi \mathrm{cm}^3\)，
大圆柱体积 \(V_2=25 \pi \times 20=500 \pi \mathrm{cm}^3\)，
小圆柱体积 \(V_3=4 \pi \times 2=8 \pi \mathrm{cm}^3\)，
\(\therefore\)盖上瓶塞后，水瓶的最大盛水量为 \(\dfrac{250}{3} \pi+500 \pi+8 \pi+52 \pi-\dfrac{10}{3} \pi=640 \pi \mathrm{cm}^3\)．
(2)(i)\(|c|\)的实际意义为倒出\(xcm^3\)体积水时，暖水瓶内水的降温速率\(|c|\)越小，
降温速率越小，保温效果越好，\(|c|\)越大，降温速率越大，保温效果越差，
\(\because x_i=30(i-1)\)，\(i=1\)，\(2\)，…，\(7\)，对于回归直线\(L_1: w=\beta x+\alpha\)，
\(\because \bar{x}=\dfrac{x_1+x_2+\cdots+x_7}{7}=90\)， \(\bar{\omega}=\dfrac{\omega_1+\omega_2+\cdots+\omega_7}{7}=1.1\)，
\(\sum_{i=1}^7\left(x_i-\bar{x}\right)\left(\omega_i-\bar{\omega}\right)=-81\)， \(\sum_{i=1}^7\left(x_i-\bar{x}\right)=25200\)，
\(\therefore \hat{\beta}=\dfrac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(\omega_i-\bar{\omega}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}=-\dfrac{81}{25200} \approx-0.0032\)，
\(\hat{\alpha}=\bar{\omega}-\hat{\beta} \cdot \bar{x}=1.1+0.0032 \times 90=1.388\)．
\(\therefore\)回归直线\(L_1\)的方程为 \(\omega=-0.0032 x+1.388\)．
(ii)联立\(\left\{\begin{array}{l} \omega=-0.0032 x+1.388 \\ \omega=0.0009 x+0.7 \end{array}\right.\)，得\(x \approx 167.8\)，
\(\therefore\)保温瓶最佳倒出体积约为 \(167.8 \mathrm{~cm}^3\)．
保温瓶盛水体积约为 \(640 \pi-167.8 \approx 640 \times 3.14-167.8=1841.8 \mathrm{~cm}^3\)，
\(\therefore\)保温瓶盛水体积约为\(1841.8 \mathrm{~cm}^3\)时保温效果最佳．
