8.1 成对数据的统计相关性
基础知识
变量的相关关系
(1) 相关关系与确定关系
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
解释
① 体重与身高的关系,一般个子高的人体重较大,但又不是一定,体重还会受饮食习惯、体育锻炼等因素影响;体重与身高为相关关系;
② 相关关系是无法直接用函数描述变量之间的关系;
③ 正方形面积与边长,圆锥的体积与底圆半径等均为确定关系;体重与身高,子女的身高与父亲的身高,空气污染指数与汽车保有量等均为相关关系.
(2) 正相关与负相关
如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,称这两个变量正相关;从散点图来看,点从左下角往右上角走.
比如 脂肪含量与年龄、子女的身高与父亲的身高正相关.
如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现减少的趋势,称这两个变量负相关;从散点图来看,点从左上角往右下角走.
比如 吸烟与健康、饮酒与记忆力负相关.
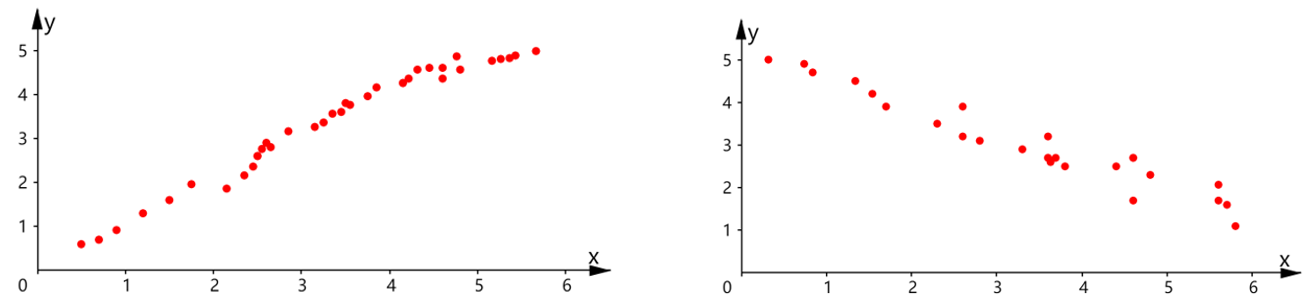
(3) 线性相关
一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关.
一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关(如下两图).
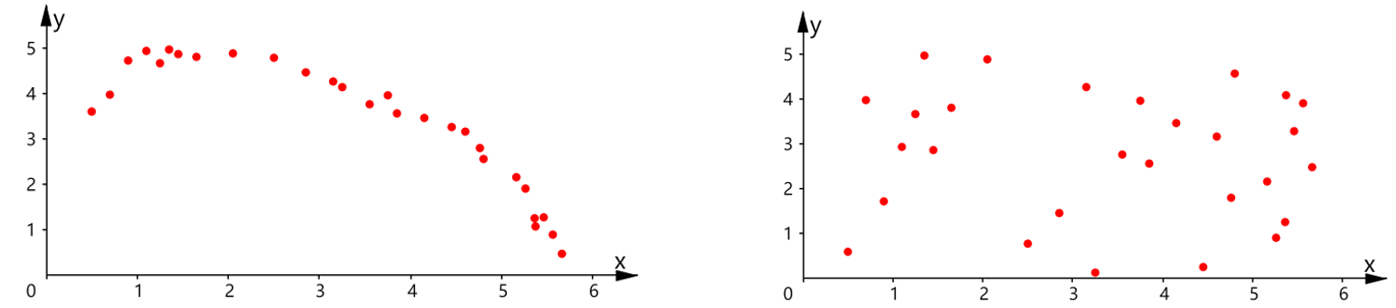
样本相关系数
对于变量\(x\)和变量\(y\),设经过随机抽样获得的成对样本数据为\((x_1 ,y_1 )\),\((x_2 ,y_2 )\) ,… ,\((x_n ,y_n)\),其中\(x_1\),\(x_2\),… ,\(x_n\)和\(y_1\),\(y_2\) ,… ,\(y_n\)的均值分别为\(\bar{x}\)和\(\bar{y}\),则
我们称\(r\)为变量\(x\)和变量\(y\)的样本相关系数.
解释
① 从散点图可知数据是正相关还是负相关,但无法对成对样本数据的相关程度;而样本相关系数可定量分析(注意理解教材中的推导分析过程及其分析思路);
② 当\(r>0\)时,称成对数据正相关;当\(r<0\)时,称成对数据负相关.
③ \(|r|\)越接近于\(1\),两个变量的线性相关性越强;
\(|r|\)接近于\(0\)时,两个变量之间几乎不存在线性相关关系.
(教材中利用\(n\)维向量数量积可知\(r\)的范围是\([-1,1]\))
④ 样本相关系数\(r\)也可以推导得到
\(r=\dfrac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \sqrt{\sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}=\dfrac{\sum_{i=1}^n x_i y_i-n \bar{x} \bar{y}}{\sqrt{\sum_{i=1}^n x_i^2-n \bar{x}^2} \sqrt{\sum_{i=1}^n y_i^2-n \bar{y}^2}}\)
基本方法
【题型1】 变量的相关关系
【典题1】 下列说法正确的是( )
A.圆的面积与半径之间的关系是相关关系
B.粮食产量与施肥量之间的关系是函数关系
C.一定范围内,学生的成绩与学习时间成正相关关系
D.人的体重与视力成负相关关系
解析 对于\(A\),圆的面积与半径之间的关系是确定的关系,是函数关系,所以\(A\)错误;
对于\(B\),粮食产量与施肥量之间的关系是不是函数关系,是相关关系,所以\(B\)错误;
对于\(C\),一定范围内,学生的成绩与学习时间是成正相关关系的,所以\(C\)正确;
对于\(D\),人的体重与视力是没有相关关系的,所以\(D\)错误.
故选:\(C\).
【典题2】 设对变量\(x\),\(y\)有如下观察的数据:
| \(x\) | \(151\) | \(152\) | \(153\) | \(154\) | \(156\) | \(157\) |
|---|---|---|---|---|---|---|
| \(y\) | \(40\) | \(41\) | \(41\) | \(41.5\) | \(42\) | \(42.5\) |
| \(x\) | \(158\) | \(159\) | \(160\) | \(162\) | \(163\) | \(164\) |
| \(y\) | \(43\) | \(44\) | \(45\) | \(45\) | \(46\) | \(45.5\) |
(1)画出散点图.
(2)判断变量\(x\),\(y\)是否具有相关关系?如果具有相关关系,那么是正相关还是负相关?
解析 (1)画出散点图.
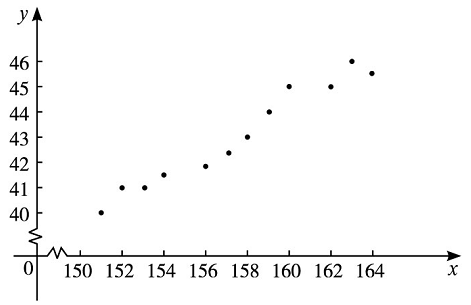
(2)具有相关关系.根据散点图,左下角到右上角的区域,变量\(x\)的值由小变大时,另一个变量\(y\)的值也由小变大,所以它们具有正相关关系.
【巩固练习】
1.下列两变量中有相关关系的是( )
A.正方体的体积与边长 \(\qquad \qquad \qquad \qquad\) B.匀速行驶车辆的行驶距离与时间
C.人的身高与视力 \(\qquad \qquad \qquad \qquad\) D.某人每日吸烟量与其身体健康情况
2.判断如图所示的图形中具有相关关系的是( )
A. \(\qquad\) B.
\(\qquad\) B. \(\qquad\) C.
\(\qquad\) C.  \(\qquad\)D.
\(\qquad\)D.
3.如下四个散点图中,正相关的是( )
A. \(\qquad \qquad\)B.
\(\qquad \qquad\)B.
C. \(\qquad \qquad\)D.
\(\qquad \qquad\)D.
4.对两个变量\(x\),\(y\)的几组观测数据统计如表,则这两个相关变量的关系是( )
| \(x\) | \(10\) | \(9\) | \(8\) | \(7\) | \(6\) | \(5\) |
|---|---|---|---|---|---|---|
| \(y\) | \(2\) | \(3\) | \(5.3\) | \(4\) | \(8.4\) | \(5\) |
A.负相关 \(\qquad \qquad \qquad\) B.正相关 \(\qquad \qquad \qquad\) C.先正后负相关 \(\qquad \qquad \qquad\) D.先负后正相关
5.已知\(10\)只狗的血细胞体积及红细胞数的测量值如下表:
| 血细胞体积\(x/mm^3\) | \(45\) | \(42\) | \(46\) | \(48\) | \(42\) |
|---|---|---|---|---|---|
| 红细胞数\(y/\)百万 | \(6.53\) | \(6.30\) | \(9.52\) | \(7.50\) | \(6.99\) |
| 血细胞体积\(x/mm^3\) | \(35\) | \(58\) | \(40\) | \(39\) | \(50\) |
| 红细胞数\(y/\)百万 | \(5.90\) | \(9.49\) | \(6.20\) | \(6.55\) | \(8.72\) |
(1)根据上表画出散点图;
(2)根据散点图,判断血细胞体积\(x\)与红细胞数\(y\)之间是否具有相关关系.
参考答案
- 答案 \(D\)
解析 对于\(A\),正方体的体积与边长是函数关系,不满足条件;
对于\(B\),匀速行驶车辆的行驶距离与时间是函数关系,不满足条件;
对于\(C\),人的身高与视力没有明显的关系,不满足条件;
对于\(D\),某人每日吸烟量与其身体健康情况是负相关关系,满足题意.
故选:\(D\). - 答案 \(C\)
解析 由题意,选项\(A\),\(B\)中的\(x\)与\(y\)的对应是确定的,
选项\(C\)、\(D\)是不确定的,
而在选项\(C\)、\(D\)中,\(C\)具有相关关系,
故选:\(C\). - 答案 \(A\)
解析 根据题意,依次分析选项:
对于\(A\),散点图中的点从左向右是上升的,且在一条直线附近,是正相关;
对于\(B\),散点图中的点从左向右是下降的,且在一条直线附近,是负相关.
对于\(C\),散点图中的点成片状分布,没有明显的相关性;
对于\(D\),散点图中的点也成片状分布,没有明显的相关性.
故选:\(A\). - 答案 \(A\)
解析 根据两个变量\(x\),\(y\)的几组观测数据统计表知,
\(y\)随\(x\)的增大而减小,所以这两个相关变量负相关.
故选:\(A\). - 答案 (1) 略;(2) 具有相关关系
解析 (1)散点图如图所示.

(2)从散点图可以看出,两个变量的对应点都集中在一条直线的附近,且\(y\)随\(x\)的增大而增大,因此血细胞体积\(x\)与红细胞数\(y\)之间具有相关关系.
【题型2】 样本相关系数
【典题1】 对某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )

A.\(r_4<r_2<0<r_1<r_3\) \(\qquad \qquad \qquad \qquad\) B.\(r_2<r_4<0<r_1<r_3\)
C.\(r_2<r_4<0<r_3<r_1\) \(\qquad \qquad \qquad \qquad\) D.\(r_4<r_2<0<r_3<r_1\)
解析 根据散点图的特征,数据大致呈增长趋势的是正相关,数据呈递减趋势的是负相关;数据越集中在一条线附近,说明相关性越强,
由题中数据可知:(1)(3)为正相关,(2)(4)为负相关;
故\(r_1>0\),\(r_3>0\);\(r_2<0\),\(r_4<0\);
又(1)与(2)中散点图更接近于一条直线,故\(r_1>r_3\),\(r_2<r_4\),
因此,\(r_2<r_4<0<r_3<r_1\).
故选:\(C\).
【典题2】 “十四五”规划纲要提出,全面推动长江经济带发展,协同推动生态环境保护和经济发展.长江水资源约占全国总量的\(36\%\),长江流域河湖、水库、湿地面积约占全国的\(20\%\),珍稀濒危植物约占全国的\(39.7\%\),淡水鱼类约占全国的\(33\%\).长江经济带在我国生态文明建设中占据重要位置.长江流域某地区经过治理,生态系统得到很大改善,水生动物数量有所增加.为调查该地区\(A\)种水生动物的数量,将其分成面积相近的\(100\)个小水域,从这些小水域中用简单随机抽样的方法抽取\(20\)个作为样本,调查得到样本数据\((x_i,y_i )\)\((i=1,2,⋯,20)\),其中\(x_i\) 和\(y_i\)分别表示第\(i\)个样本区域的水草覆盖面积(单位:公顷)和\(A\)种水生动物的数量,并计算得 \(\sum_{i=1}^{20} x_i=60\)_, _\(\sum_{i=1}^{20} y_i=1200\), \(\sum_{i=1}^{20}\left(x_i-\bar{x}\right)^2=120\),\(\sum_{i=1}^{20}\left(y_i-\bar{y}\right)^2=9000\), \(\sum_{i=1}^{20}\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)=1000\).
(1)求该地区\(A\)种水生动物数量的估计值(\(A\)种水生动物数量的估计值等于样本区域\(A\)种水生动物数量的平均数乘以小水域数);
(2)求样本\((x_i,y_i )\)\((i=1,2,⋯,20)\)的相关系数(精确到\(0.01\));
(3)根据现有统计资料,各地块间水草覆盖面积差异很大.为提高样本的代表性以获得该地区\(A\)种水生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数 \(r=\dfrac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2 \sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}\), \(\sqrt{3} \approx 1.732\).
解析 (1)样区水生动物平均数为\(\dfrac{1}{20} \sum_{i=1}^{20} y_i=\dfrac{1}{20} \times 1200=60\),地块数为\(100\),
该地区这种水生动物的估计值为\(100×60=6000\).
(2)样本\((x_i,y_i )(i=1,2,⋯,20)\)的相关系数为
\(r=\dfrac{\sum_{i=1}^{20}\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^{20}\left(x_i-x\right)^2 \sum_{i=1}^{20}\left(y_i-y\right)^2}}=\dfrac{1000}{\sqrt{120 \times 9000}}=\dfrac{5 \sqrt{3}}{9} \approx 0.96\),
(3)由(2)知各样区的这种水生动物的数量与水草覆盖面积有很强的正相关性,由于各地块间水草覆盖面积差异很大,从而各地块间这种野生动物的数量差异很大,所以采用分层抽样的方法较好地保持了样本结构与总体结构得以执行,提高了样本的代表性,从而可以获得该地区这种水生动物数量更准确的估计.
【巩固练习】
1.对相关系数\(r\),下列说法正确的是( )
A.\(r\)越大,线性相关程度越大
B.\(r\)越小,线性相关程度越大
C.\(|r|\)越大,线性相关程度越小,\(|r|\)越接近\(0\),线性相关程度越大
D.\(|r|≤1\)且\(|r|\)越接近\(1\),线性相关程度越大,\(|r|\)越接近\(0\),线性相关程度越小
2.在一组样本数据\((x_1 ,y_1 )\),\((x_2 ,y_2 )\) ,… ,\((x_n ,y_n)\),\((n⩾2\),\(x_1\),\(x_2\),⋯,\(x_n\)互不相等\()\)的散点图中,若所有样本点\((x_i,y_i )\)\((i=1,2,⋯,n)\)都在直线\(y=\dfrac{1}{3} x-5\)上,则这组样本数据的样本相关系数为( )
A. \(-\dfrac{1}{3}\) \(\qquad \qquad \qquad \qquad\) B. \(\dfrac{1}{3}\) \(\qquad \qquad \qquad \qquad\)C.\(-1\) \(\qquad \qquad \qquad \qquad\) D.\(1\)
3.已知甲、乙、丙、丁四组数据变量间对应的线性相关系数分别为\(0.46\),\(0.79\),\(-0.92\),\(0.85\),则( )
A.甲组数据变量间的线性相关程度最强 \(\qquad \qquad \qquad \qquad\) B.乙组数据变量间的线性相关程度最弱
C.丙组数据变量间的线性相关程度最强 \(\qquad \qquad \qquad \qquad\) D.丁组数据变量间的线性相关程度最强
4.对两个变量\(x\),\(y\)进行线性相关检验,得线性相关系数\(r_1=0.7859\),对两个变量\(u\),\(v\)进行线性相关检验,得线性相关系数\(r_2=-0.9568\),则下列判断正确的是( )
A.变量\(x\)与\(y\)正相关,变量\(u\)与\(v\)负相关,变量\(x\)与\(y\)的线性相关性较强
B.变量\(x\)与\(y\)负相关,变量\(u\)与\(v\)正相关,变量\(x\)与\(y\)的线性相关性较强
C.变量\(x\)与\(y\)正相关,变量\(u\)与\(v\)负相关,变量\(u\)与\(v\)的线性相关性较强
D.变量\(x\)与\(y\)负相关,变量\(u\)与\(v\)正相关,变量\(u\)与\(v\)的线性相关性较强
5.(多选)为了对变量\(x\)与\(y\)的线性相关性进行检验,由样本点\((x_1,y_1)\),\((x_2,y_2)\),…, \(\left(x_{10}, y_{10}\right)\)求得两个变量的样本相关系数为\(r\),那么下面说法中错误的有( )
A.若所有样本点都在直线\(y=-2x+1\)上,则\(r=1\)
B.若所有样本点都在直线\(y=-2x+1\)上,则\(r=-2\)
C.若\(|r|\)越大,则变量\(x\)与\(y\)的线性相关性越强
D.若\(|r|\)越小,则变量\(x\)与\(y\)的线性相关性越强
6.某消费品企业销售部对去年各销售地的居民年收入(即此地所有居民在一年内的收入的总和)及其产品销售额进行抽样分析,收集数据整理如表:
| 销售地 | \(A\) | \(B\) | \(C\) | \(D\) |
|---|---|---|---|---|
| 年收入\(x/\)亿元 | \(15\) | \(20\) | \(35\) | \(50\) |
| 销售额\(y/\)亿元 | \(16\) | \(20\) | \(40\) | \(48\) |
(1)在图中作出这些数据的散点图,并指出\(y\)与\(x\)成正相关还是负相关.
(2)求出样本相关系数\(r\),根据样本相关系数说明其相关程度和变化趋势的异同.
参考公式:样本相关系数 \(r=\dfrac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \sqrt{\sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}\)

参考答案
-
答案 \(D\)
解析 两个变量之间的相关系数,\(r\)的绝对值越接近于\(1\),
表面两个变量的线性相关性越强,
\(r\)的绝对值越接近于\(0\),表示两个变量之间几乎不存在线性相关,
故选:\(D\). -
答案 \(D\)
解析 根据回归直线方程\(y=\dfrac{1}{3} x-5\),可得这两个变量是正相关,
又因为所有样本点\((x_i,y_i )\)\((i=1,2,⋯,n)\)都在直线\(y=\dfrac{1}{3} x-5\)上,
所以\(r=1\),
故选:\(D\). -
答案 \(C\)
解析 因为线性相关系数的绝对值越大,线性相关性越强,
甲、乙、丙、丁四组数据的线性相关系数分别\(0.46\),\(0.79\),\(-0.92\),\(0.85\),
所以丙组数据的线性相关性最强.
故选:\(C\). -
答案 \(C\)
解析 由线性相关系数\(r_1=0.7859>0\)知\(x\)与\(y\)正相关,
由线性相关系数\(r_2=-0.9568<0\)知\(u\),\(v\)负相关,
又\(|r_1 |<|r_2 |\),
\(\therefore\)变量\(u\)与\(v\)的线性相关性比\(x\)与\(y\)的线性相关性强.
故选:\(C\). -
答案 \(ABD\)
解析 当所有样本点都在直线\(y=-2x+1\)上时,样本点数据完全负相关,其相关系数\(r=-1\),
所以\(A\)、\(B\)都错误;
相关系数\(|r|\)值越大,则变量\(x\)与\(y\)的线性相关性越强,\(C\)正确;
相关系数\(|r|\)值越小,则变量\(x\)与\(y\)的线性相关性越弱,\(D\)错误.
综上知,以上错误的说法是\(ABD\).
故选:\(ABD\). -
答案 (1) \(y\)与\(x\)正相关 ;(2)\(r≈0.98\),由此可推断年收入\(x\)与销售额\(y\)是正的线性相关,
即该产品的销售额与该地的居民年收入具有相同的变化趋势,且相关程度很强.
解析 (1)散点图如图所示:

由散点图可知,\(y\)与\(x\)正相关.
(2)由表中数据可得,
\(\bar{x}=\dfrac{1}{4} \times(15+20+35+50)=30\), \(\bar{y}=\dfrac{1}{4} \times(16+20+40+48)=31\),
\(\sqrt{\sum_{i=1}^4\left(x_i-\bar{x}\right)^2}=\sqrt{(-15)^2+(-10)^2+5^2+20^2}=\sqrt{750} \approx 27.39\),
\(\sqrt{\sum_{i=1}^4\left(y_i-\bar{y}\right)^2}=\sqrt{(-15)^2+(-11)^2+9^2+17^2}=\sqrt{716} \approx 26.76\),
\(\sum_{i=1}^4\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)=(-15) \times(-15)+(-10) \times(-11)+5 \times 9+20 \times 17=720\),
则 \(r \approx \dfrac{720}{27.39 \times 26.76} \approx 0.98\),
由此可推断年收入\(x\)与销售额\(y\)是正的线性相关,即该产品的销售额与该地的居民年收入具有相同的变化趋势,且相关程度很强.
分层练习
【A组---基础题】
1.关于相关关系,下列说法不正确的是( )
A.相关关系是一种非确定关系
B.相关关系\(r\)越大,两个变量的相关性越强
C.当两个变量相关且相关系数\(r>0\)时,表明两个变量正相关
D.相关系数\(r\)的绝对值越接近\(1\),表明两个变量的相关性越强
2.下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是( )

A.①③ \(\qquad \qquad \qquad \qquad\) B.①④ \(\qquad \qquad \qquad \qquad\) C.②③ \(\qquad \qquad \qquad \qquad\)D.①②
3.如图是近十年来全国城镇人口、乡村人口的折线图(数据来自国家统计局).

根据该折线图,下列说法错误的是( )
A.城镇人口与年份呈现正相关 \(\qquad \qquad \qquad \qquad\) B.乡村人口与年份的相关系数\(r\)接近\(1\)
C.城镇人口逐年增长率大致相同 \(\qquad \qquad \qquad \qquad\) D.可预测乡村人口仍呈现下降趋势
4.已知四组不同数据的两变量的线性相关系数\(r\)如下:数据组①的相关系数\(r_1=0\);数据组②的相关系数\(r_2=-0.95\);数据组③的相关系数\(|r_3 |=0.89\);数据组④的相关系数\(r_4=0.75\).则下列说法正确的是( )
A.数据组①对应的数据点都在同一直线上
B.数据组②中的两变量线性相关性最强
C.数据组③中的两变量线性相关性最强
D.数据组④中的两变量线性相关性最弱
5.在下列\(4\)组样本数据的散点图中,样本相关系数最小的是( )

A.\(r_1\) \(\qquad \qquad \qquad \qquad\) B.\(r_2\) \(\qquad \qquad \qquad \qquad\) C.\(r_3\) \(\qquad \qquad \qquad \qquad\) D.\(r_4\)
6.给出成对\(x\),\(y\)值的数据如下:
| \(x\) | \(1\) | \(2\) | \(4\) | \(8\) |
|---|---|---|---|---|
| \(y\) | \(3\) | \(5\) | \(9\) | \(71\) |
则根据数据可以判断\(x\)和\(y\)的关系是\(\underline{\quad \quad}\). (填“确定关系”“相关关系”或“没有关系”)
7.为了比较甲、乙、丙、丁四组数据的线性相关性的强弱,某人分别计算了甲、乙、丙、丁四组数据的线性相关系数,其数值分别为\(-0.95\),\(0.87\),\(0.58\),\(0.92\),则这四组数据中线性相关性最强的是\(\underline{\quad \quad}\)组数据.
8.已知变量\(X\)与\(Y\)相对应的一组数据为\((10,1)\),\((11.3,2)\),\((11.8,3)\),\((12.5,4)\),\((13,5)\),变量\(U\)与\(V\)相对应的一组数据为\((10,5)\),\((11.3,4)\),\((11.8,3)\),\((12.5,2)\),\((13,1)\).\(r_1\)表示变量\(X\)与\(Y\)之间的线性相关系数,\(r_2\)表示变量\(U\)与\(V\)之间的线性相关系数,则\(r_1\)、\(r_2\) 和\(0\)三者之间的大小关系是\(\underline{\quad \quad}\).(用符号“\(<\)”连接)
9.新冠病毒传播以来,在世界各地造成极大影响.“动态清零”政策是我国根据疫情防控经验的总结和提炼,是现阶段我们疫情防控的一个最佳选择和总方针.为落实动态清零政策下的常态化防疫,要求学校作为重点人群,每天要进行核酸检测.某高中学校核酸抽检工作:每天下午\(2:30\)开始,当天安排\(1150\)位师生核酸检测,教职员工每天都要检测,学生五天时间全员覆盖.
(1)该校教职员工有\(440\)人,高二学生有\(1200\)人,高三学生有\(1100\)人,
①用分层抽样的方法,求高一学生每天抽检人数;
②高一年级共\(20\)个班,该年级每天抽检的学生有两种安排方案,方案一:集中来自部分班级;方案二:分散来自所有班级,每班随机抽取\(20\%\).你认为哪种方案更合理,并给出理由.
(2)学校开展核酸抽检的某轮核酸抽检用时记录如下:
| 第\(x\)天 | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
|---|---|---|---|---|---|
| 用时\(y\)(小时) | \(2.5\) | \(2.3\) | \(2.1\) | \(2.1\) | \(2.0\) |
计算变量\(x\)和\(y\)的相关系数\(r\)(精确到\(0.01\)),说明两变量线性相关的强弱;并根据\(r\)的计算结果,判定变量\(x\)和\(y\)是正相关,还是负相关,给出可能的原因.
参考数据和公式: \(\sqrt{10} \approx 3.16\),相关系数 \(r=\dfrac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \sqrt{\sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}\).
参考答案
- 答案 \(B\)
解析 对于\(A\),相关关系不同于函数关系,它是一种非确定的关系,\(A\)正确;
对于\(B\),相关关系\(|r|\)越大,两个变量的相关性越强,\(\therefore B\)错误;
对于\(C\),当两个变量相关且相关系数\(r>0\)时,说明两个变量正相关,\(\therefore C\)正确;
对于\(D\),相关系数\(r\)的绝对值越接近\(1\),表明两个变量的相关性越强,\(D\)正确.
故选:\(B\). - 答案 \(B\)
解析 \(\because\)两个变量的散点图,
若样本点成带状分布,则两个变量具有线性相关关系,
\(\therefore\)两个变量具有线性相关关系的图是①和④.
故选:\(B\). - 答案 \(B\)
解析 对于\(A\)选项,由折线图可知,城镇人口与年份呈现正相关,故\(A\)正确;
对于\(B\)选项,因为乡村人口与年份呈负线性相关关系,且线性相关性很强,所以\(r\)接近\(-1\),故\(B\)错误;
对于\(C\)选项,城镇人口与年份呈现正相关,且线性相关性很强,相关系数\(r\)接近1,
故城镇人口逐年增长率大致相同,故\(C\)正确;
对于\(D\)选项,由折线图可知,乡村人口与年份呈负线性相关关系,可预测乡村人口仍呈现下降趋势,故\(D\)正确.
故选:\(B\). - 答案 \(B\)
解析 根据题意,依次分析选项:
对于\(A\),数据组①的相关系数\(r_1=0\),相关性最弱,\(A\)错误;
对于\(B\),4个数据组中,数据组②的相关系数\(r_2=-0.95\),绝对值最大,其两变量线性相关性最强,\(B\)正确;
对于\(C\),数据组①的相关系数\(r_1=0\),相关性最弱,\(C\)错误;
对于\(D\),数据组①的相关系数\(r_1=0\),相关性最弱,\(D\)错误;
故选:\(B\). - 答案 \(B\)
解析 由散点图变化趋势可知,\(r_1>0\),\(r_3>0\),\(r_2<0\),\(r_4<0\),
又图\(2\)中的散点更为集中,更接近于一条直线,
\(\therefore |r_2 |>|r_4 |\),,即\(r_2<r_4\),
故样本相关系数最小的是\(r_2\).
故选:\(B\). - 答案 确定关系
解析 由题中数据可得到每一个\(x\)都有唯一确定的\(y\)与之相对应,
故\(y\)是\(x\)的函数关系,函数解析式为\(y=2x+1\),
所以\(x\),\(y\)之间是一种确定关系,
故答案为:确定关系. - 答案 甲
解析 根据题意,因为线性相关系数的绝对值越大,线性相关性越强,
甲、乙、丙、丁四组数据的线性相关系数分别为\(-0.95\),\(0.87\),\(0.58\),\(0.92\),
所以甲组数据的线性相关性最强.
故答案为:甲. - 答案 \(r_2<0<r_1\)
解析 根据题意,由已知中的数据可知:
第一组数据中变量\(Y\)、\(X\)之间成正相关,相关系数\(r_1>0\),
第二组数据中变量\(V\)与\(U\)之间成负相关,相关系数\(r_2<0\),
即\(r_2<0<r_1\). - 答案 (1) ①\(250\)②方案二更合理;(2) \(r≈-0.95\),线性相关很强,是负相关,原因略.
解析 (1)①用分层抽样法,计算高一学生每天抽检人数为 \(1150-440-\dfrac{1200+1100}{5}=250\);
②方案二更合理,因为新冠病毒奥密克戎毒株传染性更强、潜伏期更短,
分散抽检可以全面检测年级中每个班级学生的状况,更有利于防控筛查工作;
(2)由表中数据,计算 \(\bar{x}=\dfrac{1}{5} \times(1+2+3+4+5)=3\),
\(\bar{y}=\dfrac{1}{5} \times(2.5+2.3+2.1+2.1+2.0)=2.2\),
\(\sum_{i=1}^5\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)=(-2) \times 0.3+(-1) \times 0.1+0 \times(-0.1)\) \(+1 \times(-0.1)+2 \times(-0.2)=-1.2\),
\(\sum_{i=1}^5\left(x_i-\bar{x}\right)^2=(-2)^2+(-1)^2+0^2+1^2+2^2=10\),
\(\sum_{i=1}^5\left(y_i-\bar{y}\right)^2=0.3^2+0.1^2+(-0.1)^2+(-0.1)^2+(-0.2)^2=0.16\),
所以变量\(x\)和\(y\)的相关系数 \(r=\dfrac{-1.2}{\sqrt{10} \times \sqrt{0.16}}=-\dfrac{3}{\sqrt{10}}=-\dfrac{3}{3.16} \approx-0.95\),
因为\(|r|=0.95\),说明两变量线性相关很强,根据\(r<0\)知,变量\(x\)和\(y\)是负相关,
可能的原因是,随着抽检工作的开展,学校相关管理协调工作效率提高,因此用时较短.
【B组---提高题】
1.如图所示,\(5\)组数据\((x,y)\)中去掉\(D(3,10)\)后,下列说法正确的是( )

A.偏差平方和变大 \(\qquad \qquad \qquad \qquad\) B.相关系数\(r\)变小
C.负相关变为正相关 \(\qquad \qquad \qquad \qquad\) D.解释变量\(x\)与预报变量\(y\)的相关性变强
参考答案
- 答案 \(D\)
解析 由散点图知,去掉离群点\(D(3,10)\)后,
\(y\)与\(x\)的线性相关性加强,相关系数\(r\)变大,选项\(B\)错误;
偏差平方和变小,选项\(A\)错误;
仍然是正相关,选项\(C\)错误;
解释变量\(x\)与预报变量\(y\)的相关性变强,所以选项\(D\)正确.
故选:\(D\).


