9.2.1 总体取值规律的估计
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019)]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第二册同步巩固,难度2颗星!
基础知识
画频率直方图的步骤
(1) 求极差(数据中最大值与最小值的差)
(2) 决定组距与组数(组数不要太多或太少,一般取等长组距,组距为整数)
(3) 将数据分组
(4) 列频率分布表
(5) 画频率分布直方图(纵轴表示\(\dfrac{频率}{组距}\))
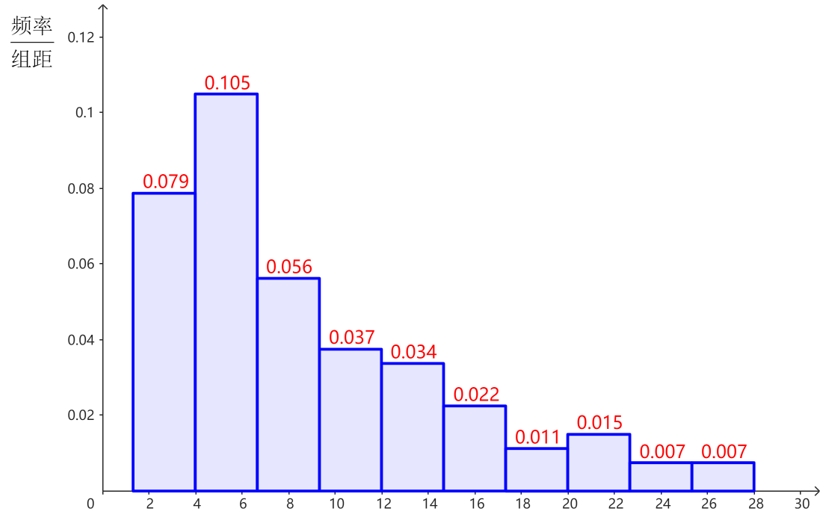
解释
当频率分布直方图的组数少、组距大时,容易从中看到数据的整体的分布特点,但由于无法看出每组内的数据分布情况,损失了较多的原始数据信息;当频率分布直方图的组数多、组距小时,保留了较多的原始数据信息,但由于小长方形较多,有时图形会变得不规则,不容易看出总体数据的分布特点.

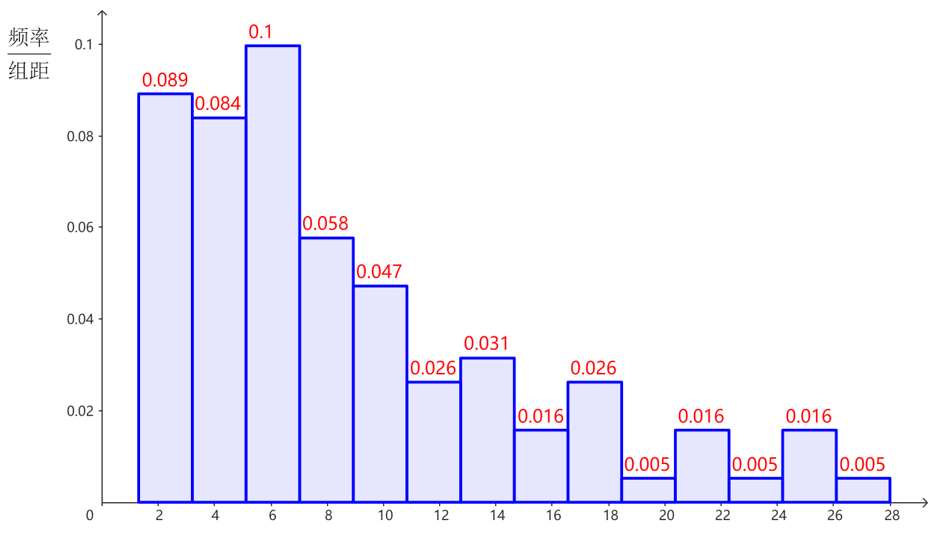
频率直方图的特点
(1) 小长方形的面积=频率
(2) 在直方图中,各小长方形的面积之和等于\(1\).
解释
(1) 频率直方图中纵轴表示\(\dfrac{频率}{组距}\),实际上是各小长方形的高,故小长方形的面积\(=组距×\dfrac{频率}{组距}=频率\);又由于频率之和为\(1\),则各小长方形的面积之和等于\(1\).
(2) 频率直方图的纵轴是\(\dfrac{频率}{组距}\),为什么不用频率呢?
① 若小长方形的高是频率,那么组距越大,小长方形越高,而两个长度不同的组距的频率比较就没意义;
② 全部小长方形面积之和为\(1\),与总体中落在全部取值范围的频率为\(1\)是一致的.
基本方法
【题型1】 画频率直方图
【典题1】 为了了解中年知识分子在知识分子中的比例,对某科研单位全体知识分子的年龄进行了登记,结果如下(单位:岁):
42,38,29,36,41,43,54,43,34,44,40,59,39,42,44,50,37,44,45,
29,48,45,53,48,37,28,46,50,37,44,42,39,51,52,62,47,59,46,
45,67,53,49,65,47,54,63,57,43,46,58.
列出样本的频率分布表,并绘制频率分布直方图.
解析 ①该单位全体知识分子的年龄中,最大值为\(67\),最小值为\(28\),
故该组数据的极差为\(67-28=39\),
②取组距为\(5\),
\(\because \dfrac{39}{5}=7.8 \approx 8\),
\(\therefore\)应将数据分为\(8\)组,分别为:\([28,33)\),\([33,38)\),\([38,43)\),\([43,48)\),\([48,53)\),\([53,58)\),\([58,63)\),\([63,68)\),
③频率分布表如下表所示:
| 分组 | 频数 | 频率 |
|---|---|---|
| \([28,33)\) | \(3\) | \(0.06\) |
| \([33,38)\) | \(5\) | \(0.10\) |
| \([38,43)\) | \(8\) | \(0.16\) |
| \([43,48)\) | \(15\) | \(0.30\) |
| \([48,53)\) | \(7\) | \(0.15\) |
| \([53,58)\) | \(5\) | \(0.10\) |
| \([58,63)\) | \(4\) | \(0.08\) |
| \([63,68)\) | \(3\) | \(0.06\) |
| 合计 | \(50\) | \(1.00\) |
④频率分布直方图如下图所示:

点拨 画频率直方图的步骤
(1) 求极差(数据中最大值与最小值的差)
(2) 决定组距与组数(组数不要太多或太少,一般取等长组距,组距为整数)
(3) 将数据分组
(4) 列频率分布表
(5) 画频率分布直方图(纵轴表示\(\dfrac{频率}{组距}\))
【巩固练习】
1.为了了解中学生的身高情况,对育才中学同龄的\(50\)名男学生的身高进行了测量,结果如下(单位:\(cm\))
175 168 180 176 167 181 162 173 171 177
171 171 174 173 174 175 177 166 163 160
166 166 163 169 174 165 175 165 170 158
174 172 166 172 167 172 175 161 173 167
170 172 165 157 172 173 166 177 169 181
列出样本的频率分布表,画出频率分布直方图.
参考答案
- 解析 在这个样本中,最大值为\(181\),最小值为\(157\),它们的差是\(24\),
可以取组距为\(4\),分成\(7\)组,根据题意列出样本的频率分布表如下:
| 分组 | 频数 | 频率 |
|---|---|---|
| \(156.5~160.5\) | \(3\) | \(0.06\) |
| \(160.5~164.5\) | \(4\) | \(0.08\) |
| \(164.5~168.5\) | \(12\) | \(0.24\) |
| \(168.5~172.5\) | \(12\) | \(0.24\) |
| \(172.5~176.5\) | \(13\) | \(0.26\) |
| \(176.5~180.5\) | \(4\) | \(0.08\) |
| \(180.5~184.5\) | \(2\) | \(0.04\) |
| 合计 | \(50\) | \(1.00\) |
频率分布直方图如下:

【题型2】 频率直方图的应用
【典题1】 某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是\([96,106]\),样本数据分组为\([96,98)\),\([98,100)\),\([100,102)\),\([102,104)\),\((104,106]\),已知样本中产品净重小于\(100\)克的个数是\(36\),则样本中净重大于或等于\(98\)克并且小于\(104\)克的产品的个数是( )

A.\(90\) \(\qquad \qquad \qquad \qquad\) B.\(75\) \(\qquad \qquad \qquad \qquad\) C.\(60\) \(\qquad \qquad \qquad \qquad\) D.\(45\)
解析 样本中产品净重小于\(100\)克的频率为\((0.050+0.100)×2=0.3\),
\(\because\)样本中产品净重小于\(100\)克的个数是\(36\),
\(\therefore\)样本总数 \(n=\dfrac{36}{0.3}=120\).
\(\therefore\)样本中净重大于或等于\(98\)克并且小于\(104\)克的产品个数为\(120×0.75=90\).
故选:\(A\).
点拨
(1) 频率直方图中小长方形的面积等于频率,在直方图中,各小长方形的面积之和等于\(1\).
(2) 频数=总数×频率,频率=频数/总数,总数=频数/频率.
【典题2】某校从高一年级学生中随机抽取\(40\)名学生作为样本,将他们的期中考试数学成绩(满分\(100\)分,成绩均为不低于\(40\)分的整数)分成六组:\([40,50)\),\([50,60)\),...,\([90,100)\)后得到如图的频率分布直方图.

(1)求图中实数\(a\)的值;
(2)若该校高一年级共有学生\(500\)人,试估计该校高一年级在考试中成绩不低于\(60\)分的人数;
(3)若从样本中数学成绩在\([40,50)\)与\([90,100]\)两个分数段内的学生中随机选取两名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于\(10\)的概率.
解析 (1)根据数据的频率之和为\(1\),得\(0.05+0.1+0.2+10a+0.25+0.1=1\),
\(\therefore a=0.03\);
(2)数学成绩不低于\(60\)分的概率为:\(0.2+0.3+0.25+0.1=0.85\),
\(\therefore\)数学成绩不低于\(60\)分的人数为\(500×0.85=425\)人
(3)数学成绩在\([40,50)\)的学生人数:\(40×0.005×10=2\)人,
数学成绩在\([50,60)\)的学生人数:\(40×0.01×10=4\)人,
设数学成绩在\([40,50)\)的学生为\(A\),\(B\);
数学成绩在\([90,100)\)的学生为\(a\),\(b\),\(c\),\(d\);
从\(6\)名学生中选两名学生的结果有:\(\{A,B\}\),\(\{A,a\}\),\(\{A,b\}\),\(\{A,c\}\),\(\{A,d\}\),\(\{B,a\}\),\(\{B,b\}\),\(\{B,c\}\),\(\{B,d\}\),\(\{a,b\}\),\(\{a,c\}\),\(\{a,d\}\),\(\{b,c\}\),\(\{b,d\}\),\(\{c,d\}\).共\(15\)种;
其中两名学生的数学成绩之差的绝对值不大于\(10\)的情况有:\(\{A,B\}\),\(\{a,b\}\),\(\{a,c\}\),\(\{a,d\}\),\(\{b,c\}\),\(\{b,d\}\),\(\{c,d\}\)共\(7\)种;
\(\therefore\)抽取的两名学生的数学成绩之差的绝对值不大于\(10\)的概率为\(\dfrac{7}{15}\).
点拨
(1) 频率直方图中小长方形的面积=频率,在直方图中,各小长方形的面积之和等于\(1\);
(2) 第二问求概率可利用枚举法或列树状图求解.
【巩固练习】
1.在样本频率分布直方图中,共有\(9\)个小长方形,若中间一个小长方形的面积等于它\(8\)个长方形的面积和的\(\dfrac{2}{5}\),且样本容量为\(140\),则中间一组的频数为( )
A.\(28\) \(\qquad \qquad \qquad \qquad\) B.\(40\) \(\qquad \qquad \qquad \qquad\)C.\(56\) \(\qquad \qquad \qquad \qquad\) D.\(60\)
2.对某次联考数学成绩(百分制)进行分析,如图为分析结果的频率分布直方图.根据标准,成绩分数在区间\([50,60)\)上为不及格,在\([60,70)\)上为一般,在\([70,80)\)上为较好,在\([80,90)\)上为良好,在\([90,100]\)上为优秀.用频率估计概率,若从参考学生中随机抽取\(1\)人,则其成绩为优良(优秀或良好)的概率为( )

A.\(0.09\) \(\qquad \qquad \qquad \qquad\) B.\(0.20\) \(\qquad \qquad \qquad \qquad\)C.\(0.25\) \(\qquad \qquad \qquad \qquad\) D.\(0.40\)
3.我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市实行阶梯水价,每人月用水量中不超过\(a\)立方米的部分按\(2.5\)元/立方米收费,超出\(a\)立方米的部分按\(7\)元/立方米收费,从该市随机调查了\(10000\)位居民,获得了他们某年的月均用水量数据,整理得到如下频率分布直方图:

如果\(a\)为整数,那么根据此次调查,为使\(80\%\)以上居民在该月的用水价格为\(2.5\)元/立方米,\(a\)至少定为( )
A.\(2\) \(\qquad \qquad \qquad \qquad\) B.\(2.5\) \(\qquad \qquad \qquad \qquad\) C.\(3\) \(\qquad \qquad \qquad \qquad\) D.\(4\)
4.学校为了调查学生在课外读物方面的支出(单位:元)情况,抽取了一个容量为\(n\)的样本,并将得到的数据分成\([10,20)\),\([20,30)\),\([30,40)\),\([40,50]\)四组,绘制成如图所示的频率分布直方图,其中支出在\([40,50]\)的同学有\(24\)人,则\(n=\)( )

A.\(80\) \(\qquad \qquad \qquad \qquad\) B.\(60\) \(\qquad \qquad \qquad \qquad\) C.\(100\) \(\qquad \qquad \qquad \qquad\) D.\(50\)
5.从某小学随机抽取\(100\)名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在\([120,130)\),\([130,140)\),\([140,150]\)三组内的学生中,用分层抽样的方法选取\(18\)人参加一项活动,则从身高在\([140,150]\)内的学生中选取的人数应为( )

A.\(2\) \(\qquad \qquad \qquad \qquad\) B.\(3\) \(\qquad \qquad \qquad \qquad\) C.\(4\) \(\qquad \qquad \qquad \qquad\) D.\(5\)
6.某网络营销部门随机抽查了某市\(200\)名网友在2018年11月11日的网购金额,所得数据如表:
已知网购金额不超过\(3\)千元与超过\(3\)千元的人数比恰为\(3:2\).
(1)试确定\(x\),\(y\),\(p\),\(q\)的值,并补全频率分布直方图(如图);
(2)该营销部门为了了解该市网友的购物体验,从这\(200\)名网友中,用分层抽样的方法从网购金额在\((1,2]\)和\((4,5]\)的两个群体中确定\(5\)人进行问卷调查,若需从这\(5\)人中随机选取\(2\)人继续访谈,则此\(2\)人来自不同群体的概率是多少?
| 网购金额(单位:千元) | 人数 | 频率 |
|---|---|---|
| \((0,1]\) | \(16\) | \(0.08\) |
| \((1,2]\) | \(24\) | \(0.12\) |
| \((2,3]\) | \(x\) | \(p\) |
| \((3,4]\) | \(y\) | \(q\) |
| \((4,5]\) | \(16\) | \(0.08\) |
| \((5,6]\) | \(14\) | \(0.07\) |
| 总计 | \(002\) | \(1.00\) |

参考答案
-
答案 \(B\)
解析 设中间一组的频数为\(x\),
因为中间一个小长方形的面积等于它\(8\)个长方形的面积和的\(\dfrac{2}{5}\),
所以其他\(8\)组的频数和为\(\dfrac{5}{2} x\),
由 \(x+\dfrac{5}{2} x=140\),解得\(x=40\).
故选:\(B\). -
答案 \(D\)
解析 根据题意,成绩在\([80,100]\)内的频率为\((0.025+0.015)×10=0.40\);
所以,成绩为优良的概率为\(0.40\).故选:\(D\). -
答案 \(C\)
解析 由频率分布直方图得:
用水量在\([0,0.5)\)的频率为\(0.08×0.5=0.04\),
用水量在\([0.5,1)\)的频率为\(0.16×0.5=0.08\),
用水量在\([1,1.5)\)的频率为\(0.30×0.5=0.15\),
用水量在\([1.5,2)\)的频率为\(0.44×0.5=0.22\),
用水量在\([2,2.5)\)的频率为\(0.50×0.5=0.25\),
用水量在\([2.5,3)\)的频率为\(0.28×0.5=0.14\),
\(\because\)用水量在\([0,2.5)\)的频率为:\(0.04+0.08+0.15+0.22+0.25=0.74\),
用水量在\([0,3)\)的频率为:\(0.04+0.08+0.15+0.22+0.25+0.14=0.88\).
\(\therefore\)根据此次调查,为使\(80\%\)以上居民在该月的用水价格为\(2.5\)元/立方米,\(a\)至少定为\(3\)元.
故选:\(C\). -
答案 \(A\)
解析 本题考查频率分布直方图,考查数据处理能力.
由频率分布直方图可得,支出在\([40,50]\)的频率为\(1-(0.01+0.024+0.036)×10=0.3\).
根据题意得 \(\dfrac{24}{n}=0.3\),解得\(n=80\).
故选:\(A\). -
答案 \(B\)
解析 \(\because\)直方图中各个矩形的面积之和为\(1\),
\(\therefore 10×(0.005+0.035+a+0.02+0.01)=1\),解得\(a=0.03\).
由直方图可知三个区域内的学生总数为\(100×10×(0.03+0.02+0.01)=60\)人.
其中身高在\([140,150]\)内的学生人数为\(10\)人,
所以身高在\([140,150]\)范围内抽取的学生人数为 \(\dfrac{18}{60} \times 10=3\)人.
故选:\(B\). -
答案 (1) \(x=80\),\(y=50\),\(p=0.4\),\(q=0.25\),补全频率分布直方图略;(2)\(\dfrac{3}{5}\).
解析 (1)依题意有: \(\left\{\begin{array}{l} 16+24+x+y+16+14=200 \\ \dfrac{16+24+x}{y+16+14}=\dfrac{3}{2} \end{array}\right.\),解得 \(\left\{\begin{array}{l} x=80 \\ y=50 \end{array}\right.\),
\(\therefore p=0.4\),\(q=0.25\).补全频率分布直方图如图.

(2)根据题意,网购金额在\((1,2]\)内的人数为\(\dfrac{24}{24+16} \times 5=3\) (人),记为\(a\),\(b\),\(c\).
网购金额在\((4,5]\)内的人数为\(\dfrac{16}{24+16} \times 5=2\)(人),记为\(A\),\(B\).
则从这\(5\)人中随机选取\(2\)人的选法为:\((a,b)\),\((a,c)\),\((a,A)\),\((a,B)\),\((b,c)\),\((b,A)\),\((b,B)\),\((c,A)\),\((c,B)\),\((A,B)\)共\(10\)种.
记\(2\)人来自不同群体的事件为\(M\),
则\(M\)中含有\((a,A)\),\((a,B)\),\((b,A)\),\((b,B)\),\((c,A)\),\((c,B)\)共\(6\)种.
\(\therefore P(M)=\dfrac{6}{10}=\dfrac{3}{5}\).
分层练习
【A组---基础题】
1.为了解某校学生的视力情况,随机抽查了该校的\(100\)名学生,得到如图所示的频率分布直方图,由于不慎将部分数据丢失,但知道前\(4\)组的频数和为\(40\),后\(6\)组的频数和为\(87\),设最大频率\(a\)视力在\(4.5\)到\(5.2\)之间的学生数\(b\),则\(a\),\(b\)的值分别为( )

A.\(0.27\),\(96\) \(\qquad \qquad \qquad \qquad\) B.\(0.27\),\(83\) \(\qquad \qquad \qquad \qquad\)C.\(2.7\),\(78\) \(\qquad \qquad \qquad \qquad\) D.\(2.7\),\(83\)
2.将某市参加高中数学建模竞赛的学生成绩分成\(6\)组,绘成频率分布直方图如图所示,现按成绩运用分层抽样的方法抽取\(100\)位同学进行学习方法座谈,则成绩为\([70,80)\)组应抽取的人数为( )

A.\(60\) \(\qquad \qquad \qquad \qquad\) B.\(50\) \(\qquad \qquad \qquad \qquad\) C.\(40\) \(\qquad \qquad \qquad \qquad\) D.\(20\)
3.某校\(100\)名学生的数学测试成绩分布直方图如图所示,分数不低于\(a\)即为优秀,如果优秀的人数为\(20\)人,则\(a\)的估计值是( )

A.\(130\) \(\qquad \qquad \qquad \qquad\) B.\(140\) \(\qquad \qquad \qquad \qquad\)C.\(133\) \(\qquad \qquad \qquad \qquad\) D.\(137\)
4.某工厂对一批产品进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是\([96,106]\),样本数据分组为\([96,98)\),\([98,100)\),\([100,102)\),\([102,104)\),\([104,106]\).已知样本中产品净重小于\(100\)克的个数是\(36\),则样本中净重大于或等于\(98\)克并且小于\(102\)克的产品的个数是( )

A.\(90\) \(\qquad \qquad \qquad \qquad\) B.\(75\) \(\qquad \qquad \qquad \qquad\)C.\(60\) \(\qquad \qquad \qquad \qquad\) D.\(45\)
5.学校为了解新课程标准提升阅读要求对学生阅读兴趣的影响情况,随机抽取了\(100\)名学生进行调查.根据调查结果绘制学生周末阅读时间的频率分布直方图如图所示:将阅读时间不低于\(30\)分钟的观众称为“阅读霸”,则下列命题正确的是( )

A.抽样表明,该校有一半学生为阅读霸
B.该校只有\(50\)名学生不喜欢阅读
C.该校只有\(50\)名学生喜欢阅读
D.抽样表明,该校有\(50\)名学生为阅读霸
6.某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为\([20,40]\),\([40,60]\),\([60,80]\),\([80,100]\),若低于\(60\)分的人数是\(15\)人,则该班的学生人数是\(\underline{\quad \quad}\) .

7.某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为\(100\)分)作为样本进行统计.若下面是尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),则\(\dfrac{a}{x}+\dfrac{b}{y}\)的值为\(\underline{\quad \quad}\).
| 分组 | 频数 | 频率 |
|---|---|---|
| \([50,60)\) | \(8\) | \(0.16\) |
| \([60,70)\) | \(a\) | ■ |
| \([70,80)\) | \(20\) | \(0.40\) |
| \([80,90)\) | ■ | \(0.08\) |
| \([90,100]\) | \(2\) | \(b\) |
| 合计 | ■ | \(1\) |

8.某制造商为2008年北京奥运会生成一批直径为\(40mm\)的乒乓球,现随机抽取\(20\)只,测得每只球的直径(单位\(mm\),保留两位小数)如下:
40.03 40.00 39.98 40.00 39.99 40.00 39.98 40.01 39.98 39.99 40.00 39.99 39.95 40.0l 40.02 39.98 40.00 39.99 40.00 39.96
(1)完成下面的频率分布表,并画出频率分布直方图;
(2)假定乒乓球的直径误差不超过\(0.02mm\)为合格品.若这批乒乓球的总数为\(10000\)只,试根据抽样检查结果估计这批产品的合格只数.
| 分组 | 频数 | 频率 | \(\dfrac{频率}{组距}\) |
|---|---|---|---|
| \([39.95,39.97)\) | |||
| \([39.97,39.99)\) | |||
| \([39.99,40.01)\) | |||
| \([40.01,40.03]\) | |||
| 合计 |

9.某校为加强党史教育,进行了一次党史知识竞赛,随机抽取的\(100\)名学生的笔试成绩均在\(75\)分以上(满分\(100\)分),分成\([75,80)\),\([80,85)\),\([85,90)\),\([90,95)\),\([95,100]\)共五组后,得到的频率分布表如下所示:
| 组号 | 分组 | 频数 | 频率 |
|---|---|---|---|
| 第\(1\)组 | \([75,80)\) | ① | |
| 第\(2\)组 | \([80,85)\) | \(0.300\) | |
| 第\(3\)组 | \([85,90)\) | \(30\) | ② |
| 第\(4\)组 | \([90,95)\) | \(20\) | \(0.200\) |
| 第\(5\)组 | \([95,100]\) | \(10\) | \(0.100\) |
| 合计 | \(100\) | \(1.00\) |
(1)请先求出频率分布表中①、②位置的相应数据,再完成频率分布直方图(用阴影表示);
(2)为能更好了解学生的知识掌握情况,学校决定在笔试成绩高的第\(3\)、\(4\)、\(5\)组中用分层抽样抽取\(6\)名学生进入第二轮面答,最终从\(6\)位学生中随机抽取\(2\)位参加市安全知识答题决赛,求抽到的\(2\)位学生不同组的概率.

参考答案
-
答案 \(A\)
解析 由频率分布直方图知组距为\(0.1\),前\(3\)组频数和为\(13\),
由\(4.6\)到\(4.7\)之间的频数最大为\(27\),故最大频率为\(a=0.27\),
视力在\(4.5\)到\(5.2\)之间的频率为\(0.96\),
故视力在\(4.5\)到\(5.2\)之间的学生数\(b=96\).
故选:\(A\). -
答案 \(C\)
解析 由频率分布直方图得:
成绩为\([70,80)\)组的频率为:\(1-(0.005+0.005+0.02+0.02+0.01)×10=0.4\),
\(\therefore\)成绩为\([70,80)\)组应抽取的人数为:\(0.4×100=40\).
故选:\(C\). -
答案 \(C\)
解析 由题意可知:\(90-100\)分的频率为\(0.005×10=0.05\),频数为\(5\)人
则\(100-110\)分的频率为\(0.018×10=0.18\),频数为\(18\)人
\(110-120\)分的频率为\(0.03×10=0.3\),频数为\(30\)人
\(120-130\)分的频率为\(0.022×10=0.22\),频数为\(22\)人
\(130-140\)分的频率为\(0.015×10=0.15\),频数为\(15\)人
\(140-150\)分的频率为\(0.010×10=0.05\),频数为\(10\)人
而优秀的人数为\(20\)人,\(140-150\)分有\(10\)人,\(130-140\)分有\(15\)人,取后\(10\)人
\(\therefore\)分数不低于\(133\)即为优秀,
故选:\(C\). -
答案 \(C\)
解析 由图可知:
\([96,98)\),频率为:\(0.05×2=0.1\);\([98,100)\),频率为:\(0.100×2=0.2\);
\([100,102)\),频率为:\(0.150×2=0.3\);\([102,104)\),频率为:\(0.125×2=0.25\);
\([104,106]\),频率为:\(0.075×2=0.15\);
\(\because\)样本中产品净重小于\(100\)克的个数是\(36\),
\(\therefore \dfrac{36}{N}=0.3\),\(N\)为样本总量,
又\(\because N=120\),
\(\therefore\)样本中净重大于或等于\(98\)克并且小于\(102\)克的产品的净重的频数为:\(0.2×120+0.3×120=60\),
故选:\(C\). -
答案 \(A\)
解析 根据频率分布直方图可列小表:
| 阅读时间(分) | $[0,10)$ | $[10,20)$ | $[20,30)$ | $[30,40)$ | $[40,50)$ | $[50,60)$ |
| 抽样人数(名) | $10$ | $18$ | $22$ | $25$ | $20$ | $5$ |
抽样\(100\)名学生中有\(50\)名为阅读霸,占一半,据此可判断该校有一半学生为阅读霸.
故选:\(A\).
-
答案 \(50\)
解析 \(\because\)成绩低于\(60\)分有第一、二组数据,
在频率分布直方图中,对应矩形的高分别为\(0.005\),\(0.01\),
每组数据的组距为\(20\),
则成绩低于\(60\)分的频率\(P=(0.005+0.010)×20=0.3\),
又\(\because\)低于\(60\)分的人数是\(15\)人,
则该班的学生人数是 \(\dfrac{15}{0.3}=50\). -
答案 \(510\)
解析 由题意可知,样本容量为\(\dfrac{8}{0.16}=50\), \(\therefore b=\dfrac{2}{50}=0.04\),
第四组的频数\(=50×0.08=4\),
\(\therefore a=50-8-20-2-4=16\),
y= \(y=\dfrac{0.04}{10}=0.004\), \(x=\dfrac{16}{50} \times \dfrac{1}{10}=0.032\).
\(\therefore a=16\),\(b=0.04\),\(x=0.032\),\(y=0.004\),
\(\therefore \dfrac{a}{x}+\dfrac{b}{y}=\dfrac{16}{0.032}+\dfrac{0.04}{0.004}=500+10=510\),
故答案为:\(510\). -
答案 (1) 略;(2) \(8500\);
解析 (1)填写频率分布表,如下;
| 分组 | 频数 | 频率 | \(\dfrac{频率}{组距}\) |
|---|---|---|---|
| \([39.95,39.97)\) | \(2\) | \(0.1\) | \(5\) |
| \([39.97,39.99)\) | \(4\) | \(0.2\) | \(10\) |
| \([39.99,40.01)\) | \(10\) | \(0.5\) | \(25\) |
| \([40.01,40.03]\) | \(4\) | \(0.2\) | \(10\) |
| 合计 | \(20\) | \(10\) |
画出频率分布直方图,如下;

(2)在抽取的\(20\)个样本中,有\(3\)个不合格产品,
\(\therefore\)不合格产品的频率是\(\dfrac{3}{20}=0.15\);
\(\therefore\)估计该批产品的合格数是\(10000×(1-0.15)=8500\)(只).
- 答案 (1) 略;(2) \(\dfrac{11}{15}\);
解析 (1)第\(2\)组的频数为\(100×0.300=30\),
所以①处应填的数为\(100-30-30-20-10=10\),
②处应填的数为\(30÷100=0.300\),
频率分布直方图如图所示,

(2)因为第\(3\)、\(4\)、\(5\)组共有\(60\)名选手,所以利用分层抽样在\(60\)名选手中抽取\(6\)名选手进入第二轮面试,每组抽取的人数分别为:
第\(3\)组: \(\dfrac{30}{60} \times 6=3\)人,第\(4\)组: \(\dfrac{20}{60} \times 6=2\)人,第\(5\)组: \(\dfrac{10}{60} \times 6=1\)人,
所以第\(3\)、\(4\)、\(5\)组分别抽取\(3\)人、\(2\)人、\(1\)人进入第二轮面试,
设第\(3\)组的\(3\)位学生为\(A_1\),\(A_2\),\(A_3\),第\(4\)组的\(2\)位学生为\(B_1\),\(B_2\),第\(5\)组的\(1\)位学生为\(C_1\),
则从这\(6\)位学生中抽取\(2\)位学生有:
\((A_1,A_2 )\),\((A_1,A_3 )\),\((A_1,B_1 )\),\((A_1,B_2 )\),\((A_1,C_1 )\),
\((A_2,A_3 )\),\((A_2,B_1 )\),\((A_2,B_2 )\),\((A_2,C_1 )\),
\((A_3,B_1)\),\((A_3,B_2 )\),\((A_3,C_1 )\),
\((B_1,B_2 )\),\((B_1,C_1)\),
\((B_2,C_1 )\),共\(15\)种情况.
抽到的\(2\)位学生不同组的有:\((A_1,B_1 )\),\((A_1,B_2 )\),\((A_1,C_1 )\),\((A_2,B_1 )\),\((A_2,B_2 )\),\((A_2,C_1 )\),\((A_3,B_1 )\),\((A_3,B_2 )\),\((A_3,C_1 )\),\((B_1,C_1 )\), \((B_2,C_1 )\),共\(11\)种情况.
所以抽到的\(2\)位学生不同组的概率为\(\dfrac{11}{15}\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号