9.1.2 分层随机抽样
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019)]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第二册同步巩固,难度2颗星!
基础知识
分层抽样的概念
一般地,按一个或多个变量把总体划分为若干个子总体,每个个体属于且仅属于一个子总体,在每个子总体中独立地进行简单随机抽样,再把所有子总体中抽取的样本合在一起作为总样本,这样的抽样方法称为分层随机抽样.
每一个子总体称为层,在分层随机抽样中,如果每层样本量都与层的大小成比例,那么成这种样本量的分配方式为比例分配.
解释
(1) 抽样最核心的问题是样本的代表性,在简单随机抽样中容易出现“极端”的样本,比如抽样调查你班里学生的平均身高,若用简单随机抽样,万一抽到“姚明”级别的一个学生或者抽到的男生明显多于女生,就会影响到数据的估计.
如何改善抽样方法?显然高中男生比女生高,故可借助“性别”这辅助信息,按照班上男女生比例进行抽样.
(2)在个体之间差异较大的情况下,只要选取的分层变量合适,使得各层间差异明显,层内差异不大,分层随机抽样的效果会比简单随机抽样好;而在分层抽样中,不同的层内除了简单随机抽样,有时层内也可以继续分层.
(3)对于按照什么标准进行分层,当然要根据调查目的而定.
若高一年级学生中男女比例是\(1:2\);学霸学渣比例是\(1:4\),调查学生身高,故采取按男女比例分层抽样;调查教学效果,则按照学霸学渣比例分层抽样;调查学生饮食习惯,可按照肥胖程度.
分层随机抽样的一般步骤
(1)根据已掌握的信息,将总体分层互不相交的\(L\)层,\(N_1\),\(N_2,\)⋯,\(N_L\);
(2)根据总体中的个体数\(N\),各层中的个体数\(N_1\),\(N_2,\)⋯,\(N_L\)和样本容量\(n\),计算第\(i\)层抽取的个体数\(n_i=\dfrac{N_i}{N} \times n\),\(i=1\),\(2\),⋯,\(L\),使得各\(n_i\)之和为\(n\);
(3)在各层中,用简单随机抽样方法抽取步骤(2)确定的个体数,合在一起得到容量为\(n\)的样本.
获取数据的途径
① 通过调查获取数据
② 通过试验获取数据
③ 通过观察获取数据
④ 通过查阅获取数据
基本方法
【题型1】 抽样方法的选择
【典题1】(多选) 对下面三个事件最适宜采用的抽样方法判断正确的是( )
①从某厂生产的\(3000\)件产品中抽取\(600\)件进行质量检验;
②一次数学竞赛中,某班有\(10\)人的成绩在\(110\)分以上,\(40\)人的成绩在\(90∼110\)分,\(10\)人的成绩低于\(90\)分,现在从中抽取\(12\)人的成绩了解有关情况;
③运动会服务人员为参加\(400 m\)决赛的\(6\)名同学安排跑道.
A.①②适宜采用分层随机抽样 \(\qquad \qquad \qquad \qquad\) B.②③适宜采用分层随机抽样
C.②适宜采用分层随机抽样 \(\qquad \qquad \qquad \qquad\) D.③适宜采用简单随机抽样
解析 从某厂生产的\(3000\)件产品中抽取\(600\)件进行质量检验,不宜采用分层抽样,
总体由差异明显且互不重叠的几部分组成,若从中抽取\(12\)人的成绩了解有关情况,宜采用分层抽样,
运动会服务人员为参加\(400 m\)决赛的\(6\)名同学安排跑道,具有随机性,适宜采用简单随机抽样.
故选:\(CD\).
点拨 简单随机抽样适合于个体间的差异不大,总体容量不大的事件;分层随机抽样适合于个体间存在较大差异.
【巩固练习】
1.分层抽样又称为类型抽样,即将相似的个体归入一类(层),然后每层各抽若干个个体构成样本,所以分层抽样为保证每个个体等可能入样,必须进行( )
A.每层内等可能抽样 \(\qquad\) B.每层内不等可能抽样 \(\qquad\) C.所有层用同一抽样比 \(\qquad\) D.所有层抽同样多样本容量
2.为了解某地区居民使用手机扫码支付的情况.拟从该地区的居民中抽取部分人员进行调查,事先已了解到该地区老、中、青三个年龄段的人员使用手机扫码支付的情况有较大差异,而男、女使用手机扫码支付的情况差异不大,在下面的抽样方法中,最合理的是( )
A.抽签法 \(\qquad\) B.按性别分层随机抽样 \(\qquad\) C.按年龄段分层随机抽样 \(\qquad\) D.随机数法
3.下列问题中,最适合用分层抽样方法抽样的是( )
A.某电影院有\(32\)排座位,每排有\(40\)个座位,座位号是\(1~40\),有一次报告会坐满了听众,报告会结束以后为听取意见,要留下\(32\)名听众进行座谈
B.从\(10\)台冰箱中抽出\(3\)台进行质量检查
C.某乡农田有山地\(8000\)亩,丘陵\(12000\)亩,平地\(24000\)亩,洼地\(4000\)亩,现抽取农田\(480\)亩估计全乡农田平均产量
D.从\(50\)个零件中抽取\(5\)个做质量检验
4.要调查全市普通高中高一年级学生中患色盲的比例, 小明根据性别对总体进行分层, 用分层随机抽样的方法进行调查. 请你查阅有关资料, 说说这样的分层是否合理. 你觉得在选择分层变量时应注意什么?
参考答案
- 答案 \(C\)
解析 由分层抽样又称为类型抽样,
为了保证每个个体入样的可能性相等必须每层等可能性抽样,故\(C\)正确.
故选:\(C\). - 答案 \(C\)
解析 因为总体中使用手机扫码支付的情况按年龄段具有明显差异,所以选择按年龄段分层随机抽样.故选:\(C\). - 答案\(C\)
解析 \(A\).总体容量较多,差异不明显,可以使用系统抽样,
\(B\).总体容量比较少,使用简单抽样即可,
\(C\).总体容量较多,样本差异比较明显,使用分层抽样,
\(D\).总体容量比较少,使用简单抽样即可,
故选:\(C\). - 解析 不合理.色盲是伴\(X\)染色体隐性遗传病. 男性发病率高于女性. 选择分层随机抽样时应注意,使得各层间差异明显,层内差异不大.
【题型2】分层随机抽样的应用
【典题1】 一个地区共有\(5\)个乡镇,共\(3\)万人,其中各个乡镇的人口比例为\(3:2:5:2:3\),从\(3\)万人中抽取\(300\)人,分析某种疾病的发病率,已知这种疾病与不同的地理位置及水土有关,问应采取什么样的抽样方法?并写出具体过程.
解析 因为疾病与地理位置和水土均有关系,所以不同乡镇的发病情况差异明显,
因此应采用分层抽样的方法,具体过程如下:
(1)将\(3\)万人分成\(5\)层,一个乡镇为一层.
(2)按照各乡镇的人口比例确定从每层抽取个体的个数.
因为\(300 \times\dfrac{3}{15}=60\),\(300 \times\dfrac{2}{15}=40\),\(300 \times\dfrac{5}{15}=100\),
\(300 \times\dfrac{2}{15}=40\), \(300 \times\dfrac{3}{15}=60\),
所以从各乡镇抽取的人数分别为\(60\),\(40\),\(100\),\(40\),\(60\).
(3)在各层分别用简单随机抽样法抽取样本.
(4)将抽取的这\(300\)人合到一起,就构成所要抽取的一个样本.
点拨
(1)分层随机抽样的一般步骤
① 根据已掌握的信息,将总体分层互不相交的\(L\)层,\(N_1\),\(N_2,\)⋯,\(N_L\);
② 根据总体中的个体数\(N\),各层中的个体数\(N_1\),\(N_2,\)⋯,\(N_L\)和样本容量\(n\),计算第\(i\)层抽取的个体数\(n_i=\dfrac{N_i}{N} \times n\),\(i=1\),\(2\),⋯,\(L\),使得各\(n_i\)之和为\(n\);
③ 在各层中,用简单随机抽样方法抽取步骤②确定的个体数,合在一起得到容量为\(n\)的样本.
(2) 计算各层的容量,需要按照分配比例确定.
【典题2】 某单位共有老年人\(120\)人,中年人\(360\)人,青年人\(n\)人,为调查身体健康状况,需要从中抽取一个容量为\(m\)的样本,用分层抽样的方法进行抽样调查,样本中的中年人为\(6\)人,则\(n\)和\(m\)的值不可以是下列四个选项中的哪组( )
A.\(n=360\),\(m=14\) \(\qquad \qquad \qquad \qquad\) B.\(n=420\),\(m=15\)
C.\(n=540\),\(m=18\) \(\qquad \qquad \qquad \qquad\) D.\(n=660\),\(m=19\)
解析 \(\because\) 某单位共有老年人\(120\)人,中年人\(360\)人,青年人\(n\)人,样本中的中年人为\(6\)人,
则样本中,老年人为\(120 \times\dfrac{6}{360}=2\),青年人为\(\dfrac{6}{360} n=\dfrac{n}{60}\),
再根据\(2+6+\dfrac{n}{60}=m\),可得\(8+\dfrac{n}{60}=m\),
代入选项计算,\(C\)不符合,
故选:\(C\).
点拨理解分层抽样的比例分配是关键,注意不混乱各数据之间的对应关系便可.
【巩固练习】
1.某大学工程学院共有本科生\(1200\)人、硕士生\(400\)人、博士生\(200\)人,要用分层抽样的方法从中抽取一个容量为\(180\)的样本,则应抽取博士生的人数为( )
A.\(20\) \(\qquad \qquad \qquad \qquad\) B.\(25\) \(\qquad \qquad \qquad \qquad\) C.\(40\) \(\qquad \qquad \qquad \qquad\) D.\(50\)
2.某大学有\(A\)、\(B\)、\(C\)三个不同的校区,其中\(A\)校区有\(4000\)人,\(B\)校区有\(3000\)人,\(C\)校区有\(2000\)人,采用按校区分层抽样的方法,从中抽取\(900\)人参加一项活动,则\(A\)、\(B\)、\(C\)校区分别抽取( )
A.\(400\)人、\(300\)人、\(200\)人 \(\qquad \qquad \qquad\) B.\(350\)人、\(300\)人、\(250\)人
C.\(250\)人、\(300\)人、\(350\)人 \(\qquad \qquad \qquad\) D.\(200\)人、\(300\)人、\(400\)人
3.某校高二年级统计了参加课外兴趣小组的学生人数,每人只参加一类,数据如下表:
| 学科类别 | 文学 | 新闻 | 经济 | 政治 |
|---|---|---|---|---|
| 人数 | \(400\) | \(300\) | \(100\) | \(200\) |
若从参加课外兴趣小组的学生中采用分层抽样的方法抽取\(50\)名参加学习需求的问卷调查,则从文学、新闻、经济、政治四类兴趣小组中抽取的学生人数分别为( )
A.\(15\),\(20\),\(10\),\(5\) \(\qquad\) B.\(15\),\(20\),\(5\),\(10\) \(\qquad\) C.\(20\),\(15\),\(10\),\(5\) \(\qquad\) D.\(20\),\(15\),\(5\),\(10\)
4.某集团校为调查学生对学校“延时服务”的满意率,想从全市\(3\)个分校区按学生数用分层随机抽样的方法抽取一个容量为\(n\)的样本.已知\(3\)个校区学生数之比为\(2:3:5\),如果最多的一个校区抽出的个体数是\(60\),那么这个样本的容量为( )
A.\(96\) \(\qquad \qquad \qquad \qquad\) B.\(120\) \(\qquad \qquad \qquad \qquad\) C.\(180\) \(\qquad \qquad \qquad \qquad\) D.\(240\)
5.某工厂生产\(A\)、\(B\)、\(C\)三种不同型号的产品,某月生产产品数量之比依次为\(m:3:2\),现用分层抽样方法抽取一个容量为\(120\)的样本,已知\(A\)种型号产品抽取了\(45\)件,则\(C\)种型号产品抽取的件数为( )
A.\(20\)\(\qquad \qquad \qquad \qquad\) B.\(30\) \(\qquad \qquad \qquad \qquad\) C.\(40\) \(\qquad \qquad \qquad \qquad\) D.\(45\)
6.(多选)某运动队由足球运动员\(12\)人,篮球运动员\(18\)人,乒乓球运动员\(6\)人组成(每人只参加一项),现从这些运动员中抽取一个容量为\(n\)的样本,若采用分层随机抽样的方法,且不用删除个体,则样本量\(n\)的取值不可能是( )
A.\(24\) \(\qquad \qquad \qquad \qquad\) B.\(20\) \(\qquad \qquad \qquad \qquad\) C.\(6\) \(\qquad \qquad \qquad \qquad\) D.\(5\)
7.(多选)某市教育局对全市高三年级的学生身高进行抽样调查,随机抽取了\(200\)名学生,他们的身高都处在\(A\),\(B\),\(C\),\(D\),\(E\)五个层次内,根据抽样结果得到统计图表,则样本中( )
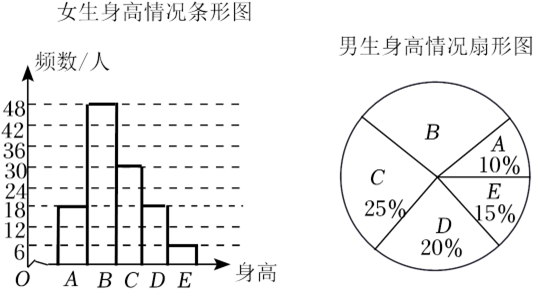
A.女生人数多于男生人数 \(\qquad \qquad \qquad \qquad\) B.\(D\)层次男生人数多于女生人数
C.\(B\)层次男生人数为\(24\)人 \(\qquad \qquad \qquad \qquad\) D.\(A\)层次人数最少
8.为了考察某校的教学水平,将抽查这个学校高三年级的部分学生本年度的考试成绩.为了全面反映实际情况,采取以下两种方式进行抽查(已知该校高三年级共有\(20\)个班,并且每个班内的学生已经按随机方式编好了学号):
①从高三年级\(20\)个班中任意抽取\(1\)个班,再从该班中任意抽取\(20\)名学生,考察他们的成绩;
②把学生按成绩分成优秀、良好、普通三个级别,按比例从中共抽取\(100\)名学生进行考察(已知该校高三学生共\(1000\)名,优秀生共\(150\)名,良好生共\(600\)名,普通生共\(250\)名).
根据上面的叙述,试回答下列问题:
(1)上面两种抽取方式的总体、个体、样本分别是什么?每一种抽取方式抽取的样本中,样本量是多少?
(2)上面两种抽取方式各自采用的是何种抽取样本的方法?
(3)试写出第二种抽取方式的步骤.
参考答案
- 答案 \(A\)
解析 \(\because\)要用分层抽样的方法从中抽取一个容量为\(180\)的样本,
\(\therefore\)抽取博士生的人数\(180 \times\dfrac{200}{200+400+200}=20\),
故选:\(A\). - 答案 \(A\)
解析 \(A\)校区有\(40004000\)人,\(B\)校区有\(3000\)人,\(C\)校区有\(2000\)人,
则\(4000:3000:2000=4:3:2\),
由分层抽样的定义得\(A\)校区中抽出的学生\(900 \times\dfrac{4}{9}=400\),
\(B\)校区中抽出的学生\(900 \times\dfrac{3}{9}=300\),\(C\)校区中抽出的学生 \(900 \times\dfrac{2}{9}=200\),
故选:\(A\). - 答案 \(D\)
解析 根据分层抽样的等比性质性质知:
文学小组抽取人数为\(50 \times\dfrac{400}{1000}=20\)人,新闻小组抽取人数为 \(50 \times\dfrac{300}{1000}=15\)人,
经济小组抽取人数为\(50 \times\dfrac{100}{1000}=5\)人,政治小组抽取人数为 \(50 \times\dfrac{200}{1000}=10\)人.
故选:\(D\). - 答案 \(B\)
解析 根据分层随机抽样法知,抽取容量为n的样本,抽样比为\(2:3:5\),
如果最多的抽出的个体数是\(60\),那么这个样本的容量为 \(n=\dfrac{60}{\frac{5}{2+3+5}}=120\).
故选:\(B\). - 答案 \(B\)
解析 \(\because\)分层抽样方法抽取一个容量为\(120\)的样本,\(A\)种型号产品抽取了\(45\)件,
\(\therefore B\)、\(C\)两种型号的产品共抽取:\(120-45=75\),
\(\because\)某工厂生产\(A\)、\(B\)、\(C\)三种不同型号的产品,某月生产产品数量之比依次为\(m:3:2\),
\(\therefore C\)种型号产品抽取的件数为:\(75 \times\dfrac{2}{3+2}=30\).
故选:\(B\). - 答案 \(BD\)
解析 总体容量\(6+12+18=36\),
则采用分层抽样的比例是\(\dfrac{n}{36}\),
分层抽样乒乓球运动员人数为\(\dfrac{n}{36} \times 6=\dfrac{n}{6}\),篮球运动员人数为 \(\dfrac{n}{36} \times 18=\dfrac{n}{2}\),足球运动员人数为 \(\dfrac{n}{36} \times 12=\dfrac{n}{3}\),
可知\(n\)应为\(6\)的倍数,\(36\)的约数,
结合选项可知,样本量\(n\)的取值不可能是\(20\),\(5\).
故选:\(BD\). - 答案 \(AC\)
解析 由条形图知,抽取女生学生有\(18+48+30+18+6=120\)(人),
所以抽取男生有\(200-120=80\)(人),女生人数多于男生人数,选项\(A\)正确;
\(D\)层次的男生有\(80×15\%=12\)(人),女生有\(18\)人,男生人数少于女生,选项\(B\)错误;
\(B\)层次的男生有\(80×(1-10\%-15\%-20\%-25\%)=24\)(人),选项\(C\)正确;
\(A\)层次有\(80×10\%+18=26\)(人),\(E\)层次有\(80×15\%+6=18\)(人),\(E\)层次的人数最少,选项\(D\)错误.
故选:\(AC\). - 答案 (1) 这两张抽取方式的总体都是该校高三全体成绩,个体都是高三年级每个学生,
其中第一种抽取方式样本量为\(20\);第二种抽取方式的样本样本量为\(100\);
(2) 第一种采用的是简单随机抽样,第二种采用的是分层随机抽样;
(3)略
解析 (1)这两张抽取方式的总体都是该校高三全体成绩,个体都是高三年级每个学生,
其中第一种抽取方式的样本为所抽取的\(20\)名学生,样本量为\(20\);
第二种抽取方式的样本为所抽取的\(100\)名学生,样本量为\(100\);
(2)两种抽取方式中,第一种采用的是简单随机抽样,第二种采用的是分层随机抽样;
(3)第二种抽取方式的步骤如下:
第一步,分层,因为优秀学生共\(150\)名,良好生共\(600\)名,普通生共\(250\)名,
所以在抽取样本时,应该把高三全体学生分成三个层次;
第二步,确定各个层次抽取的人数,因为样本量与总体中的个体数之比为\(100:1000=1:10\),
所以在优秀生、良好生、普通生中抽取的人数依次为\(\dfrac{150}{10}\), \(\dfrac{600}{10}\), \(\dfrac{250}{10}\),即\(15\),\(60\),\(25\);
第三步,按层次分别抽取,在优秀生中用简单随机抽样抽取\(15\)名学生,
在良好生中用简单随机抽样抽取\(60\)名学生,
在普通生中用简单随机抽样抽取\(25\)名学生,考察他们的成绩.
分层练习
【A组---基础题】
1.某学校要了解高一、高二和高三这三个年级学生的身体素质是否有显著差异,计划从这三个年级中抽取部分学生进行调查,则最合理的抽样方法是( )
A.按学号随机抽样 \(\qquad \qquad \qquad \qquad \qquad\) B.运动场上随机抽样
C.按性别分层抽样 \(\qquad \qquad \qquad \qquad \qquad\) D.按年级分层抽样
2.某校为了了解高二学生的身高情况,打算在高二年级\(12\)个班中抽取\(3\)个班,再按每个班男女生比例抽取样本,正确的抽样方法是( )
A.简单随机抽样 \(\qquad \qquad \qquad \qquad \qquad\) B.先用分层抽样,再用随机数表法
C.分层抽样 \(\qquad \qquad \qquad \qquad \qquad \qquad\) D.先用抽签法,再用分层抽样
3.某中学高三年级有学生\(1200\)人,高二年级有学生\(900\)人,高一年级有学生\(1500\)人,现以年级为标准,用分层抽样的方法从这三个年级中抽取一个容量为\(108\)的样本进行某项研究,则应从高三年级学生中抽取的学生人数为( )
A.\(18\) \(\qquad \qquad \qquad \qquad\) B.\(36\) \(\qquad \qquad \qquad \qquad\) C.\(72\) \(\qquad \qquad \qquad \qquad\) D.\(144\)
4.某工厂生产\(A\)、\(B\)、\(C\)三种不同型号的产品,新产品数量之比依次为\(k:5:3\),现用分层抽样的方法抽出一个容量为\(120\)的样本,已知\(A\)种产品共抽取了\(24\)件,则\(C\)种型号产品抽取的件数为( )
A.\(24\) \(\qquad \qquad \qquad \qquad\) B.\(30\)\(\qquad \qquad \qquad \qquad\) C.\(36\) \(\qquad \qquad \qquad \qquad\) D.\(40\)
5.某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为\(120\)件、\(80\)件、\(60\)件.为了解它们的产品质量是否存在显著差异,用比例分配的分层随机抽样法抽取了一个样本量为\(n\)的样本进行调查,其中从丙车间的产品中抽取了\(3\)件,则下列结论不正确的是( )
A.\(n=13\) \(\qquad\) B.\(n=12\)\(\qquad\) C.从甲车间的产品中抽取了\(6\)件 \(\qquad\) D.从乙车间的产品中抽取了\(4\)件
6.(多选)关于简单随机抽样和分层抽样之间的关系,下列说法中正确的有( )
A.都是从总体中逐个抽取
B.抽样过程中每个个体被抽到的可能性相同
C.都是将整体分成几层,然后分层进行抽取
D.分层抽样是将总体分成几层,然后按各层个体数占总体数之比,在各层中可以用简单随机抽样抽取
7.(多选)某公司为检测某型号汽车的质量问题,需对三个批次生产的该型号汽车进行检测,三个批次产量分别为\(100000\)辆、\(150000\)辆和\(250000\)辆,公司质监部门计划从中抽取\(500\)辆进行检测,则下列说法正确的是( )
A.样本容量为\(500\)
B.采用简单随机抽样比分层随机抽样合适
C.应采用分层随机抽样,三个批次的汽车被抽到的概率不相等
D.应采用分层随机抽样,三个批次分别抽取\(100\)辆、\(150\)辆、\(250\)辆
8.从一个容量为\(m(m≥3,m∈N)\)的总体中抽取一个容量为\(3\)的样本,当选取简单随机抽样方法抽取样本时,总体中每个个体被抽中的可能性是\(\dfrac{1}{3}\),则选取分层随机抽样方法抽取样本时,总体中每个个体被抽中的可能性是\(\underline{\quad \quad}\).
9.某高中共有学生\(1000\)名,其中高一年级共有学生\(380\)人,高二年级男生有\(180\)人.如果在全校学生中抽取\(1\)名学生,抽到高二年级女生的概率为\(0.19\),现采用分层抽样(按年级分层)在全校抽取\(100\)人,则应在高三年级中抽取的人数等于\(\underline{\quad \quad}\).
10.某区域大型城市、中型城市、小型城市的数量之比为\(2: m: 1\),为了解该区域城市的空气质量情况,现用比例分配的分层抽样方法抽取一个容量为\(n\)的样本.在样本中,中型城市比大型城市多\(4\)个,比小型城市多\(8\)个,则\(n=\)\(\underline{\quad \quad}\).
11.在调查某个城市的家庭年平均收入时,能否只在该市的娱乐场所(如电影院、歌剧院、游乐场、健身馆等)进行随机抽样?原因是什么?能否只在该市的公共汽车站进行随机抽样?原因是什么?
12.数据\(x_1\),\(x_2\),⋯,\(x_m\)的平均数为\(\bar{x},\), 数据\(y_1\),\(y_2\),⋯,\(y_n\)的平均数为\(\bar{y}\),
证明: \(\dfrac{\sum_{i=1}^m x_i+\sum_{i=1}^n y_i}{m+n}=\dfrac{m}{m+n} \bar{x}+\dfrac{n}{m+n} \bar{y}\).
13.\(A\)中学高一年级的\(500\)名同学中有\(218\)名女生,在调查全年级同学的平均身高时,预备抽样调查\(50\)个同学、请你做以下工作,并回答以下问题.
(1)设计一个合理的分层抽样方案.
(2)你的设计中,第\(1\)和第\(2\)层分别是什么?
(3)分层抽样是否在得到全年级同学平均身高的估计时,还分别得到了男生和女生的平均身高的估计?
参考答案
-
答案 \(D\)
解析 某学校要了解高一、高二和高三这三个年级学生的身体素质是否有显著差异,计划从这三个年级中抽取部分学生进行调查,
\(\because\) 高一、高二和高三这三个年级学生的身体素质差异明显,
\(\therefore\)最合理的抽样方法是按年级分层抽样.
故选:\(D\). -
答案 \(D\)
解析 先在高二年级\(12\)个班中抽取\(3\)个班,宜用抽签法,再按每个班男女生比例抽取样本,适合使用分层抽样,以先用抽签法,再用分层抽样.故选:\(D\). -
答案 \(B\)
解析 高三年级学生所占的比例为\(\dfrac{1200}{1200+900+1500}=\dfrac{1}{3}\),
\(\therefore\)应从高三年级学生中抽取的人数为\(108 \times\dfrac{1}{3}=36\),
故选:\(B\). -
答案 \(C\)
解析 \(\because\)新产品数量之比依次为\(k:5:3\),
\(\therefore\)由 \(\dfrac{k}{k+3+5}=\dfrac{24}{120}\),解得\(k=2\),
则\(C\)种型号产品抽取的件数为\(120 \times\dfrac{3}{10}=36\),故选:\(C\) -
答案 \(B\)
解析 \(\because\)甲、乙、丙三个车间生产的产品件数分别是\(120\),\(80\),\(60\),
\(\therefore\)甲、乙、丙三个车间生产的产品数量的比依次为\(6:4:3\),
丙车间生产产品所占的比例\(\dfrac{3}{13}\),
因为样本中丙车间生产产品有\(3\)件,占总产品的\(\dfrac{3}{13}\),
所以样本容量\(n=3 \div\dfrac{3}{13}=13\),故\(A\)正确,\(B\)错误,
从甲车间抽取了\(6\)件,从乙车间抽取了\(4\)件,故\(C\),\(D\)正确,
故选:\(B\). -
答案 \(BD\)
解析 根据简单随机抽样和分层抽样的定义可得\(B\),\(D\)选项正确;
简单随机抽样不需要分层,分层抽样将整体分成几层,然后分层进行抽取,
\(\therefore A\),\(C\)选项错误.
故选:\(BD\). -
答案 \(AD\)
解析 因为抽取\(500\)辆进行检测,所以样本容量为\(500\),故选项\(A\)正确;
因为汽车分为三个型号,故应该采用分层抽样比较合适,故选项\(B\)错误;
由分层抽样的定义可知,三个批次的汽车被抽到的概率都是相同的,故选项\(C\)错误;
设三种型号的车依次抽取\(x\),\(y\),\(z\)辆,
则有\(\left\{\begin{array}{l} \dfrac{x}{100000}=\dfrac{y}{150000}=\dfrac{z}{250000} \\ x+y+z=500 \end{array}\right.\),
解得\(x=100\),\(y=150\),\(z=250\),
所以三个批次分别抽取\(100\)辆、\(150\)辆、\(250\)辆,故选项\(D\)正确.
故选:\(AD\). -
答案 \(\dfrac{1}{3}\)
解析 \(\because\)随机抽样每个个体被抽到的概率相等,
\(\therefore\)选取分层抽样抽取样本时总体中每个个体被抽中的概率仍为\(\dfrac{1}{3}\). -
答案 \(25\)
解析 \(\because\)高中共有学生\(1000\)名,在全校学生中抽取\(1\)名学生,抽到高二年级女生的概率为\(0.19\),
\(\therefore\)高二女生共有\(1000×0.19=190\)人,则高二共有学生\(180+190=370\)人,
则高三人数为\(1000-370-380=250\)人,
则采用分层抽样(按年级分层)在全校抽取\(100\)人,
则应在高三年级中抽取的人数等于\(\dfrac{250}{1000} \times 100=25\)人,
故答案为:\(25\). -
答案 \(24\)
解析 设抽取的大中小型城市的数量分别为\(a\),\(b\),\(c\),
\(\because\)在样本中,中型城市比大型城市多\(4\)个,比小型城市多\(8\)个,
则\(b=a+4=c+8\),
又\(\because\)大型城市、中型城市、小型城市的数量之比为\(2: m: 1\),
则\(a=2c\),解得\(a=8\),\(b=12\),\(c=4\),
\(\therefore n=a+b+c=24\). -
解析 在调查某个城市的家庭年平均收入时,不能只在该市的娱乐场所(如电影院、歌剧院、游乐场、健身馆等)进行随机抽样,
因为他们不能代表全市的居民的真实情况.
也不能只在该市的公共汽车站进行随机抽样,因为在该市的公共汽车站的人不能代表全部该市全部人员.
由于要研究的对象是由具有明显不同特征的若干部分构成,
故应采用分层抽样的方法. -
证明 \(\dfrac{\sum_{i=1}^m x_i+\sum_{i=1}^n y_i}{m+n}=\dfrac{\sum_{i=1}^m x_i}{m+n}+\dfrac{\sum_{i=1}^n y_i}{m+n}\)\(=\dfrac{m \bar{x}}{m+n}+\dfrac{n \bar{y}}{m+n}=\dfrac{m}{m+n} \bar{x}+\dfrac{n}{m+n} \bar{y}\).
-
答案 (1) 略;(2) 第一层是样本中:女生\(22\)人的身高数据,第二层为男生\(28\)人的身高数据;(3)是
解析 (1)因为男生、女生身高有差异性,故按男女生在总人数中所占比例采取分层抽样.
故女生抽取人数为\(50 \times\dfrac{218}{500} \approx 22\)人;男生抽取人数为\(50 \times\dfrac{282}{500} \approx 28\)人,然后测量这\(50\)人的身高数据.从而得到\(50\)人的身高数据样本.
(2)第一层是样本中:女生\(22\)人的身高数据,第二层为男生\(28\)人的身高数据.
(3)是的,可以用男、女生身高数据之和除以各自样本中的人数,得到男、女生平均身高的估计值.
【B组---提高题】
1.某单位有老年人\(27\)人,中年人\(55\)人,青年人\(81\)人.为了调查他们的身体状况,需从他们中抽取一个容量为\(36\)的样本,最适合抽取样本的方法是( )
A.简单随机抽样
B.系统抽样
C.先从中年人中剔除一人,然后分层抽样
D.先从老年人中剔除一人,然后分层抽样
2.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组.在参加活动的职工中,青年人占\(42.5\%\),中年人占\(47.5\%\),老年人占\(10\%\).登山组的职工占参加活动总人数的\(\dfrac{1}{4}\),且该组中青年人占\(50\%\),中年人占\(40 \%\),老年人占\(10\%\).为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层随机抽样的方法从参加活动的全体职工中抽取一个容量为\(200\)的样本.
(1)试求游泳组中,青年人、中年人、老年人分别所占的比例;
(2)试求游泳组中,青年人、中年人、老年人分别应抽取的人数;
(3)如果游泳组中抽取的样本经调查得知青年人的平均满意度为\(75\%\),中年人的平均满意度为\(80\%\),老年人的平均满意度为\(90\%\),试估计游泳组中的职工的平均满意度.
参考答案
- 答案 \(C\)
解析 由于调查目的是单位人员的身体状况,明显比例以人员年纪进行分层抽样.
若直接计算抽取老年人\(36 \times\dfrac{27}{27+55+81} \approx 5.96\),结果不是整数,
故这样直接分层抽样不可取,
通过观察数值,可先从中年人中剔除一人,然后再分层,
此时总体人数是\(27+54+81=162\),每个个体被抽到的概率等于 \(\dfrac{36}{162}=\dfrac{2}{9}\),
所以老年人抽取\(27 \times\dfrac{2}{9}=6\)人,中年人\(54 \times\dfrac{2}{9}=12\)人,青年人 \(81 \times\dfrac{2}{9}=18\);
故选:\(C\). - 答案 (1) 青年人、中年人、老年人各占比例分别为\(40\%\)、\(50\%\)、\(10\%\);
(2) 青年人、中年人、老年人分别抽取的人数为:\(60\),\(75\),\(15\)人 ;
(3) \(79\%\)
解析 (1)设登山组人数为\(x\)人,游泳组中,青年人、中年人、老年人各占比例分别为\(a\)、\(b\)、\(c\),
则有\(\dfrac{x \cdot 40 \%+3 x b}{4 x}=47.5 \%\), \(\dfrac{x \cdot 10 \%+3 x c}{4 x}=10 \%\),
解得\(b=50\%\),\(c=10\%\).
故\(a=100\%-50\%-10\%=40\%\),
即游泳组中,青年人、中年人、老年人各占比例分别为\(40\%\)、\(50\%\)、\(10\%\).
(2)游泳组中,抽取的青年人数为\(200 \times\dfrac{3}{4} \times 40 \%=60\)(人);
抽取的中年人数为\(200 \times\dfrac{3}{4} \times 50 \%=75\)(人);
抽取的老年人数为\(200 \times\dfrac{3}{4} \times 10 \%=15\)(人).
(3)\(\because\)游泳组中,青年人、中年人、老年人分别抽取的人数为:\(60\),\(75\),\(15\)人;
\(\therefore\)职工的平均满意度的估计值为: \(\dfrac{60 \times 75 \%+75 \times 80 \%+15 \times 90 \%}{60+75+15} \times 100 \%=79 \%\),
\(\therefore\)估计游泳组中的职工的平均满意度为\(79\%\).


