8.6.2 直线与平面垂直
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019)]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第二册同步巩固,难度3颗星!
基础知识
定义
若一条直线垂直于平面内的任意一条直线,则这条直线垂直于平面.
符号表述:若任意\(a\subset \alpha\)都有\(l\perp a\),则\(l\perp \alpha\) .
判定定理
如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.
符号表述: \(\left.\begin{array}{c}
a, b \subset \alpha \\
a \cap b=O \\
l \perp a \\
l \perp b
\end{array}\right\} \Rightarrow l \perp \alpha \quad \text { (线线垂直 } \Rightarrow \text { 线面垂直) }\)
解释
(1) 定理中两条直线必须是相交的;
判断
① 如果一条直线与一个平面内的两条平行直线垂直,那么该直线与此平面垂直 (×)
② 如果一条直线与一个平面内的无数条直线垂直,那么该直线与此平面垂直 (×)
(2) 简证:(由向量的基本定理和线面垂直的定义可证)
设直线\(l\),\(a\),\(b\)对应的向量是\(\vec{l}\),\(\vec{a}\),\(\vec{b}\),则\(\vec{l}\cdot \vec{a}=0\),\(\vec{l}\cdot \vec{b}=0\),
由于直线\(a\),\(b\)相交,若平面 \(\alpha\)内任意直线\(c\)所对的向量\(\vec{c}=λ\vec{a}+μ\vec{b}\),
则\(\vec{l}\cdot \vec{c}=\vec{l}\cdot (λ\vec{a}+μ\vec{b} )=λ\vec{l}\cdot \vec{a}+μ\vec{l}\cdot \vec{b}=0\),则\(\vec{l}\perp\vec{c}\),
即直线\(l\)与平面\(\alpha\)内任意直线垂直,即\(l\perp \alpha\).
(3) 该定理说明线面垂直可转化为线线垂直.
性质定理
垂直同一平面的两直线平行
符号表述 :\(a\perp \alpha\),\(b\perp \alpha ⇒ a ||b\).
证明 假设\(b\)与\(a\)不平行,且\(b \cap \alpha=0\),显然点\(O\)不在直线\(a\)上,
所以点\(O\)与直线\(a\)可确定一个平面, 在该平面内过点\(O\)作直线\(b'||a\),
则直线\(b\)与\(b'\)是相交于点\(O\)的两条不同直线,所以直线\(b\)与\(b'\)可确定平面\(\beta\),
设\(\alpha \cap \beta=c\),则\(O\in c\).
因为\(a\perp \alpha\),\(b\perp \alpha\) ,所以\(a\perp c\),\(b\perp c\).
又因为\(b'||a\),所以\(b'\perp c\).
这样在平面\(\beta\)内,经过直线 \(c\)上同一点 \(O\)就有两条直线\(b\),\(b'\)与\(c\)垂直,显然不可能.
因此\(b||a\).
(证明使用了反证法)

证明线面垂直的方法
① 定义法(反证)
② 判定定理(常用)
③ \(\left.\begin{array}{l}
a / / b \\
a \perp \alpha
\end{array}\right\} \Rightarrow b \perp \alpha\)
④ \(\left.\begin{array}{c}
\alpha / / \beta \\
a \perp \alpha
\end{array}\right\} \Rightarrow a \perp \beta\)
线面所成的角
(1) 定义
如下图,平面的一条斜线(直线\(l\))和它在平面上的射影(\(AO\))所成的角,叫做这条直线和这个平面所成的角.

一条直线垂直平面,则\(\theta =90^{\circ}\);一条直线和平面平行或在平面内,则\(\theta =0^{\circ}\).
(2) 范围
直线和平面所成的角\(\theta\) 的取值范围是\(0^{\circ}≤\theta ≤90^{\circ}\).
【例】 在棱长为\(1\)的正方体\(ABCD-A'B'C'D'\)中,求直线\(C'D\)与平面\(A'B'C'D'\)所成的角,直线\(B'D\)与平面\(A'D'DA\)所成的角的余弦值.
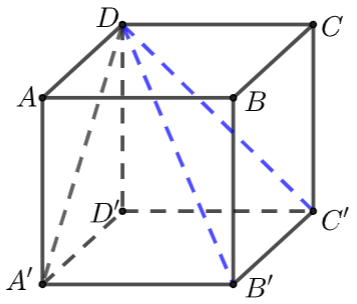
解 \(\because D'D\perp\)平面\(A'B'C'D'\),\(\therefore\)直线\(C'D\)与平面\(A'B'C'D'\)所成的角为\(∠DC' D'=45^{\circ}\);
\(\because A'B'\perp\)平面\(A'D'DA\),\(\therefore\)直线\(B'D\)与平面\(A'D'DA\)所成的角为\(∠A'DB'\),其余弦值 \(\cos \angle A^{\prime} D B^{\prime}=\dfrac{A^{\prime} D}{B^{\prime} D}=\dfrac{\sqrt{2}}{\sqrt{3}}=\dfrac{\sqrt{6}}{3}\).
距离
(1) 过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫作这个点到该平面的垂线段,垂线段的长度叫作这个点到该平面的距离;
(2) 一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫作这条直线到这个平面的距离;
(3) 两个平面平行时,其中一个平面内任意一点到另一个平面的距离,叫作两个平行平面间的距离.
基本方法
【题型1】 线面垂直的判定与性质
【典题1】 如图所示,\(Rt△ABC\)所在平面外一点\(S\),且\(SA=SB=SC\),点\(D\)为斜边\(AC\)的中点.

(1)求证:\(SD\perp\)平面\(ABC\);
(2)若\(AB=BC\),求证:\(BD\perp\) 平面\(SAC\).
证明 (1)\(\because SA=SC\),\(D\)为\(AC\)的中点,\(\therefore SD\perp AC\).
在\(Rt△ABC\)中,\(AD=DC=BD\),
又\(SA=SB\),\(\therefore △ADS≌△BDS\).
\(\therefore SD\perp BD\).
又\(AC\cap BD=D\),\(\therefore SD\perp\)平面\(ABC\).
(2)\(\because BA=BC\),\(D\)为\(AC\)的中点,\(\therefore BD\perp AC\).
又由(1)知\(SD\perp BD\),
于是\(BD\)垂直于平面\(SAC\)内的两条相交直线.
\(\therefore BD\perp\)平面\(SAC\).
点拨 线面垂直的判定定理告诉我们要证明\(l\perp \alpha\)只需要在面\(\alpha\)内找到两条相交直线均与直线\(l\)垂直便可.把线面垂直转化为线线垂直,而线线垂直常用到平几知识:等腰三角形三线合一、勾股定理逆定理、全等三角形的性质、相似三角形性质、菱形对角线垂直等.
【典题2】 如图,四边形\(ABCD\)为矩形,\(AD\perp\)平面\(ABE\),\(AE=EB=BC=2\),\(F\)为\(CE\)上的点,且\(BF\perp\)平面\(ACE\),\(BD\cap AC=G\).
(1)求证:\(AE\perp\)平面\(BCE\);
(2)求证:\(AE∥\)平面\(BFD\);
(3)求四面体\(BCDF\)的体积.

解析 (1)证明:\(\because AD\perp\)平面\(ABE\),\(AD∥BC\),\(\therefore BC\perp\)平面\(ABE\),
\(\because AE\subset\)平面\(ABE\),\(\therefore AE\perp BC\).
又\(\because BF\perp\)平面\(ACE\),\(AE\subset\)平面\(ACE\),\(\therefore BF\perp AE\),
\(\because BC\cap BF=B\),\(\therefore AE\perp\) 平面\(BCE\)
(2)证明:连接\(GF\),\(\because BF\perp\)平面\(ACE\),\(\therefore BF\perp CE\)
\(\because BE=BC\),\(\therefore F\)为\(EC\)的中点,
\(\because G\)是\(AC\)的中点,\(\therefore FG∥AE\),
\(\because FG\subset\)平面\(BFD\),\(AE\not \subset\)平面\(BFD\)
\(\therefore AE∥\)平面\(BFD\);
(3)解:取\(AB\)中点\(O\),连接\(OE\).
因为\(AE=EB\),所以\(OE\perp AB\).
因为\(AD\perp\) 面\(ABE\),\(OE\subset\)面\(ABE\),所以\(OE\perp AD\),
所以\(OE\perp\)面\(ADC\),
因为\(BF\perp\)面\(ACE\),\(AE\subset\)面\(ACE\),所以\(BF\perp AE\).
因为\(CB\perp\)面\(ABE\),\(AE\subset\) 面\(ABE\),所以\(AE\perp BC\).
又\(BF\cap BC=B\),所以\(AE\perp\)平面\(BCE\),
又\(BE\subset\)面\(BCE\),所以\(AE\perp EB\).
\(\because AE=EB=2\),\(\therefore AB=2\sqrt{2}\),\(\therefore OE=\sqrt{2}\),
\(\therefore F\)到平面\(BCD\)的距离为\(\dfrac{\sqrt{2}}{2}\),
\(\therefore\)四面体\(BCDF\)的体积\(\dfrac{1}{3} \times \dfrac{1}{2} \times 2 \times 2 \sqrt{2} \times \dfrac{\sqrt{2}}{2}=\dfrac{2}{3}\).

点拨
① 求三棱锥的体积\(V=\dfrac{1}{3} h S\),关键是确定其高\(h\)和底面积\(S\),本题是以点\(F\)到平面\(BCD\)的距离位高\(h\),底面积\(S=S_{\triangle B C D}\);以点\(D\)到平面\(BCF\)的距离为高\(h\),底面积\(S=S_{\triangle B C F}\)也可以;
② 而三棱锥的高即是点到平面的距离,本题中证明了\(OE\perp\)平面\(BCD\),即\(OE\)为点\(E\)到平面\(BCD\)的距离.以点\(D\)到平面\(BCF\)的距离为高\(h\)又如何求解呢?
【巩固练习】
1.(多选)如图,在以下四个正方体中,直线\(AB\)与平面\(CDE\)垂直的是( )
A.  \(\qquad\) B.
\(\qquad\) B. \(\qquad\)C.
\(\qquad\)C. \(\qquad\)D.
\(\qquad\)D.
2.在长方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(AB=\sqrt{2} AD\),\(E\)为棱\(CD\)的中点,则( )
A.\(A_1 E\perp DD_1\) \(\qquad \qquad\) B.\(A_1 E\perp DB\) \(\qquad \qquad\) C.\(A_1 E\perp D_1 C_1\) \(\qquad \qquad\) D.\(A_1 E\perp DB_1\)

3.如图,在三棱锥\(P-ABC\)中,\(PA\perp\)平面\(ABC\),\(AB\perp BC\),\(PA=AB\),\(D\)为\(PB\)的中点,则下列判断不正确的是( )

A.\(BC\perp\)平面\(PAB\) \(\qquad \qquad\) B.\(AD\perp PC\) \(\qquad \qquad\)C.\(AD\perp\)平面\(PBC\) \(\qquad \qquad\) D.\(PB\perp\)平面\(ADC\)
4.如图,在三棱柱\(ABC-A_1 B_1 C_1\)中,底面是以\(∠ABC\)为直角的等腰直角三角形,侧棱\(AA_1\perp\)底面\(ABC\),\(AC=2a\),\(BB_1=3a\),\(D\)是\(A_1 C_1\)的中点,点\(F\)在线段\(AA_1\)上,当\(AF=\)\(\underline{\quad \quad}\)时,\(CF\perp\)平面\(B_1 DF\).

5.如图所示,在四棱锥\(P-ABCD\)中,\(AB\perp\)平面\(PAD\),\(AB∥CD\),\(PD=AD\),\(E\)是\(PB\)中点,\(F\)是\(DC\)上的点,且\(DF=\dfrac{1}{2}AB\),\(PH\)为\(△PAD\)中\(AD\)边上的高.
(1)证明:\(PH\perp\)平面\(ABCD\);
(2)若\(PH=1\),\(AD=2\),\(FC=1\),求三棱锥\(E-BCF\)的体积;
(3)证明:\(EF\perp\)平面\(PAB\).

参考答案
-
答案 \(BD\)
解析 对于\(A\), \(\because \angle B A D=\dfrac{\pi}{4}\),\(CE∥AD\),\(\therefore AB\)与\(CE\)不垂直,
\(\because CE\subset\)平面\(CDE\),\(\therefore\)直线\(AB\)与平面\(CDE\)不垂直,故\(A\)错误;
对于\(B\),\(\because CE\perp AB\),\(DE\perp AB\),\(CE\cap DE=E\),
\(\therefore\)直线\(AB\perp\)平面\(CDE\),故\(B\)正确;
对于\(C\),\(AB\)与\(CE\)所成角为\(\dfrac{\pi}{3}\),\(\therefore\)直线\(AB\)与平面\(CDE\)不垂直,故\(C\)错误;
对于\(D\),如图,\(\because DE\perp BF\),\(DE\perp AF\),\(BF\cap AF=F\),
\(\therefore DE\perp\)平面\(ABF\),

\(\because AB\subset\)平面\(ABF\),\(\therefore DE\perp AB\),同理得\(CE\perp AB\),
\(\because DE\cap CE=E\),\(\therefore AB\perp\)平面\(CDE\),故\(D\)正确.
故选:\(BD\). -
答案 \(B\)
解析 连结\(AE\),\(BD\),因为\(AB=\sqrt{2} AD\),所以 \(\dfrac{A B}{A D}=\dfrac{A D}{D E}=\sqrt{2}\),
所以\(△ABD∽△DAE\),所以\(∠DAE=∠ABD\),
所以\(\angle E A B+\angle A B D=90^{\circ}\),即\(AE\perp BD\),
所以\(BD\perp\)平面\(A_1 AE\),所以\(A_1 E\perp DB\).
故选:\(B\). -
答案 \(D\)
解析 \(\because PA\perp\)平面\(ABC\),\(BC\subset\)平面\(ABC\),
\(\therefore PA\perp BC\),又\(AB\perp BC\),\(AB\),\(PA\subset\) 平面\(PAB\)且\(AB\cap PA=A\),
\(\therefore BC\perp\)平面 \(PAB\),故\(A\)正确,
由\(BC\perp\)平面\(PAB\),\(AD\subset\)平面\(PAB\),得\(BC\perp AD\),
又\(PA=AB\),\(D\)是\(PB\) 的中点,\(\therefore AD\perp PB\),
又\(PB\cap BC=B\),\(PB\),\(BC\subset\)平面 \(PBC\),
\(\therefore AD\perp\)平面\(PBC\),\(PC\subset\)平面\(PBC\),
\(\therefore AD\perp PC\),故\(B\),\(C\)正确,
由\(BC\perp\)平面\(PAB\),\(PB\subset\)平面\(PAB\),得\(BC\perp PB\),
因为\(BC\)与\(CD\)不平行,因此\(PB\)与\(CD\)不垂直,
从而\(PB\)不与平面\(ADC\)垂直,\(D\)错误,
故选:\(D\). -
答案 \(a\)或\(2a\)
解析 由已知得\(A_1 B_1=B_1 C_1\),又\(D\)是\(A_1 C_1\)的中点,
所以\(B_1 D\perp A_1 C_1\),又侧棱\(AA_1\perp\)底面\(ABC\),
可得侧棱\(AA_1\perp\)平面\(A_1 B_1 C_1\),
又\(B_1 D\subset\)平面\(A_1 B_1 C_1\),所以\(AA_1\perp B_1 D\),
因为\(AA_1\cap A_1 C_1=A_1\),所以\(B_1 D\perp\)平面\(AA_1 C_1 C\),
又\(CF\subset\)平面\(AA_1 C_1 C\),所以\(B_1D\perp CF\),
故若\(CF\perp\)平面\(B_1 DF\),则必有\(CF\perp DF\).
设\(AF=x(0<x<3a)\),
则 \(C F^2=x^2+4 a^2\),\(D F^2=a^2+(3 a-x)^2\),
又\(C D^2=a^2+9 a^2=10 a^2\),
所以\(10 a^2=x^2+4 a^2+a^2+(3 a-x)^2\),解得\(x=a\)或\(2a\).
故答案为:\(a\)或\(2a\). -
答案 (1) 略;(2)\(\dfrac{1}{6}\) ;(3) 略
解析 (1)由\(AB\perp\) 平面\(PAD\),\(PH\subseteq\)平面\(PAD\)可得:\(AB\perp PH\),
又\(PH\)为\(△PAD\)中边\(AD\)的高,即\(PH\perp AD\),
而\(AB\cap AD=A\),\(AB\),\(AD\subseteq\)平面\(ABCD\),
故由线面垂直的判定定理可得:\(PH\perp\)平面\(ABCD\).
(2)由\(E\)为\(PB\)中点可得:三棱锥\(E-BCF\)的体积为 \(V_{E-B C F}=\dfrac{1}{2} V_{P-B C F}\),
而又由(1)可得: \(V_{P-B C F}=\dfrac{1}{3} P H \cdot S_{\triangle B C F}=\dfrac{1}{3} P H \cdot \dfrac{1}{2} A D \cdot F C=\dfrac{1}{6} \times 1 \times 2 \times 1=\dfrac{1}{3}\),
故所求三棱锥\(E-BCF\)的体积为\(\dfrac{1}{6}\).
(3)取\(AB\)的中点\(G\),连接\(GE\),\(GF\),\(PF\),
由题意知:\(AG=\dfrac{1}{2}AB=DF\),
又\(AG∥DF\),故四边形\(ADFG\)为平行四边形,
于是得\(AD∥FG\),而\(EG\)为\(△ABP\)的中位线,故\(EG∥AP\),
又\(AD\cap AP=A\),\(EG\cap FG=G\),
可得平面\(EFG∥\)平面\(ADP\),而\(AB\perp\) 平面\(ADP\),
于是有\(AB\perp\)平面\(EFG\),
又\(EF\subseteq\)平面\(EFG\),因此,\(EF\perp AB\),
在\(Rt△PDF\)中,\(P F=\sqrt{P D^2+D F^2}\),
在\(Rt△BFG\)中, \(B F=\sqrt{F G^2+B G^2}\),
而\(PD=AD=FG\),\(BG=AG=DF\),故\(BF=PF\),
在等腰三角形\(BPF\)中,\(E\)为底边\(BP\)的中点,于是有\(EF\perp BP\),
又\(AB\cap BP=B\),\(AB\),\(BP\subseteq\)平面\(PAB\),
故由线面垂直的判定定理可得:\(EF\perp\)平面\(PAB\).

【题型2】 线面所成的角
【典题1】 如图所示,\(Rt△BMC\)中,斜边\(BM=5\),它在平面\(ABC\)上的射影\(AB\)长为\(4\),\(∠MBC=60^{\circ}\),求\(MC\)与平面\(CAB\)所成角的正弦值.

解析 由题意知,\(A\)是\(M\)在平面\(ABC\)内的射影,
\(\therefore MA\perp\)平面\(ABC\).\(\therefore MC\)在平面\(CAB\)内的射影为\(AC\).
\(\therefore ∠MCA\)即为直线\(MC\)与平面\(CAB\)所成的角.
又\(\because\)在\(Rt△MBC\)中,\(BM=5\),\(∠MBC=60^{\circ}\),
\(\therefore M C=B M \cdot \sin \angle M B C=5 \sin 60^{\circ}=5 \times \dfrac{\sqrt{3}}{2}=\dfrac{5}{2} \sqrt{3}\).
在\(Rt△MAB\)中, \(M A=\sqrt{M B^2-B A^2}=\sqrt{5^2-4^2}=3\).
在\(Rt△MAC\)中, \(\sin \angle M C A=\dfrac{M A}{M C}=\dfrac{3}{\dfrac{5}{2} \sqrt{3}}=\dfrac{2}{5} \sqrt{3}\).
即\(MC\)与平面\(CAB\)所成角的正弦值为 \(\dfrac{2}{5} \sqrt{3}\).
点拨 求线\(l\)与面\(\alpha\) 所成的角\(\theta\) ,一般的思路
如下图中,求直线\(AP\)与平面\(\alpha\)所成的角,具体步骤如下:

(1) 过点\(P\)作平面\(\alpha\)的高\(PO\),垂足为\(O\),则\(AO\)是线段\(AP\)在平面 \(\alpha\)上的投影;
(2) 找到所求角\(\theta\);
(3) 求解三角形\(APO\)进而求角\(\theta\).
(此方法难点证明到\(PO\perp\)平面\(\alpha\) )
【巩固练习】
1.如图所示,在正三棱柱\(ABC-A_1 B_1 C_1\)中,\(AA_1=AB=2\),则\(A_1 C\)与侧面\(BCC_1 B_1\)所成角的正弦值为( )

A. \(\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{\sqrt{6}}{4}\) \(\qquad \qquad \qquad \qquad\) C.\(\dfrac{\sqrt{10}}{4}\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{\sqrt{15}}{5}\)
2.在三棱锥\(A-BCD\)中,\(AB\perp\) 平面\(BCD\),\(CD\perp BC\),且\(BC=\sqrt{3} AB\),则直线\(AB\)与平面\(ACD\)所成的角为( )
A.\(\dfrac{\pi}{6}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{\pi}{4}\) \(\qquad \qquad \qquad \qquad\) C.\(\dfrac{\pi}{3}\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{\pi}{2}\)
3.在长方体\(ABCD-A_1 B_1 C_1 D_1\)中,已知\(B_1 D\)与平面\(ABCD\)和平面\(AA_1 B_1 B\)所成的角均为\(30^{\circ}\),则 ( )
A.\(AB=2AD\) \(\qquad \qquad \qquad \qquad\) B.\(AB\)与平面\(AB_1 C_1 D\)所成的角为\(30^{\circ}\)
C.\(AC=CB_1\) \(\qquad \qquad \qquad \qquad\) D.\(B_1 D\)与平面\(BB_1 C_1 C\)所成的角为\(45^{\circ}\)
4.如图,在正三棱柱\(ABC-A_1 B_1 C_1\)中,底面边长为\(a\),侧棱长为\(b\),且\(a≥b\),点\(D\)是\(BC_1\)的中点,则直线\(AD\)与侧面\(ABB_1 A_1\)所成角的正切值的最小值是( )

A.\(\dfrac{\sqrt{130}}{13}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{\sqrt{6}}{3}\) \(\qquad \qquad \qquad \qquad\) C.\(\dfrac{\sqrt{3}}{3}\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{\sqrt{39}}{13}\)
参考答案
-
答案 \(B\)
解析 如图,取\(B_1 C_1\)的中点\(E\),连接\(A_1 E\),\(CE\),
则根据题意易得\(A_1 E\perp\)侧面\(BCC_1 B_1\),\(\therefore ∠A_1 CE\)即为所求,
又根据题意易知\(A_1 E=\sqrt{3}\),\(A_1 C=2\sqrt{2}\),
\(\therefore \sin \angle A_1 C E=\dfrac{A_1 E}{A_1 C}=\dfrac{\sqrt{3}}{2 \sqrt{2}}=\dfrac{\sqrt{6}}{4},\),故选:\(B\).

-
答案 \(C\)
解析 因为\(AB\perp\)平面\(BCD\),所以\(AB\perp CD\),
又\(CD\perp BC\),\(AB\cap BC=B\),\(AB\subset\)平面\(ABC\),\(BC\subset\) 平面\(ABC\),
所以\(CD\perp\)平面\(ABC\),
又\(CD\subset\)平面\(ACD\),所以面\(ACD\perp\)平面\(ABC\),
作\(BE\perp AC\),垂足为\(E\).则\(BE\perp\)平面\(ACD\),

所以\(∠BAE\)是直线\(AB\)与平面\(ACD\)所成的角,
在直角三角形\(ABC\)中,因为\(\tan \angle B A C=\dfrac{B C}{A B}=\sqrt{3}\),
所以\(∠BAC=\dfrac{\pi}{3}\),
故选:\(C\). -
答案 \(D\)
解析 如图所示,连接\(AB_1\),\(BD\),不妨令\(AA_1=1\),

在长方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(AD\perp\)面\(AA_1 B_1 B\), 面\(ABCD\),
所以\(∠B_1 DB\)和\(∠DB_1 A\)分别为\(B_1 D\)与平面\(ABCD\)和平面\(AA_1 B_1 B\)所成的角,
即\(∠B_1 DB=∠DB_1 A=30^{\circ}\),
所以在\(RtΔBDB_1\)中,\(BB_1=AA_1=1\),\(BD=\sqrt{3}\),\(B_1 D=2\),
在\(RtΔADB_1\)中,\(DB_1=2\),\(AD=1\),\(AB_1=\sqrt{3}\),
所以\(AB=\sqrt{2}\),\(CB_1=\sqrt{2}\),\(AC=\sqrt{3}\),
故选项\(A\),\(C\)错误,
由图易知,\(AB\)在平面\(AB_1 C_1 D\)上的射影在\(AB_1\)上,
所以\(∠B_1 AB\)为\(AB\)与平面\(AB_1 C_1 D\)所成的角,
在\(Rt△ABB_1\)中, \(\sin \angle B_1 A B=\dfrac{B B_1}{A B_1}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\),故选项\(B\)错误,
如图,连接\(B_1 C\),

则\(B_1 D\)在平面\(BB_1 C_1 C\)上的射影为\(B_1 C\),
所以\(∠DB_1 C\)为\(B_1 D\)与平面\(BB_1 C_1 C\)所成的角,
在\(Rt △DB_1 C\)中,\(B_1 C=\sqrt{2}=DC\),
所以\(∠DB_1 C=45^{\circ}\),所以选项\(D\)正确,
故选:\(D\). -
答案 \(D\)
解析 取\(A_1 B_1\)的中点\(E\),连接\(BE\)、\(C_1 E\),则\(C_1 E\perp A_1 B_1\),
由正三棱柱的性质可知,面\(A_1 B_1 C_1\perp\)面\(ABB_1 A_1\),
而面\(A_1 B_1 C_1\cap\)面\(ABB_1 A_1=A_1 B_1\),\(\therefore C_1 E\perp\)面\(ABB_1 A_1\).

取\(BE\)的中点\(F\),连接\(AF\)、\(DF\),
\(\because D\)为\(CC_1\)的中点,\(\therefore DF∥C_1 E\),\(\therefore DF\perp\)面\(ABB_1 A_1\),
即点\(D\)在面\(ABB_1 A_1\)上的投影为点\(F\),
\(\therefore ∠DAF\)即为直线\(AD\)与侧面\(ABB_1 A_1\)所成角.
在\(Rt△AFD\)中, \(D F=\dfrac{1}{2} C_1 E=\dfrac{\sqrt{3}}{4} a\), \(A F=\sqrt{\left(\dfrac{3}{4} a\right)^2+\left(\dfrac{1}{2} b\right)^2}=\dfrac{\sqrt{9 a^2+4 b^2}}{4}\),
\(\therefore \tan \angle D A F=\dfrac{D F}{A F}=\dfrac{\sqrt{3} a}{\sqrt{9 a^2+4 b^2}}=\sqrt{\dfrac{1}{3+\dfrac{4 b^2}{3 a^2}}} \geq \sqrt{\dfrac{1}{3+\dfrac{4}{3}}}=\dfrac{\sqrt{39}}{13}\),
当且仅当\(a=b\)时,等号成立.
\(\therefore\)直线\(AD\)与侧面\(ABB_1 A_1\)所成角的正切值的最小值为\(\dfrac{\sqrt{39}}{13}\).故选:\(D\).
分层练习
【A组---基础题】
1.正方体\(ABCD-A_1 B_1 C_1 D_1\)中,为的中点,则直线\(CE\)垂直于( )

A.直线\(AC\) \(\qquad \qquad\) B.直线\(B_1 D_1\) \(\qquad \qquad\) C.直线\(A_1 D_1\) \(\qquad \qquad\) D.直线\(A_1 A\)
2.如图:\(PA\perp ⊙O\)所在的平面,\(AB\)是\(⊙O\)的直径,\(C\)是\(⊙O\)上的一点,\(AE\perp PC\),\(AF\perp PB\),给出下列结论①\(AE\perp BC\),②\(AE\perp PB\),③\(AF\perp BC\),④\(AE\perp\)平面\(PBC\),其中正确命题的序号是( )

A.①② \(\qquad \qquad \qquad \qquad\) B.①③ \(\qquad \qquad \qquad \qquad\) C.①②④ \(\qquad \qquad \qquad \qquad\) D.①③④
3.在长方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(AB=AA_1=1\),\(AD=2\),则直线\(A_1C\)与平面\(ABCD\)所成角的正弦为( )
A. \(\dfrac{\sqrt{6}}{6}\) \(\qquad \qquad \qquad \qquad\) B. \(\dfrac{\sqrt{5}}{5}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{\sqrt{3}}{3}\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{\sqrt{6}}{3}\)
4.已知菱形\(ABCD\)中,\(∠BAD=60^{\circ}\),\(AC\)与\(BD\)相交于点\(E\),将\(△ABD\)沿\(BD\)折起,使顶点\(A\)至点\(M\),在折起的过程中,对于下面两个命题:
①存在一个位置,使\(△CDM\)为等边三角形;②\(DM\)与\(BC\)不可能垂直,成立的是( )

A.①为假命题,②为真命题 \(\qquad\) B.①为真命题,②为假命题 \(\qquad\) C.①②均为真命题 \(\qquad\) D.①②均为假命题
5.在长方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(AA_1=AD=2AB=2\),\(AB\perp AD\),且\(P\)为\(CC_1\)中点,\(Q\)为\(AA_1\)上一动点,则( )
A.\(|PQ|\in [\sqrt{5},\sqrt{6}]\) \(\qquad \qquad \qquad \qquad \qquad\) B.三棱锥\(B-QPB_1\)的体积为 \(\dfrac{2}{3}\)
C.存在点\(Q\)使得\(BD_1\)与平面\(QPB_1\)垂直 \(\qquad\) D.存在点\(Q\)使得\(AC_1\)与平面\(QPB_1\)垂直
6.如图,已知平行四边形\(ABCD\)中,\(|AD|=4\),\(|CD|=3\),\(∠D=60^{\circ}\),\(PA\perp\)平面\(ABCD\),且\(|PA|=6\),则\(|PC|=\)\(\underline{\quad \quad}\).

7.如图,在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,点\(E\)是棱\(BC\)的中点,点\(F\)是棱\(CD\)上的动点.当 \(\dfrac{C F}{F D}=\)\(\underline{\quad \quad}\)时,\(D_1 E\perp\)平面\(AB_1 F\).

8.如图,\(∠BOC\)在平面\(\alpha\)内,\(OA\)是 \(\alpha\) 的斜线,若\(∠AOC=∠AOB=60^{\circ}\),\(OA=OB=OC=1\),\(BC=\sqrt{2}\),则\(OA\)与平面\(\alpha\)所成角是\(\underline{\quad \quad}\).

9.如图所示,在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\)是\(AB\)上一点,\(N\)是\(A_1 C\)的中点,\(MN\perp\) 平面\(A_1 DC\).

求证:(1)\(MN∥AD_1\); \(\qquad \qquad\)(2)\(M\)是\(AB\)的中点.
10.如图,菱形\(ABCD\)的边长为\(6\),\(∠BAD=60^{\circ}\),\(AC\cap BD=O\).将菱形\(ABCD\)沿对角线\(AC\)折起,得到三棱锥\(B-ACD\),点\(M\)是棱\(BC\)的中点,\(DM=3\sqrt{2}\).
(1)求证:\(OD\perp\)平面\(ABC\);
(2)求三棱锥\(M-ABD\)的体积.

11.如图,已知\(△ABC\)是正三角形,\(EA\)、\(CD\)都垂直于平面\(ABC\),且\(EA=AB=2a\),\(DC=a\),\(F\)是\(BE\)的中点,求证:
(1)\(FD∥\)平面\(ABC\);
(2)\(AF\perp\)平面\(EDB\);
(3)求直线\(AD\)与平面\(EDB\)所成角的余弦值.

参考答案
-
答案 \(B\)
解析 如图,直线\(CE\)垂直于直线\(B_1 D_1\)

事实上,\(\because AC_1\)为正方体,\(\therefore A_1 B_1 C_1 D_1\)为正方形,连结\(B_1 D_1\),
又\(\because E\)为\(A_1 C_1\)的中点,\(\therefore E\in B_1 D_1\).\(\therefore B_1 D_1\perp C_1 E\),
\(CC_1\perp\)面\(A_1 B_1 C_1 D_1\),\(\therefore CC_1\perp B_1 D_1\),
又\(CC_1\cap C_1 E=C_1\),\(\therefore B_1 D_1\perp\)面\(CC_1 E\),
而\(CE\subset\)面\(CC_1 E\),\(\therefore\)直线\(CE\)垂直于直线\(B_1 D_1\)
故选:\(B\). -
答案 \(C\)
解析 \(\because AB\)是\(⊙O\)的直径\(,\therefore AC\perp BC\),
\(\because PA\perp ⊙O\)所在平面,\(\therefore PA\perp AC\),\(PA\perp AB\),\(PA\perp BC\),
\(\therefore BC\perp\)面\(PAC\),\(\therefore BC\perp AE\),\(\therefore AE\perp PC\),
\(\because BC\cap PC=C\),\(\therefore AE\perp\) 面\(PBC\),\(\therefore\) ④正确;
\(\because BC\),\(PB\subset\)面\(PBC\),
\(\therefore AE\perp BC\),\(AE\perp PB\),\(\therefore\) ①②正确;
若\(AF\perp BC\),则\(AF\perp\)面\(PBC\),
此时\(E\),\(F\)重合,与已知矛盾.\(\therefore\)③错误;
故①②④正确.
故选\(C\). -
答案 \(A\)
解析 如图,\(\because\)长方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(A_1 A\perp\)平面\(ABCD\),
\(\therefore\)直线\(A_1 C\)与平面\(ABCD\)所成角为\(∠ACA_1\),
\(\because AB=AA_1=1\),\(AD=2\), \(\therefore A C=\sqrt{5}\),
\(\therefore\)在\(Rt△ACA_1\)中由勾股定理可得\(A_1 C=\sqrt{6}\),
\(\therefore \sin \angle A C A_1=\dfrac{A A_1}{A_1 C}=\dfrac{1}{\sqrt{6}}=\dfrac{\sqrt{6}}{6}\),
故直线\(A_1 C\)与平面\(ABCD\)所成角的正弦为 \(\dfrac{\sqrt{6}}{6}\).
故选:\(A\).

-
答案 \(B\)
解析 由题意知,\(AB=BC=CD=DA=BD\),
当四面体\(MBCD\)为正四面体时,此时\(△CDM\)为等边三角形,故①为真命题;
当三棱锥是正四面体时,设顶点\(M\)在底面\(BCD\)上的投影为\(O\),
连接\(DO\)延长交\(BC\)于\(F\),如图,

由正四面体性质可知,\(O\)是三角形\(BCD\)中心,\(F\)是\(BC\)中点,
所以\(BC\perp MO\),\(BC\perp DF\),
又\(FD\cap MO=O\),\(FD\),\(MO\subset\)平面\(MDO\),
所以\(BC\perp\)平面\(MDO\),
又\(MD\subset\) 平面\(MDO\),所以\(DM\perp BC\),所以②为假命题.
故选:\(B\). -
答案 \(AB\)
解析 对\(A\)选项,如图,当\(Q\)为\(AA_1\)的中点时,\(|PQ|\)最小,
此时 \(|P Q|=|A C|=\sqrt{1+4}=\sqrt{5}\);
当\(Q\)为\(A_1\)或\(A\)时,\(|PQ|\)最大,此时 \(|P Q|=|P A|=\sqrt{5+1}=\sqrt{6}\),
\(\therefore |PQ|\in [\sqrt{5},\sqrt{6}]\),\(\therefore A\)选项正确;
对\(B\)选项,\(\because\)三棱锥\(B-QPB_1\)的体积 \(V_{B-Q P B}=V_{Q-B P B_1}=\dfrac{1}{3} \times\left(\dfrac{1}{2} \times 2 \times 2\right) \times 1=\dfrac{2}{3}\),
\(\therefore B\)选项正确;
对\(C\),\(D\)选项,\(\because BD_1\)与\(AC_1\)与在平面\(BCC_1 B_1\)内的射影都为\(BC_1\),
而\(BC_1\) 与\(PB_1\)不垂直,根据三垂线定理可得\(PB_1\)与\(BD_1\) 、\(AC_1\)都不垂直,
\(\therefore BD_1\)和\(AC_1\)与平面\(QPB_1\)都不垂直,\(\therefore C\)、\(D\)选项错误.
故选:\(AB\).

-
答案 \(7\)
解析 由余弦定理有,\(A C^2=A D^2+C D^2-2 A D \cdot C D \cdot \cos D=16+9-2 \times 4 \times 3 \times \dfrac{1}{2}=13\),
\(\therefore A C=\sqrt{13}\),
\(\because PA\perp\)平面\(ABCD\),\(AC\)在平面\(ABCD\)内,\(\therefore PA\perp AC\),
\(\therefore P C=\sqrt{P A^2+A C^2}=\sqrt{36+13}=7\).
故答案为:\(7\). -
答案 \(1\)
解析 连接\(A_1 B\),则\(A_1 B\)是\(D_1 E\)在面\(ABB_1 A\)内的射影
\(\because AB_1\perp A_1 B\),\(\therefore D_1 E\perp AB_1\),
于是\(D_1 E\perp\)平面\(AB_1F⇔D_1 E\perp AF\).
连接\(DE\),则\(DE\)是\(D_1 E\)在底面\(ABCD\)内的射影.
\(\therefore D_1 E\perp AF⇔DE\perp AF\).
\(\because ABCD\)是正方形,\(E\)是\(BC\)的中点.
\(\therefore\)当且仅当\(F\)是\(CD\)的中点时,\(DE\perp AF\),
即当点\(F\)是\(CD\)的中点时,\(D_1 E\perp\)平面\(AB_1 F\).
\(\therefore \dfrac{C F}{F D}=1\)时,\(D_1 E\perp\)平面\(AB_1 F\). -
答案 \(\dfrac{\pi}{4}\)
解析 如图,取\(BC\)中点为\(D\),连接\(AD\),\(OD\),
\(\because OA=OC=1\),\(∠AOC=60^{\circ}\),\(\therefore AC=1\),
同理,在\(△AOB\)中,\(AB=1\),

\(\because AC=AB=1\),\(BC=\sqrt{2}\),
\(\therefore AD\perp BC\),且\(AD=\dfrac{\sqrt{2}}{2}\),
又\(\because OC=OB=1\),\(BC=\sqrt{2}\),\(\therefore OD=\dfrac{\sqrt{2}}{2}\),
\(\therefore O A^2=O D^2+A D^2\),即\(AD\perp OD\),
又因为\(BC\cap OD=D\),所以\(AD\perp\)平面\(OBC\),
所以\(∠AOD\)为\(OA\)与平面\(\alpha\)所成角,
在\(Rt△AOD\)中,\(OD=AD=\dfrac{\sqrt{2}}{2}\),所以\(∠AOD=\dfrac{\pi}{4}\),
故答案为:\(\dfrac{\pi}{4}\). -
证明 (1)\(\because\) 四边形\(ADD_1 A_1\)为正方形,\(\therefore AD_1\perp A_1 D\).
又\(\because CD\perp\)平面\(ADD_1 A_1\),\(\therefore CD\perp AD_1\).
\(\because A_1 D\cap CD=D\),\(\therefore AD_1\perp\) 平面\(A_1 DC\).
又\(\because MN\perp\)平面\(A_1 DC\),\(\therefore MN∥AD_1\).
(2)如图,连接\(ON\),在\(△A_1 DC\)中,\(A_1 O=OD\),\(A_1 N=NC\).

\(\therefore ON∥CD∥AB\).
\(\therefore ON∥AM\).又\(\because MN∥OA\),
\(\therefore\)四边形\(AMNO\)为平行四边形,
\(\therefore ON=AM\).\(\because ON=\dfrac{1}{2}AB\),\(\therefore AM=\dfrac{1}{2}AB\).
\(\therefore M\)是\(AB\)的中点. -
答案 (1) 略;(2) \(\dfrac{9 \sqrt{3}}{2}\)
解析 (1)证明:由题意,\(OM=OD=3\),
\(\therefore O M^2+O D^2=18=(3 \sqrt{2})^2=D M^2\).
\(\therefore ∠DOM=90^{\circ}\),\(\therefore OD\perp OM\).
又\(\because\) 菱形\(OM\cap AC=O\),\(\therefore OD\perp AC\).
\(\because OM\cap AC=O\),\(\therefore OD\perp\)平面\(ABC\).
(2)解:三棱锥\(M-ABD\)的体积等于三棱锥\(D-ABM\)的体积.
由(1)知,\(OD\perp\)平面\(ABC\),
\(\therefore OD=3\)为三棱锥\(D-ABM\)的高.
\(△ABM\)的面积\(=\dfrac{1}{2} B M \times B A \times \sin 120^{\circ}=\dfrac{1}{2} \times 3 \times 6 \times \dfrac{\sqrt{3}}{2}=\dfrac{9 \sqrt{3}}{2}\),
所求体积等于\(\dfrac{1}{3} \times S_{\triangle A B M} \times O D=\dfrac{9 \sqrt{3}}{2}\).

-
答案 (1) 略;(2) 略;(3) \(\dfrac{\sqrt{15}}{5}\)
解析 (1)证明:取\(AB\)的中点\(M\),连\(FM\),\(MC\),
\(\because F\)、\(M\)分别是\(BE\)、\(BA\)的中点,
\(\therefore FM∥EA\),\(FM=\dfrac{1}{2}EA\),
\(\because EA\)、\(CD\)都垂直于平面\(ABC\),\(\therefore CD∥EA\),
\(\therefore CD∥FM\),
又\(DC=a\),\(\therefore FM=DC\),
\(\therefore\)四边形\(FMCD\)是平行四边形,
\(\therefore FD∥MC\),又\(FD\not \subset\)平面\(ABC\),\(MC\subset\)平面\(ABC\),
\(\therefore FD∥\)平面\(ABC\);
(2)证明:\(\because M\)是\(AB\)的中点,\(△ABC\)是正三角形,
\(\therefore CM\perp AB\),
又\(CM\perp AE\),\(\therefore CM\perp\)面\(EAB\),\(\therefore CM\perp AF\),\(FD\perp AF\),
因\(F\)是\(BE\)的中点,\(EA=AB\),\(\therefore AF\perp EB\),
又\(FD\cap BE=F\),\(\therefore AF\perp\)平面\(EDB\).
(3)由(2)可得\(AD\)在平面\(EBD\)的射影为\(DF\),
所以直线\(AD\)与平面\(EDB\)所成角为\(∠ADF\),
\(AF=\sqrt{2} a\),\(AD=\sqrt{5} a\),\(DF=\sqrt{3} a\), \(\cos \angle A D F=\dfrac{D F}{A D}=\dfrac{\sqrt{15}}{5}\);
所以直线\(AD\)与平面\(EDB\)所成角的余弦值为\(\dfrac{\sqrt{15}}{5}\).
【B组---提高题】
1.如图,正方体\(ABCD-A_1 B_1 C_1 D_1\)的棱长为\(2\),点\(O\)为底面\(ABCD\)的中心,点\(P\)在侧面\(BB_1 C_1 C\)的边界及其内部运动,若\(D_1 O\perp OP\),则\(△D_1 C_1 P\)面积的最小值为( )

A.\(\dfrac{2 \sqrt{5}}{5}\)\(\qquad \qquad \qquad \qquad\) B.\(\dfrac{4\sqrt{5}}{5}\)\(\qquad \qquad \qquad \qquad\) C.\(\sqrt{5}\) \(\qquad \qquad \qquad \qquad\) D.\(2\sqrt{5}\)
2.已知圆锥\(DO\)的轴截面为等边三角形,\(△ABC\)是底面\(⊙O\)的内接正三角形,点\(P\)在\(DO\)上,且\(PO=λDO\).若\(PA\perp\)平面\(PBC\),则实数\(λ=\) \(\underline{\quad \quad}\) .
3.在正四棱柱\(ABCD-A_1 B_1 C_1 D_1\)中,\(B_1 C\)与平面\(ACC_1 A_1\)所成角的正弦值为\(\dfrac{\sqrt{2}}{4}\).则异面直线\(B_1 C\)与\(DC_1\)所成角的余弦值为 \(\underline{\quad \quad}\) .
参考答案
-
答案 \(B\)
解析 如图所示:
当点\(P\)在\(C\)处时,\(D_1 O\perp OC\),当点\(P\)在\(B_1 B\)的中点\(P_1\)时,
\(O P^2=(\sqrt{2})^2+1^2=3\), \(D_1 O^2=(\sqrt{2})^2+2^2=6\), \(D_1 P_1^2=(2 \sqrt{2})^2+1^2=9\),
所以 \(O P^2+D_1 O^2=D_1 P_1^2\),
所以\(D_1 O\perp OP_1\),又\(OP_1\cap OC=O\),
所以\(D_1 O\perp\)平面\(OP_1 C\),
所以点\(P\)的轨迹是线段\(P_1 C\),
因为\(D_1 C_1\perp\)平面\(P_1 C_1 C\),
所以\(△D_1 C_1 P\)面积最小时,\(C_1 P\perp P_1 C\),
此时 \(C_1 P=\dfrac{C_1 C \times B C}{P_1 C}=\dfrac{4}{\sqrt{2^2+1^2}}=\dfrac{4 \sqrt{5}}{5}\),
\(S_{\triangle D_1 C_1 P}=\dfrac{1}{2} \times 2 \times \dfrac{4 \sqrt{5}}{5}=\dfrac{4 \sqrt{5}}{5}\),
故选:\(B\).

-
答案 \(\dfrac{\sqrt{6}}{6}\)
解析 如图所示,

不妨设\(AE=AD=1\),
由\(B A=\dfrac{\sqrt{3}}{2}\), \(P O=\lambda D O=\dfrac{\sqrt{3}}{2} \lambda\), \(P A^2=P B^2=\dfrac{3}{4} \lambda^2+\dfrac{1}{4}\),
\(\because PA\perp\)平面\(PBC\),\(PB\subset\)平面\(PBC\),\(\therefore PA\perp PB\),
在\(△PAB\)中,由勾股定理有\(P A^2+P B^2=B A^2\),
\(\therefore 2\left(\dfrac{3}{4} \lambda^2+\dfrac{1}{4}\right)=\dfrac{3}{4}\),解得 \(\lambda=\dfrac{\sqrt{6}}{6}\). -
答案 \(\dfrac{3}{4}\)
解析 设\(A_1 C_1\)与\(B_1 D_1\)的交点为\(F\),连接\(CF\),则\(A_1 C_1\perp B_1 D_1\),
因为等腰三角形\(CB_1 D_1\),且点\(F\)为\(B_1 D_1\)的中点,所以\(B_1 D_1\perp CF\),
又\(A_1 C_1\cap CF=F\),\(A_1 C_1,CF\subset\)平面\(ACC_1 A_1\),
所以\(B_1 D_1\perp\)平面\(ACC_1 A_1\),
所以\(∠B_1 CF\)即为\(B_1 C\)与平面\(ACC_1 A_1\)所成角,即 \(\sin \angle B_1 C F=\dfrac{\sqrt{2}}{4}\),
设正方形\(ABCD\)的边长为\(2a\),
在\(Rt △B_1 CF\)中, \(\sin \angle B_1 C F=\dfrac{B_1 F}{B_1 C}=\dfrac{\sqrt{2} a}{B_1 C}=\dfrac{\sqrt{2}}{4}\),
所以\(B_1 C=4a\),
设\(B_1 C\)与\(BC_1\)相交于点\(E\),\(AC\)与\(BD\)相交于点\(O\),
则\(E\),\(O\)分别为\(BC_1\),\(BD\)的中点,
所以\(DC_1||OE\),
所以\(∠OEC\)或其补角即为异面直线\(B_1 C\)与\(DC_1\)所成角,
在\(△OCE\)中,\(CE=OE=\dfrac{1}{2}DC_1=2a\),\(OC=\sqrt{2} a\),
由余弦定理知, \(\cos \angle O E C=\dfrac{O E^2+C E^2-O C^2}{2 O E \cdot C E}=\dfrac{4 a^2+4 a^2-2 a^2}{2 \cdot 2 a \cdot 2 a}=\dfrac{3}{4}\),
所以异面直线\(B_1 C\)\(DC_1\)与所成角的余弦值为\(\dfrac{3}{4}\).

【C组---拓展题】
1.如图,在棱长为\(2\)的正方体中\(ABCD-A_1 B_1 C_1 D_1\),点\(M\)是\(AD\)的中点,动点\(P\)在底面\(ABCD\)内(包括边界),若\(B_1 P∥\)平面\(A_1 BM\),则\(C_1 P\)与底面\(ABCD\)所成角的正弦的取值范围是\(\underline{\quad \quad}\).

2.如图,在矩形\(ABCD\)中,\(AB=8\),\(BC=4\),\(E\)为\(DC\)边的中点,沿\(AE\)将\(△ADE\)折起,在折起过程中,正确的是\(\underline{\quad \quad}\) .
①\(ED\perp\)平面\(ACD\) \(\qquad \qquad\)②\(CD\perp\)平面\(BED\)
③\(BD\perp\)平面\(ACD\) \(\qquad \qquad\) ④\(AD\perp\)平面\(BED\).

参考答案
-
答案 \(\left[\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{30}}{6}\right]\)
解析 取\(BC\)的中点\(N\),连接\(DN\),\(B_1 N\),\(B_1 D\),
则\(DN∥BM\),\(DN\not \subset\)面\(A_1 BM\),\(BM\subset\) 面\(A_1 BM\),
所以\(DN∥\)面\(A_1 BM\),
同理:\(B_1 N∥A_1 M\),\(B_1 N\not \subset\)面\(A_1 BM\),\(A_1 M\subset\)面\(A_1 BM\),
所以\(B_1 N∥\)面\(A_1 BM\),
因为\(DN\cap B_1 N=N\),所以平面\(B_1 DN∥\)面\(A_1 BM\),
因为\(B_1 P∥\)平面\(A_1 BM\),且点\(P\)在底面\(ABCD\)内(包括边界),
所以点\(P\)在线段\(DN\)上运动,
连接\(CP\),\(C_1 P\),因为\(CC_1\perp\)面\(ABCD\),
所以\(∠C_1 PC\)即为\(C_1 P\)与底面\(ABCD\)所成角,
在\(Rt△C_1 PC\)中,\(\sin \angle C_1 P C=\dfrac{C_1 C}{C_1 P}=\dfrac{2}{C_1 P},\),
在\(Rt△CDN\)中,当点\(P\)与点\(D\)重合时\(CP\)最长为\(2\),
此时\(C_1 P\)最长为\(\sqrt{2^2+2^2}=2 \sqrt{2}\),
当\(CP\perp DN\)时,\(CP\)最短为 \(\dfrac{1 \times 2}{\sqrt{5}}=\dfrac{2 \sqrt{5}}{5}\),
此时\(C_1 P\)最短为\(\sqrt{2^2+\left(\dfrac{2 \sqrt{5}}{5}\right)^2}=\dfrac{2 \sqrt{30}}{5}\),
即\(C_1 P \in\left[\dfrac{2 \sqrt{30}}{5}, 2 \sqrt{2}\right]\), \(\dfrac{1}{C_1 P} \in\left[\dfrac{\sqrt{2}}{4}, \dfrac{\sqrt{30}}{12}\right]\),
所以\(\sin \angle C_1 P C=\dfrac{C_1 C}{C_1 P}=\dfrac{2}{C_1 P} \in\left[\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{30}}{6}\right]\),
故答案为: \(\left[\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{30}}{6}\right]\).

-
答案 ④
解析 \(\because\)在矩形\(ABCD\)中,\(AB=8\),\(BC=4\),\(E\)为\(DC\)边的中点,
\(\therefore\)设\(D\)点在平面\(BCE\)上的投影为\(Q\),在折起过程中,点\(Q\)的轨迹为下图\(Q_1\)到\(Q_2\)的四分之一圆.

此过程中始终有\(DQ\perp\)平面\(AECB\)
对于① 假设\(ED\perp\)平面\(ACD\),则\(ED\perp AC\),又\(\because DQ\perp AC\),
则\(AC\perp\) 平面\(DEQ⇒QE\perp AC\),
但由图可知\(QE\)不可能垂直\(AC\),产生了矛盾,故假设不成立,故①错误;

对于② 假设\(CD\perp\)平面\(BED\),则\(CD\perp BE\),又\(\because DQ\perp BE\),
则\(BE\perp\)平面\(CDQ⇒BE\perp CQ\),
但由图可知只有\(D\)点投影位于\(Q_2\)位置时,才有\(BE\perp CQ\),
此时\(CD\subset\)平面\(BED\),显然不能满足\(CD\perp\)平面\(BED\),产生了矛盾,故假设不成立,
故②错误;

对于③ 假设\(BD\perp\)平面\(ACD\),则\(BD\perp AC\),又\(\because DQ\perp AC\),
则\(AC\perp\)平面\(BDQ⇒AC\perp BQ\),
但由图可知\(BQ\)不可能垂直\(AC\),产生了矛盾,故假设不成立,故③错误;

对于④\(\because AD\perp ED\),\(\therefore\)若要满足\(AD\perp\)平面\(BED\),
则只需要\(AD\perp EB\),而\(DQ\perp EB\),
若\(AQ\perp EB\)便可,在折叠的过程中易得存在一个位置使得\(AQ\perp EB\)(\(Q\)为弧线\(Q_1 Q_2\)与线段\(AE\)的交点),故④正确.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号