8.5.3 平面与平面的平行
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019)]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第二册同步巩固,难度3颗星!
基础知识
定义
\(\alpha\cap\beta=\varnothing⟹\alpha|| \beta\).
判断
(1) \(\alpha\)内有无穷多条直线都与\(\beta\)平行 ( × );
(2) \(\alpha\)内的任何一条直线都与\(\beta\)平行 ( √ ) .
判定定理
如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行.
解释
(1) 符号表述:\(a\) ,\(b\subset\alpha\) ,\(a\cap b=O\) ,\(a || \beta\) ,\(b|| \beta⇒\alpha || \beta\) .

(2) 推论:一个平面内的两条相交直线分别平行于另一个平面的两条直线,那么这两个平面互相平行.
符号表述:\(a\) ,\(b\subset\alpha\) ,\(a\cap b=O\) ,\(a'\) ,\(b'\subset\beta\) ,\(a|| a'\) ,\(b ||b' ⇒\alpha|| \beta\).

面面平行的性质
(1) \(\left.\begin{array}{c}
a \subset \alpha \\
\alpha \| \beta
\end{array}\right\} \Rightarrow a \| \beta \quad \text { (面面平行 } \Rightarrow \text { 线面平行) }\)

(2) \(\left.\begin{array}{c}
\alpha \| \beta \\
\alpha \cap \gamma=a \\
\beta \cap \gamma=b
\end{array}\right\} \Rightarrow a \| b
(面面平行 \Rightarrow 线线平行)\)
证明 如下图,\(\because \alpha\cap\gamma=a\),\(\beta\cap\gamma=b\),
\(\therefore a\subset\alpha\),\(b\subset\beta\),
又\(\alpha || \beta\),\(\therefore a\),\(b\)没有公共点,
又\(a\),\(b\)同在平面\(\gamma\)内,
\(\therefore a//b\).

(3) 夹在两个平行平面间的平行线段相等.
若\(\alpha || \beta\),\(AB || CD\),\(A∈\alpha\),\(C∈\alpha\),\(B\in \beta\),\(D\in \beta\),则\(AB=CD\).

证明面面平行的方法
① 定义法;
② 判定定理及推论(常用)
基本方法
【题型1】 面面平行的判定
【典题1】 \(\alpha\),\(\beta\)是两个不重合的平面,下面说法正确的是( )
A.平面\(\alpha\)内有两条直线\(a\),\(b\)都与平面\(\beta\)平行,那么\(\alpha∥\beta\)
B.平面\(\alpha\)内有无数条直线平行于平面\(\beta\),那么\(\alpha∥\beta\)
C.若直线\(a\)与平面\(\alpha\)和平面\(\beta\)都平行,那么\(\alpha∥\beta\)
D.平面\(\alpha\)内所有的直线都与平面\(\beta\)平行,那么\(\alpha∥\beta\)
解析 \(A\),\(B\)都不能保证\(\alpha\),\(\beta\)无公共点,如图①;
\(C\)中当\(a∥\alpha\),\(a∥\beta\)时,\(\alpha\)与\(\beta\)可能相交,如图②;
只有\(D\)说明\(\alpha\),\(\beta\)一定无公共点.

【典题2】 如下图所示,在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\),\(E\),\(F\),\(N\)分别是\(A_1 B_1\),\(B_1 C_1\),\(C_1 D_1\),\(D_1 A_1\)的中点,求证:
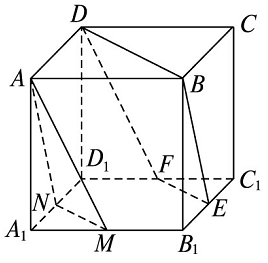
(1)\(E\),\(F\),\(B\),\(D\)四点共面;(2)平面\(MAN∥\)平面\(EFDB\).
证明 (1)连接\(B_1 D_1\),
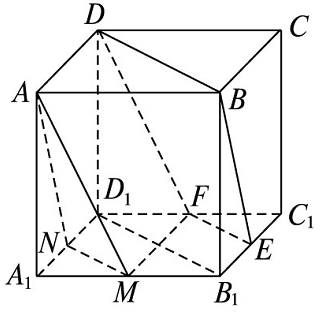
\(\because E\),\(F\)分别是边\(B_1 C_1\)和\(C_1 D_1\)的中点,\(\therefore EF∥B_1 D_1\).
而\(BD∥B_1 D_1\),\(\therefore BD∥EF\).
\(\therefore E\),\(F\),\(B\),\(D\)四点共面.
(2) \(\because MN//B_1 D_1\),\(B_1 D_1//BD\),\(\therefore MN∥BD\).
而\(MN \not \subset\)平面\(EFDB\),\(DB\subset\)平面\(EFDB\),\(\therefore MN∥\)平面\(EFDB\).
连接\(MF\),\(\because\)点\(M\),\(F\)分别是\(A_1 B_1\)与\(C_1 D_1\)的中点,
\(\therefore MF∥AD\).\(\therefore\)四边形\(MFDA\)是平行四边形.\(\therefore AM∥DF\).
\(\because AM \not \subset\)平面\(EFDB\),\(\therefore AM∥\)平面\(EFDB\).
又\(AM\cap MN=M\),
\(\therefore\)平面\(AMN∥\)平面\(EFDB\).
【巩固练习】
1.下列四个命题:①平行于同一直线的两个平面平行;②平行于同一平面的两个平面平行;③平行于两条相交直线的两个平面平行;④与无数条直线都平行的两个平面平行.则其中正确命题的序号是\(\underline{\quad \quad}\) .
2.如图,在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(O\)为底面\(ABCD\)的中心,\(P\)是\(DD_1\)的中点,设\(Q\)是\(CC_1\)上的点,当点\(Q\)在\(\underline{\quad \quad}\) 位置时,平面\(D_1 BQ∥\)平面\(PAO\).

3.如图,已知四棱锥\(P-ABCD\)中,底面\(ABCD\)为平行四边形,点\(M\),\(N\),\(Q\)分别是\(PA\),\(BD\),\(PD\)的中点上,
(1)求证:\(MN∥PC\);\(\qquad \qquad\)(2)求证:平面\(MNQ∥\)平面\(PBC\).

4.如图:正方体\(ABCD-A_1 B_1 C_1 D_1\)棱长为\(2\),\(E\),\(F\)分别为\(DD_1\),\(BB_1\)的中点.
(1)求证:\(CF∥\)平面\(A_1 EC_1\);
(2)过点\(D\)做正方体截面使其与平面\(A_1 EC_1\)平行,请给以证明并求出该截面的面积.

5.已知正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(P\)、\(Q\)分别为对角线\(BD\)、\(CD_1\)上的点,且\(\dfrac{C Q}{Q D}=\dfrac{B P}{P D}=\dfrac{2}{3}\).
(1)作出平面\(PQC\)和平面\(AA_1 D_1 D\)的交线(保留作图痕迹),并求证:\(PQ∥\)平面\(A_1 D_1 DA\);
(2)若\(R\)是\(AB\)上的点,当\(\dfrac{AR}{AB}\)的值为多少时,能使平面\(PQR∥\)平面\(A_1 D_1 DA\)?请给出证明.

参考答案
- 答案 ②③
解析 ①平行于同一直线的两个平面平行,不正确,如两相交平面,使直线与交线平行;
②平行于同一平面的两个平面平行,根据面面平行的性质可知正确;
③平行于两条相交直线的两个平面平行,根据面面平行的判定定理可知正确;
④与无数条直线都平行的两个平面平行,不正确,如无数直线是平行线就不正确了;
故答案为:②③ - 答案 \(CC_1\)的中点
解析 在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,
\(\because O\)为底面\(ABCD\)的中心,\(P\)是\(DD_1\)的中点,
\(\therefore PO∥BD_1\),
设\(Q\)是\(CC_1\)上的点,当点\(Q\)在\(CC_1\)的中点位置时,
\(PQ//AB\),\(\therefore\)四边形\(ABQP\)是平行四边形,
\(\therefore AP∥BQ\),
\(\because AP\cap PO=P\),\(BQ\cap BD_1=B\),
\(AP\)、\(PO\subset\)平面\(APO\),\(BQ\)、\(BD_1\subset\)平面\(BQD_1\),
\(\therefore\)平面\(D_1 BQ∥\)平面\(PAO\). - 证明 (1)由题意:\(P-ABCD\)是四棱锥,底面\(ABCD\)为平行四边形,
点\(M\),\(N\),\(Q\)分别是\(PA\),\(BD\),\(PD\)的中点上,连接\(AC\),\(\therefore N\)是\(AC\)的中点.
\(\therefore MN\)是三角形\(ACP\)的中位线,
\(\therefore MN∥PC\).
(2)由(1)可得\(MN∥PC\).
\(\because M\),\(Q\)分别在\(PA\),\(PD\)的中点上,
\(\therefore MQ\)是三角形\(ADP\)的中位线,
\(\therefore MQ∥PB\).
由\(MQ∥PB\),\(MN∥PC\),\(PB\subset\)平面\(PBC\),\(PC\subset\)平面\(PBC\),\(PB\cap PC=P\),
同理\(MQ\subset\)平面\(MNQ\),\(MN\subset\)平面\(MNQ\),\(MQ\cap MN=M\).
\(\therefore\)平面\(MNQ∥\)平面\(PBC\).

- 答案 (1)略 (2) \(2\sqrt{6}\).
解析 (1)证明:取\(CC_1\)中点\(M\),连接\(ME\),

由\(MC∥FB_1\)且\(MC=FB_1\)可得四边形\(MCFB_1\)为平行四边形,则\(FC∥MB_1\)
由\(ME∥A_1 B_1\)且\(ME=A_1 B_1\)可得四边形\(MEA_1 B_1\)为平行四边形,则\(A_1 E∥MB_1\),
则\(A_1 E∥FC\),又\(A_1 E\subset\)平面\(A_1 EC_1\),\(CF \not \subset\)平面\(A_1 EC_1\),则\(FC∥\)平面\(A_1 EC_1\);
(2)解:取\(AA_1\),\(CC_1\)中点\(G\),\(H\),连接\(DG\),\(CB_1\),\(B_1 H_1\),\(HD\),

\(\because\)四边形\(ADHF\)为平行四边形,\(\therefore AF∥DH\),
\(\because\)四边形\(AFB_1 G\)为平行四边形,\(\therefore GB_1∥AF∥DH\),
\(\therefore GDB_1 H\)即为过点\(D\)长方体截面,
证明如下:
\(\because DG∥A_1 E\),\(A_1 E\subset\)平面\(AEC_1\),\(DG \not \subset\)平面\(AEC_1\),\(\therefore DG∥\)平面\(AEC_1\),
\(\because DH∥C_1 E\),\(C_1 E\subset\)平面\(AEC_1\),\(DH \not \subset\)平面\(AEC_1\),\(\therefore DH∥\)平面\(AEC_1\),
又\(\because DH\cap DG=D\),\(\therefore\)平面\(DHB_1 G∥\)平面\(AEC_1\),
\(\therefore \mathrm{S}_{\mathrm{GDHB}_1}=\dfrac{1}{2} \times 2 \sqrt{2} \times 2 \sqrt{3}=2 \sqrt{6}\). - 答案 (1)略 (2) 当\(\dfrac{AR}{AB}\)的值为\(\dfrac{3}{5}\)时,能使平面\(PQR∥\)平面\(A_1 D_1 DA\).
解析 (1)连结\(CP\)并延长与\(DA\)的延长线交于\(M\)点,
则平面\(PQC\)和平面\(AA_1 D_1 D\)的线为\(D_1 M\),
因为四边形\(ABCD\)为正方形,所以\(BC∥AD\),

故\(△PBC∽△PDM\),所以\(\dfrac{C P}{P M}=\dfrac{B P}{P D}=\dfrac{2}{3}\),
又因为\(\dfrac{C Q}{Q D_1}=\dfrac{B P}{P D}=\dfrac{2}{3}\),所以\(\dfrac{C Q}{Q D_1}=\dfrac{C P}{P M}=\dfrac{2}{3}\),所以\(PQ∥MD_1\).
又\(MD_1\subset\)平面\(A_1 D_1 DA\),\(PQ\)不在平面\(A_1 D_1 DA\)内,
故\(PQ∥\)平面\(A_1 D_1 DA\).
(2)当\(\dfrac{AR}{AB}\)的值为\(\dfrac{3}{5}\)时,能使平面\(PQR∥\)平面\(A_1 D_1 DA\).

证明:因为\(\dfrac{A R}{A B}=\dfrac{3}{5}\),即\(\dfrac{B R}{R A}=\dfrac{2}{3}\),
故\(\dfrac{B R}{R A}=\dfrac{B P}{P D}\),所以\(PR∥DA\).
又\(DA\subset\)平面\(A_1 D_1 DA\),\(PR\)不在平面\(A_1 D_1 DA\)内,
所以\(PR∥\)平面\(A_1 D_1 DA\),
又\(P Q \cap P R=P\),\(PQ∥\)平面\(A_1 D_1 DA\).
所以平面\(PQR∥\)平面\(A_1 D_1 DA\).
【题型2】 面面平行的性质
【典题1】 已知两条直线\(a\),\(b\),两个平面\(\alpha\),\(\beta\),则下列结论中正确的是 ( )
A.若\(a\subset\beta\),且\(\alpha∥\beta\),则\(a∥\alpha\) \(\qquad \qquad \qquad \qquad\) B.若\(b\subset\alpha\),\(a∥b\),则\(a∥\alpha\)
C.若\(a∥\beta\),\(\alpha∥\beta\),则\(a∥\alpha\) \(\qquad \qquad \qquad \qquad\) D.若\(b∥\alpha\),\(a∥b\),则\(a∥\alpha\)
解析 \(A\): \(\because \alpha∥\beta\),又\(a\subset\beta\),\(\therefore a∥\alpha\),故\(A\)正确;
\(B\):\(\because b\subset\alpha\),\(a∥b\),若\(a\subset\alpha\),则\(a\)不可能与\(\alpha\)平行,故\(B\)错误;
\(C\): \(\because a∥\beta\),\(\alpha∥\beta\),若\(a\subset\alpha\),则结论不成立,故\(C\)错误;
\(D\): \(\because b∥\alpha\),\(a∥b\),若\(a\subset\alpha\),则结论不成立,故\(D\)错误;
故\(A\)正确.
点拨
① 线面的位置关系有三种:\(a∥\alpha\)、\(a\subset\alpha\)、\(a\cap \alpha=A\);
② 证明某些选项是错只需要举个反例,比如选项\(C\)是怎么会想到“\(a\subset\alpha\)”这个反例的呢?
运用“运动的思想”,先由\(\alpha∥\beta\)固定两个平面\(\alpha\)、\(\beta\),再由\(a∥\beta\)把线段\(a\)由上至下“运动”下来,则\(a\)、\(\alpha\)的关系有两种情况\(a\subset\alpha\)、\(a∥\alpha\).选项\(B\)、\(D\)也可类似.
【典题2】 如图所示,两条异面直线\(BA\),\(DC\)与两平行平面\(\alpha\),\(\beta\)分别交于\(B\),\(A\)点和\(D\),\(C\)点,\(M\),\(N\)分别是\(AB\),\(CD\)的中点.
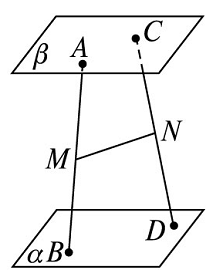
求证:\(MN∥\)平面\(\alpha\).
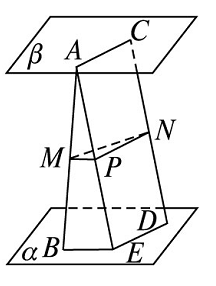
证明 过点\(A\)作\(AE∥CD\)交\(\alpha\)于\(E\),取\(AE\)的中点\(P\),连接\(MP\),\(PN\),\(BE\),\(ED\),\(AC\).
\(\because AE∥CD\),
\(\therefore AE\),\(CD\)确定平面\(AEDC\).
则平面\(AEDC\cap\)平面\(\alpha=DE\),平面\(AEDC\cap\)平面\(\beta=AC\),
\(\because \alpha∥\beta\),\(\therefore AC∥DE\).
又\(P\),\(N\)分别为\(AE\),\(CD\)的中点,\(\therefore PN∥DE\).\(PN \not \subset\alpha\),\(DE\subset\alpha\),
\(\therefore PN∥\alpha\).又\(M\),\(P\)分别为\(AB\),\(AE\)的中点,
\(\therefore MP∥BE\),且\(MP \not \subset\alpha\),\(BE\subset\alpha\),
\(\therefore MP∥\alpha\).\(\therefore\)平面\(MPN∥\)平面\(\alpha\).
又\(MN\subset\)平面\(MPN\),\(\therefore MN∥\alpha\).
【巩固练习】
1.如图,在直三棱柱\(ABC-A_1 B_1 C_1\)中,点\(E\),\(F\)分别是棱\(A_1 C_1\),\(BC\)的中点,则下列结论中不正确的是( )

A.\(CC_1∥\)平面\(A_1 ABB_1\) \(\qquad \qquad \qquad \qquad\) B.\(AF∥\)平面\(A_1 B_1 C_1\)
C.\(EF∥\)平面\(A_1 ABB_1\) \(\qquad \qquad \qquad \qquad\) D.\(AE∥\)平面\(B_1 BCC_1\)
2.如图,各棱长均为\(1\)的正三棱柱\(ABC-A_1 B_1 C_1\),\(M\),\(N\)分别为线段\(A_1 B\),\(B_1 C\)上的动点,且\(MN∥\)平面\(ACC_1 A_1\),则这样的\(MN\)有( )

A.\(1\)条 \(\qquad \qquad \qquad \qquad\) B.\(2\)条 \(\qquad \qquad \qquad \qquad\)C.\(3\)条 \(\qquad \qquad \qquad \qquad\) D.无数条
3.如图所示,\(S\)为矩形\(ABCD\)所在平面外一点,\(E\)、\(F\)分别是\(SD\)、\(BC\)上的点,且\(SE:ED=BF:FC\),求证:\(EF∥\)平面\(SAB\).

4.如图,已知\(\alpha∥\beta\),点\(P\)是平面\(\alpha\),\(\beta\)外的一点(不在\(\alpha\)与\(\beta\)之间).直线\(PB\),\(PD\)分别与\(\alpha\),\(\beta\)相交于点\(A\),\(B\)和\(C\),\(D\).

(1)求证:\(AC∥BD\);
(2)已知\(PA=4 cm\),\(AB=5 cm\),\(PC=3 cm\),求\(PD\)的长.
参考答案
-
答案 \(D\)
解析在直三棱柱\(ABC-A_1 B_1 C_1\)中,可得\(CC_1∥AA_1\),\(AA_1\subset\)平面\(A_1 ABB_1\),
\(CC_1 \not \subset\)平面\(A_1 ABB_1\),\(\therefore CC_1∥\)平面\(A_1 ABB_1\),故\(A\)正确;
\(AF\subset\)平面\(ABC\),在直三棱柱\(ABC-A_1 B_1 C_1\)中,可得平面\(ABC∥\)平面\(A_1 B_1 C_1\),
所以\(AF∥\)平面\(A_1 B_1 C_1\),故\(B\)正确;
取\(A_1 B_1\)中点\(N\),又\(E\)是\(A_1 C_1\)中点,
所以\(NE∥C_1 B_1\),且\(NE=\dfrac{1}{2}C_1 B_1\),
又\(F\)是棱\(BC\)的中点,所以\(BF=\dfrac{1}{2}C_1 B_1\),\(AF∥C_1 B_1\),
\(\therefore BF∥NE\),\(BF=NE\),
所以四边形\(BFEN\)是平行四边形,
所以\(EF∥BN\),\(BN\subset\)平面\(A_1 ABB_1\),\(EF \not \subset\)平面\(A_1 ABB_1\),
\(\therefore EF∥\)平面\(A_1 ABB_1\),故\(C\)正确;
因为\(EC_1∥AC\),但\(EC_1≠AC\),所以\(AE\)与\(CC_1\)相交,
从而有\(AE\)不平行于平面\(B_1 BCC_1\),故\(D\)错误.
故选:\(D\).

-
答案 \(D\)
解析 如图,任取线段\(A_1 B\)上一点\(M\),过\(M\)作\(MH∥AA_1\),交\(AB\)于\(H\),
过\(H\)作\(HG∥AC\)交\(BC\)于\(G\), 过\(G\)作\(CC_1\)的平行线,与\(CB_1\)一定有交点\(N\),且\(MN∥\)平面\(ACC_1 A_1\),
则这样的\(MN\)有无数个.
故选:\(D\).

-
证明 如图所示,在\(SC\)上取一点\(H\),使\(SH:HC=SE:ED\),则\(EH∥DC\).
\(\because DC∥AB\),\(\therefore EH∥AB\),
\(\because EH \not \subset\)平面\(SAB\),\(AB\subset\)平面\(SAB\),\(\therefore EH∥\)平面\(SAB\)
\(\because SE:ED=BF:FC\),\(EH∥DC\),\(\therefore SH:HC=BF:FC\),\(\therefore HF∥BS\),
\(\because HF \not \subset\)平面\(SAB\),\(BS\subset\)平面\(SAB\),\(\therefore HF∥\)平面\(SAB\)
\(\because FH\cap HE=H\).\(\therefore\)平面\(EHF∥\)平面\(SAB\).
\(\because EF\subset\)平面\(EHF\),\(\therefore EF∥\)平面\(SAB\).

-
答案 (1)略 (2) \(\dfrac{27}{4} \mathrm{~cm}\)
解析 (1)证明:\(\because PB\cap PD=P\),
\(\therefore\)直线\(PB\)和\(PD\)确定一个平面\(\gamma\),则\(\alpha\cap \gamma=AC\),\(\beta\cap \gamma=BD\).
又\(\alpha∥\beta\),\(\therefore AC∥BD\).
(2)解:由(1)得\(AC∥BD\), \(\therefore \dfrac{P A}{A B}=\dfrac{P C}{C D}\),
\(\therefore \dfrac{4}{5}=\dfrac{3}{C D}\), \(\therefore C D=\dfrac{15}{4}\).
\(\therefore P D=P C+C D=\dfrac{27}{4}(\mathrm{~cm})\).
【题型3】 综合应用
【典题1】 如图,在长方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(AD=DD_1=1\),\(AB=\sqrt{3}\),\(E\),\(F\),\(G\)分别为\(AB\),\(BC\),\(C_1 D_1\)的中点,点\(P\)在平面\(ABCD\)内,若直线\(D_1 P∥\)平面\(EFG\),则\(D_1\)与满足题意的\(P\)构成的平面截正方体的截面面积为( )

A. \(\dfrac{2 \sqrt{2}}{3}\)\(\qquad \qquad \qquad \qquad\) B. \(\dfrac{\sqrt{6}}{2}\) \(\qquad \qquad \qquad \qquad\)C.\(\dfrac{\sqrt{5}}{2}\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{\sqrt{7}}{2}\)
解析 \(\because E\)、\(F\)、\(G\)分别为\(AB\),\(BC\),\(C_1 D_1\)的中点,
\(\therefore AC∥EF\),\(AD_1∥EG\),
\(\because AC\subset\)面\(ACD_1\),\(EF \not \subset\)面\(ACD_1\),
\(\therefore EF∥\)面\(ACD_1\),
同理可证\(EG∥\)面\(ACD_1\),
又\(\because EF\subset\)面\(EFG\),\(EG\subset\)面\(EFG\),\(EF\cap EG=E\),
\(\therefore 面ACD_1∥\)面\(EFG\),
即点\(P\)在直线\(AC\)上,则\(D_1\)与满足题意的\(P\)构成的平面截正方体的截面为\(△ACD_1\),
在\(△ACD_1\)中,有\(AD_1=\sqrt{2}\),\(AC=2\),\(CD_1=2\),
\(\therefore S_{\triangle A C D_1}=\dfrac{1}{2} \times \sqrt{2} \times \sqrt{2^2-\left(\dfrac{\sqrt{2}}{2}\right)^2}=\dfrac{\sqrt{7}}{2}\),
故选:\(D\).
【巩固练习】
1.已知平面\(\alpha∥\)平面\(\beta\),\(P\)是\(\alpha\),\(\beta\)外一点,过点\(P\)的直线\(m\)与\(\alpha\),\(\beta\)分别交于点\(A\),\(C\),过点\(P\)的直线\(n\)与\(\alpha\),\(\beta\)分别交于点\(B\),\(D\),且\(PA=6\),\(AC=9\),\(PD=8\),则\(BD\)的长为( )
A.\(\dfrac{24}{5}\) \(\qquad \qquad \qquad \qquad\)B.\(\dfrac{12}{5}\) \(\qquad \qquad \qquad \qquad\) C.\(\dfrac{24}{5}\)或\(24\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{12}{5}\) 或\(12\)
2.如图,已知四棱锥\(P﹣ABCD\)的底面是平行四边形,\(AC\)交\(BD\)于点\(O\),\(E\)为\(AD\)中点,\(F\)在\(PA\)上,\(AP=λAF\),\(PC∥\)平面\(BEF\),则\(λ\)的值为( )

A.\(1\) \(\qquad \qquad \qquad \qquad\) B. \(\dfrac{3}{2}\) \(\qquad \qquad \qquad \qquad\) C.\(2\) \(\qquad \qquad \qquad \qquad\) D.\(3\)
3.如图所示,\(P\)是三角形\(ABC\)所在平面外一点,平面\(\alpha∥\)平面\(ABC\),\(\alpha\)分别交线段\(PA\)、\(PB\)、\(PC\)于\(A'\)、\(B'\)、\(C'\),若 \(P A^{\prime}: A A^{\prime}=3: 4\),则 \(S_{\triangle A^{\prime} B^{\prime} C^{\prime}}: S_{\triangle A B C}=\)\(\underline{\quad \quad}\) .

参考答案
-
答案 \(C\)
解析 连接\(AB\)、\(CD\);
①当点\(P\)在\(CA\)的延长线上,即\(P\)在平面\(\alpha\)与平面\(\beta\)的同侧时,如图\(1\);
\(\because \alpha∥\beta\),平面\(PCD\cap \alpha=AB\),平面\(PCD\cap \beta=CD\),
\(\therefore AB∥CD\), \(\therefore \dfrac{P A}{A C}=\dfrac{P B}{B D}\);
\(\because PA=6\),\(AC=9\),\(PD=8\),
\(\therefore \dfrac{6}{9}=\dfrac{8-B D}{B D}\),解得 \(B D=\dfrac{24}{5}\);
②当点\(P\)在线段\(CA\)上,即\(P\)在平面\(\alpha\)与平面\(\beta\)之间时,如图\(2\);
类似①的方法,可得 \(\dfrac{P A}{P C}=\dfrac{P B}{P D}\),
\(\because PA=6\),\(PC=AC-PA=9-6=3\),\(PD=8\),
\(\therefore \dfrac{6}{3}=\dfrac{P B}{8}\),解得\(PB=16\);
\(\therefore BD=PB+PD=24\);
综上,\(BD\)的长为\(\dfrac{24}{5}\)或\(24\).
故选:\(C\).

-
答案 \(D\)
解析 设\(AO\)交\(BE\)于点\(G\),连结\(FG\),如图所示,
因为\(E\)为\(AD\)的中点,则\(AE=\dfrac{1}{2}AD=\dfrac{1}{2}BO\),
四边形\(ABCD\)是平行四边形,\(AD∥BC\),则\(△AEG∽△CBG\),
所以\(\dfrac{A G}{G C}=\dfrac{A E}{B C}=\dfrac{1}{2}\),所以 \(\dfrac{A G}{A C}=\dfrac{1}{3}\),
又因为\(PC∥\)平面\(BEF\),\(PC\subset\)平面\(PAC\),平面\(BEF\cap\) 平面\(PAC=GF\),
所以\(GF∥PC\),
所以 \(\lambda=\dfrac{A P}{A F}=\dfrac{A C}{A G}=3\).
故选:\(D\).

-
答案 \(9:49\)
解析 由题意:\(\because\)平面\(\alpha∥\)平面\(ABC\),
\(\therefore A' B' || AB\),\(B' C' || BC\),\(A' C' || AC\),
\(\therefore\)三角\(PA'B'\)相似于三角形\(PAB\),三角形\(PB'C'\)相似于三角形\(PBC\),三角形\(PA'C'\)相似于三角形\(PAC\),
\(\therefore P A^{\prime}: P A=P B^{\prime}: P B=A^{\prime} B^{\prime}: A B\),\(P B^{\prime}: P B=P C^{\prime}: P C=B^{\prime} C^{\prime}: B C\),\(P C^{\prime}: P C=P A^{\prime}: P A=A^{\prime} C^{\prime}: A C\),
\(\therefore A^{\prime} B^{\prime}: A B=B^{\prime} C^{\prime}: B C=A^{\prime} C^{\prime}: A C\),
故得: \(S_{\triangle A^{\prime} B^{\prime} C^{\prime}} \sim S_{\triangle A B C}\).
\(\therefore S_{\triangle A^{\prime} B^{\prime} C^{\prime}}: S_{\triangle A B C}=A^{\prime} B^{\prime 2}: A B^2\).
又 \(\because P A^{\prime}: A^{\prime} A=3: 4\),
\(\therefore P A^{\prime}: P A=3: 7\),\(A^{\prime} B^{\prime}: A B=3: 7\),
所以得\(S_{\triangle A^{\prime} B^{\prime} C^{\prime}}: S_{\triangle A B C}=9: 49\).
分层练习
【A组---基础题】
1.已知直线\(a\subset\alpha\),给出以下三个命题:
①若平面\(\alpha∥\)平面\(\beta\),则直线\(a∥\)平面\(\beta\);
②若直线\(a∥\)平面\(\beta\),则平面\(\alpha∥\)平面\(\beta\);
③若直线\(a\)不平行于平面\(\beta\),则平面\(\alpha\)不平行于平面\(\beta\).
其中正确的命题是( )
A.② \(\qquad \qquad \qquad \qquad\) B.③ \(\qquad \qquad \qquad \qquad\) C.①②\(\qquad \qquad \qquad \qquad\) D.①③
2.如图在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,棱长为\(a\),\(M\),\(N\)分别为\(A_1 B\)、\(AC\)的中点,则\(MN\)与平面\(BB_1 C_1 C\)的位置关系是( )

A.相交 \(\qquad \qquad \qquad \qquad\) B.平行 \(\qquad \qquad \qquad \qquad\)C.垂直 \(\qquad \qquad \qquad \qquad\) D.不能确定
3.如图,在多面体\(ABC﹣DEFG\)中,平面\(ABC∥\)平面\(DEFG\),\(EF∥DG\),且\(AB=DE\),\(DG=2EF\),则( )

A.\(BF∥\)平面\(ACGD\) \(\qquad\) B.\(CF∥\)平面\(ABED\)\(\qquad\)C.\(BC∥FG\) \(\qquad\) D.平面\(ABED∥\)平面\(CGF\)
4.如图,在正四棱锥\(S﹣ABCD\)中,\(E\)是\(BC\)的中点,\(P\)点在侧面\(△SCD\)内及其边界上运动,并且总是保持\(PE∥\)平面\(SBD\).则动点\(P\)的轨迹与\(△SCD\)组成的相关图形最有可能是图中的( )

A. \(\qquad \qquad\) B.
\(\qquad \qquad\) B. \(\qquad \qquad\)C.
\(\qquad \qquad\)C. \(\qquad \qquad\)D.
\(\qquad \qquad\)D.
5.如图所示,在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\),\(N\),\(P\)分别是\(C_1 C\),\(C_1 B_1\),\(C_1 D_1\)的中点,点\(H\)在四边形\(A_1 ADD_1\)的边及其内部运动,则\(H\)满足条件\(\underline{\quad \quad}\) 时,有\(BH∥\)平面\(MNP\).

6.如图是一几何体的平面展开图,其中\(ABCD\)为正方形,\(E\),\(F\),\(G\),\(B\)分别为\(PA\),\(PD\),\(PC\),\(PB\)的中点.在此几何体中,给出下面四个结论:
①平面\(EFGH∥\)平面\(ABCD\);\(\qquad \qquad\)②直线\(PA∥\)平面\(BDG\);
③直线\(EF∥\)平面\(PBC\); \(\qquad \qquad\) ④直线\(EF∥\)平面\(BDG\).
其中正确的序号是\(\underline{\quad \quad}\) .

7.已知四棱锥\(P-ABCD\)中,底面\(ABCD\)为平行四边形,点\(M\),\(N\),\(Q\)分别在\(PA\),\(BD\),\(PD\)上,且\(PM∶MA=BN∶ND=PQ∶QD\).求证:平面\(MNQ∥\)平面\(PBC\).
8.正方体\(ABCD-A_1 B_1 C_1 D_1\)中.
(1)求证:平面\(A_1 BD∥\)平面\(B_1 D_1 C\);
(2)若\(E\)、\(F\)分别是\(AA_1\),\(CC_1\)的中点,求证:平面\(EB_1 D_1∥\)平面\(FBD\).

9.如图所示,正方体\(ABCD-A_1 B_1 C_1 D_1\)中,侧面对角线\(AB_1\),\(BC_1\)上分别有两点\(E\),\(F\),且\(B_1 E=C_1 F\).
求证:\(EF∥\)平面\(ABCD\).

10.如图,在四棱锥\(P-ABCD\)中,\(\angle A B C=\angle A C D=90^{\circ}\) ,\(\angle B A C=\angle C A D=60^{\circ}\),\(PA⊥\)平面\(ABCD\),\(PA=2\),\(AB=1\).设\(M\),\(N\)分别为\(PD\),\(AD\)的中点.
(1)求证:平面\(CMN∥\)平面\(PAB\);
(2)求三棱锥\(P-ABM\)的体积.

参考答案
-
答案 \(D\)
解析 ①若平面\(\alpha∥\)平面\(\beta\),则直线\(a∥\)平面\(\beta\);因为直线\(a\subset\alpha\),平面\(\alpha∥\)平面\(\beta\),
则\(\alpha\)内的每一条直线都平行平面\(\beta\).显然正确.
②若直线\(a∥\)平面\(\beta\),则平面\(\alpha∥\)平面\(\beta\);因为当平面\(\alpha\)与平面\(\beta\)相加时候,
仍然可以存在直线\(a\subset\alpha\)使直线\(a∥\)平面\(\beta\).故错误.
③若直线\(a\)不平行于平面\(\beta\),则平面\(\alpha\)不平行于平面\(\beta\),平面内有一条直线不平行与令一个平面,
两平面就不会平行.故显然正确.
故选\(D\). -
答案 \(B\)
解析 连结\(A_1 C\)、\(BC\),取\(A_1 C\)的中点\(Q\),\(A_1 B\)的中点\(P\),
连结\(NQ\)、\(PQ\)、\(MN\),
\(\because\)在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,棱长为\(a\),\(M\)、\(N\)分别为\(A_1 B\)、\(AC\)的中点,
\(\therefore NQ∥CC_1\),\(PQ∥BC\),
\(\because PQ\cap NQ=Q\),\(CC_1\cap BC=C\),\(PQ\)、\(NQ\subset\)平面\(PMN\),\(CC_1\),\(BC\subset\)平面\(A_1 BC_1\),
\(\therefore\)平面\(PNQ∥\)平面\(A_1 BC_1\),
\(\because MN\subset\)平面\(PNQ\),\(\therefore MN∥\)平面\(BB_1 C_1 C\).
故选:\(B\).

-
答案 \(A\)
解析 取\(DG\)的中点为\(M\),连结\(AM\),如图所示,
因为\(EF∥DG\),且\(DG=2EF\),所以\(DM∥EF\)且\(DM=EF\),
所以四边形\(DEFM\)是平行四边形,
所以\(DE∥FM\),且\(DE=FM\),
因为平面\(ABC∥\)平面\(DEFG\),平面\(ABC\cap\)平面\(ADEB=AB\),平面\(ADEB\cap\)平面\(DEFG=DE\),
所以\(AB∥DE\),所以\(AB∥FM\),
又\(AB=DE\),所以\(AB=FM\),
所以四边形\(ABFM\)是平行四边形,即\(BF∥AM\),
又\(BF \not \subset\)平面\(ACGD\),\(AM\subset\)平面\(ACGD\),
所以\(BF∥\)平面\(ACGD\).故选项\(A\)正确,
而根据已知条件只能推出上面的关系,无法判断\(CF\)与平面\(ABED\)是否平行,故选项\(B\)错误;
没有任何关系可以推导\(BC∥FG\),故选项\(C\)错误;
没有条件可以判断平面\(ABED\)与平面\(CGF\)是否平行,故选项\(D\)错误.
故选:\(A\).

-
答案 \(A\)
解析 取\(CD\),\(SC\)的中点\(M\),\(N\),连接\(MN\),\(ME\),\(NE\),
\(\because E\)是\(BC\)的中点,
\(\therefore EM∥BD\),\(EN∥SB\),
\(\because EM\),\(EN \not \subset\)面\(SBD\),\(BD\),\(SB\subset\)面\(SBD\),
\(\therefore EM∥\)面\(SBD\),\(EN∥\)面\(SBD\),
又\(\because EM\cap EN=E\),\(EM\),\(EN\subset\)平面\(EMN\),
\(\therefore\)面\(EMN∥\)面\(SBD\),
\(\therefore\)当\(P\)在\(MN\)上移动时,\(PE\subset\)面\(EMN\),
此时保持\(PE∥\)平面\(SBD\),
故选:\(A\).

-
答案 \(H\in\)线段\(AD_1\)
解析 连接\(CD_1\),\(B_1 D_1\),\(B_1 C\),\(A_1 B\),\(A_1 D\),\(BD\),
\(\because\)在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\),\(N\),\(P\)分别是\(C_1 C\),\(C_1 B_1\),\(C_1 D_1\)的中点,
点\(H\)在四边形\(A_1 ADD_1\)的边及其内部运动,
\(\therefore PN∥B_1 D_1\),\(PM∥D_1 C\),\(MN∥B_1 C\),
又\(BD∥B_1 D_1\),\(A_1 B∥D_1 C\),\(A_1 D∥B_1 C\),
\(\therefore PN∥BD\),\(PM∥A_1 B\),\(MN∥A_1 D\),
\(\because PN\cap PM=P\),\(A_1 B\cap BD=B\),
\(\therefore\)平面\(A_1 BD∥\)平面\(PMN\),
\(\therefore H\)满足条件\(H\in\) 线段\(AD_1\)时,有\(BH∥\)平面\(MNP\).

-
答案 ①②③
解析 作出立体图形如图所示,连接\(E\),\(F\),\(G\),\(H\)四点构成平面\(EFGH\),
对于①,因为\(E\),\(F\)分别是\(PA\),\(PD\)的中点,所以\(EF∥AD\),
又\(EF \not \subset\)平面\(ABCD\),\(AD\subset\)平面\(ABCD\),所以\(EF∥\)平面\(ABCD\),
同理\(EH∥\)平面\(ABDC\),又\(EH\cap EF=E\),\(EF\),\(EH\subset\)平面\(EFGH\),
所以平面\(EFGH∥\)平面\(ABCD\),故①正确;
对于②,连接\(AC\),\(BD\)交于点\(M\),连接\(DG\),\(BG\),则\(M\)为\(AC\),\(BD\)的中点,
所以\(MG∥PA\),又\(MG\subset\)平面\(BDG\),\(PA \not \subset\)平面\(BDG\),
所以\(PA∥\)平面\(BDG\),故②正确;
对于③,由①中的分析可知\(EF∥AD\),\(AD∥BC\),所以\(EF∥BC\),
因为\(EF \not \subset\)平面\(PBC\),\(BC\subset\)平面\(PBC\),
所以\(EF∥\)平面\(PBC\),故③正确;
对于④,根据③中的分析可知,\(EF∥BC\),再结合图形可得,\(BC\cap BD=B\),
则直线\(EF\)与平面\(BDG\)不平行,故④错误.
故答案为:①②③.

-
证明 \(\because PM∶MA=BN∶ND=PQ∶QD\),\(\therefore MQ∥AD\),\(NQ∥BP\).
\(\because BP\subset\)平面\(PBC\),\(NQ \not \subset\)平面\(PBC\),
\(\therefore NQ∥\)平面\(PBC\).又底面\(ABCD\)为平行四边形,\(\therefore BC∥AD\),
\(\therefore MQ∥BC\).\(\because BC\subset\)平面\(PBC\),\(MQ \not \subset\)平面\(PBC\),
\(\therefore MQ∥\)平面\(PBC\).
又\(MQ\cap NQ=Q\),根据平面与平面平行的判定定 理,得平面\(MNQ∥\)平面\(PBC\). -
证明 (1)由\(B_1 B//DD_1\),得四边形\(BB_1 D_1 D\)是平行四边形,\(\therefore B_1 D_1//BD\),
又\(BD \not \subset\)平面\(B_1 D_1 C\),\(B_1 D_1\subset\)平面\(B_1 D_1 C\),
\(\therefore BD∥\)平面\(B_1 D_1 C\).
同理\(A_1 D∥\)平面\(B_1 D_1 C\).
而\(A_1 D\cap BD=D\),\(\therefore\)平面\(A_1 BD∥\)平面\(B_1 CD\).
(2)由\(BD∥B_1 D_1\),得\(BD∥\)平面\(EB_1 D_1\).取\(BB_1\)中点\(G\),\(\therefore AE∥B_1 G\).
从而得\(B_1 E∥AG\),同理\(GF∥AD\).\(\therefore AG∥DF\).\(\therefore B_1 E∥DF\).
\(\therefore DF∥\)平面\(EB_1 D_1\).
\(\therefore\)平面\(EB_1 D_1∥\)平面\(FBD\). -
证明 过\(E\)作\(EG∥AB\)交\(BB_1\) 于\(G\),

连接\(GF\),则 \(\dfrac{B_1 E}{B_1 A}=\dfrac{B_1 G}{B_1 B}\),
\(\because B_1 E=C_1 F\),\(B_1 A=C_1 B\),
\(\therefore \dfrac{C_1 F}{C_1 B}=\dfrac{B_1 G}{B_1 B}\),\(\therefore FG∥B_1 C_1∥BC\),
又\(EG\cap FG=G\),\(AB\cap BC=B\),
\(\therefore\)平面\(EFG∥\)平面\(ABCD\),而\(EF\subset\)平面\(EFG\),
\(\therefore EF∥\)平面\(ABCD\). -
答案 (1)略 (2) \(\dfrac{\sqrt{3}}{3}\)
解析 (1)\(\because M\),\(N\)分别为\(PD\),\(AD\)的中点,
\(\therefore MN∥PA\).
又\(\because MN \not \subset\)平面\(PAB\),\(PA\subset\)平面\(PAB\),
\(\therefore MN∥\)平面\(PAB\).
在\(Rt△ACD\)中,\(∠CAD=60°\),\(CN=AN\),\(\therefore ∠ACN=60°\).
又\(\because ∠BAC=60°\),\(\therefore CN∥AB\).
\(\because CN \not \subset\)平面\(PAB\),\(AB\subset\)平面\(PAB\),\(\therefore CN∥\)平面\(PAB\).
又\(\because CN\cap MN=N\),\(\therefore\)平面\(CMN∥\)平面\(PAB\).
(2)由(1)知,平面\(CMN∥\)平面\(PAB\),
\(\therefore\)点\(M\)到平面\(PAB\)的距离等于点\(C\)到平面\(PAB\)的距离.
由已知,\(AB=1\),\(∠ABC=90°\),\(∠BAC=60°\),\(\therefore BC=\sqrt{3}\),
\(\therefore\) 三棱锥\(P-ABM\)的体积:
\(V=V_{M-P A B}=V_{C-P A B}=V_{P-A B C}=\dfrac{1}{3} \times \dfrac{1}{2} \times 1 \times \sqrt{3} \times 2=\dfrac{\sqrt{3}}{3}\).

【B组---提高题】
1.如图,已知平面\(\alpha\),\(\beta\),\(\gamma\),且\(\alpha∥\beta∥\gamma\),直线\(a\),\(b\)分别与平面\(\alpha\),\(\beta\),\(\gamma\)交于点\(A\),\(B\),\(C\)和\(D\),\(E\),\(F\),若\(AB=1\),\(BC=2\),\(DF=9\),则\(EF=\)\(\underline{\quad \quad}\).

2.如图,在棱长为\(2\)的正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\)是\(A_1 B_1\)的中点,点\(P\)是侧面\(CDD_1 C_1\)上的动点,且\(MP∥\)截面\(AB_1 C\),则线段\(MP\)长度的取值范围是\(\underline{\quad \quad}\).

参考答案
-
答案 \(6\)
解析 \(\because AB=1\),\(BC=2\),\(DF=9\),
若\(A\),\(B\),\(C\),\(D\),\(E\),\(F\)六点共面
由面面平行的性质定理可得\(AB∥CD∥EF\)
根据平行线分线段成比例定理可得:\(\dfrac{B C}{A C}=\dfrac{E F}{D F}=\dfrac{2}{3}=\dfrac{E F}{9}\),
\(\therefore EF=6\) ,
若\(A\),\(B\),\(C\),\(D\),\(E\),\(F\)六点不共面,
连接\(AF\),交\(\beta\)于\(M\),连接\(BM\)、\(EM\)、\(BE\).
\(\because \beta∥\gamma\),平面\(ACF\)分别交\(\beta\)、\(\gamma\)于\(BM\)、\(CF\),
\(\therefore BM∥CF\). \(\therefore \dfrac{B C}{A C}=\dfrac{M F}{A F}\),
同理 \(\dfrac{M F}{A F}=\dfrac{E F}{D F}\).
\(\therefore \dfrac{B C}{A C}=\dfrac{E F}{D F}=\dfrac{2}{3}=\dfrac{E F}{9}\), \(\therefore EF=6\),
综上所述:\(EF=6\),
故答案为:\(6\) -
答案 \([\sqrt{6},2\sqrt{2}]\)
解析 取\(CD\)的中点\(N\),\(CC_1\)的中点\(R\),\(B_1 C_1\)的中点\(H\),
则\(MN∥B_1 C∥HR\),\(MH∥AC\),
故平面\(MNRH∥\)平面\(AB_1 C\),
\(MP\subset\)平面\(MNRH\),线段\(MP\)扫过的图形是\(△MNR\),
由\(AB=2\),则\(MN=2\sqrt{2}\),\(NR=\sqrt{2}\),\(MR=\sqrt{6}\),
\(\therefore M N^2=N R^2+M R^2\),
\(\therefore ∠MRN\)是直角,
\(\therefore\)线段\(MP\)长度的取值范围是:\([MR,MN]\),即:\([\sqrt{6},2\sqrt{2}]\).
【C组---拓展题】
1.已知正方体\(ABCD-A_1 B_1 C_1 D_1\)的棱长为\(2\),\(P\)为正方形\(ABCD\)内的一动点(包含边界),\(E\)、\(F\)分别是棱\(AA_1\)、棱\(A_1 D_1\)的中点.若\(D_1 P∥\)平面\(BEF\),则\(AP\)的取值范围是\(\underline{\quad \quad}\).
参考答案
- 答案 \([0, \sqrt{5}]\)
解析 连接\(BC_1\),\(AD_1\),则\(EF∥AD_1∥BC_1\),
又\(EF\subset\)平面\(BEF\),
故\(AD_1∥\)平面\(BEF\),
设\(M\)为\(BC\)的中点,连接\(AM\),\(D_1 M\),
由于\(F\)分别是棱\(A_1 D_1\)的中点,故\(D_1 F=BM\),\(D_1 F∥BM\),
则四边形\(D_1 FBM\)为平行四边形,故\(D_1 M∥FB\),
\(FB\subset\)平面\(BEF\),故\(D_1 M∥\)平面\(BEF\),
又\(AD_1\cap D_1 M=D_1\),\(AD_1\),\(D_1 M\subset\)平面\(D_1 AM\),
故平面\(D_1 AM∥\)平面\(BEF\),
由于\(D_1 P∥\)平面\(BEF\),故\(D_1 P\subset\)平面\(D_1 AM\),
又因为\(P\)为正方形\(ABCD\)内的一动点,且平面\(D_1 AM\cap\)平面\(ABCD=AM\),
故\(AM\)即为动点\(P\)的轨迹,
又\(A M=\sqrt{2^2+1^2}=\sqrt{5}\),
故\(AP\)的取值范围是 \([0, \sqrt{5}]\).



 浙公网安备 33010602011771号
浙公网安备 33010602011771号