8.3.1 棱柱、棱锥、棱台的表面积和体积
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019)]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第二册同步巩固,难度2颗星!
基本知识
棱柱
棱柱的表面积就是围成各个面的面积的和;
体积:\(V=Sh\) (其中\(h\)是棱柱的高)
棱锥
棱锥的表面积就是围成各个面的面积的和;
棱锥体积:\(V=\dfrac{1}{3}Sh\)(其中\(h\)为棱柱的高)
棱台
棱台的表面积就是围成各个面的面积的和;
棱台体积 \(V=\dfrac{1}{3}\left(S^{\prime}+\sqrt{S S^{\prime}}+S\right) h\)
其中\(S\) ,\(S'\)分别为上,下底面面积,\(h\)为棱台的高.
解释
棱台的体积可以视为两个棱锥体积的差,简证如下
如下图,设\(S\) , \(S'\)分别为上底四边形\(A'B'C'D'\)面积,下底面四边形\(ABCD\)面积,\(h=OO'\)为高.
由相似易得, \(\dfrac{P O}{P O^{\prime}}=\sqrt{\dfrac{S}{S^{\prime}}}\),\(h=OO'=PO-PO'\),
则 \(P O^{\prime}=\dfrac{h\left(\sqrt{s s^{\prime}}+s^{\prime}\right)}{s-s^{\prime}}\), \(P O=\dfrac{h\left(\sqrt{s s^{\prime}}+s\right)}{s-s^{\prime}}\),
所以 \(V_{\text {棱台 }}=\dfrac{1}{3} \cdot P O \cdot S-\dfrac{1}{3} \cdot P O^{\prime} \cdot S^{\prime}=\dfrac{1}{3} \cdot \dfrac{h\left(\sqrt{SS^{\prime}}+S\right)}{S-S^{\prime}} \cdot S-\dfrac{1}{3} \cdot \dfrac{h\left(\sqrt{S S^{\prime}}+S^{\prime}\right)}{S-S^{\prime}} \cdot S^{\prime}\)
\(=\dfrac{1}{3}\left(S^{\prime}+\sqrt{S S^{\prime}}+S\right) h\).
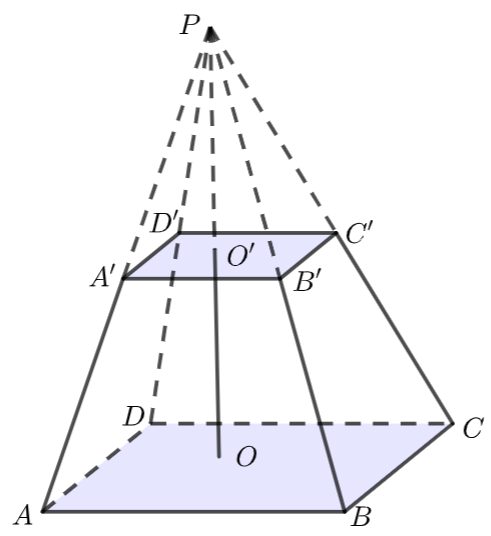
当\(S'=0\)时,棱台变成棱锥,体积公式就变成棱锥的体积公式.
基本方法
【题型1】 棱柱、棱锥、棱台的表面积
【典题1】 刍(chú)甍(méng)是中国古代算数中的一种几何体,其结构特征是:底面为长方形,顶棱和底面平行,且长度不等于底面平行的棱长的五面体,是一个对称的楔形体.已知一个刍甍底边长为\(4\),底边宽为\(3\),上棱长为\(2\),高为\(2\),则它的表面积是( )

A.\(27+3\sqrt{5}\) \(\qquad \qquad \qquad\) B.\(42+3\sqrt{5}\) \(\qquad \qquad \qquad\) C.\(27+3\sqrt{3}\) \(\qquad \qquad \qquad\) D.\(42+6\sqrt{3}\)
解析 根据题意,如图:刍甍的底面为长方形\(ABCD\),\(AB=4\),\(BC=3\),
则其面积\(S_1=4×3=12\);
侧面为两个三角形\(△ADE\)和\(△BFC\),两个梯形\(ABFE\)和\(CDEF\),
\(△BFC\)中,斜高\(F N=\sqrt{1+4}=\sqrt{5}\),则其面积 \(S_2=\dfrac{3 \sqrt{5}}{2}\),
同理:\(△ADE\)的面积 \(S_3=\dfrac{3 \sqrt{5}}{2}\),
梯形\(ABFE\)中,\(EF=2\),\(AB=4\),斜高 \(E M=\dfrac{5}{2}\),
则其面积 \(S_4=\dfrac{1}{2}(2+4) \times \dfrac{5}{2}=\dfrac{15}{2}\),
同理:梯形\(CDEF\)的面积 \(S_5=\dfrac{15}{2}\),
则它的表面积 \(S=12+\dfrac{3 \sqrt{5}}{2}+\dfrac{3 \sqrt{5}}{2}+\dfrac{15}{2}+\dfrac{15}{2}=27+3 \sqrt{5}\);
故选:\(A\).

【巩固练习】
1.已知正方体\(ABCD-A' B' C' D'\)的棱长为\(2\),棱\(AB\),\(AD\),\(AA'\)的中点分别为\(E\),\(F\),\(G\),首先截去三棱锥\(A﹣EFG\),类似的,再截去另外\(7\)个三棱锥,则余下的几何体的表面积为\(\underline{\quad \quad}\).
2.如图所示,正方体的棱长为\(4\),以其所有面的中心为顶点的多面体的表面面积为\(\underline{\quad \quad}\).

3.“李白斗酒诗百篇,长安市上酒家眠”,本诗句中的“斗”的本义是指盛酒的器具,后又作为计量蜋食的工具,某数学兴趣小组利用相关材料制作了一个如图所示的正四棱台来模拟“斗”,用它研究“斗”的相关几何性质,已知该四棱台的上、下底的边长分别是\(2\)、\(4\),高为\(1\),则该四棱台的表面积为\(\underline{\quad \quad}\).

参考答案
-
答案 \(12+4\sqrt{3}\)
解析如图, \(S_{\text {正方形GEMH }}=\sqrt{2} \times \sqrt{2}=2\), \(S_{\triangle E F G}=\dfrac{1}{2} \times \sqrt{2} \times \sqrt{2} \times \sin 60^{\circ}=\dfrac{\sqrt{3}}{2}\),
而余下的几何体的表面积等于\(6\)个正方形\(GEMN\)的面积加上\(8\)个三角形\(EFG\)的面积之和,
故所求几何体的表面积为 \(2 \times 6+\dfrac{\sqrt{3}}{2} \times 8=12+4 \sqrt{3}\),
故答案为:\(12+4\sqrt{3}\).

-
答案 \(16\sqrt{3}\)
解析 由题意知所得几何体是八面体,且八面体是两个底面边长为\(2\sqrt{2}\),高为\(2\)的四棱锥组成;
则该八面体是这两个四棱锥的侧面积之和,
由四棱锥的侧棱长为 \(l=\sqrt{2^2+2^2}=2 \sqrt{2}\),
所以该正方体各个面的中心为顶点的凸多面体的表面积为:
\(S=8×S_△=8×\dfrac{1}{2}×2\sqrt{2}×2\sqrt{2}×\sin 60^{\circ}=16\sqrt{3}\). -
答案 \(20+12\sqrt{2}\)
解析 如下图所示:\(AB=DE=1\),\(AD=\dfrac{1}{2}×2=1\),\(BC=4×\dfrac{1}{2}=2\),
所以 \(C D=\sqrt{1^2+(2-1)^2}=\sqrt{2}\),
所以该四棱台的表面积为:\(22+42+4×\dfrac{1}{2}×(2+4)×\sqrt{2}=20+12\sqrt{2}\).

【题型2】 棱柱、棱锥、棱台的体积
【典题1】 过三棱台\(ABC-A'B'C'\)上底面的一边\(A'C'\)与侧棱\(BB'\)平行的一个截面,把棱台分为两部分,截面与\(AB\),\(CB\)的交点\(D\),\(E\)分别为\(AB\),\(CB\)的中点.求棱台被分成两部分的体积的比.

解析 设棱台上底面\(△A'B'C'\)的面积为\(S'\),棱台的高为\(h\).
由题意可知\(△A'B'C'≌△DBE\).
\(∵△DBE∽△ABC\),\(D\),\(E\)分别是\(AB\),\(BC\)的中点,
\(\therefore \dfrac{S_{\triangle D B E}}{S_{\triangle A B C}}=\dfrac{1}{4}\). \(\therefore S \triangle A B C=4 S^{\prime}\).
\(\therefore V_{\text {台 } A B C-A^{\prime} B^{\prime} C^{\prime}}=\dfrac{1}{3} h \cdot\left(S^{\prime}+\sqrt{S^{\prime} \cdot 4 S^{\prime}}+4 S^{\prime}\right)=\dfrac{1}{3} h \cdot 7 S^{\prime}=\dfrac{7}{3} h \cdot S^{\prime}\),
\(V_{\text {柱 } D B E-A^{\prime} B^{\prime} C^{\prime}}=S^{\prime} \cdot h\).
\(∴\)棱台被分成的两部分体积比为\(4:3\)或\(3:4\).
【巩固练习】
1.如图,长方体\(ABCD-A_1 B_1 C_1 D_1\)的体积是\(36\),点\(E\)在棱\(CC_1\)上,且\(CE=2EC_1\),则三棱锥\(E-BCD\)的体积是( )

A.\(2\) \(\qquad \qquad \qquad \qquad\) B.\(3\) \(\qquad \qquad \qquad \qquad\) C.\(4\) \(\qquad \qquad \qquad \qquad\) D.\(6\)
2.若正三棱柱的所有棱长均为\(a\),且其体积为\(16\sqrt{3}\),则侧面积为\(\underline{\quad \quad}\) .
3.如图\(1\),在高为\(h\)的直三棱柱容器\(ABC-A_1 B_1 C_1\)中,\(AB=AC=2\),\(AB⊥AC\).现往该容器内灌进一些水,水深为\(2\),然后固定容器底面的一边\(AB\)于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰好为\(A_1 B_1 C\)(如图\(2\)),则容器的高\(h\)为\(\underline{\quad \quad}\).

4.在直三棱柱\(ABC-A_1 B_1 C_1\)中,平面\(ABC\)是下底面.\(M\)是\(BB_1\)上的点,\(AB=3\),\(BC=4\),\(AC=5\),\(CC_1=7\),过三点\(A\)、\(M\)、\(C_1\)作截面,当截面周长最小时,截面将三棱柱分成的上、下两部分的体积比为\(\underline{\quad \quad}\).
参考答案
-
答案 \(C\)
解析 根据题意可得\(V_{E-B C D}=\dfrac{2}{3} V_{C_1-B C D}=\dfrac{2}{3} \times \dfrac{1}{2} V_{C_1-\mathrm{ABCD}}\)
\(=\dfrac{2}{3} \times \dfrac{1}{2} \times \dfrac{1}{3} \mathrm{~V}_{\text {长方体 }} \mathrm{ABCD}-\mathrm{A}_1 \mathrm{~B}_1 \mathrm{C}_1 \mathrm{D}_1=\dfrac{1}{9} \times 36=4\),
故选:\(C\). -
答案 \(48\)
解析 由题意可得,正棱柱的底面是边长等于\(a\)的等边三角形,面积为 \(\dfrac{1}{2} \cdot a \cdot a \cdot \sin 60^{\circ}\),
正棱柱的高为\(a\),
\(\therefore\left(\dfrac{1}{2} \cdot a \cdot a \sin 60^{\circ}\right) \cdot a=16 \sqrt{3}\),\(∴a=4\),
侧面积为\(3×4×4=48\). -
答案 \(3\)
解析 在图\(1\)中 \(V_{\text {水 }}=\dfrac{1}{2} \times 2 \times 2 \times 2=4\),
在图\(2\)中, \(V_{\text {水 }}=V_{\mathrm{AEC}-\mathrm{A}_1 \mathrm{~B}_1 \mathrm{C}_1}-\mathrm{V}_{\mathrm{C}-\mathrm{A}_1 \mathrm{~B}_1 \mathrm{C}_1}\)
\(=\dfrac{1}{2} \times 2 \times 2 \times \mathrm{h}-\dfrac{1}{3} \times \dfrac{1}{2} \times 2 \times 2 \times \mathrm{h}=\dfrac{4}{3} \mathrm{~h}\),
\(\therefore \dfrac{4}{3} \mathrm{~h}=4\),\(∴h=3\). -
答案 \(\dfrac{11}{10}\)
解析 由\(AB=3\),\(BC=4\),\(AC=5\),得 \(A B^2+B C^2=A C^2\),
\(∴AB⊥BC\).
将平面\(ABB_1 A_1\)与平面\(BCC_1 B_1\)放在一个平面内,
连接\(AC_1\),与\(BB_1\)的交点即为\(M\),此时\(BM=3\),
设四棱锥\(A-BCC_1 M\)的体积为\(V_1\),
则 \(V_1=\dfrac{1}{3} \times \dfrac{1}{2} \times(3+7) \times 4 \times 3=20\),
三棱柱\(ABC-A_1 B_1 C_1\)的体积\(V=\dfrac{1}{2}×4×3×7=42\).
\(∴\)当截面周长最小时,截面将三棱柱分成的上、下两部分的体积比为 \(\dfrac{V-V_1}{V_1}=\dfrac{11}{10}\).

分层练习
【A组---基础题】
1.棱长均为\(1\)的正四面体的表面积是( )
A.\(\sqrt{3}\) \(\qquad \qquad \qquad \qquad\) B.\(2\sqrt{3}\) \(\qquad \qquad \qquad \qquad\) C.\(3\sqrt{3}\) \(\qquad \qquad \qquad \qquad\) D.\(4\sqrt{3}\)
2.“斗”不仅是我国古代容量单位,还是量粮食的器具,如图所示,其可近似看作正四棱台,上底面是边长为\(6dm\)的正方形,下底面是边长为\(2dm\)的正方形,高为\(4dm\).“斗”的面的厚度忽略不计,则该“斗”的所有侧面的面积之和与下底面的面积之比为( )

A.\(8\sqrt{5}\) \(\qquad \qquad \qquad \qquad\) B.\(16\) \(\qquad \qquad \qquad \qquad\) C.\(2\sqrt{5}\) \(\qquad \qquad \qquad \qquad\) D.\(4\)
3.正四棱锥底面正方形的边长为\(4\),高与斜高的夹角为\(30^{\circ}\),则该四棱锥的侧面积为( )
A.\(32\) \(\qquad \qquad \qquad \qquad\) B.\(48\) \(\qquad \qquad \qquad \qquad\) C.\(64\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{32}{3}\)
4.分别以直角三角形的斜边和两直角边所在直线为轴,将三角形旋转一周所得旋转体的体积依次为\(V_1\) 、\(V_2\) 、\(V_3\),则( )
A.\(V_1=V_2+V_3\) \(\qquad\) B. \(V_1^2=V_2^2+V_3^2\) \(\qquad\) C. \(\dfrac{1}{V_1{ }^2}=\dfrac{1}{V_2^2}+\dfrac{1}{V_3^2}\) \(\qquad\) D. \(\dfrac{1}{V_1}=\dfrac{1}{V_2}+\dfrac{1}{V_3}\)
5.如图所示,三棱柱容器的棱\(CC_1\)长为\(8\),且\(CC_1\)到侧面\(AA_1 BB_1\)的距离为\(8\sqrt{2}\),若将该容积装入容积一半的水,再以侧面\(AA_1 BB_1\)水平放置,则水面高度为( )
A.\(4\) \(\qquad \qquad \qquad \qquad\) B.\(4\sqrt{2}\) \(\qquad \qquad \qquad \qquad\) C.\(8\sqrt{2}-8\) \(\qquad \qquad \qquad \qquad\) D.\(8-4\sqrt{2}\)

6.某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样大的四面体得到的(如图).则该几何体共有\(\underline{\quad \quad}\)个面;如果被截正方体的棱长是\(50cm\),那么石凳的表面积是\(\underline{\quad \quad}\) \(\mathrm{cm}^2\).

7.如图,在直三棱柱\(ABC-A_1 B_1 C_1\)中,\(AB=1\),\(BC=2\),\(BB_1=3\),\(∠ABC=90^{\circ}\),点\(D\)为侧棱\(BB_1\)上的动点,当\(AD+DC_1\)最小时,三棱锥\(D-ABC_1\)的体积为\(\underline{\quad \quad}\).

8.已知正四棱柱\(ABCD-A_1 B_1 C_1 D_1\)中\(AB=2\),\(AA_1=3\),\(O\)为上底面中心.设正四棱柱\(ABCD-A_1 B_1 C_1 D_1\)与正四棱锥\(O-A_1 B_1 C_1 D_1\)的侧面积分别为\(S_1\),\(S_2\),则 \(\dfrac{S_2}{S_1}=\) \(\underline{\quad \quad}\).
9.一块边长为\(6cm\)的正方形铁皮按如图(1)所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正三棱锥形容器,将该容器按如图(2)放置,若其正视图为等腰直角三角形(如图(3)),则该容器的体积为\(\underline{\quad \quad}\).

10.如图所示的是一个正四棱锥\(E-ABCD\)(底面是正方形,从顶点向底面作垂线,垂足是底面中心的四棱锥),其中\(EA=5\),\(AB=6\),\(F\)为线段\(BC\)的中点,\(EO\)是正四棱锥的高.
(1)求正四棱锥\(E-ABCD\)的表面积;
(2)求正四棱锥\(E-ABCD\)的体积.

参考答案
-
答案 \(A\)
解析 \(∵\)正四面体的棱长均为\(1\)
\(∴\)正四面体每一个面均为边长等于\(1\)的等边三角形,
其面积 \(S_1=\dfrac{1}{2} \times 1 \times 1\times \sin 60^{\circ}=\dfrac{\sqrt{3}}{4}\),
因此正四面体的表面积是\(S=4S_1=\sqrt{3}\),
故选:\(A\). -
答案 \(A\)
解析 由题意可知,四棱台的侧面均为等腰梯形,则其斜高为 \(\sqrt{4^2+\left[\dfrac{1}{2}(6-2)\right]^2}=2 \sqrt{5} \mathrm{dm}\),
所以“斗”的所有侧面的面积之和为\(S_1=4×\dfrac{1}{2}(6+2)×2\sqrt{5}=32\sqrt{5}\),
下底面的面积为\(S_2=4\),
所以 \(\dfrac{S_1}{S_2}=8 \sqrt{5}\),
故选:\(A\). -
答案 \(A\)
解析 如图,正四棱锥的高\(PO\),斜高\(PE\),底面边心距\(OE\)组成直角\(△POE\).
\(∵OE=2cm\), \(\angle O P E=30^{\circ}\),
\(∴\)斜高 \(P E=\dfrac{O E}{\sin 30^{\circ}}=4\),
\(\therefore S_{\text {正四棱雉 }}=\dfrac{1}{2} C h^{\prime}=\dfrac{1}{2} \times 4 \times 4 \times 4=32\).
故选:\(A\).

-
答案 \(C\)
解析 设直角三角形的三边分别为\(a\)、\(b\)、\(c\), \(a^2+b^2=c^2\),即\(c\)为斜边,
则以边\(c\)所在直线为轴,将三角形旋转一周所得旋转体的体积为\(V_1\),
则 \(V_1=\dfrac{1}{3} \pi\left(\dfrac{a b}{c}\right)^2 \cdot c=\dfrac{1}{3} \pi a^2 \cdot b^2 \cdot \dfrac{1}{c}\),
以边\(a\)所在直线为轴,将三角形旋转一周所得旋转体的体积为\(V_2\),则 \(V_2=\dfrac{1}{3} \pi b^2 \cdot a\),
以边\(b\)所在直线为轴,将三角形旋转一周所得旋转体的体积为\(V_3\),则 \(V_3=\dfrac{1}{3} \pi a^2 \cdot b\),
\(\therefore \dfrac{1}{V_1^2}=\dfrac{1}{V_2^2}+\dfrac{1}{V_3^2} \text {, }\),
故选\(C\). -
答案 \(C\)
解析 设三棱柱中底面\(ABC\)上的高为\(h\),
则当以平面\(ABC\)为底时,水的体积 \(V=\dfrac{1}{2} h S_{\triangle A B C}\),
当以侧面\(AA_1 B_1 B\)水平放置时,水呈现为四棱柱,此时底面作图如下:

其中\(CG⊥AB\),由题意可知\(AB∥DE\),则\(CF⊥DE\),
设其底面四边形的面积为\(S\)(阴影面积),水的体积可表示为\(V=hS\),可得 \(S=\dfrac{1}{2} S_{\triangle A B C}\),
即 \(S_{\triangle C D E}=\dfrac{1}{2} S_{\triangle \mathrm{ABC}}\),则 \(\dfrac{\mathrm{CF}}{\mathrm{CG}}=\dfrac{\sqrt{2}}{2}\),即 \(F G=C G-\dfrac{\sqrt{2}}{2} C G=8 \sqrt{2}-8\),
则水面高度为\(8\sqrt{2}-8\),
故选:\(C\). -
答案 \(14\), \(2500 \sqrt{3}+7500\).
解析 由题意知截去的八个四面体是全等的正三棱锥,\(8\)个底面三角形,再加上\(6\)个小正方形,
所以该几何体共有\(14\)个面;
如果被截正方体的棱长是\(50cm\),那么石凳的表面积是
\(S_{\text {表面积 }}=8 \times \dfrac{1}{2} \times 25 \sqrt{2} \times 25 \sqrt{2} \times \sin 60^{\circ}+6 \times 25 \sqrt{2} \times 25 \sqrt{2}\)\(=2500 \sqrt{3}+7500\left(\mathrm{~cm}^2\right)\).
故答案为:\(14\), \(2500 \sqrt{3}+7500\). -
答案 \(\dfrac{1}{3}\)
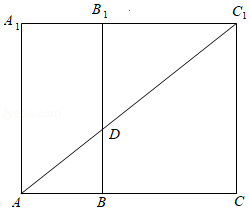
解析 将直三棱柱\(ABC-A_1 B_1 C_1\)展开成矩形\(ACC_1 A_1\),如图,
连结\(AC_1\),交\(BB_1\)于\(D\),此时\(AD+DC_1\)最小,
\(∵AB=1\),\(BC=2\),\(BB_1=3\),\(∠ABC=90°\),点\(D\)为侧棱\(BB_1\)上的动点,
\(∴\)当\(AD+DC_1\)最小时,\(BD=1\),
此时三棱锥\(D-ABC_1\)的体积
\(V_{D-A B C_1}=V_{C_1-A B D}=\dfrac{1}{3} \times S_{\triangle A B D} \times B_1 C_1=\dfrac{1}{3} \times \dfrac{1}{2} \times A B \times B D \times B_1 C_1\)\(=\dfrac{1}{3} \times \dfrac{1}{2} \times 1 \times 1 \times 2=\dfrac{1}{3}\).
故答案为 \(\dfrac{1}{3}\).
-
答案 \(\dfrac{\sqrt{10}}{6}\)
解析 如图,

正四棱柱\(ABCD-A_1 B_1 C_1 D_1\)中,\(AB=2\),\(AA_1=3\),
则正四棱柱\(ABCD-A_1 B_1 C_1 D_1\)的侧面积分别为\(S_1=4×2×3=24\);
正四棱锥\(O-A_1 B_1 C_1 D_1\)的斜高为 \(\sqrt{1^2+3^2}=\sqrt{10}\).
\(∴\)正四棱锥\(O-A_1 B_1 C_1 D_1\)的侧面积 \(S_2=4 \times \dfrac{1}{2} \times 2 \times \sqrt{10}=4 \sqrt{10}\).
\(\therefore \dfrac{S_2}{S_1}=\dfrac{4 \sqrt{10}}{24}=\dfrac{\sqrt{10}}{6}\).
故答案为: \(\dfrac{\sqrt{10}}{6}\). -
答案 \(9\sqrt{2}\)
解析 如图(2),\(△PMN\)是该四棱锥的正视图,
由图(1)知 \(PM+PN=6\),且\(PM=PN\),
由\(△PMN\)为等腰直角三角形,知\(MN=3\sqrt{2}\),\(PM=3\),
设\(MN\)中点为\(O\),则\(PO⊥\)平面\(ABCD\), \(\therefore P O=\dfrac{1}{2} M N=\dfrac{3 \sqrt{2}}{2}\),
\(∴\)该容器的体积为\(V_{P-A B C D}=\dfrac{1}{3} \times(3 \sqrt{2})^2 \times \dfrac{3 \sqrt{2}}{2}=\dfrac{1}{3} \times 18 \times \dfrac{3 \sqrt{2}}{2}=9 \sqrt{2}\).

-
答案 (1) \(84\) (2) \(12 \sqrt{7}\).
解析 (1)因为\(EB=BC\),\(F\)为线段\(BC\)的中点,所以\(EF⊥BC\).
因为\(BF=\dfrac{1}{2} BC=3\),\(EB=5\),
所以\(V_E=\sqrt{5^2-3^2}=4\),
\(S_{E-A B C D}=\left(\dfrac{1}{2} \times 6 \times 4\right) \times 4+6 \times 6=48+36=84\).
(2)因为\(EO\)是正四棱锥\(E-ABCD\)的高,所以\(EO⊥OF\).
因为\(OF=\dfrac{1}{2} AB=3\),由(1)知,\(EF=4\),
所以 \(\mathrm{EO}=\sqrt{\mathrm{EF}^2-\mathrm{OF}^2}=\sqrt{4^2-3^2}=\sqrt{7}\),
\(V_{\mathrm{E}-\mathrm{AECD}}=\dfrac{1}{3} \times 6 \times 6 \times \sqrt{7}=12 \sqrt{7}\).
【B组---提高题】
1.以\(A\)为顶点的三棱锥\(A-BCD\),其侧棱两两互相垂直,且该三棱锥外接球的表面积为\(8π\),则以\(A\)为顶点,以面\(BCD\)为下底面的三棱锥的侧面积之和的最大值为( )
A.\(2\) \(\qquad \qquad \qquad \qquad\) B.\(4\) \(\qquad \qquad \qquad \qquad\) C.\(6\) \(\qquad \qquad \qquad \qquad\) D.\(7\)
2.半径为\(2\)的球\(O\)内有一个内接正三棱柱,则正三棱柱的侧面积的最大值为( )
A.\(9\sqrt{3}\) \(\qquad \qquad \qquad \qquad\) B.\(12\sqrt{3}\) \(\qquad \qquad \qquad \qquad\) C.\(16\sqrt{3}\) \(\qquad \qquad \qquad \qquad\) D.\(18\sqrt{3}\)
参考答案
-
答案 \(B\)
解析 把三棱锥\(A-BCD\)补成长方体,如图所示:

则三棱锥\(A-BCD\)外接球即是长方体的外接球,设长方体的棱长分别为\(a\),\(b\),\(c\),
\(∵\)三棱锥\(A-BCD\)外接球的表面积为\(8π\),
\(∴\)三棱锥\(A-BCD\)外接球的半径为\(\sqrt{2}\),
\(\therefore a^2+b^2+c^2=8\),
\(\because 2 a b \leq a^2+b^2\), \(2 a c \leq a^2+c^2\), \(2 b c \leq b^2+c^2\),
\(\therefore 2(a b+a c+b c) \leq 2\left(a^2+b^2+c^2\right)\),
\(∴ab+ac+bc≤8\),
\(∴\)三棱锥的侧面积之和 \(S=\dfrac{1}{2}(a b+a c+b c) \leq 4\),
故选:\(B\). -
答案 \(B\)
解析 如图所示,
设正三棱柱上下底面的中心分别为\(O_1\),\(O_2\),底面边长与高分别为\(x\),\(h\),
则 \(O_2 A=\dfrac{\sqrt{3}}{3} x\),在\(Rt△OAO_2\)中, \(\dfrac{h^2}{4}+\dfrac{x^2}{3}=4\),
化为 \(h^2=16-\dfrac{4}{3} x^2\),
\(\because S_{\text {侧 }}=3 x h\),
\(\therefore S_{\text {侧 }}^2=9 x^2 h^2=12 x^2\left(12-x^2\right) \leq 12\left(\dfrac{x^2+12-x^2}{2}\right)^2=432\).
当且仅当\(x_2=12-x_2\),即\(x=\sqrt{6}\)时取等号,
此时\(S_{\text {侧 }}=12 \sqrt{3}\).
故选:\(B\).

【C组---拓展题】
1.如图,在\(△ABC\)中,\(AB=BC=2\),\(∠ABC=120°\).若平面\(ABC\)外的点\(P\)和线段\(AC\)上的点\(D\),满足\(PD=DA\),\(PB=BA\),则四面体\(PBCD\)的体积的最大值是\(\underline{\quad \quad}\).

参考答案
- 答案 \(\dfrac{1}{2}\)
解析 如图,\(M\)是\(AC\)的中点.
①当\(AD=t <AM=\sqrt{3}\)时,
如图,此时高为\(P\)到\(BD\)的距离,也就是\(A\)到\(BD\)的距离,即图中\(AE\),

\(DM=\sqrt{3}-t\),由\(△ADE∽△BDM\),
可得 \(\dfrac{h}{1}=\dfrac{t}{\sqrt{(\sqrt{3}-t)^2+1}}\), \(\therefore h=\dfrac{t}{\sqrt{(\sqrt{3}-t)^2+1}}\),
\(V=\dfrac{1}{3} \cdot \dfrac{1}{2} \cdot(2 \sqrt{3}-t) \cdot 1 \cdot \dfrac{t}{\sqrt{(\sqrt{3}}-t)^2+1}=\dfrac{1}{6} \cdot \dfrac{3-(\sqrt{3}-t)^2}{\sqrt{(\sqrt{3}-t)^2+1}}\),\(t∈(0,\sqrt{3})\)
②当\(AD=t>AM=\sqrt{3}\)时,
如图,此时高为\(P\)到\(BD\)的距离,也就是\(A\)到\(BD\)的距离,即图中\(AH\),

\(DM=t-\sqrt{3}\),由等面积,可得\(\dfrac{1}{2}⋅AD⋅BM=\dfrac{1}{2}⋅BD⋅AH\),
\(\therefore \dfrac{1}{2} \cdot t \cdot 1=\dfrac{1}{2} \sqrt{(t-\sqrt{3})^2+1}\),
\(\therefore h=\dfrac{t}{\sqrt{(\sqrt{3}-t)^2+1}}\),
\(\therefore V=\dfrac{1}{3} \cdot \dfrac{1}{2} \cdot(2 \sqrt{3}-t) \cdot 1 \cdot \dfrac{t}{\sqrt{(\sqrt{3}}-t)^2+1}=\dfrac{1}{6} \cdot \dfrac{3-(\sqrt{3}-t)^2}{\sqrt{(\sqrt{3}-t)^2+1}}\),\(t∈(\sqrt{3},2\sqrt{3})\)
综上所述, \(V=\dfrac{1}{6} \cdot \dfrac{3-(\sqrt{3}-t)^2}{\sqrt{(\sqrt{3}-t)^2+1}}\),\(t∈(0,2\sqrt{3})\)
令 \(m=\sqrt{(\sqrt{3}-t)^2+1} \in[1,2)\),\(∴m=1\)时, \(V_{\max }=\dfrac{1}{2}\).
故答案为\(\dfrac{1}{2}\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号