8.1 基本立体图形(2)-- 圆柱、圆锥、圆台、球
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019)]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第二册同步巩固,难度2颗星!
基础知识
圆柱
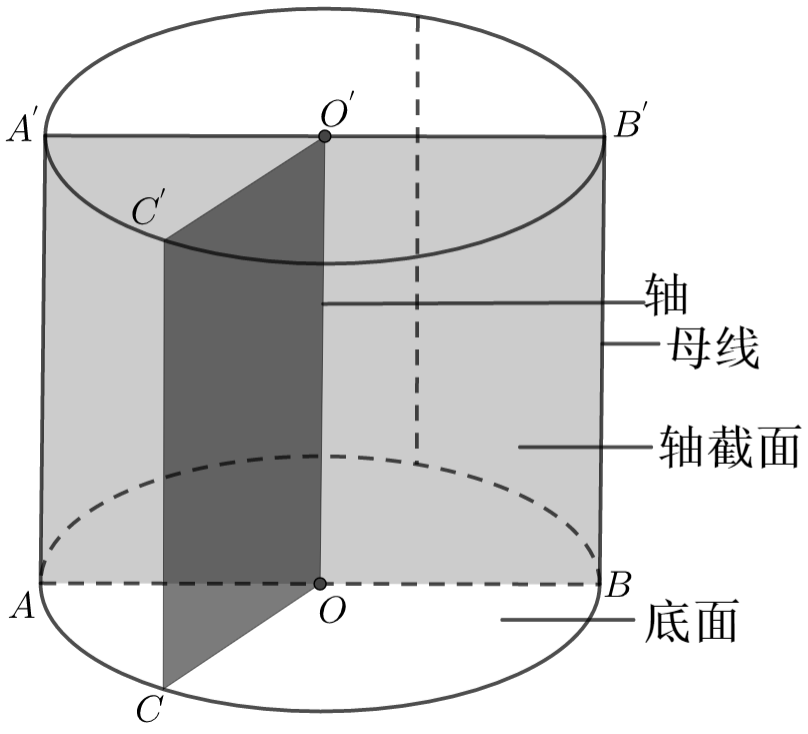
(1) 概念
以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱.
(2) 性质
上、下底及平行于底面的截面都是等圆;过轴的截面(轴截面)是全等的矩形.
(3) 侧面展开图
圆柱的侧面展开图是以底面周长和母线长为邻边的矩形.
圆锥
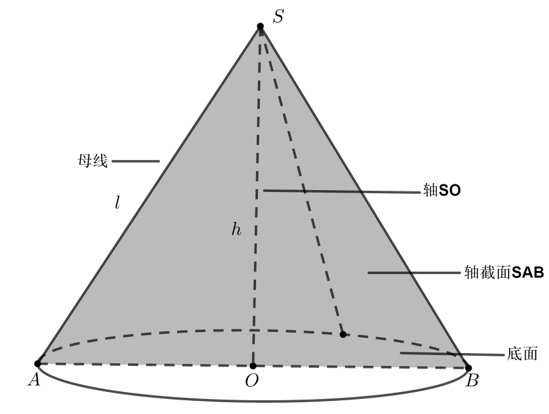
(1) 概念
以直角三角形的一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆锥.
(2) 性质
① 平行于底面的截面都是圆,截面直径与底面直径之比等于顶点到截面的距离与顶点到底面的距离之比;
② 轴截面是等腰三角形;如右图:三角形\(SAB\)
③ 如上图:\(l^2=h^2+r^2\).
(3) 侧面展开图
圆锥的侧面展开图是以顶点为圆心,以母线长为半径的扇形.
圆台
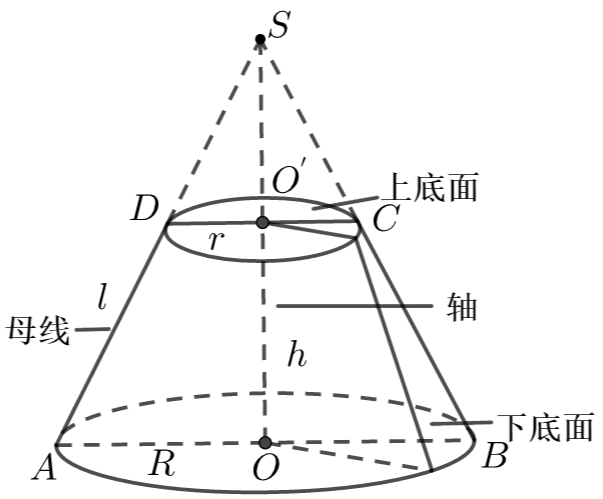
用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台.
球体
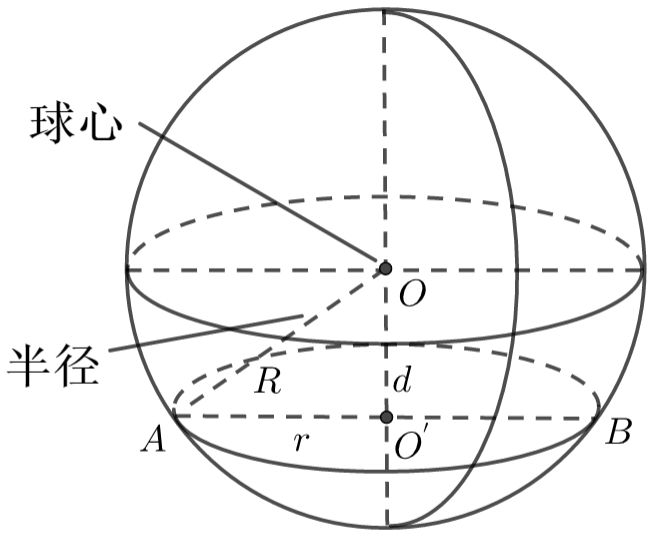
(1) 概念
以半圆的直径所在直线为旋转轴,半圆旋转一周形成的旋转体叫做球体,简称球.
(2) 性质
① 球心与截面圆心的连线垂直于截面;
② \(R^2=r^2+d^2\)(其中,球心到截面的距离为\(d\)、球的半径为\(R\)、截面的半径为\(r\)).
基本方法
【题型1】 圆柱、圆锥、圆台、球的概念
【典题1】下列叙述中,正确的个数是( )
①以直角三角形的一边为轴旋转所得的旋转体是圆锥;
②以直角梯形的一腰为轴旋转所得的几何体是圆台;
③用一个平面去截圆锥,得到一个圆锥和一个圆台;
④圆面绕它的任一直径旋转形成的几何体是球.
A.\(3\) \(\qquad \qquad \qquad\) B.\(2\) \(\qquad \qquad \qquad\) C.\(1\)\(\qquad \qquad \qquad\) D.\(0\)
解析对于①,以直角三角形的一直角边为轴旋转所得的旋转体是圆锥,故①错误;
对于②,以直角梯形的垂直于底边的一腰为轴旋转所得的几何体是圆台,故②错误;
对于③,用平行于圆锥底面的一个平面去截圆锥,得到一个圆锥和一个圆台,故③错误;
对于④,圆面绕它的任一直径旋转形成的几何体是球,故④正确.
故选:\(C\).
【巩固练习】
1.判断下列说法是否正确,并说明理由:
(1)矩形绕一直线旋转所成的旋转体是圆柱;
(2)直角三角形绕其 一边所在的直线旋转所成的旋转体是圆锥;
(3)直角梯形绕其一腰所在直线旋转所成的旋转体是圆台;
(4)圆面绕其任意一条直径旋转都能形成球.
2.用一个平面截一 个几何体,无论如何截,所得截面都是圆面,则这个几何体一定是( )
A.圆锥 \(\qquad \qquad \qquad\)B.圆柱 \(\qquad \qquad \qquad\) C.圆台 \(\qquad \qquad \qquad\) D.球体
3.下列说法正确的是( )
A.圆柱上下底面各取一点,它们的连线即为圆柱的母线
B.过球上任意两点,有且仅有一个大圆
C.圆锥的轴截面是等腰三角形
D.用一个平面去截球,所得的圆即为大圆
4.(多选)下列说法正确的是( )
A.夹在圆柱的两个平行截面间的几何体还是一个旋转体
B.圆锥用平行于底面的平面截去一个小圆锥后剩余的部分是圆台
C.圆锥的顶点与底面圆周上任意一点的连线都是母线
D.过球面上任意两不同点的大圆有且只有一个
参考答案
-
答案 (1)错;(2)错;(3)错;(4)正确;
解析(1)错.矩形绕其一边所在直线旋转形成的才是圆柱.
(2)错.直角三角形绕斜边所在的直线旋转形成的是两个同底圆锥的组合体.
(3)错.直角梯形绕垂直于底的腰所在直线旋转形成圆台,若绕另一腰所在直线旋转形成的是组合体.
(4)正确.符合球的定义. -
答案 \(D\)
-
答案 \(C\)
解析对于\(A\),圆柱上下底面各取一点,这两点的连线垂直于底面时即为圆柱的母线,所以选项\(A\)错误;
对于\(B\),当球面上的两点是球直径的端点时,过这两点的大圆有无数个,所以选项\(B\)错误;
对于\(C\),圆锥的轴截面是过顶点与底面圆心的截面,是等腰三角形,选项\(C\)正确;
对于\(D\),用一个过球的直径的平面去截球,所得的圆是大圆,所以选项\(D\)错误.
故选:\(C\). -
答案 \(BC\)
解析对于\(A\),当两个平行平面与圆柱底面平行时,夹在圆柱的两个平行截面间的几何体是旋转体,
当两个平行平面与圆柱底面不平行时,夹在圆柱的两个平行截面间的几何体不是旋转体,故\(A\)错误;
对于\(B\),根据圆台的定义,圆锥用平行于底面的平面截去一个小圆锥后剩余的部分是圆台,故\(B\)正确;
对于\(C\),由圆锥的性质得圆锥的顶点与底面圆周上任意一点的连线都是母线,故\(C\)正确;
对于\(D\),过球面上球的直径的两个端点的大圆有无数个,故\(D\)错误.
故选:\(BC\).
【题型2】 简单几何体
【典题1】请描述如图所示的组合体的结构特征.

解析(1)是由一个圆锥和一个同底的圆台拼接而成的组合体;
(2)是由一个圆台挖去一个同底的圆锥后剩下的部分得到的组合体;
(3)是由一个四棱锥和一个同 底的四棱柱拼接而成的组合体.
【巩固练习】
1.如图所示的蒙古包可以看成是由\(\underline{\quad \quad}\)构成的几何体.( )

A.三棱锥、圆锥 \(\qquad \qquad\) B.三棱锥、圆柱 \(\qquad \qquad\) C.圆锥、圆柱 \(\qquad \qquad\) D.圆锥、三棱柱
2.如图所示的组合体,其结构特征是( )

A.由两个圆锥组合成的 \(\qquad \qquad \qquad \qquad\) B.由两个圆柱组合成的
C.由一个棱锥和一个棱柱组合成的 \(\qquad \qquad\) D.由一个圆锥和一个圆柱组合成的
3.将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所得的几何体是由( )
A.一个圆台、两个圆锥构成 \(\qquad \qquad \qquad\) B.两个圆台、一个圆锥构成
C.两个圆柱、一个圆锥构成 \(\qquad \qquad \qquad\) D.一个圆柱、两个圆锥构成
4.如图的组合体的结构特征是( )

A.一个棱柱中截去一个棱柱 \(\qquad \qquad \qquad\) B.一个棱柱中截去一个圆柱
C.一个棱柱中截去一个棱锥 \(\qquad \qquad \qquad\) D.一个棱柱中截去一个棱台
5.如图所示的几何体是由下面哪一个平面图形旋转而形成的( )

A. \(\qquad \qquad\) B.
\(\qquad \qquad\) B. \(\qquad \qquad\) C.
\(\qquad \qquad\) C. \(\qquad \qquad\) D.
\(\qquad \qquad\) D.
6.图中的平面图形绕直线l旋转一周,说明形成的几何体的结构特征.

参考答案
-
答案 \(C\)
-
答案 \(D\)
解析由图形知,该几何体由一个圆锥和一个圆柱组成的简单组合体.故选:\(D\). -
答案 \(D\)
-
答案 \(C\)
解析如图所示的图形,可看成是四棱柱截取一个角
即三棱锥可得的组合体.
故为一个棱柱中截去一个棱锥所得.
故选:\(C\). -
答案 \(A\)
解析∵几何体是一个圆柱、两个圆台和一个圆锥的组合体,
\(∴\)它是由\(A\)选项中的平面图形旋转而成的.
故选:\(A\). -
答案 过原图中的折点向旋转轴引垂线,这样便可得到三个规则图形:矩形、直角梯形、直角三角形,旋转一周后便得到一个组合体,该组合体是由圆柱、圆台和圆锥组合而成的.

分层练习
【A组---基础题】
1.下列几何体是旋转体的是( )

A.①② \(\qquad \qquad \qquad\) B.②③ \(\qquad \qquad \qquad\) C.②④ \(\qquad \qquad \qquad\) D.③④
2.下列关于球体的说法中,错误的是( )
A.球面是空间中到定点的距离等于定长的点的集合
B.用一个平面去截一个球得到的截面是圆面
C.一个圆绕其直径所在直线旋转一周形成的曲面所围成的几何体是球体
D.球的对称轴只有\(1\)条
3.如图所示的平面中阴影部分绕中间轴旋转一周,形成的几何体形状为( )

A.一个球体 \(\qquad \qquad \qquad \qquad \qquad\) B.一个球体中间挖去一个圆柱
C.一个圆柱 \(\qquad \qquad \qquad \qquad \qquad\) D.一个球体中间挖去一个长方体
4.如图所示的几何体是一个正方体挖掉一个圆锥(圆锥的底面圆与正方体的上底面正方形各边相切,顶点在下底面上),用一个垂直于正方体某个面的平面截该几何体,下列图形中一定不是其截面图的是( )

A. \(\qquad\)B.
\(\qquad\)B. \(\qquad\)C.
\(\qquad\)C. \(\qquad\)D.
\(\qquad\)D.
5.一个等腰梯形绕着它的对称轴旋转一周所得各面围成的几何体是( )
A.圆柱 \(\qquad \qquad \qquad\) B.圆台 \(\qquad \qquad \qquad\) C.圆锥 \(\qquad \qquad \qquad\) D.以上都不对
6.如图中的\(△ABC\)绕直线\(BC\)旋转一周所形成的几何体是\(\underline{\quad \quad}\).

7.北方的冬天户外冰天雪地,若水管裸露在外,则管内的水就会结冰从而冻裂水管,给用户生活带来不便.每年冬天来临前,工作人员就会给裸露在外的水管“保暖” 在水管外面包裹保温带,用一条保温带盘旋而上一次包裹到位.某工作人员采用四层包裹法(除水管两端外包裹水管的保温带都是四层) 如图\(1\)所示是相邻四层保温带的下边缘轮廓线,相邻两条轮廓线的间距是带宽的四分之一.设水管的直径与保温带的宽度都为\(4cm\).在图\(2\)水管的侧面展开图中,此保温带的轮廓线与水管母线所成的角的余弦值是(保温带厚度忽略不计) .

8.说出下列几何体的结构特征.

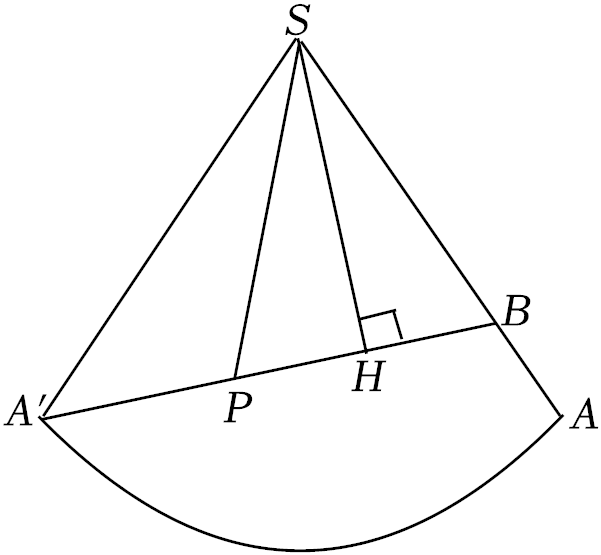
9.如图是一座山的示意图,山呈圆锥形,圆锥的底面半径为\(10\)公里,母线长为\(40\)公里,\(B\)是母线\(SA\)上一点,且\(AB=10\)公里.为了发展旅游业,要建设一条最短的从\(A\)绕山一周到\(B\)的观光铁路.这条铁路从\(A\)出发后首先上坡,随后下坡,求下坡段铁路的长度.
参考答案
-
答案 \(B\)
-
答案 \(D\)
解析对于\(A\),球面是空间中到定点的距离等于定长的点的集合,故\(A\)正确;
对于\(B\),用一个平面去截一个球得到的截面是圆面,故\(B\)正确;
对于\(C\),一个圆绕其直径所在直线旋转一周形成的曲面所围成的几何体是球体,故\(C\)正确;
对于\(D\),球的每一条直径都是对称轴,有无数条,故\(D\)错误.
故选:\(D\). -
答案 \(B\)
-
答案 \(B\)
解析用过圆锥的轴切与上底面一组对棱垂直的平面截该几何体,可得A图;
用平行于圆锥底面的平面截该几何体,可得\(C\)图;
用垂直于圆锥底面切不过圆锥的轴的平面截该几何体,可得\(D\)图;
\(B\)图中用垂直于正方体的任何面的平面截,都无法截得.
故选:\(B\). -
答案 \(B\)
-
答案 两个同底的圆锥组成的组合体
-
答案 \(\dfrac{\sqrt{1+16 \pi^2}}{1+16 \pi^2}\)
解析过点\(A\)作\(AE⊥D'B'\),垂足为\(E\),
其展开图如图所示

由水管直径为\(4cm\),所以水管的周长为\(AE=4πcm\),
则\(∠AB'E=α\),
又 \(B E=\dfrac{1}{4} \times 4=1\) , \(A B^{\prime}=\sqrt{1^2+(4 \pi)^2}=\sqrt{1+16 \pi^2}\)
所以 \(\cos \angle \alpha=\dfrac{B^{\prime} E}{A B^{\prime}}=\dfrac{1}{\sqrt{1+16 \pi^2}}=\dfrac{\sqrt{1+16 \pi^2}}{1+16 \pi^2}\). -
答案 图(1)是由一个三棱柱与一个同底的三棱锥组成的组合体;图(2)是由两个同底的圆台组成的组合体;
图(3)是由一个圆柱与一个半球组成的组合体,其中半球的半径与圆柱的底面半径相同;
图(4)是由一个圆柱挖去一个三棱柱得到的组合体,其中三棱柱的底面在圆柱的底面上. -
答案 \(18\)
解析如图,展开圆锥的侧面,过点\(S\)作\(A'B\)的垂线,垂足为\(H\),
记点\(P\)为\(A' B\)上任意一点,连接\(PS\), \(\widehat{\mathrm{A}^{\prime} \mathrm{A}}=\angle A^{\prime} O A \cdot S A=2 \pi \cdot 10 \Rightarrow \angle A^{\prime} O A=\dfrac{\pi}{2}\),
由两点之间线段最短,知观光铁路为图中的\(A' B\), \(A^{\prime} B=\sqrt{S A^{\prime 2}+S B^2}=50\),
上坡即\(P\)到山顶\(S\)的距离\(PS\)越来越小,下坡即\(P\)到山顶\(S\)的距离\(PS\)越来越大,
\(∴\)下坡段的铁路,即图中的\(HB\),
由\(Rt△SA'B∽Rt△HSB\),
可得 \(\dfrac{\mathrm{SB}}{\mathrm{HB}}=\dfrac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{SB}}\),可求出 \(H B=\dfrac{\mathrm{SB}^2}{\mathrm{~A}^{\prime} \mathrm{B}}=\dfrac{30 \times 30}{50}=18\).
即下坡段铁路的长度为\(18\)公里.
【B组---提高题】
1.如图,已知正方体\(ABCD-A_1 B_1 C_1 D_1\)上、下底面中心分别为\(O_1\),\(O_2\)将正方体绕直线\(O_1 O_2\)旋转一周,其中由线段\(BC_1\)旋转所得图形是 ( )

A. \(\qquad \qquad\)B.
\(\qquad \qquad\)B. \(\qquad \qquad\)C.
\(\qquad \qquad\)C. \(\qquad \qquad\)D.
\(\qquad \qquad\)D. 
2.已知一个圆台的上、下底面半径分别是\(1 cm\),\(2 cm\),截得圆台的圆锥的母线长为\(12 cm\).求圆台的母线长.
参考答案
-
答案 \(D\)
解析设正方体的棱长等于\(a\),
\(∵BC_1\)的中点到旋转轴的距离等于 \(\dfrac{1}{2} a\),而\(B\)、\(C_1\)两点到旋转轴的距离等于\(\dfrac{\sqrt{2}}{2} a\),
\(∴BC_1\)的中点旋转一周,得到的圆较小,可得所得旋转体的中间小,上、下底面圆较大.
由此可得\(B\)项不符合题意,舍去.
又\(∵\)在所得旋转体的侧面上有无数条直线,且直线的方向与转轴不共面,
\(∴A\)、\(C\)两项不符合题意,只有\(D\)项符合题意.
故选 \(D\) -
答案 \(6 cm\)
解析如图是几何体的轴截面,由题意知\(AO=2 cm\), \(A^{\prime} O^{\prime}=1 cm\),\(SA=12 cm\).

由\(\dfrac{A^{\prime} O^{\prime}}{A O}=\dfrac{S A^{\prime}}{S A}\),得 \(S A^{\prime}=\dfrac{A^{\prime} O^{\prime}}{A O} \cdot S A=\dfrac{1}{2} \times 12=6(\mathrm{~cm})\),
\(∴AA'=SA-SA'=6(cm)\).
\(∴\)圆台的母线长为\(6 cm\).

