8.1 基本立体图形(1) --棱柱、棱锥、棱台
基础知识
空间几何体
多面体
一般地,由若干个平面多边形围成的几何体叫做多面体。围成多面体的各个多边形叫做多面体的面,如面 ;两个面的公共边叫做多面体的棱,如棱 ,棱 ;棱与棱的公共点叫做多面体的顶点,如顶点 ,顶点 . 以前学过的长方体、正方体是多面体.
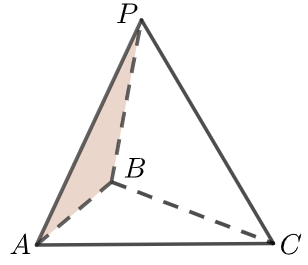
旋转体
一条平面曲线(包括直线)绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体叫做旋转体,这条定直线叫做旋转体的轴。以前学过的圆锥、圆柱是旋转体.
空间几何体的结构特征
棱柱
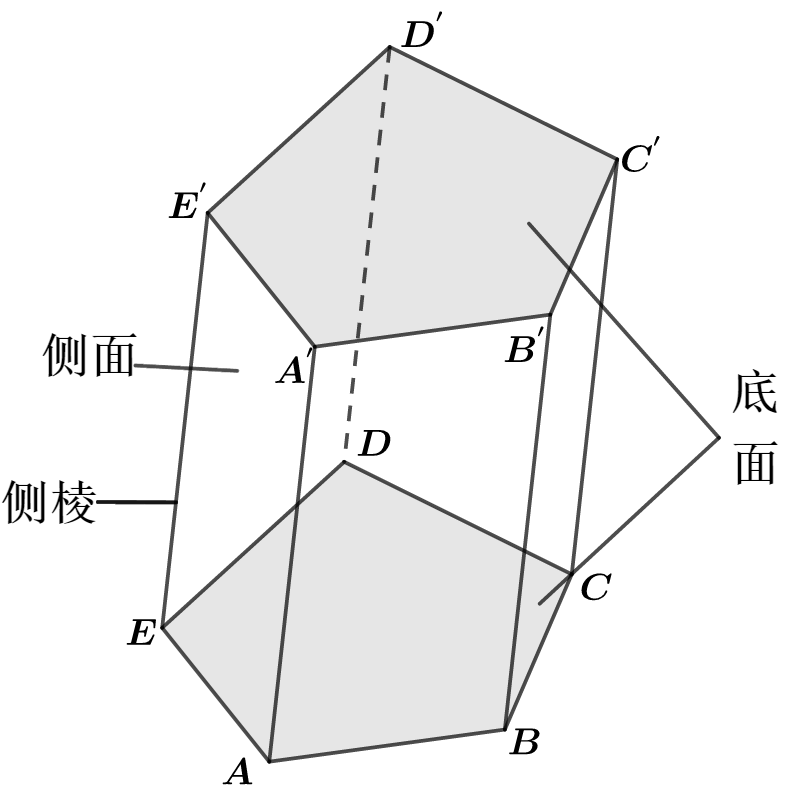
(1) 概念
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱.
(2) 性质
① 侧棱都相等,侧面是平行四边形;
② 两个底面与平行于底面的截面是全等的多边形;
③ 过不相邻的两条侧棱的截面是平行四边形;
④ 直棱柱的侧棱长与高相等,侧面与对角面是矩形.
(3) 分类
① 按底面多边形的边数分为:三棱柱,四棱柱等.
② 按侧棱是否垂直低面分为斜棱柱,直棱柱 (底面是正多边形的直棱柱,叫正棱柱;底面是平行四边形的四棱柱也叫做平行六面体)
棱锥
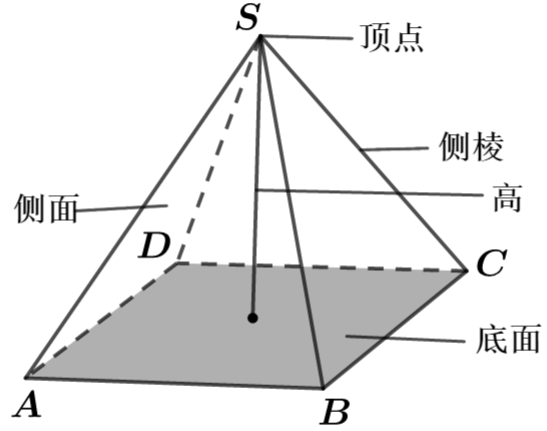
(1) 概念
有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥.
如果有一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥.
(2) 性质
① 平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的② 距离与顶点到底面的距离之比;
③ 正棱锥各侧棱相等,各侧面是全等的等腰三角形;
④ 正棱锥中六个元素,即侧棱、高、斜高、侧棱在底面内的射影、斜高在底面的射影、底面边长一半,构成四个直角三角形.)
(3) 常见棱锥
正三棱锥是底面是等边三角形,三个侧面是全等的等腰三角形的三棱锥.
正四面体是每个面都是全等的等边三角形的三棱锥,正四面体是特殊的正三棱锥.
(4) 侧面展开图
正 棱锥的侧面展开图是有 个全等的等腰三角形组成的.
棱台
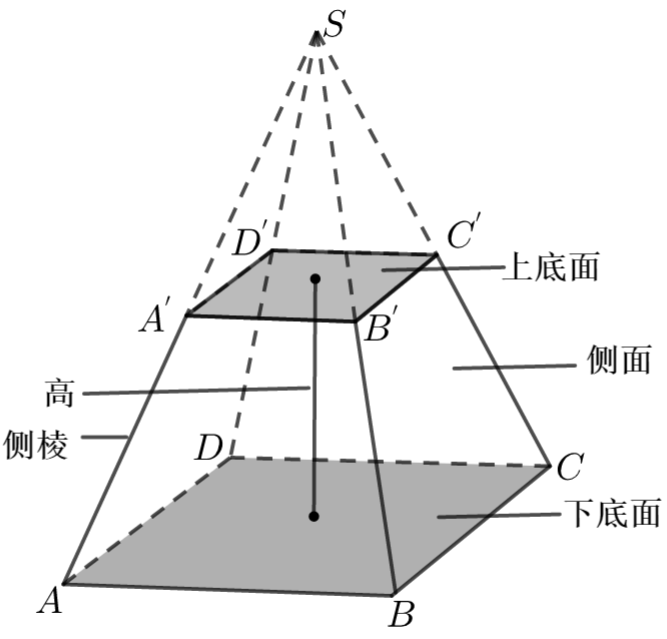
(1) 用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台.
(2) 棱台的分类:由三棱锥、四棱锥…… 截得的棱台分别叫做三棱台、四棱台…….
(3) 正棱台:由正棱锥截得的棱台叫做正棱台,正棱台各侧棱都相等,各侧面都是全等的等腰梯形.
基本方法
【题型1】 棱柱、棱锥、棱台的概念
【典题 1】有下列命题:
①有两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱;
②各个面都是三角形的几何体是三棱锥;
③用一个平行于棱锥底面的平面去截棱锥,得到的几何体叫 做棱台;
④棱 柱的各相邻侧面的公共边互相平行.
以上命题中,正确命题的序号是 .
解析 由图甲知,命题①错误;如图乙,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是棱锥,命题②错误;由棱台的定义知,命题③错误;由棱柱的特点知,命题④正确.

【典题 2】给出下列三个命题
①有四个相邻侧面互相垂直的棱柱是直棱柱;
②各侧面都是正方形的四棱柱是正方体;
③底面是正三角形,各侧面都是等腰三角形的三棱锥是正三棱锥.
其中真命题的个数是 ( )
A. B. C. D.
解析 四个侧面互相垂直的棱柱并不能保证侧棱一定垂直于底面,故①错误;
当底面是菱形时,各侧面也可以是正方形,故②错误;
当锐角为 的菱形沿短的对角线折成本棱锥时,有可能不是正三棱锥,
举个特殊的三棱锥 底面是正三角形,一个为等腰三角形的侧面与底面垂直,
这时三侧面中,有一个是正三角形,两个是等腰三角形,故③错误.
故选 .
【巩固练习】
1. 在棱柱中,( )
A.只有两个面平行 B.所有的棱都相等
C.所有的面都是平行四边形 D.两底面平行,且各侧棱也平行
2. 棱台不具有的性质是 ( )
A.两底面相似 B.侧面都是梯形
C.侧棱都平行 D.侧棱延长后都交于一点
3. 下列命题正确的是 ( )
A.棱柱的侧棱都相等,侧面都是全等的平行四边形
B.用一个平面去截棱锥,棱锥底面与截面之间的部分是棱台
C.四面体的任何一个面都可以作为棱锥的底面
D.棱台的侧棱延长后交于一点,侧面是等腰梯形
4. 下列说法中正确的是 ( )
A.棱柱中两个互相平行的平面一定是棱柱的底面
B.在平行六面体中,任意两个相对的面均互相平行,但平行六面体的任意两个相对的面不一定可当作它的底面
C.棱柱的侧面都是平行四边形,但它的底面一定不是平行四边形
D.在棱柱的面中,至少有两个面互相平行
5. 下列说法中,正确的个数为 ( )
(1) 有两个面互相平行,其余各面都是平行四边形的几何体一定是棱柱
(2) 有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台;
(3) 底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
(4) 棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是正六棱锥.
A. 个 B. 个 C. 个 D. 个
参考答案
- 答案
- 答案
- 答案
解析对于 ,棱柱的侧棱都相等,但侧面不一定是全等的平行四边形, 错误;
对于 ,用一个平行于底面的平面去截棱锥,棱锥底面与截面之间的部分才是棱台, 错误;
对于 ,四面体的任何一个面都可以作为棱锥的底面, 正确;
对于 ,棱台的侧棱延长后交于一点,但侧面不一定是等腰梯形, 错误.
故选:. - 答案
解析对于 ,棱柱的侧面也可以互相平行,即 错误;
对于 ,底面是平行四边形的四棱柱是平行六面体,它的侧面是互相平行的平行四边形,可以作为底面,即 错误;
对于 ,正四棱柱是棱柱,且正四棱柱的底面是平行四边形,即 错误;
对于 ,棱柱的上下底面一定是平行的,故至少有两个面互相平行,即 正确.
故选:. - 答案
解析 (1) 中,有两个面互相平行,其余各面都是平行四边形,且每相邻两个四边形的公共边互相平行的几何体一定是棱柱,故 (1) 不正确;
(2) 中,有两个面互相平行,其余四个面都是等腰梯形的六面体不一定是棱台,只有当四个等腰梯形的腰延长后交于一点时,这个六面体才是棱台,故 (2) 不正确;
(3) 中,底面是等边三角形,侧面都是等腰三角形的三棱锥不一定是正三棱锥,只有当三棱锥的顶点在底面的射影是底面中心时,才是正三棱锥,故 (3) 不正确;
(4) 中,因为正六棱锥的底面是正六边形,侧棱在底面内的射影与底面边长相等,所以正六棱锥的侧棱长一定大于底面边长,故 (4) 不正确.
故选:.
【题型2】 简单几何体的表面展开与折叠问题
【典题 1】(1) 请画出如图所示的几何体的表面展开图.

(2) 将各平面图形折起后形成的空间图形如图所示:

解析 (1) 展开图如图所示:

(2) 根据下图所给的平面图形,画出立体图形.

【典题 2】如图一个封闭的立方体,它 个表面各标出 、、、、、 这 个数字,现放成下面 个不同的位置,则数字 、、 对面的数字是 ( )

A.、、 B.、、 C.、、 D.、、
解析 第一个正方体已知 、、 第二个正方体已知 、、
第三个正方体已知 、, 且不同的面上写的数字各不相同,
则可知 对面标的是 , 对面标的是 , 对面标的是
故选 .
【典题 3】如图,已知三棱柱 ,底面是边长为 的正三角形,侧面为全等的矩形且高为 ,求自一点 出发沿着三棱柱的侧面绕行一周后到达 点的最短路线长.
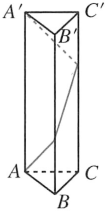
解析 将正三棱柱 沿侧棱展开,其侧面展开图如图所示,

依题意 ,,
依题意沿着三棱柱的侧面绕行一周到达点 的最短路线为:
.
【巩固练习】
1. 下图中能围成正方体的是 .(填序号)

2. 水平放置的正方体的六个面分别用 “前面、后面、上面、下面、左面、右面” 表示,如图是一个正方体的表面展开图,若图中 “努” 在正方体的后面,那么这个正方体的前面是 .

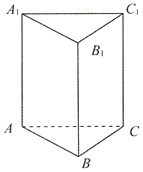
3. 如图所示,在所有棱长均为 的三棱柱上,有一只蚂蚁从点 出发,围着三棱柱的侧面爬行一周到达点 ,则爬行的最短路线长为 .
参考答案
-
答案 ①②③
-
答案 有
解析 这是一个正方体的平面展开图,共有六个面,其中面 “努” 与面 “有” 相对,所以图中 “努” 在正方体的后面,则这个正方体的前面是 “有”.

-
答案
解析正三棱柱的侧面展开图如图所示的矩形,
矩形的长为 ,宽为 ,则其对角线 的长为最短路程.
因此蚂蚁爬行的最短路程为:.

分层练习
【A组---基础题】
1. 下列几何体中,棱柱有 ( )

A. 个 B. 个 C. 个 D. 个
2. 下列说法正确的是 ( )
A.三棱柱有三个侧面、三条侧棱和三个顶点
B.四面体有四个面、六条棱和四个顶点
C.六棱锥有七个顶点
D.棱柱的各条侧棱可以不相等
3. 下列命题中正确的是 ( )
A.有一个面是多边形,其余各面是三角形的几何体是棱锥
B.有两个面平行且相似,其余各面都是梯形的多面体是棱台
C.长方体是正四棱柱
D.四个面都是等边三角形的四面体是正四面体
4. 下面的多面体是棱台的是 ( )
A.两底面是相似多边形的多面体
B.侧面是梯形的多面体
C.两底面平行的多面体
D.两底面平行,侧棱延长后交于一点的多面体
5. 下列命题正确的是 ( )
A.棱柱的底面一定是平行四边形
B.棱锥被平面分成的两部分不可能都是棱锥
C.棱锥的底面一定是三角形
D.棱柱被平面分成的两部分可以都是棱柱
6. 下列说法中正确的个数为 ( )
①各侧棱都相等的棱锥为正棱锥;
②各侧面都是面积相等的等腰三角形的棱锥为正棱锥;
③各侧面都是全等的等腰三角形的棱锥是正棱锥;
④底面是正多边形且各侧面是全等三角形的棱锥为正棱锥.
A. B. C. D.
7. 在下面四个平面图形中,哪几个是各侧棱都相等的四面体的展开图?其序号是 .(把你认为正确的序号都填上)

8. 在正方形 中,, 分别为 , 的中点,现沿 ,, 把 ,, 折起,使 ,, 三点重合,则折成的几何体为 .

9. 如图,在三棱柱 中,, 分别是 与 的中点,试判断几何体 是什么几何体,并指出它的底面与侧面.

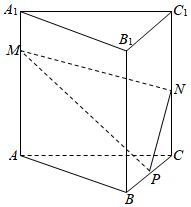
10. 如图,在正三棱柱 中,,, 为 的中点, 是 上一点,且由 沿棱柱侧面经过棱 到 的最短路线长为 ,设这条最短路线与 的交点为 ,求:
(1) 该三棱柱的侧面展开图的对角线的长;
(2) 和 的长.
参考答案
- 答案
- 答案
- 答案
解析对于 ,有一个面是多边形,其余各面是三角形,
若其余各面没有一个共同的顶点的几何体就不是棱锥,故 错误;
对于 ,有两个面平行且相似,其余各面都是梯形,
若侧棱不相交于一点的多面体不是棱台,故 错误;
对于 ,长方体中有一组相对的面是正方体时是正四棱柱,故 错误;
对于 ,四个面都是等边三角形的四面体是正四面体,故 正确.
故选:. - 答案
- 答案
解析对于 ,棱柱的底面不一定是平行四边形,也可以是三角形或六边形等,所以 错误;
对于 ,棱锥被平面分成的两部分也可能都是棱锥,如过棱锥顶点的平面与底面相交把棱锥分成的两部分,所以 错误;
对于 ,棱锥的底面不一定是三角形,也可以是四边形或其他平面图形,所以 错误;
对于 ,棱柱被平面分成的两部分可以都是棱柱,如用平行于底面的平面截棱柱分成的两部分,所以 正确.
故选:. - 答案
解析对于①,各侧棱都相等,但无法保证底面为正多边形,①错误;
对于②,各侧面都是面积相等的等腰三角形,但无法保证各个等腰三角形全等且腰长均为侧棱长,②错误;
对于③,各侧面都是全等的等腰三角形,但无法保证等腰三角形的腰长为侧棱长,③错误;
对于④,底面是正多边形,各侧面是全等三角形,则可以保证顶点在底面射影为底面中心,满足正棱锥定义,④正确.
故选:. - 答案 ①②
- 答案三棱锥
- 答案几何体 是三棱台.其中 是下底面, 是上底面,四边形 ,四边形 ,四边形 是侧面.
解析 , 分别是 与 的,且 ,,,
.
且 ,, 延长后交于一点.
又平面 平行于平面 ,
几何体 是三棱台.
其中 是下底面, 是上底面,四边形 ,四边形 ,四边形 是侧面. - 答案 (1); (2) ,
解析 (1) 正三棱柱 的侧面展开图是一个长为 ,宽为 的矩形,其对角线长 ;
(2) 如图,将侧面 绕棱 旋转 使其与侧面 在同一平面上,点 运动到点 的位置,
连接 ,则 就是由点 沿棱柱侧面经过棱 到点 的最短路线,

设 ,则 ,在 中,由勾股定理得 ,
求得 ,,
, .
【B组---提高题】
1. 给出下列命题
①底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
②若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
③一个棱锥可以有两条侧棱和底面垂直;
④一个棱锥可以有两个侧面和底面垂直;
⑤所有侧面都是正方形的四棱柱一定是正方体.
其中正确的命题是 ( )
A.①②③ B.①③ C.②③④ D.④
2. 如图所示,在正三棱柱 中,,,由顶点 沿棱柱侧面 (经过棱 ) 到达顶点 ,与 的交点记为 . 求:

(1) 三棱柱侧面展开图的对角线长;
(2) 从 经 到 的最短路线长及此时 的值.

参考答案
-
答案
解析对于①,底面是等边三角形,侧面都是等腰三角形的三棱锥不一定是正三棱锥,
如图所示,
若 ,且 平面 ,但三棱锥 表示正三棱锥,
①错误;
对于②,当有两个侧面垂直于底面时,该四棱柱不一定为直四棱柱,
如两个侧面不是相邻的时,侧棱与底面不一定垂直,②错误;
对于③,一个棱锥不能有两条侧棱和底面垂直,否则,这两条侧棱互相平行,
③错误;
对于④,一个棱锥可以有两个侧面和底面垂直,如①中图形,④正确;
对于⑤,所有侧面都是正方形的四棱柱不一定是正方体,
各相邻侧面并不一定都互相垂直,∴⑤错误.
综上,正确的命题是④.
故选 .

-
答案 (1) (2) ,
解析沿侧棱 将正三棱柱的侧面展开,得到一个矩形 .
(1) 矩形 的长 ,宽 .
所以三棱柱侧面展开图的对角线长为 .
(2) 由侧面展开图可知:当 ,, 三点共线时,由 经 到 点的路线最短.
所以最短路线长为 .
显然 ,
所以 ,即 .




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 按钮权限的设计及实现