7.3 复数的三角形表示(选学)
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019)]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第二册同步巩固,难度2颗星!
基础知识
复数的三角表示
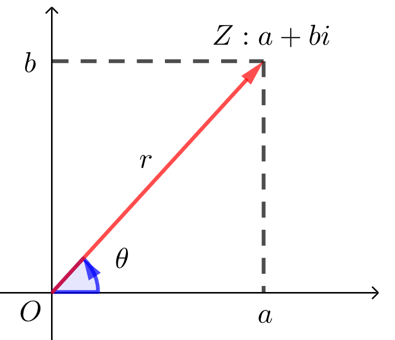
一般地,任何一个复数\(z=a+bi\)都可以表示成
的形式,其中,\(r\)是复数\(z\)的模,\(θ\)是以\(x\)轴的非负半轴为始边,向量\(\overrightarrow{O Z}\)所在射线为终边的角,叫做复数\(z=a+bi\)的辐角,\(r(\cos θ+i\sin θ)\)叫做复数\(z=a+bi\)的三角形表示式,简称三角形式. \(a+bi\)简称为代数形式.
解释
① 如下图,向量\(\overrightarrow{O Z}\)的大小由其模\(|\overrightarrow{O Z} |=r\),其方向角度\(θ\)决定;而复数\(z=a+bi\)与向量\(\overrightarrow{O Z}=(a,b)\)一一对应,故复数也可以用\(r\)、\(θ\)表示.由图显然可得, \(\left\{\begin{array}{l}
a=r \cos \theta \\
b=r \sin \theta
\end{array}\right.\).
即\(z=a+bi=r(\cos θ+i\sin θ)\)
② 显然,辐角有无限个,且这些值相差\(2π\)的整数倍.
规定:在\(0≤θ<2π\)范围内的辐角\(θ\)的值为辐角的主值,通常记作\(\arg z\),即\(0≤\arg z<2π\).
例如\(\arg 1=0\),\(\arg i=\dfrac{\pi}{2}\),\(\arg (-1)=π\).
③ 复数的代数形式与三角形式可互换,根据不同的运算需要,它们各有优势.
【例】 画出复数\(z=1+\sqrt{3} i\)对应的向量,并表示成三角形式.
解 复数\(z=1+\sqrt{3} i\)对应的向量如图所示,则 \(r=\sqrt{1^2+(\sqrt{3})^2}=2\),\(\cos θ=\dfrac{1}{2}\),
所以\(\arg (1+\sqrt{3} i)=\dfrac{\pi}{3}\),于是\(1+\sqrt{3} i=2(\cos \dfrac{\pi}{3}+i\sin \dfrac{\pi}{3})\).
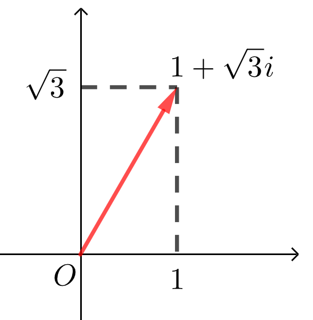
\(θ\)不一定要去主值, \(1+\sqrt{3} i=2\left(\cos \dfrac{7 \pi}{3}+i \sin \dfrac{7 \pi}{3}\right)\)也可以.
复数乘、除运算的三角表示及其几何意义
设\(z_1=r_1\left(\cos \theta_1+i \sin \theta_1\right)\), \(z_2=r_2\left(\cos \theta_2+i \sin \theta_2\right)\)
则 \(z_1 z_2=r_1 r_2\left[\cos \left(\theta_1+\theta_2\right)+i \sin \left(\theta_1+\theta_2\right)\right]\), \(\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}\left[\cos \left(\theta_1-\theta_2\right)+i \sin \left(\theta_1-\theta_2\right)\right]\)
解释
① 证明 \(z_1 z_2=r_1\left(\cos \theta_1+i \sin \theta_1\right) \cdot r_2\left(\cos \theta_2+i \sin \theta_2\right)\)
\(=r_1 r_2\left(\cos \theta_1+i \sin \theta_1\right)\left(\cos \theta_2+i \sin \theta_2\right)\)
\(=r_1 r_2\left[\left(\cos \theta_1 \cos \theta_2-\sin \theta_1 \sin \theta_2\right)+\mathrm{i}\left(\sin \theta_1 \cos \theta_2+\cos \theta_1 \sin \theta_2\right)\right]\)
\(=r_1 r_2\left[\cos \left(\theta_1+\theta_2\right)+i \sin \left(\theta_1+\theta_2\right)\right]\).
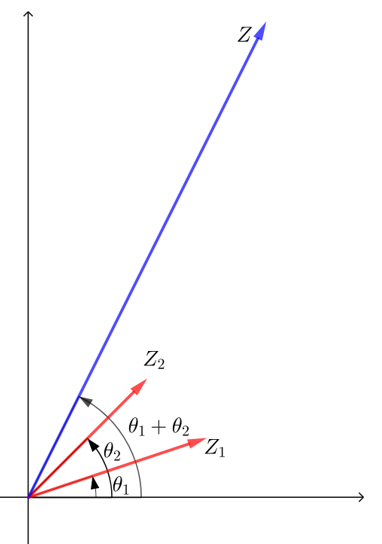
② 两个复数\(z_1\),\(z_2\)相乘时,可以如图,先分别画出与\(z_1\),\(z_2\)对应的向量 \(\overrightarrow{O Z_1}\), \(\overrightarrow{O Z_2}\),然后把向量 \(\overrightarrow{O Z_1}\)绕点\(O\)按逆时针旋转角\(θ_2\)(如果 \(\theta_2<0\),就要把\(\overrightarrow{O Z_1}\)绕点\(O\)按顺时针旋转角\(|θ_2 |\)),再把它的模变为原来的\(r_2\)倍,得到向量\(\overrightarrow{O Z}\),\(\overrightarrow{O Z}\)表示的复数就是\(z_1 z_2\),这就是复数乘法的几何意义.
【例】 若 \(z_1=\dfrac{3}{2}\left(\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)\), \(z_2=2\left(\cos \dfrac{\pi}{3}+i \sin \dfrac{\pi}{3}\right)\),求\(z_1 z_2\).
解 \(z_1 z_2=\dfrac{3}{2}\left(\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right) \times 2\left(\cos \dfrac{\pi}{3}+i \sin \dfrac{\pi}{3}\right)\)
\(=\dfrac{3}{2} \times 2\left[\cos \left(\dfrac{\pi}{6}+\dfrac{\pi}{3}\right)+i \sin \left(\dfrac{\pi}{6}+\dfrac{\pi}{3}\right)\right]\)
\(=3\left(\cos \dfrac{\pi}{2}+i \sin \dfrac{\pi}{2}\right)=3\).
③ 复数的除法可看成是乘法的逆运算.
基本方法
【题型1】 复数的三角形式与代数形式的互换
【典题1】 复数的代数形式与三角形式互化:
(1)\(-1+\sqrt{3} i\);\(\qquad \qquad\) (2) \(2\left(\cos \dfrac{5 \pi}{6}+i \sin \dfrac{5 \pi}{6}\right)\).
解析 (1) \(-1+\sqrt{3} i=2\left(-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2} i\right)=2\left(\cos \dfrac{2 \pi}{3}+i \sin \dfrac{2 \pi}{3}\right)\);
(2) \(2\left(\cos \dfrac{5 \pi}{6}+i \sin \dfrac{5 \pi}{6}\right)=2\left(-\dfrac{\sqrt{3}}{2}+\dfrac{1}{2} i\right)=-\sqrt{3}+i\).
点拨 复数的代数形式\(z=a+bi\)与三角形式\(r(\cos θ+i\sin θ)\)的互换: \(\left\{\begin{array}{l}
a=r \cos \theta \\
b=r \sin \theta
\end{array}\right.\).
【巩固练习】
1.已知复数\(z=-1+\sqrt{3}i\),则它的共轭复数\(\bar{z}\)的辐角主值是( )
A.\(\dfrac{2\pi}{3}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{4\pi}{3}\) \(\qquad \qquad \qquad \qquad\)C.\(\dfrac{5\pi}{6}\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{7\pi}{6}\)
2.已知复数\(z-1\)的辐角为\(\dfrac{5\pi}{6}\),\(z+1\)的辐角为\(\dfrac{\pi}{3}\),则复数\(z\)等于( )
A.\(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2} i\) \(\qquad \qquad\) B.\(-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2} i\) \(\qquad \qquad\)C.\(\dfrac{1}{2}±\dfrac{\sqrt{3}}{2} i\) \(\qquad \qquad\) D.\(-\dfrac{1}{2}±\dfrac{\sqrt{3}}{2} i\)
3.\(-1-\sqrt{3} i\)的三角形式是( )
A.\(-2\left(\cos \dfrac{\pi}{3}+i \sin \dfrac{\pi}{3}\right)\) \(\qquad \qquad \qquad\) B. \(2\left[\cos \left(-\dfrac{2 \pi}{3}\right)+i \sin \left(-\dfrac{2 \pi}{3}\right)\right]\) \(\qquad \qquad \qquad\)
C. \(2\left(\sin \dfrac{7 \pi}{6}+i \cos \dfrac{7 \pi}{6}\right)\) \(\qquad \qquad \qquad\) D. \(2\left(\cos \dfrac{7 \pi}{6}+i \sin \dfrac{7 \pi}{6}\right)\)
参考答案
-
答案 \(B\)
解析 \(\because z=-1+\sqrt{3}i\),\(\therefore \bar{z}=-1-\sqrt{3} i\),则\(|\bar{z}|=2\),
\(\therefore \bar{z}=2\left(-\dfrac{1}{2}-\dfrac{\sqrt{3}}{2} i\right)\),则\(\bar{z}\)的辐角主值是\(\dfrac{4\pi}{3}\).
故选:\(B\). -
答案 \(B\)
解析 \(\because C\)和\(D\)均有两组答案,\(\therefore\)不合题意.
在\(A\)中,\(\because z=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2} i\),\(\therefore z-1=-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2} i\),辐角为\(\dfrac{2\pi}{3}\);
\(z+1=\dfrac{3}{2}+\dfrac{\sqrt{3}}{2} i\),辐角为\(\dfrac{\pi}{6}\).
故\(A\)不正确.
在\(B\)中,\(z=-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2} i\),\(\therefore z-1=-\dfrac{3}{2}+\dfrac{\sqrt{3}}{2} i\),辐角为\(\dfrac{5\pi}{6}\);
\(z+1=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2} i\),辐角为\(\dfrac{\pi}{3}\).故\(B\)正确.
故选:\(B\). -
答案 \(B\)
解析 \(-1-\sqrt{3} i=2\left(-\dfrac{1}{2}-\dfrac{\sqrt{3}}{2} i\right)=2\left[\cos \left(-\dfrac{2 \pi}{3}\right)+i \sin \left(-\dfrac{2 \pi}{3}\right)\right]\).故选:\(B\).
【题型2】 复数乘、除运算的三角表示
【典题1】 \(\frac{1}{2}\left(\cos 30^{\circ}+i \sin 30^{\circ}\right) \times 2\left(\cos 60^{\circ}+i \sin 60^{\circ}\right) \times 3 \times\left(\cos 45^{\circ}+i \sin 45^{\circ}\right)=\)( )
A. \(\dfrac{3 \sqrt{2}}{2}+\dfrac{3 \sqrt{2}}{2} i\) \(\qquad \qquad \qquad \qquad\) B. \(\dfrac{3 \sqrt{2}}{2}-\dfrac{3 \sqrt{2}}{2} i\)
C. \(-\dfrac{3 \sqrt{2}}{2}+\dfrac{3 \sqrt{2}}{2} i\) \(\qquad \qquad \qquad \qquad\) D. \(-\dfrac{3 \sqrt{2}}{2}-\dfrac{3 \sqrt{2}}{2} i\)
解析 \(\dfrac{1}{2}\left(\cos 30^{\circ}+i \sin 30^{\circ}\right) \times 2\left(\cos 60^{\circ}+i \sin 60^{\circ}\right) \times 3 \times\left(\cos 45^{\circ}+i \sin 45^{\circ}\right)\)
\(=3\left(\cos 135^{\circ}+i \sin 135^{\circ}\right)=3\left(-\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2} i\right)=-\dfrac{3 \sqrt{2}}{2}+\dfrac{3 \sqrt{2}}{2} i\).
故选:\(C\).
【典题2】已知\(z_1=\sqrt{5}(\cos α+i\sin α)\), \(z_2=\sqrt{10}(\cos \beta+i \sin \beta)\),其中 \(\alpha\), \(\beta \in\left(0, \dfrac{\pi}{2}\right)\),\(i\)是虚数单位,且 \(\tan \alpha=\dfrac{1}{2}\), \(\tan \beta=\dfrac{1}{3}\),则\(z_1 z_2\)的值是\(\underline{\quad \quad}\) .
解析 \(\tan \alpha=\dfrac{1}{2}\), \(\tan \beta=\dfrac{1}{3}\),可得 \(\tan (\alpha+\beta)=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{1-\dfrac{1}{2} \times \dfrac{1}{3}}=1\),
\(\alpha\), \(\beta \in\left(0, \dfrac{\pi}{2}\right)\),所以 \(\alpha+\beta=\dfrac{\pi}{4}\),
\(z_1=\sqrt{5}(\cos α+i\sin α)\), \(z_2=\sqrt{10}(\cos \beta+i \sin \beta)\),
所以 \(z_1 z_2=\sqrt{5} \times \sqrt{10}(\cos (\alpha+\beta)+i \sin (\alpha+\beta))\)\(=5 \sqrt{2}\left(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2} i\right)=5+5 i\).
【巩固练习】
1.已知 \(z=(1-\sqrt{3} i) \times\left(-\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)\),则\(\arg z=\)( )
A.\(\dfrac{\pi}{3}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{\pi}{2}\) \(\qquad \qquad \qquad \qquad\) C.\(\dfrac{2\pi}{3}\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{5\pi}{6}\)
2.\(\dfrac{1}{2}\left(\cos 60^{\circ}-i \sin 240^{\circ}\right) \times 6\left(\cos 30^{\circ}-i \sin 210^{\circ}\right)=\) \(\underline{\quad \quad}\) .
3.复数 \((1+i)\left(\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)\)的三角形式是\(\underline{\quad \quad}\) .
4.计算 \(10\left(\cos \dfrac{\pi}{3}+i \sin \dfrac{\pi}{3}\right) \div(-2 \sqrt{3}+2 i)\)的结果是\(\underline{\quad \quad}\).
参考答案
-
答案 \(B\)
解析 \(z=(1-\sqrt{3} i) \times\left(-\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{\sqrt{3}}{2} i\right) \times\left(\cos \dfrac{5 \pi}{6}+i \sin \dfrac{5 \pi}{6}\right)\)
\(=2\left[\cos \left(-\dfrac{\pi}{3}\right)+i \sin \left(-\dfrac{\pi}{3}\right)\right] \times\left(\cos \dfrac{5 \pi}{6}+i \sin \dfrac{5 \pi}{6}\right)\)
\(=2\left[\cos \left(\dfrac{5 \pi}{6}-\dfrac{\pi}{3}\right)+i \sin \left(\dfrac{5 \pi}{6}-\dfrac{\pi}{3}\right)\right]\)
\(=2\left(\cos \dfrac{\pi}{2}+i \sin \dfrac{\pi}{2}\right)\).
\(\therefore \arg z=\dfrac{\pi}{2}\).
故选:\(B\). -
答案 \(3i\)
解析 \(\dfrac{1}{2}\left(\cos 60^{\circ}-i \sin 240^{\circ}\right) \times 6\left(\cos 30^{\circ}-i \sin 210^{\circ}\right)\)
\(=3\left(\cos 90^{\circ}+i \sin 90^{\circ}\right)=3 i=\dfrac{1}{2}\left(\cos 60^{\circ}+i \sin 60^{\circ}\right) \times 6\left(\cos 30^{\circ}+i \sin 30^{\circ}\right)\)
\(=3\left(\cos 90^{\circ}+i \sin 90^{\circ}\right)=3 i\).
故答案为:\(3i\). -
答案 \(\sqrt{2}\left(\cos \dfrac{5 \pi}{12}+i \sin \dfrac{5 \pi}{12}\right)\)
解析 \(\because(1+i)\left(\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)=\sqrt{2}\left[\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2} i\right]\left(\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)\)
\(=\sqrt{2}\left(\cos \dfrac{\pi}{4}+i \sin \dfrac{\pi}{4}\right)\left(\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)\)
\(=\sqrt{2}\left[\cos \left(\dfrac{\pi}{4}+\dfrac{\pi}{6}\right)+i \sin \left(\dfrac{\pi}{4}+\dfrac{\pi}{6}\right)\right]\)
\(=\sqrt{2}\left(\cos \dfrac{5 \pi}{12}+i \sin \dfrac{5 \pi}{12}\right)\).
\(\therefore\)复数 \((1+i)\left(\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)\)的三角形式是\(\sqrt{2}\left(\cos \dfrac{5 \pi}{12}+i \sin \dfrac{5 \pi}{12}\right)\). -
答案 \(-\dfrac{5}{2} i\)
解析 \(10\left(\cos \dfrac{\pi}{3}+i \sin \dfrac{\pi}{3}\right) \div(-2 \sqrt{3}+2 i)\)
\(=10\left(\cos \dfrac{\pi}{3}+i \sin \dfrac{\pi}{3}\right) \div 4\left(\cos \dfrac{5 \pi}{6}+i \sin \dfrac{5 \pi}{6}\right)\)
\(=\dfrac{5}{2}\left(\cos \left(-\dfrac{\pi}{2}\right)+i \sin \left(-\dfrac{\pi}{2}\right)\right)=-\dfrac{5}{2} i\),
故答案为: \(-\dfrac{5}{2} i\).
【题型3】复数三角形式的运用
【典题1】 如下图,复平面内的\(∆ABC\)是等边三角形,它的两个顶点\(A\),\(B\)的坐标分别为\((1,0)\),\((2,1)\),求点\(C\)的坐标.
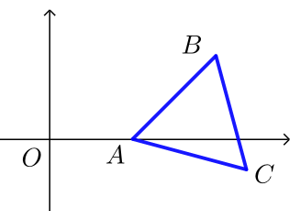
解析向量\(\overrightarrow{A B}\)对应的复数为 \(z_1=1+\mathrm{i}=\sqrt{2}\left(\cos 45^{\circ}+i \sin 45^{\circ}\right)\),
向量\(\overrightarrow{A C}\)对应的复数为 \(z_2=\sqrt{2}\left[\cos \left(45^{\circ}-60^{\circ}\right)+i \sin \left(45^{\circ}-60^{\circ}\right)\right]\)
\(=\sqrt{2}\left(\cos 15^{\circ}-i \sin 15^{\circ}\right)=\dfrac{\sqrt{3}+1}{2}-\dfrac{\sqrt{3}-1}{2} i\),
\(\therefore \overrightarrow{A C}=\left(\dfrac{\sqrt{3}+1}{2},-\dfrac{\sqrt{3}-1}{2}\right)\), \(\therefore C\left(\dfrac{\sqrt{3}+3}{2}, \dfrac{1-\sqrt{3}}{2}\right)\).
【巩固练习】
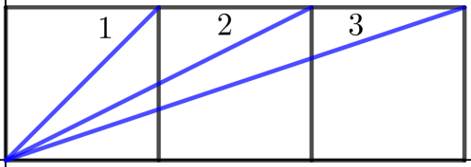
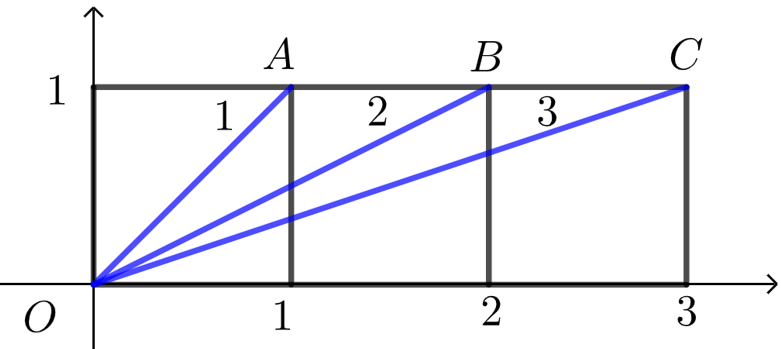
1.如下页图, 已知平面内并列的三个全等的正方形, 利用复数证明\(∠1+∠2+∠3=\dfrac{\pi}{2}\).
参考答案
- 证明 如图所示, 向量\(\overrightarrow{OA}\)对应的复数 \(z_1=1+i=\sqrt{2}(\cos \angle 1+i \sin \angle 1)\),
向量\(\overrightarrow{OB}\)对应的复数 \(z_2=2+\mathrm{i}=\sqrt{5}(\cos \angle 2+\mathrm{i} \sin \angle 2)\),
向量\(\overrightarrow{OC}\)对应的复数 \(z_3=3+\mathrm{i}=\sqrt{10}(\cos \angle 3+\mathrm{i} \sin \angle 3)\),
\(z_1 z_2 z_3=10[\cos (\angle 1+\angle 2+\angle 3)+i \sin (\angle 1+\angle 2+\angle 3)]=(1+i)(2+i)(3+i)=10 \mathrm{i}\),
\(\therefore \cos (\angle 1+\angle 2+\angle 3)+\mathrm{i} \sin (\angle 1+\angle 2+\angle 3)=\mathrm{i}\),
\(\therefore\left\{\begin{array}{l} \cos (\angle 1+\angle 2+\angle 3)=0 \\ \sin (\angle 1+\angle 2+\angle 3)=1 \end{array}\right.\), \(\therefore \angle 1+\angle 2+\angle 3=\dfrac{\pi}{2}\).
分层练习
【A组---基础题】
1.复数\(z=\sqrt{2}-\sqrt{2} i\)的三角形式是( )
A. \(2\left(\cos \dfrac{\pi}{4}+i \sin \dfrac{\pi}{4}\right)\) \(\qquad \qquad \qquad\) B. \(2\left(\cos \dfrac{3 \pi}{4}+i \sin \dfrac{3 \pi}{4}\right)\)
C. \(2\left(\cos \dfrac{7 \pi}{4}+i \sin \dfrac{7 \pi}{4}\right)\) \(\qquad \qquad \qquad\) D. \(2\left(\cos \dfrac{5 \pi}{4}+i \sin \dfrac{5 \pi}{4}\right)\)
2.瑞士数学家欧拉在1748年得到复数的三角形式: \(e^{i \theta}=\cos \theta+i \sin \theta\),(\(i\)为虚数单位),根据该式,计算 \(e^{\pi i}+1\)的值为( )
A.\(-1\) \(\qquad \qquad \qquad \qquad\) B.\(0\) \(\qquad \qquad \qquad \qquad\) C.\(1\) \(\qquad \qquad \qquad \qquad\) D.\(i\)
3.已知 \(z_1=\cos 120^{\circ}+i \sin 120^{\circ}\), \(z_2=\cos 330^{\circ}+i \sin 330^{\circ}\),则 \(\dfrac{2 z_1^2}{z_2}\)的辐角主值是( )
A.\(30^∘\) \(\qquad \qquad \qquad \qquad\) B.\(150^∘\) \(\qquad \qquad \qquad \qquad\) C.\(270^∘\) \(\qquad \qquad \qquad \qquad\) D.\(-90^∘\)
4.(多选)已知 \(z_1=\dfrac{3}{2}\left(\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)\), \(z_2=a\left(\cos \dfrac{\pi}{3}+i \sin \dfrac{\pi}{3}\right)(a \in(1,3))\),则\(z_1 z_2\)的值可以是( )
A.\(i\) \(\qquad \qquad \qquad \qquad\) B.\(2i\) \(\qquad \qquad \qquad \qquad\) C.\(2\sqrt{2} i\) \(\qquad \qquad \qquad \qquad\) D.\(3i\)
5.写出复数\(z=\sqrt{3}+i\)的三角形式是 \(\underline{\quad \quad}\).(辐角\(θ∈[0,2π)\))
6.设 \(z_1=2\left(\cos \dfrac{\pi}{3}+i \sin \dfrac{\pi}{3}\right)\), \(z_2=4\left(\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)\),则\(z_1 z_2=\)\(\underline{\quad \quad}\).
7.已知复数 \(z=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2} i\), \(\omega=\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2} i\).求复数\(zω+zω^3\)的模及辐角主值.
8.设复数\(z_1=1-i\),\(z_2=\cos θ+i\sin θ\),其中\(θ∈[0,π]\).
(1)若复数 \(z=\overline{z_1} \cdot z_2\)为实数,求\(θ\)的值;
(2)求\(|3z_1+z_2 |\)的取值范围.
参考答案
-
答案 \(C\)
解析 \(z=\sqrt{2}-\sqrt{2} i=2\left(\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2} i\right)=2\left(\cos \dfrac{7 \pi}{4}+i \sin \dfrac{7 \pi}{4}\right)\),故选:\(C\). -
答案 \(B\)
解析 由 \(e^{i x}=\cos x+i \sin x\),则 \(e^{i \pi}+1=\cos \pi+i \sin \pi+1=0\),故选:\(B\). -
答案 \(C\)
解析 \(\because z_1=\cos 120^{\circ}+i \sin 120^{\circ}\), \(z_2=\cos 330^{\circ}+i \sin 330^{\circ}\),
\(\therefore \dfrac{2 z_1^2}{z_2}=\dfrac{2\left(\cos 240^{\circ}+i \sin 240^{\circ}\right)}{\cos 330^{\circ}+i \sin 330^{\circ}}\)
\(=2\left[\cos \left(-90^{\circ}\right)+i \sin \left(-90^{\circ}\right)\right]=2\left(\cos 270^{\circ}+i \sin 270^{\circ}\right)\).
\(\therefore \dfrac{2 z_1^2}{z_2}\)的辐角主值是\(270^∘\).
故选:\(C\). -
答案 \(BCD\)
解析 \(z_1=\dfrac{3}{2}\left(\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)\), \(z_2=a\left(\cos \dfrac{\pi}{3}+i \sin \dfrac{\pi}{3}\right)(a \in(1,3))\),
则 \(z_1 z_2=\dfrac{3 a}{2}\left(\cos \dfrac{\pi}{2}+i \sin \dfrac{\pi}{2}\right)=\dfrac{3 a}{2} i\),\(\dfrac{3 a}{2} \in\left(\dfrac{3}{2}, \dfrac{9}{2}\right)\)
故选:\(BCD\). -
答案 \(2\left(\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)\).
-
答案 \(8i\)
解析 \(\because z_1=2\left(\cos \dfrac{\pi}{3}+i \sin \dfrac{\pi}{3}\right)\), \(z_2=4\left(\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right)\),
\(\therefore z_1 z_2=8\left(\cos \left(\dfrac{\pi}{3}+\dfrac{\pi}{6}\right)+i \sin \left(\dfrac{\pi}{3}+\dfrac{\pi}{6}\right)\right)=8\left(\cos \dfrac{\pi}{2}+i \sin \dfrac{\pi}{2}\right)=8 i\),
故答案为:\(8i\). -
答案 模为\(\sqrt{2}\),辐角主值为\(\frac{5\pi}{6}\).
解析 解法一:将已知复数化为复数三角形式: \(z=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2} i=\cos \dfrac{\pi}{3}+i \sin \dfrac{\pi}{3}\),
\(\omega=\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2} i=\cos \dfrac{\pi}{4}+i \sin \dfrac{\pi}{4}\),
依题意有 \(z \omega+z \omega^3=\left(\cos \dfrac{7 \pi}{12}+i \sin \dfrac{7 \pi}{12}\right)+\left(\cos \dfrac{13 \pi}{12}+i \sin \dfrac{13 \pi}{12}\right)\)
\(=\left(\cos \dfrac{7 \pi}{12}+\cos \dfrac{13 \pi}{12}\right)+i\left(\sin \dfrac{7 \pi}{12}+\sin \dfrac{13 \pi}{12}\right)=\sqrt{2}\left(\cos \dfrac{5 \pi}{6}+i \sin \dfrac{5 \pi}{6}\right)\),
故复数\(zω+zω^3\)的模为\(\sqrt{2}\),辐角主值为\(\dfrac{5\pi}{6}\).
解法二: \(z \omega+z \omega^3=z \omega\left(1+\omega^2\right)=\left(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2} i\right)\left(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2} i\right)(1+i)\)
\(=\sqrt{2}\left(-\dfrac{\sqrt{3}}{2}+\dfrac{1}{2} i\right)=\sqrt{2}\left(\cos \dfrac{5 \pi}{6}+i \sin \dfrac{5 \pi}{6}\right)\).
故复数\(zω+zω^3\)的模为\(\sqrt{2}\),辐角主值为\(\dfrac{5\pi}{6}\). -
答案 (1)\(\dfrac{3 \pi}{4}\) (2)\([3\sqrt{2}-1,5]\)
解析 (1)\(\because\) 复数\(z_1=1-i\),
\(\therefore \overline{z_1}=1+i\),
\(\therefore z=(1+i)(\cos \theta+i \sin \theta)=(\cos \theta-\sin \theta)+(\sin \theta+\cos \theta) i\),
\(\because\) 复数\(z=\overline{z_1} \cdot z_2\)为实数,
\(\therefore \sin θ+\cos θ=0\),即\(\tanθ=-1\),
\(\because θ∈[0,π]\),\(\therefore θ=\dfrac{3\pi}{4}\).
(2)\(\because z_1=1-i\),\(z_2=\cos θ+i\sin θ\),
\(\therefore 3z_1+z_2=3-3i+\cos θ+\sin θi=(3+\cos θ)+(\sin θ-3)i\),
\(\therefore\left|3 z_1+z_2\right|=\sqrt{(3+\cos \theta)^2+(\sin \theta-3)^2}=\sqrt{19+6(\cos \theta-\sin \theta)}\)
\(=\sqrt{19+6 \sqrt{2} \cos \left(\theta+\dfrac{\pi}{4}\right)}\),
\(\because θ∈[0,π]\), \(\therefore-1 \leqslant \cos \left(\theta+\dfrac{\pi}{4}\right) \leqslant \dfrac{\sqrt{2}}{2}\),
即 \(-6 \sqrt{2} \leqslant 6 \sqrt{2} \cos \left(\theta+\dfrac{\pi}{4}\right) \leqslant 6\),
\(\therefore\left|3 z_1+z_2\right|\)的取值范围为\([3\sqrt{2}-1,5]\).
【B组---提高题】
1.(多选)任何一个复数\(z=a+bi\)(其中\(a\),\(b∈R\),\(i\)为虚数单位)都可以表示成\(x=r(\cos θ+i\sin θ)\)(其中\(r⩾0\),\(θ∈R\))的形式,通常称之为复数\(z\)的三角形式.法国数学家棣莫弗发现: \([r(\cos \theta+i \sin \theta)]^n=r^n(\cos n \theta+i \sin n \theta)\left(n \in N^*\right)\).我们称这个结论为棣莫弗定理.则下列判断正确的是( )
A.复数\(z=1-\sqrt{3} i\)的三角形式为 \(z=2\left(\cos \dfrac{\pi}{3}-i \sin \dfrac{\pi}{3}\right)\)
B.\(r=1\),\(θ=\dfrac{\pi}{3}\)时,\(z^3=-1\)
C.\(r=1\),\(θ=\dfrac{\pi}{2}\)时, \(z+z^2+z^3+\cdots+z^{2021}=i\)
D.\(r=1\),\(θ=\dfrac{\pi}{4}\),“\(n\)为偶数”是“\(z^n\)为纯虚数”的必要不充分条件
2.设复数\(z=\cos θ+i\sin θ\),\(θ∈(π,2π)\),求复数\(z^2+z\)的模和辐角.
参考答案
-
答案 \(BCD\)
解析 对于\(A\)选项, \(z=2\left(\cos \dfrac{\pi}{3}-i \sin \dfrac{\pi}{3}\right)\)不是 \(z=r(\cos θ+i\sin θ)\)的形式,故A错误;
对于\(B\)选项,易知\(z=\cos \dfrac{\pi}{3}+i\sin \dfrac{\pi}{3}\),根据棣莫弗定理有\(z^3=\cos \left(3 \times \dfrac{\pi}{3}\right)+i \sin \left(3 \times \dfrac{\pi}{3}\right)=-1\),
故\(B\)正确;
对于\(C\)选项,易知\(z=\cos \dfrac{\pi}{2}+i\sin \dfrac{\pi}{2}=i\),
所以 \(z+z^2+z^3+\cdots+z^{2021}=i+i^2+i^3+\cdots+i^{2021}=i\),故\(C\)正确;
对于\(D\)选项,易知\(z=\cos \dfrac{\pi}{4}+i\sin \dfrac{\pi}{4}\),根据棣莫弗定理有\(z^n=\cos \dfrac{n\pi}{4}+i\sin \dfrac{n\pi}{4}\),
若\(z^n\)为纯虚数,则\(\cos \dfrac{n\pi}{4}=0\)且\(\sin \dfrac{n\pi}{4}≠0\),即\(\dfrac{n\pi}{4}=kπ+\dfrac{\pi}{2}\),所以\(n=2k+2\),
所以“\(n\)为偶数”是“\(z^n\)为纯虚数”的必要不充分条件,故\(D\)正确.
故选:\(BCD\). -
答案 模为 \(-2 \cos \left(\dfrac{\theta}{2}\right)\),辐角 \((2 k-1) \pi+\dfrac{3 \theta}{2}(k \in z)\).
解析 \(z^2+z=(\cos \theta+i \sin \theta)^2+(\cos \theta+i \sin \theta)=\cos 2 \theta+i \sin 2 \theta+\cos \theta+i \sin \theta\)
\(=2 \cos \dfrac{3 \theta}{2} \cos \dfrac{\theta}{2}+i\left(2 \sin \dfrac{3 \theta}{2} \cos \dfrac{\theta}{2}\right)=2 \cos \dfrac{\theta}{2}\left(\cos \dfrac{3 \theta}{2}+i \sin \dfrac{3 \theta}{2}\right)\)
\(=-2 \cos \dfrac{\theta}{2}\left[\cos \left(-\pi+\dfrac{3 \theta}{2}\right)+i \sin \left(-\pi+\dfrac{3 \theta}{2}\right)\right]\),
\(\because θ∈(π,2π)\), \(\therefore \dfrac{\theta}{2} \in\left(\dfrac{\pi}{2}, \pi\right)\), \(\therefore-2 \cos \left(\dfrac{\theta}{2}\right)>0\)
所以复数\(z^2+z\)的模为 \(-2 \cos \left(\dfrac{\theta}{2}\right)\),辐角 \((2 k-1) \pi+\dfrac{3 \theta}{2}(k \in z)\).


