欢迎到学科网下载资料学习
[【基础过关系列】高一数学同步精品讲义与分层练习 (人教 A 版 2019)]
(https://www.zxxk.com/docpack/2921718.html)
跟贵哥学数学,soeasy!
必修第二册同步巩固,难度 2 颗星!
基础知识
虚数单位的性质
i 叫做虚数单位,并规定:
① i 可与实数进行四则运算;
② i2=−1,这样方程 x2=−1 就有解了,解为 x=−i,x=i.
③ i2=−1 ,i3=−i ,i4=1 ,in 以 4 为周期,即 i4+n=in.
【例】 i2023=––––– .
解 i2023=i4×550+3=i3=−i.
复数的概念
1 定义
形如 a+bi(a,b∈R) 的数叫做复数,其中 i 叫做虚数单位,a 叫做实部,b 叫做虚部.
全体复数所成的集合 C 叫做复数集.
复数通常用 z 字母表示,即 z=a+bi(a,b∈R).
【例】 z=3−4i 的实部是 3,虚部是 −4.
2 分类
z=a+bi=⎧⎪⎨⎪⎩b=0 实数 b≠0 虚数 a=0 且 b≠0 纯虚数
理解:当复数 z=a+bi 中不存在 i,它就是实数,那显然 b=0;若复数 z 是虚数,则 z 中要存在 i,则 b≠0.
【例】 1+2i,−12−√2i,3i 是虚数,而其中 3i 是纯虚数.
复数的几何意义
1 复平面的概念
建立直角坐标系来表示复数的平面叫做复平面,x 轴叫做实轴,y 轴叫做虚轴.
显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.
复数 z=a+bi一一 对应⟷ 复平面内的点 Z(a,b),
【例】 复数 1−2i 对应复平面上的点 (1,−2),复数 3i 对应复平面上的点 (0,3).
2 复数的几何意义
复数 z=a+bi 与复平面内的点 Z(a,b) 及平面向量 −−→OZ=(a,b) (a,b∈R) 是一一对应关系 (复数的实质是有序实数对,有序实数对既可以表示一个点,也可以表示一个平面向量) 相等的向量表示同一个复数.
3 复数的模
向量 −−→OZ 的模叫做复数 z=a+bi 的模,记作 |z| 或 |a+bi|,表示点 (a,b) 到原点的距离,
即 |z|=|a+bi|=√a2+b2 ,|z|=|¯z|,
【例】 若 z=3+4i,则 z 的模 |z|=√32+42=5.
复数相等
a+bi=c+di⇔a=c,b=d(a,b,c,d∈R)
也就是说,两个复数相等,充要条件是他们的实部和虚部分别相等.
PS 只有两个复数全是实数,才可以比较大小,否则无法比较大小,比如说 1+3i>1+2i 是错误的.
共轭复数
z=a+bi 的共轭复数记作 ¯z=a−bi(a,b∈R),易得 z⋅¯z=a2+b2.
【例】 复数 z=1−2i 的共轭复数 ¯z=1+2i.
基本方法
【题型1】 复数的概念与分类
【典题 1】 i+i2+i3+⋯+i2017= –––––.
解析 ∵i+i2+i3+i4=i−1−i+1=0 且 in 以 4 为周期,
∴i+i2+i3+⋯+i2017=0×504+i2017=i.
点拨 i2=−1 ,i3=−i ,i4=1 ,in 以 4 为周期,即 i4+n=in.
【典题 2】求当 a 为何实数时,复数 z=(a2−2a−3)+(a2+a−12)i 满足:
(1)z 为实数; (2)z 为纯虚数;
解析 复数 z=(a2−2a−3)+(a2+a−12)i.
(1) 若 z 为实数,则 a2+a−12=0,解得 a=−4 或 a=3;
(2) 若 z 为纯虚数,则 {a2−2a−3=0a2+a−12≠0,解得 a=−1.
【巩固练习】
1. 复数 3−4i 的虚部是 –––––.
2. 若复数 (m2−3m)+(m2−5m+6)i 是纯虚数,则实数 m 的值为 –––––.
3. 若复数 z=(m−2)+(m+1)i 为纯虚数 (i 为虚数单位),其中 m∈R,则 |z|= –––––.
4. 当实数 x 取何值时,复数 z=(x2−1)+(x+1)i.
(1) 是实数? (2) 是纯虚数?
参考答案
-
答案 −4
-
答案 0
解析 ∵ 复数 (m2−3m)+(m2−5m+6)i 是纯虚数,
∴m2−3m=0 且 m2−5m+6≠0,
∴m=0,m=3 且 m≠2,m≠3,
∴m=0.
-
答案 3
解析 由 z 是纯虚数可知 m=2,这时 z=3i,故 |z|=|3i|=3.
-
答案 (1) x=−1;(2)x=1.
解析 (1) ∵z 是实数,∴x+1=0,解得 x=−1;
(2) ∵z 是纯虚数, ∴{x2−1=0x+1≠0,解得 x=1.
【题型2】 复数的几何意义
【典题 1】 在复平面内,复数 6+5i,−2+3i 对应的点分别为 A,B.若 C 为线段 AB 的中点,则点 C 对应的复数是 ( )
A.4+8i B.8+2i C.2+4i D.4+i
解析 复数 6+5i 对应 A 点坐标为 (6,5),−2+3i 对应 B 点坐标为 (−2,3).
由中点坐标公式知 C 点坐标为 (2,4),
∴ 点 C 对应的复数为 2+4i.故选 C.
点拨 复数 z=a+bi 在复平面内对应点 (a,b).
【典题 2】设 z∈C,满足下列条件的点 Z 的集合是什么图形?
①|z|=√2; ②|z|≤3.
解析 设 z=x+yi(x,y∈R),
①|z|=√2,∴ 点 Z 的集合是以原点为圆心,以 √2 为半径的圆.
②|z|≤3,∴ 点 Z 的集合是以原点为圆心,以 3 为半径的圆及其内部.
【典题 3】已知复数 z1=−3+4i ,z2=a−3i(a∈R).z1,z2 对应的向量分别为 −−→OZ1, −−→OZ2,且 −−→OZ1⊥−−→OZ2,则 a= –––––.
解析 依题意 −−→OZ1=(−3,4), −−→OZ2=(a,−3),
由于 −−→OZ1⊥−−→OZ2,
所以 −−→OZ1⋅−−→OZ2=0,
即 −3a−12=0,解得 a=−4.
【巩固练习】
1. 在复平面内,复数 z=−√3+i(i 为虚数单位)对应的点位于第 ––––– 象限.
2. 已知复数 z 是纯虚数,且 |z|=4,则复数 z 在复平面内对应的点的坐标是 –––––.
3. 已知复数 x2−6x+5+(x−2)i 在复平面内对应的点在第三象限,则实数 x 的取值范围为 –––––.
4. 在复平面内,向量 −−→OA 表示的复数为 1+i,将向量 −−→OA 向右平移 1 个单位后,再向上平移 2 个单位,得到向量 −−−→O′A′,则向量 −−−→O′A′ 对应的复数是 –––––.
5. 已知向量 −−→OA 对应的复数是 4+3i,点 A 关于实轴的对称点为 A1,将向量 −−→OA1 平移,使其起点移动到 A 点,这时终点为 A2.
(1) 求向量 −−→OA1 对应的复数; (2) 求点 A2 对应的复数.
参考答案
-
答案 二
解析 复数 z=−√3+i 对应的点 (−√3,1) 位于第二象限.
-
答案 (0,4) 或 (0,−4)
解析 设 z=bi(b∈R,且 b≠0),由 |z|=4 得 √b2=4,所以 b=±4,即 z=±4i,
故 z 对应的点的坐标是 (0,4) 或 (0,−4).
-
答案 1<x<2
解析 因为复数 x2−6x+5+(x−2)i 在复平面内对应的点在第三象限,
所以 {x2−6x+5<0x−2<0,所以 {1<x<5x<2,所以 1<x<2.
即 1<x<2 为所求实数 x 的取值范围.
-
答案 1+i
解析 在复平面内,一个向量作平移变换,从一个位置无论平移到哪一个位置,平移后的向量和原来的向 量都是相等向量,对应的复数也都相等,所以 −−−→O′A′=−−→OA.因此向量 −−−→O′A′ 对应的复数仍然是 1+i.
-
答案 (1) 4−3i ;(2) 8
解析 (1)∵ 向量 −−→OA 对应的复数是 4+3i,
∴ 点 A 对应的复数也是 4+3i,
因此点 A 坐标为 (4,3),
∴ 点 A 关于实轴的对称点 A1 为 (4,−3),
故向量 −−→OA1 对应的复数是 4−3i;
(2) 依题意知 −−→OA1=−−→AA2,而 −−→OA1=(4,−3),
设 A2(x,y),则有 (4,−3)=(x−4,y−3),
∴x=8,y=0,即 A2(8,0),
∴ 点 A2 对应的复数是 8.
分层练习
【A组---基础题】
1. 复数 i+i2+i3+⋯…+i2020+i2021 的值为 ( )
A.0 B.i C.1+i D.−1−i
2. 已知 x,y∈R,i 为虚数单位,且 (x−2)i−y=1+i,则 (1+i)x+y 的值为 ( ).
A.4 B.−4 C.4+4i D.2i
3. 若 a 为实数,复数 z=a−2i 在复平面上位于第四象限,且 |z|=√5,则 a=( )
A.±1 B.−1 C.1 D.2
4. 给出复平面内的以下各点:A(3,1),B(−2,0),C(0,4),D(0,0),E(−1,−5),则这些点中对应的复数为虚数的点的个数是 ( )
A.1 B.2 C.3 D.4
5. 若 z=2−i2023,则 z 在复平面内对应的点位于第 ––––– 象限.
6. 设 z 为纯虚数,且 |z−1|=|−1+i|,则复数 z= –––––.
7. 已知 a∈R,则复数 (a2+a+1)−(a2−2a+3)i 对应的点在复平面内的第 ––––– 象限.
8. 设 z=a+bi(a,b∈R),求在复平面上满足下列条件的点的集合所组成的图形.
(1)|a|<2,且 |b|<2; (2)|z|≤2,且 |b|>1; (3)|z|=2,且 a>b.
参考答案
-
答案 B
解析 ∵i2=−1,i3=−i,i4=1,
∴i+i2+i3+i4+⋯+i2021=505(i+i2+i3+i4)+i2021
=505(i−1−i+1)+(i2)1010⋅i=0+i=i
故选:B.
-
答案 D
解析 由 (x−2)i−y=1+i,可得 {x−2=1−y=1⟹{x=3y=−1,
∴(1+i)x+y=(1+i)2=2i,故选 D.
-
答案 C
解析 由 z=a−2i 在复平面上位于第四象限知 a>0,
由 |z|=√5 得 a2+4=5,∴a=1,
故选 C.
-
答案 C
解析 A,C,E 三点对应的复数分别为 3+i,4i,−1−5i,是虚数,B,D 对应的是实数,因此共有 3 个点.
-
答案 一
解析 i2023=(i4)505⋅i3=−i,
则 z=2−i2023=2+i
故 z 在复平面内对应的点 (2,1) 位于第一象限.
-
答案 ±i
解析 ∵z 为纯虚数,
∴ 设 z=ai(a∈R,且 a≠0),则 |z−1|=|ai−1|=√a2+1.
又 ∵|−1+i|=√2,
∴√a2+1=√2,即 a2=1,
∴a=±1,即 z=±i.
-
答案 四
解析 由 a2+a+1=(a+12)2+34>0,−(a2−2a+3)=−(a−1)2−2<0,
故复数对应点在第四象限.
-
答案 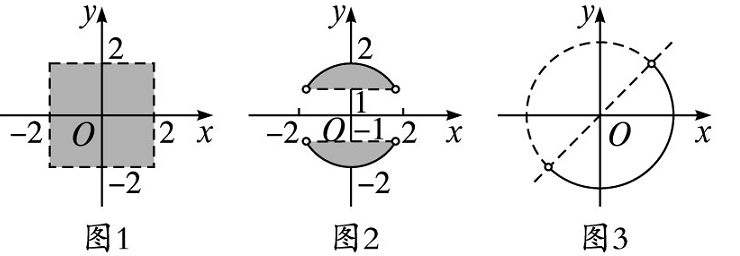
解析 (1) 在复平面上,满足不等式 |a|<2 的点组成的图形是位于两条平行直线 x=±2 之间的长条带状 (不包括两条平行直线).满足不等式 |b|<2 的点组成的图形是位于两条平行直线 y=±2 之间的长条带状 (不包括两条平行直线),两者的公共部分即为所求.即以原点为中心,边长等于 4,各边分别平行于坐标轴的正方形内部的点,但不包括边界,如图 1 所示.
(2) 不等式 |z|≤2 的解集对应的点是以原点为圆心,以 2 为半径的圆的内部及其边界上的点组成的图形.满足条件 |b|>1 的点是直线 y=1 以上及直线 y=−1 以下的点,两者的公共部分即为所求.即以原点为圆心、以 2 为半径的圆被直线 y=±1 所截得的两个弓形,但不包括弦上的点,如图 2 所示.
(3) 方程 |z|=2 的对应点的集合是以原点为圆心,以 2 为半径的圆周.满足条件 a>b 的点组成的图形是位于直线 y=x 下方的半平面,其中不包括直线 y=x 上的点.两者的公共部分即为所求,如图 3 所示.

【B组---提高题】
1. 已知关于 x 的方程,x2+2(1+i)x+ab+(a+b)i=0(a,b∈R+) 总有实数解,则 a+b 的取值范围是 –––––.
2. 若 θ∈(3π4,5π4),则复数 z=(cosθ+sinθ)+(sinθ−cosθ)i 在复平面内所对应的点在第 ––––– 象限.
3. 已知 z1=x2+√x2+1i,z2=(x2+a)i 对任意的 x∈R 均有 |z1|>|z2| 成立,试求实数 a 的取值范围.
参考答案
-
答案 [2,+∞)
解析 ∵x2+2(1+i)x+ab+(a+b)i=0
得 x2+2x+ab+(a+b+2x)i=0 有实数解,
∴x2+2x+ab=0,a+b+2x=0,
消去 x 得 14(a+b)2-(a+b)+ab=0,
∵ab≤(a+b2)2,
∴0=14(a+b)2−(a+b)+ab≤14(a+b)2−(a+b)+(a+b2)2,
即 14(a+b)2-(a+b)+14(a+b)2≥0
则 12(a+b)2-(a+b)≥0
∵a,b∈R+,∴a+b>0,
即 a+b≥2,
即 a+b 的取值范围是 [2,+∞),
故答案为 [2,+∞).
-
答案 二
解析 cosθ+sinθ=√2sin(θ+π4), sinθ−cosθ=√2sin(θ−π4).
因为 θ∈(3π4,5π4),所以 θ+π4∈(π,3π2), θ−π4∈(π2,π).
因此 cosθ+sinθ<0, sinθ−cosθ>0,
所以复数 z 在复平面内对应的点在第二象限.
-
答案 {a∣−1<a≤12}
解析 ∵z1=x2+√x2+1i,z2=(x2+a)i,且 |z1|>|z2|,
∴√x4+x2+1>∣∣x2+a∣∣⇔(1−2a)x2+(1−a2)>0 恒成立.
不等式等价于①:1−2a=0⇒a=12,
即 a=12 时,0⋅x2+(1−14)>0 恒成立.
或②: {1−2a>0Δ=−4(1−2a)(1−a2)<0⇒−1<a<12.
∴a∈(−1,12).
综上可得,a 的取值范围是 {a∣−1<a≤12}.






【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战