欢迎到学科网下载资料学习
[【基础过关系列】高一数学同步精品讲义与分层练习 (人教 A 版 2019)]
(https://www.zxxk.com/docpack/2921718.html)
跟贵哥学数学,soeasy!
必修第二册同步巩固,难度 2 颗星!
基础知识
解三角形
一般地,三角形的三个角 A,B,C 和它们的对边 a,b,c 叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫做解三角形.
余弦定理
(1) 内容
三角形中任何一边的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.
即 a2=b2+c2−2bccosA ,b2=a2+c2−2accosB,c2=a2+b2−2abcosC.
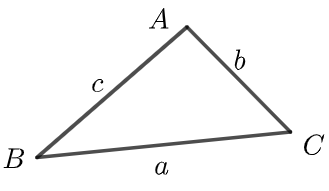
证明 因为 |−−→BC|2=−−→BC2=(−−→AC−−−→AB)2=−−→AC2−2−−→AC⋅−−→AB+−−→AB2
=−−→AC2−2|−−→AC|⋅|−−→AB|cosA+−−→AB2
所以 a2=b2+c2−2bccosA,
同理可得 b2=a2+c2−2accosB,c2=a2+b2−2abcosC.
(2) 变形
cosA=b2+c2−a22bc , cosB=a2+c2−b22ac , cosC=a2+b2−c22ab
(3) 利用余弦定理可以解决下列两类三角形的问题
① 已知三边,可求三个角;
【例】 在 △ABC 中,若 a=4 , b=3, c=√13,则角 C=––––– .
解 cosC=a2+b2−c22ab=16+9−1324=12⇒C=π3.
② 已知两边和一角,求第三边和其他两个角.
【例 1】 在 △ABC 中,A=30° , b=√3,c=1,则 a=––––– .(角 A 为两边的夹角)
解 a2=b2+c2−2bccosA=3+1−3=1⇒a=1.
【例 2】 在 △ABC 中,A=30° , b=3√3,a=3, 则边 c=–––––. (角 A 不为两边的夹角)
解 a2=b2+c2−2bccosA⇒9=27+c2−9c⇒c=3 或 c=6.
三角形类型的判断
∠A=π2⇒b2+c2=a2;
∠A>π2⇒cosA=b2+c2−a22bc<0⇒b2+c2<a2;
∠A<π2⇒cosA=b2+c2−a22bc>0⇒b2+c2>a2.
射影定理
a=c⋅cosB+b⋅cosC ,b=a⋅cosC+c⋅cosA,c=b⋅cosA+a⋅cosB
基本方法
【题型1】 余弦定理解三角形
【典题 1】 若 △ABC 的三边长分别为 3、6、7,则该三角形最大角的余弦值为 –––––.
解析 ∵△ABC 的三边长分别为 3、6、7,
∴ 该三角形最大角的余弦值为 32+62−722×3×6=−19.
点拨 三角形中大角对大边;已知三角形的三边可用余弦定理求三内角.
【典题 2】△ABC 的内角 A,B,C 和它们的对边 a,b,c,已知 a=√5,c=2, cosA=23,则 b=–––––.
解析 因为 a=√5,c=2,cosA=23,
所以由余弦定理可得: cosA=b2+c2−a22bc,即 23=b2+4−54b,
整理可得:3b2−8b−3=0,解得 b=3 或 −13(舍去),
所以 b=3.
点拨 已知三角形的两边与一角,可用余弦定理求第三边。余弦定理有三条,那一般题中涉及哪个角就用对应的余弦定理公式.
【巩固练习】
1. 在 △ABC 中,A=30°,b=√3,c=1,则 a=( )
A.2 B.√3 C.√2 D.1
2. 在 △ABC 中,内角 A,B,C 和它们的对边 a,b,c.若 a=3,A=30°,b=3√3,则 c 值为 ( )
A.3 B.3 或 6 C.√3 D.√3 或 6
3. 在 △ABC 中,已知角 A,B,C 和它们的对边 a,b,c,a=1,b=√2,C=45∘,则边 c 等于 ––––– .
4. 在 △ABC 中,若 ac=8,a+c=7, B=π3,则 b=–––––.
参考答案
-
答案 D
解析 因为 A=30°,b=√3,c=1,
∴a2=b2+c2−2bcosA=√32+12−2×√3×1×cos30∘=1,
故 a=1.
故选:D.
-
答案 B
解析 由余弦定理可得 a2=b2+c2-2bccosA,
即 9=27+c2-9c,即 c2-9c+18=0,解得 c=3 或 c=6,
故选:B.
-
答案 1
解析 由余弦定理得, c=√a2+b2−2abcosC=√1+2−2×1×√2×√22=1.
-
答案 5
解析 由余弦定理知,b2=a2+c2−2accosB=(a+c)2−2ac−2accosB
=49−2×8−2×8×12=25,所以 b=5.
【题型2】 余弦定理的运用
【典题 1】 已知 △ABC 中,角 A,B,C 和它们的对边 a,b,c.若 2bcosC=a+2ccosB,b=√2c,则 cosC=–––––.
解析 由余弦定理及 2bcosC=a+2ccosB 知, 2b⋅a2+b2−c22ab=a+2c⋅a2+c2−b22ac,
化简可得 a2=2(b2−c2),
因为 b=√2c,所以 a2=2(2c2−c2)=2c2,即 a=√2c,
由余弦定理知, cosC=a2+b2−c22ab=2c2+2c2−c22⋅√2c⋅√2c=34.
点拨 遇到类似 "2bcosC=a+2ccosB" 含角含边的等式,可化为仅含角或仅含边的等式.
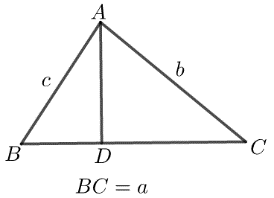
【典题 2】在 △ABC 中,角 A,B,C 和它们的对边 a,b,c,已知 a=4,b=5,c=6,则 BC 边上的中线长 AD=–––––.
解析 因为 a=4,b=5,c=6,
所以 cosB=a2+c2−b22ac=16+36−252×4×6=916,
又 AD 为 BC 边上的中线长,
所以 BD=a2=2,
在 △ABD 中,由余弦定理可得 AD2=c2+(a2)2−2⋅c⋅a2⋅cosB=36+4−2×6×2×916=532,
可得 AD=√1062.

点拨 对于类似本题图象含有多个三角形的问题,一是尽量去思考在每个三角形中哪些角哪些边可求尽量先确定;二是注意公角或公边的三角形间条件转换.
【巩固练习】
1. 在 △ABC 中,角 A,B,C 和它们的对边 a,b,c.若 b2+c2−a2=65bc,则 sinA 的值为 –––––.
2. 在 △ABC 中,内角 A,B,C 和它们的对边 a,b,c,若 2a2=2b2+bc, cosA=14,则 bc= ––––– .
3. 设 △ABC 的内角 A,B,C 和它们的对边 a,b,c.若 b2=ac,a+c=4, −−→BA⋅−−→BC=3,则 cosB=–––––.
4. 在钝角三角形 ABC 中,a=1,b=2,则边 c 的取值范围是 –––––.
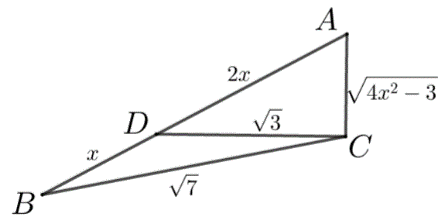
5. 在 △ABC 中,D 是 AB 边上一点,AD=2DB,DC⊥AC,DC=√3, BC=√7,则 AB=–––––.
参考答案
-
答案 45
解析 ∵b2+c2−a2=65bc,
又由余弦定理可得,b2+c2−a2=2bc⋅cosA,
∴65bc=2bc⋅cosA,即 cosA=35,
∴sinA=√1−cos2A=45.
-
答案 1
解析 在 △ABC 中,2a2=2b2+bc,整理得 b2=a2−12bc,
由余弦定理: cosA=b2+c2−a22bc=c2−12bc2bc=2c−b4b=14,
整理得 bc=1.
-
答案 910
解析 由 −−→BA⋅−−→BC=3,得 cacosB=3,
结合余弦定理可得 ac⋅a2+c2−b22ac=3,
∴a2+c2−b2=6.∴(a+c)2−2ac−b2=6,
∴3b2=10, ∴b2=103,
∴cosB=910 .
-
答案 1<c<√3 或 √5<c<3.
解析 ①∵ 当 ∠C 是钝角时,有 ∠C>90°,
∴c>√a2+b2=√5,
又 a+b>c,可得 c<1+2=3,
∴ 可得边 c 的取值范围是 (√5,3);
②当 ∠B 是钝角时,有 ∠B>90°,
∴b2>a2+c2,可得 4>1+c2,解得 c<√3,
又 c>b-a=1,
∴1<c<√3,
综上,边 c 的取值范围是 1<c<√3 或 √5<c<3.
-
答案 1
解析 如图,设 BD=x,则由余弦定理可得, cosA=√4x2−32x,
又由余弦定理可得, 7=BC2=9x2+(4x2−3)−2⋅3x⋅√4x2−3cosA
=13x2−6x⋅√4x2−3×√4x2−32x−3,
即 7=6+x2,解得 x=1,
∴AB=3.
故答案为:1.
分层练习
【A组---基础题】
1. 已知 a,b,c 分别为 △ABC 内角 A,B,C 的对边,若 c=3,b=√3,B=30°,则 a=( )
A.3 B.2√3 C.√3 或 2√3 D.3 或 2√3
2. 在 △ABC 中,角 A,B,C 和它们的对边 a,b,c,若 a=4,b=3, c=√13,则 C=( )
A.30° B.45° C.60° D.120°
3.(多选) 已知 △ABC 中,角 A,B,C 和它们的对边 a,b,c,且满足 B=π3,a+c=√3b,则 ac=( )
A.2 B.3 C. 12 D. 13
4. 在 △ABC 中,a2=b2+c2+bc,则 ∠A=––––– .
5. 在 △ABC 中,若 a=2,b=4, cosC=14,则 △ABC 的周长等于 –––––.
6. 已知 △ABC 中,角 A,B,C 和它们的对边 a,b,c,且满足 accosB=a2−b2+12bc,则 A=–––––.
7. 在 △ABC 中,角 A,B,C 和它们的对边 a,b,c.已知 C=π3, b2−c2=12a2,则 cosA=–––––.
8. 在 △ABC 中,内角 A,B,C 和它们的对边 a,b,c.已知 c=2,b=1, cosC=14.则 △ABC 的中线 AD 的长为 –––––.
9. 如图所示,在平面四边形 ABCD 中, AB=√10,BC=3,AC=5,CD=2√2,∠BCD=135∘.
(1) 求 sin∠ACB; (2) 求 AD 的长.

参考答案
-
答案 C
解析 ∵c=3,b=√3,B=30°,
∴ 由余弦定理可得:b2=a2+c2-2accosB,
可得 3=a2+32−2×a×3×√32,,可得 a2-3√3a+6=0,
∴ 解得 a=√3,或 2√3.
故选:C.
-
答案 C
解析 由余弦定理可得, cosC=a2+b2−c22ab=16+9−132×4×3=12,
因为 C 为三角形的内角,故 C=13π,
故选:C.
-
答案 AC
解析 由余弦定理知, cosB=a2+c2−b22ac=a2+c2−(a+c√3)22ac,
∵B=π3,a+c=√3b,
∴12=a2+c2−(a+c√3)22ac,化简得 2a2−5ac+2c2=0,
解得 a=12c 或 a=2c,
∴ac=12 或 2.
故选:AC.
-
答案 120∘
解析 因为在 中,设 A,B,C 和它们的对边 a,b,c,若 a2=b2+c2+bc,
由余弦定理可知 cosA=−12,所以 A=120∘.
-
答案 10
解析 因为 a=2,b=4, cosC=14,
由余弦定理得: c2=a2+b2−2abcosC=4+16−2×2×4×14=16,
所以 c=4.
所以 △ABC 的周长为 a+b+c=2+4+4=10.
-
答案 π3
解析 accosB=a2−b2+12bc,
直接利用余弦定理 cosB=a2+c2−b22ac,
转换为 b2+c2−a2=bc,整理得 cosA=b2+c2−a22bc=12,
由于 0<A<π,所以 A=π3.
-
答案 2√77
解析 △ABC 中,角 A,B,C 和它们的对边 a,b,c,C=π3, b2−c2=12a2,
由余弦定理可得 c2=a2+b2−2ab⋅cosC=a2+b2−ab,
即 b2−c2=ab−a2,
∴a22=ab−a2, b=3a2,
再把 b=3a2 代入 b2−c2=12a2,可得 c=√72a.
则 cosA=b2+c2−a22bc=2√77.
-
答案 √62
解析 如图所示,

△ABC 中,c=2,b=1, cosC=14,
由余弦定理得,c2=a2+b2-2accosC,即 4=a2+1−2a×1×14,
整理得 2a2-a-6=0,解得 a=2 或 a=−32(舍去);
所以 CD=12a=1,
由余弦定理得, AD2=12+12−2×1×1×14=32,
解得 AD=√62,
所以 △ABC 的中线 AD 的长为 √62.
故答案为:√62.
-
答案 (1) 35; (2) √37.
解析 (1) 在 △ABC 中,AB=√10,BC=3,AC=5,
由余弦定理可得 cos∠ACB=AC2+BC2−AB22AC⋅BC=25+9−102×5×3=45,
∴sin∠ACB=√1−cos2∠ACB=35;
(2) 结合 (1) 可知 cos∠ACD=cos(135∘−∠ACB)=cos135∘cos∠ACB+sin135∘sin∠ACB
=−√22×45+√22×35=−√210,
∵CD=2√2,AC=5,
∴ 在 △ACD 中,由余弦定理可得
AD=√AC2+CD2−2AC⋅CD⋅cos∠ACD=
⎷52+(2√2)2−2×5×2√2×(−√210)=√37.
【B组---提高题】
1.ΔABC 中三边上的高依次为 113, 15, 111,判定 ΔABC 的形状.
2. 在 △ABC 中,∠C=90°,M 是 BC 边上一点,且满足 −−→CM=2−−→MB,若 sin∠BAM=15,则 sin∠BAC=–––––.
参考答案
-
答案 钝角三角形
解析 设 ΔABC 三边分别为 a,b,c, S△ABC=12a⋅113=12b⋅111=12c⋅15,
所以 a13=b11=c5,设 a=13k,b=11k,c=5k(k>0) .
因为 11k+5k>13k,
故能构成三角形,取大角 A ,
cosA=b2+c2−a22bc=112+52−1322×11×5<0,
所以 A 为钝角,所以 ΔABC 为钝角三角形.
-
答案 √155
解析 记 ∠BAM=θ,则 sinθ=15,
设 BC=3,因 −−→CM=2−−→MB,所以 BM=1,MC=2,
设 CA=t,由 ∠C=90°,得 AB=√9+t2, AM=√4+t2,
因 sinθ=15,所以 cosθ=2√65,
因 BM2=AB2+AM2−2AB⋅AMcosθ,
即 1=9+t2+4+t2−2√9+t2√4+t2⋅2√65,
整理得:t4-12t2+36=0,即 (t2-6)2=0,所以 t2=6,
所以 AB=√9+t2=√9+6=√15,
所以 sin∠BAC=3√15=√155.
故答案为: √155.










【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!