6.4.1—6.4.2 平面向量的应用
${\color{Red}{欢迎到学科网下载资料学习 }}$
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019)]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第二册同步巩固,难度2颗星!
基础知识
平面几何中的向量方法
① 由于向量的线性运算和数量积运算具有鲜明的几何背景,平面几何图形的许多性质,如全等、相似、长度、夹角等都可以由向量的线性运算及数量积表示出来,因此平面几何中的许多问题都可用向量运算的方法加以解决.
② 用向量方法解决平面几何问题的“三部曲”
(1) 建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2) 通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3) 把运算结果“翻译”成几何关系.
Eg 点\(A\)、\(B\)、\(C\)、\(D\)不在同一直线上
(1)证明直线平行或共线: \(A B / / C D \Leftrightarrow \overrightarrow{A B} / / \overrightarrow{C D}\);
(2)证明直线垂直: \(A B \perp C D \Leftrightarrow \overrightarrow{A B} \cdot \overrightarrow{C D}=0\);
(3)求线段比值: \(\dfrac{A B}{C D}=|\lambda|\)且 \(A B / / C D \Leftrightarrow \overrightarrow{A B}=\lambda \overrightarrow{C D}\);
(4)证明线段相等: \(\overrightarrow{A B}^2=\overrightarrow{C D}^2 \Leftrightarrow A B=C D\).
向量在物理中的应用
① 速度、力是向量,都可以转化为向量问题;
② 力的合成与分解符合平行四边形法则.
基本方法
【题型1】 向量在几何中的应用
【典题1】 证明对角线互相平分的四边形是平行四边形.

证明 设四边形\(ABCD\)的对角线\(AC\)、\(BD\)交于点\(O\),且\(AO=OC\),\(BO=OD\)
\(\because \overrightarrow{A B}=\dfrac{1}{2} \overrightarrow{A C}+\dfrac{1}{2} \overrightarrow{D B}, \quad \overrightarrow{D C}=\dfrac{1}{2} \overrightarrow{D B}+\dfrac{1}{2} \overrightarrow{A C}\),\(\overrightarrow{DC}=\dfrac{1}{2} \overrightarrow{DB}+\dfrac{1}{2} \overrightarrow{A C}\),
\(\therefore \overrightarrow{A B}=\overrightarrow{D C}\),
即\(AB=DC\)且\(AB//DC\),
所以四边形\(ABCD\)是平行四边形
即对角线互相平分的四边形是平行四边形.
点拨 证明直线平行或共线: \(A B / / C D \Leftrightarrow \overrightarrow{A B} / / \overrightarrow{C D}\).若\(\overrightarrow{A B}=\overrightarrow{DC}\),则\(AB=DC\)且\(AB//DC\).
【典题2】 用向量方法证明三角形三条高线交于一点.
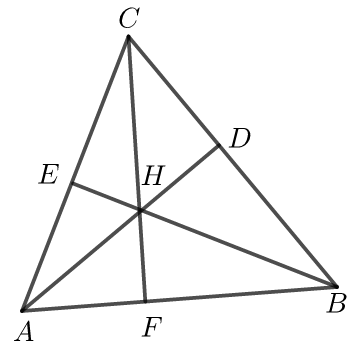
证明 设\(H\)是高线\(BE\)、\(CF\)的交点,
则有\(\overrightarrow{BH}=\overrightarrow{AH}-\overrightarrow{A B}\),\(\overrightarrow{CH}=\overrightarrow{AH}-\overrightarrow{A C}\),\(\overrightarrow{BC}=\overrightarrow{A C}-\overrightarrow{A B}\),
\(\because \overrightarrow{BH}⊥\overrightarrow{A C}\),\(\overrightarrow{CH}⊥\overrightarrow{A B}\),
\(\therefore (\overrightarrow{AH}-\overrightarrow{A B})⋅\overrightarrow{A C}=(\overrightarrow{AH}-\overrightarrow{A C})⋅\overrightarrow{A B}=0\),
化简得\(\overrightarrow{AH}⋅(\overrightarrow{A C}-\overrightarrow{A B} )=0\),\(\therefore \overrightarrow{AH}⋅\overrightarrow{BC}=0\)
则\(AH⊥BC\),
所以三角形三条高线交于一点.
点拨 证明直线垂直: \(A B \perp C D \Leftrightarrow \overrightarrow{A B} \cdot \overrightarrow{C D}=0\).
【巩固练习】
1.已知\(DE\)是\(∆ABC\)的中位线,用向量的方法证明\(DE=\dfrac{1}{2} BC\),且\(DE//BC\).

2.用向量方法证明对角线相等的平行四边形是矩形.

3.证明三角形三条中线交于一点.
4.已知平行四边形\(ABCD\)的对角线为\(AC\)、\(BD\),求证 \(A C^2+B D^2=2\left(A B^2+A D^2\right)\) (即对角线的平方和等于邻边平方和的\(2\)倍).

参考答案
-
证明 已知\(\overrightarrow{A D}=\dfrac{1}{2} \overrightarrow{A B}\), \(\overrightarrow{A E}=\dfrac{1}{2} \overrightarrow{A C}\)
所以 \(\overrightarrow{D E}=\overrightarrow{A E}-\overrightarrow{A D}=\dfrac{1}{2}(\overrightarrow{A C}-\overrightarrow{A B})=\dfrac{1}{2} \overrightarrow{B C}\)
即\(DE=\dfrac{1}{2} BC\),
又\(D\)不在\(BC\)上,所以\(DE//BC\). -
证明 如图,平行四边形\(ABCD\)对角线\(AC\)、\(BD\)交于点\(O\),
设\(OA=a\),\(\because\)对角线相等\(\therefore OB=OD=a\)
\(\because \overrightarrow{A B}=\overrightarrow{AO}+\overrightarrow{OB}\),\(\overrightarrow{A D}=\overrightarrow{AO}+\overrightarrow{OD}\)
\(\therefore \overrightarrow{A B}\cdot \overrightarrow{A D}=(\overrightarrow{AO}+\overrightarrow{OB} )(\overrightarrow{AO}+\overrightarrow{OD} )\)\(=\overrightarrow{AO}^2+\overrightarrow{AO}\cdot \overrightarrow{OD}+\overrightarrow{OB}⋅\overrightarrow{AO}+\overrightarrow{OB}⋅\overrightarrow{OD}\)
\(=a^2+\overrightarrow{AO}(\overrightarrow{OD}+\overrightarrow{OB} )-a^2=0\),
\(\therefore \overrightarrow{A B}⊥\overrightarrow{A D}\) , 即\(AB⊥AD\),
\(\therefore\)四边形\(ABCD\)是矩形. -
证明 \(AF\)、\(CD\)、\(BE\)是三角形\(ABC\)的三条中线
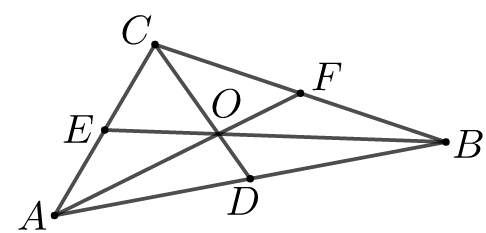
\(\because\)点\(D\)是中点, \(\therefore \overrightarrow{C D}=\dfrac{1}{2}(\overrightarrow{C A}+\overrightarrow{C B})\)
连接\(EF\),易所以 \(\overrightarrow{D E}=\overrightarrow{A E}-\overrightarrow{A D}=\dfrac{1}{2}(\overrightarrow{A C}-\overrightarrow{A B})=\dfrac{1}{2} \overrightarrow{B C}\)
即\(DE=\dfrac{1}{2} BC\),
又\(D\)不在\(BC\)上,所以\(DE//BC\).\(∆AOB~∆FOE\),且相似比是\(2:1\),
\(\therefore B O=\dfrac{2}{3} B E\),
\(\therefore \overrightarrow{C O}=\overrightarrow{C B}+\overrightarrow{B O}=\overrightarrow{C B}+\dfrac{2}{3} \overrightarrow{B E}=\overrightarrow{C B}+\dfrac{2}{3}(\overrightarrow{B A}+\overrightarrow{A E})\)
\(=\overrightarrow{C B}+\dfrac{2}{3}\left(\overrightarrow{B C}+\overrightarrow{C A}+\dfrac{1}{2} \overrightarrow{A C}\right)=\dfrac{1}{3}(\overrightarrow{C A}+\overrightarrow{C B})\)
\(\therefore \overrightarrow{C O}=\dfrac{2}{3} \overrightarrow{C D}\) ,即\(C\)、\(O\)、\(D\)三点共线,
\(\therefore AF\)、\(CD\)、\(BE\)交于一点,
即三角形三条中线交于一点. -
证明 由 \(|\overrightarrow{A C}|^2=\overrightarrow{A C}^2=(\overrightarrow{A B}+\overrightarrow{A D})^2=|\overrightarrow{A B}|^2+|\overrightarrow{A D}|^2+2 \overrightarrow{A B} \cdot \overrightarrow{A D}\) \(|\overrightarrow{D B}|^2=\overrightarrow{D B}^2=(\overrightarrow{A B}-\overrightarrow{A D})^2=|\overrightarrow{A B}|^2+|\overrightarrow{A D}|^2-2 \overrightarrow{A B} \cdot \overrightarrow{A D}\)
两式相加得 \(|\overrightarrow{A C}|^2+|\overrightarrow{D B}|^2=2\left(|\overrightarrow{A B}|^2+|\overrightarrow{A D}|^2\right)\)
即\(A C^2+B D^2=2\left(A B^2+A D^2\right)\)
【题型2】 向量在物理中的应用
【典题1】 如图所示,一个物体被两根轻质细绳拉住,且处于平衡状态,已知两条绳上的拉力分别是\(F_1\),\(F_2\),且\(F_1\),\(F_2\)与水平夹角均为\(45°\),\(|\overrightarrow{F_1} |=|\overrightarrow{F_2} |=10 \sqrt{2} N\),则物体的重力大小为 \(\underline{\quad \quad}\) .

解析 如图,\(\because |\overrightarrow{F_1} |=|\overrightarrow{F_2} |=10 \sqrt{2} N\),

\(\therefore |\overrightarrow{F_1}+\overrightarrow{F_2}|=10 \sqrt{2}× \sqrt{2} N=20N\),
\(\therefore\) 物体的重力大小为\(20\).
故答案 为 \(20\).
点拨 力的分解与合成符合平行四边形法则.由于物体是静止的,所以两个力在水平方向是相反向量,在垂直方向两个力的合力大小等于重力.
【典题2】如图,已知河水自西向东流速为\(|v_0 |=1m/s\),设某人在静水中游泳的速度为\(v_1\),在流水中实际速度为\(v_2\).
(1)若此人朝正南方向游去,且\(|v_1 |= \sqrt{3} m/s\),求他实际前进方向与水流方向的夹角\(α\)和\(v_2\)的大小;
(2)若此人实际前进方向与水流垂直,且\(|v_2 |= \sqrt{3} m/s\),求他游泳的方向与水流方向的夹角\(β\)和\(v_1\)的大小.

解析 如图,设\(\overrightarrow{OA}=\overrightarrow{v_0}\),\(\overrightarrow{OB}=\overrightarrow{v_1}\),\(\overrightarrow{OC}=\overrightarrow{v_2}\),

则由题意知\(\overrightarrow{v_2}=\overrightarrow{v_0}+\overrightarrow{v_1}\),\(|\overrightarrow{OA}|=1\),
根据向量加法的平行四边形法则得四边形\(OACB\)为平行四边形.
(1)由此人朝正南方向游去得四边形\(OACB\)为矩形,且\(|\overrightarrow{OB}|=AC= \sqrt{3}\),如下图所示,
则在直角\(△OAC\)中, \(\left|\overrightarrow{v_2}\right|=O C=\sqrt{O A^2+A C^2}=2\),
\(\tan \angle A O C=\dfrac{\sqrt{3}}{1}=\sqrt{3}\),又 \(\alpha=\angle A O C \in\left(0, \dfrac{\pi}{2}\right)\),所以 \(\alpha=\dfrac{\pi}{3}\);
(2)由题意知 \(\alpha=\angle O C B=\dfrac{\pi}{2}\),且\(|\overrightarrow{v_2}|=|OC|= \sqrt{3}\),\(BC=1\),如下图所示,

则在直角\(△OBC\)中, \(\left|\overrightarrow{v_1}\right|=O B=\sqrt{O C^2+B C^2}=2\), \(\tan \angle B O C=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\),
又 \(\angle A O C \in\left(0, \dfrac{\pi}{2}\right)\),所以 \(\angle B O C=\dfrac{\pi}{6}\),
则 \(\beta=\dfrac{\pi}{2}+\dfrac{\pi}{6}=\dfrac{2 \pi}{3}\),
答 (1)他实际前进方向与水流方向的夹角\(α\)为\(\dfrac{ \pi}{3}\),\(v_2\)的大小为\(2m/s\);
(2)他游泳的方向与水流方向的夹角\(β\)为\(\dfrac{2 \pi}{3}\),\(v_1\)的大小为\(2m/s\).
【巩固练习】
1.如图 一个力\(\overrightarrow{F}\)作用于小车\(G\),使小车\(G\)发生了\(40\)米的位移,\(\overrightarrow{F}\)的大小为\(50\)牛,且与小车的位移方向的夹角为\(60°\),则\(\overrightarrow{F}\)在小车位移方向上的正射影的数量为\(\underline{\quad \quad}\),力\(\overrightarrow{F}\)做的功为\(\underline{\quad \quad}\) 牛米.

2.(多选)如图所示,小船被绳索拉向岸边,设船在水中运动时水的阻力大小不变,那么小船匀速靠岸过程中,下列说法中正确的是( )

A.绳子的拉力不断增大 \(\qquad \qquad \qquad \qquad\) B.绳子的拉力不断变小
C.船的浮力不断小 \(\qquad \qquad\qquad \qquad\) D.船的浮力保持不变
3.已知,一艘船以\(5km/h\)的速度向垂直于对岸方向行驶,航船实际航行方向与水流方向成\(30°\)角,求水流速度和船实际速度.
4.如图,一条河两岸平行,河的宽度\(AC= \sqrt{3} km\),一艘船从河边的\(A\)点出发到达对岸的\(B\)点,船只在河内行驶的路程\(AB=2km\),行驶时间为\(0.2h\).已知船在静水中的速度\(v_1\)的大小为\(|v_1 |\),水流的速度\(v_2\)的大小为\(|v_2 |=2km/h\).
求:
(1)\(|v_1 |\);
(2)船在静水中速度\(v_1\)与水流速度\(v_2\)夹角的余弦值.

参考答案
-
答案 \(25\)牛,\(1000\).
解析 如图,\(\because |\overrightarrow{F}|=50\),且\(\overrightarrow{F}\)与小车的位移方向的夹角为\(60°\),
\(\therefore \overrightarrow{F}\)在小车位移方向上的正射影的数量为
\(|\overrightarrow{F}|cos60°=50×\dfrac{1}{2}=25\)(牛).
力\(\overrightarrow{F}\)作用于小车\(G\),使小车\(G\)发生了\(40\)米的位移,
\(\therefore\)力\(\overrightarrow{F}\)做的功\(w=25×40=1000\)(牛米).
故答案 为\(25\)牛,\(1000\). -
答案 \(AC\)
解析 设水的阻力为\(\overrightarrow{f}\),绳子的拉力为\(\overrightarrow{F}\),\(\overrightarrow{F}\)与水平方向的夹角为\(\theta\left(0<\theta<\dfrac{\pi}{2}\right)\),
则 \(|\vec{F}| \cos \theta=|\vec{f}|\),所以 \(|\vec{F}|=\dfrac{|\vec{f}|}{\cos \theta}\),
因为\(θ\)增大,\(\cos θ\)减小,则\(|\overrightarrow{F}|\)增大,
因为\(|\overrightarrow{F}|\cos θ\)增大,且\(|\overrightarrow{F}|\sin θ\)加上浮力等于船的重力,
所以船的浮力减小.
故选:\(AC\). -
答案 船实际航行速度的大小为\(10km/h\),水流速度\(5 \sqrt{3} km/h\).
解析 如图,设\(\overrightarrow{A D}\)表示船垂直于对岸的速度,\(\overrightarrow{A B}\)表示水流的速度,
以\(AD\),\(AB\)为邻边作平行四边形\(ABCD\),则\(\overrightarrow{A C}\)就是船实际航行的速度.
在\(Rt△ABC\)中,\(∠CAB=30°\),\(|\overrightarrow{A D}|=|\overrightarrow{BC}|=5\),
\(\therefore|\overrightarrow{A C}|=\dfrac{|\overrightarrow{B C}|}{\sin 30^{\circ}}=10\), \(|\overrightarrow{A B}|=\dfrac{|\overrightarrow{B C}|}{\tan 30^{\circ}}=5 \sqrt{3}\).
故船实际航行速度的大小为\(10km/h\),水流速度\(5 \sqrt{3} km/h\).

-
答案 (1)\(2 \sqrt{21 }km/h\); (2) \(\dfrac{\sqrt{21}}{14}\)
解析 (1)如图,\(\because\) 河的宽度\(AC= \sqrt{3} km\),\(AB=2km\),
\(\therefore \sin \angle A B C=\dfrac{A C}{A B}=\dfrac{\sqrt{3}}{2}\),\(\therefore ∠ABC=60^∘\),
设合速 \(\vec{v}=\overrightarrow{O E}\), \(\overrightarrow{v_2}=\overrightarrow{O F}\),船在静水中的速度 \(\overrightarrow{v_1}=\overrightarrow{F E}\),
则 \(\vec{v}=\overrightarrow{v_1}+\overrightarrow{v_2}\),
由题意可得\(O E=|\vec{v}|=\dfrac{2}{0.2}=10 \mathrm{~km} / \mathrm{h}\),且\(∠EOF=∠ABC=60^∘\),
又\(O F=\left|\overrightarrow{v_2}\right|=2 \mathrm{~km} / \mathrm{h}\),\(\therefore\) 在\(△EOF\)中由余弦定理可得:
\(\left|\overrightarrow{v_1}\right|=E F=\sqrt{O E^2+O F^2-2 \times O E \times O F \times \cos 60^{\circ}}\)
\(=\sqrt{100+4-2 \times 10 \times 2 \times \dfrac{1}{2}}=2 \sqrt{21} \mathrm{~km} / \mathrm{h}\);
(2)由(1)\(EF=2 \sqrt{2}\),\(OE=10\),\(OF=2\),
\(\therefore\)由余弦定理可得 \(\cos \angle O F E=\dfrac{4+84-100}{2 \times 2 \times 2 \sqrt{21}}=-\dfrac{\sqrt{21}}{14}\),
又 \(\left\langle\overrightarrow{v_1}, \overrightarrow{v_2}\right\rangle=180^{\circ}-\angle O F E\),
\(\therefore \cos \left\langle\overrightarrow{v_1}, \overrightarrow{v_2}\right\rangle=\cos \left(180^{\circ}-\angle O F E\right)=-\cos \angle O F E=\dfrac{\sqrt{21}}{14}\).

分层练习
【A组---基础题】
1.一质点在平面上的三个力\(F_1\),\(F_2\),\(F_3\)的作用下处于平衡状态,已知\(F_1\),\(F_2\)成\(90^∘\)角,且\(F_1\),\(F_2\)的大小分别为\(2N\)和\(4N\),则\(F_3\)的大小为( )
A.\(6N\) \(\qquad \qquad \qquad\) B.\(2N\) \(\qquad \qquad \qquad\) C.\(2 \sqrt{5} N\) \(\qquad \qquad \qquad\) D.\(2 \sqrt{7} N\)
2.一条渔船以\(6km/h\)的速度向垂直于对岸的方向行驶,同时河水的流速为\(2km/h\),则这条渔船实际航行的速度大小
为( )
A. \(2 \sqrt{10} \mathrm{~km} / \mathrm{h}\) \(\qquad \qquad \qquad\) B.\(4 \sqrt{2} km/h\) \(\qquad \qquad \qquad\) C.\(2 \sqrt{3} km/h\) \(\qquad \qquad \qquad\) D.\(3km/h\)
3.(多选)一物体受到\(3\)个力的作用,其中重力\(G\)的大小为\(2N\),水平拉力\(F_1\)的大小为\(1N\),力\(F_2\)未知,则( )
A.当该物体处于平衡状态时,\(|F_2 |= \sqrt{5} N\)
B.当物体所受合力为\(F_1\)时,\(|F_2 |= \sqrt{5} N\)
C.当\(|F_2 |=1N\)时, \((\sqrt{5}-1) \mathrm{N} \leqslant\left|F_1+F_2+G\right| \leqslant(\sqrt{5}+2) \mathrm{N}\)
D.当\(|F_2 |=1N\)时,必存在实数\(λ\),使得\(G=F_2+λF_1\)
4.用向量方法证明对角线互相垂直的平行四边形是菱形.

5.证明勾股定理,在\(Rt∆ABC\)中,\(AC⊥BC\),\(AC=b\),\(BC=a\),\(AB=c\),则\(c^2=a^2+b^2\).

6.用向量方法证明设平面上\(A\),\(B\),\(C\),\(D\)四点满足条件\(AD⊥BC\),\(BD⊥AC\),则\(AB⊥CD\).
7.已知向量 \(\overrightarrow{O P}_1\)_、 _\(\overrightarrow{O P}_2\)、 \(\overrightarrow{O P}_3\)满足 \(\overrightarrow{O P}_1+\overrightarrow{O P}_2+\overrightarrow{O P}_3=\overrightarrow{0}\), \(\left|\overrightarrow{O P}_1\right|=\left|\overrightarrow{O P}_2\right|=\left|\overrightarrow{O P}_3\right|=1\).求证\(△P_1 P_2 P_3\)是正三角形.
参考答案
-
答案 \(C\)
解析 根据题意, \(\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{0}\),所以 \(\overrightarrow{F_3}=-\left(\overrightarrow{F_1}+\overrightarrow{F_2}\right)\),
故 \(\vec{F}_3^2=\vec{F}_1^2+{\overrightarrow{F_2}}^2+2 \overrightarrow{F_1} \cdot \overrightarrow{F_2}\),
又\(F_1\),\(F_2\)成\(90^∘\)角,则\(\overrightarrow{F_1}⋅\overrightarrow{F_2}=0\),
则\(\vec{F}_3^2=\vec{F}_1^2+\vec{F}_2^2=22+42=20\),
则\(F_3\)的大小为\(2 \sqrt{5} N\),
故选:\(C\). -
答案 \(A\)
解析 如图所示,渔船实际航行的速度为 \(\overrightarrow{v_{A C}}=\overrightarrow{v_{\text {船 }}}+\overrightarrow{v_{\text {水 }}}\);
大小为 \(\left|\overrightarrow{v_{A C}}\right|=\left|\overrightarrow{v_{\text {船 }}}+\overrightarrow{v_{\text {水 }}}\right|=\sqrt{6^2+2^2}=2 \sqrt{10} \mathrm{~km} / \mathrm{h}\).
故选\(A\).

-
答案 \(ABD\)
解析 对于\(A\),当该物体所受合力处于平衡状态时,如图\(1\),
此时\(\overrightarrow{F_1}\),\(\overrightarrow{F_2}\)的合力大小为\(2N\),方向与重力方向相反,\(\therefore |\overrightarrow{F_2} |= \sqrt{5}\),故\(A\)正确;
对于\(B\),当物体所受合力为\(\overrightarrow{F_1}\)时,结合向量加法的平行四边形法则,如图\(2\),\(|\overrightarrow{F_2} |= \sqrt{5}\),
故\(B\)正确;
对于\(C\),当\(|\overrightarrow{F_2} |=1N\)时,设重力\(\vec{G}\)与水平拉力\(\overrightarrow{F_1}\)的合力为\(\overrightarrow{F}\),大小为\(|\overrightarrow{F}|= \sqrt{5} N\),如图\(3\),
当\(\overrightarrow{F_2}\)与\(\overrightarrow{F}\)方向相同时, \(\left|\overrightarrow{F_1}+\overrightarrow{F_2}+\vec{G}\right|\)取得最大值\(( \sqrt{5}+1)N\)
当\(\overrightarrow{F_2}\)与\(\overrightarrow{F}\)方向相反时,\(\left|\overrightarrow{F_1}+\overrightarrow{F_2}+\vec{G}\right|\)取得最小值\(( \sqrt{5}-1)N\),
故\((\sqrt{5}-1) \mathrm{N} \leqslant \left|\overrightarrow{F_1}+\overrightarrow{F_2}+\vec{G}\right| \leqslant(\sqrt{5}+1) \mathrm{N}\) ,故\(C\)错误;
对于\(D\),当\(|\overrightarrow{F_2} |=1N\)时,若存在实数\(λ\),使得\(\vec{G}=\overrightarrow{F_2}+λ\overrightarrow{F_1}\),
则 \(\lambda^2=\left(G-F_2\right)^2=4+1-2 \times 2 \times 1 \times \cos \theta=5-4 \cos \theta \in[1,9]\),
其中\(θ\)为力 \(\vec{G}\),\(\overrightarrow{F_2}\)的夹角,
\(\therefore\) 存在实数\(λ\),使得 \(\vec{G}=\overrightarrow{F_2}+\lambda \overrightarrow{F_1}\),故\(D\)正确.

故选:\(ABD\). -
证明 如图平行四边形\(ABCD\)对角线\(AC\)、\(BD\)交于点\(O\),
\(\because \overrightarrow{A B}=\overrightarrow{AO}+\overrightarrow{OB}\),\(\overrightarrow{BC}=\overrightarrow{BO}+\overrightarrow{OC}\)
\(\therefore |\overrightarrow{A B} |^2=(\overrightarrow{AO}+\overrightarrow{OB} )^2=|\overrightarrow{AO} |^2+2\overrightarrow{AO}⋅\overrightarrow{OB}+|\overrightarrow{OB} |^2=|\overrightarrow{AO} |^2+|\overrightarrow{OB} |^2\)
\(|\overrightarrow{BC} |^2=(\overrightarrow{BO}+\overrightarrow{OC} )^2=|\overrightarrow{BO} |^2+2\overrightarrow{BO}⋅\overrightarrow{OC}+|\overrightarrow{OC} |^2=|\overrightarrow{BO} |^2+|\overrightarrow{OC} |^2\)
\(\therefore |\overrightarrow{A B} |=|\overrightarrow{BC} |\)
\(\therefore\) 四边形\(ABCD\)是菱形. -
证明 由\(\overrightarrow{A B}=\overrightarrow{A C}+\overrightarrow{CB}\),得\(\overrightarrow{A B}^2=(\overrightarrow{A C}+\overrightarrow{CB} )^2=\overrightarrow{A C}^2+2\overrightarrow{A C}⋅\overrightarrow{CB}+\overrightarrow{CB}^2\)
即\(|\overrightarrow{A B}|^2=|\overrightarrow{A C}|^2+|\overrightarrow{CB}|^2\)
故\(c^2=a^2+b^2\). -
证明 因\(AD⊥BC\),所以\(\overrightarrow{A D}⋅\overrightarrow{BC}=\overrightarrow{A D}⋅(\overrightarrow{A C}-\overrightarrow{A B})=0\),
因\(BD⊥AC\),所以\(\overrightarrow{A C}⋅\overrightarrow{BD}=\overrightarrow{A C}⋅(\overrightarrow{A D}-\overrightarrow{A B})=0\),
于是\(\overrightarrow{A D}⋅\overrightarrow{A C}=\overrightarrow{A D}⋅\overrightarrow{A B}\),\(\overrightarrow{A C}⋅\overrightarrow{A D}=\overrightarrow{A C}⋅\overrightarrow{A B}\)
所以\(\overrightarrow{A D}⋅\overrightarrow{A B}=\overrightarrow{A C}⋅\overrightarrow{A B}\),\((\overrightarrow{A D}-\overrightarrow{A C})⋅\overrightarrow{A B}=0\),
即 \(\overrightarrow{C D} \cdot \overrightarrow{A B}=0\),所以 \(\overrightarrow{C D} \perp \overrightarrow{A B}\),即\(AB⊥CD\). -
证明 法一 \(\because \overrightarrow{O P}_1+\overrightarrow{O P}_2+\overrightarrow{O P}_3=\overrightarrow{0}\), \(\therefore \overrightarrow{O P}_1+\overrightarrow{O P}_2=-\overrightarrow{O P}_3\),
\(\therefore\left|\overrightarrow{O P}_1+\overrightarrow{O P}_2\right|=\left|-\overrightarrow{O P}_3\right|\).
\(\therefore\left|\overrightarrow{O P}_1\right|^2+\left|\overrightarrow{O P}_2\right|^2+2 \overrightarrow{O P_1} \cdot \overrightarrow{O P}_2=\left|\overrightarrow{O P}_3\right|^2\).
又\(\because\left|\overrightarrow{O P}_1\right|=\left|\overrightarrow{O P}_2\right|=\left|\overrightarrow{O P}_3\right|=1\),
\(\therefore \overrightarrow{O P}_1 \cdot \overrightarrow{O P}_2=-\dfrac{1}{2}\), \(\therefore\left|\overrightarrow{O P}_1\right|\left|\overrightarrow{O P}_2\right| \cos \angle P_1 O P_2=-\dfrac{1}{2}\)
即\(∠P_1 OP_2=120^∘\).
同理\(∠P_1 OP_3=∠P_2 OP_3=120^∘\).
\(\therefore △P_1 P_2 P_3\)为等边三角形.
法二 以\(O\)点为坐标原点建立直角坐标系,设 \(P_1\left(x_1, y_1\right)\), \(P_2\left(x_2, y_2\right)\), \(P_3\left(x_3, y_3\right)\),
则 \(\overrightarrow{O P}_1=\left(x_1, y_1\right)\), \(\overrightarrow{O P}_2=\left(x_2, y_2\right)\), \(\overrightarrow{O P}_3=\left(x_3, y_3\right)\).
由 \(\overrightarrow{O P}_1+\overrightarrow{O P}_2+\overrightarrow{O P}_3=\overrightarrow{0}\),得 \(\left\{\begin{array}{l} x_1+x_2+x_3=0 \\ y_1+y_2+y_3=0 \end{array}\right.\),
\(\therefore\left\{\begin{array}{l} x_1+x_2=-x_3 \\ y_1+y_2=-y_3 \end{array}\right.\),
由\(\left|\overrightarrow{O P}_1\right|=\left|\overrightarrow{O P}_2\right|=\left|\overrightarrow{O P}_3\right|=1\),得 \(x_1^2+y_1^2=x_2^2+y_2^2=x_3^2+y_3^2=1\)
\(\therefore 2+2\left(x_1 x_2+y_1 y_2\right)=1\),
\(\therefore\left|\overrightarrow{P_1 P_2}\right|=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\)
\(=\sqrt{x_1^2+x_2^2+y_1^2+y_2^2-2 x_1 x_2-2 y_1 y_2}\)
\(=\sqrt{2\left(1-x_1 x_2-y_1 y_2\right)}=\sqrt{3}\)
同理 \(\left|\overrightarrow{P_1 P_3}\right|=\sqrt{3}\), \(\left|\overrightarrow{P_2 P_3}\right|=\sqrt{3}\)
\(\therefore △P_1 P_2 P_3\)为正三角形.
【B组---提高题】
1.在\(△ABC\)内使\(A P^2+B P^2+C P^2\)的值最小的点\(P\)是\(△ABC\)的( )
A.外心 \(\qquad \qquad \qquad \qquad\) B.内心\(\qquad \qquad \qquad \qquad\) C.垂心 \(\qquad \qquad \qquad \qquad\) D.重心
2.如图,一条河的两岸平行,河的宽度\(d=600m\),一艘客船从码头\(A\)出发匀速驶往河对岸的码头\(B\).已知\(|AB|=1km\),水流速度为\(2km/h\),若客船行驶完航程所用最短时间为\(6\)分钟,则客船在静水中的速度大小为( )

A.\(8km/h\) \(\qquad \qquad \qquad\) B.\(6 \sqrt{2} km/h\) \(\qquad \qquad \qquad\) C.\(2 \sqrt{34} km/h\) \(\qquad \qquad \qquad\) D.\(10km/h\)
3.如图,\(E\),\(F\)分别是四边形\(ABCD\)的边\(AD\),\(BC\)的中点,\(AB=1\),\(CD=2\),\(∠ABC=75°\),\(∠BCD=45°\),则线段\(EF\)的长是\(\underline{\quad \quad}\).

参考答案
-
答案 \(D\)
解析 令\(\overrightarrow{CA}=\overrightarrow{a}\),\(\overrightarrow{CB}=\overrightarrow{b}\),设\(\overrightarrow{C P}=\vec{m}\),则 \(\overrightarrow{A P}=\vec{m}-\vec{a}\), \(\overrightarrow{B P}=\vec{m}-\vec{b}\),

于是 \(A P^2+B P^2+C P^2=\overrightarrow{A P^2}+\overrightarrow{B P^2}+\overrightarrow{C P^2}=(\vec{m}-\vec{a})^2+(\vec{m}-\vec{b})^2+\vec{m}^2\)
\(=3 \vec{m}^2-2(\vec{a}+\vec{b}) \cdot \vec{m}+\vec{a}^2+\vec{b}^2=3\left[\vec{m}-\dfrac{1}{3}(\vec{a}+\vec{b})\right]^2-\dfrac{1}{3}(\vec{a}+\vec{b})^2+\vec{a}^2+\vec{b}^2\).
所以当 \(\vec{m}=\dfrac{1}{3}(\vec{a}+\vec{b})\)时, \(A P^2+B P^2+C P^2\)最小,
设\(AB\)的中点为\(D\),
\(\because \overrightarrow{m}=\dfrac{1}{3}(\overrightarrow{a}+\overrightarrow{b})\), \(\therefore 3 \vec{m}=\vec{a}+\vec{b} \Rightarrow \dfrac{3}{2} \vec{m}=\dfrac{\vec{a}+\vec{b}}{2} \Rightarrow \dfrac{3}{2} \vec{m}=\overrightarrow{C D}\),
\(\therefore\)点\(P\)在边\(AB\)的中线上,同理点\(P\)在边\(AC\)、\(BC\)的中线上
\(\therefore\)点\(P\)为\(△ABC\)的重心.
故选 \(D\). -
答案 \(B\)
解析 设客船在静水中的速度大小为\(\overrightarrow{v_{\text {静 }}} \mathrm{km} / \mathrm{h}\),水流速度为 \(\overrightarrow{v_{\text {水 }}}\),则| \(\left|\overrightarrow{v_{\text {水 }}}\right|=2 \mathrm{~km} / \mathrm{h}\),
则船实际航行的速度 \(\vec{v}=\overrightarrow{v_{\text {静 }}}+\overrightarrow{v_{\text {水 }}}\), \(t=\dfrac{6}{60}=0.1 h\).
由题意得 \(|\vec{v}| \leqslant \dfrac{|\overrightarrow{A B}|}{0.1}=10\).
把船在静水中的速度正交分解为 \(\overrightarrow{v_{\text {静 }}}=\overrightarrow{v_x}+\overrightarrow{v_y}\).
\(\therefore\left|\overrightarrow{v_y}\right|=\dfrac{0.6}{0.1}=6\),
在\(Rt△ABC\)中, \(B C=\sqrt{1^2-0 \cdot 6^2}=0.8\).
\(\because\left|\overrightarrow{v_x}+\overrightarrow{v_{\text {水 }}}\right|=\left|\overrightarrow{v_x}\right|+\left|\overrightarrow{v_{\text {水 }}}\right|=\dfrac{B C}{0.1}=8\),
\(\therefore\left|\overrightarrow{v_x}\right|=8-2=6\),
\(\therefore\left|\overrightarrow{v_{\text {静 }}}\right|=\left.\sqrt{\mid \overrightarrow{v_x}}\right|^2+\left|\overrightarrow{v_y}\right|^2=6 \sqrt{2}\). \(\therefore \overrightarrow{v_{\text {静 }}}=6 \sqrt{2} \mathrm{~km} / \mathrm{h}\).
设\(\left\langle\overrightarrow{v_{\text {静 }}}, \overrightarrow{v_{\text {水 }}}\right\rangle=\theta\),则\(\mid \tan \theta=\dfrac{\left|\overrightarrow{v_y}\right|}{\left|\overrightarrow{v_x}\right|}=1\), \(\therefore \cos \theta=\dfrac{\sqrt{2}}{2}\).
此时 \(|\vec{v}|=\left|\overrightarrow{v_{\text {静 }}}+\overrightarrow{v_{\text {水 }}}\right|=\sqrt{\left|\overrightarrow{v_{\text {静 }}}\right|^2+2 \overrightarrow{v_{\text {静 }}} \cdot \overrightarrow{v_{\text {水 }}}+\left|\overrightarrow{v_{\text {水 }}}\right|^2}\)
\(=\sqrt{(6 \sqrt{2})^2+2 \times 6 \sqrt{2} \times 2 \cos \theta+2^2}\)\(=\sqrt{72+24 \sqrt{2} \times \dfrac{\sqrt{2}}{2}+4}=10 \leqslant 10\),满足条件.
故选:\(B\).

-
答案 \(\dfrac{\sqrt{7}}{2}\)
解析 由图象,得 \(\overrightarrow{E F}=\overrightarrow{E A}+\overrightarrow{A B}+\overrightarrow{B F}\), \(\overrightarrow{E F}=\overrightarrow{E D}+\overrightarrow{D C}+\overrightarrow{C F}\).
\(\because E\),\(F\)分别是四边形\(ABCD\)的边\(AD\),\(BC\)的中点,
\(\therefore 2 \overrightarrow{E F}=(\overrightarrow{E A}+\overrightarrow{E D})+(\overrightarrow{A B}+\overrightarrow{D C})+(\overrightarrow{B F}+\overrightarrow{C F})=\overrightarrow{A B}+\overrightarrow{D C}\).
\(\because∠ABC=75°\),\(∠BCD=45°\), \(\therefore<\overrightarrow{A B}, \overrightarrow{D C}>=60^{\circ}\),
\(\therefore|\overrightarrow{E F}|=\dfrac{1}{2} \sqrt{(\overrightarrow{A B}+\overrightarrow{D C})^2}=\dfrac{1}{2} \sqrt{\overrightarrow{A B^2}+\overrightarrow{D C^2}+2|\overrightarrow{A B}| \cdot|\overrightarrow{D C}| \cos <\overrightarrow{A B}, \overrightarrow{D C}>}\) \(=\dfrac{1}{2} \sqrt{1^2+2^2+2 \times 1 \times 2 \times \dfrac{1}{2}}=\dfrac{\sqrt{7}}{2}\).
\(\therefore EF\)的长为\(\dfrac{\sqrt{7}}{2}\).
故答案 为 \(\dfrac{\sqrt{7}}{2}\).
【C组---拓展题】
1.在日常生活中,我们会看到如图所示的情境,两个人共提一个行李包.假设行李包所受重力为\(G\),作用在行李包上的两个拉力分别为\(\overrightarrow{F_1}\),\(\overrightarrow{F_2}\),且\(|\overrightarrow{F_1} |=|\overrightarrow{F_2} |\),\(|\overrightarrow{F_1} |\)与\(|\overrightarrow{F_1} |\)的夹角为\(θ\).给出以下结论
①\(θ\)越大越费力,\(θ\)越小越省力; ②\(θ\)的范围为\([0,π]\);
③当 \(\theta=\dfrac{\pi}{2}\)时, \(\left|\overrightarrow{F_1}\right|=|\vec{G}|\); ④当 \(\theta=\dfrac{2 \pi}{3}\)时, \(\left|\overrightarrow{F_1}\right|=|\vec{G}|\).
其中正确结论的序号是\(\underline{\quad \quad}\).

2.如图,重为\(10N\)的匀质球,半径\(R\)为\(6cm\),放在墙与均匀的\(AB\)木板之间,\(A\)端锁定并能转动,\(B\)端用水平绳索\(BC\)拉住,板长\(AB=20cm\),与墙夹角为\(α\),如果不计木板的重量,则\(α\)为何值时,绳子拉力最小?最小值是多少?

参考答案
- 答案 ①④
解析 对于①,由\(|\vec{G}|=\left|\overrightarrow{F_1}+\overrightarrow{F_2}\right|\)为定值,
所以 \(\vec{G}^2=\left|\vec{F}_1\right|^2+\left|\vec{F}_2\right|^2+2\left|\overrightarrow{F_1}\right| \times\left|\vec{F}_2\right| \times \cos \theta=2\left|\vec{F}_1\right|^2(1+\cos \theta)\),
解得 \(\left|\overrightarrow{F_1}\right|^2=\dfrac{|\vec{G}|^2}{2(1+\cos \theta)}\);
由题意知\(θ∈(0,π)\)时,\(y=\cos θ\)单调递减,所以\(\left|\overrightarrow{F_1}\right|^2\)单调递增,
即\(θ\)越大越费力,\(θ\)越小越省力;①正确.
对于②,由题意知,\(θ\)的取值范围是\((0,π)\),所以②错误.
对于③,当 \(\theta=\dfrac{\pi}{2}\)时, \(\left|\overrightarrow{F_1}\right|^2=\dfrac{\vec{G}^2}{2}\),所以 \(\left|\overrightarrow{F_1}\right|=\dfrac{\sqrt{2}}{2}|\vec{G}|\),③错误.
对于④,当\(\theta=\dfrac{2 \pi}{3}\)时, \(\left|\overrightarrow{F_1}\right|^2=|\vec{G}|^2\),所以\(\left|\overrightarrow{F_1}\right|=|\vec{G}|\),④正确.
综上知,正确结论的序号是①④.
故答案 为 ①④. - 答案 \(α=60°\)时,\(\overrightarrow{f}\)有最小值\(12N\).
解析 如图 设木板对球的支持力为\(\overrightarrow{n}\),则 \(\vec{N}=\dfrac{10}{\sin \alpha}\),
设绳子的拉力为\(\overrightarrow{f}\).
又 \(A C=20 \cos \alpha\), \(A D=\dfrac{6}{\tan \dfrac{\alpha}{2}}\),
由动力矩等于阻力矩得 \(\vec{f} \times 20 \cos \alpha=\vec{N} \times \dfrac{6}{\tan \dfrac{\alpha}{2}}=\dfrac{60}{\sin \alpha \cdot \tan \dfrac{\alpha}{2}}\),
\(\therefore \vec{f}=\dfrac{60}{20 \cos \alpha \cdot \sin \alpha \cdot \tan \dfrac{\alpha}{2}}=\dfrac{3}{\cos \alpha(1-\cos \alpha)} \geq \dfrac{3}{\left(\dfrac{\cos \alpha+1-\cos \alpha}{2}\right)^2}=\dfrac{3}{\dfrac{1}{4}}=12\),
\(\therefore\)当且仅当\(\cos α=1-\cosα\)即\(\cos α=\dfrac{1}{2}\),亦即\(α=60°\)时,\(\overrightarrow{f}\)有最小值\(12N\).


