6.3.5 平面向量数量积的坐标表示
${\color{Red}{欢迎到学科网下载资料学习 }}$
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019)]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第二册同步巩固,难度2颗星!
基础知识
平面向量数量积的坐标表示
设\(\vec{a}=(x_1 ,y_1)\),\(\vec{b}=(x_2 ,y_2)\),\(\theta\)为\(\vec{a}\)与\(\vec{b}\)的夹角,则
(1) 数量积\(\vec{a}⋅\vec{b}=x_1 x_2+y_1 y_2\);
(2) 夹角余弦值 \(\cos \theta=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{x_1 x_2+y_1 y_2}{\sqrt{x_1^2+y_1^2} \cdot \sqrt{x_2^2+y_2^2}}\).
证明 (1)因为\(\vec{a}=x_1 \vec{i}+y_1 \vec{j}\),\(\vec{b}=x_2 \vec{i}+y_2 \vec{j}\),
所以\(\vec{a}⋅\vec{b}=(x_1 \vec{i}+y_1 \vec{j} )⋅(x_2 \vec{i}+y_2 \vec{j} )=x_1 x_2 \vec{i}^2+x_1 y_2 \vec{i}⋅\vec{j}+y_1 x_2 \vec{j}⋅\vec{i}+y_1 y_2 \vec{j}^2\)
又\(\vec{i}⋅\vec{i}=1\),\(\vec{j}⋅\vec{j}=1\),\(\vec{i}⋅\vec{j}=\vec{j}⋅\vec{i}=0\),
所以\(\vec{a}⋅\vec{b}=x_1 x_2+y_1 y_2\);
(2)因为\(\vec{a}⋅\vec{b}=|\vec{a}||\vec{b}|\cos\theta\),所以\(\cos \theta=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{x_1 x_2+y_1 y_2}{\sqrt{x_1^2+y_1^2} \cdot \sqrt{x_2^2+y_2^2}}\).
【例】 已知\(\vec{a}=(-1,2)\),\(\vec{b}=(3,4)\),\(\theta\)为\(\vec{a}\)与\(\vec{b}\)的夹角,求\(\vec{a}⋅\vec{b}\)和\(\cos \theta\).
解 \(\vec{a}⋅\vec{b}=-1×3+2×4=5\),
又因为\(|\vec{a}|=\sqrt{5}\),\(|\vec{b} |=5\),所以 \(\cos \theta=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{5}{5 \sqrt{5}}=\dfrac{\sqrt{5}}{5}\).
平面向量垂直
若 \(\vec{a}(x_1 ,y_1)\),\(\vec{b}(x_2 ,y_2)\),则\(\vec{a}⊥ \vec{b}⇒ x_1 x_2+y_1 y_2=0\).
证明 因为\(\vec{a}⊥ \vec{b}\),所以\(\vec{a}\)与\(\vec{b}\)的夹角为 \(\dfrac{\pi}{2}\),
所以 \(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \dfrac{\pi}{2}=0\),
又\(\vec{a}⋅\vec{b}=x_1 x_2+y_1 y_2\),所以\(x_1 x_2+y_1 y_2=0\).
【例】 已知\(\vec{a}=(4,2)\),\(\vec{b}=(2,m)\),且\(\vec{a}⊥\vec{b}\),求\(m\).
解 \(\because \vec{a}⊥\vec{b}\),\(\therefore \vec{a}⋅ \vec{b}=0\),\(\therefore 4×2+2m=0\),解得\(m=-4\).
基本方法
【题型1】 平面向量数量积的坐标表示
【典题1】 已知\(\overrightarrow{A B}=(2,3)\),\(\overrightarrow{A C}=(1,t)\),\(|\overrightarrow{BC}|=1\),则\(\overrightarrow{A B}⋅\overrightarrow{BC}\)=\(\underline{\quad \quad}\) .
解析 由\(\overrightarrow{A B}=(2,3)\),\(\overrightarrow{A C}=(1,t)\),则\(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{A B}=(-1,t-3)\),
即\(|\overrightarrow{B C}|=\sqrt{1+(t-3)^2}=1\),即\(t=3\),
则\(\overrightarrow{A B}⋅\overrightarrow{BC}=(2,3)⋅(-1,0)=-2\).
点拨 题中的向量均是坐标表示,则可把其他向量均用向量表示求解.
【典题2】已知向量\(\vec{a}=(-1,-2)\),\(\vec{b}=(2,λ)\),且\(\vec{a}\)与\(\vec{b}\)的夹角为钝角,则实数\(λ\)的取值范围是\(\underline{\quad \quad}\) .
解析 向量\(\vec{a}=(-1,-2)\),\(\vec{b}=(2,λ)\),且\(\vec{a}\)与\(\vec{b}\)的夹角为钝角,
所以\(\vec{a}⋅\vec{b}<0\),且\(\vec{a}\)与\(\vec{b}\)不共线;
所以\(\left\{\begin{array}{l}
-2-2 \lambda<0 \\
-\lambda \neq-4
\end{array}\right.\),解得\(\lambda>-1\)且\(\lambda≠4\),
所以实数\(\lambda\)的取值范围是\((-1,4)∪(4,+∞)\).
点拨 \(\vec{a}\)与\(\vec{b}\)的夹角为钝角,则\(\vec{a}⋅\vec{b}<0\),且\(\vec{a}\)与\(\vec{b}\)不共线(注意\(\vec{a}\)与\(\vec{b}\)是方向相反的向量);\(\vec{a}\)与\(\vec{b}\)的夹角为锐角,则\(\vec{a}⋅\vec{b}>0\).
【巩固练习】
1.已知\(\vec{a}=(2,1)\),\(\vec{b}=(-4,3)\),则\(\vec{a}\)在\(\vec{b}\)方向上射影的数量\(\underline{\quad \quad}\).
2.已知向量\(\vec{a}=(\sqrt{3}, 1)\), \(\vec{b}=(2,2 \sqrt{3})\),则向量\(\vec{a}\),\(\vec{b}\)的夹角为\(\underline{\quad \quad}\).
3.已知\(\vec{a}=(4,-3)\),\(\vec{b}=(2,1)\),若\(\vec{a}+t\vec{b}\)与\(\vec{b}\)的夹角为\(45^∘\),则实数\(t=\)\(\underline{\quad \quad}\).
参考答案
- 答案 \(-1\)
解析 \(\vec{a}=(2,1)\),\(\vec{b}=(-4,3)\);\(\therefore \vec{a}⋅\vec{b}=-8+3=-5\), \(|\vec{b}|=5\);
\(\therefore \vec{a}\)在\(\vec{b}\)方向上的射影为 \(|\vec{a}| \cos <\vec{a}, \vec{b}>=|\vec{a}| \cdot \dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{b}|}=\dfrac{-5}{5}=-1\). - 答案 \(\dfrac{\pi}{6}\)
解析 \(\because \cos \langle\vec{a}, \vec{b}\rangle=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{2 \sqrt{3}+2 \sqrt{3}}{2 \times 4}=\dfrac{\sqrt{3}}{2}\),且\(0⩽⟨\vec{a},\vec{b}⟩⩽π\),
\(\therefore \vec{a}\),\(\vec{b}\)的夹角为\(\dfrac{\pi}{6}\). - 答案 \(1\)
解析 \(\because \vec{a}=(4,-3)\),\(\vec{b}=(2,1)\),
\(\therefore |\vec{a}|=5\), \(|\vec{b}|=\sqrt{5}\),\(\vec{a}⋅\vec{b}=5\), \(|\vec{a}+t \vec{b}|=\sqrt{5 t^2+10 t+25}\)
\(\because \vec{a}+t\vec{b}\)与\(\vec{b}\)的夹角为\(45^∘\),
\(\therefore(\vec{a}+t \vec{b}) \cdot \vec{b}=|\vec{a}+t \vec{b}| \cdot|\vec{b}| \cos 45^{\circ}\),
即\(5+5 t=\sqrt{5 t^2+10 t+25} \cdot \sqrt{5} \times \dfrac{\sqrt{2}}{2}\),则 \(5+5 t \geqslant 0\),即\(t\geqslant -1\),
平方整理得 \(5 t^2+10 t-15=0\),\(t^2+2 t-3=0\)
即\((t+3)(t-1)=0\),解得\(t=-3\)(舍去)或\(t=1\),
故答案为:\(1\).
【题型2】 平面向量垂直
【典题1】已知\(\vec{a}=(2,-1)\),\(\vec{b}=(x+1,4)\),且\(\vec{a}⊥\vec{b}\),则\(|2\vec{a}+\vec{b}|=\)( )
A.\(\sqrt{5}\)\(\qquad \qquad \qquad\) B.\(2\sqrt{5}\)\(\qquad \qquad \qquad\) C.\(\sqrt{10}\) \(\qquad \qquad \qquad\)D.\(2\sqrt{10}\)
解析 因为\(\vec{a}=(2,-1)\),\(\vec{b}=(x+1,4)\),且\(\vec{a}⊥\vec{b}\),
所以\(\vec{a}⋅\vec{b}=2x+2-4=0\),
所以\(x=1\),\(\vec{b}=(2,4)\),\(2\vec{a}+\vec{b}=(6,2)\),
则\(|2\vec{a}+\vec{b}|=\sqrt{36+4} =2\sqrt{10}\).
故选:\(D\).
点拨 若\(\vec{a}(x_1 ,y_1)\),\(\vec{b}(x_2 ,y_2)\),则\(\vec{a}⊥ \vec{b}⇒\vec{a}⋅ \vec{b}=0⇒ x_1 x_2+y_1 y_2=0\).
【典题2】已知向量\(\vec{a}=(2,1)\),\(\vec{b}=(3,-1)\).
(1)求\(\vec{a}\)与\(\vec{b}\)的夹角;
(2)求\(|2\vec{a}+\vec{b}|\);
(3)若\((k\vec{a}-\vec{b})⊥\vec{b}\),求实数\(k\)的值.
解析 (1)\(\because \vec{a}=(2,1)\),\(\vec{b}=(3,-1)\),
\(\therefore \vec{a}⋅\vec{b}=2×3+1×(-1)=5\), \(|\vec{a}|=\sqrt{2^2+1}=\sqrt{5}\), \(|\vec{b}|=\sqrt{3^2+(-1)^2}=\sqrt{10}\),
设向量\(\vec{a}\)与\(\vec{b}\)的夹角为\(\theta\),则\(\cos \theta=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{5}{\sqrt{5} \times \sqrt{10}}=\dfrac{\sqrt{2}}{2}\),
又由\(\theta∈[0,π]\),\(\theta=\dfrac{\pi}{4}\),即向量\(\vec{a}\)与\(\vec{b}\)的夹角为\(\dfrac{\pi}{4}\);
(2) \(|2 \vec{a}+\vec{b}|=\sqrt{(2 \vec{a}+\vec{b})^2}=\sqrt{4 \vec{a}^2+\vec{b}^2+4 \vec{a} \cdot \vec{b}}\)\(=\sqrt{20+10+20}=5 \sqrt{2}\);
(3)\(k\vec{a}-\vec{b}=(2k-3,k+1)\),且\((k\vec{a}-\vec{b})⊥\vec{b}\),
\(\therefore 3×(2k-3)-(k+1)=0\),解得:\(k=2\).
【巩固练习】
1.已知向量\(\vec{a}=(1,m)\),\(\vec{b}=(2,-1)\),且\((2\vec{a}+\vec{b})⊥\vec{b}\),则实数\(m=\)\(\underline{\quad \quad}\).
2.在\(△ABC\)中,三顶点的坐标分别为\(A(3,t)\),\(B(t,-1)\),\(C(-3,-1)\),\(△ABC\)为以\(B\)为直角顶点的直角三角形,则\(t=\)\(\underline{\quad \quad}\).
3.已知向量\(\vec{a}=(1,2)\),\(\vec{b}=(-3,4)\).
(1)求\(\vec{a}+\vec{b}\)与\(\vec{a}-\vec{b}\)的夹角;
(2)若\(\vec{a}⊥(\vec{a}+\lambda\vec{b})\),求实数\(\lambda\)的值.
参考答案
- 答案 \(\dfrac{9}{2}\)
解析 根据题意,向量\(\vec{a}=(1,m)\),\(\vec{b}=(2,-1)\),则\(2\vec{a}+\vec{b}=(4,2m-1)\),
若\((2\vec{a}+\vec{b})⊥\vec{b}\),则\((2\vec{a}+\vec{b})⋅\vec{b}=8-(2m-1)=9-2m=0\),解可得\(m=\dfrac{9}{2}\). - 答案 \(3\)
解析 \(\overrightarrow{A B}=(t-3,-1-t)\),\(\overrightarrow{BC}=(-t-3,0)\)
\(\because △ABC\)为以\(B\)为直角顶点的直角三角形,
\(\therefore \overrightarrow{A B}⋅\overrightarrow{BC}=(t-3)(-t-3)+0=0\),解得\(t=±3\).
\(t=-3\)时,点\(B\),\(C\)重合,因此舍去.
故答案为 \(3\). - 答案 (1) \(\dfrac{3 \pi}{4}\) ; (2) \(-1\)
解析 (1) 向量\(\vec{a}=(1,2)\),\(\vec{b}=(-3,4)\),
\(\therefore \vec{a}+\vec{b}=(-2,6)\),\(\vec{a}-\vec{b}=(4,-2)\),
\(\therefore (\vec{a}+\vec{b})⋅(\vec{a}-\vec{b})=-8-12=-20\),
\(\therefore \cos \langle\vec{a}+\vec{b}, \vec{a}-\vec{b}\rangle=\dfrac{(\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})}{|\vec{a}+\vec{b}||\vec{a}-\vec{b}|}=\dfrac{-20}{\sqrt{40} \cdot \sqrt{20}}=-\dfrac{\sqrt{2}}{2}\),
\(\therefore \vec{a}+\vec{b}\)与\(\vec{a}-\vec{b}\)的夹角为\(\dfrac{3 \pi}{4}\) .
(2)\(\because \vec{a}⊥(\vec{a}+\lambda\vec{b})\),\(\therefore \vec{a}⋅(\vec{a}+\lambda\vec{b})=0\),
\(\therefore (1,2)⋅(1-3\lambda,2+4\lambda)=0\),
化为\(1-3\lambda+4+8\lambda=0\),解得\(\lambda=-1\).
【题型3】综合运用
【典题1】已知\(A(4,1)\),\(B(1,4)\),\(C(-4,-1)\),\(D(-1,-4)\),通过作图判断四边形\(ABCD\)的形状,并证明你的结论.
解析 如图,
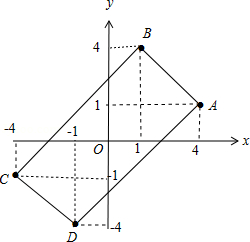
四边形\(ABCD\)为长方形.
\(\because A(4,1)\),\(B(1,4)\),\(C(-4,-1)\),\(D(-1,-4)\),
\(\therefore \overrightarrow{A B}=(-3,3)\), \(\overrightarrow{D C}=(-3,3)\), \(\overrightarrow{C B}=(5,5)\), \(\overrightarrow{D A}=(5,5)\).
\(\therefore AB||CD\),\(AD||BC\),\(AB⊥BC\).
则四边形\(ABCD\)为长方形.
【典题2】如图,在直角梯形\(ABCD\)中,已知\(AB∥DC\),\(∠DAB=90°\),\(AB=2\),\(AD=CD=1\),对角线\(AC\)交\(BD\)于点\(O\),点\(M\)在\(AB\)上,且满足\(OM⊥BD\),则 \(\overrightarrow{A M} \cdot \overrightarrow{B D}\)的值为\(\underline{\quad \quad}\) .

解析 如图以\(A\)为坐标原点,\(AB\)所在直线为\(x\)轴,\(AD\)所在直线为\(y\)轴建立平面直角坐标系;
则\(A(0,0)\),\(B(2,0)\),\(C(1,1)\),\(D(0,1)\);
则 \(\overrightarrow{B D}=(-2,1)\),
由相似三角形易得 \(O\left(\dfrac{2}{3}, \dfrac{2}{3}\right)\).
设\(M(\lambda,0)\),则 \(\overrightarrow{O M}=\left(\lambda-\dfrac{2}{3},-\dfrac{2}{3}\right)\),
因为\(OM⊥BD\),所以 \(\overrightarrow{O M} \cdot \overrightarrow{B D}=-2\left(\lambda-\dfrac{2}{3}\right)-\dfrac{2}{3}=0\),解得 \(\lambda=\dfrac{1}{3}\).
则 \(\overrightarrow{A M}=\left(\dfrac{1}{3}, 0\right)\)
所以 \(\overrightarrow{A M} \cdot \overrightarrow{B D}=\left(\dfrac{1}{3}, 0\right)(-2,1)=-\dfrac{2}{3}\).
故答案为: \(-\dfrac{2}{3}\).

点拨 题中出现垂直关系,有助于建系;建系后向量用坐标表示,处理向量问题或纯几何问题使得问题简便些.
【巩固练习】
1.已知点\(A(2,3)\),\(B(-2,6)\),\(C(6,6)\),\(D(10,3)\),则以\(A\)、\(B\)、\(C\),\(D\)为顶点的四边形是( )
A.梯形 \(\qquad \qquad \qquad \qquad\) B.邻边不等的平行四边形
C.菱形 \(\qquad \qquad \qquad \qquad\) D.两组对边均不平行的四边形
2.已知\(A(-5,0)\),\(B(5,0)\),若对任意实数\(t∈R\),点\(P\)都满足 \(|\overrightarrow{A P}-t \overrightarrow{A B}| \geq 3\),则 \(\overrightarrow{P A} \cdot \overrightarrow{P B}\)的最小值为\(\underline{\quad \quad}\).
3.如图,已知\(O\)为矩形\(ABCD\)内的一点,且\(OA=2\),\(OC=4\),\(AC=5\),则 \(\overrightarrow{O B} \cdot \overrightarrow{O D}=\)\(\underline{\quad \quad}\).

4.如图,菱形\(ABCD\)的边长为\(\sqrt{5}\),对角线\(AC=4\),边\(DC\)上点\(P\)与\(CB\)的延长线上点\(Q\)满足 \(D P=B Q=\dfrac{\sqrt{5}}{3}\),则向量 \(\overrightarrow{P A} \cdot \overrightarrow{P Q}\)的值是\(\underline{\quad \quad}\) .

5.在平面上, \(\overrightarrow{A B_1} \perp \overrightarrow{A B_2}\), \(\left|\overrightarrow{O B_1}\right|=\left|\overrightarrow{O B_2}\right|=1\), \(\overrightarrow{A P}=\overrightarrow{A B_1}+\overrightarrow{A B_2}\).若 \(|\overrightarrow{O P}|<\dfrac{1}{2}\),
则 \(|\overrightarrow{O A}|\)的取值范围是 \(\underline{\quad \quad}\) .
参考答案
-
答案 \(B\)
解析 \(\because \overrightarrow{A B}=(-4,3)\), \(\overrightarrow{D C}=(-4,3)\), \(\overrightarrow{A D}=(8,0)\),
\(\therefore \overrightarrow{A B}=\overrightarrow{D C}\)可得\(AB\)、\(DC\)平行且相等,
可得四边形\(ABCD\)是平行四边形,
又 \(\because|\overrightarrow{A B}|=\sqrt{(-4)^2+3^2}=5\), \(|\overrightarrow{A D}|=8\),
\(\therefore|\overrightarrow{A B}| \neq|\overrightarrow{A D}|\),
由此可得四边形\(ABCD\)是邻边不等的平行四边形
故选 \(B\). -
答案 \(-16\);\(6\).
解析 \(\because A(-5,0)\)和\(B(5,0)\)在中点为原点\(O(0,0)\),
不妨以\(A\),\(B\)的中点为原点,\(AB\)所在直线为\(x\)轴,
过\(O\)且垂直于\(AB\)的直线为轴建立平面直角坐标系,如图所示,

设 \(\overrightarrow{A H}=t \overrightarrow{A B},\),\(H\)为\(AB\)上一点, \(|\overrightarrow{A P}-t \overrightarrow{A B}|=|\overrightarrow{A P}-\overrightarrow{A H}|=|\overrightarrow{H P}| \geq 3\),
故 \(|\overrightarrow{H P}|_{\min }=3\),
所以,\(P\)到直线\(AB\)的距离为\(3\),
则\(P\)点在直线\(L:y=3\)上,
可得:\(A(-5,0)\),\(B(5,0)\),\(P(x,3)\),
则 \(\overrightarrow{P A} \cdot \overrightarrow{P B}=(-5-x,-3) \cdot(5-x,-3)=x^2-25+9=x^2-16\),
当且仅当\(x=0\)时, \(\overrightarrow{P A} \cdot \overrightarrow{P B}\)取最小值\(-16\),
此时\(P(0,3)\), \(|\overrightarrow{P A}+\overrightarrow{P B}|=|(-5, \quad-3)+(5,-3)|=|(0,-6)|=6\).
故答案为:\(-16\);\(6\). -
答案 \(-\dfrac{5}{2}\)
解析 以\(A\)为原点,以\(AB\),\(AD\)为坐标轴建立平面直角坐标系,
设\(O(m,n)\),\(B(a,0)\),\(D(0,b)\),则\(C(a,b)\),
\(\because OA=2\),\(OC=4\),\(AC=5\),
\(\therefore\left\{\begin{array}{l} a^2+b^2=25 \\ m^2+n^2=4 \\ (m-a)^2+(n-b)^2=16 \end{array}\right.\),整理可得: \(a m+b n=\dfrac{13}{2}\).
又 \(\overrightarrow{O B}=(a-m,-n)\), \(\overrightarrow{O D}=(-m, b-n)\),
\(\therefore \overrightarrow{O B} \cdot \overrightarrow{O D}=m(m-a)+n(n-b)=m^2+n^2-(a m+b n)=4-\dfrac{13}{2}=-\dfrac{5}{2}\).

-
答案 \(\dfrac{44}{9}\)
解析 取\(AC\)的中点\(O\),以点\(O\)为原点,直线\(AC\)为\(x\)轴,建立如图所示平面直角坐标系,

则:\(A(-2,0)\),\(D(0,1)\), \(P\left(\dfrac{2}{3}, \dfrac{2}{3}\right)\), \(Q\left(-\dfrac{2}{3},-\dfrac{4}{3}\right)\) ,
\(\therefore \overrightarrow{P A}=\left(-\dfrac{8}{3},-\dfrac{2}{3}\right)\), \(\overrightarrow{P Q}=\left(-\dfrac{4}{3},-2\right)\),
\(\therefore \overrightarrow{P A} \cdot \overrightarrow{P Q}=\dfrac{32}{9}+\dfrac{4}{3}=\dfrac{44}{9}\).
故答案为: \(\dfrac{44}{9}\). -
答案 \(\left(\dfrac{\sqrt{7}}{2}, \sqrt{2}\right]\)
解析 根据 \(\overrightarrow{A B_1} \perp \overrightarrow{A B_2}\), \(\overrightarrow{A P}=\overrightarrow{A B_1}+\overrightarrow{A B_2}\)知,四边形\(AB_1 PB_2\)是矩形.
如图,以\(AB_1\),\(AB_2\)所在直线为坐标轴建立直角坐标系.

设\(|AB_1 |=a\),\(|AB_2 |=b\),点\(O\)的坐标为\((x,y)\),点\(P (a,b)\),
\(\because\left|\overrightarrow{O B}_1\right|=\left|\overrightarrow{O B}_2\right|=1\), \(\therefore\left\{\begin{array}{l} (x-a)^2+y^2=1 \\ x^2+(y-b)^2=1 \end{array}\right.\), \(\therefore\left\{\begin{array}{l} (x-a)^2=1-y^2 \\ (y-b)^2=1-x^2 \end{array}\right.\).
\(\because|\overrightarrow{O P}|<\dfrac{1}{2}\), \(\therefore(x-a)^2+(y-b)^2<\dfrac{1}{4}\),
\(\therefore 1-x^2+1-y^2<\dfrac{1}{4}\), \(\therefore x^2+y^2>\dfrac{7}{4}\)①.
\(\because(x-a)^2+y^2=1\), \(\therefore y^2 \leq 1\),同理 \(x^2 \leq 1\), \(\therefore x^2+y^2 \leq 2\) ②.
由 ①②可知, \(\dfrac{7}{4}<x^2+y^2 \leq 2\)
\(\because|\overrightarrow{O A}|=\sqrt{x^2+y^2}\), \(\therefore \dfrac{\sqrt{7}}{2}<|\overrightarrow{O A}| \leq \sqrt{2}\).
\(\therefore|\overrightarrow{O A}|\)的取值范围为 \(\left(\dfrac{\sqrt{7}}{2}, \sqrt{2}\right]\).
分层练习
【A组---基础题】
1.已知向量\(\vec{a}=(2,-3)\),\(\vec{b}=(m,1)\),若\(|\vec{a}+2\vec{b}|=|\vec{a}-2\vec{b}|\),则\(m=\)( )
A. \(\dfrac{3}{2}\)\(\qquad \qquad \qquad \qquad\) B.\(-\dfrac{3}{2}\) \(\qquad \qquad\qquad \qquad\) C.\(\dfrac{2}{3}\) \(\qquad\qquad \qquad \qquad\) D.\(-\dfrac{2}{3}\)
2.设 \(P_1(1-\sin \alpha, 0)\), \(P_2(0,-\cos \alpha)\),则 \(\left|\overrightarrow{O P_1}-\overrightarrow{O P_2}\right|\)的最大值是( )
A.\(1\)\(\qquad \qquad \qquad \qquad\) B.\(\sqrt{2}\)\(\qquad \qquad \qquad \qquad\) C.\(\sqrt{3}\)\(\qquad\qquad \qquad \qquad\) D.\(2\)
3.在平面四边形\(ABCD\)中,\(\overrightarrow{AC}=(1,3)\), \(\overrightarrow{B D}=(-9,3)\),则四边形\(ABCD\)的面积为( )
A.\(\dfrac{7 \sqrt{10}}{2}\)\(\qquad \qquad \qquad \qquad\) B.\(\dfrac{27}{2}\) \(\qquad \qquad \qquad \qquad\) C.\(15\) \(\qquad\qquad \qquad \qquad\) D.\(\dfrac{9 \sqrt{10}}{2}\)
4.(多选)向量\(\vec{a}=(2,0)\),\(\vec{b}=(x,1)\),则下列说法正确的是 ( )
A.若\(x=2\),则\(\vec{a}||\vec{b}\)
B.若\(\vec{a}⊥\vec{b}\),则\(x=0\)
C.若\(|\vec{b}|=2|\vec{a}|\),则 \(x=\sqrt{15}\)
D.若\(\vec{a}\)与\(\vec{a}-\vec{b}\)夹角的余弦值为 \(\dfrac{\sqrt{2}}{2}\),则\(x=1\)或\(3\)
5.向量\(\vec{a}\),\(\vec{b}\),\(\vec{c}\)在正方形(边长均为 网格中的位置如图所示,则\(\vec{a}⋅\vec{b}=\) \(\underline{\quad \quad}\) .

6.已知向量\(\vec{a}=(1,0)\),\(\vec{b}=(0,1)\),若\((k\vec{a}+\vec{b})⊥(3\vec{a}-\vec{b})\),则实数\(k=\)\(\underline{\quad \quad}\) .
7.已知向量\(\vec{a}=(1,2)\),\(\vec{b}=(t,1)\),若\(\vec{a}\),\(\vec{b}\)夹角的余弦值为 \(\dfrac{\sqrt{5}}{5}\),则实数\(t\)的值为\(\underline{\quad \quad}\) .
8.在平面直角坐标系中,\(O\)为坐标原点,已知\(A(-2,0)\),\(B(0,-2)\),\(C(\cos φ,\sin φ)\),其中\(0<φ<π\).
(1)若 \(\overrightarrow{A C} \cdot \overrightarrow{B C}=\dfrac{5}{3}\),求\(\sin 2φ\)的值;
(2)若 \(|\overrightarrow{O A}+\overrightarrow{O C}|=\sqrt{3}\),求\(\overrightarrow{O B}\)与 \(\overrightarrow{O C}\)的夹角\(\theta\).
9.如图所示,在矩形\(ABCD\)中,\(AB=3\),\(BC=2\),点\(M\)为边\(BC\)的中点,点\(N\)在边\(CD\)上.
(1)若点\(N\)为线段\(CD\)上靠近\(D\)的三等分点,求\(\overrightarrow{A M} \cdot \overrightarrow{A N}\)的值;
(2)若 \(\overrightarrow{A M} \cdot \overrightarrow{A N}=8\),求此时点\(N\)的位置.

10.如图,在矩形\(ABCD\)中,\(BC=3AB=6\),\(E\)为\(AB\)的中点,\(F\)是\(BC\)边上靠近点\(B\)的三等分点,\(AF\)与\(DE\)于点\(G\).设\(\overrightarrow{A B}=\vec{a}\), \(\overrightarrow{A D}=\vec{b}\).
(1)求\(∠EGF\)的余弦值. \(\qquad \qquad\) (2)用\(\vec{a}\)和\(\vec{b}\)表示 \(\overrightarrow{A G}\);

参考答案
-
答案 \(A\)
解析 \(\because |\vec{a}+2\vec{b}|=|\vec{a}-2\vec{b}|\),
\(\therefore (\vec{a}+2\vec{b})^2=(\vec{a}-2\vec{b})^2\),即\(\vec{a}⋅\vec{b}=0\)
\(\because \vec{a}=(2,-3)\),\(\vec{b}=(m,1)\),
\(\therefore \vec{a}⋅\vec{b}=2m-3=0\),解得 \(m=\dfrac{3}{2}\).
故选:\(A\). -
答案 \(D\)
解析 因为\(P_1(1-\sin \alpha, 0)\), \(P_2(0,-\cos \alpha)\),
所以 \(\overrightarrow{O P}_1-\overrightarrow{O P}_2=(1-\sin \alpha, \cos \alpha)\),
\(\left(\overrightarrow{O P_1}-\overrightarrow{O P_2}\right)^2=(1-\sin \alpha)^2+\cos ^2 \alpha=2-2 \sin \alpha\),
当\(\sin α=-1\)时, \(\left(\overrightarrow{O P_1}-\overrightarrow{O P_2}\right)^2\)取得最大值为\(2-2×(-1)=4\),
所以 \(\left|\overrightarrow{O P_1}-\overrightarrow{O P_2}\right|\)的最大值是\(2\).
故选:\(D\). -
答案 \(C\)
解析 在平面四边形\(ABCD\)中,\(\overrightarrow{AC}=(1,3)\), \(\overrightarrow{B D}=(-9,3)\),
\(\because \overrightarrow{A C} \cdot \overrightarrow{B D}=0\), \(\therefore \overrightarrow{A C} \perp \overrightarrow{B D}\).
\(\therefore|\overrightarrow{A C}|=\sqrt{10}\), \(|\overrightarrow{B D}|=\sqrt{(-9)^2+3^2}=3 \sqrt{10}\),
\(\therefore\) 四边形\(ABCD\)的面积为 \(\dfrac{1}{2} \cdot \sqrt{10} \cdot 3 \sqrt{10}=15\),
故选 \(C\). -
答案 \(BD\)
解析 根据题意,依次分析选项:
对于\(A\),若\(x=2\),\(\vec{b}=(2,1)\),\(\vec{a}=(2,0)\),\(\vec{a}||\vec{b}\)不成立,\(A\)错误;
对于\(B\),若\(\vec{a}⊥\vec{b}\),则\(\vec{a}⋅\vec{b}=2x=0\),则\(x=0\),\(B\)正确;
对于\(C\),若\(|\vec{b}|=2|\vec{a}|=4\),则有\(x^2+1=16\),解可得 \(x= \pm \sqrt{15}\),\(C\)错误,
对于\(D\),\(\vec{a}-\vec{b}=(2-x,-1)\),若\(\vec{a}\)与\(\vec{a}-\vec{b}\)夹角的余弦值为 \(\dfrac{\sqrt{2}}{2}\),
则有 \(\dfrac{\sqrt{2}}{2}=\dfrac{\vec{a} \cdot(\vec{a}-\vec{b})}{|\vec{a}| \cdot|\vec{a}-\vec{b}|}=\dfrac{4-2 x}{2 \times \sqrt{(2-x)^2+1}}\),解可得\(x=1\)或\(3\),\(D\)正确;
故选:\(BD\). -
答案 \(-3\)
解析 建立如图的平面直角坐标系,将\(\vec{a}\),\(\vec{b}\)平移到起点为原点时终点坐标即为向量坐标,
\(\therefore \vec{a}=(-1,1)\),\(\vec{b}=(4,1)\),\(\therefore \vec{a}⋅\vec{b}=-1×4+1×1=-3\).

-
答案 \(\dfrac{1}{3}\)
解析 \(\because\) 向量\(\vec{a}=(1,0)\),\(\vec{b}=(0,1)\),
\(\therefore k\vec{a}+\vec{b}=(k,1)\),\(3\vec{a}-\vec{b}=(3,-1)\),
又\((k\vec{a}+\vec{b})⊥(3\vec{a}-\vec{b})\),
\(\therefore 3k-1=0\),解得\(k=\dfrac{1}{3}\). -
答案 \(-\dfrac{3}{4}\)
解析 \(|\vec{a}|=\sqrt{5}\), \(|\vec{b}|=\sqrt{t^2+1}\), \(\vec{a} \cdot \vec{b}=t+2\), \(\cos \langle\vec{a}, \vec{b}\rangle=\dfrac{\sqrt{5}}{5}\)
\(\therefore t+2=\sqrt{5} \cdot \sqrt{t^2+1} \cdot \dfrac{\sqrt{5}}{5}\),整理得, \(t+2=\sqrt{t^2+1}\),解得 \(t=-\dfrac{3}{4}\).
故答案为: \(-\dfrac{3}{4}\). -
答案 (1) \(-\dfrac{8}{9}\);(2) \(\dfrac{5 \pi}{6}\).
解析 (1) \(\overrightarrow{A C}=(\cos \varphi+2 \sin \varphi)\), \(\overrightarrow{B C}=(\cos \varphi,\sin \varphi+2)\), \(\overrightarrow{A C} \cdot \overrightarrow{B C}=\dfrac{5}{3}\),
\(\therefore \cos \varphi(\cos \varphi+2)+\sin \varphi(\sin \varphi+2)=\dfrac{5}{3}\),
\(\therefore \cos \varphi+\sin \varphi=\dfrac{1}{3}\),两边平方可得 \(\sin 2 \varphi=-\dfrac{8}{9}\).
(2) \(\because|\overrightarrow{O A}+\overrightarrow{O C}|=\sqrt{3}\),
\(\therefore \sqrt{(\cos \varphi-2)^2+\sin ^2 \varphi}=\sqrt{3}\),化为 \(\cos \varphi=\dfrac{1}{2}\),
\(\because 0<φ<π\), \(\therefore \varphi=\dfrac{\pi}{3}\).
\(\therefore C\left(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right)\).
\(\therefore \cos \theta=\dfrac{\overrightarrow{O B} \cdot \overrightarrow{O C}}{|\overrightarrow{O B}||\overrightarrow{O C}|}=\dfrac{-\sqrt{3}}{2 \times 1}=-\dfrac{\sqrt{3}}{2}\),
\(\therefore \theta=\dfrac{5 \pi}{6}\).即\(\overrightarrow{O B}\)与\(\overrightarrow{O C}\)的夹角为\(\dfrac{5 \pi}{6}\). -
答案 (1) \(5\) ;(2) 点\(N\)的位置为线段\(CD\)上靠近\(C\)的三等分点
解析 (1)由题意,以\(A\)为原点,\(AB\)所在的直线为\(x\)轴,\(AD\)所在的直线为\(y\)轴,
建立如下图所示的平面直角坐标系,

则\(A(0,0)\),\(M(3,1)\),\(N(1,2)\),\(\overrightarrow{A M}=(3,1)\), \(\overrightarrow{A N}=(1,2)\),
\(\therefore \overrightarrow{A M} \cdot \overrightarrow{A N}=3 \times 1+1 \times 2=5\).
(2)由题意,设\(N\)点坐标为\((a,2)\),\(a∈[0,3]\),
则 \(\overrightarrow{A M}=(3,1)\), \(\overrightarrow{A N}=(a, 2)\),
\(\therefore \overrightarrow{A M} \cdot \overrightarrow{A N}=3 \times a+1 \times 2=3 a+2=8\),解得\(a=2\),
\(\therefore N\)点坐标为\((2,2)\),
故 点\(N\)的位置为线段\(CD\)上靠近\(C\)的三等分点. -
答案 (1) \(-\dfrac{5 \sqrt{74}}{74}\); (2) \(\overrightarrow{A G}=\dfrac{3}{7} \vec{a}+\dfrac{1}{7} \vec{b}\).
解析 (1)建立坐标系如图:
\(\because BC=3AB=6\),\(E\)为\(AB\)的中点,\(F\)是\(BC\)边上靠近点\(B\)的三等分点,
\(\therefore AB=2\),\(AE=1\),\(BF=2\),
则\(A(0,0)\),\(B(2,0)\),\(C(2,6)\),\(D(0,6)\),\(E(1,0)\),\(F(2,2)\).
则\(AF:y=x\),\(DE:y=-6(x-1)\),
由 \(\left\{\begin{array}{l} y=x \\ y=-6(x-1) \end{array}\right.\)得 \(\left\{\begin{array}{l} x=\dfrac{6}{7} \\ y=\dfrac{6}{7} \end{array}\right.\),即\(G\left(\dfrac{6}{7}, \dfrac{6}{7}\right)\),
则 \(\overrightarrow{G E}=\left(\dfrac{1}{7},-\dfrac{6}{7}\right)\), \(\overrightarrow{G F}=\left(\dfrac{8}{7}, \dfrac{8}{7}\right)\),
则 \(\overrightarrow{G E} \cdot \overrightarrow{G E}=\left(\dfrac{1}{7},-\dfrac{6}{7}\right) \cdot\left(\dfrac{8}{7}, \dfrac{8}{7}\right)=-\dfrac{40}{49}\), \(|\overrightarrow{G E}|=\dfrac{\sqrt{37}}{7}\), \(|\overrightarrow{G F}|=\dfrac{8 \sqrt{2}}{7}\),
则 \(\cos \langle\overrightarrow{G E}, \overrightarrow{G F}\rangle=\dfrac{-\dfrac{40}{49}}{\dfrac{\sqrt{37}}{7} \times \dfrac{8 \sqrt{2}}{7}}=-\dfrac{40}{8 \sqrt{74}}=-\dfrac{5 \sqrt{74}}{74}\),
则即 \(\cos \angle E G F=-\dfrac{5 \sqrt{74}}{74}\).
(2) \(\overrightarrow{A G}=\left(\dfrac{6}{7}, \dfrac{6}{7}\right)\), \(\overrightarrow{A B}=\vec{a}=(2,0)\), \(\overrightarrow{A D}=\vec{b}=(0,6)\),
设 \(\overrightarrow{A G}=x \vec{a}+y \vec{b}\),即 \(\left\{\begin{array}{l} 2 x=\dfrac{6}{7} \\ 6 y=\dfrac{6}{7} \end{array}\right.\), 解得\(\left\{\begin{array}{l} x=\frac{3}{7} \\ y=\frac{1}{7} \end{array}\right.\),即 \(\overrightarrow{A G}=\dfrac{3}{7} \vec{a}+\dfrac{1}{7} \vec{b}\).
【B组---提高题】
1.\(P\)是边长为\(2\)的正方形\(ABCD\)边界或内部一点,且 \(\overrightarrow{P B}+\overrightarrow{P C}=\overrightarrow{P M}\),则\(\overrightarrow{A P} \cdot \overrightarrow{A M}\)的最大值是 \(\underline{\quad \quad}\) .
2.如图,矩形\(ABCD\)中,\(AB=2\),\(AD=1\),\(P\)是矩形\(ABCD\)内的动点,且点\(P\)到点\(A\)距离为\(1\),则\(\overrightarrow{P C} \cdot \overrightarrow{P D}\)的最小值为 \(\underline{\quad \quad}\) .

参考答案
-
答案 \(5\)
解析 建立如图所示坐标系;

则\(A(0,2)\),\(B(0,0)\),\(C(2,0)\),\(D(2,2)\);
设\(P(x,y)\),\(0≤x≤2\),\(0≤y≤2\);
取\(BC\)的中点为\(E\),则\(E(1,0)\)
\(\because \overrightarrow{P B}+\overrightarrow{P C}=\overrightarrow{P M}\),
则 \(\overrightarrow{P M}=2 \overrightarrow{P E}\);
则 \(\overrightarrow{A P} \cdot \overrightarrow{A M}=(\overrightarrow{A E}+\overrightarrow{E P})(\overrightarrow{A E}+\overrightarrow{E M})=(\overrightarrow{A E}+\overrightarrow{E P})(\overrightarrow{A E}-\overrightarrow{E P})\)
\(=\overrightarrow{A E^2}+\overrightarrow{A E}(\overrightarrow{E P}-\overrightarrow{E P})-\overrightarrow{E P}^2=\overrightarrow{A E}^2-\overrightarrow{E P^2}\)
\(=2^2+1^2-\left[(x-1)^2+y^2\right]=5-\left[(x-1)^2+y^2\right]\);
故当\(x=1\),\(y=0\)时 \(\overrightarrow{A P} \cdot \overrightarrow{A M}\)取最大值\(5\). -
答案 \(2-2 \sqrt{2}\).
解析 如图,取\(A\)为原点,\(AB\)边所在的直线为\(x\)轴,建立平面直角坐标系,
则\(D(0,1)\),\(C(2,1)\),设 \(P(\cos \theta, \sin \theta)\), \(\left(\theta \in\left(0, \dfrac{\pi}{2}\right)\right)\),

\(\therefore \overrightarrow{P C}=(2-\cos \theta, 1-\sin \theta)\),\(\overrightarrow{P D}=(-\cos \theta, 1-\sin \theta)\)
\(\therefore \overrightarrow{P C} \cdot \overrightarrow{P D}=-2 \cos \theta+\cos ^2 \theta+1-2 \sin \theta+\sin ^2 \theta\)
\(=2-2(\sin \theta+\cos \theta)=2-2 \sqrt{2} \sin \left(\theta+\dfrac{\pi}{4}\right)\),
\(\therefore \sin \left(\theta+\dfrac{\pi}{4}\right)=1\),即 \(\theta=\dfrac{\pi}{4}\)时, \(\overrightarrow{P C} \cdot \overrightarrow{P D}\)取最小值 \(2-2 \sqrt{2}\).
故答案为:\(2-2 \sqrt{2}\).
【C组---拓展题】
1.如图,在正方形\(ABCD\)中,\(AB=2\),\(E\)为\(BC\)的中点,点\(P\)是以\(AB\)为直径的圆弧上任一点.设\(\overrightarrow{A P}=x \overrightarrow{A E}+y \overrightarrow{A D}\),
(1)求\(x-2y\)的最大值、最小值. \(\qquad \qquad\)(2)求\(x+y\)的取值范围.

参考答案
- 答案 (1) 最大值为\(2\),最小值为 \(1-\sqrt{2}\); (2) \(\left[0, \dfrac{\sqrt{5}+1}{4}\right]\)
解析 (1)如图,取\(AB\)中点\(O\),以\(O\)点为原点,以\(AB\)所在直线为\(x\)轴,如图建立平面直角坐标系,
设\(∠POB=\theta\),结合题意,可知\(A(-1,0)\),\(B(1,0)\),\(C(1,2)\),
\(D(-1,2)\),\(E(1,1)\), \(P(\cos \theta, \sin \theta)(\theta \in[0, \pi])\),
所以 \(\overrightarrow{A P}=(\cos \theta+1, \sin \theta), \overrightarrow{A E}=(2,1)\), \(\overrightarrow{A D}=(0,2)\)
又 \(\overrightarrow{A P}=x \overrightarrow{A E}+y \overrightarrow{A D}=x(2,1)+y(0,2)=(2 x, x+2 y)\),
所以\((2x,x+2y)=(\cos \theta+1,\sin \theta)\),
即 \(\left\{\begin{array} { l } { 2 x = \operatorname { c o s } \theta + 1 } \\ { x + 2 y = \operatorname { s i n } \theta } \end{array} \Rightarrow \left\{\begin{array}{l} x=\dfrac{\cos \theta+1}{2} \\ y=\dfrac{2 \sin \theta-\cos \theta-1}{4} \end{array}\right.\right.\),
则有 \(x-2 y=\cos \theta-\sin \theta+1=\sqrt{2} \cos \left(\theta+\dfrac{\pi}{4}\right)+1\),
又由\(\theta∈[0,π]\),则 \(\theta+\dfrac{\pi}{4} \in\left[\dfrac{\pi}{4}, \dfrac{5 \pi}{4}\right]\),
当\(\theta=0\)时, \((x-2 y)_{\max }=2\),
当 \(\theta=\dfrac{3 \pi}{4}\)时, \((x-2 y)_{\text {min }}=1-\sqrt{2}\);
故\(x+2y\)的最大值为\(2\),最小值为 \(1-\sqrt{2}\),
(2)根据题意, \(\left\{\begin{array}{l} x=\dfrac{\cos \theta+1}{2} \\ y=\dfrac{2 \sin \theta-\cos \theta-1}{4} \end{array}\right.\),
则 \(x+y=\dfrac{\cos \theta+1}{2}+\dfrac{2 \sin \theta-\cos \theta-1}{4}=\dfrac{1}{4}(2 \sin \theta+\cos \theta+1)=\dfrac{\sqrt{5}}{4} \sin (\theta+\varphi)+\dfrac{1}{4}\),
其中 \(\tan \varphi=\dfrac{1}{2}\),\(φ\)为锐角)
因为 \(\varphi \leq \theta+\varphi \leq \pi+\varphi\),所以 \(\sin (\pi+\varphi) \leq \sin (\theta+\varphi) \leq 1\),
所以 \(-\dfrac{1}{\sqrt{5}} \leq \sin (\theta+\varphi) \leq 1\),所以 \(0 \leq x+y \leq \dfrac{\sqrt{5}+1}{4}\),
即\(x+y\)的取值范围为\(\left[0, \dfrac{\sqrt{5}+1}{4}\right]\).



