导数专题 函数零点个数
基础知识
函数的零点、方程的实数根
函数的零点、方程的实数根与两函数的交点可视为同一问题,
函数\(h(x)=f(x)-g(x)\)的零点个数
\(⇔\)方程\(f(x)=g(x)\)实数根个数
\(⇔\)函数\(y=f(x)\)与函数\(y=g(x)\)交点个数.
函数零点存在定理
如果函数\(y=f(x)\)在\([a ,b]\)上的图象是连续不断的,且\(f(a)f(b)<0\),那么函数\(y=f(x)\)在\((a ,b)\)至少有一个零点\(c\),即存在\(c∈(a ,b)\),使得\(f(c)=0\),这个\(c\)也就是方程\(f(x)=0\)的解.
求函数零点个数的方法
对于复杂的函数(特别是含参函数)需要利用导数的方法求解
(1) 直接法
直接法,即直接对所求函数进行分析,
(i)对于不含参函数,比如\(f(x)=x^3-2x^2-x\),\(f(x)=e^x-2x^2+x\)等,
求零点个数的思路是:求导→求单调性→求极值最值→结合函数图象分析零点个数;
(ii)对含参函数,进行分类讨论就行.
(2) 分离参数法
对于求含参函数的零点个数,采取分离参数法可把问题转化为求不含参函数问题;
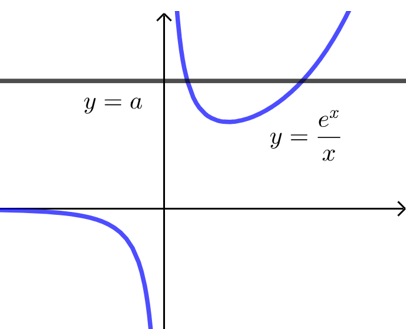
比如求函数\(f(x)=e^x-ax\)的零点个数,
采取分离参数法相当于求函数\(y=\dfrac{e^x}{x}\)与函数\(y=a\)的交点个数.
(3) 切线法
切线法,即利用导数的几何意义求两函数相切的“临界值”,再结合图象判断交点个数;
若所求函数能“分离”出一次函数或“分离”两函数有明显“凹凸性”,可考虑切线法;
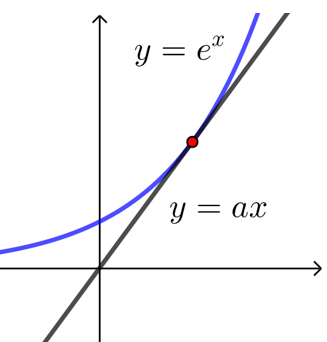
比如求函数\(f(x)=e^x-ax\)的零点个数,可转化为\(y=e^x\)与\(y=ax\)的交点个数,
此时先确定当\(a\)为何值时两函数相切,再结合图象分析交点个数.
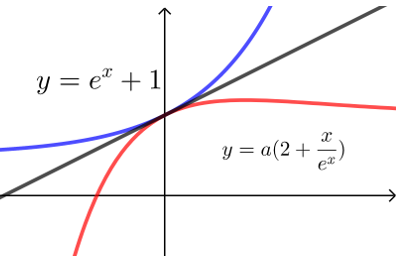
比如求函数\(f(x)=e^x+1-a\left(2+\dfrac{x}{e^x}\right)\)的零点个数,可转化为\(y=e^x+1\)与 \(y=a\left(2+\dfrac{x}{e^x}\right)\)的交点个数,此时先确定当\(a\)为何值时两函数相切,再结合图象分析交点个数.
注意事项
(1) 求函数零点个数时,时常要结合函数图象,所以尽量图象准确,不要想当然;
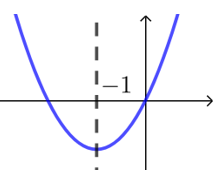
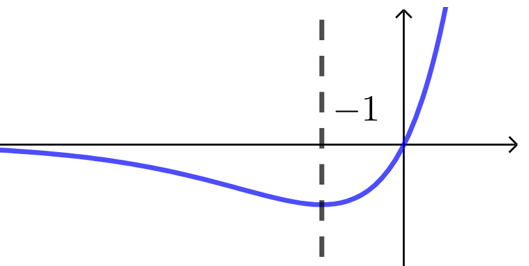
【例】求函数\(f(x)=xe^x\)的零点个数.
(注 函数零点明显仅有\(0\),以下讨论仅为表达画图的重要性)
\(\because f'(x)=(x+1)e^x\),
\(\therefore\)函数\(f(x)\)在\((-∞,-1)\)递减,在\((-1,+∞)\)递增,最小值\(f(-1)=-\dfrac{1}{e}<0\),
此时就以为函数图象是左图,那就得到“有两个零点”的错误结论,
严谨的表达是,\(\because x⟶-∞\),\(f(x)⟶0\),\(\therefore f(x)\)在\((-∞,-1)\)不存在零点,
\(\because f(1)=e>0\), \(\therefore f(-1)f(1)<0\),
由函数零点存在定理可得\(f(x)\)在\((-1,+∞)\)存在\(1\)个零点,
故函数\(f(x)=xe^x\)实际的图象如右图,仅有一个零点.
(2) 要避免上诉“想当然”的情况需要在零点旁边找两个函数值异号的点,方法有二种,
(i)利用极限的思路,比如判断\(x→x_0\)时,\(y→y_0\);\(x→-∞\)时,\(y→+∞\)之类的;
此时会涉及到函数增长快慢问题,但若涉及大学的内容(比如洛必达法则),则解答不会得满分;
(ii) 找到“实实在在”的点;
(3) 对某些含参函数,分离变量的方法行不通,比如因为需要洛必达法则、求导困难等,需要用直接法进行分类讨论.
极限问题
(1) 函数的增长速度
一般地,如果一个函数在某一范围内导数的绝对值\(|f'(x)|\)较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
【例】指数函数\(y=a^x (a>1)\)在\((0,+∞)\)的增长速度是“爆发式”的,
幂函数\(y=x^n (n>0)\)在\((0,+∞)\)的增长速度较快,指数\(n\)越大,增长速度越快.
一次函数\(y=kx+b(k>0)\)的增长的速度不变,\(k\)越大,其增长得越快.
对数函数\(y=\log _ax(a>1)\)在\((1,+∞)\)的增长速度很慢.
(2) 极限
对于某函数\(y=f(x)\),当\(x→a\)时,\(y\)趋向什么”属于极限问题,本质是求\(\lim _{x \rightarrow a} f(x)\).
以下举几个例子,大家细品下,
① \(f(x)=e^x\),当\(x→0\)时,\(y→e^0=1\);即函数\(y=e^x\)能取到\(0\),直接代入便可;
② \(f(x)=\dfrac{1}{x}\),当\(x→+∞\)时,\(y→0\);可想象下\(x\)取一很大的数\(10000\),对应函数值\(y=\dfrac{1}{10000}\)很小,接近\(0\);
③ \(f(x)=\dfrac{\ln x}{x^2}\) ,当\(x→+∞\)时,分子\(\ln x→+∞\),分母\(x^2→+∞\),那\(\dfrac{\ln x}{x^2}\)趋向什么呢?
因为函数\(y=\ln x\)较函数\(y=x^2\)在\((0,+∞)\)增长得慢很多,所以当\(x→+∞\)时, \(\dfrac{\ln x}{x^2} \rightarrow 0\);
这需要了解函数间在某区间的增长速度的比较;
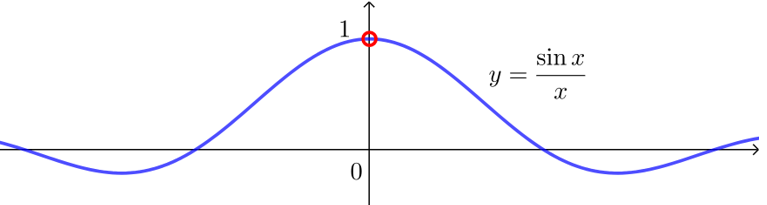
④ \(f(x)=\dfrac{\sin x}{x}\),当\(x→0\)时,分子\(\sin x→0\),分母\(x→0\),那\(\dfrac{\sin x}{x}\)趋向什么呢?
此时\(y=x\)与\(y=\sin x\)在\(x=0\)附近的增速在高中无法确定,
其实\(x→0\)时, \(\dfrac{\sin x}{x} \rightarrow 1\)的,为什么呢?(用洛必达法则可求,但在高中用导数的定义也可求)
其实\(\lim _{x \rightarrow 0} \dfrac{\sin x}{x}=\lim _{x \rightarrow 0} \dfrac{\sin x-0}{x-0}=\lim _{x \rightarrow 0} \dfrac{g(x)-f(0)}{x-0}=g^{\prime}(0)=1\),(\(g(x)=\sin x\),\(g'(x)=\cos x\))
如下图
基本方法
【题型1】 求不含参函数的零点个数
【典题1】判断\(g(x)=2\ln x-\dfrac{1}{2} x^2+x\)的零点个数.
解析 \(g(x)=2\ln x-\dfrac{1}{2} x^2+x\)的定义域是\((0,+∞)\),
\(g^{\prime}(x)=\dfrac{2}{x}-x+1=\dfrac{(-x+2)(x+1)}{x}\),
由\(g'(x)=0\)得\(x=2\),
所以当\(x∈(0,2)\)时,\(g'(x)>0\),\(g(x)\)单调递增;
当\(x∈(2,+∞)\)时,\(g'(x)<0\),\(g(x)\)单调递减,
所以\(x=2\)是\(g(x)\)唯一的极值点且为极大值点,
故\(g_{\max }(x)=g(2)=2 \ln 2>0\),
又\(g\left(\dfrac{1}{e}\right)=-2-\dfrac{1}{2 e^2}-\dfrac{1}{e}<0\),
\(g\left(e^2\right)=4-\dfrac{1}{2} e^4+e^2=-\dfrac{1}{2}\left(e^2-1\right)^2+\dfrac{9}{2}<0\),
由零点的存在性定理知,\(g(x)\)在\(\left(\dfrac{1}{e}, 2\right)\)和\((2,e^2 )\)上分别有一个零点,
故\(g(x)\)有\(2\)个零点.
点拨 解题时多结合导函数“穿线图”与原函数“趋势图”,关于本题的取点,在\((0,2)\)上取\(x=\dfrac{1}{e}\),在\((2,+∞)\)上取\(x=e^2\),取点一要看取点范围,二看函数特征,而函数中含\(\ln x\)多取\(x=1\)、\(e\)、\(\dfrac{1}{e}\) 、\(e^2\)之类的,若失败了多尝试,比如本题中取\(g(e)=2-\dfrac{e^2}{2}+e>0\)失败就再取大些的\(x=e^2\)等.若本题是非解答题,不要取点,直接由\(x→-∞\),\(y→-∞\)和\(x→+∞\),\(y→-∞\)可得.
【巩固练习】
1.在函数\(f(x)=ax^3+bx(a≠0)\)图像在点\((1,f(1))\)处的切线与直线\(6x+y+7=0\)平行,导函数\(f'(x)\)的最小值为\(-12\).
(1)求\(a\)、\(b\)的值;
(2)判断方程\(f(x)=0\)解的个数.
2.证明函数\(f(x)=\ln (x+1)-\sin x\)在\(\left(\dfrac{\pi}{2},+\infty\right)\)上有且仅有一个零点.
参考答案
- 答案 (1)\(a=2\),\(b=-12\);(2)\(3\).
解析 (1)\(a=2\),\(b=-12\)(过程略).
(2)由(1)知\(f(x)=2x^3-12x\),
\(\therefore f^{\prime}(x)=6 x^2-12=6(x+\sqrt{2})(x-\sqrt{2})\),列表如下:
| $x$ | $(-∞,-\sqrt{2})$ | $-\sqrt{2}$ | $(-\sqrt{2},\sqrt{2})$ | $\sqrt{2}$ | $(\sqrt{2},+∞)$ |
| $f'(x)$ | $+$ | $0$ | $-$ | $0$ | $+$ |
| $f(x)$ | ↗ | 极大值 | ↘ | 极小值 | ↗ |
\(\therefore f(x)\)的极大值是\(f(-\sqrt{2})=8\sqrt{2}\),极小值是\(f(\sqrt{2})=-8\sqrt{2}\),
且当\(f(-3)=-18<0\),\(f(3)=18>0\),
\(\therefore f(-3)\cdot f(-\sqrt{2})<0\),\(f(3)\cdot f(\sqrt{2})>0\),
\(\therefore f(x)\)在\((-∞,-\sqrt{2})\)、\((-\sqrt{2},\sqrt{2})\)、\((\sqrt{2},∞)\)上各有\(1\)个零点,
故函数\(f(x)\)有三个零点,即方程\(f(x)=0\)解的个数是\(3\).
- 证明 \(f^{\prime}(x)=\dfrac{1}{x+1}-\cos x\),
当\(x \in\left(\dfrac{\pi}{2}, \pi\right)\)时,\(-\cos x>0\), \(\dfrac{1}{x+1}>0\),
\(\therefore f^{\prime}(x)=\dfrac{1}{x+1}-\cos x>0\),\(\therefore f(x)\)单调递增,
而\(f\left(\dfrac{\pi}{2}\right)=\ln \left(\dfrac{\pi}{2}+1\right)-1<0\),\(f(π)=\ln (π+1)>0\),
所以\(f(x)\)在\(\left(\dfrac{\pi}{2}, \pi\right)\)上有且仅有一个零点\(x_0\);
当\(x∈[π,+∞)\)时,\(f(x)=\ln (x+1)-\sin x>\ln (π+1)-1>0\),
所以以\(f(x)\)在\([π,+∞)\)上无零点;
综上所述,\(f(x)\)有且仅有一个零点.
【题型2】 分离参数法
【典题1】 若\(f(x)=ae^2x+(a-2)e^x-x\)有两个零点,求\(a\)的取值范围.
解析 依题意, \(f(x)=0 \Leftrightarrow a\left(e^{2 x}+e^x\right)=2 e^x+x \Leftrightarrow a=\dfrac{2 e^x+x}{e^{2 x}+e^x}\),
令\(g(x)=\dfrac{2 e^x+x}{e^{2 x}+e^x}\),
则\(g^{\prime}(x)=\dfrac{\left(2 e^x+1\right)\left(e^{2 x}+e^x\right)-\left(2 e^x+x\right)\left(2 e^{2 x}+e^x\right)}{\left(e^{2 x}+e^x\right)^2}=\dfrac{\left(2 e^x+1\right)\left(1-e^x-x\right)}{e^x\left(e^x+1\right)^2}\),
令\(h(x)=1-e^x-x\),
显然函数\(h(x)\)是\(R\)上的减函数,而\(h(0)=0\),
当\(x<0\)时,\(h(x)>0\),\(g'(x)>0\),当\(x>0\)时,\(h(x)<0\),\(g'(x)<0\),
因此,函数\(g(x)\)在\((-∞,0)\)上单调递增,在\((0,+∞)\)上单调递减,
当\(x=0\)时,\(g(x)_{max}=g(0)=1\),
而\(g(-1)=\dfrac{2-e}{e^{-1}+1}<0\),
又当\(x>0\)时,\(g(x)>0\)恒成立,
函数\(f(x)\)有两个零点,等价于直线\(y=a\)与函数\(y=g(x)\)的图象有两个公共点,
在同一坐标系内作出直线\(y=a\)与函数\(y=g(x)\)的图象,如图,

由图象知,当且仅当\(0<a<1\)时,直线\(y=a\)与函数\(y=g(x)\)的图象有两个公共点,
所以\(a\)的取值范围是\((0,1)\).
点拨 利用分离参数法,能把含参函数问题转化为不含参函数问题.
【巩固练习】
1.已知函数\(f(x)=(x-a)\ln x(a∈R)\),若函数\(f(x)\)存在三个单调区间,则实数\(a\)的取值范围是\(\underline{\quad \quad}\) .
2.讨论函数\(g(x)=\dfrac{1}{x}-\dfrac{m}{x^2}-\dfrac{x}{3}(x>0)\)零点的个数.
3.已知函数\(f(x)=\dfrac{x^2+2 x+4}{x+2}\).
(1)求函数\(f(x)\)在区间\([-1,1]\)上的最值;
(2)若关于\(x\)的方程\((x+2)f(x)-ax=0\)在区间\((0,3)\)内有两个不等实根,求实数\(a\)的取值范围.
参考答案
-
答案 \(\left(-\dfrac{1}{e^2}, 0\right)\)
解析 \(f^{\prime}(x)=\ln x+\dfrac{1}{x}(x-a)=\ln x+1-\dfrac{a}{x}\),
函数\(f(x)=(x-a)\ln x(a∈R)\),若函数\(f(x)\)存在三个单调区间,
即\(f'(x)=0\)有两个不等实根,即\(a=x(\ln x+1)\)有两个不等实根,
转化为\(y=a\)与\(y=x(\ln x+1)\)的图像有两个不同的交点,
\(y'=\ln x+2\),令\(\ln x+2=0\),即\(x=\dfrac{1}{e^2}\) ,
即\(y=x(\ln x+1)\)在\(\left(0, \dfrac{1}{e^2}\right)\)上单调递减,在\(\left(\dfrac{1}{e^2},+\infty\right)\)上单调递增 ,
\(y_{min}=-\dfrac{1}{e^2}\),
当\(x\in \left(0, \dfrac{1}{e^2}\right)\)时,\(y<0\),
所以\(a\)的范围为\(\left(-\dfrac{1}{e^2}, 0\right)\). -
答案 当\(m>\dfrac{2}{3}\)时,函数\(g(x)\)无零点;
当\(m=\dfrac{2}{3}\)或\(m≤0\)时,函数\(g(x)\)有且仅有一个零点;
当\(0<m<\dfrac{2}{3}\)时,函数\(g(x)\)有两个零点.
解析 令\(g(x)=0\),得\(m=-\dfrac{1}{3} x^3+x(x>0)\),
设\(h(x)=-\dfrac{1}{3} x^3+x(x>0)\),
所以\(h'(x)=-x^2+1=-(x-1)(x+1)\),
当\(x\in (0,1)\)时,\(h'(x)>0\),此时\(h(x)\)在\((0,1)\)上为增函数;
当\(x\in (1,+∞)\)时,\(h'(x)<0\),此时\(h(x)\)在\((1,+∞)\)上为减函数,
所以当\(x=1\)时,\(h(x)\)取极大值\(h(1)=-1+\dfrac{1}{3}=\dfrac{2}{3}\),
且\(x→0\)时\(h(x)→0\),\(x→+∞\)时\(h(x)→-∞\),

故当\(m>\dfrac{2}{3}\)时,函数\(y=m\)和函数\(y=h(x)\)无交点;
当\(m=\dfrac{2}{3}\)时,函数\(y=m\)和函数\(y=h(x)\)有且仅有一个交点;
当\(0<m<\dfrac{2}{3}\)时,函数\(y=m\)和函数\(y=h(x)\)有两个交点;
当\(m≤0\)时,函数\(y=m\)和函数\(y=h(x)\)有且仅有一个交点.
综上所述,当\(m>\dfrac{2}{3}\)时,函数\(g(x)\)无零点;
当\(m=\dfrac{2}{3}\)或\(m≤0\)时,函数\(g(x)\)有且仅有一个零点,
当\(0<m<\dfrac{2}{3}\)时,函数\(g(x)\)有两个零点. -
答案 (1)最大值为\(3\),最小值为\(2\);(2) \(\left(6, \dfrac{19}{3}\right)\).
解析 (1)最大值为\(3\),最小值为\(2\)(过程略).
(2)因为关于于\(x\)的方程\((x+2)f(x)-ax=0\)在区间\((0,3)\)内有两个不等实根,
则\((x+2) \cdot \dfrac{x^2+2 x+4}{x+2}-a x=0\)在区间\((0,3)\)内有两个不等实根,
所以\(x^2+2x+4-ax=0\)在区间\((0,3\))内有两个不等实根,
所以\(a=\dfrac{x^2+2 x+4}{x}\)在区间\((0,3)\)内有两个不等实根,
令\(g(x)=\dfrac{x^2+2 x+4}{x}\),\(x\in (0,3)\),
\(g(x)=x+2+\dfrac{4}{x} \geqslant 2 \sqrt{x \cdot \dfrac{4}{x}}+2=6\) (当且仅当\(x=2\)时,取等号),
\(x→0\)时,\(g(x)→+∞\); \(g(3)=\dfrac{3^2+2 \times 3+4}{3}=\dfrac{19}{3}\),
所以\(a\)的取值范围为 \(\left(6, \dfrac{19}{3}\right)\).
【题型3】直接法
【典题1】 讨论函数\(f(x)=x\ln x-\dfrac{1}{2} x^2+(a-1)x(a\in R)\)的极值点的个数.
解析 \(f(x)\)的定义域是\((0 ,+∞)\),\(f'(x)=\ln x-x+a\),
令\(g(x)=\ln x-x+a\),则\(f'(x)=\ln x-x+a\),(构造函数,二次求导)
当\(x\in (0 ,1)\)时,\(g^{\prime}(x)>0\),\(g(x)\)单调递增,即\(f'(x)\)单调递增;
当\(x\in (1 ,+∞)\)时,\(g'(x)<0\), \(g(x)\)单调递减,即\(f'(x)\)单调递减;
所以当\(x=1\)时,\(f'(x)\)有极大值\(f'(1)=a-1\),也是最大值,
(确定\(f'(x)\)的最大值\(a-1\),想下函数图象\(a-1\)与\(0\)的大小比较决定导函数\(y=f'(x)\)是否存在零点)
① 当\(a-1≤0\),即\(a≤1\)时,
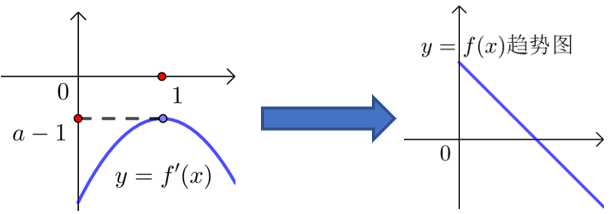
所以\(f(x)\)在\((0 ,+∞)\)上单调递减,此时\(f(x)\)无极值,
② 当\(a>1\)时,\(f'(1)=a-1>0\),
\(f^{\prime}\left[\left(\dfrac{1}{e}\right)^{a+1}\right]=\ln \left(\dfrac{1}{e}\right)^{a+1}-\left(\dfrac{1}{e}\right)^{a+1}+a\)\(=-a-1-\left(\dfrac{1}{e}\right)^{a+1}+a=-1-\left(\dfrac{1}{e}\right)^{a+1}<0\),
易证\(x>1\)时,\(e^x>2x\),
所以\(a>1\),\(f'(e^a )=2a-e^a<0\),

故存在\(x_1\) ,\(x_2\)满足\(0<\left(\dfrac{1}{e}\right)^{a+1}<x_1<1<x_2<e^a\),\(f'(x_1)=f'(x_2)=0\),
当\(x\in (0 ,x_1)\)时,\(f(x)\)单调递减,
当\(x\in (x_1 ,x_2)\)时,\(f(x)\)单调递增,
当\(x\in (x_2 ,+∞)\)时,\(f(x)\)单调递减,
所以\(f(x)\)在\(x=x_1\)处有极小值,在\(x=x_2\)处有极大值.
综上所述,当\(a≤1\)时,\(f(x)\)没有极值点;当\(a>1\)时,\(f(x)\)有\(2\)个极值点.
点拨
① 求出导函数\(f'(x)=\ln x-x+a\),它的图象很难确定,不知道是否存在零点(这与原函数单调性有关),则考虑二次求导进行分析;
② 当\(a>1\)时,导函数\(f'(x)=\ln x-x+a\)存在零点\(x_1\) ,\(x_2\)是怎么确定的?
误区1:\(y=f'(x)\)最大值在\(x\)轴上方且是“先增后减”,想当然说它有两个零点是不严谨的.因为\(y=f'(x)\)的图象可能如下左图,则只有一个零点;如右图,甚至没有零点;
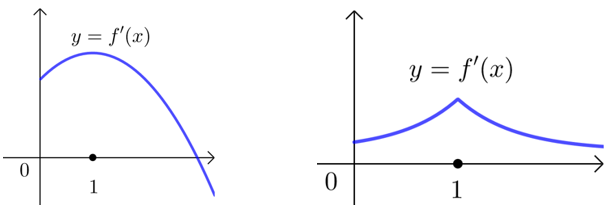
误区2:当\(x→0\)时,显然\(f'(x)→-∞\),当\(x→+∞\)时,显然\(f'(x)→-∞\),
那可知\(y=f'(x)\)存在两个零点,也不够严谨;
而因\(f^{\prime}\left[\left(\dfrac{1}{e}\right)^{a+1}\right]<0\), \(f'(e^a)=2a-e^a<0\),
由零点判定定理可确定\(y=f'(x)\)有两个零点\(x_1\)、\(x_2\).
③ 那“取点”\(\left(\dfrac{1}{e}\right)^{a+1}\)、\(e^a\)是怎么想到的呢?这需要些技巧,导函数\(f'(x)=\ln x-x+a\)中有参数\(a>1\),\(x\)取常数是不行的;因有\(\ln x\),想到含\(a\)的\(e\)指数幂,多尝试就可以!
【典题2】已知函数\(f(x)=\dfrac{1}{x}+a\ln x-a-1\),\(a\in R\).
(1)讨论函数\(f(x)\)的单调性;(2)讨论函数\(f(x)\)的零点个数.
解析 (1) \(f^{\prime}(x)=-\dfrac{1}{x^2}+\dfrac{a}{x}=\dfrac{a x-1}{x^2}\),
当\(a≤0\)时,\(f'(x)<0\),故\(f(x)\)在\((0,+∞)\)上单调递减,
当\(a>0\)时, \(f^{\prime}(x)>0 \Rightarrow x>\dfrac{1}{a}\),
\(f(x)\)在\(\left(0, \dfrac{1}{a}\right)\)上单调递减,在\(\left(\dfrac{1}{a},+\infty\right)\)上单调递增.
(2)当\(a≤0\)时, \(f\left(\dfrac{1}{e}\right)=e-2 a-1 \geq e-1>0\),\(f(e)=\dfrac{1}{e}-1<0\),\(f(x)\)有唯一零点;
当\(a>0\)时,\(f(1)=-a<0\),
(不用最小值\(f\left(\dfrac{1}{a}\right)=-a\ln a-1<0\),因为这个还要证明,用\(f(1)=-a<0\)容易,接着要在\(x=1\)两边各取点\(0<x_1<1\),\(x_2>1\)使得\(f(x_1 )>0\),\(f(x_2 )>0\), 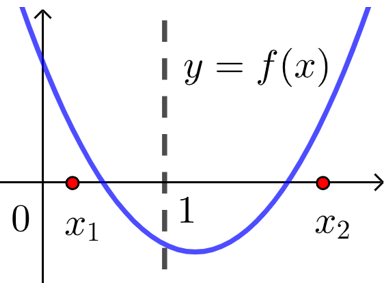 )
)
而\(e^{1+\frac{1}{a}}>1,\), \(f\left(e^{1+\frac{1}{a}}\right)=\dfrac{1}{e^{1+\frac{1}{a}}}+a\left(1+\dfrac{1}{a}\right)-a-1=\dfrac{1}{e^{1+\frac{1}{a}}}>0\),(取 \(x_2=e^{1+\frac{1}{a}}\))
\(\therefore f(x)\)在 \(\left(1, e^{1+\frac{1}{a}}\right)\)内有一个零点;
\(f\left(e^{-a-1}\right)=e^{a+1}-(a+1)^2\),(取 \(x_1=e^{-a-1}<1\))
令\(g(t)=e^t-t^2\),则\(g'(t)=e^t-2t\),\(g'' (t)=e^t-2\),
当\(t>1\)时,\(g'' (t)>e-2>0\),\(\therefore g'(t)\)单调递增,
\(\therefore g'(t)>g'(1)=e-2>0\),\(\therefore g(t)\)单调递增,
\(\therefore g(t)>g(1)=e-1>0\),故 \(f\left(e^{-a-1}\right)>0\),
\(\because e^{-a-1}<1\),\(\therefore f(x)\)在\((e^{-a-1},1)\)内有一个零点;
\(\therefore\)当\(a>0\)时\(f(x)\)有两个零点.
综上,当\(a≤0\)时\(f(x)\)有一个零点,当\(a>0\)时\(f(x)\)有两个零点.
【巩固练习】
1.若函数\(f(x)=-\dfrac{1}{3} x^3+a x^2+3 a^2 x-\dfrac{5}{3}\)仅有一个零点,求实数\(a\)的取值范围.
2.讨论函数\(f(x)=2 e^{2 x}-\dfrac{a}{x}\),\(x\in (0,1)\)的零点的个数.
3.已知函数\(f(x)=ax⋅\ln x\)(其中\(a≠0\),\(a\in R\)), \(g(x)=\dfrac{x-1}{x+1}\).
(1)若存在实数\(a\)使得\(f(x)<\dfrac{1}{e}\)恒成立,求\(a\)的取值范围;
(2)当\(a⩽\dfrac{1}{2}\)时,讨论函数\(y=f(x)-g(x)\)的零点个数.
参考答案
-
答案 \(\left(-1, \dfrac{\sqrt[3]{5}}{3}\right)\)
解析 函数\(f(x)\)只有一个零点,
因为\(f'(x)=-x^2+2ax+3a^2=-(x-3a)(x+a)\),
①当\(a<0\)时,由\(f'(x)>0\),解得\(3a<x<-a\),
所以函数\(f(x)\)在区间\((3a,-a)\)上单调递增,
由\(f'(x)<0\),解得\(x<3a\)或\(x>-a\),
所以函数\(f(x)\)在区间\((-∞,3a)\),\((-a,+∞)\)上单调递减,
又\(f(0)=-\dfrac{5}{3}<0\),
所以只需要\(f(-a)<0\),解得\(-1<a<0\),
所以实数\(a\)的取值范围为\((-1,0)\).
②当\(a=0\)时,显然\(f(x)\)只有一个零点成立,
③当\(a>0\)时,由\(f'(x)>0\),解得\(-a<x<3a\),
即\(f(x)\)在区间\((-a,3a)\)上单调递增,
由\(f'(x)<0\),解得\(x<-a\)或\(x>3a\),
即函数\(f(x)\)在区间\((-∞,-a)\),\((3a,+∞)\)上单调递减,
又\(f(0)=-\dfrac{5}{3}<0\),
所以只需\(f(3a)<0\),解得 \(0<a<\dfrac{\sqrt[3]{5}}{3}\),
综上,实数\(a\)的取值范围为\(\left(-1, \dfrac{\sqrt[3]{5}}{3}\right)\). -
答案 当\(a≤0\)或\(a≥2e^2\)时,\(f(x)\)无零点;当\(0<a<2e^2\)时,\(f(x)\)存在\(1\)个零点 .
解析 \(f^{\prime}(x)=4 e^{2 x}+\dfrac{a}{x^2}\)
①当\(a≤0\)时,\(f(x)>0\)恒成立,在\((0,1)\)上恒成立,\(\therefore f(x)\)在\((0,1)\)上无零点;
②当\(a≥2e^2\)时, \(\because f^{\prime}(x)=4 e^{2 x}+\dfrac{a}{x^2}>0\),在\((0,1)\)上恒成立,
\(\therefore f(x)\)在\((0,1)\)上单调递增,
\(\therefore f(x)<f(1)=2e^2-a<0\),\(\therefore f(x)\)在\((0,1)\)上无零点;
③当\(0<a<2e^2\)时, \(\because f^{\prime}(x)=4 e^{2 x}+\dfrac{a}{x^2}>0\)在\((0,1)\)上恒成立,
\(\therefore f(x)\)在\((0,1)\)上单调递增.
又\(\because\)当\(x\)趋向于\(0\)时,\(f(x)\)趋向于\(-∞\);且\(f(1)=2e^2-a>0\).
故由零点存在性定理可知:\(f(x)\)在\((0,1)\)上存在唯一一个零点,
综上:当\(a≤0\)或\(a≥2e^2\)时,\(f(x)\)在\((0,1)\)上无零点;
当\(0<a<2e^2\)时,\(f(x)\)在\((0,1)\)上存在唯一一个零点 . -
答案 (1)\((-1,0)\);
(2) 当\(a<0\)或\(a=\dfrac{1}{2}\)时,\(h(x)\)有\(1\)个零点,当\(0<a<\dfrac{1}{2}\)时,\(h(x)\)有\(2\)个零点.
解析 (1)因为\(f(x)=ax\ln x\),\(a≠0\),要使得\(f(x)<\dfrac{1}{e}\)在\((0,+∞)\)上恒成立,
所以\(a<0\),由\(f'(x)=a(\ln x+1)\),
由\(f'(x)=a(\ln x+1)>0\),解得\(0<x<\dfrac{1}{e}\),
由\(f'(x)=a(\ln x+1)<0\),解得\(x>\dfrac{1}{e}\) ,
所以\(f(x)_{\max }=f\left(\dfrac{1}{e}\right)=-\dfrac{a}{e}\),
所以\(-\dfrac{a}{e}<\dfrac{1}{e}\),所以\(-1<a<0\),
所以\(a\)的取值范围为\((-1,0)\).
(2)①当\(a<0\)时,当\(x\in (0,1)\)时,\(f(x)>0\),\(g(x)<0\),
所以\(y=f(x)-g(x)\)恒大于零,
当\(x=1\)时,\(y=f(x)-g(x)=0\),
令\(h(x)=f(x)-g(x)\),
所以\(a<0\)时,令\(h(x)\)在\((0,+∞)\)只有\(1\)个零点,
②当\(a>0\)时,令\(h(x)=f(x)-g(x)\),
则\(h(x)=a x \ln x-1+\dfrac{2}{x+1}(x>0)\),
\(h^{\prime}(x)=a(\ln x+1)-\dfrac{2}{(x+1)^2}\), \(h^{\prime \prime}(x)=\dfrac{a}{x}+\dfrac{4}{(x+1)^3}\),
因为\(x>0\),所以\(h'' (x)>0\)恒成立,
所以\(h'(x)\)在\((0,+∞)\)上单调递增,
因为\(h(1)=0\),当\(h'(1)=0\),即\(a=\dfrac{1}{2}\)时,
\(h'(x)\)在\((0,1)\)上恒小于零,在\((1,+∞)\)上恒大于零,
即 在\((0,1)\)上单调递减,在\((1,+∞)\)上单调递增,
所以\(h(x)⩾h(1)=0\),\(y=h(x)\)在\((0,+∞)\)只有\(1\)个零点,
若\(0<a<\dfrac{1}{2}\)时,\(h'(1)=a-\dfrac{1}{2}<0\),
由于\(h'(x)\)在\((0,+∞)\)上单调递增,
所以\(h'(x)\)在\((0,1]\)上恒小于零,\(h(x)\)在\((0,1]\)上单调递减,
因为\(h(1)=0\),所以\(h(x)\)在\((0,1]\)上有唯一零点\(1\),
又因为\(h'(1)=a-\dfrac{1}{2}<0\), \(h^{\prime}\left(e^{\frac{2}{a}-1}\right)=2-\dfrac{2}{\left(e^{\frac{2}{a}-1}+1\right)^2}>0\),
所以存在 \(x_0 \in\left(1, e^{\frac{2}{a}-1}\right)\),使得\(h'(x_0 )=0\),
由于\(h'(x)\)在\((0,+∞)\)上单调递增, (1) ,
所以\(h(x)\)在\((1,x_0 )\)上单调递减,在\((x_0,+∞)\)上单调递增, \(x_0 \in\left(1, e^{\frac{2}{a}-1}\right)\),
所以\(h(x_0 )<h(1)=0\),
又\(0<a<\dfrac{1}{2}\), \(e^{\frac{1}{a}}>1\), \(h\left(e^{\frac{1}{a}}\right)=e^{\frac{1}{a}}-1+\dfrac{2}{e^{\frac{1}{a}+1}}>0\),
所以 \(x_0<e^{\frac{1}{a}}\),
结合\(h(x)\)在\((x_0,+∞)\)单调递增,\(h(x)\)在\((1,+∞)\)上有唯一零点,
又\(h(1)=0\),
所以\(0<a<\dfrac{1}{2}\)时,\(h(x)\)在(0,+∞)上有唯一零点,
又因为\(h(1)=0\),
所以\(0<a<\dfrac{1}{2}\)时,\(h(x)\)在\((0,+∞)\)上有\(2\)个零点,
综上所述,当\(a<0\)或\(a=\dfrac{1}{2}\)时,\(h(x)\)在\((0,+∞)\)只有\(1\)个零点,
当\(0<a<\dfrac{1}{2}\)时,\(h(x)\)在\((0,+∞)\)上有\(2\)个零点.
【题型4】几何法
【典题1】 函数\(g(x)=(x^2+1) e^x-mx-1\)在\([-1,+∞)\)有两个零点,求\(m\)的取值范围.
解析 函数\(g(x)=(x^2+1) e^x-mx-1\)在\([-1,+∞)\)有两个零点,
等价于\(s(x)=(x^2+1) e^x\)与\(t(x)=mx+1\)在\([-1,+∞)\)有两个交点,
\(\because s'(x)=(x+1)^2 e^x≥0\),\(\therefore s(x)\)在\([-1,+∞)\)单调递增,
又 \(s(-1)=\dfrac{2}{e}\),\(s(0)=1\),
而函数\(t(x)=mx+1\)是过定点\((0,1)\)的直线,且斜率为\(m\),
则 \(\dfrac{1-\dfrac{2}{e}}{0-(-1)}=1-\dfrac{2}{e} \leq m<1\),或\(m>s'(0)=1\),
故m的取值范围为 \(1-\dfrac{2}{e} \leqslant m<1\)或\(m>1\).
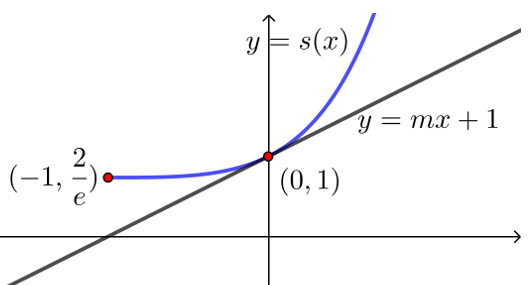
点拨 函数能够转化为一次函数与其他形式函数的交点问题,可考虑这种方法;但还要注意到\(s(x)=(x^2+1) e^x\)是凹函数,因为\(s'' (x)>0\),若\(s(x)\)是凸函数,则\(m\)的范围就不一样了,但内容超纲不适合处理解答题,第二问利用分离参数法有难度 \(m=\dfrac{\left(x^2+1\right) e^x-1}{x}\),出现洛必达法则、隐零点.
【巩固练习】
1.函数 \(F(x)=\dfrac{a x-a}{e^x}+1(a<0)\)没有零点,求实数\(a\)的取值范围.
参考答案
- 答案 \((-e^2,0)\)
解析 由已知有 \(F(x)=\dfrac{a x-a+e^x}{e^x}=0\)没有解,即\(e^x=-a(x-1)\)无解,
\(\therefore y_1=e^x\)与\(y_2=-a(x-1)\)两图象无交点,
设两图象相切于\((m,n)\)两点,
\(\therefore\left\{\begin{array}{l} e^m=-a(m-1) \\ e^m=-a \end{array}\right.\),\(\therefore m=2\),\(a=-e^2\),
\(\because\)两图象无交点,\(\therefore\)故\(a\)的取值范围是\((-e^2,0)\).
分层练习
【A组---基础题】
1.已知函数\(f(x)=ax^3+bx^2+cx\)在点\(x_0\)处取得极小值\(-4\),使其导数\(f'(x)>0\)的\(x\)的取值范围为\((1,3)\),
(1)求\(f(x)\)的解析式;
(2)若过点\(P(-1,m)\)作曲线\(y=f(x)\)的三条切线,求实数\(m\)的取值范围.
2.证明:\(a>1\), \(f(x)=(1+x^2 ) e^x-a\)在 \((-∞,+∞)\)上有且仅有一个零点.
3.已知函数 \(f(x)=\dfrac{1}{3} x^3-\dfrac{(k+1)}{2} x^2\),\(g(x)=\dfrac{1}{3}-kx\),且\(f(x)\)在区间\((2,+∞)\)上为增函数.
(1)求实数\(k\)的取值范围;
(2)若函数\(f(x)\)与\(g(x)\)的图象有三个不同的交点,求实数\(k\)的取值范围.
4.已知函数\(f(x)=ax^2+x-\ln x(a\in R)\).
(1)当\(a=1\)时,求\(f(x)\)在区间 \(\left[\dfrac{1}{3}, 1\right]\)上的最值;
(2)若\(g(x)=f(x)-x\)在定义域内有两个零点,求\(a\)的取值范围.
5.若 \(f(x)=e^{x-2}-a x\)有两个零点,求实数\(a\)的取值范围.
6.已知函数\(f(x)=x^2-a\ln x\),
(1)求\(f(x)\)的单调区间;
(2)如果\(a>0\),讨论函数\(y=f(x)\)在区间\((1,e)\)上零点的个数.
7.已知函数\(f(x)=x^3+ax+\dfrac{1}{4}\),\(g(x)=-\ln x\).用\(\min \{m,n\}\)表示\(m\),\(n\)中的最小值,设函数 \(h(x)=\min \{f(x), g(x)\}(x>0)\),讨论\(h(x)\)零点的个数 .
8.若\(f(x) =m^2 x^2-\ln x\)的图象与直线\(y=mx\)交于\(M(x_M,y_M )\),\(N(x_N,y_N )\),两点,且\(x_M>x_N>1\),求实数\(m\)的取值范围.
9.已知\(g(x)=a^x+b^x-2(0<a<1,b>1)\)有且只有\(1\)个零点,求\(ab\)的值.
10.已知\(a>0\),函数\(f(x)=ae^x-x-2\),函数\(g(x)=\ln (x+2)-x-\ln a\).
(1)若对\(∀x\in R\),\(f(x)⩾0\)恒成立,求\(a\)的取值范围;
(2)若方程\(f(x)=g(x)\)有两个根,求\(a\)的取值范围.
参考答案
-
答案 (1)\(f(x)=-x^3+6x^2-9x\);(2) \((-11,16)\) .
解析 (1)\(f(x)=-x^3+6x^2-9x\)(过程略).
(2)设切点\((t,f(t))\),\(y-f(t)=f'(t)(x-t)\)
\(y=(-3t^2+12t-9)(x-t)+(-t^3+6t^2-9t)\)
\(=(-3t^2+12t-9)x+t(3t^2-12t+9)-t(t^2-6t+9)\)
\(=(-3t^2+12t-9)x+t(2t^2-6t)\)过\((-1,m)\)
\(\therefore m=(-3t^2+12t-9)(-1)+2t^3-6t^2\),
\(\therefore 2t^3-3t^2-12t+9-m=0\),
设\(g(t)=2t^3-3t^2-12t+9-m\),
令\(g'(t)=6t^2-6t-12=6(t^2-t-2)=0\),
求得\(t=-1\),\(t=2\),
若要方程\(g(t)=0\)有三个根,
需\(\left\{\begin{array} { l } { g ( - 1 ) > 0 } \\ { g ( 2 ) < 0 } \end{array} \Rightarrow \left\{\begin{array} { l } { - 2 - 3 + 1 2 + 9 - m > 0 } \\ { 1 6 - 1 2 - 2 4 + 9 - m < 0 } \end{array} \Rightarrow \left\{\begin{array}{l} m<16 \\ m>-11 \end{array}\right.\right.\right.\)
故\(-11<m<16\);因此所求实数\(m\)的范围为:\((-11,16)\). -
证明 \(f'(x)=e^x (x^2+2x+1)=e^x (x+1)^2\),\(\therefore f'(x)≥0\),
\(\therefore f(x)=(1+x^2 ) e^x-a\)在\((-∞,+∞)\)上为增函数.
而\(f(0)=1-a<0\), \(f(\sqrt{a})=(1+a) e^{\sqrt{a}}-a=e^{\sqrt{a}}+a\left(e^{\sqrt{a}}-1\right)>0\),
\(\therefore f(x)\)在\((-∞,+∞)\)上有且只有一个零点. -
答案 (1) \(k≤1\);(2) \(k<1-\sqrt{3}\).
解析 (1)\(k≤1\)(过程略).
(2)欲使\(f(x)\)与\(g(x)\)的图象有三个不同的交点,
即函数\(h(x)=f(x)-g(x)\)有三个不同的零点,
设 \(h(x)=f(x)-g(x)=\dfrac{x^3}{3}-\dfrac{(k+1)}{2} x^2+k x-\dfrac{1}{3}\),
\(h'(x)=x^2-(k+1)x+k=(x-k)(x-1)\),
令\(h'(x)=0\)得\(x=k\)或\(x=1\),
由(1)知\(k≤1\),
①当\(k=1\)时,\(h'(x)=(x-1)^2≥0\),\(h(x)\)在\(R\)上递增,显然不合题意.
②当\(k<1\)时,\(h(x)\),\(h'(x)\)随\(x\)的变化情况如下表:
| $x$ | $(-∞,k)$ | $k$ | $(k,1)$ | $1$ | $(1,+∞)$ |
| $h'(x)$ | $+$ | $0$ | $-$ | $0$ | $+$ |
| $h(x)$ | $↗$ | 极大值 $-\dfrac{k^3}{6}+\dfrac{k^2}{2}-\dfrac{1}{3}$ | $↘$ | 极小值 $\dfrac{k-1}{2}$ | $↗$ |
由于 \(h(1)=\dfrac{k-1}{2}<0\)且当\(x→+∞\)时,\(y→+∞\),当\(x→-∞\)时\(,y→-∞\),
若要函数\(h(x)=f(x)-g(x)\)有三个不同的零点,
故需 \(-\dfrac{k^3}{6}+\dfrac{k^2}{2}-\dfrac{1}{3}>0\),即\((k-1)(k^2-2k-2)<0\),
\(\therefore\left\{\begin{array}{l}
k<1 \\
k^2-2 k-2>0
\end{array}\right.\),解得 \(k<1-\sqrt{3}\),
综上,所求\(k\)的取值范围为\(k<1-\sqrt{3}\).
-
答案 (1)\(f(x)_{min}=\ln 2+\dfrac{3}{4}\),\(f(x)_{max}=2\);(2) \(\left(0, \dfrac{1}{2 e}\right)\).
解析 (1) \(f(x)_{min}=\ln 2+\dfrac{3}{4}\),\(f(x)_{max}=2\)(过程略)
(2)令\(g(x)=f(x)-x=0\),得 \(a=\dfrac{\ln x}{x^2}\),
设 \(h(x)=\dfrac{\ln x}{x^2}(x>0)\),
\(\because g(x)=f(x)-x\)在定义域内有两个零点,
\(\therefore\)函数\(y=h(x)\)与\(y=a\)与在定义域内有两个交点
\(\because h^{\prime}(x)=\dfrac{1-2 \ln x}{x^3}\) ,
令\(h'(x)>0\)得:\(0<x<\sqrt{e}\);令\(h'(x)<0\)得:\(x>\sqrt{e}\),
\(\therefore h(x)\)在\((0,\sqrt{e})\)单调递增,在\((\sqrt{e},+∞)\)单调递减,
又\(\because h(\sqrt{e})=\dfrac{1}{2e}\),且当\(x→0\)时,\(h(x)→-∞\),当\(x→+∞\)时,\(h(x)→0\),
画出函数\(h(x)\)的大致图像,如图所示:

由图象可得, \(a \in\left(0, \dfrac{1}{2 e}\right)\),
\(\therefore a\)的取值范围为 \(\left(0, \dfrac{1}{2 e}\right)\). -
答案 \(\left(\dfrac{1}{e},+\infty\right)\).
解析 方法1
因为\(f(x)=e^{x-2}-ax\),所以 \(f^{\prime}(x)=e^{x-2}-a\),
当\(a⩽0\)时,\(f'(x)>0\),\(f(x)\)在\(R\)上单调递增,
故\(f(x)\)至多存在一个零点,不合题意;
当\(a>0\)时,由\(f'(x)=e^{x-2}-a=0\)得:\(x=2+\ln a\),
当\(x\in (-∞,2+\ln a)\)时,\(f'(x)<0\),\(f(x)\)在\((-∞,2+\ln a)\)上单调递减;
当\(x\in (2+\ln a,+∞)\)时,\(f'(x)>0\),\(f(x)\)在\((2+\ln a,+∞)\)上单调递增;
所以当\(x=2+\ln a\)时,\(f(x)\)取到最小值,且最小值为\(f(2+\ln a)=-a(1+\ln a)\).
①当\(0<a⩽\dfrac{1}{e}\)时,\(f(2+\ln a)⩾0\),\(f(x)\)在\(R\)上至多存在一个零点,不合题意;
②当\(a>\dfrac{1}{e}\)时,\(f(2+\ln a)<0\).
由于 \(f(0)=e^{-2}>0\),
所以\(f(x)\)在\((-∞,2+\ln a)\)上存在唯一零点.
\(f(4+2 \ln a)=e^{2 \ln a+2}-a(4+2 \ln a)=e^2 a^2-a(4+2 \ln a)=a\left(e^2 a-2 \ln a-4\right)\).
设\(g(a)=e^2 a-2\ln a-4\),
则 \(g^{\prime}(a)=e^2-\dfrac{2}{e}=\dfrac{e^2 a-2}{a}=\dfrac{e^2}{a}\left(a-\dfrac{2}{e^2}\right)\),
当\(a>\dfrac{1}{e}\)时,\(g'(a)>0\),
所以\(g(a)\)在\(\left(\dfrac{1}{e},+\infty\right)\)上单调递增.
因为\(g\left(\dfrac{1}{e}\right)=e+2-4>0\),
所以\(g(a)>g\left(\dfrac{1}{e}\right)>0\),即\(f(4+2\ln a)>0\).
从而\(f(x)\)在\(R\)上有两个零点.
综上所述,\(a\)的取值范围为\(\left(\dfrac{1}{e},+\infty\right)\).
方法2 几何法
函数\(f(x)=e^{x-2}-ax\)有两个零点等价于函数\(g(x)=e^{x-2}\)与函数\(y=ax\)有两个交点,
设函数\(y=kx\)与函数\(g(x)=e^{x-2}\)相切,切点\(P(x_0,y_0)\),
\(\because g'(x)=e^{x-2}\),\(\therefore k=g'(x_0 )=e^{x_0-2}\),
即切线方程为\(y=e^{x_0-2} x\),则\(y_0=e^{x_0-2} x_0\),
又\(g(x_0 )=e^{x_0-2}\),即\(y_0=e^{x_0-2}\),\(\therefore x_0=1\),
\(\therefore k=e^{x_0-2}=\dfrac{1}{e}\),
\(\therefore\)若函数\(g(x)=e^{x-2}\)与函数\(y=ax\)有两个交点,则\(a>\dfrac{1}{e}\),
所以\(a\)的取值范围为 \(\left(\dfrac{1}{e},+\infty\right)\).

-
答案 (1)当\(a≤0\),\(f(x)\)在\((0,+∞)\)上递增;
当\(a>0\),\(f(x)\)的增区间为\(\left(\sqrt{\dfrac{a}{2}},+\infty\right)\),减区间为\(\left(0, \sqrt{\dfrac{a}{2}}\right)\);
(2)当\(0<a<2e\)时,函数\(f(x)\)无零点;
当\(a=2e\)或\(a≥e^2\)时,函数\(f(x)\)有\(1\)零点;
当\(2e<a<e^2\)时,函数\(f(x)\)有\(2\)个零点.
解析(1)函数\(f(x)=x^2-a\ln x\)的导数 \(f^{\prime}(x)=2 x-\dfrac{a}{x}=\dfrac{2 x^2-a}{x}(x>0)\),
若\(a≤0\),则\(f'(x)>0\),即有\(f(x)\)在\((0,+∞)\)上递增;
若\(a>0\),由\(f'(x)>0\)得到\(x>\sqrt{\dfrac{a}{2}}\),由\(f'(x)<0\)得到\(0<x<\sqrt{\dfrac{a}{2}}\),
即有\(a>0\)时,\(f(x)\)的增区间为\(\left(\sqrt{\dfrac{a}{2}},+\infty\right)\),减区间为\(\left(0, \sqrt{\dfrac{a}{2}}\right)\);
(2)由(1)知\(f(x)\)的极小值为 \(f\left(\sqrt{\dfrac{a}{2}}\right)=\dfrac{a}{2}\left(1-\ln \dfrac{a}{2}\right)\),也为最小值.
① 当\(\dfrac{a}{2}\left(1-\ln \dfrac{a}{2}\right)>0\),即\(0<a<2e\),\(f(x)\)的最小值大于\(0\),
则\(y=f(x)\)在区间\((1,e)\)上无零点;
② 当\(\dfrac{a}{2}\left(1-\ln \dfrac{a}{2}\right)=0\),即\(a=2e\),即有\(1<\sqrt{\dfrac{a}{2}}<e\),
而\(f(1)=1>0\), \(f\left(\sqrt{\dfrac{a}{2}}\right)=0\),\(f(e)>0\),
则\(f(x)\)在\((1,e)\)上有一个零点;
③ 当\(\dfrac{a}{2}\left(1-\ln \dfrac{a}{2}\right)<0\),即\(a>2e\),即有\(\sqrt{\dfrac{a}{2}}>\sqrt{e}>1\),
(i)若\(\sqrt{\dfrac{a}{2}}<e\),即\(2e<a<2e^2\),而\(f(e)=e^2-a\),
当\(2e<a<e^2\)时,\(f(e)≥0\),则\(f(x)\)在\((1,e)\)上有\(2\)零点.
当\(e^2≤a<2e^2\)时,\(f(e)≤0\),则\(f(x)\)在\((1,e)\)上有\(1\)个零点;
(ii)若\(\sqrt{\dfrac{a}{2}}≥e\),即\(a≥2e^2\),而\(f(1)>0\),\(f(e)<0\),
则\(f(x)\)在\((1,e)\)上有\(1\)零点.
综上所述:当\(0<a<2e\)时,函数\(f(x)\)无零点;
当\(a=2e\)或\(a≥e^2\)时,函数\(f(x)\)有\(1\)零点;
当\(2e<a<e^2\)时,函数\(f(x)\)有\(2\)个零点. -
答案 当\(a>-\dfrac{3}{4}\),\(h(x)\)有\(0\)个零点,
当 \(a=-\dfrac{3}{4}\)或\(a≤-\dfrac{5}{4}\)时,\(h(x)\)有一个零点,
当\(-\dfrac{5}{4}<a<-\dfrac{3}{4}\)时,\(h(x)\)有两个零点.
解析 当 \(x\in (1,+∞)\)时,\(g(x)=-\ln x<0\),
\(\therefore\) 函数 \(h(x)=\min \{f(x), g(x)\} \leq g(x)<0\),
故\(h(x)\)在\((1,+∞)\)时无零点.
当\(x=1\)时,若\(a≥-\dfrac{5}{4}\),则\(f(1)=a+\dfrac{5}{4}≥0\),
\(\therefore h(x)=\min \{f(1), g(1)\}=g(1)=0\),
故\(x=1\)是函数\(h(x)\)的一个零点;
若\(a<-\dfrac{5}{4}\),则\(f(1)=a+\dfrac{5}{4}<0\),
\(\therefore h(x)=\min \{f(1), g(1)\}=f(1)<0\),
故\(x=1\)不是函数\(h(x)\)的零点;
当 \(x\in (0,1)\)时,\(g(x)=-\ln x>0\),
所以只需考虑\(f(x)\)在\((0,1)\)的零点个数,
(i)若\(a≤-3\)或\(a≥0\),则\(f'(x)=3x^2+a\),
当\(a≥0\)时,\(f(x)\)在\((0,1)\)无零点,
当\(a≤-3\)时,\(f(x)\)在\((0,1)\)单调,
而\(f(0)=\dfrac{1}{4}\),\(f(1)=a+\dfrac{5}{4}\),\(f(x)\)在\((0,1)\)有一个零点,
(ii)若\(-3<a<0\),
则\(f(x)\)在\(\left(0, \sqrt{-\dfrac{a}{3}}\right)\)单调递减,在\(\left(\sqrt{-\dfrac{a}{3}}, 1\right)\)单调递增,
故当 \(x=\sqrt{-\dfrac{a}{3}}\)时,\(f(x)\)取得最小值,最小值为 \(f\left(\sqrt{-\dfrac{a}{3}}\right)=\dfrac{2 a}{3} \sqrt{-\dfrac{a}{3}}+\dfrac{1}{4}\),
①若\(f\left(\sqrt{-\dfrac{a}{3}}\right)>0\),即\(-\dfrac{3}{4}<a<0\),\(f(x)\)在\((0,1)\)无零点,
②若\(f\left(\sqrt{-\dfrac{a}{3}}\right)=0\),即\(a=-\dfrac{3}{4}\),则\(f(x)\)在\((0,1)\)有唯一零点,
③若\(f\left(\sqrt{-\dfrac{a}{3}}\right)<0\),即\(-3<a<-\dfrac{3}{4}\),由于\(f(0)=\dfrac{1}{4}\),\(f(1)=a+\dfrac{5}{4}\),
所以当\(-\dfrac{5}{4}<a<-\dfrac{3}{4}\)时,\(f(x)\)在\((0,1)\)有两个零点,
当\(-3<a≤-\dfrac{5}{4}\)时,\(f(x)\)在\((0,1)\)有一个零点,
综上所述,当\(a>-\dfrac{3}{4}\),\(h(x)\)有\(0\)个零点,
当 \(a=-\dfrac{3}{4}\)或\(a≤-\dfrac{5}{4}\)时,\(h(x)\)有一个零点,
当\(-\dfrac{5}{4}<a<-\dfrac{3}{4}\)时,\(h(x)\)有两个零点. -
答案 \(\left(-\dfrac{1}{2 e^{\frac{3}{4}}}, 0\right)\)
解析 令 \(m^2 x^2-\ln x=mx\) ,
则由题意可知\(m^2 x^2-\ln x-mx=0\)有两个大于\(1\)的实数根,显然\(m≠0\).
令\(F(x)=m^2 x^2-\ln x-mx\),
则 \(F^{\prime}(x)=2 m^2 x-\dfrac{1}{x}-m=\dfrac{(2 m x+1)(m x-1)}{x}\).
若\(m>0\),则当 \(x \in\left(0, \dfrac{1}{m}\right)\)时,\(F'(x)<0\),
当 \(x \in\left(-\dfrac{1}{2 m}, \quad+\infty\right)\)时,\(F'(x)>0\),
要满足已知条件,必有 \(\left\{\begin{array}{c} F(1)=m^2-m>0 \\ F\left(\dfrac{1}{m}\right)=-\ln \dfrac{1}{m}<0 \\ \dfrac{1}{m}>1 \end{array}\right.\)此时无解;
若\(m<0\),则当 \(x \in\left(0,-\dfrac{1}{2 m}\right)\)时,\(F'(x)<0\),
当 \(x \in\left(-\dfrac{1}{2 m},+\infty\right)\)时,\(F'(x)>0\),
要满足已知条件,必有\(\left\{\begin{array}{c} F(1)=m^2-m>0, \\ F\left(-\dfrac{1}{2 m}\right)=\dfrac{3}{4}+\ln (-2 m)<0 \\ -\dfrac{1}{2 m}>1 \end{array}\right.\),解得\(-\dfrac{1}{2 e^{\dfrac{3}{4}}}<m<0\).
当\(-\dfrac{1}{2 e^{\dfrac{3}{4}}}<m<0\)时,\(F(x)\)在\(\left(1,-\dfrac{1}{2 m}\right)\)上单调递减,\(F(1) \cdot F\left(-\dfrac{1}{2 m}\right)<0\),
故函数\(F(x)\)在\(\left(1,-\dfrac{1}{2 m}\right)\)上有一个零点.
易知 \(\dfrac{1}{m^2}>-\dfrac{1}{2 m}\),且 \(F\left(\dfrac{1}{m^2}\right)=\dfrac{1}{m^2}-\dfrac{1}{m}-\ln \dfrac{1}{m^2}>\dfrac{1}{m^2}-\ln \dfrac{1}{m^2}\) ,
下证:\(x-\ln x>0\).
令\(g(x)=x-\ln x\),则\(g'(x)=1-\dfrac{1}{x}\),当\(0<x<1\)时\(g'(x)<0\),
当\(x>1\)时,\(g'(x)>0\),
故\(g(x)≥g(1)=1-\ln 1>0\),即\(x-\ln x>0\),
故\(F\left(\dfrac{1}{m^2}\right)>\dfrac{1}{m^2}-\ln \dfrac{1}{m^2}>0\),
故\(F\left(-\dfrac{1}{2 m}\right) \cdot F\left(\dfrac{1}{m^2}\right)<0\),
又\(F(x)\)在 \(\left(-\dfrac{1}{2 m},+\infty\right)\)上单调递增,
故\(F(x)\)在 \(\left(-\dfrac{1}{2 m},+\infty\right)\)上有一个零点.
综上所述,实数\(m\)的取值范围为 \(\left(-\dfrac{1}{2 e^{\frac{3}{4}}}, 0\right)\). -
答案 \(1\)
解析 \(\because g(0)=0\),由题意知\(0\)为\(g(x)=f(x)-2\)的唯一零点,
因为\(g'(x)=a^x \ln a+b^x \ln b\),且\(0<a<1\),\(b>1\),
故\(\ln a<0\),\(\ln b>0\),
所以\(g'(x)=0\)有唯一解 \(x_0=\log _{\frac{b}{a}}\left(-\dfrac{\ln a}{\ln b}\right)\),
令\(h(x)=g'(x)\),则\(h'(x)=(a^x \ln a+b^x \ln b)'=a^x (\ln a)^2+b^x (\ln b)^2\),
对于任意\(x\in R\),都有\(h'(x)>0\),
故\(g'(x)=h(x)\)在\(R\)上单调递增,
则\(x\in (-∞,x_0 )\)时,\(g'(x)<0\),\(x\in (x_0,+∞)\)时,\(g'(x)>0\),
故函数\(g(x)\)在\((-∞,x_0 )\)时单调递减,在\((x_0,+∞\))时单调递增,
故\(g(x)_{min}=g(x_0 )\);
若\(g(x_0 )<0\),当\(x<\log _a2\)时, \(a^x>a^{\log _a2}=2\),\(b^x>0\),
则\(g(x)>0\),因此当\(x_1<\log _a2\)且\(x_1<x_0\)时,\(g(x_1 )>0\),
此时\(g(x)\)在\((x_1,x_0 )\)内有零点,则\(g(x)\)至少有两个零点,与题意不符;
故\(g(x_0)≥0\),则\(g(x)\)的最小值为\(g(x_0)=0\),
因为由题意知\(0\)为\(g(x)\)的唯一零点,故\(x_0=0\),
即\(x_0=\log_ \frac{b}{a}\left(-\dfrac{\ln a}{\ln b}\right)=0\), \(-\dfrac{\ln a}{\ln b}=1\),
则\(\ln a+\ln b=0\),\(\ln ab=0\),\(ab=1\),
即\(ab\)值为\(1\). -
答案 (1)\([e,+∞)\);(2)\((0,e)\) .
解析 (1)\([e,+∞)\)(过程略);
(2)由题意得\(ae^x-x-2-\ln (x+2)+x+\ln a=0\)在\(x>-2\)上有两个根,
即 \(e^{x+\ln a}+x+\ln a=\ln (x+2)+x+2=e^{\ln (x+2)}+\ln (x+2)\),(同构)
令\(h(x)=x+e^x\),则\(h(x)\)单调递增,而\(h(x+\ln a)=h(\ln (x+2))\)
所以\(x+\ln a=\ln (x+2)\),问题转化为\(\ln a=\ln (x+2)-x\)在\(x>-2\)时有\(2\)实根,
令\(t(x)=\ln (x+2)-x\),则 \(t^{\prime}(x)=-\dfrac{x+1}{x+2}\),
当\(-2<x<-1\)时,\(t'(x)>0\),\(t(x)\)单调递增,
当\(x<-2\)或\(x>-1\)时,\(t'(x)<0\),\(t(x)\)单调递减,
所以\(t(x)⩽t(-1)=1\),且在\((-2,-1)\),\((-1,+∞)\)上的值域都为\((-∞,-1]\),
综上\(\ln a<1\),所以\(0<a<e\).
故\(a\)的取值范围为\((0,e)\).
【B组---提高题】
1.己知函数\(f(x)=e^x-1-x+\dfrac{1}{2} ax^2\).
(1)当\(a≥0\)时,求\(f(x)\)的单调区间和极值;
(2)讨论\(f(x)=e^x-1-x+\dfrac{1}{2} ax^2\)的零点的个数.
2.已知函数\(f(x)=(x-2)e^x+a(x-1)^2\)有两个零点,求\(a\)的取值范围.
参考答案
- 答案 (1)单调递减区间为\((-∞,0)\),单调递增区间为\((0,+∞)\);极小值为\(0\),无极大值;
(2) 当\(a≥0\)或\(a=-1\)时,\(f(x)\)有\(1\)个零点;
当\(a<0\)且\(a≠-1\)时,\(f(x)\)有\(2\)个零点.
解析 (1)\(f(x)=e^x-1-x+\dfrac{1}{2} ax^2\)的定义域为\((-∞,+∞)\),\(f'(x)=e^x-1+ax\),
\(\because a≥0\),\(\therefore f'' (x)=e^x+a>0\),
则\(f'(x)=e^x-1+ax\)在\((-∞,+∞)\)上单调递增,
又\(f'(0)=0\),
所以当\(x\in (-∞,0)\)时,\(f'(x)<0\),当\(x\in (0,+∞)\)时,\(f'(x)>0\),
即\(f(x)\)的单调递减区间为\((-∞,0)\),单调递增区间为\((0,+∞)\);
\(f(x)\)的极小值为\(f(0)=0\),\(f(x)\)无极大值;
(2)当\(a≥0\)时,由(1)知\(f(x)≥f(0)=0\),
故\(f(x)\)仅有一个零点\(x=0\);
当\(a<0\)时,\(f'' (x)=e^x+a\),
令\(f'' (x)=0⇒x=\ln (-a)\);
令\(f'' (x)>0⇒x>\ln (-a)\),
所以\(f'(x)\)在\(x\in (\ln (-a),+∞)\)上单调递增;
令\(f'' (x)<0⇒x<\ln (-a)\),
所以\(f'(x)\)在\(x\in (-∞,\ln (-a))\)上单调递减,且\(f'(0)=0\),\(f(0)=0\),
所以\(f'(x)≥f'(\ln (-a))\),
最小值\(f'(\ln (-a))\)与\(0\)的比较等价于\(\ln (-a)\)与\(0\)的大小比较,
所以分三类进行讨论:
①当\(-1<a<0\)时,即\(\ln (-a)<0\)时,
由\(f'(x)\)在\(x\in (-∞,\ln (-a))\)上单调递减及在\(x\in (\ln (-a),+∞)\)上单调递增,
且\(f'(0)=0\),\(x→-∞⇒f'(x)→+∞\)
由零点存在定理,得\(f'(x)\)在\(x\in (-∞,\ln (-a))\)上存在唯一零点,设为\(x_0\),所以
| $x$ | $(-∞,x_0 )$ | $x_0$ | $(x_0,0)$ | $0$ | $(0,+∞)$ |
| $f'(x)$ | $+$ | $0$ | $-$ | $0$ | $+$ |
| $f(x)$ | 递增 | 极大值 | 递减 | 极小值 $f(0)=0$ | 递增 |
又\(f(0)=0\)及\(x→-∞⇒f(x)→-∞\)由零点存在定理,
得\(f(x)\)在\(x\in (-∞,0)\)上存在唯一零点,设为\(x_1\),
综上,当\(-1<a<0\)时,\(f(x)\)在\((-∞,+∞)\)上存在\(2\)个零点(一个为\(x=0\),一个为\(x_1\in (-∞,0)\));
②当\(a=-1\)时,即\(\ln (-a)=0\)时,
由\(f'(x)\)在\(x\in (-∞,0)\)上单调递减及在\(x\in (0,+∞)\)上单调递增,且\(f'(x)≥f'(0)=0\),
得\(f(x)\)在\((-∞,+∞)\)上单调递增,
故\(f(x)\)在\((-∞,+∞)\)上只有一个零点\(x=0\);
③当\(a<-1\)时,
同理可得\(f(x)\)在\((-∞,+∞)\)上存在\(2\)个零点:一个为\(x=0\),一个为\(x_2\in (0,+∞)\),
综上可得,当\(a≥0\)或\(a=-1\)时,\(f(x)\)有\(1\)个零点;
当\(a<0\)且\(a≠-1\)时,\(f(x)\)有\(2\)个零点.
- 答案 \((0,+∞)\)
解析 法一 分类讨论
\(\because\)函数\(f(x)=(x-2)e^x+a(x-1)^2\),
\(\therefore f'(x)=(x-1)e^x+2a(x-1)=(x-1)(e^x+2a)\),
①若\(a=0\),那么\(f(x)=0⇔(x-2)e^x=0⇔x=2\),
函数\(f(x)\)只有唯一的零点\(2\),不合题意;
②若\(a>0\),那么\(e^x+2a>0\)恒成立,
当\(x<1\)时,\(f'(x)<0\),此时函数为减函数;
当\(x>1\)时,\(f'(x)>0\),此时函数为增函数;
此时当\(x=1\)时,函数\(f(x)\)取极小值\(-e\),
由\(f(2)=a>0\),可得:函数\(f(x)\)在\(x>1\)存在一个零点;
当\(x<1\)时,\(e^x<e\),\(x-2<x-1<0\),
\(\therefore f(x)=(x-2)e^x+a(x-1)^2>(x-2)e+a(x-1)^2=a(x-1)^2+e(x-1)-e\),
(使用放缩法)
方程\(a(x-1)^2+e(x-1)-e=0\)显然由两个不相等的实数根,
设为两根为\(t_1\),\(t_2\),且\(t_1<1<t_2\),
则当\(x<t_1\)时, \(f(x)>a(x-1)^2+e(x-1)-e>0\),
(由\(x→-∞\)时,\(y=x-2→-∞\),\(y=e^x→0\),\(y=a(x-1)^2→+∞\),而二次函数比一次函数的增长速度快,\(f(x)→+∞\)可得函数\(f(x)\)在\(x<1\)存在一个零点,以上的证法更严谨但难度较大)
故函数\(f(x)\)在\(x<1\)存在一个零点;
即函数\(f(x)\)在\(R\)是存在两个零点,满足题意;
③若 \(-\dfrac{e}{2}<a<0\),则\(\ln (-2a)<\ln e=1\),
当\(x<\ln (-2a)\)或\(x>1\)时,\(f'(x)=(x-1)(e^x+2a)>0\)恒成立,
故\(f(x)\)单调递增,
当\(\ln (-2a)<x<1\)时,\(f'(x)=(x-1)(e^x+2a)<0\)恒成立,
故\(f(x)\)单调递减,
故当\(x= \ln (-2a)\)时,函数取极大值,
由\(f(\ln (-2a))=[\ln (-2a)-2](-2a)+a[\ln (-2a)-1]^2=a{[\ln (-2a)-2]^2+1}<0\)得:函数\(f(x)\)在\(R\)上至多存在一个零点,不合题意;
④若 \(a=-\dfrac{e}{2}\),则\(\ln (-2a)=1\),函数\(f(x)\)在\(R\)上单调递增,
函数\(f(x)\)在\(R\)上至多存在一个零点,不合题意;
⑤若\(a<-\dfrac{e}{2}\),则\(\ln (-2a)>\ln e=1\),
当\(x<1\)或\(x>\ln (-2a)\)时,\(f'(x)=(x-1)(e^x+2a)>0\)恒成立,
故\(f(x)\)单调递增,
当\(1<x<\ln (-2a)\)时,\(f'(x)=(x-1)(e^x+2a)<0\)恒成立,
故\(f(x)\)单调递减,
故当\(x=1\)时,函数取极大值,
由\(f(1)=-e<0\)得:函数\(f(x)\)在\(R\)上至多存在一个零点,不合题意;
综上所述,\(a\)的取值范围为\((0,+∞)\).
法二 分类参数
解:显然\(x=1\)不是函数\(f(x)\)的零点,
当\(x≠1\)时,方程\(f(x)=0\)等价于 \(-a=\dfrac{x-2}{(x-1)^2} \cdot e^x\),
设 \(g(x)=\dfrac{x-2}{(x-1)^2} \cdot e^x\),求导 \(g^{\prime}(x)=e^x \cdot \dfrac{x^2-4 x+5}{(x-1)^3}\),
当\(x<1\)时,\(g'(x)<0\);当\(x>1\)时,\(g'(x)>0\);
\(\therefore\)函数\(g(x)\)在\((-∞,1)\)上单调递减,在\((1,+∞)\)上单调递增,
且\(x→-∞\)时,\(g(x)→0\);\(x→1\)时,\(g(x)→-∞\);\(x→+∞\)时,\(g(x)→+∞\);
\(\therefore\)函数\(g(x)\)在\((-∞,1)\)上的值域为\((-∞,0)\),在\((1,+∞)\)上的值域为\((-∞,+∞)\),
\(\therefore\)当\(-a<0\)时,函数\(f(x)\)有两个零点,
故所求\(a\)取值范围为\((0,+∞)\).

【C组---拓展题】
1.已知函数\(f(x)=\ln x\).
(1)若\(af(x)⩽e^{x-1}-1\)恒成立,求实数\(a\)的值;
(2)若关于\(x\)的方程\(f\left(x^2\right)-x+\dfrac{m}{x}-\ln m=0\)有四个不同的实数根,则实数\(m\)的取值范围.
2.已知函数\(f(x)=\ln x-a^2 x^2+ax\).
(1)求函数\(f(x)\)在定义域内的最值.
(2)当\(a>0\)时,若\(y=f'(x)\)有两个不同的零点\(x_1\),\(x_2\),求证:\(a(x_1+x_2 )>2\).
参考答案
-
答案 (1) \(a=1\);(2) \((0,1)\) .
解析 (1)\(a=1\).(过程略)
(2)解法一:由题意知,\(m>0\), \(h(x)=\ln x^2-x+\dfrac{m}{x}-\ln m\),
\(h^{\prime}(x)=\dfrac{2}{x}-1-\dfrac{m}{x^2}=\dfrac{-x^2+2 x-m}{x^2}\),
当\(x<0\)时,\(h'(x)<0\),\(h(x)\)在区间\((-∞,0)\)单调递减,
又 \(h(-\sqrt{m})=0\),故\(h(x)\)在区间\((-∞,0)\)有唯一实根,
若\(m⩾1\),\(-x^2+2x-m=-(x-1)^2+1-m⩽0\),
当\(x>0\)时,\(h'(x)≤0\),\(h(x)\)在区间\((0,+∞)\)单调递减,
故\(h(x)\)在区间\((0,+∞)\)至多有一个实根,不符合题意,
若\(0<m<1\),令\(x_1,x_2 (x_1<x_2 )\)是方程\(-x^2+2x-m=0\)的两不同实根,
易得\(0<x_1<1<x_2\),
故\(h(x)\)在区间\((0,x_1 )\),\((x_2,+∞)\)上单调递减,在区间\((x_1,x_2 )\)上单调递增.
\(h\left(x_1\right)=\ln x_1^2-x_1+\dfrac{m}{x_1}-\ln m=\ln x_1^2-x_1+\dfrac{-x_1^2+2 x_1}{x_1}-\ln \left(-x_1^2+2 x_1\right)\)
\(=-2x_1+2+\ln x_1-\ln (2-x_1 )\),
设\(φ(x)=-2x+2+\ln x-\ln (2-x)(0<x<1)\),
则 \(\varphi^{\prime}(x)=-2+\dfrac{1}{x}+\dfrac{1}{2-x}=\dfrac{2(x-1)^2}{x(2-x)}>0\),
\(φ(x)<φ(1)=0\),\(h(x_1 )<0\),
同理可证\(h(x_2 )>0\),
取 \(x_3=\left(1+\sqrt{2+\dfrac{1}{m}}\right)^2>x_2=1+\sqrt{1-m}\), \(h\left(x_3\right)<2 \sqrt{x_3}-x_3+1+\dfrac{1}{m}=0\).
取 \(x_4=\min \left\{\ln \dfrac{1}{m}, \dfrac{m^2}{4}\right\}\), \(x_4 \leqslant \dfrac{m^2}{4}<\dfrac{m}{2}<x_1=1-\sqrt{1-m}\),
\(h\left(x_4\right)>2 \sqrt{x_4}-\dfrac{2}{\sqrt{x_4}}+\dfrac{m}{x_4}+\left(\ln \dfrac{1}{m}-x_4\right)=2 \sqrt{x_4}+\dfrac{m-2 \sqrt{x_4}}{x_4}+\left(\ln \dfrac{1}{m}-x_4\right)>0\).
故\(h(x)\)在\((x_4,x_1 )\),\((x_1,x_2 )\),\((x_2,x_3 )\)各存在一个零点,
实数\(m\)的取值范围是\((0,1)\).
解法二:由题意知,\(m>0\), \(h(x)=\ln x^2-x+\dfrac{m}{x}-\ln m\),
\(h^{\prime}(x)=\dfrac{2}{x}-1-\dfrac{m}{x^2}=\dfrac{-x^2+2 x-m}{x^2}\),
当\(x<0\)时,\(h'(x)<0\),\(h(x)\)在区间\((-∞,0)\)单调递减,
又 \(h(-\sqrt{m})=0\),故\(h(x)\)在区间\((-∞,0)\)有唯一实根,
因此当\(x>0\)时,\(\ln x-x=\ln \dfrac{m}{x}-\dfrac{m}{x}\)有三个实根,
当\(x=\dfrac{m}{x}\), \(x=\sqrt{m}\)是方程的一个实根,
若\(x \neq \dfrac{m}{x}\), \(\ln x-\ln \dfrac{m}{x}=x-\dfrac{m}{x}\), \(\dfrac{1}{\sqrt{m}}>\dfrac{\ln x-\ln \dfrac{m}{x}}{x -\dfrac{m}{x}}=1\)(对数均值不等式),
所以\(0<m<1\).
故\(m\)的取值范围为\((0,1)\). -
答案 (1) 最大值\(-\ln a\),无最小值;(2)略 .
解析 (1)函数\(f(x)=\ln x-a^2 x^2+ax\)的定义域为\((0,+∞)\),
\(f^{\prime}(x)=\dfrac{1}{x}-2 a^2 x+a=-\dfrac{(2 a x+1)(a x-1)}{x}\),
当\(a=0\)时,\(f(x)=\ln x\),
此时函数\(f(x)\)为增函数,无最值,
当\(a≠0\)时,令\(f'(x)=0\),得\(x=-\dfrac{1}{2a}\)或\(x=\dfrac{1}{a}\),
①若\(a<0\),则\(-\dfrac{1}{2a}>0\),\(\dfrac{1}{a} <0\),
由\(f'(x)>0\),得\(0<x<-\dfrac{1}{2a}\),\(f(x)\)单调递增,
由\(f'(x)<0\),得\(x>-\dfrac{1}{2a}\),\(f(x)\)单调递减,
所以函数\(f(x)\)在定义域内有最大值\(f\left(-\dfrac{1}{2 a}\right)=\ln \left(-\dfrac{1}{2 a}\right)-a^2\left(-\dfrac{1}{2 a}\right)^2+a\cdot \left(-\dfrac{1}{2 a}\right)=\ln \left(-\dfrac{1}{2 a}\right)-\dfrac{3}{4}\),无最小值.
②若\(a>0\),则\(-\dfrac{1}{2a}<0\),\(\dfrac{1}{a} >0\),
由\(f'(x)>0\),得\(0<x<\dfrac{1}{a}\) ,\(f(x)\)单调递增,
由\(f'(x)<0\),得\(x>\dfrac{1}{a}\),\(f(x)\)单调递减,
所以\(f(x)\)定义域内有最大值\(f\left(\dfrac{1}{a}\right)=\ln \left(\dfrac{1}{a}\right)-a^2\left(\dfrac{1}{a}\right)^2+a\cdot \dfrac{1}{a} =-\ln a\),无最小值.
(2)证明:由(1)知,当\(a>0\)时,函数\(f(x)\)在定义域内的最大值为\(f\left(\dfrac{1}{a}\right)=-\ln a\),
因为\(y=f(x)\)有两个不同的零点\(x_1\),\(x_2\),
所以\(-\ln a>0\),解得\(-\ln a>0\), 解得\(0<a<1\),
不妨设\(0<x_1<\dfrac{1}{a} <x_2\),
由题意知\(f(x_1 )=\ln x_1-a^2 x_1^2+ax_1=0\),\(f(x_2 )=\ln x_2-a^2 x_2^2+ax_2=0\),
所以\(\ln x_2-\ln x_1=a^2 (x_2^2-x_1^2 )-ax_2+ax_1\),
即\(\ln \dfrac{\ln x_2-\ln x_1}{x_2-x_1}=a\left[a\left(x_2+x_1\right)-1\right]\),
即\(\dfrac{\ln \dfrac{x_2}{x_1}}{\dfrac{x_2}{x_1}-1}=a\left[a\left(x_1+x_2\right)-1\right] x_1\),
设 \(h(t)=\ln t-\dfrac{2(t-1)}{t+1}(t>1)\),
则 \(h^{\prime}(t)=\dfrac{1}{t}-\dfrac{4}{(t+1)^2}=\dfrac{(t-1)^2}{t(t+1)^2}(t>1)\),
所以当\(t>1\)时,\(h'(t)>0\),\(h(t)\)单调递增,
所以\(h(t)>h(1)=0\),
即\(\ln t-\dfrac{2(t-1)}{t+1}>0\),所以 \(\dfrac{\ln t}{t-1}>\dfrac{2}{t+1}\),
令\(t=\dfrac{x_2}{x_1}\) ,
则上式可化为 \(\dfrac{\ln \dfrac{x_2}{x_1}}{\dfrac{x_2}{x_1}-1}>\dfrac{2}{\dfrac{x_2}{x_1}+1}\),
所以 \(a\left[a\left(x_1+x_2\right)-1\right] x_1>\dfrac{2}{\dfrac{x_2}{x_1}+1}\),
所以 \(a\left[a\left(x_1+x_2\right)-1\right] x_1>\dfrac{2}{x_1+x_2}\),
即\(a^2 (x_1+x_2 )^2-a(x_1+x_2 )-2>0\),
所以\([a(x_1+x_2 )-2][a(x_1+x_2 )+1]>0\),
又因为\(a(x_1+x_2 )+1>0\)恒成立,
所以\(a(x_1+x_2 )>2\).

