导数专题 导数的几何意义
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高二数学同步精品讲义与分层练习(人教A版2019）]
( https://www.zxxk.com/docpack/2875423.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)
选择性第二册同步巩固，难度3颗星！
基础知识
函数\(y=f(x)\)在点\(x=x_0\)处的导数的几何意义是曲线\(y=f(x)\)在点\(P(x_0 ，f(x_0))\)处的切线的斜率，
即：曲线\(y=f(x)\)在点\(P(x_0 ，f(x_0))\)处的切线l的斜率\(k=f'(x_0)\)，
切线\(l\)的方程为\(y-f(x_0)=f'(x_0)(x-x_0)\)．
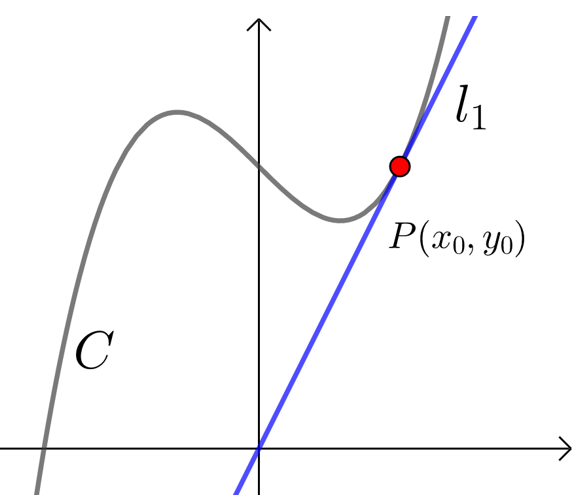
解释
"过点\(x=x_0\)”与"在点\(x=x_0\)处"的区别
曲线\(C：y=f(x)\)在点\(P(x_0 ，y_0)\)处的切线指的是\(P\)为切点的切线，如图一；
过点\(P(x_0 ，y_0)\)的切线是指切线过点\(P\)，点\(P\)是否切点均可，切线可多条，如图二.
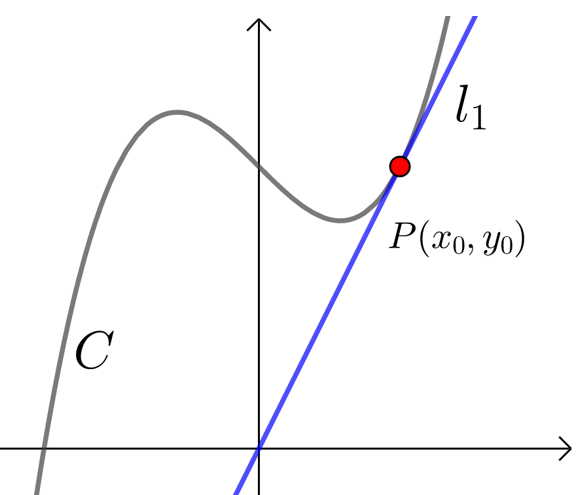\(\qquad \qquad\)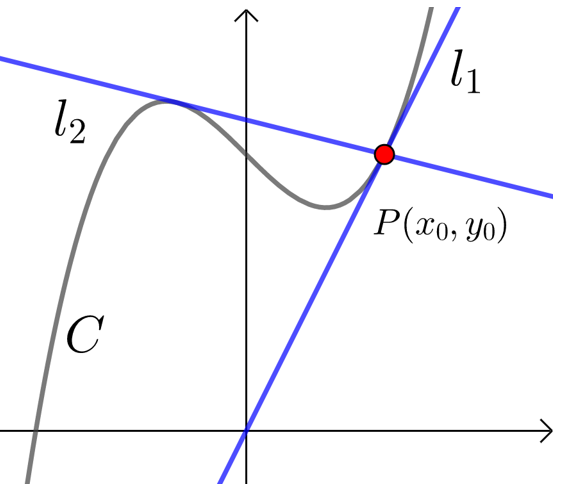 
基本方法
【题型1】在某点处的切线
【典题1】 (多选)若函数\(f(x)\)的图象上存在两个不同的点\(A\)，\(B\)，使得曲线\(y=f(x)\)在这两点处的切线重合，称函数\(f(x)\)具有\(T\)性质．下列函数中具有\(T\)性质的有( )
A．\(y=e^x-x\) \(\qquad \qquad \qquad \qquad\) B．\(y=x^4-x^2\) \(\qquad \qquad \qquad \qquad\) C．\(y=x^3\) \(\qquad \qquad \qquad \qquad\) D．\(y=x+\sin x\)
解析 由题意可得，性质T指函数\(f(x)\)图象上有两个不同点的切线是重合的，即两个不同点所对应的导数值相等，且该点处函数的切线方程也相同．
对于\(A\)选项，\(y=e^x-x\)，则\(y'=e^x-1\)，导函数为增函数，不存在不同的两个\(x\)使得导数值相等，故\(A\)不符合；
对于\(B\)选项，\(y'=4x^3-2x\)，
设两切点分别为\((x_1，x_1^4-x_1^2 )\)，\((x_2，x_2^4-x_2^2 )\)，且\(4x_1^3-2x_1=4x_2^3-2x_2\)，
取\(x_1=-\dfrac{\sqrt{2}}{2}\)，\(x_2=\dfrac{\sqrt{2}}{2}\)，
则\(y_1=-\dfrac{1}{4}=y_2\)，两切点处的导数值为\(y'=0\)，
两切点连线的直线斜率为\(k=\dfrac{y_2-y_1}{x_2-x_1}=0\)，
所以两切点处的导数值等于两切点连线的斜率，
符合性质\(T\)，所以\(B\)选项符合；
对于\(C\)选项，设两切点分别为\((x_1，x_1^3 )\)和\((x_2，x_2^3 )\)，
则两切点处的导数值相等有：\(3x_1^2=3x_2^2\)，解得：\(x_1=-x_2\)，
令\(x_1=a\)，则\(x_2=-a\)，两切点处的导数\(y'=3a^2\)，
两切点连线的斜率为 \(k=\dfrac{a^3-\left(-a^3\right)}{a-(-a)}=a^2\)，
则\(3a^2=a^2\)，得\(a=0\)，两切点重合，不符合题意，所以\(C\)选项不符合；
对于\(D\)选项，\(y'=1+\cos x\)，设两切点的横坐标分别为\(x_1\)和\(x_2\)，
则\(1+\cos x_1=1+\cos x_2\)，所以\(\cos x_1=\cos x_2\)，
取\(x_1=\dfrac{\pi}{2}\)，\(x_2=\dfrac{5\pi}{2}\)，则\(y_1=\dfrac{\pi}{2}+1\)，\(y_2=\dfrac{5\pi}{2}+1\)，
两切点处的导数值为\(y'=1\)，两切点连线的直线斜率为 \(k=\dfrac{y_2-y_1}{x_2-x_1}=1\)，
所以两切点处的导数值等于两切点连线的斜率，符合性质\(T\)，所以\(D\)选项符合．
故选：\(BD\)．
【典题2】 已知函数 \(f(x)=\dfrac{1}{2} \sin \left(2 x+\dfrac{\pi}{3}\right)\)的图像在\((x_1，f(x_1 ))\)处的切线与在\((x_2，f(x_2 ))\)处的切线相互垂直，那么\(|x_1-x_2 |\)的最小值是( )
A． \(\dfrac{\pi}{4}\) \(\qquad \qquad \qquad \qquad\) B．\(\dfrac{\pi}{2}\)\(\qquad \qquad \qquad \qquad\) C．\(π\) \(\qquad \qquad \qquad \qquad\) D．\(2π\)
解析 由函数 \(f(x)=\dfrac{1}{2} \sin \left(2 x+\dfrac{\pi}{3}\right)\)得： \(f^{\prime}(x)=\cos \left(2 x+\dfrac{\pi}{3}\right)\)，
显然若图象在\((x_1，f(x_1 ))\)处的切线与在\((x_2，f(x_2 ))\)处的切线相互垂直，
只需\(f' (x_1 ) f' (x_2 )=-1\)，
不妨设\(2x_1+\dfrac{\pi}{3}=2nπ\)，\(n∈Z\)，\(2x_2+\dfrac{\pi}{3}=2mπ+π\)，\(m∈Z\)，
显然\(x_1-x_2=(n-m)π-\dfrac{\pi}{2}\)，
显然当\(n=m\)时，\(|x_1-x_2 |\)的最小值是\(\dfrac{\pi}{2}\)．
故选：\(B\)．
【巩固练习】
1.若函数\(f(x)=2\ln x+4x^2+bx+5\)的图象上的任意一点的切线斜率都大于\(0\)，则\(b\)的取值范围是( )
A．\((-∞，-8)\) \(\qquad \qquad\) B．\((-8，+∞)\) \(\qquad \qquad\) C．\((-∞，8)\) \(\qquad \qquad\) D．\((8，+∞)\)
2.(多选)若以曲线\(y=f(x)\)上任意一点\(M(x，y)\)为切点作切线\(l\)，曲线上总存在异于点\(M\)的点\(N(x'，y')\)，使得以点\(N\)为切点的切线l'满足\(l∥l'\)，则称曲线\(y=f(x)\)具有“可平行性”．下列曲线具有“可平行性”的是( )
A．\(y=x+\dfrac{1}{x}\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) B．\(y=x^3-x\)
C．\(y=\sin x\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) D．\(y=(x-2)^2+\ln x\)
3.设对于曲线\(f(x)=-e^x-x\)上任一点处的切线\(l_1\)，总存在曲线\(g(x)=kx+\cos x\)上一点处的切线\(l_2\)，使得\(l_1⊥l_2\)，则实数\(k\)的取值范围是\(\underline{\quad \quad}\) .
4.若函数\(f(x)=ax+\sin x\)的图象上存在互相垂直的切线，则实数\(a\)的值为\(\underline{\quad \quad}\)．
参考答案
-
答案 \(B\)
解析 根据题意，函数\(f(x)=2\ln x+4x^2+bx+5\)，其定义域为\((0，+∞)\)，
其导数\(f'(x)=\dfrac{2}{x}+8x+b\)，
若函数\(f(x)\)的图象上的任意一点的切线斜率都大于\(0\)，
则有\(f'(x)=\dfrac{2}{x}+8x+b>0\)在\((0，+∞)\)上恒成立，
变形可得\(b>-\left(\dfrac{2}{x}+8 x\right)\)在\((0，+∞)\)上恒成立，
又由\(\dfrac{2}{x}+8 x \geq 2 \times \sqrt{\dfrac{2}{x} \times 8 x}=8\)，
当且仅当\(x=\dfrac{1}{2}\)时等号成立，即\(\dfrac{2}{x}+8x\)有最小值\(8\)，
若 \(b>-\left(\dfrac{2}{x}+8 x\right)\)在\((0，+∞)\)上恒成立，
必有\(b>-8\)，即\(b\)的取值范围为\((-8，+∞)\)；
故选\(B\)． -
答案 \(AC\)
解析 设\(f'(x)\)的值域为\(Q\)，
由题意，曲线\(y=f(x)\)具有“可平行性”等价于对任意的\(a∈Q\)，
方程\(y'=a\)至少有两个根，
对于\(A\)，由\(y'=1-\dfrac{1}{x^2} =a\)(\(x≠0\)且\(a<1\))，得\(\dfrac{1}{x^2} =1-a\)，
此方程有两个不同的根，符合题意；
对于\(B\)，由\(y'=-1\)时，\(x\)的取值唯一，只有\(0\)，不合题意；
对于\(C\)，由\(y'=\cos x\)和三角函数的周期性可知，\(\cos x=a(-1≤a≤1)\)的解有无穷多个，符合题意；
对于\(D\)，\(y'=2x－4+\dfrac{1}{x}\)，
令\(2x-4+\dfrac{1}{x}=a(a≥2\sqrt{2}-4)\)，则有\(2x^2-(4+a)x+1=0\)，
当\(△=0\)时解唯一，不合题意．
故选：\(AC\)． -
答案 \([0，1]\)
解析 \(f(x)=-e^x-x\)，其导数\(f' (x)=-e^x-1\)，
有\(f' (x)<-1\)，则\(-f' (x)>1\)，则\(\dfrac{1}{-f^{\prime}(x)} \in(0，1)\)，
由\(g(x)=kx+\cos x\)，得\(g' (x)=k-\sin x\)，
\(\because -\sin x∈[-1，1]\)，\(\therefore k-\sin x∈[-1+k，1+k]\)，
要使过曲线\(f(x)=-e^x-x\)上任一点处的切线\(l_1\)，总存在曲线\(g(x)=kx+\cos x\)上一点处的切线\(l_2\)，使得\(l_1⊥l_2\)，
则有\(\left\{\begin{array}{l} -1+k \leqslant 0 \\ 1+k \geqslant 1 \end{array}\right.\)，解得\(0⩽k⩽1\)．
\(\therefore\)实数\(k\)的取值范围是\([0，1]\)． -
答案 \(0\)
解析 \(\because f(x)=ax+\sin x\)，\(\therefore f'(x)=a+\cos x\)，
假设函数\(f(x)=ax+\sin x\)的图象上存在互相垂直的切线，
不妨设在\(x=m\)与\(x=n\)处的切线互相垂直
则\((a+\cos m)(a+\cos n)=-1\)
\(\therefore a^2+(\cos m+\cos n)a+(\cos m\cos n+1)=0 \quad (*)\)
因为\(a\)的值必然存在，即方程\((*)\)必然有解，所以
判别式\(△=(\cos m+\cos n)^2-4(\cos m\cos n+1)≥0\)
所以\(\cos ^2m+\cos ^2n-2\cos m\cos n=(\cos m-\cos n)^2≥4\)
解得\(\cos m-\cos n≥2\)或\(\cos m-\cos n≤-2\)
由于\(|\cos x|≤1\)，
所以有\(\cos m=1\)，\(\cos n=-1\)或\(\cos m=-1\)，\(\cos n=1\)，且\(△=0\)
所以\((*)\)变为：\(a^2=0\)所以\(a=0\).
故答案为：\(0\) .
【题型2】过某点处的切线
【典题1】 已知函数\(f(x)=2x^3-ax\)，若\(a=1\)时，直线\(y=k(x-1)+1\)与曲线\(y=f(x)\)相切，则\(k\)的所有可能的取值为\(\underline{\quad \quad}\)；若\(a∈R\)时，直线\(y=k(x-2)\)与曲线\(y=f(x)\)相切，且满足条件的\(k\)的值有且只有\(3\)个，则\(a\)的取值范围为\(\underline{\quad \quad}\)．
解析 当\(a=1\)时，\(f(x)=2x^3-x\)，求导得\(f' (x)=6x^2-1\)，
设直线\(y=k_1 (x-1)+1\)与曲线\(y=f(x)\)相切的切点为\((x_0，2x_0^3-x_0 )\)，
则\(k_1=f' (x_0 )=6x_0^2-1\)，且\(2x_0^3-x_0=k_1 (x_0-1)+1\)，
即\(2x_0^3-x_0=(6x_0^2-1)(x_0-1)+1\)，
整理得\((x_0-1)^2 (2x_0+1)=0\)，解得\(x_0=-\dfrac{1}{2}\)或\(x_0=1\)，
则\(k_1=f' \left(-\dfrac{1}{2}\right)=\dfrac{1}{2}\)或\(k_1=f' (1)=5\)，
所以\(k_1\)的所有可能的取值为\(\dfrac{1}{2}\)，\(5\)；
由\(f(x)=2x^3-ax\)，求导得\(f' (x)=6x^2-a\)，
设直线\(y=k(x-2)\)与曲线\(y=f(x)\)相切的切点为\((t，2t^3-at)\)，
于是得\(k=f' (t)=6t^2-a\)，且\(2t^3-at=k(t-2)\)，则\(k=2t^3\)，
显然函数\(y=2t^3\)在\(R\)上单调递增，
因直线\(y=k(x-2)\)与曲线\(y=f(x)\)相切的\(k\)的值有且只有\(3\)个，
则有直线\(y=k(x-2)\)与曲线\(y=f(x)\)相切的切点横坐标值有且只有\(3\)个，
即方程\(a=6t^2-2t^3\)有\(3\)个不等实根，
令\(g(t)=2t^3-6t^2+a\)，求导得\(g' (t)=6t^2-12t=6t(t-2)\)，
当\(t<0\)或\(t>2\)时，\(g' (t)>0\)，当\(0<t<2\)时，\(g' (t)<0\)，
即函数\(g(t)\)在\((-∞，0)\)，\((2，+∞)\)上递增，在\((0，2)\)上递减，
当\(t=0\)时，\(g(t)\)取得极大值\(g(0)=a\)，
当\(t=2\)时，\(g(t)\)取得极小值\(g(2)=a-8\)，
方程\(a=6t^2-2t^3\)有\(3\)个不等实根，当且仅当函数\(g(t)\)有\(3\)个不同的零点，
因此 \(\left\{\begin{array}{l}
a>0 \\
a-8<0
\end{array}\right.\)，解得\(0<a<8\)，
所以\(a\)的取值范围为\((0，8)\)．
故答案为：\(\dfrac{1}{2}\)，\(5\)；\((0，8)\)．
【典题2】 已知函数\(f(x)=x+\dfrac{1}{x}\)，过点\(P(1，0)\)作函数\(y=f(x)\)图像的两条切线，切点分别为\(M\)，\(N\)．则下列说法正确的是( )
A．\(PM⊥PN\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) B．直线\(MN\)的方程为\(2x-y+1=0\)
C． \(|M N|=2 \sqrt{10}\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) D．\(△PMN\)的面积为\(3\sqrt{2}\)
解析 因为\(f(1)=1+1=2\)，所以\(P(1，0)\)没有在函数的图象上，
\(f^{\prime}(x)=1-\dfrac{1}{x^2}=\dfrac{x^2-1}{x^2}\)，
设切点坐标为\((a，b)(a≠0)\)，
当\(a=1\)时，\(f(1)=2\)，\(x=1\)不与\(f(x)=x+\dfrac{1}{x}\)相切，所以\(a≠1\)，
\(f^{\prime}(a)=\dfrac{a^2-1}{a^2}=\dfrac{b}{a-1}\)，
又因为 \(a+\dfrac{1}{a}=b\)，解得\(a=-1±\sqrt{2}\)，
即\((-1-\sqrt{2}，-2\sqrt{2})\)，\((-1+\sqrt{2}，2\sqrt{2})\)，
所以 \(k_{P M} \times k_{P N}=\dfrac{2 \sqrt{2}}{2+\sqrt{2}} \times \dfrac{2 \sqrt{2}}{\sqrt{2}-2}=-4 \neq-1\)，故\(A\)错误；
\(k_{N M}=\dfrac{2 \sqrt{2}+2 \sqrt{2}}{2 \sqrt{2}}=2\)，
所以直线\(MN\)的方程为\(y=2(x-1)\)，即\(2x-y+2=0\)，故\(B\)错误；
\(|M N|=\sqrt{(-1+\sqrt{2}+1+\sqrt{2})^2+(2 \sqrt{2}+2 \sqrt{2})^2}=2 \sqrt{10}\)，故\(C\)正确；
\(P(1，0)\)到直线\(MN\)的距离为 \(d=\dfrac{|2-0+2|}{\sqrt{4+1}}=\dfrac{4 \sqrt{5}}{5}\)，
所以\(△PMN\)的面积为\(\dfrac{1}{2}|M N| d=\dfrac{1}{2} \times 2 \sqrt{10} \times \dfrac{4 \sqrt{5}}{5}=4 \sqrt{2}\)，故\(D\)错误．
故选：\(C\)．
【巩固练习】
1.已知曲线\(y=\ln x\)的切线过原点，则此切线的斜率为( )
A．\(e\) \(\qquad \qquad \qquad \qquad\) B．\(-e\) \(\qquad \qquad \qquad \qquad\) C．\(\dfrac{1}{e}\) \(\qquad \qquad \qquad \qquad\) D．\(-\dfrac{1}{e}\)
2.过直线\(y=x-1\)上一点\(P\)可以作曲线\(f(x)=x-\ln x\)的两条切线，则点\(P\)横坐标\(t\)的取值范围为( )
A．\(0<t<1\) \(\qquad \qquad\) B．\(1<t<e\) \(\qquad \qquad\) C．\(0<t<e\) \(\qquad \qquad\) D．\(\dfrac{1}{e}<t<1\)
3.(多选)若过点\((1，a)\)可以作出曲线\(y=(x-1)e^x\)的切线\(l\)，且\(l\)最多有\(n\)条，\(n∈N^*\)，则( )
A．\(a≤0\) \(\qquad \qquad \qquad \qquad \qquad \qquad \qquad\) B．当\(n=2\)时，\(a\)值唯一
C．当\(n=1\)时， \(a<-\dfrac{4}{e}\) \(\qquad \qquad \qquad \qquad\) D．\(na\)的值可以取到\(-4\)
参考答案
-
答案 \(C\)
解析 设切点坐标为\((a，\ln a)\)，
\(\because y=\ln x\)，\(\therefore y'=\dfrac{1}{x}\)，切线的斜率是\(\dfrac{1}{a}\)，
切线的方程为\(y-\ln a=\dfrac{1}{a}(x-a)\)，
将\((0，0)\)代入可得\(\ln a=1\)，\(\therefore a=e\)，
\(\therefore\)切线的斜率是\(\dfrac{1}{a}=\dfrac{1}{e}\)；
故选：\(C\)． -
答案 \(C\)
解析 设切点为\((m，m-\ln m)\)，\(m>0\)，
由\(f(x)=x-\ln x\)的导数为\(f' (x)=1-\dfrac{1}{x}\)，
可得切线的斜率为 \(1-\dfrac{1}{m}\)，
又\(P(t，t-1)\)，可得 \(\dfrac{m-\ln m-t+1}{m-t}=1-\dfrac{1}{m}\)，
化为\(t=2m-m\ln m\)，
设\(g(x)=2x-x\ln x\)，
可得\(g' (x)=2-(1+\ln x)=1-\ln x\)，
当\(x>e\)时，\(g' (x)<0\)，\(g(x)\)递减；
当\(0<x<e\)时，\(g' (x)>0\)，\(g(x)\)递增．
可得\(g(x)\)在\(x=e\)处取得最大值\(e\)，
可得当\(0<t<e\)时，方程\(t=2m-m\ln m\)有两解，
故选：\(C\)． -
答案 \(ABD\)
解析 \(y'=e^x+(x-1)e^x=xe^x\)，
设切线\(l\)的切点为\((x_0，y_0 )\)，则切线\(l\)的斜率为\(k=x_0 e^{x_0}\)，
又\(y_0=(x_0-1) e^{x_0}\)，
故由点斜式方程可知切线l的方程为\(y-(x_0-1) e^{x_0}=x_0 e^{x_0} (x-x_0 )\)，
\(\therefore x_0 e^{x_0}=\dfrac{\left(x_0-1\right) e^{x_0-a}}{x_0-1}=e^{x_0}-\dfrac{a}{x_0-1}\)，
则\(a=-e^{x_0} (x_0-1)^2\)，
对于\(A\)，由于\(a=-e^{x_0} (x_0-1)^2\)，\(e^{x_0}>0，(x_0-1)^2⩾0\)，
故\(a≤0\)，选项\(A\)正确；
对于\(B\)，令\(g(x)=-e^x (x-1)^2\)，则\(g' (x)=-e^x (x-1)(x+1)\)，
易知\(g(x)\)在\((-∞，-1)\)，\((1，+∞)\)上单调递减，在\((-1，1)\)上单调递增，
且 \(g(-1)=-\dfrac{4}{e}\)，\(g(1)=0\)，当\(x→-∞\)，时，\(g(x)→0\)，
当\(x→+∞\)时，\(g(x)→-∞\)，
作出函数\(g(x)\)的草图如下，
当\(n=2\)时，即\(x_0\)的值有两个，由图象可知，
当且仅当 \(a=g(-1)=-\dfrac{4}{e}\)时，\(x_0\)的值有两个，选项\(B\)正确；
对于\(C\)，由图象可知，当\(a=0\)或\(a<-\dfrac{4}{e}\)时，\(x_0\)的值唯一，此时\(n=1\)，选项\(C\)错误；
对于\(D\)，由图象可知，\(n=1\)或\(2\)或\(3\)，若\(na=-4\)，则当\(n=1\)时，\(a=-4\)，
由选项\(C\)可知，此时\(a=0\)或\(a<-\dfrac{4}{e}\)，而 \(-4<-\dfrac{4}{e}\)，
故\(na\)可能取到\(-4\)，选项\(D\)正确．
故选：\(ABD\)．
【题型3】两曲线的公切线
【典题1】 若直线\(y=kx+b\)是曲线 \(y=e^{x-2}\)的切线，也是曲线\(y=e^x-1\)的切线，则\(b=\)\(\underline{\quad \quad}\)．
解析 设直线\(y=kx+b\)是曲线 \(y=e^{x-2}\)和\(y=e^x-1\)的切点分别为 \(\left(x_1， e^{x_1-2}\right)\)和 \(\left(x_2， e^{x_2}-1\right)\)，
则切线分别为 \(y-e^{x_1-2}=e^{x_1-2}\left(x-x_1\right)\)， \(y-e^{x_2}+1=e^{x_2}\left(x-x_2\right)\)，
化简得： \(y=e^{x_1-2} x+e^{x_1-2}-x_1 e^{x_1-2}\)， \(y=e^{x_2} x+e^{x_2}-1-x_2 e^{x_2}\)，
依题意有： \(\left\{\begin{array}{l}
e^{x_1-2}=e^{x_2} \\
e^{x_1-2}-x_1 e^{x_1-2}=e^{x_2}-1-x_2 e^{x_2}
\end{array}\right.\)，
\(\therefore x_1-2=x_2\)，\(x_2=-\ln 2\)，
则 \(b=e^{x_2}-1-x_2 e^{x_2}=\dfrac{1}{2} \ln 2-\dfrac{1}{2}\)．
故答案为：\(\dfrac{1}{2} \ln 2-\dfrac{1}{2}\) ．
【典题2】 若曲线\(C_1:y=ax^2 (a>0)\)与曲线\(C_2:y=e^x\)存在公共切线，则\(a\)的取值范围为( )
A． \(\left[\dfrac{e^2}{8}，+\infty\right)\) \(\qquad \qquad\) B． \(\left(0， \dfrac{e^2}{8}\right]\) \(\qquad \qquad\)C． \(\left[\dfrac{e^2}{4}，+\infty\right)\) \(\qquad \qquad\) D． \(\left(0， \dfrac{e^2}{4}\right]\)
解析 由\(y=ax^2 (a>0)\)，得\(y'=2ax\)，
由\(y=e^x\)，得\(y'=e^x\)，
\(\because\)曲线\(C_1:y=ax^2 (a>0)\)与曲线\(C_2:y=e^x\)存在公共切线，则
设公切线与曲线\(C_1\)切于点\((x_1，ax_1^2)\)，与曲线\(C_2\)切于点\((x_2，e^{x_2})\)，
则\(2 a x_1=e^{x_2}=\dfrac{e^{x_2}-a x_1{ }^2}{x_2-x_1}\)，
将\(e^{x_2}=2 a x_1\)代入 \(2 a x_1=\dfrac{e^{x_2}-a x_1{ }^2}{x_2-x_1}\)，可得\(2x_2=x_1+2\)，
\(\therefore a=\dfrac{e^{\frac{x_1}{2}+1}}{2 x_1}\)，记 \(f(x)=\dfrac{e^{\frac{x}{2}+1}}{2 x}\)，
则\(f^{\prime}(x)=\dfrac{e^{\frac{x}{2}+1}(x-2)}{4 x^2}\)，当\(x∈(0，2)\)时，\(f'(x)<0\)．
\(\therefore\)当\(x=2\)时， \(f(x)_{\min }=\dfrac{e^2}{4}\)．
\(\therefore a\)的范围是\(\left[\dfrac{e^2}{4}，+\infty\right)\) ．
故选：\(C\)．
【巩固练习】
1.若曲线\(y=x-\ln x\)与曲线\(y=ax^3+x+1\)在公共点处有相同的切线，则实数\(a\)等于( )
A． \(\dfrac{e^2}{3}\) \(\qquad \qquad \qquad \qquad\) B．\(-\dfrac{e^2}{3}\) \(\qquad \qquad \qquad \qquad\) C．\(-\dfrac{e}{3}\) \(\qquad \qquad \qquad \qquad\) D．\(\dfrac{e}{3}\)
2.若二次函数\(f(x)=x^2+1\)的图象与曲线\(C:g(x)=ae^x+1(a>0)\)存在公共切线，则实数\(a\)的取值范围为\(\underline{\quad \quad}\) ．
参考答案
-
答案 \(B\)
解析 设公共点的横坐标为\(t\)，由\(y'=1-\dfrac{1}{x}\)，以及\(y'=3ax^2+1\)，
则\(\left\{\begin{array}{l} t-\ln t=a t^3+t+1 \\ 1-\dfrac{1}{t}=3 a t^2+1 \end{array}\right.\)，由第二个方程得\(t^3=-\dfrac{1}{3 a}\)，
①再代入第一个方程\(\ln t=-\dfrac{2}{3}\)，结合①解得\(a=-\dfrac{e^2}{3}\)．
故选：\(B\)． -
答案 \(\left(0， \dfrac{4}{e^2}\right]\)
解析 \(f(x)=x^2+1\)的导数为\(f'(x)=2x\)，
\(g(x)=ae^x+1\)的导数为\(g'(x)=ae^x\)，
设公切线与\(f(x)=x^2+1\)的图象切于点\((x_1，x_1^2+1)\)，
与曲线\(C:g(x)=ae^x+1\)切于点 \(\left(x_2， a e^{x^2+1}\right)\)，
\(\therefore 2 x_1=a e^{x 2}=\dfrac{a e^{x_2}+1-\left(x_1{ }^2+1\right)}{x_2-x_1}=\dfrac{a e^{x_2}-x_1{ }^2}{x_2-x_1}\)，
化简可得\(2 x_1=\dfrac{2 x_1-x_1^2}{x_2-x_1}\)，得\(x_1=0\)或\(2x_2=x_1+2\)，
\(\because 2x_1=ae^{x_2}\)，且\(a>0\)，\(\therefore x_1>0\)，
则\(2x_2=x_1+2>2\)，即\(x_2>1\)，
由\(2 x_1=a e^{x_2}\)，得\(a=\dfrac{2 x_1}{e^{x_2}}=\dfrac{4\left(x_2-1\right)}{e^{x_2}}\)，
设\(h(x)=\dfrac{4(x-1)}{e^x}(x>1)\)，则\(h^{\prime}(x)=\dfrac{4(2-x)}{e^x}\)，
\(\therefore h(x)\)在\((1，2)\)上递增，在\((2，+∞)\)上递减，
\(\therefore h(x)_{\max }=h(2)=\dfrac{4}{e^2}\)，
\(\therefore\)实数\(a\)的取值范围为\(\left(0， \dfrac{4}{e^2}\right]\)，
故答案为：\(\left(0， \dfrac{4}{e^2}\right]\)．
【题型4】综合运用
【典题1】 对任意的\(x>0\)， 总有\(f(x)=a-x-|\lg x|≤0\)， 则\(a\)的取值范围是\(\underline{\quad \quad}\).
解析 原问题即\(|\lg x |≥-x+a\)在区间\((0，+∞)\)上恒成立， 考查临界情况，
即函数\(g(x)=|\lg x|\)与\(h(x)=-x+a\)相切时的情形，很明显切点横坐标位于区间\((0，1)\)内，
此时，\(g(x)=-\lg x\)， \(g^{\prime}(x)=\dfrac{1}{x \ln 10}\)，
由\(g' (x)=-1\)可得: \(x=-\dfrac{1}{\ln 10}=-\lg e\)，
则切点坐标为:\((-\lg e，-\lg (\lg e))\)，
切线方程为：\(y+\lg (\lg e)=x+\lg e\)，
令\(x=0\)可得纵截距为：\(\lg e-\lg (\lg e)\)，
结合如图所示的函数图象可得则\(a\)的取值范围是\((-∞，\lg e-\lg (\lg e)]\).
【典题2】 直线\(y=m\)分别与曲线\(y=2(x+1)\)， 与\(y=x+\ln x\)交于点\(A\)，\(B\)，则\(|AB|\)的最小值为\(\underline{\quad \quad}\).
解析 作出曲线\(y=2(x+1)\)， 与\(y=x+\ln x\)草图如下
过\(B\)作\(BC⊥AC\)， \(|A B|=\dfrac{|B C|}{\sin 60^{\circ}}=\dfrac{|B C|}{\dfrac{\sqrt{3}}{2}}\)，
要使\(|AB|\)取到最小值， 只需\(|BC|\)取到最小值即可，
为此对\(y=x+\ln x\)进行求导得\(y'=1+\dfrac{1}{x}\)，
令\(y'=2\)， 解得\(x=1\)， 代入\(y=x+\ln x\)，知\(y=1\)，
所以当\(|BC|\)取到最小值时，\(m=1\)，
易知 \(|A B|=1-\left(-\dfrac{1}{2}\right)=\dfrac{3}{2}\).
【巩固练习】
1.已知\(M(1，0)\)，\(N\)是曲线\(y=e^x\)上一点，则\(|MN|\)的最小值为( )
A．\(1\) \(\qquad \qquad \qquad \qquad\) B．\(\sqrt{2}\) \(\qquad \qquad \qquad \qquad\) C．\(e\) \(\qquad \qquad \qquad \qquad\) D． \(\sqrt{e^4+1}\)
2.已知定义在 \(\left[\dfrac{1}{\pi}， \pi\right]\)上的函数\(f(x)\)，满足 \(f(x)=f\left(\dfrac{1}{x}\right)\)，且当\(x∈[1，π]\)时\(f(x)=\ln x\)，若函数\(g(x)=f(x)-ax\)在 \(\left[\dfrac{1}{\pi}， \pi\right]\)上有唯一的零点，则实数\(a\)的取值范围是\(\underline{\quad \quad}\).
参考答案
-
答案 \(B\)
解析 \(y=e^x\)的导数为\(y'=e^x\)．
设\(N(m，e^m)\)，可得过\(N\)的切线的斜率为\(e^m\)．
当\(MN\)垂直于切线时，\(|MN|\)取得最小值，
可得 \(\dfrac{e^m}{m-1}=-\dfrac{1}{e^m}\)，则 \(e^{2 m}+m=1\)．
因为\(f(x)=e^{2x}+x\)单调递增，且\(f(0)=1\)，所以\(m=0\)．
所以\(|MN|\)的最小值为 \(\sqrt{1^2+1^2}=\sqrt{2}\)．
故选：\(B\)． -
答案 \(\left(\dfrac{1}{e}， \pi \ln \pi\right] \cup\{0\}\).
解析 \(\because f(x)=f\left(\dfrac{1}{x}\right)\)，\(x∈[1，π]\)时\(f(x)=\ln x\)，
\(\therefore x \in\left(-\dfrac{1}{\pi}， 1\right]\)时，\(\dfrac{1}{x}∈[1，π]\)， \(f\left(\dfrac{1}{x}\right)=\ln \dfrac{1}{x}=f(x)\)，
\(f(x)=-\ln x\)，\(g(x)\)零点， 就是\(y=f(x)\))与\(y=ax\)的交点，
画出两函数图象，如图，由图知， \(k_{O A}=\pi \ln \pi\)，
过原点与\(y=\ln x\)相切的直线斜率为\(\dfrac{1}{e}\)，
所有直线与曲线有一个交点的\(a\)的范围是\(\left(\dfrac{1}{e}， \pi \ln \pi\right] \cup\{0\}\).
分层练习
【A组---基础题】
1.若函数\(y=f(x)\)的图象上存在两点，使得函数的图象在这两点处的切线互相垂直，则称\(y=f(x)\)具有\(T\)性质.下列函数中具有\(T\)性质的是( )
A. \(y=\sin x\) \(\qquad \qquad \qquad \qquad\) B. \(y=\ln x\) \(\qquad \qquad \qquad \qquad\) C. \(y=e^x\) \(\qquad \qquad \qquad \qquad\) D.\(y=x^3\)
2.若过点\(P(－1，m)\)可以作三条直线与曲线\(C:y=xe^x\)相切，则\(m\)的取值范围是( )
A．\(\left(-\dfrac{3}{e^2}，+\infty\right)\) \(\qquad \qquad\) B．\(\left(-\dfrac{1}{e}， 0\right)\) \(\qquad \qquad\) C．\((0，+∞)\) \(\qquad \qquad\) D． \(\left(-\dfrac{3}{e^2}，-\dfrac{1}{e^2}\right)\)
3.曲线\(y=e^x\)上的点到直线\(x-y-3=0\)的距离的最小值为( )
A．\(\sqrt{2}\) \(\qquad \qquad \qquad \qquad\) B．\(2\) \(\qquad \qquad \qquad \qquad\) C．\(2\sqrt{2}\) \(\qquad \qquad \qquad \qquad\) D．\(4\)
4.已知函数\(f(x)=\sin x-\cos x\)， 直线L过原点且与曲线\(y=f(x)\)相切， 其切点的横坐标从小到大依次排列为 \(x_1\)，\(x_2\)，\(x_3\)，⋯，\(x_n\)，⋯， 则下列说法正确的是 ( )
A. \(|f(x_n )|=1\) \(\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\) B.数列 \(\left\{x_n\right\}\)为等差数列
C. \(x_n=\tan \left(x_n+\dfrac{\pi}{4}\right)\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) D. \(\left[f\left(x_n\right)\right]^2=\dfrac{2 x_n^2}{x_n^2+1}\)
5.过平面内一点\(P\)作曲线\(y=|\ln x|\)两条互相垂直的切线\(l_1\)，\(l_2\)，切点为\(P_1\)，\(P_2\) (\(P_1\)，\(P_2\) 不重合)，设直线\(l_1\)，\(l_2\)分别与\(y\)轴交于点\(A\)，\(B\)，则下列结论正确的个数是( )
①\(P_1 P_2\)两点的横坐标之积为定值； ②直线\(P_1 P_2\)的斜率为定值；
③线段\(AB\)的长度为定值； ④三角形\(ABP\)面积的取值范围为\((0，1]\)．
A．\(1\) \(\qquad \qquad \qquad \qquad\) B．\(2\) \(\qquad \qquad \qquad \qquad\) C．\(3\) \(\qquad \qquad \qquad \qquad\) D．\(4\)
6.已知函数\(f(x)=\ln x-x+t\)，直线\(l:y=-\dfrac{1}{2} x+\ln 2+2\)，点\(P(x_0，f(x_0 ))\)在函数\(y=f(x)\)图像上，则以下说法正确的是( )
A．若直线\(l\)是曲线\(y=f(x)\)的切线，则\(t=-3\)
B．若直线\(l\)与曲线\(y=f(x)\)无公共点，则\(t>-3\)
C．若\(t=-2\)，则点\(P\)到直线\(l\)的最短距离为 \(\sqrt{5}\)
D．若\(t=-2\)，当点\(P\)到直线\(l\)的距离最短时，\(x_0=2\)
7.(多选)若过点\(P(-1，t)\)最多可以作出\(n(n∈N^* )\)条直线与函数 \(f(x)=\dfrac{x+1}{e^x}\)的图像相切，则( )
A．\(th\)可以等于\(2022\) \(\qquad \qquad \qquad \qquad\) B．\(n\)不可以等于\(3\)
C．\(te+n>3\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) D．\(n=1\)时， \(t \in\{0\} \cup\left(\dfrac{4}{e}，+\infty\right)\)
8.已知曲线\(y=x^2+\dfrac{5}{4}\)在点\(\left(\dfrac{1}{2}， \dfrac{3}{2}\right)\)处的切线为\(l\)，数列\(\left\{a_n\right\}\)的首项为\(1\)，点\(\left(a_n， a_{n+1}\right)\)\((n∈N^* )\)为切线\(l\)上一点，则数列\(\left\{a_n\right\}\)的前n项和为 \(\underline{\quad \quad}\) .
9.若直线\(y=kx+b\)是曲线\(y=\ln x+2\)的切线，也是曲线\(y=\ln (x+2)\)的切线，则\(b=\)\(\underline{\quad \quad}\)．
10.曲线\(y=\ln (2x-1)\)上的点到直线\(2x-y+8=0\)的最短距离是\(\underline{\quad \quad}\) .
11.设函数\(y=2x^2-2(0⩽x⩽1)\)的图象为曲线\(C\)，\(R(x_0，y_0 )\)为曲线\(C\)上任意一点过点\(R\)的直线\(PQ\)与曲线\(C\)相切，且与\(x\)轴交于点\(P\)，与\(y\)轴交于点\(Q\)．当三角形\(POQ\)的面积取得最小值时，\(x_0\)的值为 \(\underline{\quad \quad}\) .
参考答案
-
答案 \(A\)
解析 当\(y=\sin x\)时，\(y'=\cos x\)，有\(\cos 0⋅\cos π=-1\)，
所以在函数\(y=\sin x\)图象存在两点\(x=0\)，\(x=π\)使条件成立，
故\(A\)正确；
函数\(y=\ln x\)，\(y=e^x\)，\(y=x^3\)的导数值均非负，不符合题意， 故选\(A\). -
答案 \(D\)
解析 设切点为\((x_0，y_0)\)，过点\(P\)的切线方程为\(y=(x_0+1)e^{x_0} (x-x_0)+x_0 e^{x_0}\)，
代入点\(P\)坐标化简为\(m=(-x_0^2 -x_0-1)e^{x_0}\)，即这个方程有三个不等根即可，
令\(f(x)=(-x^2_0 -x_0-1)e^{x_0}\)，求导得到\(f' (x)=(-x-1)(x+2) e^x\)，
函数在\((-∞，-2)\)上单调递减，在\((-2，-1)\)上单调递增，在\((-1，+∞)\)上单调递减，
故得到\(f(-2)<m<f(-1)\)，即\(\left(-\dfrac{3}{e^2}，-\dfrac{1}{e^2}\right)\)，
故选：\(D\)． -
答案 \(C\)
解析 由\(y=e^x\)，得\(y'=e^x\)，
设曲线在\(P(x_0，e^{x_0} )\)处的切线与直线\(x-y-3=0\)平行，
则\(e^{x_0}=1\)，所以\(x_0=0\)，切点\(P(0，1)\)，
所以与已知直线平行且与曲线相切的直线为\(x-y+1=0\)，
所以曲线\(y=e^x\)上的点到直线\(x-y-3=0\)的距离的最小值为 \(d=\dfrac{|0-1-3|}{\sqrt{2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)．
故选：\(C\)． -
答案 \(D\)
解析 设直线\(L\)的方程为\(y=k_n x\)，切点为\((x_n，y_n )\)，
由导数的几何意义可得 \(\left\{\begin{array}{l} y_n=\sin x_n-\cos x_n \\ y_n=k_n x_n \\ \cos x_n+\sin x_n=k_n \end{array}\right.\)，
\(\therefore x_n=\dfrac{y_n}{k_n}=\dfrac{\sin x_n-\cos x_n}{\sin x_n+\cos x_n}=\dfrac{\tan x_n-1}{1+\tan x_n}=\tan \left(x_n-\dfrac{\pi}{4}\right)\)．故\(C\)错误．
作出\(y=x\)与\(y=\tan \left(x-\dfrac{\pi}{4}\right)\)的函数图象如图所示：
由图象可知\(\left\{x_n\right\}\)不是等差数列．故\(B\)错误．
由\(\left\{\begin{array}{l} y_n=\sin x_n-\cos x_n \\ y_n=k_n x_n \\ \cos x_n+\sin x_n=k_n \end{array}\right.\)，可得\(\left\{\begin{array}{l} y_n^2=1-2 \sin x_n \cos x_n \\ y_n^2=k_n^2 x_n^2 \\ k_n^2=1+2 \sin x_n \cos x_n \end{array}\right.\)，
\(\therefore y_n^2+k_n^2=2\)，\(\therefore k_n^2 x_n^2+k_n^2=2\)，
\(\therefore k_n^2=\dfrac{2}{x_n^2+1}\)，
\(\therefore\left[f\left(x_n\right)\right]^2=y_n^2=2-k_n^2=\dfrac{2 x_n^2}{x_n^2+1}\)，故\(A\)错误，\(D\)正确．
故选：\(D\)． -
答案 \(C\)
解析 作出曲线\(y=|\ln x|\)的图象，可知，
过平面内一点\(P\)作曲线\(y=|\ln x|\)两条互相垂直的切线\(l_1\)，\(l_2\)，
切点为\(P_1\)，\(P_2\) (\(P_1\)，\(P_2\) 不重合)，
则切点\(P_1\)的横坐标在\(x_2∈(0，1)\)，\(P_2\)的横坐标在\(x_1∈(1，+∞)\)，
当\(x∈(0，1)\)，\(y=-\ln x\)，\(y'=-\dfrac{1}{x}\)，\(\therefore k_2=-\dfrac{1}{x_2}\)，
当\(x∈(1，+∞)\)，\(y=\ln x\)，\(y'=\dfrac{1}{x}\)，\(\therefore k_1=\dfrac{1}{x_1}\)，
\(\therefore -\dfrac{1}{x_2} ×\dfrac{1}{x_1} =-1\)，\(\therefore x_1 x_2=1\)，故①正确；
直线\(P_1 P_2\)的斜率为\(\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{-\ln x_2-\ln x_1}{x_2-x_1}=-\dfrac{\ln x_1 x_2}{x_2-x_1}=0\)，故\(B\)正确；
过\(P_1\)的切线方程为\(y-y_1=\dfrac{1}{x_1}\left(x-x_1\right)\)，
令\(x=0\)，\(\therefore y=y_1-1\)，即点\(A(0，y_1-1)\)，
即同理可得\(B(0，y_2+1)\)，
\(\therefore |AB|=|y_2-y_1+2|=|-\ln x_2-\ln x_1+2|=2\)，故③正确；
由切线\(l_1\)，\(l_2\)联立解得交点\(P\)的横坐标为\(x_P=\dfrac{2 x_1 x_2}{x_1+x_2} \leqslant \dfrac{2}{2 \sqrt{x_1 x_2}}=1\)，
又因为\(P_1\)，\(P_2\)不重合，故等号不成立，
\(\therefore P\)的横坐标\(x_P∈(0，1)\)，故\(S_{\triangle A B P}=\dfrac{1}{2}|A B| \cdot\left|x_P\right| \in(0，1)\)，故④错误．
故选：\(C\)．
-
答案 \(D\)
解析 \(f' (x)=\dfrac{1}{x}-1\)，
\(A\)选项：因为直线为\(f(x)\)的切线，故\(k=-\dfrac{1}{2}\)，
故\(\dfrac{1}{x}-1=-\dfrac{1}{2}\)，解得\(x=2\)，
又\(f(2)=\ln 2-2+t\)，
故将\((2，\ln 2-2+t)\)代入直线计算可得\(t=3\)，故\(A\)选项错误；
\(B\)选项：因为\(f' (x)=\dfrac{1}{x}-1\)，
令\(f' (x)=\dfrac{1}{x}-1>0\)，解得\(0<x<1\)，
故\(f(x)\)在\((0，1)\)递增，\((1，+∞)\)递减，
故\(f(x)\)的最大值为\(f(1)=t\)，
又因为直线\(y=-\dfrac{1}{2} x+\ln 2+2\)在\(R\)上单调递减，
当\(x=1\)时，\(y=\ln 2+\dfrac{3}{2}\)，
故要使得直线与\(f(x)\)无公共点，仅需\(t<\ln 2+\dfrac{3}{2}\)，故\(B\)选项错误；
\(C\)选项：当\(t=-2\)时，\(f(x)=\ln x-x-2\)，要使得到直线距离最短，
即\(f' (x)=\dfrac{1}{x}-1=-\dfrac{1}{2}\)，解得\(x=2\)，
故\(P(2，\ln 2-4)\)，
故\(P\)点到直线的距离 \(d=\dfrac{\left|-\dfrac{1}{2} \times 2-\ln 2+4+\ln 2+2\right|}{\sqrt{\dfrac{1}{4}+1}}=2 \sqrt{5}\)，
故\(C\)选项错误；
\(D\)选项：由\(C\)选项可知距离最小时，\(P\)横坐标为\(2\)，故\(D\)选项正确．
故选：\(D\)． -
答案 \(AD\)
解析 设过点\(P(-1，t)\)的直线与函数\(f(x)=\dfrac{x+1}{e^x}\)的图像相切时的切点为\((a，b)\)，
则\(b=\dfrac{a+1}{e^a}\) ，
因为\(f(x)=\dfrac{x+1}{e^x}\)， \(f^{\prime}(x)=\dfrac{e^x-(x+1) e^x}{e^{2 x}}=-\dfrac{x}{e^x}\) ，
所以切线方程为\(y-\dfrac{a+1}{e^a}=-\dfrac{a}{e^a}(x-a)\)，
又\(P(-1，t)\)在切线上，
所以\(t-\dfrac{a+1}{e^a}=-\dfrac{a}{e^a}(-1-a)\)，整理得\(t=\dfrac{(a+1)^2}{e^a}\)，
令\(g(a)=\dfrac{(a+1)^2}{e^a}\)，
则过点\(P(-1，t)\)的直线与函数\(f(x)=\dfrac{x+1}{e^x}\)的图像相切的切线条数
即为直线\(y=t\)与曲线\(g(a)=\dfrac{(a+1)^2}{e^a}\)的图象的公共点的个数，
因为\(g^{\prime}(a)=\dfrac{2(a+1) e^a-(a+1)^2 e^a}{e^{2 a}}=\dfrac{-(a+1)(a-1)}{e^a}\)，
令\(g' (a)=0\)，得\(a=±1\)，
所以，当\(a<-1\)时，\(g' (a)<0\)，\(g(a)\)单调递减，
当\(-1<a<1\)时，\(g' (a)>0\)，\(g(a)\)单调递增，
当\(a>1\)时，\(g' (a)<0\)，\(g(a)\)单调递减，
因为\(g(-1)=0\)， \(g(1)=\dfrac{4}{e}\)，\(g(0)=1\)，
所以函数\(g(a)\)的图像大致如图：
由图可知当\(t<0\)时，直线\(y=t\)与曲线\(g(a)=\dfrac{(a+1)^2}{e^a}\)的图像没有公共点，即\(n=0\)，
当\(t=0\)或 \(t>\dfrac{4}{e}\)时，直线\(y=t\)与曲线\(g(a)=\dfrac{(a+1)^2}{e^a}\)的图像有\(1\)个公共点，即\(n=1\)，
当 \(t=\dfrac{4}{e}\)时，直线\(y=t\)与曲线\(g(a)=\dfrac{(a+1)^2}{e^a}\)的图像有\(2\)个公共点，即\(n=2\)，
当\(0<t<\dfrac{4}{e}\)时，直线\(y=t\)与曲线\(g(a)=\dfrac{(a+1)^2}{e^a}\)的图像有\(3\)个公共点，即\(n=3\)，
对于\(A\)，当 \(t=2022>\dfrac{4}{e}\)，此时\(n=1\)，则\(tn=2022\)符合题意，故\(A\)正确；
对于\(B\)，当\(0<t<\dfrac{4}{e}\)时，\(n=3\)，故\(B\)错误；
对于\(C\)，当\(t=0\)时，\(n=1\)，则\(te+n=1<3\)，故\(C\)错误；
对于\(D\)，当\(t=0\)或 \(t>\dfrac{4}{e}\)时，\(n=1\)，
则当\(n=1\)时， \(t \in\{0\} \cup\left(\dfrac{4}{e}，+\infty\right)\)，故\(D\)正确．
故选：\(AD\)． -
答案 \(\dfrac{n(n+1)}{2}\)
解析 由\(y=x^2+\dfrac{5}{4}\)，得\(y'=2x\)，则 \(y^{\prime} |_{x=\dfrac{1}{2}}=1\)，
\(\therefore\)切线 \(l: y-\dfrac{3}{2}=1 \times\left(x-\dfrac{1}{2}\right)\)，即\(y=x+1\)，
\(\because\)点 \(\left(a_n， a_{n+1}\right)\)\((n∈N^* )\)为切线\(l\)上一点，
\(\therefore a_{n+1}=a_n+1\)，
则数列\(\left\{a_n\right\}\)是首项为\(1\)，公差为\(1\)的等差数列，
\(\therefore\)数列\(\left\{a_n\right\}\)的前\(n\)项和为\(S_n=n+\dfrac{n(n-1)}{2} \times 1=\dfrac{n(n+1)}{2}\)． -
答案 \(1\)
解析 设\(y=kx+b\)与\(y=\ln x+2\)和\(y=\ln (x+2)\)的切点分别为\((x_1，kx_1+b)\)、\((x_2，kx_2+b)\)；
由导数的几何意义可得 \(k=\dfrac{1}{r}=\dfrac{1}{x+1}\)，得\(x_1=x_2+2\)，
切线方程分别为\(y-\left(\ln x_1+2\right)=\dfrac{1}{x_1}\left(x-x_1\right)\)，即为 \(y=\dfrac{x}{x_1}+\ln x_1+1\)，
或 \(y-\ln \left(x_2+2\right)=\dfrac{1}{x_2+2}\left(x-x_2\right)\)，即为 \(y=\dfrac{x}{x_1}+\dfrac{2-x_1}{x_1}+\ln x_1\)，
\(\therefore \dfrac{2-x_1}{x_1}=1\)，解得\(x_1=1\)，\(\therefore b=1\)．
故答案为\(1\)． -
答案 \(2 \sqrt{5}\)
解析 \(\because\)曲线\(y=\ln (2x-1)\)，\(\therefore y^{\prime}=\dfrac{2}{2 x-1}\)，
分析知直线\(2x-y+8=0\)与曲线\(y=\ln(2x-1)\)相切的点到直线\(2x-y+8=0\)的距离最短，
\(y^{\prime}=\dfrac{2}{2 x-1}=2\)， 解得\(x=1\)，把\(x=1\)代入\(y=\ln (2x-1)\)，
\(\therefore y=0\)，\(\therefore\)点\((1，0)\)到直线\(2x-y+8=0\)的距离最短，
\(\therefore d=\dfrac{|2+8|}{\sqrt{4+1}}=2 \sqrt{5}\). -
答案 \(\dfrac{\sqrt{3}}{3}\)
解析 由\(y=2x^2-2\)，得\(y'=4x\)，
则切线\(PQ\)的方程为\(y-(2x_0^2-2)=4x_0 (x-x_0 )\)，
化简得\(4x_0 x-y-2(x_0^2+1)=0\)，
所以 \(|O P|=\dfrac{x_0^2+1}{2 x_0}，|O Q|=2\left(x_0^2+1\right)\)，
所以三角形\(POQ\)的面积为\(\dfrac{1}{2} \cdot 2\left(x_0^2+1\right) \cdot \dfrac{x_0^2+1}{2 x_0}=\dfrac{\left(x_0^2+1\right)^2}{2 x_0}=\dfrac{1}{2}\left(x_0^3+2 x_0+\dfrac{1}{x_0}\right)\)，
令\(v=x_0^3+2x_0+\dfrac{1}{x_0}\) ，
\(u=v^{\prime}=\left(x_0^3+2 x_0+\dfrac{1}{x_0}\right)^{\prime}=3 x_0^2+2-\dfrac{1}{x_0^2}=\dfrac{3 x_0^4+2 x_0^2-1}{x_0^2}\)，
令\(x_0^2=t∈[0，1]\)，则 \(u=\dfrac{3 t^2+2 t-1}{t}\)．
令\(u=0\)，解得\(t=\dfrac{1}{3}\)或\(-1\) (舍去)，
所以当\(t \in\left[0， \dfrac{1}{3}\right)\)时，\(u<0\)， \(v=x_0^3+2 x_0+\dfrac{1}{x_0}\)单调递减；
当\(t \in\left(\dfrac{1}{3}， 1\right]\)时，\(u>0\)，\(v=x_0^3+2x_0+\dfrac{1}{x_0}\) 单调递增，
又\(x_0∈[0，1]\)，
所以当且仅当\(x_0=\dfrac{\sqrt{3}}{3}\)时，三角形\(POQ\)的面积取得最小值．
【B组---提高题】
1.若直线\(y=k_1 (x+1)-1\)与曲线\(y=e^x\)相切，直线\(y=k_2 (x+1)-1\)与曲线\(y=\ln x\)相切．则\(k_1 k_2\)的值为( )
A．\(\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) B．\(1\) \(\qquad \qquad \qquad \qquad\) C．\(e\)\(\qquad \qquad \qquad \qquad\) D．\(e^2\)
2.若曲线\(C_1：y=ax^2 (a>0)\)与曲线\(C_2：y=\ln x\)有唯一的公共点，则实数\(a\)的值为\(\underline{\quad \quad}\)．
3.已知\(a\)，\(b\)，\(c∈R\)， 且满足\(b^2+c^2=1\)， 如果存在两条相互垂直的直线与函数\(f(x)=ax+b\cos x+ c\sin x\)的图象都相切，则\(a+\sqrt{2} b+\sqrt{3} c\)的取值范围是\(\underline{\quad \quad}\) .
参考答案
-
答案 \(B\)
解析 \(y=e^x\)的导数为\(y'=e^x\)，\(y=\ln x\)的导数为\(y'=\dfrac{1}{x}\)，
设与曲线\(y=e^x\)相切的切点为\((m，n)\)，
直线\(y=k_2 (x+1)-1\)与曲线\(y=\ln x\)相切的切点为\((s，t)\)，
所以\(k_1=e^m\)， \(k_2=\dfrac{1}{s}，\)，即\(m=\ln k_1\)， \(s=\dfrac{1}{k_2}\)，
\(n=k_1=k_1 (1+\ln k_1 )-1\)，即 \(\ln k_1=\dfrac{1}{k_1}\)，
又 \(t=\ln s=-\ln k_2=k_2\left(1+\dfrac{1}{k_2}\right)-1\)，
即\(-\ln k_2=k_2\)，可得 \(e^{k_2}=\dfrac{1}{k_2}\) ，
考虑\(k_1\)\(\ln x=\dfrac{1}{x}\)为方程的根，\(k_2\)为方程\(e^x=\dfrac{1}{x}\)的根，
分别画出\(y=e^x\)，\(y=\ln x\)和\(y=\dfrac{1}{x}\)，\(y=x\)的图像，
可得\(y=e^x\)和\(y=\dfrac{1}{x}\)的交点与\(y=\ln x\)和\(y=\dfrac{1}{x}\)的交点关于直线\(y=x\)对称，
则\(k_1=\dfrac{1}{k_2}\)，即\(k_1 k_2=1\)．
故选：\(B\)．
-
答案 \(\dfrac{1}{2e}\)
解析 由\(y=ax^2\)，得\(y'=2ax\)，
由\(y=\ln x\)，得\(y^{\prime}=\dfrac{1}{x}\)，
曲线\(y=ax^2 (a>0)\)与曲线\(y=\ln x\)有唯一的公共点，
则该公共点为两曲线公切线的切点，设为\((s，t)\)，
则\(\left\{\begin{array}{l} 2 a s=\dfrac{1}{s} \\ t=a s^2 \\ t=\ln s \end{array}\right.\)，解得\(a=\dfrac{1}{2 e}\)．
故答案为：\(\dfrac{1}{2e}\)． -
答案 \([-\sqrt{5}，\sqrt{5}]\)
解析 因为\(b^2+c^2=1\)， 故可设\(b=\cos θ\)，\(c=\sin θ\)，\(θ∈[0，2π)\)，
\(\because f(x)=ax+b\cos x+c\sin x\)，
\(\therefore f' (x)=a-b\sin x+c\cos x=a-\cos θ\sin x+\sin θ\cos x=a-\sin (x-θ)\)，
\(\therefore a-1≤f' (x)≤a+1\) 且\(a-1\)，\(a+1\)异号，
\(\because\)存在两条相互垂直的直线与函数\(f(x)\)的图象都相切，
\(\therefore\)存在\(x_1\)，\(x_2\)， 使得\(f' (x_1 ) f' (x_2 )=-1\)，
只需\(|a-1||a+1|=|a^2-1|≥1\)， 即\(a^2-1≤-1\)，
\(\therefore a^2≤0\)，\(\therefore a=0\)，
\(\therefore a+\sqrt{2} b+\sqrt{3} c=\sqrt{2} b+\sqrt{3} c=\sqrt{2} \cos \theta+\sqrt{3} \sin \theta=\sqrt{5} \sin (\theta+\varphi)\)，
其中 \(\tan \varphi=\dfrac{\sqrt{2}}{\sqrt{3}}=\dfrac{\sqrt{6}}{3}\)，
\(\therefore-\sqrt{5} \leq a+\sqrt{2} b+\sqrt{3} c \leq \sqrt{5}\).
【C组---拓展题】
1.若直线\(y=k_1 x+b_1\)与直线\(y=k_2 x+b_2 (k_1≠k_2 )\)是曲线\(y=\ln x\)的两条切线，也是曲线\(y=e^x\)的两条切线，则\(k_1 k_2+b_1+b_2\)的值为\(\underline{\quad \quad}\) .
2.若实数\(a\)，\(b\)，\(c\)， \(d\)满足\(|b+a^2-4\ln a|+|2c-d+2|=0\)， 则\((a-c)^2+(b-d)^2\)的最小值为\(\underline{\quad \quad}\).
参考答案
-
答案 \(-1\)
解析 由\(y=e^x\)和\(y=\ln x\)互为反函数可知，
两条公切线\(y=k_1 x+b_1\)和\(y=k_2 x+b_2\)也互为反函数，
即\(x=\dfrac{1}{k_1} y-\dfrac{b_1}{k_1}\)满足 \(\dfrac{1}{k_1}=k_2\)， \(-\dfrac{b_1}{k_1}=b_2\)，
即\(k_1 k_2=1\)， \(b_2=-\dfrac{b_1}{k_1}\) ，
设直线\(y=k_1 x+b_1\)与\(y=e^x\)和\(y=\ln x\)分别切于点\(\left(x_1， e^{x_1}\right)\)和\((x_2，\ln x_2 )\)，
可得切线方程为\(y-e^{x_1}=e^{x_1}\left(x-x_1\right)\)和 \(y-\ln x_2=\dfrac{1}{x_2}\left(x-x_2\right)\)，
整理得：\(y=e^{x_1} x+e^{x_1}-x e^{x_1}\)和 \(y=\dfrac{1}{x_2} x-1+\ln x_2\)，
则\(k_1=e^{x_1}=\dfrac{1}{x_2}\) ， \(b_1=e^{x_1}\left(1-x_1\right)=-1+\ln x_2\)，
由\(e^{x_i}=\dfrac{1}{x_2}\) ，得 \(x_1=\ln \dfrac{1}{x_2}=-\ln x_2\)，且 \(b_1=\dfrac{1}{x_2}\left(1-x_1\right)=-1+\ln x_2\)，
则\(b_1=\dfrac{1}{x_2}\left(1-x_1\right)=-1-x_1\)，
所以\(x_2=\dfrac{1-x_1}{-1-x_1}\)，
所以 \(k_1 k_2+b_1+b_2=1+b_1-\dfrac{b_1}{k_1}=1+b_1\left(1-\dfrac{1}{k_1}\right)=1+b_1\left(1-x_2\right)\)
\(=1+\left(-1-x_1\right)\left(1-\dfrac{1-x_1}{-1-x_1}\right)=1+\left(-1-x_1\right)-\left(1-x_1\right)=-1\). -
答案 \(5\)
解析 \(\because |b+a^2-4\ln a|+|2c-d+2|=0\)，
\(\therefore b+a^2-4\ln a=0\)，\(2c-d+2=0\).
将\(b+a^2-4\ln a=0\)看成\(y+x^2-4\ln x=0\)，
即曲线\(y=-x^2+4\ln x\)，
将\(2c-d+2=0\)看成\(2x-y+2=0\)， 即直线\(y=2x+2\)，
\((a-c)^2+(b-d)^2\)表示曲线\(y=-x^2+4\ln x\)上的点与直线\(y=2x+2\)上的点间的距离的平方，
作与直线\(y=2x+2\)平行的曲线的切线，
由\(y=-x^2+4\ln x\)， 得 \(y^{\prime}=-2 x+\dfrac{4}{x}\)，
令 \(y^{\prime}=-2 x+\dfrac{4}{x}=2\)， 得\(x^2+x-2=0\)，解得\(x=1\)或\(x=-2\)(舍去)
所以切点为\((1，-1)\)，
故点\((1，-1)\)到直线\(2x-y+2=0\)的距离为 \(d=\dfrac{|2 \times 1-(-1)+2|}{\sqrt{5}}=\sqrt{5}\)，
故曲线上的点到直线的最小距离为\(\sqrt{5}\)，
\(\therefore (a-c)^2+(b-d)^2\)的最小值为\(5\).
