5.3.2(3) 导数在函数中的应用
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高二数学同步精品讲义与分层练习(人教A版2019）]
( https://www.zxxk.com/docpack/2875423.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)
选择性第二册同步巩固，难度2颗星！
基础知识
函数单调性与导数
在某个区间\((a ，b)\)内，若\(f'(x)>0\)，则函数\(y=f(x)\)在这个区间内单调递增；
若\(f'(x)<0\)，则函数\(y=f(x)\)在这个区间内单调递减．
函数增长快慢
一般地，如果一个函数在某一范围内导数的绝对值较大，那么函数在这个范围内变化得较快，这时函数的图象就比较“陡峭”（向上或向下）；反之，函数在这个范围内变化得较慢，函数的图象就比较“平缓”.
求函数的极值的方法
解方程\(f'(x)=0\)，当\(f'(x_0)=0\)时：
(1) 如果在\(x_0\)附近的左侧\(f'(x)>0\)，右侧\(f'(x)<0\)，那么\(f(x_0)\)是极大值；
(2) 如果在\(x_0\)附近的左侧\(f'(x)<0\)，右侧\(f'(x)>0\)，那么\(f(x_0)\)是极小值．
函数y=f(x)在[a，b]上的最大值与最小值的步骤
(1)求函数\(y=f(x)\)在\((a ，b)\)内的极值；
(2)将函数\(y=f(x)\)的各极值与端点处的函数值\(f(a)\)，\(f(b)\)比较，其中最大的一个是最大值，最小的一个是最小值．
基本方法
【题型1】 函数的大致图象
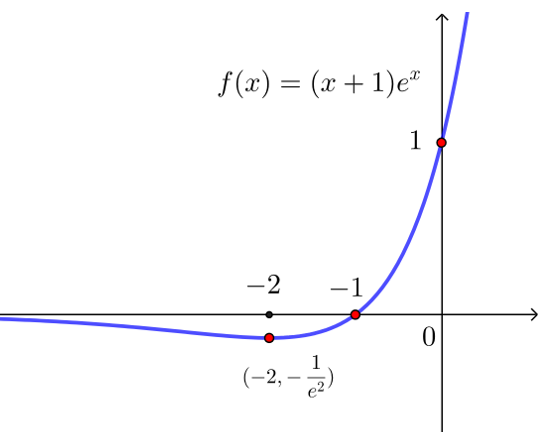
【典题1】 画出函数\(f(x)=(x+1) e^x\)的大致图象.
解析 函数的定义域为\(R\)，\(f'(x)=e^x+(x+1) e^x=(x+2) e^x\)，
当\(x>-2\)时，\(f'(x)>0\)；当\(x<-2\)时，\(f'(x)<0\)；
所以\(f(x)\)在\((-∞，-2)\)上单调递减，在\((-2，+∞)\)上单调递增，
且极小值\(f(-2)=-\dfrac{1}{e ^2}\)，过点\((-1，0)\)，\((0，1)\)，
当\(x→-∞\)时，\(y=x+1→-∞\)，\(y=e^x→0\)，
则\(f(x)=(x+1) e^x<0\)且趋向于\(0\)，
当\(x→+∞\)时，\(f(x)=(x+1) e^x→+∞\)，\(f'(x)→+∞\)，
根据以上信息，可画出函数\(f(x)=(x+1) e^x\)的大致图象如下：
点拨
1.画函数\(y=f(x)\)在区间\((a，b)\)上的大致图象步骤：
① 求函数单调性，再求极值与最值；
② 求出一些关键点，比如函数零点等；
③ 确定当\(x→a\)，\(x→b\)时，函数值的变化.
2.函数增长快慢：导函数的绝对值\(|f'(x)|\)大小决定函数\(f(x)\)的增长快慢.
3.类似“当\(x\)趋向某值时，函数值y会怎么变化”的问题，要注意函数的类型及其增长的快慢；
比如对于\(y=e^x\)，当\(x→0\)时，\(y→e^0=1\)(函数\(y=e^x\)能取到\(0\)，直接代入便可)；
当\(x→-∞\)时，\(y→0\)(可想象下\(x\)取一很小的负数\(-10000\)，对应函数值 \(y=\dfrac{1}{e^{10000}}\)很小)；
对于函数 \(y=\dfrac{\ln x}{x^2}\)，当\(x→+∞\)时，分母\(x^2→+∞\)，分子\(\ln x→+∞\)，那 \(\dfrac{\ln x}{x^2}\)趋向什么呢？
因为函数\(y=\ln x\)较函数\(y=x^2\)在\((0，+∞)\)增长得慢很多，所以当\(x→+∞\)时， \(\dfrac{\ln x}{x^2} \rightarrow 0\).
4.我们在解题中会经常遇到如下的六个超越函数，掌握它们的图象及性质便于找到解题思路与提高解题速度：
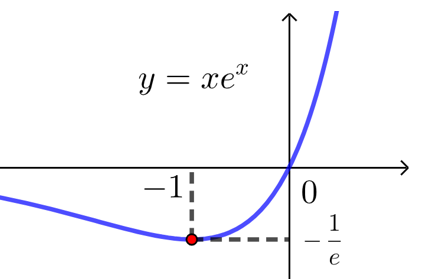
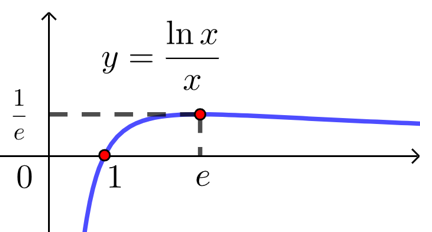
| 函数 | \(f(x)=x\cdot \ln x\) | \(f(x)=x\cdot e^x\) | \(f(x)=\dfrac{\ln x}{x}\) |
|---|---|---|---|
| 图象 |  |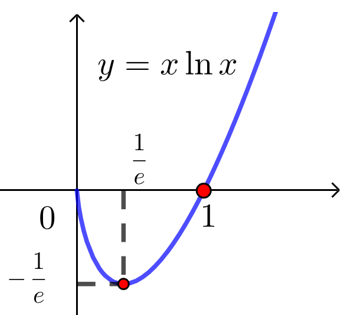
 |
 |
| 函数 | \(f(x)=\dfrac{x}{\ln x}\) | \(f(x)=\dfrac{e^x}{x}\) | \(f(x)=\dfrac{x}{e^x}\) |
| 图象 |  |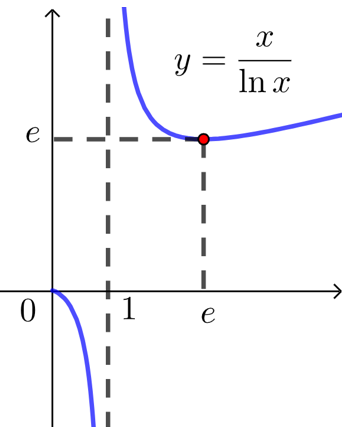
 |
 |
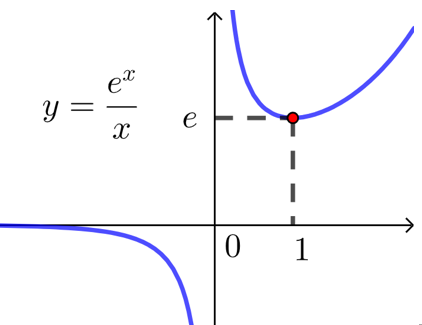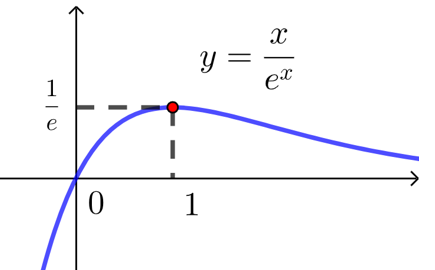【巩固练习】
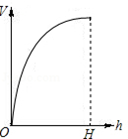
1.向高为\(H\)的水瓶中注水，注满为止，如果注水量\(V\)与水深\(H\)的函数关系的图象如上图所示，那么水瓶的形状是( )
A．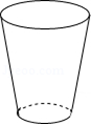
\(\qquad \qquad\) B．
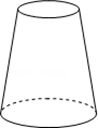\(\qquad \qquad\) C． 
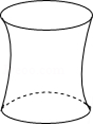\(\qquad \qquad\) D．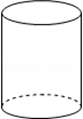 
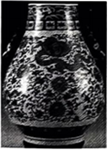
2.青花瓷，又称白地青花瓷，常简称青花，是中国瓷器的主流品种之一．如图，这是景德镇青花瓷，现往该青花瓷中匀速注水，则水的高度\(y\)与时间\(x\)的函数图象大致是( )
A．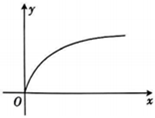
\(\qquad \qquad \qquad\) B．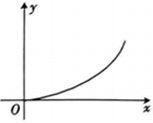
C．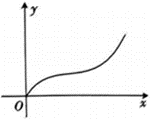
\(\qquad \qquad \qquad\) D． 
3.画出函数\(f(x)=\dfrac{e^x}{x}\)的大致图象.
参考答案
-
答案 \(B\)
解析 因为高度不是均匀上升的，应排除\(D\)；图象中没有出现对称情况，应排除\(C\)；随着\(V\)的不断增加，\(H\)的改变越来越快，图象应是越来越窄．
故选：\(B\)． -
答案 \(C\)
解析 由图可知，青花瓷上下细，中间粗，则在一定时间匀速注水过程中，水的高度先一直增高，且开始时水的高度增高得速度越来越慢，到达青花瓷最粗处之后，水的高度增高得越来越快，结合选项可知，选项\(C\)符合题意．
故选：\(C\)． -
答案
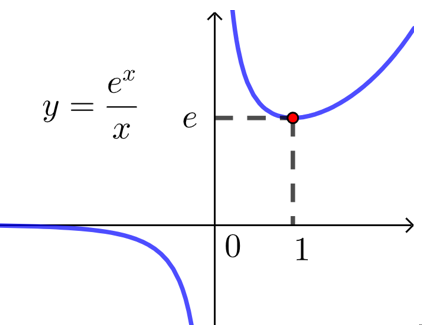
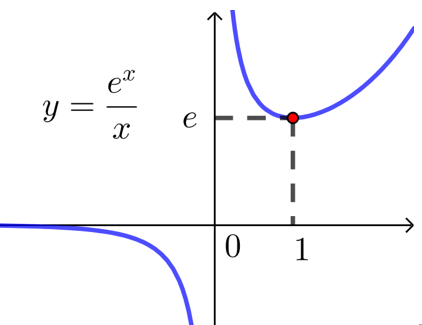
解析 函数的定义域为\(\{x|x≠0\}\)， \(f^{\prime}(x)=\dfrac{(x-1) e^x}{x^2}\)，
当\(x<0\)时，\(f'(x)<0\)；当\(0<x<1\)时，\(f'(x)<0\)；当\(x>1\)时，\(f'(x)>0\)；
所以\(f(x)\)在\((-∞，0)\)，\((0，1)\)上单调递减，在\((1，+∞)\)上单调递增，且极小值\(f(1)=e\)，
当\(x→-∞\)时， \(f(x)=\dfrac{e^x}{x} \rightarrow 0\)；当\(x<0\)且\(x→0\)时， \(f(x)=\dfrac{e^x}{x} \rightarrow-\infty\)；
当\(x>0\)且\(x→0\)时， \(f(x)=\dfrac{e^x}{x} \rightarrow+\infty\)；
根据以上信息，可画出函数\(f(x)=\dfrac{e^x}{x}\)的大致图象如下：
【题型2】 函数零点个数
【典题1】 若\(f(x)=x^3-3ax+a(a\in R)\)仅有一个零点，求\(a\)的取值范围.
解析 因为\(f(x)=x^3-3ax+a(a\in R)\)，
所以\(f'(x)=3x^2-3a=3(x^2-a)\)．
①当\(a⩽0\)时，\(f'(x)⩾0\)恒成立，
\(f(x)\)在\(R\)上单调递增，易知其有\(1\)个零点，满足题意；
②当\(a>0\)时，\(x\in (-∞，-\sqrt{a})∪(\sqrt{a}，+∞)\)时，\(f'(x)>0\)；
\(x\in (-\sqrt{a}，\sqrt{a})\)时，\(f'(x)<0\)；
故\(f(x)\)在\((-∞，-\sqrt{a})\)和\((\sqrt{a}，+∞)\)上单调递增，在\((-\sqrt{a}，\sqrt{a})\)上单调递减，
而\(f(-\sqrt{a})=2 a \sqrt{a}+a>0\)，\(f(\sqrt{a})=-2a\sqrt{a}+a\)，
由题意知：\(f(x)\)仅有\(1\)个零点，
所以\(f(\sqrt{a})=-2a\sqrt{a}+a>0\)，即\(0<a<\dfrac{1}{4}\)．
综上，\(a\)的取值范围为 \(\left(-\infty， \dfrac{1}{4}\right]\)．
【典题2】 已知函数\(f(x)=\dfrac{1}{x} +a\ln x-a-1\)，\(a\in R\)．
(1)讨论函数\(f(x)\)的单调性；\(\qquad \qquad\) (2)讨论函数\(f(x)\)的零点个数．
解析 \(f^{\prime}(x)=-\dfrac{1}{x^2}+\dfrac{a}{x}=\dfrac{a x-1}{x^2}\) ，
当\(a≤0\)时，\(f'(x)<0\)，故\(f(x)\)在\((0，+∞)\)上单调递减，
当\(a>0\)时，\(f'(x)>0⇒x>\dfrac{1}{a}\)，
\(f(x)\)在 \(\left(0， \dfrac{1}{a}\right)\)上单调递减，在 \(\left(\dfrac{1}{a}，+\infty\right)\)上单调递增．
(2)当\(a≤0\)时， \(f\left(\dfrac{1}{e}\right)=e-2 a-1 \geq e-1>0\)，\(f(e)=\dfrac{1}{e} -1<0\)，
\(f(x)\)有唯一零点；
当\(a>0\)时，\(f(1)=-a<0\)，
由\(e^x≥x+1\)知 \(e^{-a-1}<\dfrac{1}{a}\)， \(e^{1+\frac{1}{a}}>\dfrac{1}{a}\) ，
\(f\left(e^{1+\frac{1}{a}}\right)>\dfrac{1}{1+\frac{1}{a}}+a\left(1+\frac{1}{a}\right)-a-1>0\)，
\(f\left(e^{-a-1}\right)=e^{a+1}-(a+1)^2\)，
令\(g(t)=e^t-t^2\)，则\(g'(t)=e^t-2t\)，\(g'' (t)=e^t-2\)，
当\(t>1\)时，\(g'' (t)>e-2>0\)，\(\therefore g'(t)\)单调递增，
\(\therefore g'(t)>g'(1)=e-2>0\)，\(\therefore g(t)\)单调递增，
\(\therefore g(t)>g(1)=e-1>0\)，故 \(f\left(e^{-\alpha-1}\right)>0\)，
\(\therefore f(x)\)在 \(\left(0， \dfrac{1}{a}\right)\)和 \(\left(\dfrac{1}{a}，+\infty\right)\)内各有一个零点．
综上，当\(a≤0\)时\(f(x)\)有一个零点，当\(a>0\)时\(f(x)\)有两个零点．
【巩固练习】
1.已知函数\(f(x)=x^3+ax^2-6x+b(b>0)\)在\(x=2\)处的切线与x轴平行．
(1)求\(f(x)\)在区间\([-2，4]\)上的最值；
(2)若\(f(x)\)恰有两个零点，且\(f(x)⩾c+10\)在\((0，+∞)\)时恒成立，求实数\(c\)的取值范围．
2.已知函数\(f(x)=\dfrac{a \ln x}{x}-\dfrac{1}{2} x+a-1(a \in R)\)，记\(g(x)=xf(x)\)．
(1)当\(a<1\)时，求\(g(x)\)在区间\([1，3]\)上的最大值；
(2)当\(a=2\)时，试判断\(f(x)\)的零点个数．
3.设函数\(f(x)=x^2-(a-2)x-a\ln x\)．
(1)求函数的单调区间；
(2)若函数\(f(x)\)有两个零点，求正整数\(a\)的最小值．
参考答案
- 答案 (1)最小值为\(-10+b\)，最大值为\(16+b\)；(2)\(c⩽-10\) .
解析 (1)依题意，\(f'(x)=3x^2+2ax-6\)由已知\(f'(2)=0\)，
即\(12+4a-6=4a+6=0\)，解得\(a=-\dfrac{3}{2}\)．
所以\(f'(x)=3x^3-3x-6=3(x+1)(x-2)\)．
| \(x\) | \(-2\) | \((-2，-1)\) |
\(-1\) | \((-1，2)\) |
\(2\) | \((2，4)\) |
\(4\) |
|---|---|---|---|---|---|---|---|
| \(f'(x)\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) | ||
| \(f(x)\) | \(-2+b\) | 递增 | \(\dfrac{7}{2}+b\) | 递减 | \(-10+b\) | 递增 | \(16+b\) |
由上表可知\(f(x)\)的最小值为\(-10+b\)，最大值为\(16+b\)．
(2)由(1)知\(f(x)\)的极大值点为\(x=-1\)，
因为\(b>0\)，所以\(f(x)\)的极大值\(f(-1)=b+\dfrac{7}{2}>0\)，
故若\(f(x)\)恰有两个零点，则\(f(x)\)的极小值\(f(2)=b-10=0\)．
由(1)\(y=f(x)\)在\((0，+∞)\)上的最小值为\(0\)．
即有\(0⩾c+10\)．所以\(c⩽-10\)．
-
答案 (1)\(a-\dfrac{3}{2}\) ；(2)\(2\).
解析 (1)由题意知，\(g(x)=xf(x)=a\ln x-\dfrac{1}{2} x^2+(a-1)x(1⩽x⩽3)\)，
则 \(g^{\prime}(x)=\dfrac{a}{x}-x+a-1=\dfrac{-x^2+(a-1) x+a}{x}=\dfrac{(-x+a)(x+1)}{x}\)，
当\(a<1\)且\(1⩽x⩽3\)时，\(g'(x)<0\)恒成立，
从而\(g(x)\)在\([1，3]\)单调递减，
故\(g(x)\)的最大值为\(g(1)=a-\dfrac{3}{2}\)．
(2)由题意知，判断\(f(x)\)的零点个数，即判断\(g(x)\)的零点个数，
当\(a=2\)时，\(g(x)=2\ln x-\dfrac{1}{2} x^2+x(x>0)\)，
\(g^{\prime}(x)=\dfrac{2}{x}-x+1=\dfrac{(-x+2)(x+1)}{x}\)，
由\(g'(x)=0\)得\(x=2\)，
所以当\(x\in (0，2)\)时，\(g'(x)>0\)，\(g(x)\)单调递增；
当\(x\in (2，+∞)\)时，\(g'(x)<0\)，\(g(x)\)单调递减，
所以\(x=2\)是\(g(x)\)唯一的极值点且为极大值点，
故 \(g_{\max }(x)=g(2)=2 \ln 2>0\)，
又\(g\left(\dfrac{1}{e}\right)=-2-\dfrac{1}{2 e^2}-\dfrac{1}{e}<0\)，
\(g\left(e^2\right)=4-\dfrac{1}{2} e^4+e^2=-\dfrac{1}{2}\left(e^2-1\right)^2+\dfrac{9}{2}<0\)，
由零点的存在性定理知，\(g(x)\)在\(\left(\dfrac{1}{e}， 2\right)\)和\((2，e^2 )\)上分别有一个零点，
故\(f(x)\)有\(2\)个零点． -
答案 (1) 单调增区间为\(\left(\dfrac{a}{2}，+\infty\right)\)，单调减区间为\(\left(0， \dfrac{a}{2}\right)\)；(2) \(3\).
解析 (1) \(f^{\prime}(x)=2 x-(a-2)-\dfrac{a}{x}=\dfrac{2 x^2-(a-2) x-a}{x}=\dfrac{(2 x-a)(x+1)}{x}(x>0)\)，
当\(a⩽0\)时，\(f'(x)>0\)，函数\(f(x)\)在区间\((0，+∞)\)内单调递增，
所以函数\(f(x)\)的单调增区间为\((0，+∞)\)，无单调减区间；
当\(a>0\)时，由\(f'(x)>0\)，得\(x>\dfrac{a}{2}\)；由\(f'(x)<0\)，得\(0<x<\dfrac{a}{2}\)．
所以函数\(f(x)\)的单调增区间为\(\left(\dfrac{a}{2}，+\infty\right)\)，单调减区间为\(\left(0， \dfrac{a}{2}\right)\)，
(2)由(1)知：如果函数\(f(x)\)有两个零点，则\(a>0\)，且 \(f\left(\dfrac{a}{2}\right)<0\)，
即\(-a^2+4a-4a\ln \dfrac{a}{2}<0\)，即\(a+4\ln \dfrac{a}{2}-4>0\)，
令\(h(a)=a+4\ln \dfrac{a}{2}-4\)，
可知\(h(a)\)在区间\((0，+∞)\)内为增函数，
且\(h(2)=-2<0\)， \(h(3)=4 \ln \dfrac{3}{2}-1=\ln \dfrac{81}{16}-1>0\)，
所以存在\(a_0\in (2，3)\)，\(h(a_0 )=0\)，
当\(a>a_0\)时，\(h(a)>0\)；当\(0<a<a_0\)时，\(h(a)<0\)．
所以，满足条件的最小正整数\(a=3\)．
又当\(a=3\)时，\(f(x)=x^2-x-3\ln x\)．
\(f(x)\)在\(\left(0， \dfrac{3}{2}\right)\)上单调递减，在\(\left(\dfrac{3}{2}，+\infty\right)\)上单调递增，
\(f(1)=0\)，\(f\left(\dfrac{3}{2}\right)<0\)，\(f(e)=e^2-e-3>e^2-6>0\)，
所以存在唯一 \(x_0 \in\left(\dfrac{3}{2}， e\right)\)，使得\(f(x_0 )=0\)，
所以\(f(x)\)有两个零点，\(a=3\)符合题意，
综上所述，正整数\(a\)的最小值为\(3\)．
【题型3】生活问题应用
【典题1】 如图所示，\(ABCD\)是边长\(AB=24cm\)，\(AD=9cm\)的矩形硬纸片，在硬纸片的四角切去边长相等的小正方形后，再沿虚线折起，做成一个无盖的长方体盒子，\(M\)、\(N\)是\(AB\)上被切去的小正方形的两个顶点，设\(AM=x(cm)\)．
(1)将长方体盒子体积\(V(cm^3 )\)表示成\(x\)的函数关系，并求其定义域；
(2)当\(x\)为何值时，此长方体盒子体积\(V(cm^3 )\)最大？并求出最大体积．
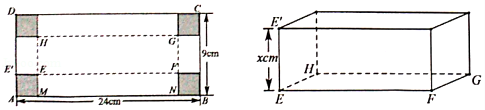
解析 长方体盒子长\(EF=(24-2x)cm\)，宽\(FG=(9-2x)cm\)，高\(EE'=xcm\)．
(1)长方体盒子体积\(V=x(24-2x)(9-2x)\)，
由 \(\left\{\begin{array}{l}
x>0 \\
24-2 x>0 \\
9-2 x>0
\end{array}\right.\)，得\(0<x<\dfrac{9}{2}\)，故定义域为\(\left(0， \dfrac{9}{2}\right)\)．
(2)长方体盒子体积\(V=x(24-2x)(9-2x)=2(2x^3-33x^2+12×9x)\)
由\(V'=2(6x^2-66x+12×9)=12(x^2-11x+2×9)=0\)
得\(x=2 \in\left(0， \dfrac{9}{2}\right)\)， \(x=9 \notin\left(0， \dfrac{9}{2}\right)\) (舍去)
\(\therefore V\)在\((0，2)\)单增，在\(\left(2， \dfrac{9}{2}\right)\)单减，
\(\therefore V\)在\(x=2\)取得极大值也是最大值．此时\(V=200cm^3\)．
故当\(x=2\)时长方体盒子体积\(V(cm^3 )\)最大，此时最大体积为\(200cm^3\)．
点拨 处理实际问题要注意不要忽略自变量的取值范围.
【巩固练习】
1.一船在航行中的燃料费与其速度\(v\)的立方成正比，已知\(v=10km/h\)时燃料费是\(6\)元 \(/h\)，而其他与\(v\)无关的费用是\(96\)元 \(/h\)，问\(v\)为何值时可使航行每公里所需费用的总和最小？
2.如图，某景区内有两条道路\(AB\)，\(AP\)，现计划在\(AP\)上选择一点\(C\)，新建道路\(BC\)，并把\(△ABC\)所在的区域改造成绿化区域．已知\(∠BAC=\dfrac{\pi}{6}\)，\(AB=2km\)，\(AP=2\sqrt{3} km\)．若绿化区域\(△ABC\)改造成本为\(10\)万元\(/km^2\)，新建道路\(BC\)成本为\(10\)万元\(/km\)．
(1)①设\(∠ABC=θ\)，写出该计划所需总费用\(F(θ)\)的表达式，并写出\(θ\)的范围；
②设\(AC=x\)，写出该计划所需总费用\(F(x)\)的表达式，并写出\(x\)的范围；
(2)从上面两个函数关系中任选一个，求点\(C\)在何处时改造计划的总费用最小．
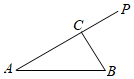
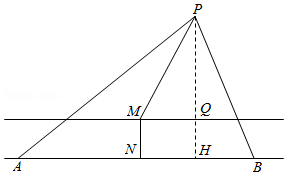
3.如图，一条小河岸边有相距\(8km\)的\(A\)，\(B\)两个村庄(村庄视为岸边上\(A\)，\(B\)两点)，在小河另一侧有一集镇\(P\)(集镇视为点\(P\))，\(P\)到岸边的距离\(PQ\)为\(2km\)，河宽\(OH\)为\(0.05km\)，通过测量可知，\(∠PAB\)与\(∠PBA\)的正切值之比为\(1:3\)．当地政府为方便村民出行，拟在小河上建一座桥\(MN\)(\(M\)，\(N\)分别为两岸上的点，且\(MN\)垂直河岸，\(M\)在\(Q\)的左侧)，建桥要求：两村所有人到集镇所走距离之和最短，已知\(A\)，\(B\)两村的人口数分别是\(1000\)人、\(500\)人，假设一年中每人去集镇的次数均为\(m\)次．设\(∠PMQ=θ\)．(小河河岸视为两条平行直线)
(1)记\(L\)为一年中两村所有人到集镇所走距离之和，试用\(θ\)表示\(L\)；
(2)试确定\(θ\)的余弦值，使得\(L\)最小，从而符合建桥要求．
参考答案
-
答案 \(20\)公里/小时
解析 设船速度为\(x(x>0)\)时，燃料费用为\(Q\)元，则\(Q=kx^3\)，
由\(6=k×10^3\)可得 \(k=\dfrac{3}{500}\)， \(\therefore Q=\dfrac{3}{500} x^3\)，
\(\therefore\)总费用 \(y=\left(\dfrac{3}{500} x^3+96\right) \cdot \dfrac{1}{x}=\dfrac{3}{500} x^2+\dfrac{96}{x}\)，
\(\therefore y^{\prime}=\dfrac{6}{500} x-\dfrac{96}{x^2}\) ，令\(y'=0\)得\(x=20\)，
当\(x\in (0，20)\)时，\(y'<0\)，此时函数单调递减，
当\(x\in (20，+∞)\)时，\(y'>0\)，此时函数单调递增，
\(\therefore\)当\(x=20\)时，\(y\)取得最小值，
答：此轮船以\(20\)公里/小时的速度使行驶每公里的费用总和最小． -
答案 (1) \(F(x)=10 \times\left(\dfrac{1}{2} x+\sqrt{x^2+4-2 \sqrt{3} x}\right)(0<x \leqslant 2 \sqrt{3})\)；
(2) \(A C=\dfrac{2 \sqrt{3}}{3}\)时，改造计划的总费用最小.
解析 (1)设\(∠ABC=θ\)，
由正弦定理得， \(\dfrac{A C}{\sin \theta}=\dfrac{2}{\sin \left(\dfrac{5 \pi}{6}-\theta\right)}=\dfrac{B C}{\sin \dfrac{\pi}{6}}\)，
\(\therefore B C=\dfrac{1}{\sin \left(\dfrac{5 \pi}{6}-\theta\right)}\)， \(A C=\dfrac{2 \sin \theta}{\sin \left(\dfrac{5 \pi}{6}-\theta\right)}\)， \(F(\theta)=\dfrac{10 \sin \theta+10}{\sin \left(\dfrac{5 \pi}{6}-\theta\right)}\) ，
当点\(C\)与点\(P\)重合的时候，\(θ=\dfrac{2\pi}{3}\) ，所以 \(\theta \in\left(0， \dfrac{2 \pi}{3}\right]\)．
设\(AC=x\)， \(B C=\sqrt{x^2+4-2 \sqrt{3} x}\)，
\(F(x)=10 \times\left(\dfrac{1}{2} x+\sqrt{x^2+4-2 \sqrt{3} x}\right)(0<x \leqslant 2 \sqrt{3})\)．
(2) \(F(\theta)=\dfrac{20 \sin \theta+20}{\cos \theta+\sqrt{3} \sin \theta}\)，
则\(F^{\prime}(\theta)=\dfrac{20 \cos \theta(\cos \theta+\sqrt{3} \sin \theta)-(20 \sin \theta+20)(-\sin \theta+\sqrt{3} \cos \theta)}{(\cos \theta+\sqrt{3} \sin \theta)^2}\)\(=\dfrac{40 \sin \left(\theta-\dfrac{\pi}{3}\right)+20}{(\cos \theta+\sqrt{3} \sin \theta)^2}\)，
因为\(F'(θ)=0\)，且\(\theta-\dfrac{\pi}{3} \in\left[-\dfrac{\pi}{3}， \dfrac{\pi}{3}\right]\)，所以\(θ=\dfrac{\pi}{6}\)，
当\(\theta \in\left(0， \dfrac{\pi}{6}\right)\)时，\(F'(θ)<0\)，\(F(θ)\)单调递减；
当\(\theta \in\left(\dfrac{\pi}{6}， \dfrac{2 \pi}{3}\right)\)时，\(F'(θ)>0\)，\(F(θ)\)单调递增．
所以当\(θ=\dfrac{\pi}{6}\) ，即\(A C=\dfrac{2 \sqrt{3}}{3}\)时，改造计划的总费用最小． -
答案 (1)\(L=7075 m+1000 m\left(\dfrac{3}{\sin \theta}-\dfrac{1}{\tan \theta}\right)\)，\(\theta \in\left(0， \dfrac{\pi}{2}\right)\) ；(2)\(\cos \theta=\dfrac{1}{3}\).
解析 (1)因\(∠PAB\)与\(∠PBA\)的正切值之比为\(1:3\)，
所以\(\dfrac{P H}{H A}: \dfrac{P H}{H B}=1: 3\)，
所以\(HB:HA=1:3\)，即\(AH=6\)，\(HB=2\)，
因\(PQ=2\)，所以 \(P M=\dfrac{2}{\sin \theta}\)， \(M Q=\dfrac{2}{\tan \theta}\) ，
所以\(L=1000(AN+MN+MP)+500(BN+MN+MP)\)，
所以\(L=1000 m\left(6-\dfrac{2}{\tan \theta}+0.05+\dfrac{2}{\sin \theta}\right)+500 m\left(2+\dfrac{2}{\tan \theta}+0.05+\dfrac{2}{\sin \theta}\right)\)，
化简得 \(L=7075 m+1000 m\left(\dfrac{3}{\sin \theta}-\dfrac{1}{\tan \theta}\right)\)， \(\theta \in\left(0， \dfrac{\pi}{2}\right)\)．
(2)由(1)知\(L=7075 m+1000 m\left(\dfrac{3-\cos \theta}{\sin \theta}\right)\)，
所以\(L^{\prime}=1000 m \cdot \dfrac{(3-\cos \theta)^{\prime} \sin \theta-(3-\cos \theta)(\sin \theta)^{\prime}}{\sin ^2 \theta}\)，
化简得\(L^{\prime}=1000 m \cdot \dfrac{1-3 \cos \theta}{\sin ^2 \theta}\)，
由\(L'=0\)，得\(\cos θ=\dfrac{1}{3}\)，
令\(\cos θ_0=\dfrac{1}{3}\)，且 \(\theta_0 \in\left(0， \dfrac{\pi}{2}\right)\)，
当\(θ\in (0，θ_0 )\)时，\(\cos θ>\dfrac{1}{3}\)，\(L'<0\)；
当 \(\theta \in\left(\theta_0， \dfrac{\pi}{2}\right)\)时，\(\cos θ<\dfrac{1}{3}\)，\(L'>0\)；
所以函数\(L(θ)\)在\((0，θ_0 )\)上单调递减；在\(\left(\theta_0， \dfrac{\pi}{2}\right)\)上单调递增；
所以\(θ=θ_0\)时函数\(L(θ)\)取最小值，即当\(\cos θ=\dfrac{1}{3}\)时，符合建桥要求，
答：(1) \(L=7075 m+1000 m\left(\dfrac{3}{\sin \theta}-\dfrac{1}{\tan \theta}\right)\)， \(\theta \in\left(0， \dfrac{\pi}{2}\right)\) ；
(2)当 \(\cos \theta=\dfrac{1}{3}\)时，符合建桥要求．
分层练习
【A组---基础题】
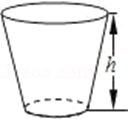
1.向如图所示的高为\(H\)的水杯中注水，注满为止，那么注水量\(V\)与水深\(h\)的函数关系的图象是( )
A．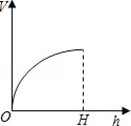
\(\qquad\) B．
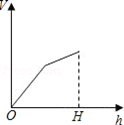\(\qquad\) C．
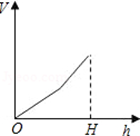\(\qquad\) D．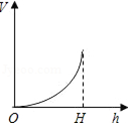 
2.函数 \(f(x)=-\dfrac{x}{\mathrm{e}^x}\)的图象大致是( )
A.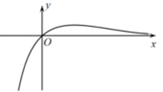 
\(\qquad\) B. 
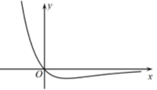\(\qquad\) C. 
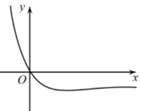\(\qquad\) D.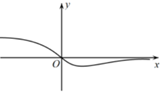 
3.画出函数\(f(x)=\dfrac{\ln x}{x}\)的大致图象.
4.某分公司经销某种品牌产品，每件产品的成本为\(30\)元，并且每件产品需向总公司缴纳\(5\)元的管理费，根据多年的管理经验，预计当每件产品的售价为\(x\)元时，产品一年的销售量为\(\dfrac{k}{e^x}\) (\(e\)为自然对数的底数)万件．已知每件产品的售价为\(40\)元时，该产品的一年销售量为\(500\)万件，经物价部门核定每件产品的售价\(x\)最低不低于\(35\)元，最高不超过\(41\)元．
(1)求\(k\)的值；
(2)求分公司经营该产品一年的利润\(L(x)\)(万元)与每件产品的售价\(x\)(元 的函数关系式；
(3)当每件产品的售价为多少元时，分公司一年的利润\(L(x)\)最大，并求出\(L(x)\)的最大值．
5.如图：已知某公园的四处景观分别位于等腰梯形\(ABCD\)的四个顶点处，其中\(A\)，\(B\)两地的距离为\(4\)千米，\(C\)，\(D\)两地的距离为\(2\)千米，\(∠DAB=∠B=60^∘\)．现拟规划在\(CD\) (不包括端点)路段上增加一个景观\(P\)，并建造观光路直接通往\(A\)处，造价为每千米\(10\)万元，又重新装饰\(PC\)路段，造价为每千米\(8\)万元．
(1)若拟修建观光路\(AP\)路段长为 \(\sqrt{7}\)千米，求\(PC\)路段的造价；
(2)设\(∠BAP=θ\)，当\(\cos θ\)为何值时，\(AP\)，\(PC\)段的总造价最低．
6.已知函数\(f(x)=ax^2+x-\ln x(a\in R)\)．
(1)当\(a=1\)时，求\(f(x)\)在区间 \(\left[\dfrac{1}{3}， 1\right]\)上的最值；
(2)若\(g(x)=f(x)-x\)在定义域内有两个零点，求\(a\)的取值范围．
7.已知函数\(f(x)=-\dfrac{1}{3} x^3+ax^2+3a^2 x-\dfrac{5}{3}\)．
(1)若\(a=-1\)时，求\(f(x)\)在区间\([-4，2]\)上的最大值与最小值；
(2)若函数\(f(x)\)仅有一个零点，求实数\(a\)的取值范围．
参考答案
-
答案 \(D\)
解析 根据图形的形状可知，注水量增加的越来越多．故选：\(D\)． -
答案 \(B\)
解析 函数 \(f(x)=-\dfrac{x}{\mathrm{e}^x}\)的定义域为\(R\)，\(x>0\)时\(f(x)<0\)，排除\(A\)；
\(f^{\prime}(x)=\dfrac{x-1}{\mathrm{e}^x}\)，当\(x<1\)时，\(f'(x)<0\)，当\(x>1\)时，\(f'(x)>0\)，
所以\(f(x)\)在\((-∞，1)\)递减，在\((1，+∞)\)递增，
且\(x→-∞\)时，\(f(x)→+∞\)，\(x→+∞\)时，\(f(x)→0\)，
故选\(B\). -
答案
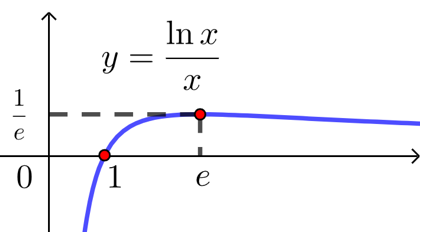
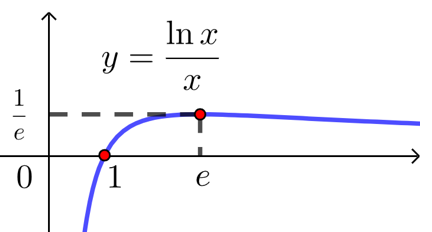
解析 函数的定义域为 \(\{x \mid x>0\}\)， \(f^{\prime}(x)=\dfrac{1-\ln x}{x^2}\) ，
当\(0<x<e\)时，\(f'(x)>0\)；当\(x>e\)时，\(f'(x)<0\)；
所以\(f(x)\)在\((0，e)\)上单调递减，在\((e，+∞)\)上单调递增，且极大值\(f(e)=\dfrac{1}{e}\)，
当\(x→0\)时， \(f(x)=\dfrac{\ln x}{x} \rightarrow-\infty\)；当\(x→+∞\)时， \(f(x)=\dfrac{\ln x}{x} \rightarrow 0\)；
根据以上信息，可画出函数\(f(x)=\dfrac{\ln x}{x}\)的大致图象如下：
-
答案 (1) \(500e^{40}\)；(2) \(L(x)=500(x-35) e^{40-x}(35 \leqslant x \leqslant 41)\)；(3) \(500e^4\) .
解析 (1)由题意，该产品一年的销售量为 \(y=\dfrac{k}{e^x}\) ，
将\(x=40\)，\(y=500\)代入得 \(k=500 e^{40}\)．
(2)由(1)知该产品的销售量为 \(y=500 e^{40-x}\)，
所以 \(L(x)=(x-30-5) y=500(x-35) e^{40-x}(35 \leqslant x \leqslant 41)\)．
(3)由(2)知， \(L^{\prime}(x)=500\left[e^{40-x}-(x-35) e^{40-x}\right]=500 e^{40-x}(36-x)(35 \leqslant x \leqslant 41)\)，
所以在\((35，36)\)上，\(L'(x)>0\)，\(L(x)\)单调递增，
在\((36，41)\)上，\(L'(x)<0\)，\(L(x)\)单调递减，
所以 \(L(x)_{\max }=L(36)=500 e^4\)． -
答案 (1) \(8\)；(2) 当\(\cos θ=\dfrac{4}{5}\) 时，\(AP\)，\(PC\)段的总造价最低.
解析 (1)作\(ED⊥AB\)，\(CF⊥AB\)，垂足分别为\(E\)，\(F\)，
则有\(DC=EF\)，所以\(AE=BF=1\)，所以\(AD=2\)．
设\(PD=x\)，
在三角形\(APD\)中，由余弦定理\(AP^2=AD^2+PD^2-2AD⋅DP⋅\cos ∠ADP\)
得到\(7=4+x^2-4x\cos 120^∘\)，整理得到\(x^2+2x-3=0\)，
所以\(x=1\)或\(x=-3\)(舍) ，所以\(PC=1\)，\(PC\)段造价为\(8\)万元．
答：\(PC\)段造价为\(8\)万元．
(2)因为在三角形\(APD\)中，\(∠APD=∠PAB=θ\)，\(∠ADP=120^∘\)，
所以\(∠DAB=60^∘-θ\)，
由正弦定理得， \(\dfrac{A P}{\sin \angle A D P}=\dfrac{A D}{\sin \theta}=\dfrac{P D}{\sin \left(60^{\circ}-\theta\right)}\)，
所以\(A P=\dfrac{\sqrt{3}}{\sin \theta}\)， \(P D=\dfrac{2 \sin \left(60^{\circ}-\theta\right)}{\sin \theta}\)．
设总造价为\(y\)，
则 \(y=10 A P+8(2-P D)=\dfrac{10 \sqrt{3}}{\sin \theta}+16-\dfrac{16 \sin \left(60^{\circ}-\theta\right)}{\sin \theta}\)\(=\dfrac{2 \sqrt{3}(5-4 \cos \theta)}{\sin \theta}+8\)， \(0<\theta<\dfrac{\pi}{3}\) ，
则有\(y^{\prime}=\dfrac{2 \sqrt{3}(4-5 \cos \theta)}{\sin ^2 \theta}\)，
令\(y'=0\)，得\(\cos θ=\dfrac{4}{5}\)，令\(\cos θ_0=\dfrac{4}{5}\) ，\(\theta_0 \in\left(0， \dfrac{\pi}{3}\right)\)，
列表：
| \(θ\) | \((0，θ_0 )\) |
\(θ_0\) | \(\left(\theta_0， \dfrac{\pi}{3}\right)\) |
|---|---|---|---|
| \(y'\) | \(-\) | \(0\) | \(+\) |
| \(y\) | \(\downarrow\) | 极小值 | \(\uparrow\) |
由列表当\(θ=θ_0\)，即\(\cos θ=\dfrac{4}{5}\) 时，有最小值．
答：当\(\cos θ=\dfrac{4}{5}\) 时，\(AP\)，\(PC\)段的总造价最低．
-
答案 (1) \(f(x)_{\min }=\ln 2+\dfrac{3}{4}\)， \(f(x)_{\max }=2\)；(2) \(\left(0， \dfrac{1}{2 e}\right)\) .
解析 (1)当\(a=1\)时，\(f(x)=x^2+x-\ln x\)， \(f^{\prime}(x)=\dfrac{(2 x-1)(x+1)}{x}\)，
\(\therefore f(x)\)在 \(\left[\dfrac{1}{3}， \dfrac{1}{2}\right)\)单调递减，在 \(\left(\dfrac{1}{2}， 1\right]\)单调递增，
\(\therefore f(x)_{\min }=\ln 2+\dfrac{3}{4}\)， \(f(x)_{\max }=2\)．
(2)令\(g(x)=f(x)-x=0\)，得 \(a=\dfrac{\ln x}{x^2}\)，设 \(h(x)=\dfrac{\ln x}{x^2}(x>0)\)，
\(\because g(x)=f(x)-x\)在定义域内有两个零点，
\(\therefore\)函数\(y=h(x)\)与\(y=a\)与在定义域内有两个交点
\(\because h^{\prime}(x)=\dfrac{1-2 \ln x}{x^3}\)，
令\(h'(x)>0\)得：\(0<x<\sqrt{e}\)；令\(h'(x)<0\)得：\(x>\sqrt{e}\)，
\(\therefore h(x)\)在\((0，\sqrt{e})\)单调递增，在\((\sqrt{e}，+∞)\)单调递减，
又 \(\because h(\sqrt{e})=\dfrac{1}{2 e}\)，且当\(x→0\)时，\(h(x)→-∞\)，当\(x→+∞\)时，\(h(x)→0\)，
画出函数\(h(x)\)的大致图像，如图所示：
由图象可得， \(a \in\left(0， \dfrac{1}{2 e}\right)\)，
\(\therefore a\)的取值范围为 \(\left(0， \dfrac{1}{2 e}\right)\)． -
答案 (1) 最大值为\(0\)，最小值为 \(-\dfrac{32}{3}\) ；(2)\(\left(-1， \dfrac{\sqrt[3]{5}}{3}\right)\).
解析 (1)由题意得\(f'(x)=-x^2+2ax+3a^2=-(x-3a)(x+a)\)，
当\(a=-1\)时，\(f'(x)=-(x-1)(x+3)\)，\(x\in [-4，2]\)，
由\(f'(x)>0\)，解得\(-3<x<1\)，
由\(f'(x)<0\)，解得\(-4⩽x<-3\)或\(1<x⩽2\)，
所以函数\(f(x)\)在区间\((-3，1)\)上单调递增，在区间\((-4，-3)\)，\((1，2)\)上单调递减，
又\(f(-4)=- \dfrac{25}{3}\)，\(f(-3)=-\dfrac{32}{3}\)，\(f(1)=0\)， \(f(2)=-\dfrac{7}{3}\)，
所以函数\(f(x)\)在区间\((-4，-2)\)上的最大值为\(0\)，最小值为\(-\dfrac{32}{3}\)．
(2)函数\(f(x)\)只有一个零点，
因为\(f'(x)=-x^2+2ax+3a^2=-(x-3a)(x+a)\)，
①当\(a<0\)时，由\(f'(x)>0\)，解得\(3a<x<-a\)，
所以函数\(f(x)\)在区间\((3a，-a)\)上单调递增，
由\(f'(x)<0\)，解得\(x<3a\)或\(x>-a\)，
所以函数\(f(x)\)在区间\((-∞，3a)\)，\((-a，+∞)\)上单调递减，
又\(f(0)=-\dfrac{5}{3}<0\)，
所以只需要\(f(-a)<0\)，解得\(-1<a<0\)，
所以实数\(a\)的取值范围为\((-1，0)\)．
②当\(a=0\)时，显然\(f(x)\)只有一个零点成立，
③当\(a>0\)时，由\(f'(x)>0\)，解得\(-a<x<3a\)，
即\(f(x)\)在区间 \((-a，3a)\)上单调递增，
由\(f'(x)<0\)，解得\(x<-a\)或\(x>3a\)，
即函数\(f(x)\)在区间\((-∞，-a)\)，\((3a，+∞)\)上单调递减，
又\(f(0)=-\dfrac{5}{3}<0\)，
所以只需\(f(3a)<0\)，解得 \(0<a<\dfrac{\sqrt[3]{5}}{3}\)，
综上，实数\(a\)的取值范围为\(\left(-1， \dfrac{\sqrt[3]{5}}{3}\right)\).
【B组---提高题】
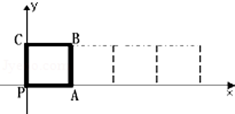
1.如图放置的边长为\(1\)的正方形\(PABC\)沿\(x\)轴正方向滚动．设顶点\(P(x，y)\)的轨迹方程是\(y=f(x)\)，设\(y=f(x)\)在其两个相邻零点间的图象与\(x\)轴所围区域为\(S\)，则直线\(x=t\)从\(t=0\)到\(t=4\)所匀速移动扫过区域\(S\)的面积\(D\)与\(t\)的函数图象大致为( )
A．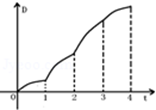
\(\qquad\) B．
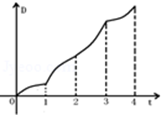\(\qquad\) C．
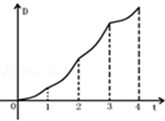\(\qquad\) D．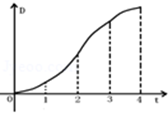 
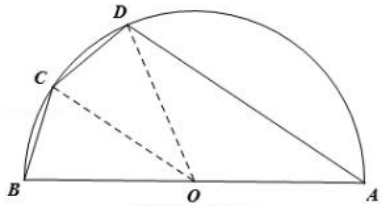
2.如图，某专用零件四边形\(ABCD\)由平面图是一个半圆形钢板切割而成，其中\(O\)为圆心，\(AB=2\)，\(OC\)平分角\(∠BOD\)交圆于点\(C\)，\(D\)为圆弧上一点，设\(∠BOC=θ\)．
(1)当\(θ=\dfrac{\pi}{6}\)时，求该零件的面积；
(2)若该零件周长为函数\(f(θ)\)，且\(2f(θ)-m^2-4m⩽0\)恒成立，求实数\(m\)的取值范围．
3.已知函数\(f(x)=ax⋅\ln x\)(其中\(a≠0\)，\(a\in R\))， \(g(x)=\dfrac{x-1}{x+1}\)．
(1)若存在实数\(a\)使得 \(f(x)<\dfrac{1}{e}\)恒成立，求\(a\)的取值范围；
(2)当\(a⩽\dfrac{1}{2}\)时，讨论函数\(y=f(x)-g(x)\)的零点个数．
参考答案
-
答案 \(D\)
解析 由题意得，从顶点\(A\)落在\(x\)轴上的时候开始计算，到下一次\(A\)点落在\(x\)轴上，
这个过程中四个顶点依次落在了\(x\)轴上，而每两个顶点间距离为正方形的边长\(1\)，
下面考查\(P\)点的运动轨迹，知正方形向右滚动，
\(P\)点从 轴上开始运动的时候，首先是围绕\(A\)点运动\(\dfrac{1}{4}\)个圆，该圆半径为\(1\)，
然后以\(B\)点为中心，滚动到\(CP\)点落地，其间是以\(BP\)为半径，旋转\(90^∘\)，再以\(C\)为圆心，旋转\(90^∘\)，这时候以\(CP\)为半径，因此\(y=f(x)\)最终构成图象如下：
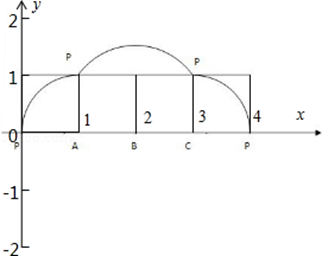
由图得，两个相邻零点间的图象与 轴所围区域\(S\)为曲线与\(x\)轴围成的封闭图形，
则直线\(x=t\)从\(t=0\)到\(t=4\)所匀速移动扫过区域\(S\)的面积\(D\)与\(t\)的函数变化：
从\(O\)到\(B\)面积相同时间内越来越大，\(D\)随着\(t\)变化得越来越快，从\(B\)到\(D\)面积相同时间内越来越小，\(D\)随着\(t\)变化得越来越慢，故\(D\)与\(t\)的函数变化图象大致为\(D\)中的图象，
故选：\(D\)． -
答案 (1) \(\dfrac{2+\sqrt{3}}{4}\)；(2) \((-\infty，-5] \cup[1，+\infty)\).
解析 (1)\(\because OC\)平分角\(∠BOD\)交圆于点\(C\)，\(D\)为圆弧上一点，\(∠BOC=θ=\dfrac{\pi}{6}\)，\(\therefore ∠AOD=\dfrac{2\pi}{3}\)，
\(\because AB=2\)，\(\therefore OA=OB=OC=OD=1\)，
\(\therefore S_{\text {四边形 } A B C D}=S_{\triangle B O C}+S_{\triangle C O D}+S_{\triangle A O D}\)
\(=\dfrac{1}{2} \times 1 \times 1 \times \sin \dfrac{\pi}{6} \times 2+\dfrac{1}{2} \times 1 \times 1 \times \sin \dfrac{2 \pi}{3}=\dfrac{1}{2}+\dfrac{\sqrt{3}}{4}=\dfrac{2+\sqrt{3}}{4}\)．
(2)由题意，在\(△BOC\)中， \(\angle O B C=\angle O C B=\dfrac{\pi-\theta}{2}\)，
由正弦定理 \(\dfrac{B C}{\sin \theta}=\dfrac{O B}{\sin \left(\dfrac{\pi-\theta}{2}\right)}=\dfrac{1}{\cos \dfrac{\theta}{2}}\)，
\(\therefore B C=C D=\dfrac{\sin \theta}{\cos \dfrac{\theta}{2}}=2 \sin \dfrac{\theta}{2}\)，
同理在 \(△AOD\)中，\(∠OAD=θ\)，\(∠DOA=π-2θ\)，
由正弦定理 \(\dfrac{D A}{\sin (\pi-2 \theta)}=\dfrac{O D}{\sin \theta}\) ，
\(\therefore D A=\dfrac{\sin 2 \theta}{\sin \theta}=2 \cos \theta\)，
\(\therefore f(\theta)=2+4 \sin \dfrac{\theta}{2}+2 \cos \theta=2+4 \sin \dfrac{\theta}{2}+2\left(1-2 \sin ^2 \dfrac{\theta}{2}\right)\)，\(0<θ<\dfrac{\pi}{2}\)，
令 \(t=\sin \dfrac{\theta}{2}\left(0<t<\dfrac{\sqrt{2}}{2}\right)\)，
\(\therefore f(\theta)=2+4 t+2\left(1-2 t^2\right)=4+4 t-4 t^2=-4\left(t-\dfrac{1}{2}\right)^2+5\)，
\(\therefore t=\dfrac{1}{2}\)时，即\(θ=\dfrac{\pi}{3}\) ，\(f(θ)\)的最大值为\(5\)，
\(\because f(θ)-m^2-4m⩽0\)，\(\therefore m^2+4m⩽f(θ)\)恒成立，
\(\therefore m^2+4m⩾5\)，\(\therefore m⩾1\)或\(m⩽-5\)，
即实数\(m\)的取值范围为 \((-\infty，-5] \cup[1，+\infty)\)． -
答案 (1) \((-1，0)\)；
(2) 当\(a<0\)或\(a=\dfrac{1}{2}\)时，\(h(x)\)在\((0，+∞)\)只有\(1\)个零点，
当\(0<a<\dfrac{1}{2}\)时，\(h(x)\)在\((0，+∞)\)上有\(2\)个零点．
解析 (1)因为\(f(x)=ax\ln x\)，\(a≠0\)，要使得\(f(x)<\dfrac{1}{e}\)在\((0，+∞)\)上恒成立，
所以\(a<0\)，由\(f'(x)=a(\ln x+1)\)，
由\(f'(x)=a(\ln x+1)>0\)，解得\(0<x<\dfrac{1}{e}\)，
由\(f'(x)=a(\ln x+1)<0\)，解得\(x>\dfrac{1}{e}\) ，
所以 \(f(x)_{\max }=f\left(\dfrac{1}{e}\right)=-\dfrac{a}{e}\)，
所以 \(-\dfrac{a}{e}<\dfrac{1}{e}\)，所以\(-1<a<0\)，
所以\(a\)的取值范围为\((-1，0)\)．
(2)①当\(a<0\)时，当\(x\in (0，1)\)时，\(f(x)>0\)，\(g(x)<0\)，
所以\(y=f(x)-g(x)\)恒大于零，
当\(x=1\)时，\(y=f(x)-g(x)=0\)，
令\(h(x)=f(x)-g(x)\)，
所以\(a<0\)时，令\(h(x)\)在\((0，+∞)\)只有\(1\)个零点，
②当\(a>0\)时，令\(h(x)=f(x)-g(x)\)，
则 \(h(x)=a x \ln x-1+\dfrac{2}{x+1}(x>0)\)，
\(h^{\prime}(x)=a(\ln x+1)-\dfrac{2}{(x+1)^2}，\)， \(h^{\prime \prime}(x)=\dfrac{a}{x}+\dfrac{4}{(x+1)^3}\)，
因为\(x>0\)，所以\(h'' (x)>0\)恒成立，
所以\(h'(x)\)在\((0，+∞)\)上单调递增，
因为\(h(1)=0\)，当\(h'(1)=0\)，即\(a=\dfrac{1}{2}\)时，
\(h'(x)\)在\((0，1)\)上恒小于零，在\((1，+∞)\)上恒大于零，
即\(h(x)\)在\((0，1)\)上单调递减，在\((1，+∞)\)上单调递增，
所以\(h(x)⩾h(1)=0\)，\(y=h(x)\)在\((0，+∞)\)只有\(1\)个零点，
若\(0<a<\dfrac{1}{2}\)时，\(h'(1)=a-\dfrac{1}{2}<0\)，
由于\(h'(x)\)在\((0，+∞)\)上单调递增，
所以\(h'(x)\)在\((0，1]\)上恒小于零，\(h(x)\)在\((0，1]\)上单调递减，
因为\(h(1)=0\)，所以\(h(x)\)在\((0，1]\)上有唯一零点\(1\)，
又因为\(h'(1)=a-\dfrac{1}{2}<0\)， \(h^{\prime}\left(e^{\frac{2}{a}-1}\right)=2-\dfrac{2}{\left(e^{\frac{2}{a}-1}+1\right)^2}>0\)，
所以存在 \(x_0 \in\left(1， e^{\frac{2}{a}-1}\right)\)，使得\(h'(x_0 )=0\)，
由于\(h'(x)\)在\((0，+∞)\)上单调递增，\(h^{\prime}(1)=a-\frac{1}{2}<0\) ， \(h^{\prime}\left(x_0\right)=0\)，
所以\(h(x)\)在\((1，x_0 )\)上单调递减，在\((x_0，+∞)\)上单调递增， \(x_0 \in\left(1， e^{\frac{2}{a}-1}\right)\)，
所以\(h(x_0 )<h(1)=0\)，
又\(0<a<\dfrac{1}{2}\)， \(e^{\frac{1}{a}}>1\)， \(h\left(e^{\frac{1}{a}}\right)=e^{\frac{1}{a}}-1+\dfrac{2}{e^{\frac{1}{a}+1}}>0\)，
所以\(x_0<e^{\frac{1}{a}}\)，
结合\(h(x)\)在\((x_0，+∞)\)单调递增，\(h(x)\)在\((1，+∞)\)上有唯一零点，
又\(h(1)=0\)，
所以\(0<a<\dfrac{1}{2}\)时，\(h(x)\)在(0，+∞)上有唯一零点，
又因为\(h(1)=0\)，
所以\(0<a<\dfrac{1}{2}\)时，\(h(x)\)在\((0，+∞)\)上有\(2\)个零点，
综上所述，当\(a<0\)或\(a=\dfrac{1}{2}\)时，\(h(x)\)在\((0，+∞)\)只有\(1\)个零点，
当\(0<a<\dfrac{1}{2}\)时，\(h(x)\)在\((0，+∞)\)上有\(2\)个零点．
【C组---拓展题】
1.已知函数\(f(x)=\ln x-a^2 x^2+ax\)．
(1)求函数\(f(x)\)在定义域内的最值．
(2)当\(a>0\)时，若\(y=f'(x)\)有两个不同的零点\(x_1\)，\(x_2\)，求证：\(a(x_1+x_2 )>2\)．
参考答案
- 答案 (1) 最大值\(-\ln a\)，无最小值；(2)略 .
解析 (1)函数\(f(x)=\ln x-a^2 x^2+ax\)的定义域为\((0，+∞)\)，
\(f^{\prime}(x)=\dfrac{1}{x}-2 a^2 x+a=-\dfrac{(2 a x+1)(a x-1)}{x}\)，
当\(a=0\)时，\(f(x)=\ln x\)，
此时函数\(f(x)\)为增函数，无最值，
当\(a≠0\)时，令\(f'(x)=0\)，得\(x=-\dfrac{1}{2a}\)或\(x=\dfrac{1}{a}\)，
①若\(a<0\)，则\(-\dfrac{1}{2a}>0\)，\(\dfrac{1}{a} <0\)，
由\(f'(x)>0\)，得\(0<x<-\dfrac{1}{2a}\)，\(f(x)\)单调递增，
由\(f'(x)<0\)，得\(x>-\dfrac{1}{2a}\)，\(f(x)\)单调递减，
所以函数\(f(x)\)在定义域内有最大值\(f\left(-\dfrac{1}{2 a}\right)=\ln \left(-\dfrac{1}{2 a}\right)-a^2\left(-\dfrac{1}{2 a}\right)^2+a\left(\dfrac{1}{a}\right)=\ln \left(-\dfrac{1}{2 a}\right)-\dfrac{3}{4}\)，无最小值．
②若\(a>0\)，则\(-\dfrac{1}{2a}<0\)，\(\dfrac{1}{a} >0\)，
由\(f'(x)>0\)，得\(0<x<\dfrac{1}{a}\) ，\(f(x)\)单调递增，
由\(f'(x)<0\)，得\(x>\dfrac{1}{a}\)，\(f(x)\)单调递减，
所以\(f(x)\)定义域内有最大值\(f\left(\dfrac{1}{a}\right)=\ln \left(\dfrac{1}{a}\right)-a^2\left(\dfrac{1}{a}\right)^2+a\left(-\dfrac{1}{2 a}\right)=-\ln a\)，无最小值．
(2)证明：由(1)知，当\(a>0\)时，函数\(f(x)\)在定义域内的最大值为 \(f\left(\dfrac{1}{a}\right)=-\ln a\)，
因为\(y=f(x)\)有两个不同的零点\(x_1\)，\(x_2\)，
所以\(-\ln a>0\)，解得\(-\ln a>0\)， 解得\(0<a<1\)，
不妨设\(0<x_1<\dfrac{1}{a} <x_2\)，
由题意知\(f(x_1 )=\ln x_1-a^2 x_1^2+ax_1=0\)，\(f(x_2 )=\ln x_2-a^2 x_2^2+ax_2=0\)，
所以\(\ln x_2-\ln x_1=a^2 (x_2^2-x_1^2 )-ax_2+ax_1\)，
即\(\ln \dfrac{\ln x_2-\ln x_1}{x_2-x_1}=a\left[a\left(x_2+x_1\right)-1\right]\)，
即\(\dfrac{\ln \dfrac{x_2}{x_1}}{\dfrac{x_2}{x_1}-1}=a\left[a\left(x_1+x_2\right)-1\right] x_1\)，
设\(h(t)=\ln t-\dfrac{2(t-1)}{t+1}(t>1)\)，
则\(h^{\prime}(t)=\dfrac{1}{t}-\dfrac{4}{(t+1)^2}=\dfrac{(t-1)^2}{t(t+1)^2}(t>1)\)，
所以当\(t>1\)时，\(h'(t)>0\)，\(h(t)\)单调递增，
所以\(h(t)>h(1)=0\)，
即\(\ln t-\dfrac{2(t-1)}{t+1}>0\)，所以\(\dfrac{\ln t}{t-1}>\dfrac{2}{t+1}\)，
令\(t=\dfrac{x_2}{x_1}\) ，
则上式可化为 \(\dfrac{\ln \dfrac{x_2}{x_1}}{\dfrac{x_2}{x_1}-1}>\dfrac{2}{\dfrac{x_2}{x_1}+1}\)，
所以\(a\left[a\left(x_1+x_2\right)-1\right] x_1>\dfrac{2}{\dfrac{x_2}{x_1}+1}\)，
所以 \(a\left[a\left(x_1+x_2\right)-1\right] x_1>\dfrac{2}{x_1+x_2}\)，
即\(a^2 (x_1+x_2 )^2-a(x_1+x_2 )-2>0\)，
所以\([a(x_1+x_2 )-2][a(x_1+x_2 )+1]>0\)，
又因为\(a(x_1+x_2 )+1>0\)恒成立，所以\(a(x_1+x_2 )>2\)．
