5.3.2(2) 导数与函数的最值
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高二数学同步精品讲义与分层练习(人教A版2019)]
( https://www.zxxk.com/docpack/2875423.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性第二册同步巩固,难度2颗星!
基础知识
函数\(y=f(x)\)在\([a,b]\)上的最大值与最小值的步骤
(1)求函数\(y=f(x)\)在\((a ,b)\)内的极值;
(2)将函数\(y=f(x)\)的各极值与端点处的函数值\(f(a)\),\(f(b)\)比较,其中最大的一个是最大值,最小的一个是最小值.
解释
(1) 极大值不一定是最大值,极小值不一定是最小值.
(2) 一般地,如果在区间\([a,b]\)上函数\(y=f(x)\)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
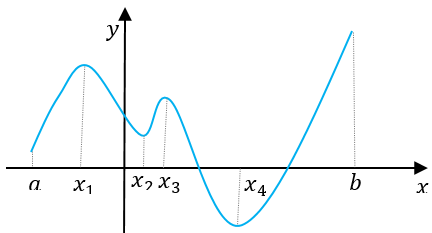
【例】 如下图,可知函数\(y=f(x)\)在区间\([a,b]\)上的极大值为\(f(x_1 )\),\(f(x_3 )\);极小值为\(f(x_2 )\),\(f(x_4 )\);最大值为\(f(b)\),最小值为\(f(x_4 )\).
基本方法
【题型1】 求函数的最值
【典题1】 设\(a∈R\),函数\(f(x)=x^3-x^2-x+a\).
(1)求\(f(x)\)的极值;\(\qquad \qquad\) (2)若\(x∈[-1,2]\),求函数\(f(x)\)的值域.
解析 (1) \(f'(x)=3x^2-2x-1\),若\(f'(x)=0\),则\(x=-\dfrac{1}{3}\),\(1\).
当\(x\)变化时,\(f'(x)\),\(f(x)\)变化情况如下表:
| \(x\) | \(\left(-\infty,-\dfrac{1}{3}\right)\) |
\(-\dfrac{1}{3}\) | \(\left(-\dfrac{1}{3}, 1\right)\) |
\(1\) | \((1,+∞)\) |
|---|---|---|---|---|---|
| \(f'(x)\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| \(f(x)\) | \(\uparrow\) | 极大值 | \(\downarrow\) | 极小值 | \(\uparrow\) |
所以\(f(x)\)的极大值是\(f\left(-\dfrac{1}{3}\right)=\dfrac{5}{27}+a\),极小值是\(f(1)=a-1\).
(2)因为\(x∈\left[-1,2\right]\),由(1)知, \(f\left(-\dfrac{1}{3}\right)=\dfrac{5}{27}+a\),
\(f(1)=a-1\),\(f(-1)=a-1\),\(f(2)=a+2\).
则\(f(x)\)的值域为\(\left[a-1,a+2\right]\).
点拨 函数\(y=f(x)\)在\(\left[a,b\right]\)上的最大值与最小值的步骤
(1)求函数\(y=f(x)\)在\((a ,b)\)内的极值;
(2)将函数\(y=f(x)\)的各极值与端点处的函数值\(f(a)\),\(f(b)\)比较,其中最大的一个是最大值,最小的一个是最小值.
【典题2】 已知函数\(f(x)=e^x (x-a-1)\).
(1)当\(a=0\)时,求曲线\(y=f(x)\)在\((0,f(0))\)处的切线方程;
(2)求\(f(x)\)的单调性;
(3)求函数\(f(x)\)在\(\left[0,1\right]\)上的最小值.
解析 (1)当\(a=0\)时,\(f(x)=e^x (x-1)\),\(f'(x)=e^x (x-1)+e^x=xe^x\),
切线的斜率为\(k=f'(0)=0\),
又\(f(0)=-1\),
所以切线方程为\(y-f(0)=k(x-0)\),即\(y=-1\).
(2) \(f'(x)=e^x (x-a-1)+e^x=e^x (x-a)\),
当\(x⩾a\)时,\(f'(x)⩾0\),\(f(x)\)单调递增,
当\(x<a\)时,\(f'(x)<0\),\(f(x)\)单调递减,
所以\(f(x)\)的单调递增区间为\((a,+∞)\),单调递减区间为\((-∞,a)\).
(3)当\(a⩾1\)时,\(f(x)\)在\((0,1)\)上单调递减,
所以\(f(x)_{\min }=f(1)=e a\),
当\(a⩽0\)时,\(f(x)\)在 上单调递增,
所以\(f(x)_{\min }=f(0)=-a-1\),
当\(0<a<1\)时,\(f(x)\)在\((0,a)\)上单调递减,在\((a,+∞)\)上单调递增,
所以 \(f(x)_{\min }=f(a)=e^a(a-a-1)=-e^a\),
综上所述, \(f(x)_{\min }=\left\{\begin{array}{l}
-a-1, a \leqslant 0 \\
-e^a, 0<a<1 \\
-a e, a \geqslant 1
\end{array}\right.\).
【巩固练习】
1.函数\(y=\dfrac{x}{2}+\cos x, x \in\left[0, \dfrac{\pi}{2}\right]\)的最大值为 ( )
A.\(\dfrac{\sqrt{3}}{3}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{\pi}{12}+\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{\pi}{6}+\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{\sqrt{3}}{2}\)
2.已知函数\(f(x)=e^x (2x^2-3x)\).则函数\(f(x)\)在区间\(\left[0,2\right]\)上的最大值为\(\underline{\quad \quad}\).
3.已知函数\(f(x)=x-\dfrac{a}{e^x}\).
(1)当\(a=-1\)时,求函数\(f(x)\)的单调区间;
(2)若函数\(f(x)\)在\(\left[0,1\right]\)上的最小值为\(\dfrac{3}{2}\),求实数\(a\)的值.
参考答案
-
答案 \(B\)
解析 \(f'(x)=\dfrac{1}{2}-\sin x\),
令\(f'(x)=0\),得\(x=\dfrac{\pi}{6}\),
当\(0≤x<\dfrac{\pi}{6}\)时,\(f'(x)>0\),\(f(x)\)单调递增,
当\(\dfrac{\pi}{6}<x≤\dfrac{\pi}{2}\)时,\(f'(x)<0\),\(f(x)\)单调递减,
所以当\(x=\dfrac{\pi}{6}\)时,\(f(x)\)取得极大值,也是最大值,
即\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\pi}{12}+\dfrac{\sqrt{3}}{2}\),
故选:\(B\). -
答案 \(2e^2\)
解析 \(f(x)=e^x (2x^2-3x)\),
\(f'(x)=e^x (2x^2+x-3)=e^x (2x+3)(x-1)\),\(x∈[0,2]\),
所以\(f'(x)\)和\(f(x)\)在区间\(\left[0,2\right]\)上随\(x\)变化的情况如下:
| \(x\) | \(0\) | \((0,1)\) |
\(1\) | \((1,2)\) |
\(2\) |
|---|---|---|---|---|---|
| \(f'(x)\) | \(-\) | \(0\) | \(+\) | ||
| \(f(x)\) | \(0\) | \(\downarrow\) | \(-e\) | \(\uparrow\) | \(2e^2\) |
所以\(f(x)\)在\([0,2]\)单调递减区间为\([0,1)\),单调递增区间为\((1,2]\),
可知:当\(x=2\)时,\(f(x)\)取得最大值\(2e^2\),
故答案为\(2e^2\).
- 答案 (1) \(f(x)\)在\((-∞,0)\)递减,在\((0,+∞)\)递增;(2) \(a=-\sqrt{e}\).
解析 (1)\(f(x)\)的定义域是\(R\),且 \(f^{\prime}(x)=1+\dfrac{a}{e^x}=\dfrac{e^x+a}{e^x}\),
\(a=-1\)时, \(f^{\prime}(x)=\dfrac{e^x-1}{e^x}\),
由\(f'(x)>0\),得\(x∈(0,+∞)\),由\(f'(x)<0\),得\(x∈(-∞,0)\),
\(\therefore f(x)\)在\((-∞,0)\)递减,在\((0,+∞)\)递增;
(2)由(1)得 \(f^{\prime}(x)=\dfrac{e^x+a}{e^x}\),
①若\(a≥-1\),则\(e^x+a≥0\),即\(f'(x)≥0\)在\(\left[0,1\right]\)上恒成立,
\(f(x)\)在\(\left[0,1\right]\)上是增函数,
\(\therefore f(x)_{\min }=f(0)=-a=\dfrac{3}{2}\),\(\therefore a=-\dfrac{3}{2}\)(舍);
②若\(a≤-e\),则\(e^x+a≤0\),即\(f'(x)≤0\)在\((0,1 ]\)恒成立,
\(f(x)\)在\(\left[0,1\right]\)递减, \(\therefore f(x)_{\min }=f(1)=1-\dfrac{a}{e}=\dfrac{3}{2}\), \(\therefore a=-\dfrac{e}{2}\)(舍);
③若\(-e<a<-1\),当\(0<x<\ln (-a)\)时,\(f'(x)<0\),
\(\therefore f(x)\)在\((0,\ln (-a))\)递减,
当\(\ln (-a)<x<1\)时,\(f'(x)>0\),
\(\therefore f(x)\)在\((\ln (-a),1)\)递增;
\(\therefore f(x)_{min}=f(\ln (-a))=\ln (-a)+1=\dfrac{3}{2}\),
\(\therefore a=-\sqrt{e}\),
综上所述:\(a=-\sqrt{e}\).
【题型2】 证明不等式
【典题1】 证明:不等式\(\ln x≤x-1\).
证明 设\(f(x)=\ln x-x+1\),
\(\therefore\)函数定义域是\((0,+∞)\), \(f^{\prime}(x)=\dfrac{1}{x}-1=\dfrac{1-x}{x}\),
令\(f'(x)=0\),得\(x=1\),
当\(x>1\)时,\(f'(x)<0\),\(f(x)\)单调递减;
当\(x<1\)时,\(f'(x)>0\),\(f(x)\)单调递增;
所以\(f(x)\)在\(x=1\)处取到最大值\(f(1)=0\),
即\(f(x)=\ln x-x+1≤0\),所以\(\ln x≤x-1\).
点拨 构造函数证明不等式恒成立.
【典题2】 已知函数\(f(x)=\dfrac{\ln x}{x}\).
(1)求函数\(f(x)\)的单调区间;
(2)已知\(a\)、\(b∈R\),\(a>b>e\), (其中\(e\)是自然对数的底数), 求证: \(b^a>a^b\).
解析 (1)\(f(x)=\dfrac{\ln x}{x}\), \(\therefore f^{\prime}(x)=\dfrac{1-\ln x}{x^2}\)
当\(x>e\)时, \(f'(x)<0\),\(\therefore\)函数\(f(x)\)在\((e,+∞)\)上是单调递减.
当\(0<x<e\)时, \(f'(x)>0\),\(\therefore\)函数\(f(x)\)在\((0,e)\)上是单调递增.
\(\therefore f(x)\)的增区间是\((0,e)\),减区间是\((e,+∞)\).
(2)证明: \(\because b^a>0\),\(a^b>0\),
要证: \(b^a>a^b\),
只要证: \(a\ln b>b\ln a\),
只要证\(\dfrac{\ln b}{b}>\dfrac{\ln a}{a}\).\((\because a>b>e)\),
由(1)得函数\(f(x)\)在\((e,+∞)\)上是单调递减.
当\(a>b>e\)时,有\(f(b)>f(a)\)即 \(\dfrac{\ln b}{b}>\dfrac{\ln a}{a}\).
\(\therefore b^a>a^b\).
点拨 类似\(b^a>a^b\)这样的指数式不等式,可两边去对数,化为对数式 \(\dfrac{\ln b}{b}>\dfrac{\ln a}{a}\),可构造函数 \(f(x)=\dfrac{\ln x}{x}\).
【巩固练习】
1.证明:不等式\(e^x-x-1≥0\)成立.
2.证明 \(\sin x>\dfrac{2 x}{\pi}\), \(x \in\left(0, \dfrac{\pi}{2}\right)\).
3.已知函数\(f(x)=xe^ax-e^x\).
(1)当\(a=\dfrac{1}{2}\)时,判断\(f(x)\)在\([0,+∞)\)的单调性;
(2)设\(n∈N^*\),证明:\(\dfrac{1}{\sqrt{1^2+1}}+\dfrac{1}{\sqrt{2^2+2}}+\cdots+\dfrac{1}{\sqrt{n^2+n}}>\ln (n+1)\).
参考答案
-
证明 设\(f(x)=e^x-x-1\),\(\therefore f'(x)=e^x-1\),
令\(f'(x)=0\),得\(x=0\),
当\(x>0\)时,\(f'(x)>0\),\(f(x)\)单调递增;
当\(x<0\)时,\(f'(x)<0\),\(f(x)\)单调递减;
所以\(f(x)\)在\(x=0\)处取到最小值\(f(0)=0\),
即\(f(x)=e^x-x-1≥0\). -
证明 令 \(f(x)=\dfrac{\sin x}{x}\),\(x \in\left(0, \dfrac{\pi}{2}\right)\),
则 \(f^{\prime}(x)=\dfrac{x \cdot \cos x-\sin x}{x^2}\),
令\(g(x)=x\cdot \cos x-\sin x\),
则\(g'(x)=\cos x-x\cdot \sin x-\cos x=-x\cdot \sin x\),
当 \(x \in\left(0, \dfrac{\pi}{2}\right)\)时,\(g'(x)<0\),则\(g(x)\)在\(\left(0, \dfrac{\pi}{2}\right)\)上递减,
则\(g(x)<g(0)=0\),
即当 \(x \in\left(0, \dfrac{\pi}{2}\right)\)时,\(f'(x)<0\),所以\(f(x)\)在\(\left(0, \dfrac{\pi}{2}\right)\)上递减,
所以 \(f(x)>f\left(\dfrac{\pi}{2}\right)=\dfrac{2}{\pi}\),
即 \(\dfrac{\sin x}{x}>\dfrac{2}{\pi} \Rightarrow \sin x>\dfrac{2 x}{\pi}\),\(x \in\left(0, \dfrac{\pi}{2}\right)\). -
答案 (1)\(f(x)\)在\([0,+∞)\)上单调递减;(2) 略.
解析 (1)解:当\(a=\dfrac{1}{2}\)时, \(f(x)=x e^{\frac{1}{2} x}-e^x\),
则 \(f^{\prime}(x)=e^{\frac{1}{2} x}+\frac{1}{2} x e^{\frac{1}{2} x}-e^x=e^{\frac{1}{2} x}\left(1+\dfrac{1}{2} x-e^{\frac{1}{2} x}\right)\),
令 \(g(x)=1+\dfrac{1}{2} x-e^{\frac{1}{2} x}\),\(x\in [0,+∞)\),
则\(g^{\prime}(x)=\dfrac{1}{2}-\dfrac{1}{2} e^{\frac{1}{2} x} \leq 0\),
即\(g(x)=1+\dfrac{1}{2} x-e^{\frac{1}{2} x}\),\(x\in [0,+∞)\)为减函数,
又\(g(0)=0\),则\(g(x)≤0\),即\(f'(x)≤0\),
即当\(a=\dfrac{1}{2}\)时,\(f(x)\)在\([0,+∞)\)上单调递减;
(2)证明:由(1)可得: \(x e^{\frac{1}{2} x}-e^x \leq-1\),当且仅当\(x=0\)时取等号,
令\(t=e^x\),\(x>0\),则\(t>1\),
则\(\sqrt{t} \ln t<t-1\),即 \(\sqrt{t}-\dfrac{1}{\sqrt{t}}>\ln t\),
令\(t=\dfrac{n+1}{n}\),则 \(\sqrt{\dfrac{n+1}{n}}-\dfrac{1}{\sqrt{\dfrac{n+1}{n}}}>\ln \dfrac{n+1}{n}\),
即\(\dfrac{1}{\sqrt{n(n+1)}}=\dfrac{1}{\sqrt{n^2+n}}>\ln \dfrac{n+1}{n}\),
则\(\dfrac{1}{\sqrt{1^2+1}}+\dfrac{1}{\sqrt{2^2+2}}+\cdots+\dfrac{1}{\sqrt{n^2+n}}>\ln \dfrac{2}{1}+\ln \dfrac{3}{2}+\cdots+\ln \dfrac{n+1}{n}\)\(=\ln \left(\dfrac{2}{1} \times \dfrac{3}{2} \times \ldots \times \dfrac{n+1}{n}\right)=\ln (n+1)\),
故 \(\dfrac{1}{\sqrt{1^2+1}}+\dfrac{1}{\sqrt{2^2+2}}+\cdots+\dfrac{1}{\sqrt{n^2+n}}>\ln (n+1)\).
【题型3】 函数的最值综合运用
【典题1】 已知函数\(f(x)=x^2-2 \ln x-m\), \(g(x)=\left(\dfrac{1}{2}\right)^x+m\).
(1)存在\(x_1\in \left[1,4\right]\),对任意\(x_2\in \left[1,4\right]\),有不等式\(f(x_1 )⩽g(x_2 )\)成立,求实数\(m\)的取值范围;
(2)如果存在\(x_1\)、\(x_2\in \left[1,4\right]\),使得\(f(x_1 )-f(x_2 )⩾M\)成立,求满足条件的最大整数\(M\).
解析 (1)存在\(x_1\in \left[1,4\right]\),对任意\(x_2\in \left[1,4\right]\),有不等式\(f(x_1 )⩽g(x_2 )\)成立,
所以 \(f(x)_{\min } \leqslant g(x)_{\min }\),因为\(f(x)=x^2-2\ln x-m\),
所以 \(f^{\prime}(x)=2 x-\dfrac{2}{x}=\dfrac{2 x^2-2}{x}=\dfrac{2(x-1)(x+1)}{x} \geqslant 0\)对任意的\(x\in \left[1,4\right]\)恒成立,
所以函数\(y=f(x)\)在区间\(\left[1,4\right]\)上单调递增,
所以\(f(x)_{\min }=f(1)=1-m,\),函数 \(g(x)=\left(\dfrac{1}{2}\right)^x+m\)在区间\(\left[1,4\right]\)上的单调递减,
所以\(g(x)_{\min }=g(4)=m+\dfrac{1}{16}\),
所以 \(1-m \leqslant m+\dfrac{1}{16}\),解得 \(m \geqslant \dfrac{15}{32}\).
所以实数\(m\)的取值范围是\(\left[\dfrac{15}{32},+\infty\right)\).
(2)存在存在\(x_1\)、\(x_2\in \left[1,4\right]\),使得\(f(x_1 )-f(x_2 )⩾M\)成立,
所以 \(M \leqslant\left[f\left(x_1\right)-f\left(x_2\right)\right]_{\text {max }}\),即 \(M \leqslant f(x)_{\text {max }}-f(x)_{\text {min }}\) ,
由(1)可知,函数\(y=f(x)\)在区间\(\left[1,4\right]\)上单调递增,
所以\(f(x)_{min}=f(1)=1-m\),\(f(x)_{max}=16-4\ln 2-m\)
所以 \(M \leqslant f(x)_{\max }-f(x)_{\min }=15-4 \ln 2\),
所以满足条件的最大整数\(M\)的值为\(12\).
【巩固练习】
1.已知函数\(f(x)=x\ln x\).
(1)求\(f(x)\)的最小值;
(2)若对所有\(x≥1\)都有\(f(x)≥ax-1\),求实数\(a\)的取值范围.
2.己知函数\(f(x)=bx\ln x+3(b≠0)\),\(f'(e)=4\),\(g(x)= -x^2+ax\).
(l)求函数\(f(x)\)的极值;
(2)若对\(∀x\in (0,+∞)\)有\(f(x)-g(x)≥0\)恒成立,求实数\(a\)的取值范围.
参考答案
-
答案 (1) \(-\dfrac{1}{e}\);(2) \(a≤1\).
解析 (1)函数的定义域\((0,+∞)\),
\(f'(x)=\ln x+1\),令\(f'(x)>0\)得\(x>\dfrac{1}{e}\),此时\(f(x)\)递增,
令\(f'(x)<0\)得\(0<x<\dfrac{1}{e}\),此时\(f(x)\)递减,\(f(x)\)最小值为\(-\dfrac{1}{e}\);
(2)方法一 分离参数法
由题意得\(a≤\ln x+\dfrac{1}{x}\),令\(g(x)=\ln x+\dfrac{1}{x}\),
当\(x≥1\)时, \(g^{\prime}(x)=\dfrac{1}{x}-\dfrac{1}{x^2}=\dfrac{x-1}{x^2} \geq 0\),
所以\(g(x)\)递增,\(g(x)\)的最小值为\(g(1)=1\),
所以\(a≤1\).
方法二 直接构造函数法
对所有\(x≥1\)都有\(f(x)≥ax-1\)等价于\(x\ln x-ax+1≥0\),
令\(h(x)=x\ln x-ax+1\),则\(h'(x)=\ln x+1-a\),
令\(h'(x)=0\)解得 \(x=e^{a-1}\),
当\(0<x<e^{a-1}\)时,\(h'(x)<0\),\(h(x)\)递减;
当\(x>e^{a-1}\)时,\(h'(x)>0\),\(h(x)\)递增;
\(\therefore h(x)≥h(e^{a-1} )=e^{a-1} (a-1)-ae^{a-1}+1=1-e^{a-1}\),
若要满足题意,则\(1-e^{a-1}≥0\),解得\(a≤1\). -
答案 (1) 极小值\(3-\dfrac{2}{e}\),无极大值;(2) \(a≤4\).
解析 (1)\(f'(x)=b(\ln x+1)\),
由\(f'(e)=4\)得\(2b=4\),解得\(b=2\),
所以\(f(x)=2x\ln x+3\),\(f'(x)=2(\ln x+1)\),
令\(f'(x)=0\)得\(x=\dfrac{1}{e}\),
当\(x<\dfrac{1}{e}\)时,\(f'(x)<0\);当\(x>\dfrac{1}{e}\)时,\(f'(x)>0\);
所以函数\(f(x)\)的极小值\(f\left(\dfrac{1}{e}\right)=3-\dfrac{2}{e}\),无极大值.
(2) 对\(∀x\in (0,+∞)\)有\(2x\ln x+3+x^2-ax≥0\)恒成立
等价于对\(∀x\in (0,+∞)\)有 \(a \leq 2 \ln x+x+\dfrac{3}{x}\)恒成立
令\(g(x)=2 \ln x+x+\dfrac{3}{x}\),
则\(g^{\prime}(x)=\dfrac{2}{x}+1-\dfrac{3}{x^2}=\dfrac{x^2+2 x-3}{x^2}=\dfrac{(x-1)(x+3)}{x^2}\),
所以当\(x<1\)时,\(g'(x)<0\);当\(x>1\)时,\(g'(x)>0\);
所以\(g(x)≥g(1)=4\),
所以\(a≤4\).
分层练习
【A组---基础题】
1.函数\(y=x^3+x^2-x+1\)在区间\(\left[-2,1\right]\)上的最小值为( )
A. \(\dfrac{22}{27}\) \(\qquad \qquad \qquad \qquad\) B.\(2\) \(\qquad \qquad \qquad \qquad\) C.\(-1\) \(\qquad \qquad \qquad \qquad\) D.\(-4\)
2.若函数\(f(x)=\ln x-ax\)在区间\((0,+∞)\)上的最大值为\(0\),则\(f(e)=\) ( )
A.\(0\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{1}{e}\) \(\qquad \qquad \qquad \qquad\) C.\(1\) \(\qquad \qquad \qquad \qquad\) D.\(e\)
3.函数\(f(x)=ax-\ln x⩾0(a\in R)\)恒成立的一个必要不充分条件是( )
A. \(a \in\left[\dfrac{1}{e},+\infty\right)\) \(\qquad\) B. \(a∈[0,+∞)\) \(\qquad\) C.\(a\in [1,+∞)\) \(\qquad\) D.\(a\in (-∞,e ]\)
4.函数\(y=x+2\cos x\)在区间 \(\left[0, \dfrac{\pi}{2}\right]\)上的最大值是\(\underline{\quad \quad}\),最小值是\(\underline{\quad \quad}\).
5.若函数\(f(x)=\dfrac{x^3}{3}+x^2-2\)在区间\((a-4,a)\)上存在最小值,则\(a\)的取值范围是\(\underline{\quad \quad}\).
6.已知函数\(f(x)=x^3-3x^2-9x\).
(1)求函数\(f(x)\)在点\((0,0)\)处的切线方程;
(2)求函数\(f(x)\)在区间\(\left[-2,2\right]\)的最大值和最小值.
7.已知函数\(f(x)=x\ln x\),\(g(x)=-x^2+ax-3\).
(1)求函数\(f(x)\)的图象在点\((1,0)\)处的切线方程;
(2)若对\(∀x\in (0,+∞)\)有\(2f(x)≥g(x)\)恒成立,求实数\(a\)的取值范围.
8.已知函数\(f(x)=x-1-\ln x\).
(1)求证:\(f(x)≥0\);
(2)求证:对于任意正整数\(n\),\(\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{2^2}\right) \cdots\left(1+\dfrac{1}{2^n}\right)<e\).
9.已知函数\(f(x)=e^x-a(x+1)\).
(1)若\(f(x)≥0\)恒成立,求\(a\)的取值范围;
(2)证明:当\(a=0\)时,曲线\(y=f(x)(x>0)\)总在曲线\(y=2+\ln x\)的上方.
参考答案
-
答案 \(C\)
解析 \(y'=3x^2+2x-1=(3x-1)(x+1)\),
令\(y'>0\),解得:\(x>\dfrac{1}{3}\)或\(x<-1\),令\(y'<0\),解得:\(-1<x<\dfrac{1}{3}\),
\(\therefore\)函数在\([-2,-1)\)递增,在\(\left(-1, \dfrac{1}{3}\right)\)递减,在\(\left(\dfrac{1}{3}, 1\right]\)递增,
\(\therefore x=-1\)时,取极大值,极大值是\(2\),\(x=\dfrac{1}{3}\)时,函数取极小值,极小值是\(\dfrac{22}{27}\),
而\(x=-2\)时,\(y=-1\),\(x=1\)时,\(y=2\),
故函数的最小值是\(-1\),
故选:\(C\). -
答案 \(B\)
解析 \(f^{\prime}(x)=\dfrac{1}{x}-a=\dfrac{1-a x}{x}\),\(x>0\),
当\(a⩽0\)时,在\((0,+∞)\)上\(f'(x)>0\),\(f(x)\)单调递增,
所以\(f(x)\)没有最大值,不合题意,
当\(a>0\)时,令\(f'(x)=0\),得\(x=\dfrac{1}{a}\),
所以在 \(\left(0, \dfrac{1}{a}\right)\)上,\(f'(x)>0\),\(f(x)\)单调递增,
在\(\left(\dfrac{1}{a},+\infty\right)\)上,\(f'(x)<0\),\(f(x)\)单调递减,
所以\(f(x)_{\max }=f\left(\dfrac{1}{a}\right)=\ln \dfrac{1}{a}-a \times \dfrac{1}{a}=\ln \dfrac{1}{a}-1=0\),
所以\(\dfrac{1}{a}=e\),所以\(a=\dfrac{1}{e}\),
故选:\(B\). -
答案 \(B\)
解析 根据题意,函数\(f(x)=ax-\ln x\),其定义域为\((0,+∞)\),
若\(f(x)=ax-\ln x⩾0(a\in R)\)恒成立,必有 \(a \geqslant \dfrac{\ln x}{x}\),
设 \(g(x)=\dfrac{\ln x}{x}\),其导数 \(g^{\prime}(x)=\dfrac{1-\ln x}{x^2}\),
在区间\((0,e)\)上, \(g^{\prime}(x)=\dfrac{1-\ln x}{x^2}>0\),则\(g(x)\)在\((0,e)\)上单调递增,
在\((e,+∞)\)上,\(g^{\prime}(x)=\dfrac{1-\ln x}{x^2}<0\) ,则\(g(x)\)在\((e,+∞)\)上单调递减,
故\(g(x)_{max}=g(e)=\dfrac{1}{e}\),
若\(a \geqslant \dfrac{\ln x}{x}\)恒成立,必有\(a⩾\dfrac{1}{e}\),
依次分析选项:
对于\(A\), \(a \in\left[\dfrac{1}{e},+\infty\right)\)是\(f(x)=ax-\ln x⩾0\)恒成立的充分必要条件,不符合题意,
对于\(B\), \(a \in[0,+\infty)\)是\(f(x)=ax-\ln x⩾0\)恒成立的一个必要不充分,符合题意,
对于\(C\),\(a\in [1,+∞)\)是\(f(x)=ax-\ln x⩾0\)恒成立的一个充分不必要,不符合题意,
对于\(D\),\(a\in (-∞,e ]\)是\(f(x)=ax-\ln x⩾0\)恒成立的既不充分也不必要条件,不符合题意,
故选:\(B\). -
答案 \(\dfrac{\pi}{6}+\sqrt{3}\);\(\dfrac{\pi}{2}\)
解析 由题意,可知:
当\(x\in \left[0,\dfrac{\pi}{2}\right]\)时,\(y'=1-2\sin x\).
①当\(y'=0\)时,即\(1-2\sin x=0\),\(\sin x=\dfrac{1}{2}\),\(x=\dfrac{\pi}{6}\)时,函数取极值\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\pi}{6}+\sqrt{3}\).
②当\(y'>0\)时,即\(1-2\sin x>0\),\(\sin x<\dfrac{1}{2}\),\(0≤x<\dfrac{\pi}{6}\)时,函数\(f(x)\)单调递增.
③当\(y'<0\)时,即\(1-2\sin x<0\),\(\sin x>\dfrac{1}{2}\),\(\dfrac{\pi}{6}<x≤\dfrac{\pi}{2}\)时,函数\(f(x)\)单调递减.
\(\because f(0)=2\),\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\pi}{6}+\sqrt{3}\),\(f\left(\dfrac{\pi}{2}\right)=\dfrac{\pi}{2}\).
\(\therefore f(x)\)在区间\(\left[0,\dfrac{\pi}{2}\right]\)上的图象大致如下:

则由图象可知:
在区间\(\left[0,\dfrac{\pi}{2}\right]\)上,当\(x=\dfrac{\pi}{6}\)时,\(f(x)\)取最大值\(\dfrac{\pi}{6}+\sqrt{3}\);
当\(x=\dfrac{\pi}{2}\)时,\(f(x)\)取最小值\(\dfrac{\pi}{2}\).
故答案为:\(\dfrac{\pi}{6}+\sqrt{3}\);\(\dfrac{\pi}{2}\). -
答案 \([1,4)\)
解析 \(f^{\prime}(x)=x^2+2 x=x(x+2)\),
令\(f'(x)>0\),解得:\(x>0\)或\(x<-2\),
令\(f'(x)<0\),解得:\(-2<x<0\),
故\(f(x)\)在\((-∞,-2)\)递增,在\((-2,0)\)递减,在\((0,+∞)\)递增,
故 \(f(x)_{\text {min }}=f(x)_{\text {极小值 }}=f(0) \text {, }\),
若\(f(x)\)在区间\((a-4,a)\)上存在最小值,
则\(f(a-4)≥f(0)\)
即 \(\dfrac{1}{3}(a-4)^3+(a-4)^2-2 \geq-2\),解得:\(a≥1\)①,
而\(a-4<0<a\),解得:\(0<a<4\)②,
综合①②得:\(1≤a<4\). -
答案 (1) \(y=-9x\);(2)\(f(x)_{max}=5\),\(f(x)_{min}=-22\).
解析 (1) \(f'(x)=3x^2-6x-9\),则\(f'(0)=-9\),
所以函数在点\((0,0)\)处的切线方程为\(y=-9x\);
(2)由(1)得\(f'(x)=3x^2-6x-9=3(x-3)(x+1)\),
由\(f'(x)=0\),得\(x=3\),或\(x=-1\).
令\(f'(x)>0\),得\(x<-1\)或\(x>3\);令\(f'(x)<0\),得\(-1<x<3\),
所以\(f(x)\)在\([-2,-1)\)上单调递增,在\((-1,2 ]\)上单调递减,
因为\(f(-2)=-2\),\(f(2)=-22\),\(f(-1)=5\),
所以\(f(x)_{max}=5\),\(f(x)_{min}=-22\). -
答案 (1) \(y=x-1\);(2)\((-∞,4 ]\).
解析 (1)\(\because f'(x)=1+\ln x\),\(\therefore f'(1)=1=k\),
故切线方程是:\(y=x-1\);
(2)由题意,不等式化为\(ax≤2x\ln x+x^2+3\),因为\(x>0\),
所以 \(a \leq 2 \ln x+x+\dfrac{3}{x}\),当\(x>0\)时恒成立.
令\(h(x)=2 \ln x+x+\dfrac{3}{x}\),
则\(h^{\prime}(x)=\dfrac{2}{x}-\dfrac{3}{x^2}+1=\dfrac{(x+3)(x-1)}{x^2}\),
当\(0<x<1\)时,\(h'(x)<0\),\(x>1\)时,\(h'(x)>0\),
所以\(h(x)\)在\((0,1)\)上递减,在\((1,+∞)\)上递增.
故\(h(x)_{min}=h(1)=2\ln 1+1+3=4\).所以\(a≤4\).
故所求\(a\)的范围是\((-∞,4 ]\). -
答案 (1) 略;(2)略 .
解析 证明:(1) \(f^{\prime}(x)=1-\dfrac{1}{x}=\dfrac{x-1}{x}\),
当\(x>1\)时\(f'(x)>0\),\(f(x)\)单调增,
当\(0<x<1\)时\(f'(x)<0\),\(f(x)\)单调减,
所以 \(f(x)\)的最小值为\(f(1)=0\);
(2)由(1)知\(\ln x≤x-1\),
令\(x=1+\dfrac{1}{2^n }\)得\(\ln (1+\dfrac{1}{2^n })<\dfrac{1}{2^n }\),
所以\(\ln \left(1+\dfrac{1}{2}\right)+\ln \left(1+\dfrac{1}{2^2}\right)+\cdots \ln \left(1+\dfrac{1}{2^2}\right)<\dfrac{1}{2^1}+\dfrac{1}{2^2}+\cdots \dfrac{1}{2^n}\)\(=\dfrac{\dfrac{1}{2}\left(1-\left(\dfrac{1}{2}\right)^n\right)}{1-\dfrac{1}{2}}=1-\left(\dfrac{1}{2}\right)^n<1\),
所以 \(\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{2^2}\right) \cdots\left(1+\dfrac{1}{2^n}\right)<e\). -
答案 (1)\((0,1 ]\);(2) 略.
解析 (1)\(f'(x)=e^x-a(x\in R)\)
当\(a=0\)时,\(f(x)=e^x>0\)符合题意,
当\(a<0\)时,取\(x_0=-1+\dfrac{1}{a}\),
则\(f(x_0 )=e^{-1+\frac{1}{a}}-a(-1+\frac{1}{a}+1)=e^{-1+\frac{1}{a}}-1<0\),不符合题意,
③当\(a>0\)时,令\(f'(x)=0\),得\(x=\ln a\),
所以在\((-∞,\ln a)\)上,\(f'(x)<0\),\(f(x)\)单调递减,
在\((\ln a,+∞)\)上,\(f'(x)>0\),\(f(x)\)单调递增,
所以\(f(x)_{\min }=f(\ln a)=a-a(1+\ln a)=-a \ln a\),
若\(f(x)≥0\)恒成立,则\(f(x)\)的最小值大于等于\(0\),即\(-a \ln a≥0\),
因为\(a>0\),所以\(0<a⩽1\),
综上所述,\(a\)的取值范围为\((0,1 ]\).
(2)证明:
当\(a=0\)时,令\(h(x)=f(x)-(2+\ln x)=e^x-\ln x-2(x>0)\),
所以\(h'(x)=e^x-\dfrac{1}{x}\)在\((0,+∞)\)上单调递增,
又\(h'\left(\dfrac{1}{2}\right)=e^{\frac{1}{2}}-2<0\),\(h'(1)=e-1>0\),
所以存在\(x_0\in (0,+∞)\),使得\(h'(x_0 )=e^{x_0}-\dfrac{1}{x}_0 =0\),
即\(e^{x_0}=\dfrac{1}{x}_0\),且\(\dfrac{1}{2}<x_0<1\),
所以在\((0,x_0 )\)上,\(g'(x)<0\),\(g(x)\)单调递减,
在\((x_0,+∞)\)上,\(g'(x)>0\),\(g(x)\)单调递增,
所以\(h(x)_{min}=h(x_0 )=e^{x_0}-\ln x_0-2=\dfrac{1}{x}_0 +x_0-2\),
因为\(x_0 \in\left(\dfrac{1}{2}, 1\right)\),
所以\(h\left(x_0\right)=\dfrac{1}{x_0}+x_0-2>2 \sqrt{\dfrac{1}{x_0} \cdot x_0}-2=0\),
所以当\(a=0\)时,\(f(x)>2+\ln x(x>0)\),
所以当\(a=0\)时,曲线\(y=f(x)(x>0)\)总在曲线\(y=2+\ln x\)的上方.
【B组---提高题】
1.(多选)下列不等式中恒成立的有( )
A.\(\ln (x+1) \geq \dfrac{x}{x+1}\),\(x>-1\) \(\qquad \qquad \qquad\) B.\(\ln x \leq \dfrac{1}{2}\left(x-\dfrac{1}{x}\right)\),\(x>0\)
C.\(e^x≥x+1\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) D.\(\cos x≥1-\dfrac{1}{2} x^2\)
2.(多选)设 \(f(x)=\dfrac{\sin x}{x^a}\) , \(x \in\left[\dfrac{\pi}{6}, \dfrac{\pi}{3}\right]\)的最大值为\(M\),则( )
A.当\(a=-1\)时,\(M>\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad \qquad\) B.当\(a=1\)时,\(M<1\)
C.当\(a=2\)时,\(M<\sqrt{3}\) \(\qquad \qquad \qquad \qquad\) D.当\(a=3\)时,\(M<2\sqrt{3}\)
3.已知函数\(f(x)=ax^2\),\(g(x)=x\ln x\).
(1)若\(f(x)⩾g(x)\)恒成立,求实数\(a\)的取值范围;
(2)若\(a=1\),\(G(x)=f(x)-g(x)-1\),且\(mn>1\),证明:\(G(m)+G(n)>0\).
参考答案
-
答案 \(ACD\)
解析 选项\(A\),设 \(f(x)=\ln (x+1)-\dfrac{x}{x+1}(x>-1)\),
则 \(f^{\prime}(x)=\dfrac{1}{x+1}-\dfrac{1}{(x+1)^2}=\dfrac{x}{(x+1)^2}\),
当\(-1<x<0\)时,\(f'(x)<0\),\(f(x)\)单调递减;
当\(x>0\)时,\(f'(x)>0\),\(f(x)\)单调递增.
\(\therefore f(x)_{min}=f(0)=0\),即\(f(x)≥0\)在\((-1,+∞)\)上恒成立,
\(\therefore \ln (x+1) \geq \dfrac{x}{x+1}(x>-1)\)恒成立,即\(A\)正确;
选项\(B\),设 \(g(x)=\ln x-\dfrac{1}{2}\left(x-\dfrac{1}{x}\right)(x>0)\),
则 \(g^{\prime}(x)=\dfrac{1}{x}-\dfrac{1}{2}\left(1+\dfrac{1}{x^2}\right)=-\dfrac{(x-1)^2}{2 x^2} \leq 0\)恒成立,
\(\therefore g(x)\)在\((0,+∞)\)上单调递减,
又\(g(1)=0\),\(\therefore g(x)≤0\)在\((0,+∞)\)上不可能恒成立,
\(\therefore \ln x \leq \dfrac{1}{2}\left(x-\dfrac{1}{x}\right)(x>0)\)不恒成立,即\(B\)错误;
选项\(C\),设\(h(x)=e^x-x-1\),则\(h'(x)=e^x-1\),
令\(h'(x)=0\),解得\(x=0\),
当\(x<0\)时,\(h'(x)<0\),\(h(x)\)单调递减;
当\(x>0\)时,\(h'(x)>0\),\(h(x)\)单调递增.
\(\therefore h(x)_{min}=h(0)=0\),即\(h(x)≥0\)在\(R\)上恒成立,
\(\therefore e^x≥x+1\)恒成立,即\(C\)正确;
选项\(D\),设\(t(x)=\cos x-1+\dfrac{1}{2} x^2\),
则\(t'(x)=-\sin x+x\),
令\(m(x)=t'(x)=-\sin x+x\),
则\(m'(x)=-\cos x+1≥0\)恒成立,即\(m(x)\)在\(R\)上单调递增,
又\(m(0)=0\),
\(\therefore\)当\(x<0\)时,\(m(x)<0\),\(t'(x)<0\),\(t(x)\)单调递减;
当\(x>0\)时,\(m(x)>0\),\(t'(x)>0\),\(t(x)\)单调递增.
\(\therefore t(x)_{min}=t(0)=0\),即\(t(x)≥0\)在\(R\)上恒成立,
\(\therefore \cos x≥1-\dfrac{1}{2} x^2\)恒成立,即\(D\)正确.
故选:\(ACD\). -
答案 \(AB\)
解析 对于\(A\):当\(a=-1\)时,\(f(x)=x\sin x\),
\(f'(x)=\sin x+x\cos x>0\),\(x \in\left[\dfrac{\pi}{6}, \dfrac{\pi}{3}\right]\),
故\(f(x)\)在\(\left[\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\)递增,
故\(M=f\left(\dfrac{\pi}{3}\right)=\dfrac{\pi}{3} \sin \dfrac{\pi}{3}=\dfrac{\sqrt{3} \pi}{6}>\dfrac{\sqrt{3}}{2}\),故\(A\)正确;
对于\(B\):\(a=1\)时, \(f(x)=\dfrac{\sin x}{x}\),
\(f^{\prime}(x)=\dfrac{x \cos x-\sin x}{x^2}\),
令\(h(x)=x\cos x-\sin x\),\(x\in \left[\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\),
则\(h'(x)=\cos x-x\sin x-\cos x=-x\sin x<0\),
\(h(x)\)在\(x\in \left[\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\)递减,
而\(h\left(\dfrac{\pi}{6}\right)=\dfrac{\pi}{6} \times \dfrac{\sqrt{3}}{2}-\dfrac{1}{2}<0\),
故\(f'(x)<0\),\(f(x)\)在\(x\in \left[\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\)递减,
故\(M=f\left(\dfrac{\pi}{6}\right)=\dfrac{\frac{1}{2}}{\frac{\pi}{6}}=\dfrac{3}{\pi}<1\),故\(B\)正确;
对于\(C\):\(a=2\)时, \(f(x)=\dfrac{\sin x}{x^2}\) ,
则\(f^{\prime}(x)=\dfrac{x \cos x-2 \sin x}{x^3}\),
令\(h(x)=x\cos x-2\sin x\),\(x\in \left[\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\),
则\(h'(x)=\cos x-x\sin x-2\cos x=-\cos x-x\sin x<0\),
故\(h(x)\)在\(x\in \left[\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\)递减,
而\(h\left(\dfrac{\pi}{6}\right)<0\),\(h(x)\)在\(x\in \left[\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\)递减,
而\(h\left(\dfrac{\pi}{6}\right)<0\),即\(f'(x)<0\),\(f(x)\)在\(x\in \left[\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\)递减,
故\(M=f\left(\dfrac{\pi}{6}\right)=\dfrac{\frac{1}{2}}{\frac{\pi^2}{36}}=\dfrac{18}{\pi^2}>\sqrt{3}\),故\(C\)错误;
对于\(D\):\(a=3\)时, \(f(x)=\dfrac{\sin x}{x^3}\),
则\(f^{\prime}(x)=\dfrac{x \cos x-3 \sin x}{x^4}\),
令\(h(x)=x\cos x-3\sin x\),\(x\in \left[\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\),
则\(h'(x)=\cos x-x\sin x-3\cos x=-2\cos x-x\sin x<0\),
故\(h(x)\)在\(x\in \left[\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\)递减,
而\(h\left(\dfrac{\pi}{6}\right)<0\),\(h(x)\)在\(x\in \left[\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\)递减,
而\(h\left(\dfrac{\pi}{6}\right)<0\),即\(f'(x)<0\),\(f(x)\)在\(x\in \left[\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\)递减,
故 \(M=f\left(\dfrac{\pi}{6}\right)=\dfrac{108}{\pi^3}>\sqrt{3}\),故\(D\)错误;
故选:\(AB\). -
答案 (1) \(\left[\dfrac{1}{e},+∞\right)\);(2)略.
解析 (1) \(f(x)=ax^2\),\(g(x)=x\ln x\),\(x\in (0,+∞)\)
\(f(x)⩾g(x)\)恒成立 \(\Leftrightarrow a \geqslant \dfrac{\ln x}{x}\),\(x\in (0,+∞)\).
令\(u(x)=\dfrac{\ln x}{x}\),\(x\in (0,+∞)\).
则\(u^{\prime}(x)=\dfrac{1-\ln x}{x^2}\),令 \(u^{\prime}(x)=\dfrac{1-\ln x}{x^2}=0\),解得\(x=e\).
可得\(x\in (0,e)\)时,\(u'(x)>0\),函数\(u(x)\)单调递增;
\(x\in (e,+∞)\)时,\(u'(x)<0\),函数\(u(x)\)单调递减.
可得\(x=e\)时,函数\(u(x)\)取得极大值即最大值,\(u(e)=\dfrac{1}{e}\),
\(\therefore a⩾\dfrac{1}{e}\),
\(\therefore\)实数\(a\)的取值范围是\(\left[\dfrac{1}{e},+∞\right)\).
(2)证明:若\(a=1\),
则\(G(x)=f(x)-g(x)-1=x^2-x\ln x-1\),\(x\in (0,+∞)\).
\(G'(x)=2x-\ln x-1=H(x)\), \(H^{\prime}(x)=2-\dfrac{1}{x}=\dfrac{2 x-1}{x}\),
\(\therefore x=\dfrac{1}{2}\)时,函数\(H(x)\)取得极小值即最小值,
\(\therefore G'(x)=H(x)⩾H\left(\dfrac{1}{2}\right)=1-\ln \dfrac{1}{2}-1=\ln 2>0\),
\(\therefore\)函数\(G(x)\)在\(x\in (0,+∞)\)上单调递增,\(G(1)=0\).
不妨设\(n⩽m\).
由\(mn>1\),若\(m>n⩾1\)时,则\(G(m)+G(n)>0\)成立.
若\(m>1⩾n>0\)时,\(\because mn>1\), \(\therefore m>\dfrac{1}{n}>1\),
则\(G(m)+G(n)>G\left(\dfrac{1}{n}\right)+G(n)\),
要证明\(G(m)+G(n)>0\),只要证明\(G\left(\dfrac{1}{n}\right)+G(n) \geqslant 0\)即可.
令\(F(x)=G(x)+G\left(\dfrac{1}{x}\right)=x^2-x \ln x-1+\dfrac{1}{x^2}-\dfrac{1}{x} \ln \dfrac{1}{x}-1\)
\(=\left(x-\dfrac{1}{x}\right)^2+\left(\dfrac{1}{x}-x\right) \ln x=\dfrac{\left(1-x^2\right)\left(1-x^2+x \ln x\right)}{x^2}\) ,\(x\in (0,1)\),
令\(h(x)=1-x^2+x\ln x\),\(x\in (0,1)\),\(h(1)=0\),
\(h'(x)=-2x+\ln x+1\), \(h^{\prime \prime}(x)=-2+\dfrac{1}{x}=\dfrac{1-2 x}{x}\),
可得\(x=\dfrac{1}{2}\)时,函数\(h'(x)\)取得极大值即最大值,\(h^{\prime}\left(\dfrac{1}{2}\right)=-1+\ln \dfrac{1}{2}+1=-\ln 2<0\),
\(\therefore h(x)=1-x^2+x\ln x\)在\(x\in (0,1)\)上单调递减,
\(\therefore h(x)>h(1)=0\),
\(\therefore F(x)>F(1)=0\),\(x\in (0,1)\),
\(\therefore G(m)+G(n)>0\)成立.
综上可得:\(mn>1\),\(G(m)+G(n)>0\)成立.
【C组---拓展题】
1.已知函数\(f(x)=x+a\ln x+\dfrac{1}{e^x} -x^a (a<0)\),若\(f(x)≥0\)在\(x\in [2,+∞)\)上恒成立,则实数\(a\)的取值范围为\(\underline{\quad \quad}\).
2.已知\(f(x)=x\ln x-\dfrac{1}{2} mx^2-x\),\(m\in R\).若\(f(x)\)有两个极值点\(x_1\),\(x_2\),且\(x_1<x_2\),求证:\(x_1 x_2>e^2\) (\(e\)为自然对数的底数).
参考答案
-
答案 \([-e,+∞)\)
解析 由\(f(x)≥0\)在\(x\in [2,+∞)\)上恒成立,
得\(\ln x^a-x^a \geq \ln e^{-x}-e^{-x}\) 在\(x\in [2,+∞)\)上恒成立,
易知当\(x\in [2,+∞)\),\(a<0\)时,\(0<x^a<1\), \(0<e^{-x}<1\),
令函数\(g(t)=\ln t-t(0<t<1)\),
则\(a=\dfrac{1}{t}-1>0\),\(g(t)\)单调递增,
故有 \(x^a \geq e^{-x}\),
则\(a \geq \log _x e^{-x}=-\dfrac{x}{\ln x}\)在\(x\in [2,+∞)\)上恒成立,
令\(F(x)=-\dfrac{x}{\ln x}(x \geq 2)\),
则\(F^{\prime}(x)=\dfrac{1-\ln x}{(\ln x)^2}\),
易得\(F(x)\)在\([2,e)\)上单调递增,在\([e,+∞)\)上单调递减,
故\(F(x)_{max}=F(e)=-e\),
故\(a≥-e\),
即实数\(a\)的取值范围是\([-e,+∞)\).
故答案为:\([-e,+∞)\). -
证明 欲证\(x_1 x_2>e^2\),需证\(\ln x_1+\ln x_2>2\).
若\(f(x)\)有两个极值点\(x_1\),\(x_2\),即函数\(f'(x)\)有两个零点.
又\(f'(x)=\ln x-mx\),所以\(x_1\),\(x_2\)是方程\(f'(x)=0\)的两个不同实根.
于是,有\(\left\{\begin{array}{l} \ln x_1-m x_1=0 \\ \ln x_2-m x_2=0 \end{array}\right.\),解得 \(m=\dfrac{\ln x_1+\ln x_2}{x_1+x_2}\).
另一方面,由 \(\left\{\begin{array}{l} \ln x_1-m x_1=0 \\ \ln x_2-m x_2=0 \end{array}\right.\),得\(\ln x_2-\ln x_1=m\left(x_2-x_1\right)\),
从而可得\(\dfrac{\ln x_2-\ln x_1}{x_2-x_1}=\dfrac{\ln x_1+\ln x_2}{x_1+x_2}\).
于是, \(\ln x_1+\ln x_2=\dfrac{\left(\ln x_2-\ln x_1\right)\left(x_2+x_1\right)}{x_2-x_1}=\dfrac{\left(1+\dfrac{x_2}{x_1}\right) \ln \dfrac{x_2}{x_1}}{\dfrac{x_2}{x_1}-1}\).
又\(0<x_1<x_2\),设 \(z=\dfrac{x_2}{x_1}\),则\(t>1\).
因此\(\ln x_1+\ln x_2=\dfrac{(1+t) \ln t}{t-1}\),\(t>1\).
要证\(\ln x_1+\ln x_2>2\),即证 \(\dfrac{(t+1) \ln t}{t-1}>2\),\(t>1\).
即当\(t>1\)时,有 \(\ln t>\dfrac{2(t-1)}{t+1}\).
设函数 \(h(t)=\ln t-\dfrac{2(t-1)}{t+1}\),\(t≥1\),
则\(h^{\prime}(t)=\dfrac{1}{t}-\dfrac{2(t+1)-2(t-1)}{(t+1)^2}=\dfrac{(t-1)^2}{t(t+1)^2} \geq 0\),
所以\(h(t)\)为\((1,+∞)\)上的增函数.注意到\(h(1)=0\),
因此\(h(t)≥h(1)=0\).
于是,当\(t>1\)时,有 \(\ln t>\dfrac{2(t-1)}{t+1}\).
所以有\(\ln x_1+\ln x_2>2\)成立,\(x_1 x_2>e^2\).

