5.7 三角函数的应用
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步巩固,难度2颗星!
基础知识
三角函数模型
现实生活中存在大量具有周而复始、循环往复特点的周期运动变化现象,如果某种变化着的现象具有周期性,那么就可以考虑借助三角函数来描述.比如农业中筒车中盛水筒距离水面的相对高度与时间的关系,物理中的简谐运动等.
简谐运动
现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的振动等等.这些都是物体在某一中心位置附近循环往复的运动.在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为 “简谐运动”. 可以证明,在适当的直角坐标系下,简谐运动可以用函数\(y=A\sin \left(ωx+φ\right),x\in\left[0,+∞\right)\)表示,其中\(A>0\),\(ω>0\).描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关:
\(A\)就是这个简谐运动的振幅,它是做简谐运动的物体离开平衡位置的最大距离;
这个简谐运动的周期是 \(T=\dfrac{2 \pi}{\omega}\),它是做简谐运动的物体往复运动一次所需要的时间;
这个简谐运动的频率由公式 \(f=\dfrac{1}{T}=\dfrac{\omega}{2 \pi}\)给出,它是做简谐运动的物体在单位时间内往复运动的次数;
\(ωx+φ\)称为相位;\(x=0\)时的相位\(φ\)称为初相.
基本方法
【题型1】 函数解析式的应用
【典题1】 水车是一种利用水流动力进行灌溉的工具,是人类一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个水车的示意图,已知水车逆时针匀速旋转一圈的时间是\(80\)秒,半径为\(3\)米,水车中心(即圆心)距水面\(1.5\)米若.以水面为\(x\)轴,圆心到水面的垂线为\(y\)轴建立直角坐标系,水车的一个水斗从出水面点\(A\)处开始计时,经过\(t\)秒后转到\(P\)点的位置,则点\(P\)到水面的距离\(h\)与时间\(t\)的函数关系式为( )

A.\(h=3\sin \left(\dfrac{\pi}{40}t-\dfrac{\pi}{6}\right)+1.5\) \(\qquad \qquad \qquad \qquad\) B.\(h=1.5\cos \left(\dfrac{\pi}{40}t+\dfrac{\pi}{6}\right)+3\)
C.\(h=3\cos \left(\dfrac{\pi}{40}t-\dfrac{\pi}{3}\right)+1.5\) \(\qquad \qquad \qquad \qquad\) D.\(h=1.5\sin \left(\dfrac{\pi}{40}t+\dfrac{\pi}{3}\right)+3\)
解析 由题意,如图,过\(P\)向\(x\)轴作垂线,垂足为\(E\),

则\(h=PE=PD+1.5\),
\(\because r=3\),\(BO=1.5\),可得\(∠CBA=∠BAO=\dfrac{\pi}{6}\),
\(\because\) 水车的角速度\(ω=\dfrac{2\pi}{80}=\dfrac{\pi}{40}\),
\(\therefore\)由题意可得,\(∠PBA=\dfrac{\pi}{40} t\),可得\(∠PBD=∠PBA-∠CBA=\dfrac{\pi}{40} t-\dfrac{\pi}{6}\),
\(\therefore\)在\(△PBD\)中,\(PD=PB\sin ∠PBD=3\sin \left(\dfrac{\pi}{40} t-\dfrac{\pi}{6}\right)\),
\(\therefore\) 点\(P\)到水面的距离\(h=PD+1.5=3\sin \left(\dfrac{\pi}{40 }t-\dfrac{\pi}{6}\right)+1.5\).
故选:\(A\).
【典题2】 设\(y=f\left(t\right)\)是某港口水的深度\(y\left(m\right)\)关于时间\(t\)(时)的函数,其中\(0≤t≤24\),下表是该港口某一天从\(0\)时至\(24\)时记录的时间\(t\)与水深\(y\)的关系:
| \(t\) | \(0\) | \(3\) | \(6\) | \(9\) | \(12\) | \(15\) | \(18\) | \(21\) | \(24\) |
|---|---|---|---|---|---|---|---|---|---|
| \(y\) | \(12\) | \(15.1\) | \(12.1\) | \(9.1\) | \(11.9\) | \(14.9\) | \(11.9\) | \(8.9\) | \(12.1\) |
经长期观察,函数\(y=f\left(x\right)\)的图象可近似地看成函数\(y=k+A\sin \left(ωt+φ\right)\)的图象,下面的函数中,最能近似表示表中数据的对应关系的函数是( )
A.\(y=12+3\sin \dfrac{\pi}{6} t,t\in\left[0,24\right]\) \(\qquad \qquad \qquad \qquad\) B.\(y=12+3\sin \left(\dfrac{\pi}{6} t+π\right),t\in\left[0,24\right]\)
C.\(y=12+3\sin \dfrac{\pi}{12} t,t\in\left[0,24\right]\) \(\qquad \qquad \qquad \qquad\) D.\(y=12+3\sin \left(\dfrac{\pi}{12} t+\dfrac{\pi}{2}\right),t\in\left[0,24\right]\)
解析 \(\because y=f\left(x\right)\)的图象可以近似地看成\(y=k+A\sin \left(ωt+φ\right)\)的图象,
\(\therefore y=f\left(x\right)\)具有周期性.当\(t=3,15\)时,\(y\)取得最大值,
\(\therefore T=15-3=12\),
则 \(\omega=\dfrac{2 \pi}{T}=\dfrac{2 \pi}{12}=\dfrac{\pi}{6}\),\(\therefore\) 排除\(C\)、\(D\).
下面将点\(\left(3,15.1\right)\)的坐标分别代入\(A\)、\(B\)验证.
将\(t=3\)代入\(A\),得\(y=12+3\sin \left(\dfrac{\pi}{6}×3\right)=15\);
代入\(B\),得\(y=12+3\sin \left(\dfrac{\pi}{6}×3+π\right)=9\),与\(15.1\)相差太多.
\(\therefore\) 应选\(A\).
【典题3】 已知电流\(I\)与时间\(t\)的关系为\(I=A\sin \left(ωt+φ\right)\).
\(\left(1\right)\)如图所示的是\(I=A\sin \left(ωt+φ\right)\left(ω>0,|φ|<\dfrac{\pi}{2}\right)\)在一个周期内的图象,根据图中数据求\(I=A\sin \left(ωt+φ\right)\)的解析式;

\(\left(2\right)\)如果\(t\)在任意一段 \(\dfrac{1}{150}\)秒的时间内,电流\(I=A\sin \left(ωt+φ\right)\)都能取得最大值和最小值,那么\(ω\)的最小正整数值是多少?
解析 \(\left(1\right)\)由图知\(A=300\),设\(t_1=-\dfrac{1}{900}\), \(t_2=\dfrac{1}{180}\),
则周期 \(T=2\left(t_2-t_1\right)=2\left(\dfrac{1}{180}+\dfrac{1}{900}\right)=\dfrac{1}{75}\).
\(\therefore \omega=\dfrac{2 \pi}{T}=150 \pi\).
又当 \(t=\dfrac{1}{180}\)时,\(I=0\),即 \(\sin \left(150 \pi \cdot \dfrac{1}{180}+\varphi\right)=0\).
而\(|φ|<\dfrac{\pi}{2}\),\(\therefore φ=\dfrac{\pi}{6}\).
故所求的解析式为 \(I=300 \sin \left(150 \pi t+\dfrac{\pi}{6}\right)\).
\(\left(2\right)\)依题意,周期 \(T \leq \dfrac{1}{150}\),即 \(\dfrac{2 \pi}{\omega} \leq \dfrac{1}{150}(\omega>0)\),
\(\therefore ω≥300π>942\).
又\(ω\in N^*\),
故所求最小正整数\(ω=943\).
【巩固练习】
1.某游乐场中半径为\(30\)米的摩天轮逆时针(固定从一侧观察)匀速旋转,每\(5\)分钟转一圈,其最低点离底面\(5\)米,如果以你从最低点登上摩天轮的时刻开始计时,那么你与底面的距离高度\(y\)(米)随时间\(t\)(秒)变化的关系式为( )
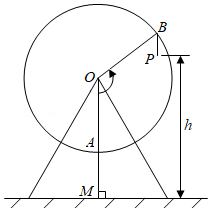
A.\(y=30\sin \left(\dfrac{2 \pi}{5} t-\dfrac{\pi}{2}\right)+35\) \(\qquad \qquad \qquad \qquad\) B. \(y=30 \sin \left(\dfrac{\pi}{150} t-\dfrac{\pi}{2}\right)+35\)
C.\(y=30\sin \left(\dfrac{2 \pi}{5} t+\dfrac{\pi}{2}\right)+5\) \(\qquad \qquad \qquad \qquad\) D. \(y=30 \sin \left(\dfrac{\pi}{150} t-\dfrac{\pi}{2}\right)+5\)
2.如图,半径为\(4m\)的水轮绕着圆心\(O\)逆时针做匀速圆周运动,每分钟转动\(4\)圈,水轮圆心\(O\)距离水面\(2m\),如果当水轮上点\(P\)从离开水面的时刻\(P_0\)开始计算时间.
\(\left(1\right)\)将点\(P\)距离水面的高度\(y\left(m\right)\)与时间\(t\left(s\right)\)满足的函数关系;
\(\left(2\right)\)求点\(P\)第一次到达最高点需要的时间.

3.已知某海滨浴场水浪的高度\(y\)(米)是时间\(t(0≤t≤24,\)单位:小时\()\)的函数,记作:\(y=f\left(t\right)\),下表是某日各时的浪高数据:
| \(t\)(时) | \(0\) | \(3\) | \(6\) | \(9\) | \(12\) | \(15\) | \(18\) | \(21\) | \(24\) |
|---|---|---|---|---|---|---|---|---|---|
| \(y\)(米) | \(1.5\) | \(1.0\) | \(0.5\) | \(1.0\) | \(1.5\) | \(1.0\) | \(0.5\) | \(0.99\) | \(1.5\) |
经长期观测,\(y=f\left(t\right)\)的曲线可近似地所成是函数\(y=A\cos ωt+b\)的图象.
\(\left(1\right)\)根据以上数据,求函数\(y=A\cos ωt+b\)的函数表达式;
\(\left(2\right)\)依据规定,当水浪高度高于\(1\)米时才对冲浪爱好者开放,请依据\(\left(1\right)\)的结论,判断一天内的上午\(8.00\)时至晚上\(20:00\)的之间,有多少时间可供冲浪者进行运动?
参考答案
-
答案 \(B\)
解析 设\(y=A\sin \left(ωt+φ\right)+B\),
由题意可得\(A=30\), \(\omega=\dfrac{2 \pi}{300}=\dfrac{\pi}{150}\),\(B=30×2+5-30=35\),
\(\left(0,5\right)\)为最低点,代入可得\(5=30\sin φ+35\),,\(\sin φ=-1\)
\(φ=-\dfrac{\pi}{2}+2kπ\),\(k=0\)时,\(φ=-\dfrac{\pi}{2}\),
\(y=30 \sin \left(\dfrac{\pi}{150} t-\dfrac{\pi}{2}\right)+35\),
故选:\(B\). -
答案 \(\left(1\right) y=4\sin \left(\dfrac{2 \pi}{15} t-\dfrac{\pi}{6}\right)+2\);\(\left(2\right) 5s\).
解析 \(t\left(s\right)\left(1\right)\)以\(O\)为原点建立如图所示的直角坐标系.
由于水轮绕着圆心\(O\)做匀速圆周运动,
可设点\(P\)到水面的距离\(y\left(m\right)\)与时间\(t\left(s\right)\)满足函数关系\(y=A\sin \left(\omega t+φ\right)+2,\left(-\dfrac{\pi}{2}<φ<\dfrac{\pi}{2}\right)\),
\(\because\)水轮每分钟旋转\(4\)圈, \(\therefore T=\dfrac{60}{4}=15\), \(\therefore \omega=\dfrac{2 \pi}{T}=\dfrac{2 \pi}{15}\).
\(\because\)水轮半径为\(4 m\),\(\therefore A=4\).
\(\therefore y=4\sin \left(\dfrac{2 \pi}{15} t+φ\right)+2,\left(-\dfrac{\pi}{2}<φ<0\right)\).
当\(t=0\)时,\(y=0\).
\(\therefore φ=-\dfrac{\pi}{6}\).\(\therefore y=4\sin \left(\dfrac{2 \pi}{15} t-\dfrac{\pi}{6}\right)+2\).
\(\left(2\right)\)由于最高点距离水面的距离为\(6\),\(\therefore 6=4\sin \left(\dfrac{2 \pi}{15}t-\dfrac{\pi}{6}\right)+2\).
\(\therefore \sin \left(\dfrac{2 \pi}{15}t-\dfrac{\pi}{6}\right)=1\).
\(\therefore \dfrac{2 \pi}{15} t-\dfrac{\pi}{6}=\dfrac{\pi}{2}+2 k \pi(k \in Z)\).
\(\therefore t=5+15k \left(k\in Z \right)\).
\(\therefore\)当\(k=0\)时,即\(t=5\left(s\right)\)时,点\(P\)第一次达到最高点.

-
答案 \(\left(1\right) y=\dfrac{1}{2} \cos \dfrac{\pi}{6} t+1\);\(\left(2\right) 6\)个小时.
解析 \(\left(1\right)\)由表中数据知周期\(T=12\),
\(\therefore \omega=\dfrac{2 \pi}{T}=\dfrac{2 \pi}{12}=\dfrac{\pi}{6}\),
由\(t=0\),\(y=1.5\),得\(A+b=1.5\).
由\(t=3\),\(y=1.0\),得\(b=1.0\).
\(\therefore A=0.5\),\(b=1\),\(\therefore y=\dfrac{1}{2} \cos \dfrac{\pi}{6} t+1\).
\(\left(2\right)\)由题知,当\(y>1\)时才可对冲浪者开放,
\(\therefore \dfrac{1}{2} \cos \dfrac{\pi}{6} t+1>1\),\(\therefore \cos \dfrac{\pi}{6} t>0\),
\(\therefore 2kπ-\dfrac{\pi}{2}<\dfrac{\pi}{6} t<2kπ+\dfrac{\pi}{2},k\in Z\),
即\(12k-3<t<12k+3,k\in Z\).①
\(\because 0≤t≤24\),故可令①中\(k\)分别为\(0\),\(1\),\(2\),
得\(0≤t<3\)或\(9<t<15\)或\(21<t≤24\).
\(\therefore\)在规定时间上午\(8:00\)至晚上\(20:00\)之间,
有\(6\)个小时时间可供冲浪者运动,即上午\(9:00\)至下午\(3:00\).
【题型2】综合应用
【典题1】 水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为\(R\)的水车,一个水斗从点\(A\left(3\sqrt{3},-3\right)\)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时\(60\)秒.经过\(t\)秒后,水斗旋转到\(P\)点,设\(P\)的坐标为\(\left(x,y\right)\),其纵坐标满足\(y=f\left(t\right)=R\sin \left(ωt+φ\right)\)\(\left(t≥0,ω>0,|φ|<\dfrac{\pi}{2}\right)\).则下列叙述错误的是( )

A.\(R=6\),\(ω=\dfrac{\pi}{30}\),\(φ=-\dfrac{\pi}{6}\)
B.当\(t\in \left[35,55\right]\)时,点\(P\)到\(x\)轴的距离的最大值为\(6\)
C.当\(t\in \left[10,25\right]\)时,函数\(y=f\left(t\right)\)单调递减
D.当\(t=20\)时,\(|PA|=6\sqrt{3}\)
解析 由题意, \(R=\sqrt{27+9}=6\), \(T=60=\dfrac{2 \pi}{\omega}\), \(\therefore \omega=\dfrac{\pi}{30}\),
点\(A\left(3\sqrt{3},-3\right)\)代入可得\(-3=6\sin φ\),\(\because |φ|<\dfrac{\pi}{2}\),\(\therefore φ=-\dfrac{\pi}{6}\).故\(A\)正确;
\(f\left(t\right)=6\sin \left(\dfrac{\pi}{30} t-\dfrac{\pi}{6}\right)\),当\(t\in \left[35,55\right]\)时,\(\dfrac{\pi}{30} t-\dfrac{\pi}{6}\in \left[π, \dfrac{5}{3} π\right]\),
\(\therefore\)点\(P\)到\(x\)轴的距离的最大值为\(6\),正确;
当\(t\in \left[10,25\right]\)时,\(\dfrac{\pi}{3}0 t-\dfrac{\pi}{6}\in \left[\dfrac{\pi}{6},2\dfrac{\pi}{3}\right]\),函数\(y=f\left(t\right)\)单调递减,不正确;
当\(t=20\)时,\(\dfrac{\pi}{30} t-\dfrac{\pi}{6}=\dfrac{\pi}{2}\),\(P\)的纵坐标为\(6\), \(|P A|=\sqrt{27+81}=6 \sqrt{3}\),\(D\)正确,
故选:\(C\).
【典题2】 如图,已知扇形\(AOB\)的半径为\(1\),中心角为\(60°\),四边形\(PQRS\)是扇形的内接矩形,\(P\)为 \(\widehat{A B}\)上一动点,问:点\(P\)在怎样的位置时,矩形\(PQRS\)的面积的最大?并求出这个最大值.

解析 如图,在\(Rt△OPS\)中,设\(∠POS=α\),则\(OS=\cos α\),\(PS=\sin α\),
在\(Rt△ORQ\)中, \(\dfrac{Q R}{O R}=\tan 60^{\circ}=\sqrt{3}\),所以 \(O R=\dfrac{\sqrt{3}}{3} Q R=\dfrac{\sqrt{3}}{3} \sin \alpha\).
\(\therefore RS=OS-OR=\cos α-\dfrac{\sqrt{3}}{3} \sin α\).
设矩形\(ABCD\)的面积为\(S\),
则\(S=\left(\cos α-\dfrac{\sqrt{3}}{3} \sin α\right)\sin α=\sin α\cos α-\dfrac{\sqrt{3}}{3} \sin ^2α\)
\(=\dfrac{1}{2} \sin 2 \alpha+\dfrac{\sqrt{3}}{6} \cos 2 \alpha-\dfrac{\sqrt{3}}{6}=\dfrac{\sqrt{3}}{3}\left(\dfrac{\sqrt{3}}{2} \sin 2 \alpha+\dfrac{1}{2} \cos 2 \alpha\right)-\dfrac{\sqrt{3}}{6}\)
\(=\dfrac{\sqrt{3}}{3} \sin \left(2 \alpha+\dfrac{\pi}{6}\right)-\dfrac{\sqrt{3}}{6}\).
由于\(0<α<\dfrac{\pi}{3}\),
所以当\(2α+\dfrac{\pi}{6}=\dfrac{\pi}{2}\),即\(α=\dfrac{\pi}{6}\)时, \(S_{\max }=\dfrac{\sqrt{3}}{3}-\dfrac{\sqrt{3}}{6}=\dfrac{\sqrt{3}}{6}\).
因此,当\(α=\dfrac{\pi}{6}\)时,矩形\(PQRS\)的面积最大,最大面积为 \(\dfrac{\sqrt{3}}{6}\).

【典题3】 如图,\(ABCD\)是块边长为\(100m\)的正方形地皮,其中扇形\(AST\)是一半径为\(90m\)的扇形小山,其余部分都是平地,一开发商想在平地上建一个矩形停车场,使矩形的一个顶点\(P\)在弧 \(\widehat{S T}\)上,相邻两边\(CQ\)、\(CR\)落在正方形的边\(BC\)、\(CD\)上.
\(\left(1\right)\)设\(∠PAB=θ\),把矩形停车场\(PQCR\)的面积表示为\(θ\)的函数
\(\left(2\right)\)求矩形\(PQCR\)面积的最大值和最小值.

解析 \(\left(1\right)\)设\(∠PAB=θ\)(其中\(0°≤θ≤90°\)),延长\(RT\)交\(AB\)于\(M\),
所以\(AM=90\cos θ\),\(MP=90\sin θ\),
所以\(PQ=MB=100-90\cos θ\),
所以\(PR=MR-MP=100-90\sin θ\),
所以矩形\(PQRC\)的面积为 \(S_{\text {矩形 } P Q R C}=P Q \cdot P R=(100-90 \cos \theta)(100-90 \sin \theta)\)
\(=10000-9000\left(\sin θ+\cos θ\right)+8100\sin θ\cos θ\),(其中\(0°≤θ≤90°\));
\(\left(2\right)\)令\(t=\sin θ+\cos θ\)(其中\(1≤t≤\sqrt{2}\)),
则 \(\sin \theta \cos \theta=\dfrac{t^2-1}{2}\);
所以 \(S_{\text {知形 } P Q R C}=10000-9000 t+8100 \cdot \dfrac{t^2-1}{2}=4050\left(t-\dfrac{10}{9}\right)^2+950\);
所以当 \(t=\dfrac{10}{9}\)时,\(S\)取得最小值为\(950m^2\),
当\(t=\sqrt{2}\)时 \(S\)取得最大值为\(\left(14050-9000\sqrt{2}\right)m^2\).
【巩固练习】
1.如图是半径为\(1\)的半圆,且\(PQRS\)是半圆的内接矩形,设\(∠SOP=α\),则其值为\(\underline{\quad \quad}\)时,矩形的面积最大,最大面积为\(\underline{\quad \quad}\).

2.如图,某正方形公园\(ABCD\),在\(ABD\)区域内准备修建三角形花园\(BMN\),满足\(MN\)与\(AB\)平行(点\(N\)在\(BD\)上),且\(AB=AD=BM=2\)(单位:百米).设\(∠ABM=θ\),\(△BMN\)的面积为\(S\)(单位:百米平方).
\(\left(1\right)\)求\(S\)关于\(θ\)的函数解析式
\(\left(2\right)\)求\(S\left(θ\right)\)的最大值,并求出取到最大值时\(θ\)的值.

3.如图,半圆\(O\)的直径为\(2\),\(A\)为直径延长线上的一点,\(OA=2\),\(B\)为半圆上任意一点,以\(AB\)为一边作等边三角形\(ABC\),设\(∠AOB=α\left(0<α<π\right)\).
\(\left(1\right)\)当\(α\)为何值时,四边形\(OACB\)面积最大,最大值为多少;
\(\left(2\right)\)当\(α\)为何值时,\(OC\)长最大,最大值为多少.

参考答案
-
答案 \(\dfrac{\pi}{4}\),\(1\)
解析 \(∠SOP=α\),\(PS=\sin α\),\(SR=2\cos α\),
\(\therefore\)矩形\(PQRS\)的面积\(S=SR\cdot PS=2\cos α \cdot\sin α=\sin 2α\),
当\(α=\dfrac{\pi}{4}\)时,\(S_{\max}=1\),
故答案为:\(\dfrac{\pi}{4}\),\(1\). -
答案 \(\left(1\right) S\left(θ\right)2=\sin θ \left(\cos θ-\sin θ\right) \left(θ\in \left(0,\dfrac{\pi}{4}\right)\right)\);
\(\left(2\right) S\left(θ\right)\)的最大值为\(\sqrt{2}-1\)百米平方,此时\(θ=\dfrac{\pi}{8}\).
解析 \(\left(1\right)\)依题意得,\(∠ABD=∠CBD=\dfrac{\pi}{4}\),延长\(MN\)交\(BC\)于点\(H\).

因为\(MN∥AB\),且四边形\(ABCD\)为正方形,
所以\(∠NMB=∠ABM=θ\),\(∠HNB=∠CBD=\dfrac{\pi}{4}\),
在\(Rt△BMH\)中,\(BH=BM\sin θ=2\sin θ\).\(MH=BM\cos θ=2\cos θ\),
在\(Rt△BNH\)中,因为\(∠HNB=∠CBD=\dfrac{\pi}{4}\),
所以\(NH=BH=2\sin θ\).
所以\(MN=MH-NH=2\left(\cos θ-\sin θ\right)\),
所以\(S\left(θ\right)= \dfrac{1}{2} MN⋅BH=2\sin θ\left(\cos θ-\sin θ\right)\left(θ\in \left(0,\dfrac{\pi}{4}\right)\right)\).
\(\left(2\right)\)由\(\left(1\right)\)得,
\(S\left(θ\right)=2\sin θ\left(\cos θ-\sin θ\right)=\sin 2θ-\left(1-\cos 2θ\right)=\sin 2θ+\cos 2θ-1\)
\(=\sqrt{2}\sin \left(2θ+\dfrac{\pi}{4}\right)-1\),
因为\(θ\in \left(0,\dfrac{\pi}{4}\right)\),所以\(2θ+\dfrac{\pi}{4}\in \left(\dfrac{\pi}{4},\dfrac{3\pi}{4}\right)\),
所以当\(2θ+\dfrac{\pi}{4}=\dfrac{\pi}{2}\),即\(θ=\dfrac{\pi}{8}\)时,\(S\left(θ\right)_{\max}=\sqrt{2}-1\),
答:\(S\left(θ\right)\)的最大值为\(\sqrt{2}-1\)百米平方,此时\(θ=\dfrac{\pi}{8}\). -
答案 \(\left(1\right)\)当 \(\alpha=\dfrac{5}{6} \pi\),四边形\(OABC\)面积最大值为 \(2+\dfrac{5}{4} \sqrt{3}\);
\(\left(2\right)\)当 \(\alpha=\dfrac{2}{3} \pi\)时,\(OC\)有最大值\(3\).
解析 \(\left(1\right)\)由题意,在\(△OAB\)中,\(AB^2=5-4\cos α\),
三角形\(S_{△AOB}=\sin α\),三角形 \(S_{\triangle A B C}=\dfrac{\sqrt{3}}{4} A B^2=\dfrac{5}{4} \sqrt{3}-\sqrt{3} \cos \alpha\)
四边形\(OABC\)的面积为 \(S=S_{\triangle A O B}+S_{\triangle A B C}=2 \sin \left(\alpha-\dfrac{\pi}{3}\right)+\dfrac{5}{4} \sqrt{3}\).
\(\because 0<α<π\),
\(\therefore\)当\(α-\dfrac{\pi}{3}=\dfrac{\pi}{2}\),即 \(\alpha=\dfrac{5}{6} \pi\)时,四边形\(OABC\)的面积最大,
故得当 \(\alpha=\dfrac{5}{6} \pi\),四边形\(OABC\)的面积最大且最大值为 \(2+\dfrac{5}{4} \sqrt{3}\).
\(\left(2\right)△OAB\)中, \(\sin \angle O A B=\dfrac{O B \sin \angle A O B}{A B}=\dfrac{\sin \alpha}{\sqrt{5-4 \cos \alpha}}\)
\(\therefore \cos \angle O A B=\sqrt{1-\sin ^2 \angle O A B}=\dfrac{2-\cos \alpha}{\sqrt{5-4 \cos \alpha}}\)
\(\therefore \cos \angle O A C=\cos \left(\angle O A B+60^{\circ}\right)=\dfrac{2-\cos \alpha-\sqrt{3} \sin \alpha}{2 \sqrt{5-4 \cos \alpha}}\).
\(△OAC\)中,\(OC^2=OA^2+AC^2-2\cdot OA\cdot AC\cdot \cos ∠OAC=2\sqrt{3} \sin α-2\cos α+5\)
即 \(O C=\sqrt{4 \sin \left(\alpha-\dfrac{\pi}{6}\right)+5}(\alpha \in(0, \pi))\)
\(\because \alpha-\dfrac{\pi}{6} \in\left(-\dfrac{\pi}{6}, \dfrac{5 \pi}{6}\right)\) , \(\therefore \alpha-\dfrac{\pi}{6}=\dfrac{\pi}{2}\),\(\therefore α-\dfrac{\pi}{6}=\dfrac{\pi}{2}\),
即 \(\alpha=\dfrac{2}{3} \pi\)时,\(OC\)有最大值.
故得当 \(\alpha=\dfrac{2}{3} \pi\)时,\(OC\)有最大值\(3\).
分层练习
【A组---基础题】
1.如图所示为一简谐振动的图象,则下列判断正确的是( )

A.该质点的振动周期为\(0.7 s\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) B.该质点的振幅 为\(5 cm\)
C.该质点在\(0.1 s\)和\(0.5 s\)时振动速度最大 \(\qquad \qquad \qquad \quad\) D.该质点在\(0.3 s\)和\(0.7 s\)时振动速度为零
2.电流\(I\left(A\right)\)随时间\(t\left(s\right)\)变化的关系式是\(I=5\sin \left(100πt+\dfrac{\pi}{3}\right)\),则当\(t= \dfrac{1}{2 00 }s\)时,电流\(I\)为( )
A.\(5 A\) \(\qquad \qquad \qquad \qquad\) B.\(2.5 A\) \(\qquad \qquad \qquad \qquad\) C.\(2 A\) \(\qquad \qquad \qquad \qquad\) D.\(-5 A\)
3.一个匀速旋转的摩天轮每\(12\)分钟旋转一周,最低点距地面\(2\)米,最高点距地面\(18\)米,\(P\)是摩天轮轮周上的定点,点\(P\)在摩天轮最低点开始计时,\(t\)分钟后\(P\)点距地面高度为\(h\)(米),设\(h=A\sin \left(ωt+φ\right)+B\)\(\left(A>0,ω>0,φ\in \left[0,2π\right)\right)\),则下列结论错误的是( )
A.\(A=8\) \(\qquad \qquad \qquad \qquad\) B.\(ω=\dfrac{\pi}{6}\) \(\qquad \qquad \qquad \qquad\) C.\(φ=\dfrac{\pi}{2}\) \(\qquad \qquad \qquad \qquad\) D.\(B=10\)
4.(多选)如图,摩天轮的半径为\(40m\),其中心\(O\)点距离地面的高度为\(50m\),摩天轮按逆时针方向做匀速转动,且\(20\min\)转一圈,若摩天轮上点\(P\)的起始位置在最高点处,则摩天轮转动过程中( )

A.经过\(10\min\)点\(P\)距离地面\(10m\)
B.若摩天轮转速减半,则其周期变为原来的\(\dfrac{1}{2}\)倍
C.第\(17\min\)和第\(43\min\)时\(P\)点距离地面的高度相同
D.摩天轮转动一圈,\(P\)点距离地面的高度不低于\(70m\)的时间为\(\dfrac{20}{3} \min\)
5.如图,单摆从某点开始来回摆动,离开平衡位置\(O\)的距离\(s cm\)和时间\(t s\)的函数关系式为 \(s=6\sin \left(2πt+\dfrac{\pi}{6}\right)\),那么单摆来回摆动一次所需的时间为\(\underline{\quad \quad}\).

6.下面是一半径为\(2\)米的水轮,水轮的圆心\(O\)距离水面\(1\)米,已知水轮自点\(M\)开始以\(1\)分钟旋转\(4\)圈的速度顺时针旋转,点\(M\)距水面的高度\(d\)(米)(在水平面下\(d\)为负数)与时间\(t\)(秒)满足函数关系式\(d=A \sin (\omega t+\varphi)+1\)\(\left(A>0, \omega>0,|\varphi|<\dfrac{\pi}{2}\right)\),则函数关系式为\(\underline{\quad \quad}\).

7.如图,一个半径为\(4\)米的筒车按逆时针方向每\(π\)分钟转\(1\)圈,筒车的轴心\(O\)距水面的高度为\(2\)米.设筒车上的某个盛水筒\(W\)到水面的距离为\(d\)(单位:米)(在水面下\(d\)则为负数).若以盛水筒\(W\)刚浮出水面时开始计算时间,则\(d\)与时间\(t\)(单位:分钟)之间的关系为\(d=A\sin \left(ωt+φ\right)+K\left(A>0 ,ω>0 ,-\dfrac{\pi}{2}<φ<\dfrac{\pi}{2}\right)\).
\(\left(1\right)\)求\(A\) ,\(ω\) ,\(φ\) ,\(K\)的值;
\(\left(2\right)\)求盛水筒\(W\)出水后至少经过多少时间就可到达最高点?
\(\left(3\right)\)某时刻\(t_0\)(单位:分钟)时,盛水筒\(W\)在过点\(O\)的竖直直线的左侧,到水面的距离为\(5\)米,再经过\(\dfrac{\pi}{6}\)分钟后,盛水筒\(W\)是否在水中?

8.已知函数\(f\left(x\right)=A\sin \left(ωx+φ\right)+B\left(A>0,ω>0,|φ|<\dfrac{\pi}{2}\right)\)的一系列对应值如下表:
| \(x\) | \(-\dfrac{\pi}{6}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{5\pi}{6}\) | \(\dfrac{4\pi}{3}\) | \(\dfrac{11\pi}{6}\) | \(\dfrac{7\pi}{3}\) | \(\dfrac{17\pi}{6}\) |
|---|---|---|---|---|---|---|---|
| \(y\) | \(-1\) | \(1\) | \(3\) | \(1\) | \(-1\) | \(1\) | \(3\) |
\(\left(1\right)\) 根据表格提供的数据求出函数\(f\left(x\right)\)的一个解析式;
\(\left(2\right)\)根据\(\left(1\right)\)的结果,若函数\(y=f\left(kx\right)\left(k>0\right)\)的周期为\(2\dfrac{\pi}{3}\),当\(x\in \left[0,\dfrac{\pi}{3}\right]\)时,方程\(f\left(kx\right)=m\)恰有两个不同的解,求实数\(m\)的取值范围.
9.某农场有一块扇形农田,如图所示.已知扇形\(OAB\)的圆心角为\(\dfrac{\pi}{4}\),半径为\(80\)米,点\(P\)在 \(\widehat{A B}\)上,\(PC⊥OA\)于\(C\),\(PD⊥OB\)于\(D\).现要在\(△OPC\)和\(△OPD\)区域中分别种植甲、乙两种蔬菜,且甲、乙两种蔬菜单位面积年产值之比为\(1:\sqrt{3}\).设\(∠AOP=θ\),\(0<θ<\dfrac{\pi}{4}\).
\(\left(1\right)\)用\(θ\)分别表示\(△OPC\)和\(△OPD\)的面积;
\(\left(2\right)\)当\(θ\)为何值时,读农场种植甲、乙两种蔬菜的年总产值最大?

10.如图,\(OPQ\)是半径为\(2\).圆心角为\(\dfrac{\pi}{3}\)的扇形,点\(A\)在\(\widehat{P Q}\)上(异于点\(P\),\(Q\)),过点\(A\)作\(AB⊥OP\),\(AC⊥OQ\),垂足分别为\(B\),\(C\),记\(∠AOB=θ\),四边形\(ACOB\)的面积为\(S\).
\(\left(1\right)\)求\(S\)关于\(θ\)的函数关系式;
\(\left(2\right)\)当\(θ\)为何值时,\(S\)有最大值,并求出这个最大值.

参考答案
-
答案 \(B\)
解析 由图知该质点振动的周期要大于\(0.7 s\),振幅为\(5 cm\),在\(0.1s\)和\(0.5s\)时振动速度为\(0\),在\(0.3 s\)和\(0.7 s\)时振动速度为最大.故选\(B\). -
答案 \(B\)
解析 将\(t= \dfrac{1}{200}\)代入\(I=5\sin \left(100πt+\dfrac{\pi}{3}\right)\)得\(I=2.5 A\). -
答案 \(C\)
解析 由摩天轮最低点距地面\(2\)米,最高点距地面\(18\)米,
得 \(\left\{\begin{array}{l} A+B=18 \\ -A+B=2 \end{array}\right.\),解得 \(\left\{\begin{array}{l} A=8 \\ B=10 \end{array}\right.\),
因此\(A\),\(D\)都正确;又由摩天轮每\(12\)分钟旋转一周,得\(T=12\),
而 \(T=\dfrac{2 \pi}{\omega}\),所以\(ω=\dfrac{\pi}{6}\),则\(B\)正确;
又由\(P\)是摩天 轮轮周上的定点,从\(P\)在摩天轮最低点开始计时,
得\(8\sin \left(\dfrac{\pi}{6}×0+φ\right)+10=2\),所以\(\sin φ=-1\),
而\(φ\in \left[0,2π\right)\),所以\(φ=\dfrac{3\pi}{2}\),所以\(C\)错误. -
答案 \(ACD\)
解析 依题意,\(A=40\),\(h=50\),\(T=20\),
则 \(\omega=\dfrac{2 \pi}{20}=\dfrac{\pi}{10}\),且\(f\left(0\right)=40\sin φ+50=90\),所以\(φ=\dfrac{\pi}{2}\);
所以\(f\left(t\right)=40\sin \left(\dfrac{\pi}{10} t+\dfrac{\pi}{2}\right)+50\),\(\left(t≥0\right)\).
对于\(A\).\(f\left(10\right)=40\sin \left(\dfrac{\pi}{10} ×10+\dfrac{\pi}{2}\right)+50=10\),\(A\)正确;
对于\(B\),若摩天轮转速减半,则其周期变为原来的\(2\)倍,\(B\)错误;
对于\(C\),\(f\left(17\right)=40\sin \left(\dfrac{\pi}{10} ×17+\dfrac{\pi}{2}\right)+50=-40\cos \dfrac{7\pi}{10} +50=40\cos \dfrac{3\pi}{10} +50\),
\(f\left(43\right)=40\sin \left(\dfrac{\pi}{10} ×43+\dfrac{\pi}{2}\right)+50=40\cos \dfrac{3\pi}{10} +50\);
所以\(f\left(17\right)=f\left(43\right)\),\(C\)正确;
对于\(D\),令\(f\left(t\right)≥70\),得\(40\sin \left(\dfrac{\pi}{10} t+\dfrac{\pi}{2}\right)+50≥70\),
所以\(\cos \dfrac{\pi}{10} t≥ \dfrac{1}{2}\),
所以\(-\dfrac{\pi}{3}+2kπ≤\dfrac{\pi}{10} t≤\dfrac{\pi}{3}+2kπ\),\(k\in Z\);
解得 \(-\dfrac{10}{3}+20 k \leq t \leq \dfrac{10}{3}+20 k\),\(k\in Z\);
\(\dfrac{10}{3}-\left(-\dfrac{10}{3}\right)=\dfrac{20}{3}\),
即摩天轮转动一圈,\(P\)点距离地面的高度不低于\(70m\)的时间为 \(\dfrac{20}{3} \min\),\(D\)正确.
故选:\(ACD\). -
答案 \(1\)
解析 由题易知,单摆来回摆动一次所需的时间恰好为一个周期,即\(T=\dfrac{2\pi}{2π}=1\). -
答案 \(d=2 \sin \left(\dfrac{2 \pi}{15} t-\dfrac{\pi}{6}\right)+1\)
解析 由题意知水轮的半径为\(2\),水轮圆心\(O\)距离水面\(1\),所以\(A=2\);
又水轮每分钟旋转\(4\)圈,所以转一圈需要\(15\)秒,
所以 \(T=15=\dfrac{2 \pi}{\omega}\),解得 \(\omega=\dfrac{2 \pi}{15}\);
由顺时针旋转\(t=0\)时,\(ωt+φ=2kπ-\dfrac{\pi}{6}\),解得\(φ=2kπ-\dfrac{\pi}{6}\left(k\in Z\right)\),
又\(|φ|<\dfrac{\pi}{2}\),所以\(φ=\dfrac{\pi}{6}\);
所以函数关系式为 \(d=2 \sin \left(\dfrac{2 \pi}{15} t-\dfrac{\pi}{6}\right)+1\). -
答案 \(\left(1\right) A=4\),\(K=2\),\(ω=2\),\(φ=-\dfrac{\pi}{6}\);\(\left(2\right) \dfrac{\pi}{3}\)分钟;\(\left(3\right)\)不在水中.
解析 \(\left(1\right)\)由题意,\(d=A\sin \left(ωt+φ\right)+K\),
由图可知\(d\)的最大值为\(6\),最小值为\(-2\),
即 \(\left\{\begin{array}{l} A+K=6 \\ -A+K=-2 \end{array}\right.\),解得\(A=4\) ,\(K=2\),
\(\because\) 每\(π\)分钟转\(1\)圈,
\(\therefore\)函数的周期为 \(T=\dfrac{2 \pi}{\omega}=\pi\),可得\(ω=2\),可得\(d=4\sin \left(2t+φ\right)+2\),
\(\because\)依题意,可知当\(t=0\)时,\(d=0\),即\(0=4\sin φ+2\),可得\(\sin φ=- \dfrac{1}{2}\) ,
由\(-\dfrac{\pi}{2}<φ<\dfrac{\pi}{2}\),可得\(φ=-\dfrac{\pi}{6}\).
\(\left(2\right)\)由\(\left(1\right)\)可得\(d=4\sin \left(2t-\dfrac{\pi}{6}\right)+2\),
令\(6=4\sin \left(2t-\dfrac{\pi}{6}\right)+2\),得\(\sin \left(2t-\dfrac{\pi}{6}\right)=1\),
取\(2t-\dfrac{\pi}{6}=\dfrac{\pi}{2}\),解得\(t=\dfrac{\pi}{3}\),
故经过\(\dfrac{\pi}{3}\)分钟后盛水筒\(W\)出水后就可到达最高点.
\(\left(3\right)\)由题意,\(5=4\sin \left(2t_0-\dfrac{\pi}{6}\right)+2\),
可得 \(\sin \left(2 t_0-\dfrac{\pi}{6}\right)=\dfrac{3}{4}\),可得 \(\cos \left(2 t_0-\dfrac{\pi}{6}\right)=-\dfrac{\sqrt{7}}{4}\)或 \(\dfrac{\sqrt{7}}{4}\)(舍去),
所以 \(\sin \left[2\left(t_0+\dfrac{\pi}{6}\right)-\dfrac{\pi}{6}\right]=\sin \left[\left(2 t_0-\dfrac{\pi}{6}\right)+\dfrac{\pi}{3}\right]\)
\(=\dfrac{3}{4} \times \dfrac{1}{2}+\left(-\dfrac{\sqrt{7}}{4}\right) \times \dfrac{\sqrt{3}}{2}=\dfrac{3-\sqrt{21}}{8}\),
所以再经过\(\dfrac{\pi}{6}\)分钟,可得 \(d=4 \times \dfrac{3-\sqrt{21}}{8}+2=\dfrac{7-\sqrt{21}}{2}>0\),
故盛水筒不在水中. -
答案 \(\left(1\right) f\left(x\right)=2\sin \left(x-\dfrac{\pi}{3}\right)+1\); \(\left(2\right) \left[\sqrt{3}+1,3\right)\).
解析 \(\left(1\right)\)设\(f\left(x\right)\)的最小正周期为\(T\),得\(T=\dfrac{11\pi}{6}-\left(-\dfrac{\pi}{6}\right)=2π\).
由 \(T=\dfrac{2 \pi}{\omega}\)得\(ω=1\).
又 \(\left\{\begin{array}{l} B+A=3 \\ B-A=-1 \end{array}\right.\)解得 \(\left\{\begin{array}{l} A=2 \\ B=1 \end{array}\right.\),
令\(ω⋅\dfrac{5\pi}{6}+φ=\dfrac{\pi}{2}+2kπ\),
即\(\dfrac{5\pi}{6}+φ=\dfrac{\pi}{2}+2kπ,k\in Z\),又\(|φ|<\dfrac{\pi}{2}\),解得\(φ=-\dfrac{\pi}{3}\).
\(\therefore f\left(x\right)=2\sin \left(x-\dfrac{\pi}{3}\right)+1\).
\(\left(2\right)\because\) 函数\(y=f\left(kx\right)=2\sin \left(kx-\dfrac{\pi}{3}\right)+1\)的周期为\(\dfrac{2\pi}{3}\),
又\(k>0\),\(\therefore k=3\).
令\(t=3x-\dfrac{\pi}{3}\),\(\because x\in \left[0,\dfrac{\pi}{3}\right]\),\(\therefore t\in \left[-\dfrac{\pi}{3},\dfrac{2\pi}{3}\right]\).
如图,\(\sin t=s\)在\(\left[-\dfrac{\pi}{3},\dfrac{2\pi}{3}\right]\)上有两个不同的解的条件是\(s\in \left[\dfrac{\sqrt{3}}{2} ,1\right)\),
\(\therefore\)方程\(f\left(kx\right)=m\)在\(x\in \left[0,\dfrac{\pi}{3}\right]\)时恰好有两个不同的解的条件是\(m\in \left[\sqrt{3}+1,3\right)\),
即实数\(m\)的取值范围是\(\left[\sqrt{3}+1,3\right)\).

-
答案 \(\left(1\right) △OPC\)的面积为\(1600\sin 2θ\),\(△OPD\)的面积为\(1600\cos 2θ\); \(\left(2\right) \dfrac{\pi}{12}\).
解析 \(\left(1\right)\)直角三角形\(OPC\)中,\(PC=OP\sin θ=80\sin θ\),\(OC=OP\cos θ=80\cos θ\),
所以\(△OPC\)的面积为\(\dfrac{1}{2} ×PC×OC=3200\sin θ\cos θ=1600\sin 2θ\),
同理\(△OPD\)的面积为\(1600\sin 2\left(\dfrac{\pi}{4}-θ\right)=1600\cos 2θ\).
\(\left(2\right)\)设农场种植甲,乙两种蔬菜的年总产值为\(y\),
甲,乙两种蔬菜每平方米年产值分别为\(t\),\(\sqrt{3} t\left(t>0\right)\),
则\(y=1600\sin 2θ\cdot t+1600\cos 2θ\cdot\sqrt{3} t=3200t\sin \left(2θ+\dfrac{\pi}{3}\right)\),
\(\because 0<θ<\dfrac{\pi}{4}\),\(\therefore \dfrac{\pi}{3}<2θ+\dfrac{\pi}{3}<\dfrac{5\pi}{6}\).
\(\therefore\)当\(2θ+\dfrac{\pi}{3}=\dfrac{\pi}{2}\),即\(θ=\dfrac{\pi}{12}\)时,\(y\)取得最大值.
答:\(\left(1\right)△OPC\)和\(△OPD\)的面积分别为\(1600\sin 2θ\)平方米,\(1600\cos 2θ\)平方米;
\(\left(2\right)\)当\(θ=\dfrac{\pi}{12}\)时,该农场种植甲,乙两种蔬菜的年总产值量大. -
答案 \(\left(1\right) S=\sin 2θ+\sin \left(2\dfrac{\pi}{3}-2θ\right),\left(0<θ<\dfrac{\pi}{3}\right)\);
\(\left(2\right)\)当\(θ\)为\(\dfrac{\pi}{6}\)时,面积\(S\)有最大值\(\sqrt{3}\).
解析 \(\left(1\right)\)因为\(AB⊥OP\),所以在\(Rt△OAB\)中,\(AB=OA\sin θ=2\sin θ\),\(OB=OA\cos θ=2\cos θ\),
\(S_{\triangle A B O}=\dfrac{1}{2} O B \times A B=2 \sin \theta \cos \theta=\sin 2 \theta\),
因为\(AC⊥OQ\),\(∠POQ=\dfrac{\pi}{3}\),所以\(∠AOC=\dfrac{\pi}{3}-θ\);
同理: \(S_{\triangle A C O}=2 \sin \left(\dfrac{\pi}{3}-\theta\right) \cos \left(\dfrac{\pi}{3}-\theta\right)=\sin \left(\dfrac{2 \pi}{3}-2 \theta\right)\);
从而\(S\)关于\(θ\)的解析式为 \(S=S_{\triangle A B O}+S_{\triangle A C O}=\sin 2 \theta+\sin \left(\dfrac{2 \pi}{3}-2 \theta\right),\left(0<\theta<\dfrac{\pi}{3}\right)\);
\(\left(2\right)\)化简函数 \(S=\sin 2 \theta+\sin \left(\dfrac{2 \pi}{3}-2 \theta\right)=\sin 2 \theta+\sin \dfrac{2 \pi}{3} \cos 2 \theta-\cos \dfrac{2 \pi}{3} \sin 2 \theta\)
\(=\dfrac{3}{2} \sin 2 \theta+\dfrac{\sqrt{3}}{2} \cos 2 \theta=\sqrt{3}\left(\dfrac{\sqrt{3}}{2} \sin 2 \theta+\dfrac{1}{2} \cos 2 \theta\right)\)
\(=\sqrt{3}\left(\sin 2 \theta \cos \dfrac{\pi}{6}+\cos 2 \theta \sin \dfrac{\pi}{6}\right)=\sqrt{3} \sin \left(2 \theta+\dfrac{\pi}{6}\right)\),
因为\(0<θ<\dfrac{\pi}{3}\),所以\(\dfrac{\pi}{6}<2θ+\dfrac{\pi}{6}<\dfrac{5\pi}{6}\),
故当\(2θ+\dfrac{\pi}{6}=\dfrac{\pi}{2}\),即\(θ=\dfrac{\pi}{6}\)时\(S\)有最大值,最大值为\(\sqrt{3}\).
答:当\(θ\)为\(\dfrac{\pi}{6}\)时,面积\(S\)有最大值,最大值为\(\sqrt{3}\).
【B组---提高题】
1.如图,一个水轮的半径为\(6m\),水轮轴心\(O\)距离水面的高度为\(3m\),已知水轮按逆时针匀速转动,每分钟转动\(5\)圈,当水轮上点\(P\)从水中浮现时的起始(图中点\(P_0\))开始计时,记\(f\left(t\right)\)为点\(P\)距离水面的高度关于时间\(t\left(s\right)\)的函数,则下列结论正确的是( )

A.\(f\left(3\right)=9\)
B.\(f\left(1\right)=f\left(7\right)\)
C.若\(f\left(t\right)≥6\),则\(t\in \left[2+12k,5+12k\right]\left(k\in N\right)\)
D.不论\(t\)为何值,\(f\left(t\right)+f\left(t+4\right)+f\left(t+8\right)\)是定值
2.如图,正方形\(ABCD\)的边长为\(10\)米,以点\(A\)为顶点,引出放射角为\(\dfrac{\pi}{6}\)的阴影部分的区域,其中\(∠EAB=x\),\(\dfrac{\pi}{12}≤x≤\dfrac{\pi}{4}\),记\(AE\),\(AF\)的长度之和为\(f\left(x\right)\).则\(f\left(x\right)\)的最大值为\(\underline{\quad \quad}\) .

3.如图,某登山队在山脚\(A\)处测得山顶\(B\)的仰角为\(45°\),沿倾斜角为\(α\)(其中\(\tan α= \dfrac{1}{2}\) )的斜坡前进\(\sqrt{5} km\)后到达\(D\)处,休息后继续行驶\(\sqrt{5} km\)到达山顶\(B\).
\(\left(1\right)\)求山的高度\(BE\);
\(\left(2\right)\)现山顶处有一塔 \(C B=\dfrac{3}{8} k m\).从\(A\)到\(D\)的登山途中,队员在点\(P\)处测得塔的视角为\(θ\)(\(∠CPB=θ\)).若点\(P\)处高度\(PF\)为\(xkm\),则\(x\)为何值时,视角\(θ\)最大?

参考答案
-
答案 \(BD\)
解析 设\(f\left(t\right)=A\sin \left(ωx+φ\right)+B\),依题意可知\(f\left(t\right)\)的最大值为\(9\),最小为\(-3\),
\(\therefore A+B=9\),且\(-A+B=-3\),可得\(A=6\),\(B=3\);
\(\because OP\)每秒钟内所转过的角为\(\dfrac{5 \times 2 \pi}{60}=\dfrac{\pi}{6}\),得\(f\left(t\right)=6\sin \left(\dfrac{\pi}{6} t+φ\right)+3\),
当\(t=0\)时,\(f\left(t\right)=0\),得\(\sin φ=- \dfrac{1}{2}\),即\(φ=-\dfrac{\pi}{6}\),
故所求的函数解析式为\(f\left(t\right)=6\sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)+3\),
对于\(A\),\(f\left(3\right)=6\sin \left(\dfrac{\pi}{6}×3-\dfrac{\pi}{6}\right)+3=3\sqrt{3}+3\),即\(A\)错误;
对于\(B\),\(f\left(1\right)=6\sin \left(\dfrac{\pi}{6}×1-\dfrac{\pi}{6}\right)+3=3\),\(f\left(7\right)=6\sin \left(\dfrac{\pi}{6}×7-\dfrac{\pi}{6}\right)+3=3\),
即\(B\)正确;
对于\(C\),因为\(f\left(t\right)≥6\),所以\(6\sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)+3≥6\),即\(\sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)≥ \dfrac{1}{2}\),
所以\(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\in \left[\dfrac{\pi}{6}+2kπ,\dfrac{5\pi}{6}+2kπ\right]\),解得\(t\in \left[2+12k,6+12k\right]\),\(k\in N\),
即\(C\)错误;
对于\(D\),\(f\left(t\right)+f\left(t+4\right)+f\left(t+8\right)\)
\(=6\sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)+3+6\sin \left[\dfrac{\pi}{6}\left(t+4\right)-\dfrac{\pi}{6}\right]+3+6\sin \left[\dfrac{\pi}{6}\left(t+8\right)-\dfrac{\pi}{6}\right]+3\)
\(=6\sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)+6\sin \left(\dfrac{\pi}{6} t+\dfrac{\pi}{2}\right)+6\sin \left(\dfrac{\pi}{6} t+7\dfrac{\pi}{6}\right)+9\)
\(=6\left[\sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)+\cos \dfrac{\pi}{6} t-\sin \left(\dfrac{\pi}{6} t+\dfrac{\pi}{6}\right)\right]+9\),
因为\(\sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)+\cos \dfrac{\pi}{6} t-\sin \left(\dfrac{\pi}{6} t+\dfrac{\pi}{6}\right)\)
\(=\left(\sin \dfrac{\pi}{6} t⋅\cos \dfrac{\pi}{6}-\cos \dfrac{\pi}{6} t⋅\sin \dfrac{\pi}{6}\right)+\cos \dfrac{\pi}{6} t-\left(\sin \dfrac{\pi}{6} t⋅\cos \dfrac{\pi}{6}+\cos \dfrac{\pi}{6} t⋅\sin \dfrac{\pi}{6}\right)=0\),
所以\(f\left(t\right)+f\left(t+4\right)+f\left(t+8\right)=9\),即\(D\)正确.
故选:\(BD\). -
答案 \(10\sqrt{6}\).
解析 由题设,\(A E=\dfrac{A B}{\cos x}=\dfrac{10}{\cos x}\), \(\dfrac{\pi}{12} \leq x \leq \dfrac{\pi}{4}\),
而\(∠FAD=∠EAB+∠EAF\in \left[\dfrac{\pi}{4},\dfrac{5\pi}{12}\right]\),
故\(∠DAF=\dfrac{\pi}{3}-x\in \left[\dfrac{\pi}{12},\dfrac{\pi}{4}\right]\),
所以 \(A F=\dfrac{A D}{\cos \left(\dfrac{\pi}{3}-x\right)}=\dfrac{10}{\cos \left(\dfrac{\pi}{3}-x\right)}\),
综上\(f(x)=10\left[\dfrac{1}{\cos x}+\dfrac{1}{\cos \left(\dfrac{\pi}{3}-x\right)}\right]\),且\(\dfrac{\pi}{12}≤x≤\dfrac{\pi}{4}\),
所以 \(f(x)=10\left(\dfrac{1}{\cos x}+\dfrac{2}{\cos x+\sqrt{3} \sin x}\right)\)\(=10 \cdot \dfrac{3 \cos x+\sqrt{3} \sin x}{\cos x(\cos x+\sqrt{3} \sin x)}=\dfrac{20 \sqrt{3} \sin \left(x+\dfrac{\pi}{3}\right)}{\sin \left(2 x+\dfrac{\pi}{6}\right)+\dfrac{1}{2}}\),
令 \(t=\sin \left(x+\dfrac{\pi}{3}\right) \in\left[\dfrac{\sqrt{6}+\sqrt{2}}{4}, 1\right]\),
则 \(t^2=\sin ^2\left(x+\dfrac{\pi}{3}\right)=\dfrac{1-\cos \left(2 x+\dfrac{2 \pi}{3}\right)}{2}\)\(=\dfrac{1-\cos \left(\dfrac{\pi}{2}+2 x+\dfrac{\pi}{6}\right)}{2}=\dfrac{1+\sin \left(2 x+\dfrac{\pi}{6}\right)}{2}\),
所以\(f\left(2x+\dfrac{\pi}{6}\right)=2t^2-1\),
故 \(f(x)=g(t)=\dfrac{20 \sqrt{3}}{2 t-\dfrac{1}{2 t}}\)在 \(t \in\left[\dfrac{\sqrt{6}+\sqrt{2}}{4}, 1\right]\)上递减,
所以 \(f(x)_{\max }=g(t)_{\max }=g\left(\dfrac{\sqrt{6}+\sqrt{2}}{4}\right)=\dfrac{20 \sqrt{3}}{\dfrac{\sqrt{6}+\sqrt{2}}{2}-\dfrac{2}{\sqrt{6}+\sqrt{2}}}=10 \sqrt{6},\),
此时\(x=\dfrac{\pi}{12}\)或\(x=\dfrac{\pi}{4}\).
故答案为:\(10\sqrt{6}\). -
答案 \(\left(1\right) 3 km\); \(\text { (2) } \dfrac{3}{4} \mathrm{~km}\).
解析 \(\left(1\right)\)因为\(\tan α= \dfrac{1}{2}\) ,\(α\)是锐角,所以\(\sin α=\dfrac{1}{\sqrt{5}}\),\(\cos α=\dfrac{2}{\sqrt{5}}\),
所以\(\cos ∠BAD=\cos \left(\dfrac{\pi}{4}-α\right)=\cos \dfrac{\pi}{4} \cos α+\sin \dfrac{\pi}{4} \sin α\)\(= \dfrac{1}{\sqrt{2}}×\dfrac{2}{\sqrt{5}}+ \dfrac{1}{\sqrt{2}}×\dfrac{3}{\sqrt{5}}==\dfrac{3 \sqrt{10}}{10}\);
在\(△ABD\)中,过\(D\)作\(DM⊥AB\),垂足为\(M\),
如图1所示

因为\(AD=BD=\sqrt{5}\),
所以\(AB=2AM=2AD\cos ∠BAD=2\sqrt{5}⋅\dfrac{3 \sqrt{10}}{10}=3\sqrt{2}\);
在\(△ABE\)中,\(BE=AB\cos 45°=3\),
所以山的高度为\(3 km\).
\(\left(2\right)\)过\(P\)作\(PN⊥BE\)于\(N\),如图3所示;

因为\(PF=x\),所以\(AF=2x\),
因为\(P\)在\(AD\)上,\(DG=1\),所以\(x\in \left[0,1\right]\),
所以\(\tan ∠BPN=\dfrac{B N}{P N}=\dfrac{3-x}{3-2 x}\), \(\tan \angle C P N=\dfrac{C N}{P N}=\dfrac{3+\dfrac{3}{8}-x}{3-2 x}=\dfrac{\dfrac{27}{8}-x}{3-2 x}\),
所以 \(\tan \theta=\tan (\angle C P N-\angle B P N)=\dfrac{\tan \angle C P N-\tan \angle B P N}{1+\tan \angle C P N \cdot \tan \angle B P N}\)
\(=\dfrac{\dfrac{\frac{27}{8}-x}{3-2 x}-\dfrac{3-x}{3-2 x}}{1+\dfrac{\frac{27}{8}-x}{3-2 x} \times \dfrac{3-x}{3-2 x}}=\dfrac{\dfrac{3}{8}}{(3-2 x)+\dfrac{\left(\frac{27}{8}-x\right)(3-x)}{3-2 x}}\) ,\(x\in \left[0,1\right]\);
令\(t=3-2x\in \left[1,3\right]\),所以 \(x=\dfrac{3-t}{2}\),
则 \(\tan \theta=\dfrac{\dfrac{3}{8}}{t+\dfrac{\left(\dfrac{15}{8}+\dfrac{t}{2}\right)\left(\dfrac{3}{2}+\dfrac{t}{2}\right)}{t}}=\dfrac{6}{5\left(4 t+\dfrac{9}{t}\right)+27} \leq \dfrac{6}{5 \cdot 2 \sqrt{4 t \cdot \dfrac{9}{t}+27}}=\dfrac{2}{29}\),
当且仅当 \(4 t=\dfrac{9}{t}\),即 \(t=\dfrac{3}{2} \in[1,3]\)时,即 \(x=\dfrac{3}{4}\)时\(\tan θ\)取得最大值 \(\dfrac{2}{29}\).
所以当 \(x=\dfrac{3}{4} k m\)时,视角\(θ\)最大.
【C组---拓展题】
1.如图,半圆的直径\(AB=2\),\(O\)为圆心,\(C\),\(D\)为半圆上的点.
\(\left(1\right)\)请你为\(C\)点确定位置,使\(△ABC\)的周长最大,并说明理由;
\(\left(2\right)\)已知\(AD=DC\),设\(∠ABD=θ\),当\(θ\)为何值时,
\(\qquad\)\(\left(i\right)\)四边形\(ABCD\)的周长最大,最大值是多少?
\(\qquad\)\(\left(ii\right)\)四边形\(ABCD\)的面积最大,最大值是多少?

参考答案
- 答案 \(\left(1\right)\)点\(C\)是半圆的中点;\(\left(2\right) \left(i\right) 5\); \(\text { (ii) } \dfrac{3 \sqrt{3}}{4}\).
解析 \(\left(1\right)\)点\(C\)在半圆中点位置时,\(△ABC\)周长最大;理由如下:

因为点\(C\)在半圆上,且\(AB\)是圆的直径,
所以\(∠ACB=\dfrac{\pi}{2}\),即\(△ABC\)是直角三角形;
设\(BC=a\),\(AC=b\),\(AB=c\),\(∠ABC=α\left(0<α<\dfrac{\pi}{2}\right)\),
则\(a=c\cdot \cos α\),\(b=c\cdot \sin α\),
所以\(△ABC\)周长为\(L=a+b+c=c\cdot\cos α+c\cdot\sin α+c\)\(=2\left(\cos α+\sin α\right)+2=2\sqrt{2}\sin \left(α+\dfrac{\pi}{4}\right)+2\),
因为\(0<α<\dfrac{\pi}{2}\),所以\(\dfrac{\pi}{4}<α+\dfrac{\pi}{4}<\dfrac{3\pi}{4}\);
所以当\(α+\dfrac{\pi}{4}=\dfrac{\pi}{2}\),即\(α=\dfrac{\pi}{4}\)时,\(△ABC\)周长取得最大值为\(2\sqrt{2}+2\);
此时点\(C\)是半圆的中点.
\(\left(2\right) \left(i\right)\)因为\(AD=DC\),

所以\(∠ABD=∠DBC=θ\);
所以\(AD=DC=AB\cdot \sin θ\),\(CB=AB\cdot \cos 2θ\);
设四边形\(ABCD\)的周长为\(p\),
则\(p=AD+DC+CB+AB=2AB\sin θ+AB\cos 2θ+2\)
\(=4\sin θ+2\left(1-2\sin^2 θ\right)+2=5-4\left(\sin θ- \dfrac{1}{2} \right)^2\);
显然\(θ\in \left(0,\dfrac{\pi}{4}\right)\),所以当\(θ=\dfrac{\pi}{6}\)时,\(p\)取得最大值\(5\).
\(\left(ii\right)\)过\(O\)作\(OE⊥BC\)于\(E\),
设四边形\(ABCD\)的面积为\(s\),四边形\(AOCD\)的面积为\(s_1\),\(△BOC\)的面积为\(s_2\),

则\(s=s_1+s_2= \dfrac{1}{2} AC⋅OD+ \dfrac{1}{2} BC⋅OE= \dfrac{1}{2} AB\sin 2θ⋅1+ \dfrac{1}{2} AB\cos 2θ⋅\sin 2θ\)
\(=\sin 2θ+\cos 2θ\cdot \sin 2θ=\sin 2θ\left(1+\cos 2θ\right)\);
所以\(s^2=\sin ^22θ \left(1+\cos 2θ\right)^2=\left(1-\cos ^22θ \right) \left(1+\cos 2θ\right)^2\)
\(=\left(1-\cos 2θ\right) \left(1+\cos 2θ\right)^3\)
\(=\dfrac{3}{3}(1-\cos 2 \theta)(1+\cos 2 \theta)^3\)
\(\leq \dfrac{1}{3}\left[\dfrac{3(1-\cos 2 \theta)+(1+\cos 2 \theta)}{2}\right]^2(1+\cos 2 \theta)^2\)
\(=\dfrac{1}{3}\left[\dfrac{3(1-\cos 2 \theta)+(1+\cos 2 \theta)}{2}(1+\cos 2 \theta)\right]^2\)\(\leq \dfrac{1}{3}\left[\dfrac{\dfrac{3(1-\cos 2 \theta)+(1+\cos 2 \theta)}{2}+(1+\cos 2 \theta)}{2}\right]^{2 \times 2}\)
\(=\dfrac{1}{3}\left[\dfrac{3(1-\cos 2 \theta)+(1+\cos 2 \theta)+2(1+\cos 2 \theta)}{4}\right]^4=\dfrac{1}{3}\left(\dfrac{3}{2}\right)^4=\dfrac{27}{16}\).
当且仅当\(3\left(1-\cos 2θ\right)=1+\cos 2θ\),即\(\cos 2θ= \dfrac{1}{2}\) 时,等号成立;
显然\(θ\in \left(0,\dfrac{\pi}{4}\right)\),所以\(2θ\in \left(0,\dfrac{\pi}{2}\right)\),所以此时\(θ=\dfrac{\pi}{6}\);
所以当\(θ=\dfrac{\pi}{6}\)时, \(s=\dfrac{3 \sqrt{3}}{4}\),即四边形\(ABCD\)的最大面积是 \(\dfrac{3 \sqrt{3}}{4}\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号