5.4.2 正弦函数、余弦函数的性质2 (单调性与最值)
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步巩固,难度2颗星!
基础知识
正弦函数,余弦函数的图像与性质
注 表中的\(k∈Z\)
| \(y=\sin x\) | \(y=\cos x\) | |
|---|---|---|
| 图像 | 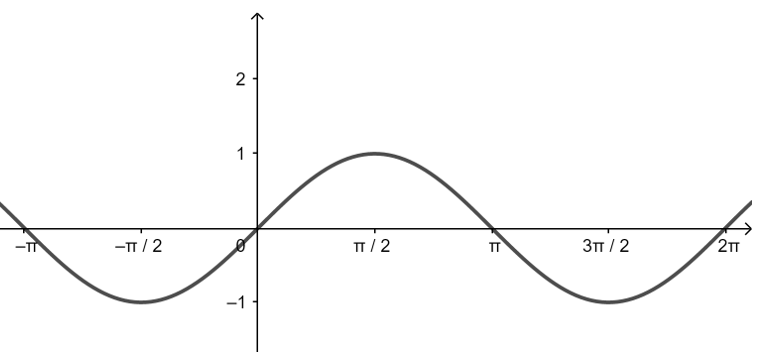 |
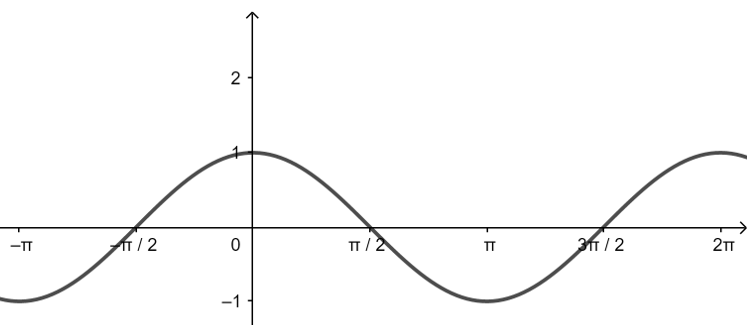 |
| 定义域 | \(R\) | \(R\) |
| 值域 | \(\left[-1 ,1\right]\) | \(\left[-1 ,1\right]\) |
| 周期性 | \(2π\) | \(2π\) |
| 对称中心 | \((kπ ,0)\) | \(\left(kπ+\dfrac{\pi}{2},0\right)\) |
| 对称轴 | \(x=kπ+\dfrac{\pi}{2}\) | \(x=kπ\) |
| 单调性 | 在\(\left[-\dfrac{\pi}{2}+2kπ ,\dfrac{\pi}{2}+2kπ\right]\)上是增函数; 在\(\left[\dfrac{\pi}{2}+2kπ ,3\dfrac{\pi}{2}+2kπ\right]\)上是减函数. |
在\(\left[-π+2kπ ,2kπ\right]\)上是增函数; 在\(\left[2kπ ,π+2kπ\right]\)上是减函数. |
| 最值 | 当\(x=\dfrac{\pi}{2}+2kπ\)时,\(y_{\max}=1\); 当\(x=-\dfrac{\pi}{2}+2kπ\)时,\(y_{\min}=-1\). |
当\(x=2kπ\)时,\(y_{\max}=1\); 当\(x=π+2kπ\)时,\(y_{\min}=-1\). |
解释
如何理解三角函数的单调性、最值?
主要是结合图象及其周期性,比如如何理解正弦函数\(f(x)=\sin x\)在\(\left[-\dfrac{\pi}{2}+2kπ ,\dfrac{\pi}{2}+2kπ\right]\)单调递增?
① 在一个周期\(\left[-\dfrac{\pi}{2},\dfrac{3\pi}{2}\right)\)内,找到一个单调增区间\(\left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\);
② 接着每隔一个周期\(2π\)个单位就有一个增区间,则\(\left[-\dfrac{\pi}{2}+2kπ ,\dfrac{\pi}{2}+2kπ\right]\)是\(f(x)=\sin x\)的增区间.
类似可得到正弦函数的减区间与最值,余弦函数的单调性与最值.
(也可以利用单位圆的性质研究正弦函数、余弦函数的性质)
【例】 求正弦函数\(f(x)=\sin x\)、余弦函数\(f(x)=\cos x\)在\(\left[0,2π\right]\)的单调性.
解 结合图象可得,正弦函数\(f(x)=\sin x\)的增区间是\(\left[0,\dfrac{\pi}{2}\right)\),\(\left[\dfrac{3\pi}{2},2π\right]\),减区间是\(\left[\dfrac{\pi}{2},\dfrac{3\pi}{2}\right]\);
余弦函数\(f(x)=\cos x\)的增区间是\(\left(π,2π\right]\),减区间是\([0,π)\).
基本方法
【题型1】 单调性
【典题1】 求下列函数的单调递减区间.
(1) \(y=\cos \left(2x+\dfrac{\pi}{3}\right)\);$\qquad \qquad $ (2)\(y=2\sin \left(\dfrac{\pi}{4}-x\right)\).
解析 (1) 令\(z=2x+\dfrac{\pi}{3}\),而函数\(y=\cos z\) 的递减区间是\(\left[2kπ,2kπ+π\right](k∈Z)\).
\(\therefore\)原函数递减时,可得\(2kπ≤2x+\dfrac{\pi}{3}≤2kπ+π(k∈Z)\),
解得\(kπ-\dfrac{\pi}{6}≤x≤kπ+\dfrac{\pi}{3}(k∈Z)\).
\(\therefore\) 原函数的递减区间是\(\left[kπ-\dfrac{\pi}{6},kπ+\dfrac{\pi}{3}\right](k∈Z)\).
(2)\(y=2\sin \left(\dfrac{\pi}{4}-x \right)=-2\sin \left(x-\dfrac{\pi}{4} \right)\),
令\(z=x-\dfrac{\pi}{4}\),
而函数\(y=-2\sin z\)的递减区间是\(\left[2kπ-\dfrac{\pi}{2},2kπ+\dfrac{\pi}{2}\right](k∈Z)\).
\(\therefore\) 原函数递减时,得\(2kπ-\dfrac{\pi}{2}≤x-\dfrac{\pi}{4}≤2kπ+\dfrac{\pi}{2}(k∈Z)\),
得\(2kπ-\dfrac{\pi}{4}≤x≤2kπ+\dfrac{3\pi}{4}(k∈Z)\).
\(\therefore\)原函数的递减区间是\(\left[2kπ-\dfrac{\pi}{4},2kπ+\dfrac{3\pi}{4}\right](k∈Z)\).
点拨 求三角函数\(f(x)=A\sin (ωx+φ)(ω>0)\)的单调性,利用换元法\(z=ωx+φ\),把\(ωx+φ\)代入\(y=\sin z\)对应的单调区间;而由复合函数的单调性“同增异减”,\(y=2\sin \left(\dfrac{\pi}{4}-x \right)\)与\(y=2\sin \left(x-\dfrac{\pi}{4} \right)\)的单调性相反.
【典题2】 下列关系式中正确的是( )
A.\(\sin 11°<\cos 10°<\sin 168°\) \(\qquad \qquad \qquad \qquad\) B.\(\sin 168°<\sin 11°<\cos 10°\) \(\qquad \qquad \qquad \qquad\)
C.\(\sin 11°<\sin 168°<\cos 10°\) \(\qquad \qquad \qquad \qquad\) D.\(\sin 168°<\cos 10°<\sin 11°\)
解析 \(\cos 10°=\sin 80°,\sin 168°=\sin 12°\).
因为\(y=\sin x\)在\(\left[0,\dfrac{\pi}{2}\right]\)上递增,所以\(\sin 11°<\sin 12°<\sin 80°\),
即\(\sin 11°<\sin 168°<\cos 10°\),故选\(C\).
点拨 本题利用函数的单调性比较大小,思路是统一函数名,把角度限制在一范围.
【典题3】 已知函数\(y=\sin \left(ωx+\dfrac{\pi}{3} \right)(ω>0)\)在区间\(\left(-\dfrac{\pi}{6},\dfrac{\pi}{3} \right)\)上单调递增,则\(ω\)的取值范围是( )
A.\(\left(0,\dfrac{1}{2}\right]\) \(\qquad \qquad \qquad \qquad\) B.\(\left[\dfrac{1}{2},1\right]\) \(\qquad \qquad \qquad \qquad\) C.\(\left(\dfrac{1}{3}, \dfrac{3}{2} \right]\) $\qquad \qquad \qquad \qquad $ D.\(\left[\dfrac{3}{2} ,2\right]\)
解析 由\(2kπ-\dfrac{\pi}{2}≤ωx+\dfrac{\pi}{3}≤2kπ+\dfrac{\pi}{2}\),\(k∈Z\),
得\(2kπ-\dfrac{5\pi}{6}≤ωx≤2kπ+\dfrac{\pi}{6}\),\(k∈Z\),
即 \(\dfrac{2 k \pi-\dfrac{5 \pi}{6}}{\omega} \leq x \leq \dfrac{2 k \pi+\dfrac{\pi}{6}}{\omega}\),\(k∈Z\),
\(\because f(x)\)在区间\(\left(-\dfrac{\pi}{6},\dfrac{\pi}{3} \right)\)上单调递增,\(\therefore\)此时函数单调递增区间经过原点,
则当\(k=0\)时,增区间为\(\left[-\dfrac{5\pi}{6ω},\dfrac{\pi}{6ω}\right]\).
此时满足 \(\left\{\begin{array}{l}
-\dfrac{5 \pi}{6 \omega} \leq-\dfrac{\pi}{6} \\
\dfrac{\pi}{6 \omega} \geq \dfrac{\pi}{3}
\end{array}\right.\),得 \(\left\{\begin{array}{l}
\omega \leq 5 \\
\omega \leq \dfrac{1}{2}
\end{array}\right.\),解得\(0<ω≤\dfrac{1}{2}\),
即\(ω\)的取值范围是\(\left(0,\dfrac{1}{2}\right]\),
故选:\(A\).
【巩固练习】
1.函数\(f(x)=\sin \left(2x+\dfrac{\pi}{6} \right)\)的单调递增区间是( )
A.\(\left[kπ+\dfrac{\pi}{6},kπ+2\dfrac{\pi}{3}\right]\),\((k∈Z)\) \(\qquad \qquad \qquad \qquad\) B.\(\left[kπ,kπ+\dfrac{\pi}{2}\right]\),\((k∈Z)\)
C.\(\left[kπ-\dfrac{\pi}{3},kπ+\dfrac{\pi}{6}\right]\),\((k∈Z)\) \(\qquad \qquad \qquad \qquad\) D.\(\left[kπ-\dfrac{\pi}{2},kπ\right]\),\((k∈Z)\)
2.已知函数\(f(x)=\cos (ωx+φ)(ω>0,0<φ<π)\)为奇函数,\(f(x)=f(2-x)\),当\(ω\)取最小值时,\(f(x)\)的一个单调递减区间是( )
A.\(\left[-1,1\right]\) $\qquad \qquad \qquad $ B.\(\left[- \dfrac{3}{2},\dfrac{1}{3}\right]\) \(\qquad \qquad \qquad\) C.\(\left[\dfrac{\pi}{3},\dfrac{5\pi}{6}\right]\) \(\qquad \qquad \qquad\) D.\(\left[0,\dfrac{\pi}{3}\right]\)
3.若\(f(x)=\sin \left(2x-\dfrac{\pi}{4} \right)\),则( )
A.\(f(1)>f(2)>f(3)\) \(\qquad\) B.\(f(3)>f(2)>f(1)\) \(\qquad\) C.\(f(2)>f(1)>f(3)\) \(\qquad\) D.\(f(1)>f(3)>f(2)\)
4.设\(f(x)=3\sin \left(ωx-\dfrac{\pi}{12} \right)+1\),若\(f(x)\)在\(\left[-\dfrac{\pi}{3},\dfrac{\pi}{6}\right]\)上为增函数,则\(ω\)的取值范围是( )
A.\(\left[ \dfrac{5}{12}, \dfrac{7}{2}\right]\) \(\qquad \qquad\) B.\(\left[ \dfrac{5}{4}, \dfrac{7}{2}\right]\) \(\qquad \qquad\) C.\(\left(0, \dfrac{7}{4}\right]\) \(\qquad \qquad\) D.\(\left(0, \dfrac{5}{4}\right]\)
5.设函数\(f(x)=\sin (ωx+ϕ)\),\(A>0\),\(ω>0\),若\(f(x)\)在区间\(\left[\dfrac{\pi}{6},\dfrac{\pi}{2}\right]\)上单调,且\(f\left(\dfrac{\pi}{2} \right)=f\left(\dfrac{2\pi}{3} \right)=-f\left(\dfrac{\pi}{6} \right)\),
则\(f(x)\)的最小正周期为\(\underline{\quad \quad}\).
参考答案
-
答案 \(C\)
解析 对于函数\(f(x)=\sin \left(2x+\dfrac{\pi}{6} \right)\),令\(2kπ-\dfrac{\pi}{2}≤2x+\dfrac{\pi}{6}≤2kπ+\dfrac{\pi}{2}\),
求得\(kπ-\dfrac{\pi}{3}≤x≤kπ+\dfrac{\pi}{6}\),
故函数的单调增区间为\(\left[kπ-\dfrac{\pi}{3},kπ+\dfrac{\pi}{6}\right],k∈Z\),
故选:\(C\). -
答案 \(A\)
解析 函数\(f(x)=\cos (ωx+φ)(ω>0,0<φ<π)\)为奇函数,
则\(φ=\dfrac{\pi}{2}\),\(f(x)=-\sin ωx\),\(ω>0\);
由\(f(x)=f(2-x)\)知函数\(f(x)\)的图象关于直线\(x=1\)对称,
由\(f(x)\)是\(R\)上的奇函数知\(f(2-x)=-f(x-2)\),\(f(x-4)=-f(4-x)\)
在\(f(2-x)=f(x)\)中,以\(x-2\)代\(x\)得:\(f(2-(x-2))=f(x-2)\)
即\(f(4-x)=f(x-2)\),
所以\(f(x)=f(2-x)=-f(4-x)=f(x-4)\) , 即\(f(x+4)=f(x)\),
所以\(f(x)\)是以\(4\)为周期的周期函数;
所以 \(T=\dfrac{2 \pi}{\omega}=4\),解得\(ω=\dfrac{\pi}{2}\);
当\(ω\)取最小值\(\dfrac{\pi}{2}\)时,\(f(x)=-\sin \dfrac{\pi}{2} x\);
令\(-\dfrac{\pi}{2}+2kπ≤\dfrac{\pi}{2} x≤\dfrac{\pi}{2}+2kπ\),\(k∈Z\);解得\(-1+4k≤x≤1+4k\),\(k∈Z\);
令\(k=0\),得\(-1≤x≤1\),
所以\(f(x)\)的一个单调递减区间是\(\left[-1,1\right]\).
故选:\(A\). -
答案 \(A\)
解析 利用函数的单调性:由于函数\(f(x)\)在区间\(\left[\dfrac{\pi}{2},\dfrac{3\pi}{2}\right]\)上单调递减,
故:\(\dfrac{\pi}{2}≤2x-\dfrac{\pi}{4}≤\dfrac{3\pi}{2}\),解得:\(\dfrac{3\pi}{8}≤x≤\dfrac{7\pi}{8}\),
所以\(f(1)\)的值在\(x=\dfrac{3\pi}{8}\)的左边且离得比较近,接近于最大值,故\(f(1)\)最大,
由于\(\dfrac{3\pi}{8}≤2<x<3≤\dfrac{7\pi}{8}\),故:\(f(2)>f(3)\),
所以\(f(1)>f(2)>f(3)\).
故选: \(A\). -
答案 \(D\)
解析 设\(f(x)=3\sin \left(ωx-\dfrac{\pi}{12} \right)+1\),在\(\left[-\dfrac{\pi}{3},\dfrac{\pi}{6}\right]\)上,\(\omega x-\dfrac{\pi}{12} \in\left[-\dfrac{\omega \pi}{3}-\dfrac{\pi}{12}, \dfrac{\omega \pi}{6}-\dfrac{\pi}{12}\right]\),
由于\(f(x)\)为增函数, \(\therefore\left\{\begin{array}{l} -\dfrac{\omega \pi}{3}-\dfrac{\pi}{12} \geq-\dfrac{\pi}{2} \\ \dfrac{\omega \pi}{6}-\dfrac{\pi}{12} \leq \dfrac{\pi}{2} \end{array}\right.\),即 \(\left\{\begin{array}{l} \omega \leq \dfrac{5}{4} \\ \omega \leq \dfrac{7}{2} \end{array}\right.\),求得 \(0<\omega \leq \dfrac{5}{4}\),
故选:\(D\). -
答案 \(π\)
解析 函数\(f(x)=\sin (ωx+ϕ)\),\(A>0\),\(ω>0\),若\(f(x)\)在区间\(\left[\dfrac{\pi}{6},\dfrac{\pi}{2}\right]\)上单调,
则 \(\dfrac{T}{2}=\dfrac{\pi}{\omega} \geq \dfrac{\pi}{2}-\dfrac{\pi}{6}\),\(\therefore 0<ω≤3\).
\(\because f\left(\dfrac{\pi}{2} \right)=f\left(\dfrac{2\pi}{3} \right)=-f\left(\dfrac{\pi}{6} \right)\),
\(\therefore x=\dfrac{\dfrac{\pi}{2}+\dfrac{2 \pi}{3}}{2}=\dfrac{7 \pi}{12}\),为\(f(x)=\sin (ωx+φ)\)的一条对称轴,
且 \(\left(\dfrac{\frac{\pi}{6}+\frac{\pi}{2}}{2}, 0\right)\)即\((\dfrac{\pi}{3},0)\)为\(f(x)=\sin (ωx+φ)\)的一个对称中心,
\(\therefore \dfrac{T}{4}=\dfrac{1}{4} \cdot \dfrac{2 \pi}{\omega}=\dfrac{7 \pi}{12}-\dfrac{\pi}{3}=\dfrac{\pi}{4}\),解得\(ω=2∈\left(0,3\right]\),
\(\therefore T=\dfrac{2\pi}{2}=π\),
故答案为:\(π\).
【题型2】 最值
【典题1】 求使下列函数取得最大值、最小值的自变量\(x\)的集合,并分别写出最大值、最小值:
(1)\(y=3-2\sin x\);\(\qquad \qquad\) (2)\(y=\cos \left(2x-\dfrac{\pi}{3} \right)\),\(x∈\left[\dfrac{\pi}{12},\dfrac{\pi}{2}\right]\).
解析 (1)\(\because -1≤\sin x≤1\),\(\therefore\)当\(\ \sin x=-1\),
即\(x=2kπ+\dfrac{3\pi}{2}\),\(k∈Z\)时,
\(y\)有最大值\(5\),相应\(x\)的集合为\(\{x∣x=2kπ+\dfrac{3\pi}{2},k∈Z\}\).
当\(\sin x=1\),即\(x=2kπ+\dfrac{\pi}{2}\),\(k∈Z\)时,
\(y\)有最小值\(1\),相应\(x\)的集合为\(\{x∣x=2kπ+\dfrac{\pi}{2},k∈Z\}\).
(2)令\(z=2x-\dfrac{\pi}{3}\),
\(\because \dfrac{\pi}{12}≤x≤\dfrac{\pi}{2}\),
\(\therefore -\dfrac{\pi}{6}≤2x-\dfrac{\pi}{3}≤\dfrac{2\pi}{3}\),即\(-\dfrac{\pi}{6}≤z≤\dfrac{2\pi}{3}\),
\(\therefore -\dfrac{1}{2}≤\cos z≤1\),\(\therefore y=\cos \left(2x-\dfrac{\pi}{3} \right)\),\(x∈\left[\dfrac{\pi}{12},\dfrac{\pi}{2}\right]\)的最大值为\(1\),最小值为\(-\dfrac{1}{2}\);
当\(z=0\)时,\(y=\cos z\)取得最大值;当\(z=\dfrac{2\pi}{3}\)时,\(y=\cos z\)取得最小值;
\(\therefore\)当\(2x-\dfrac{\pi}{3}=0\),即\(x=\dfrac{\pi}{6}\)时, \(y=\cos \left(2x-\dfrac{\pi}{3} \right)\)取得最大值;
当\(2x-\dfrac{\pi}{3}=\dfrac{2\pi}{3}\),即\(x=\dfrac{\pi}{2}\)时,\(y=\cos \left(2x-\dfrac{\pi}{3} \right)\)取得最小值.
【典题2】 求函数\(y=\cos ^2 x+2\sin x\)的值域.
解析 \(y=\cos ^2 x+2\sin x=-\sin ^2 x+2\sin x+1=-(\sin x-1)^2+2\).
令\(t=\sin x\),
则\(y=-(t-1)^2+2,(-1≤t≤1)\),
\(\therefore -2≤y≤2\),
即函数\(y=\cos ^2 x+2\sin x\)的值域为\(y∈\left[-2,2\right]\).
点拨 利用\(\sin ^2 x+\cos ^2 x=1\),把函数化为仅含\(\sin x\),再利用换元法(注意\(-1≤\sin x≤1\)取值范围)转化为二次函数的值域问题.
【巩固练习】
1.函数\(y=2 \sin \left(\dfrac{\pi x}{6}-\dfrac{\pi}{3}\right)(0 \leq x \leq 9)\)的最大值与最小值之和为( )
A.\(2-\sqrt{3}\) \(\qquad \qquad \qquad \qquad\) B.\(0\) \(\qquad \qquad \qquad \qquad\) C.\(-1\) \(\qquad \qquad \qquad \qquad\) D.\(-1-\sqrt{3}\)
2.函数\(y=\cos \left(x+\dfrac{\pi}{6} \right)\),\(x∈\left[0,\dfrac{\pi}{2}\right]\)的值域是\(\underline{\quad \quad}\) .
3.求函数\(y=\cos ^2 x-\sin x\),\(x∈\left[-\dfrac{\pi}{4},\dfrac{\pi}{4}\right]\)的值域 \(\underline{\quad \quad}\).
4.已知函数\(f(x)=\cos \left(ωx+\dfrac{\pi}{6} \right)(ω>0)\)在区间\(\left[0,π\right]\)上的值域为\(\left[-1, \dfrac{\sqrt{3}}{2}\right]\),则\(ω\)的取值范围为\(\underline{\quad \quad}\).
参考答案
-
答案 \(A\)
解析 由\(0≤x≤9\)可得,\(-\dfrac{\pi}{3}≤\dfrac{\pi}{6} x-\dfrac{\pi}{3}≤7\dfrac{\pi}{6}\),
所以\(-\sqrt{3}≤2\sin \left(\dfrac{\pi}{6} x-\dfrac{\pi}{3} \right)≤2\),
所以最大值为\(2\),最小值为\(-\sqrt{3}\),最大值与最小值 之差为\(2-\sqrt{3}\). -
答案 \(\left[-\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right]\).
解析 由\(x∈\left[0,\dfrac{\pi}{2}\right]\),可得\(x+\dfrac{\pi}{6}∈\left[\dfrac{\pi}{6},\dfrac{2\pi}{3}\right]\),\(\therefore\) 函数\(y=\cos \left(x+\dfrac{\pi}{6} \right)∈\left[-\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right]\). -
答案 \(\left[\dfrac{1}{2}-\dfrac{\sqrt{2}}{2}, \dfrac{5}{4}\right]\)
解析 \(y=\cos ^2 x-\sin x=1-\sin ^2 x-\sin x=-(\sin x+\dfrac{1}{2})^2+\dfrac{5}{4}\).
\(\because -\dfrac{\pi}{4}≤x≤\dfrac{\pi}{4}\),
\(\therefore\)当 \(x=-\dfrac{\pi}{6}\),即\(\sin x=-\dfrac{1}{2}\)时,\(y_{\max}=\dfrac{5}{4}\);
当\(x=\dfrac{\pi}{4}\),即 \(\sin x=\dfrac{\sqrt{2}}{2}\)时, \(y_{\min }=\dfrac{1}{2}-\dfrac{\sqrt{2}}{2}\).
故函数\(y=\cos ^2 x-\sin x\),\(x∈\left[-\dfrac{\pi}{4},\dfrac{\pi}{4}\right]\)的值域为\(\left[\dfrac{1}{2}-\dfrac{\sqrt{2}}{2}, \dfrac{5}{4}\right]\). -
答案 \(\left[\dfrac{5}{6}, \dfrac{5}{3}\right]\).
解析 在区间\(\left[0,π\right]\)上,\(ωx+\dfrac{\pi}{6}∈\left[\dfrac{\pi}{6},ωπ+\dfrac{\pi}{6}\right]\),
\(f(x)=\cos \left(ωx+\dfrac{\pi}{6} \right)\)的值域为 \(\left[-1, \dfrac{\sqrt{3}}{2}\right]\),
\(\therefore ωπ+\dfrac{\pi}{6}∈\left[π,11\dfrac{\pi}{6}\right]\),\(\therefore ωπ∈\left[\dfrac{5\pi}{6},\dfrac{5\pi}{3}\right]\),\(\therefore ω∈\left[\dfrac{5}{6}, \dfrac{5}{3}\right]\).
【题型3】三角函数综合
【典题1】 设函数\(f(x)=\cos \left(2x-\dfrac{\pi}{3} \right)\),则下列结论错误的是( )
A.\(f(x)\)的一个周期为\(-π\) \(\qquad \qquad \qquad \qquad \qquad\) B.\(f(x)\)的图象关于直线\(x=\dfrac{2\pi}{3}\)对称
C.\(f\left(x+\dfrac{\pi}{2} \right)\)的一个零点为\(x=-\dfrac{\pi}{3}\) \(\qquad \qquad \qquad\) D.\(f(x)\)在区间\(\left[\dfrac{\pi}{3},\dfrac{\pi}{2}\right]\)上单调递减
解析 根据题意,依次分析选项:
对于 \(A\)、\(f(x)=\cos \left(2x-\dfrac{\pi}{3} \right)\),其周期\(T=\dfrac{2\pi}{2}=π\), \(A\)正确;
对于\(B\)、\(f(x)=\cos \left(2x-\dfrac{\pi}{3} \right)\),令\(2x-\dfrac{\pi}{3}=kπ\),解可得\(x=\dfrac{k\pi}{2}+\dfrac{\pi}{6}\),
即\(y=f(x)\)的对称轴为\(x=\dfrac{k\pi}{2}+\dfrac{\pi}{6}\),
当\(k=1\)时,\(x=\dfrac{2\pi}{3}\),即\(y=f(x)\)的图象关于直线\(x=\dfrac{2\pi}{3}\)对称,\(B\)正确;
对于\(C\)、\(f\left(x+\dfrac{\pi}{2} \right)=\cos \left(2x+π-\dfrac{\pi}{3} \right)=\cos \left(2x+\dfrac{2\pi}{3} \right)\),
当\(x=-\dfrac{\pi}{3}\)时,\(f\left(x+\dfrac{\pi}{2} \right)=\cos 0=1\),
则\(x=-\dfrac{\pi}{3}\)不是\(f\left(x+\dfrac{\pi}{2} \right)\)的零点,\(C\)错误;
对于\(D\)、\(f(x)=\cos \left(2x-\dfrac{\pi}{3} \right)\),\(2kπ≤2x-\dfrac{\pi}{3}≤2kπ+π\),
解可得\(kπ+\dfrac{\pi}{6}≤x≤kπ+\dfrac{2\pi}{3}\),即函数\(f(x)\)的递减区间为\(\left[kπ+\dfrac{\pi}{6},kπ+\dfrac{2\pi}{3}\right]\),
则函数在\(\left[\dfrac{\pi}{6},\dfrac{2\pi}{3}\right]\)上递减,
又由\(\left[\dfrac{\pi}{3},\dfrac{\pi}{2}\right]∈\left[\dfrac{\pi}{6},\dfrac{2\pi}{3}\right]\),则\(f(x)\)在区间\(\left[\dfrac{\pi}{3},\dfrac{\pi}{2}\right]\)上递减,\(D\)正确;
故选:\(C\).
【典题2】 已知\(f(x)=-\dfrac{\sqrt{2}}{2} \sin \left(2 x+\dfrac{\pi}{4}\right)+2\),求:
(1)\(f(x)\)的最小正周期及对称轴方程;
(2)\(f(x)\)的单调递增区间;
(3)若方程\(f(x)-m+1=0\)在\(x∈\left[0,\dfrac{\pi}{2}\right]\)上有解,求实数\(m\)的取值范围.
解析 (1)由于 \(f(x)=-\dfrac{\sqrt{2}}{2} \sin \left(2 x+\dfrac{\pi}{4}\right)+2\),它的最小正周期为\(\dfrac{2\pi}{2}=π\),
令\(2x+\dfrac{\pi}{4}=kπ+\dfrac{\pi}{2}\),求得\(x=\dfrac{k\pi}{2}+\dfrac{\pi}{8}\),\(k∈Z\),
故函数\(f(x)\)的图象的对称轴方程为\(x=\dfrac{k\pi}{2}+\dfrac{\pi}{8}\),\(k∈Z\).
(2)令\(2kπ+\dfrac{\pi}{2}≤2x+\dfrac{\pi}{4}≤2kπ+\dfrac{3\pi}{2}\),求得 \(kπ+\dfrac{\pi}{8}≤x≤kπ+\dfrac{5\pi}{8}\),
可得函数\(f(x)\)的增区间为\(\left[kπ+\dfrac{\pi}{8},kπ+\dfrac{5\pi}{8}\right]\),\(k∈Z\).
(3)若方程\(f(x)-m+1=0\)在\(x∈\left[0,\dfrac{\pi}{2}\right]\)上有解,
则函数\(f(x)\)的图象和直线\(y=m-1\)在\(x∈\left[0,\dfrac{\pi}{2}\right]\)上有交点.
\(\because x∈\left[0,\dfrac{\pi}{2}\right]\),\(\therefore 2x+\dfrac{\pi}{4}∈\left[\dfrac{\pi}{4},\dfrac{5\pi}{4}\right]\),\(\sin \left(2x+\dfrac{\pi}{4} \right)∈\left[-\dfrac{\sqrt{2}}{2},1\right]\),
\(\therefore f(x) \in\left[2-\dfrac{\sqrt{2}}{2}, \dfrac{5}{2}\right]\),
故\(m-1∈\left[2-\dfrac{\sqrt{2}}{2}, \dfrac{5}{2}\right]\),
\(\therefore m \in\left[3-\dfrac{\sqrt{2}}{2}, \dfrac{7}{2}\right]\).
【巩固练习】
1.已知函数\(f(x)=3\sin \left(2x-\dfrac{\pi}{3} \right)\),下列结论中正确的是( )
A.函数\(f(x)\)的最小正周期为\(2π\) \(\qquad \qquad \qquad \qquad\) B.函数\(f(x)\)的图象关于直线\(x=\dfrac{\pi}{6}\)对称
C.函数\(f(x)\)的图象关于点\(\left(-\dfrac{\pi}{6},0 \right)\)对称 \(\qquad \qquad\) D.函数\(f(x)\)在\(\left(-\dfrac{\pi}{12},\dfrac{5\pi}{12} \right)\)内是增函数
2.同时具有以下性质:①最小正周期是\(π\);②图象关于直线\(x=\dfrac{\pi}{3}\)对称;③在\(\left[-\dfrac{\pi}{6},\dfrac{\pi}{3}\right]\)上是增函数;
④一个对称中心为\(\left(\dfrac{\pi}{12},0 \right)\)的一个函数是( )
A.\(y=\sin \left(\dfrac{x}{2}+\dfrac{\pi}{6} \right)\) \(\qquad \qquad \qquad \qquad \qquad\) B.\(y=\sin \left(2x+\dfrac{\pi}{3} \right)\)
C.\(y=\sin \left(2x-\dfrac{\pi}{6} \right)\) \(\qquad \qquad \qquad \qquad \qquad\) D.\(y=\sin \left(2x-\dfrac{\pi}{3} \right)\)
3.设函数\(f(x)=\sin \left(2x+\dfrac{2\pi}{3} \right)\),则下列结论中正确的是( )
A.\(f(x)\)的图象关于点\(\left(\dfrac{\pi}{3},0 \right)\)对称 \(\qquad \qquad \qquad\) B.\(f(x)\)的图象关于直线\(x=\dfrac{\pi}{3}\)对称
C.\(f(x)\)在\(\left[0,\dfrac{\pi}{3}\right]\)上单调递减 \(\qquad \qquad \qquad \qquad\) D.\(f(x)\)在\(\left[-\dfrac{\pi}{6},0\right]\)上的最小值为\(0\)
4.若函数\(f(x)=\cos (ωx+φ)\left(ω>0,|φ|<\dfrac{\pi}{2} \right)\)的一个零点和与之相邻的对称轴之间的距离为\(\dfrac{\pi}{4}\),
且当\(x=\dfrac{2\pi}{3}\)时,\(f(x)\)取得最小值.
(1)求\(f(x)\)的解析式及其单调递减区间;
(2)若\(x∈\left[\dfrac{\pi}{4},\dfrac{5\pi}{6}\right]\),求\(f(x)\)的值域.
参考答案
-
答案 \(D\)
解析 \(A\)错,最小正周期为\(π\),当\(x=\dfrac{\pi}{6}\)时,\(f(x)≠1\),\(B\)错,
\(f\left(-\dfrac{\pi}{6} \right)=3\sin \left(-\dfrac{2\pi}{3} \right)≠0\),\(C\)错,
当\(x∈\left(-\dfrac{\pi}{12},\dfrac{5\pi}{12} \right)\)时,\(2x-\dfrac{\pi}{3}∈(-\dfrac{\pi}{2},\dfrac{\pi}{2})\),\(f(x)\)单调递增,\(D\)成立,
故选:\(D\). -
答案 \(C\)
解析 由“①最小正周期是\(π\),可得\(ω=2\),排除 \(A\);
②图象关于直线\(x=\dfrac{\pi}{3}\)对称;可得:\(\dfrac{2\pi}{3}+φ=\dfrac{\pi}{3}+kπ\),\(k∈Z\).
对于\(D\)选项:\(φ=-\dfrac{\pi}{3}\),不满足,排除\(D\);
④一个对称中心为\(\left(\dfrac{\pi}{12},0 \right)\)带入函数y中,\(B\)选项不满足.排除\(B\);
故选:\(C\). -
答案 \(C\)
解析 对于函数\(f(x)=\sin \left(2x+\dfrac{2\pi}{3} \right)\),令\(x=\dfrac{\pi}{3}\),求得\(f(x)=-\sqrt{3}\),不是最值,
可得\(y=f(x)\)的图象不关于点\(\left(\dfrac{\pi}{3},0 \right)\)对称,也不关于直线\(x=\dfrac{\pi}{3}\)对称,故\(A\)、\(B\)都不正确;
在\(\left[0,\dfrac{\pi}{3}\right]\)上,\(2x+\dfrac{2\pi}{3}∈\left[\dfrac{2\pi}{3},\dfrac{4\pi}{3}\right]\),故\(f(x)\)在\(\left[0,\dfrac{\pi}{3}\right]\)上单调递减,故\(C\)正确;
在\(\left[-\dfrac{\pi}{6},0\right]\)上,\(2x+\dfrac{2\pi}{3}∈\left[\dfrac{\pi}{3},\dfrac{2\pi}{3}\right]\),
故\(f(x)\)在\(\left[0,\dfrac{\pi}{3}\right]\)上没有单调性,最小值为\(f(-\dfrac{\pi}{6})=f(0)=\dfrac{\sqrt{3}}{2}\),故\(D\)不正确,
故选:\(C\). -
答案 (1)\(f(x)=\cos \left(2x-\dfrac{\pi}{3} \right)\),\(\left[kπ+\dfrac{\pi}{6},kπ+\dfrac{2\pi}{3}\right]\),\(k∈Z\); (2) \(\left[-1,\dfrac{\sqrt{3}}{2}\right]\).
解析 (1)由题意,函数\(f(x)\)的一个零点和与之相邻的对称轴之间的距离为\(\dfrac{\pi}{4}\),
可得\(f(x)\)的周期\(T=π\),即 \(\dfrac{2 \pi}{\omega}=\pi\),解得\(ω=2\),
又因为当\(x=\dfrac{2\pi}{3}\)时,\(f(x)\)取得最小值,
所以\(f\left(\dfrac{2\pi}{3} \right)=\cos \left(\dfrac{4\pi}{3}+φ \right)=-1\),
所以\(\dfrac{4\pi}{3}+φ=2kπ+π\),\(k∈Z\),解\(φ=2kπ-\dfrac{\pi}{3}\),\(k∈Z\),
因为\(|φ|<\dfrac{\pi}{2}\),所以\(φ=-\dfrac{\pi}{3}\),所以\(f(x)=\cos (2x-\dfrac{\pi}{3})\).
令\(2kπ≤2x-\dfrac{\pi}{3}≤2kπ+π\),\(k∈Z\),解得\(kπ+\dfrac{\pi}{6}≤x≤kπ+\dfrac{2\pi}{3}\),\(k∈Z\),
所以\(f(x)\)的单调递减区间为\(\left[kπ+\dfrac{\pi}{6},kπ+\dfrac{2\pi}{3}\right]\),\(k∈Z\);
(2)因为\(x∈\left[\dfrac{\pi}{4},\dfrac{5\pi}{6}\right]\),可得\(\dfrac{\pi}{6}≤2x-\dfrac{\pi}{3}≤\dfrac{4\pi}{3}\),
所以当\(2x-\dfrac{\pi}{3}=π\)时,\(f(x)\)取得最小值\(-1\),
当\(2x-\dfrac{\pi}{3}=\dfrac{\pi}{6}\)时,\(f(x)\)取得最大值为 \(\dfrac{\sqrt{3}}{2}\),
所以函数\(f(x)\)的值域是\(\left[-1,\dfrac{\sqrt{3}}{2}\right]\).
分层练习
【A组---基础题】
1.下列区间中是函数\(y=\sin \left(x+\dfrac{\pi}{4} \right)\)的单调递增区间的是( )
A.\(\left[\dfrac{\pi}{2},π\right]\) $\qquad \qquad \qquad \qquad $ B.\(\left[0,\dfrac{\pi}{4}\right]\) $\qquad \qquad \qquad \qquad $ C.\(\left[-π,0\right]\) $\qquad \qquad \qquad \qquad $ D.\(\left[\dfrac{\pi}{4}, \dfrac{\pi}{2}\right]\)
2.函数\(y=2\sin 2x\),\(x∈\left[0,\dfrac{\pi}{6}\right]\)的值域为( )
A.\(\left[-2,2\right]\) $\qquad \qquad \qquad \qquad $ B.\(\left[-1,0\right]\) $\qquad \qquad \qquad \qquad $ C.\(\left[0,\sqrt{3}\right]\) $\qquad \qquad \qquad \qquad $ D.\(\left[0,1\right]\)
3.函数\(f(x)=\cos \left(2x-\dfrac{\pi}{3} \right)\)在\(\left[0,\dfrac{\pi}{2}\right]\)上的最小值是( )
A.\(-\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad \qquad \qquad\) D.\(1\)
4.下列函数中,以\(π\)为周期且在区间\(\left(\dfrac{\pi}{2},π \right)\)单调递增的是( )
A.\(f(x)=|\cos 2x|\) \(\qquad \qquad\) B.\(f(x)=|\sin 2x|\) \(\qquad \qquad\) C.\(f(x)=|\cos x|\) \(\qquad \qquad\) D.\(f(x)=|\sin x|\)
5.已知函数\(f(x)=\sin x+|\sin x|\),则下列结论正确的是( )
A.\(f(x+π)=f(x)\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) B.\(f(x)\)的值域为\(\left[0,1\right]\)
C.\(f(x)\)在\(\left[\dfrac{\pi}{2},π\right]\)上单调递减 \(\qquad \qquad \qquad \qquad\) D.\(f(x)\)的图象关于点\((π,0)\)对称
6.函数\(f(x)=\cos \left(ωx+\dfrac{\pi}{6} \right)(ω>0)\)的最小正周期为\(π\),则\(f(x)\)满足( )
A.在\(\left(0,\dfrac{\pi}{3} \right)\)上单调递增 \(\qquad \qquad \qquad \qquad\) B.图象关于直线\(x=\dfrac{\pi}{6}\)对称
C.\(f\left(\dfrac{\pi}{3} \right)=\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad \qquad \qquad \qquad\) D.当\(x=\dfrac{5\pi}{12}\)时有最小值\(-1\)
7.关于函数\(f(x)=|\sin x|+\cos x\)有下述四个结论:
①\(f(x)\)是周期函数;\(\qquad \qquad \qquad\) ②\(f(x)\)的最小值为\(-\sqrt{2}\);
③\(f(x)\)的图象关于\(y\)轴对称;\(\qquad \qquad\) ④\(f(x)\)在区间\(\left(\dfrac{\pi}{4},\dfrac{\pi}{2} \right)\)单调递增.
其中所有正确结论的编号是( )
A.①② \(\qquad \qquad \qquad \qquad\) B.①③ \(\qquad \qquad \qquad \qquad\) C.②③ \(\qquad \qquad \qquad \qquad\) D.②④
8.已知函数\(f(x)=\sin (ωx+φ)\left(ω>0,0<φ<\dfrac{\pi}{2} \right)\)的最小正周期为\(π\),且关于\(\left(-\dfrac{\pi}{8},0 \right)\)中心对称,则下列结论正确的是( )
A.\(f(1)<f(0)<f(2)\) \(\qquad \qquad \qquad \qquad\) B.\(f(0)<f(2)<f(1)\)
C.\(f(2)<f(0)<f(1)\) \(\qquad \qquad \qquad \qquad\) D.\(f(2)<f(1)<f(0)\)
9.已知函数\(f(x)=\sin ωx\)的图象关于点\(\left(\dfrac{2\pi}{3},0 \right)\)对称,且\(f(x)\)在\(\left[0,\dfrac{\pi}{4}\right]\)上为增函数,则\(ω=\)\(\underline{\quad \quad}\).
10.若\(f(x)=2\sin (2x+φ)(φ>0)\)的图象关于直线\(x=\dfrac{\pi}{12}\)对称,且当\(φ\)取最小值时,\(∃x_0∈\left(0,\dfrac{\pi}{2} \right)\),使得\(f(x_0)=a\),则\(a\)的取值范围是\(\underline{\quad \quad}\).
11.已知点\(A\left(\dfrac{\pi}{24},0 \right)\)在函数\(f(x)=\cos (2ωx+φ)(ω>0\)且\(ω∈N^*,0<φ<π)\)的图象上,直线\(x=\dfrac{\pi}{6}\)是函数\(f(x)\)的图象的一条对称轴.若\(f(x)\)在区间\(\left(\dfrac{\pi}{6},\dfrac{\pi}{3} \right)\)内单调,则\(φ=\)\(\underline{\quad \quad}\).
12.已知\(f(x)=\sqrt{2} \sin \left(2x+\dfrac{\pi}{4} \right)\).
(1)求函数\(f(x)\)图象的对称轴方程.
(2)求\(f(x)\)的单调递增区间.
(3)当\(x∈\left[\dfrac{\pi}{4},\dfrac{3\pi}{4}\right]\)时,求函数\(f(x)\)的最大值和最小值.
参考答案
-
答案 \(B\)
解析 \(\because\)函数\(y=\sin x\)的单调递增区间为\(\left[2kπ-\dfrac{\pi}{2},2kπ+\dfrac{\pi}{2}\right](k∈Z)\),
由\(2kπ-\dfrac{\pi}{2}≤x+\dfrac{\pi}{4}≤2kπ+\dfrac{\pi}{2}\),得\(2kπ-\dfrac{3\pi}{4}≤x≤2kπ+\dfrac{\pi}{4}(k∈Z)\).
令\(k=0\),得\(-\dfrac{3\pi}{4}≤x≤\dfrac{\pi}{4}\),
\(\therefore\)只有\(\left[0,\dfrac{\pi}{4}\right]⊆\left[-\dfrac{3\pi}{4},\dfrac{\pi}{4}\right]\),故选\(B\). -
答案 \(C\)
解析 \(\because 0≤x≤\dfrac{\pi}{6}\),\(\therefore 0≤2x≤\dfrac{\pi}{3}\),\(\therefore 0≤\sin 2x≤\dfrac{\sqrt{3}}{2}\),\(\therefore y∈\left[0,\sqrt{3}\right]\). -
答案 \(A\)
解析 \(x∈\left[0,\dfrac{\pi}{2}\right]\)时,\(2x-\dfrac{\pi}{3}∈\left[-\dfrac{\pi}{3},\dfrac{2\pi}{3}\right]\),
\(\therefore x=\dfrac{\pi}{2}\)时,\(\cos \left(2x-\dfrac{\pi}{3} \right)=\cos \dfrac{2\pi}{3}=-\dfrac{1}{2}\);
\(\therefore\)函数\(f(x)=\cos \left(2x-\dfrac{\pi}{3} \right)\)在\(\left[0,\dfrac{\pi}{2}\right]\)上的最小值是\(-\dfrac{1}{2}\).
故选: \(A\). -
答案 \(C\)
解析 由于\(f(x)=|\cos 2x|\)的周期为\(\dfrac{1}{2}\cdot \dfrac{2\pi}{2}=\dfrac{\pi}{2}\),故 \(A\)不满足条件;
由于\(f(x)=|\sin 2x|\)的周期为\(\dfrac{1}{2}\cdot \dfrac{2\pi}{2}=\dfrac{\pi}{2}\),故\(B\)不满足条件;
由于\(f(x)=|\cos x|\)的最小正周期为\(\dfrac{1}{2}\cdot 2π=π\),
在区间\(\left(\dfrac{\pi}{2},π \right)\)上,\(f(x)=|\cos x|=-\cos x\)单调递增,故\(C\)满足条件;
由于\(f(x)=|\sin x|\)的最小正周期为\(\dfrac{1}{2}\cdot 2π=π\),
在区间\(\left(\dfrac{\pi}{2},π \right)\)上,\(f(x)=\sin x\)单调递减,故\(D\)不满足条件,
故选:\(C\). -
答案 \(C\)
解析 函数 \(f(x)=\sin x+|\sin x|=\left\{\begin{array}{l} 2 \sin x, x \in[0, \pi] \\ 0, x \in(\pi, 2 \pi] \end{array}\right.\),
故函数的周期为\(2π\),即\(f(x+2π)=f(x)\),故排除 \(A\);
显然,函数的值域为\(\left[0,2\right]\),故排除\(B\);
在\(\left[\dfrac{\pi}{2},π\right]\)上,函数\(t=\sin x\)单调递减,故函数\(y=2\sin x\)单调递减,故\(C\)正确;
根据故函\(f(x)\)的图象特征,可得它的图象不关于点\((π,0)\)对称,故排除\(D\),
故选:\(C\). -
答案 \(D\)
解析 函数\(f(x)=\cos \left(ωx+\dfrac{\pi}{6} \right)(ω>0)\)的最小正周期为 \(T=\dfrac{2 \pi}{\omega}=\pi\),\(\therefore ω=2\),
\(\therefore f(x)=\cos (2x+\dfrac{\pi}{6})\);
当\(x∈\left(0,\dfrac{\pi}{3} \right)\)时,\(2x+\dfrac{\pi}{6}∈\left(\dfrac{\pi}{6},\dfrac{5\pi}{6} \right)\),\(f(x)\)单调递减,\(\therefore A\)错误;
\(x=\dfrac{\pi}{6}\)时,\(2x+\dfrac{\pi}{6}=\dfrac{\pi}{2}\),\(f\left(\dfrac{\pi}{6} \right)=0\),其图象不关于直线\(x=\dfrac{\pi}{6}\)对称,\(B\)错误;
\(f\left(\dfrac{\pi}{3} \right)=\cos \left(2×\dfrac{\pi}{3}+\dfrac{\pi}{6} \right)=-\dfrac{\sqrt{3}}{2}\),\(C\)错误;
\(x=\dfrac{5\pi}{12}\)时,\(f(x)=\cos (2×\dfrac{5\pi}{12}+\dfrac{\pi}{6})=-1\),\(D\)正确.
故选:\(D\). -
答案 \(B\)
解析 函数\(f(x)=|\sin x|+\cos x\),其中\(|\sin x|\)的周期为\(π\),\(\cos 2x\)的周期为\(2π\),
所以函数的最小正周期为\(2π\),故函数为周期函数.①\(f(x)\)是周期函数;正确.
②函数的最小值为\(-1\),所以:\(f(x)\)的最小值为\(-\sqrt{2}\);错误.
③由于\(f(-x)=f(x)\),\(f(x)\)的图象关于\(y\)轴对称;
④\(f(x)\)在区间\(\left(\dfrac{\pi}{4},\dfrac{\pi}{2} \right)\)单调递减.故错误.
故选:\(B\). -
答案 \(D\)
解析 \(\because\)函数的最小周期是\(π\), \(\therefore \dfrac{2 \pi}{\omega}=\pi\),得\(ω=2\),则\(f(x)=\sin (2x+φ)\),
\(\because f(x)\)关于\(\left(-\dfrac{\pi}{8},0 \right)\)中心对称,
\(\therefore 2×\left(-\dfrac{\pi}{8} \right)+φ=kπ\),\(k∈Z\),即\(φ=kπ+\dfrac{\pi}{4}\),\(k∈Z\),
\(\because 0<φ<\dfrac{\pi}{2}\),\(\therefore\)当\(k=0\)时,\(φ=\dfrac{\pi}{4}\),即\(f(x)=\sin \left(2x+\dfrac{\pi}{4} \right)\),
则函数在\(\left[-\dfrac{\pi}{8}, \dfrac{\pi}{8}\right]\)上递增,在\(\left[\dfrac{\pi}{8},\dfrac{5\pi}{8}\right]\)上递减,\(f(0)=f\left(\dfrac{\pi}{4} \right)\),
\(\because \dfrac{\pi}{4}<1<2\),\(\therefore f\left(\dfrac{\pi}{4} \right)>f(1)>f(2)\),即\(f(2)<f(1)<f(0)\),
故选:\(D\). -
答案 \(\dfrac{3}{2}\)
解析 依题意:\(f\left(\dfrac{2\pi}{3} \right)=\sin \left(\dfrac{2\pi}{3} ω \right)=0\),\(\therefore \dfrac{2\pi}{3} ω=kπ\),\(k∈Z\),
\(\therefore \omega=\dfrac{3 k}{2}\),\(k∈Z\),
又\(f(x)=\sin ωx\)在\(\left[0,\dfrac{\pi}{4}\right]\)上递增,
\(\therefore 0<ω⋅\dfrac{\pi}{4}≤\dfrac{\pi}{2}\),即\(0<ω≤2\),
\(\therefore k=1\),\(ω=\dfrac{3}{2}\). -
答案 \(\left(-\sqrt{3},2\right]\)
解析 \(f(x)=2\sin (2x+φ)(φ>0)\)的图象关于直线\(x=\dfrac{\pi}{12}\)对称,
所以\(2×\dfrac{\pi}{12}+φ=kπ+\dfrac{\pi}{2}(k∈Z)\),解得\(φ=kπ+\dfrac{\pi}{3}\),
当\(k=0\)时,\(φ=\dfrac{\pi}{3}\).所以\(f(x)=2\sin \left(2x+\dfrac{\pi}{3} \right)\).
由于\(∃x_0∈\left(0,\dfrac{\pi}{2} \right)\),所以\(\dfrac{\pi}{3}<2x_0+\dfrac{\pi}{3}<\dfrac{4\pi}{3}\),
所以\(-\sqrt{3}<f(x_0)≤2\),即\(a\)的范围为\(\left(-\sqrt{3},2\right]\). -
答案 \(\dfrac{\pi}{3}\)
解析 由题意得, \(\dfrac{\pi}{6}-\dfrac{\pi}{24}=\dfrac{\pi}{8} \geq \dfrac{T}{4}\),得 \(\dfrac{1}{4} \times \dfrac{2 \pi}{2 \omega} \leq \dfrac{\pi}{8}\),得\(ω≥2\),
又因为\(f(x)\)在区间\(\left(\dfrac{\pi}{6},\dfrac{\pi}{3} \right)\)内单调,
所以 \(\dfrac{\pi}{3}-\dfrac{\pi}{6} \leq \dfrac{T}{2}\),得 \(\dfrac{1}{2} \times \dfrac{2 \pi}{2 \omega} \geq \dfrac{\pi}{6}\),得\(ω≤3\).所以\(2≤ω≤3\).
又因为\(ω∈N^*\),所以\(ω=2\)或\(3\).
当\(ω=2\)时,\(\cos \left(4×\dfrac{\pi}{24}+φ \right)=0\),得\(φ=kπ+\dfrac{\pi}{3}\),
又\(0<φ<π\),所以\(φ=\dfrac{\pi}{3}\),
此时直线\(x=\dfrac{\pi}{6}\)是函数\(f(x)\)的图象的一条对称轴,且\(f(x)\)在区间\(\left(\dfrac{\pi}{6},\dfrac{\pi}{3} \right)\)内单调.
所以\(φ=\dfrac{\pi}{3}\).
当\(ω=3\)时,\(\cos \left(6×\dfrac{\pi}{24}+φ \right)=0\),得\(φ=kπ+\dfrac{\pi}{4}\),
又\(0<φ<π\),所以\(φ=\dfrac{\pi}{4}\),此时\(\cos \left(6×\dfrac{\pi}{6}+\dfrac{\pi}{4} \right)=-\dfrac{\sqrt{2}}{2}≠±1\),
所以直线\(x=\dfrac{\pi}{6}\)不是函数\(f(x)\)的图象的一条对称轴.
所以\(ω=2\),\(φ=\dfrac{\pi}{3}\). -
答案 (1) \(x=\dfrac{k\pi}{2}+\dfrac{\pi}{8}\),\(k∈Z\); (2) \(\left[kπ-\dfrac{3\pi}{8},kπ+\dfrac{\pi}{8}\right]\),\(k∈Z\);
(3)最大值为 \(1\),最小值为\(-\sqrt{2}\).
解析 (1)由\(f(x)=\sqrt{2} \sin \left(2x+\dfrac{\pi}{4} \right)\),
令\(2x+\dfrac{\pi}{4}=kπ+\dfrac{\pi}{2}\),\(k∈Z\),解得\(x=\dfrac{k\pi}{2}+\dfrac{\pi}{8}\),\(k∈Z\);
所以函数\(f(x)\)图象的对称轴方程是\(x=\dfrac{k\pi}{2}+\dfrac{\pi}{8}\),\(k∈Z\);
(2)令\(2kπ-\dfrac{\pi}{2}≤2x+\dfrac{\pi}{4}≤2kπ+\dfrac{\pi}{2}\),\(k∈Z\),解得\(kπ-\dfrac{3\pi}{8}≤x≤kπ+\dfrac{\pi}{8}\),\(k∈Z\);
所以\(f(x)\)的单调递增区间为\(\left[kπ-\dfrac{3\pi}{8},kπ+\dfrac{\pi}{8}\right]\),\(k∈Z\);
(3)当\(x∈\left[\dfrac{\pi}{4},\dfrac{3\pi}{4}\right]\)时,\(\dfrac{3\pi}{4}≤2x+\dfrac{\pi}{4}≤\dfrac{7\pi}{4}\),
所以\(-1≤\sin \left(2x+\dfrac{\pi}{4} \right)≤\dfrac{\sqrt{2}}{2}\),所以\(-\sqrt{2}≤f(x)≤1\);
所以当\(x∈\left[\dfrac{\pi}{4},\dfrac{3\pi}{4}\right]\)时,函数\(f(x)\)的最大值为\(1\),最小值为\(-\sqrt{2}\).
【B组---提高题】
1.已知函数\(f(x)=\left|\cos \left(ω x+\dfrac{\pi}{3} \right) \right|(ω>0)\)在区间\(\left[-\dfrac{\pi}{3},\dfrac{5\pi}{6}\right]\)上单调,则\(ω\)的取值范围为( )
A.\(\left(0,\dfrac{12}{15} \right]\) \(\qquad \qquad \qquad \qquad\) B.\(\left(0,\dfrac{1}{5} \right]\) \(\qquad \qquad \qquad \qquad\) C.\(\left[\dfrac{1}{5} ,\dfrac{12}{15} \right]\) \(\qquad \qquad \qquad \qquad\) D.\(\left[\dfrac{12}{15} ,1\right]\)
2.已知函数\(f(x)=\sin \left(ωx+\dfrac{\pi}{3} \right),(ω>0)\)在区间\(\left[-\dfrac{2\pi}{3},\dfrac{5\pi}{6}\right]\)上是增函数,且在区间\(\left[0,π\right]\)上恰好取得一次最大值\(1\),则\(ω\)的取值范围是( )
A. \(\left(0,\dfrac{1}{5} \right]\) \(\qquad \qquad \qquad \qquad\) B.\(\left[\dfrac{1}{2},\dfrac{3}{5}\right]\) \(\qquad \qquad \qquad \qquad\) C.\(\left[\dfrac{1}{6},\dfrac{1}{5}\right]\) \(\qquad \qquad \qquad \qquad\) D.\(\left[\dfrac{1}{2},\dfrac{5}{2}\right)\)
3.若方程\(\sin \left(2x-\dfrac{\pi}{6} \right)=\dfrac{3}{5}\) 在\((0,π)\)上的解为\(x_1\) 、\(x_2\),且\(x_1>x_2\),则\(\sin (x_1-x_2)=\) \(\underline{\quad \quad}\).
参考答案
-
答案 \(B\)
解析 \(y=|\cos x|\)的单调递减区间为\(\left[kπ,kπ+\dfrac{\pi}{2}\right]\),\(k∈Z\),
由\(kπ≤ωx+\dfrac{\pi}{3}≤kπ+\dfrac{\pi}{2}\),\(k∈Z\),得 \(\dfrac{k \pi-\frac{\pi}{3}}{\omega} \leq x \leq \dfrac{k \pi+\frac{\pi}{6}}{\omega}\),
即函数的单调递减区间为 \(\left[\dfrac{k \pi-\frac{\pi}{3}}{\omega}, \dfrac{k \pi+\frac{\pi}{6}}{\omega}\right]\),\(k∈Z\),
若\(f(x)\)在区间\(\left[-\dfrac{\pi}{3},\dfrac{5\pi}{6}\right]\)上单调递减,
则\(\dfrac{k \pi-\dfrac{\pi}{3}}{\omega} \leq-\dfrac{\pi}{3}\)且 \(\dfrac{k \pi+\dfrac{\pi}{6}}{\omega} \geq \dfrac{5 \pi}{6}\),得 \(\left\{\begin{array}{l} \omega \leq \dfrac{6}{5} k+\dfrac{1}{5} \\ \omega \leq-3 k+1 \end{array}\right.\),\(k∈Z\),
当\(k=0\)时, \(\left\{\begin{array}{l} \omega \leq \dfrac{1}{5} \\ \omega \leq 1 \end{array}\right.\),即\(0<ω≤\dfrac{1}{5}\),即\(ω\) 的取值范围是 \(\left(0,\dfrac{1}{5} \right]\).
当\(f(x)\)在区间\(\left[-\dfrac{\pi}{3},\dfrac{5\pi}{6}\right]\)上单调递增时,\(ω\)无解,
故选:\(B\). -
答案 \(C\)
解析 方法一(复合函数法):令\(X=ωx+\dfrac{\pi}{3}\),\(-\dfrac{2\pi}{3}≤x≤\dfrac{5\pi}{6}\),
则\(-\dfrac{2 \pi \omega}{3}+\dfrac{\pi}{3} \leq X \leq \dfrac{5 \pi \omega}{6}+\dfrac{\pi}{3}\).
\(\therefore\)函数\(y=\sin X\)在区间 上\(\left[-\dfrac{2 \pi \omega}{3}+\dfrac{\pi}{3}, \dfrac{5 \pi \omega}{6}+\dfrac{\pi}{3}\right]\)单调递增,
\(\therefore\left[-\dfrac{2 \pi \omega}{3}+\dfrac{\pi}{3}, \dfrac{5 \pi \omega}{6}+\dfrac{\pi}{3}\right] \subseteq\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right]\),\(\therefore ω≤\dfrac{1}{5}\).
当\(0≤x≤π\)时,\(\dfrac{\pi}{3}≤X≤πω+\dfrac{\pi}{3}\),
\(\therefore\)函数\(y=\sin X\)在区间\(\left[\dfrac{\pi}{3},πω+\dfrac{\pi}{3}\right]\)恰好取一次最大值\(1\),
\(\therefore \dfrac{\pi}{2}≤πω+\dfrac{\pi}{3}<\dfrac{5\pi}{2}\), \(\therefore \dfrac{1}{6} \leq \omega \leq \dfrac{13}{6}\),
综上所知 \(\dfrac{1}{6} \leq \omega \leq \dfrac{1}{5}\),故选\(C\).
方法二(特殊值法):当\(ω=\dfrac{1}{2}\)时,令 \(X=\dfrac{x}{2}+\dfrac{\pi}{3}\), \(-\dfrac{2 \pi}{3} \leq x \leq \dfrac{5 \pi}{6}\),
则\(0≤X≤\dfrac{3\pi}{4}\),则函数\(y=\sin X\)在区间\(\left[0,\dfrac{3\pi}{4}\right]\)上不单调,
\(\therefore ω=\dfrac{1}{2}\)不合题意,排除\(BD\).
当 \(\omega=\dfrac{1}{12}\)时,令 \(X=\dfrac{x}{12}+\dfrac{\pi}{3}\),\(0≤x≤π\),
则\(\dfrac{\pi}{3}≤X≤\dfrac{5\pi}{12}\),则函数\(y=\sin X\)在区间\(\left[\dfrac{\pi}{3},\dfrac{5\pi}{12}\right]\)取不到最大值\(1\),
\(\therefore \omega=\dfrac{1}{12}\)不合题意,排除 \(A\).
故选:\(C\). -
答案 \(\left[2-\sqrt{2},2\sqrt{2}\right]\)
解析 令\(2x-\dfrac{\pi}{6}=\dfrac{1}{2} π+kπ\)可得,\(x=\dfrac{1}{3} π+\dfrac{1}{2} kπ\),
由于\(y=\sin \left(2x-\dfrac{\pi}{6} \right)=\dfrac{3}{5}\)在\((0,π)\)上的解为\(x_1\) 、\(x_2\),且\(x_1>x_2\),
故\(x_1\),\(x_2\)关于\(x=\dfrac{1}{3} π\)对称,即\(x_1+x_2=\dfrac{2\pi}{3}\),\(\therefore x_2=\dfrac{2\pi}{3}-x_1\),
\(\because x_1>x_2\),\(\therefore π>x_1>\dfrac{2\pi}{3}-x_1>0\),解可得\(\dfrac{1}{3} π<x_1<\dfrac{2\pi}{3}\),
又因为\(\sin (2x_1-\dfrac{\pi}{6})=\dfrac{3}{5}\)且 \(2 x_1-\dfrac{1}{6} \pi \in\left(\dfrac{1}{2} \pi, \dfrac{7 \pi}{6}\right)\),
故\(\cos (2x_1-\dfrac{\pi}{6})=-\dfrac{4}{5}\),
则\(\sin (x_1-x_2 )=\sin \left(2x_1-\dfrac{2\pi}{3}\right)=\sin \left(2x_1-\dfrac{\pi}{6}-\dfrac{1}{2} π\right)\)\(=-\cos \left(2x_1-\dfrac{\pi}{6}\right)=\dfrac{4}{5}\).
故答案为: \(\dfrac{4}{5}\).
【C组---拓展题】
1.已知函数\(f(x)=2\cos \left(2x-\dfrac{\pi}{3}\right)\)在\(\left[a-\dfrac{\pi}{4},a\right](a∈R)\)上的最大值为\(y_1\),最小值为\(y_2\),则\(y_1-y_2\)的取值范围是\(\underline{\quad \quad}\) .
2.已知函数\(f(x)=\cos \left(ωx+\dfrac{\pi}{3}\right)(ω>0)\),图象上任意两条相邻对称轴间的距离为\(\dfrac{\pi}{2}\).
(1)求函数的单调区间和对称中心.
(2)若关于\(x\)的方程\(2 \sin ^2x-m\cos x-4=0\)在\(x∈\left(0 ,\dfrac{\pi}{2}\right)\)上有实数解,求实数\(m\)的取值范围.
参考答案
-
答案 \(\left[2-\sqrt{2},2\sqrt{2}\right]\)
解析 函数\(f(x)=2\cos \left(2x-\dfrac{\pi}{3}\right)\)的周期为\(π\),
且对称轴为\(x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\),对称中心\(\left(\dfrac{5\pi}{12}+kπ,0\right)\),\(k∈Z\),
\(f(x)\)的图象大致如图所示;

区间\(\left[a-\dfrac{\pi}{4},a\right]\)正好是函数\(\dfrac{1}{4}\)个周期,在一个周期内讨论就行,
设\(\left[a-\dfrac{\pi}{4},a\right]\)的中点为\(P\),
由图可知,当点\(P\)落在对称轴上,即\(a-\dfrac{\pi}{8}=\dfrac{\pi}{6}\)时,\(y_1=2\),\(y_2=\sqrt{2}\),
此时\(y_1-y_2\)取得最小值为\(2-\sqrt{2}\);
当点\(P\)落在对称中心上,即\(a-\dfrac{\pi}{8}=\dfrac{5\pi}{12}\)时, \(y_1=\sqrt{2}\),\(y_2=-\sqrt{2}\),
此时\(y_1-y_2\)的值为\(2\sqrt{2}\);
\(\therefore y_1-y_2\)的取值范围是\(\left[2-\sqrt{2},2\sqrt{2}\right]\). -
答案 (1)单调递增区间\(\left[kπ-\dfrac{2\pi}{3} ,kπ-\dfrac{\pi}{6}\right]\) ,单调递减区间\(\left[kπ-\dfrac{\pi}{6} ,kπ+\dfrac{\pi}{3}\right]\) , 对称中心为\(\left(\dfrac{1}{2} kπ+\dfrac{\pi}{12} ,0\right)\), \(k∈Z\), (2)\(\{m|m<-4\}.\)
解析 (1)函数\(f(x)=\cos \left(ωx+\dfrac{\pi}{3}\right)(ω>0)\),图象上任意两条相邻对称轴间的距离为\(\dfrac{\pi}{2}\).
\(\therefore\)周期\(\dfrac{1}{2} T=\dfrac{\pi}{2}\),即\(T=π\),那么 \(\dfrac{2 \pi}{\omega}=\pi\),可得\(ω=2\).
\(\therefore f(x)=\cos (2x+\dfrac{\pi}{3})\),
令\(2kπ-π≤2x+\dfrac{\pi}{3}≤2kπ\),\(k∈Z\),可得\(kπ-\dfrac{2\pi}{3}≤x≤kπ-\dfrac{\pi}{6}\),
\(\therefore\)可得函数的单调递增区间\(\left[kπ-\dfrac{2\pi}{3},kπ-\dfrac{\pi}{6}\right]\),\(k∈Z\),
令\(2kπ≤2x+\dfrac{\pi}{3}≤2kπ+π\),\(k∈Z\),
可得\(kπ-\dfrac{\pi}{6}≤x≤kπ+\dfrac{\pi}{3}\),
\(\therefore\)可得函数的单调递减区间\(\left[kπ-\dfrac{\pi}{6},kπ+\dfrac{\pi}{3}\right]\),\(k∈Z\),
令\(2x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+kπ\),可得\(x=\dfrac{1}{2} kπ+\dfrac{\pi}{12}\),
可得函数的对称中心为\(\left(\dfrac{1}{2} kπ+\dfrac{\pi}{12},0 \right)\), \(k∈Z\),
(2)方程\(2 \sin ^2x-m\cos x-4=0\)在\(x∈\left(0,\dfrac{\pi}{2}\right)\)上有实数解,
\(\because \sin ^2x=1-\cos ^2x\),\(\therefore 2(1-\cos ^2x )-m\cos x-4=0\),
即\(2 \cos ^2x+m\cos x+2=0\),
令\(t=\cos x\),
\(\because x∈(0,\dfrac{\pi}{2})\)上,
\(\therefore t∈(0,1)\),则\(2t^2+mt+2=0\)在\((0,1)\)上有解, \(m=-2\left(t+\dfrac{1}{t}\right)\),
令 \(f(t)=t+\dfrac{1}{t} \geq 2 \sqrt{t \cdot \dfrac{1}{t}}=2\),当且仅当\(t=1\)时,取等号.
即 \(-2\left(t+\dfrac{1}{t}\right) \leq-4\).
任取\(0<t_1<t_2<1\),有 \(f\left(t_1\right)-f\left(t_2\right)=\left(t_1-t_2\right)\left(1-\dfrac{1}{t_1 \cdot t_2}\right)>0\).
因此\(f(t)\)在\((0,1)\)上单调递减,因此\(m<-2k(1)=-4\),
所以\(m\)范围\(\{m|m<-4\}\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号