5.4.2 正弦函数、余弦函数的性质1(周期性与奇偶性)
${\color{Red}{欢迎到学科网下载资料学习 }}$
【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步巩固,难度2颗星!
基础知识
周期函数
一般地,对于函数\(f(x)\),如果存在一个非零常数\(T\),使得定义域内的每一个\(x\)值,都满足\(f(x+T)=f(x)\),那么函数\(f(x)\)就叫做周期函数,\(T\)叫做该函数的周期.
解释
(1)从解析式\(f(x+T)=f(x)\)来看:任一自变量\(x\)对应函数值\(y\)与\(x\)增加\(T\)后对应函数值相等;
(2)从图象看:整体函数图象是由一部分图象像“分身术”一样向两边延申,而那一部分图象的水平长度就是其正周期!

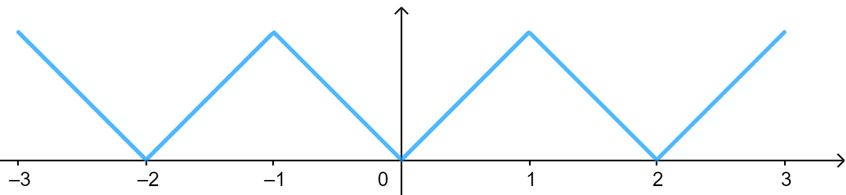
周期函数的周期不止一个,可正可负,比如上面第\(2\)图对应的函数\(f(x)\)的周期有\(-2\),\(-4\),…及其\(2\),\(4\),…等.
(3) 如果在周期函数\(f(x)\)的所有周期中存在一个最小的正数,那么这个最小的正数叫做\(f(x)\)的最小正周期.
【例】 若\(f(x-4)=f(x)\),那\(f(x)\)的一个正周期是多少?
解 \(∵f(x-4)=f(x)\),\(∴f(x)=f(x+4)\),所以\(f(x)\)的一个正周期是\(4\).
正弦函数,余弦函数的图像与性质
注 表中的\(k∈Z\)
| \(y=\sin x\) | \(y=\cos x\) | |
|---|---|---|
| 图像 | 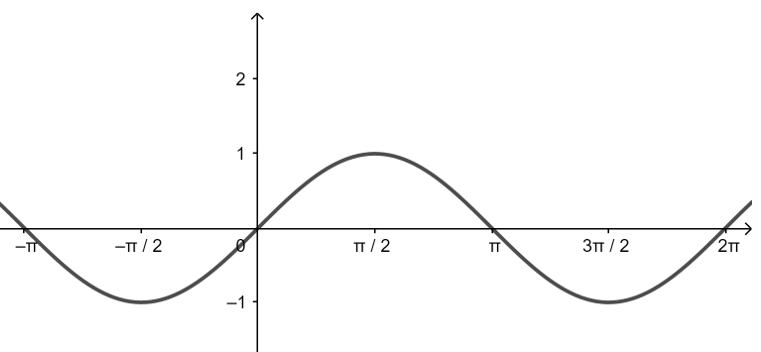 |
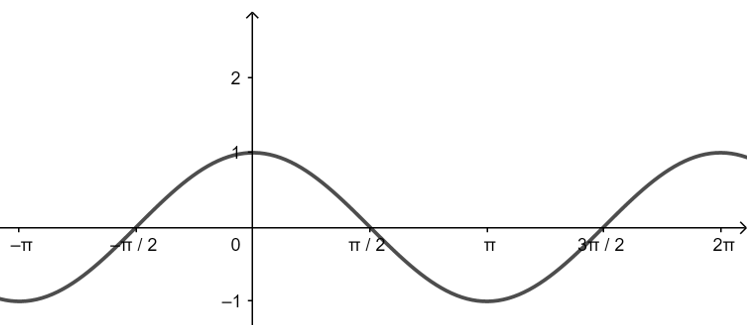 |
| 定义域 | \(R\) | \(R\) |
| 值域 | \([-1 ,1]\) | \([-1 ,1]\) |
| 周期性 | \(2π\) | \(2π\) |
| 对称中心 | \((kπ ,0)\) | \(\left(kπ+\dfrac{\pi}{2},0\right)\) |
| 对称轴 | \(x=kπ+\dfrac{\pi}{2}\) | \(x=kπ\) |
解释
(1) 周期
根据周期的定义,由于\(\sin (x+2kπ)=\sin x\) ,\(\cos (x+2kπ)=\cos x\)可知\(2π\),\(4π\),\(-2π\),\(-4π\)….都是正弦函数、余弦函数的周期,其中\(2π\)是最小正周期.
三角函数\(f(x)=A \sin (ωx+φ)\)或\(f(x)=A \cos (ωx+φ)\)的最小正周期 \(T=\dfrac{2 \pi}{|\omega|}\).
(2) 奇偶性
由\(\sin (-x)=-\sin x\),\(\cos (-x)=\cos x\),或者看正弦曲线关于原点对称,余弦曲线关于\(y\)轴对称,均可知正弦函数是奇函数,余弦函数是偶函数.
(3) 如何理解三角函数的对称轴、对称中心?
主要是结合图象及其周期性,比如如何理解正弦函数\(f(x)=\sin x\)对称中心\((kπ ,0)\)?
① 在一个周期\([0,2π)\)内,找到一个对称中心\((0,0)\);
② 接着每隔半个周期\(π\)个单位就有一个对称中心,则\((0+kπ,0)\)即\((kπ ,0)\)是其对称中心.
类似可得到正弦函数的对称轴方程,余弦函数的对称轴方程与对称中心.
【例】判断函数\(f(x)=\cos |x|\)的奇偶性.
解析 函数\(f(x)=\cos |x|\)的定义域是\(R\),且\(\cos |-x|=\cos |x|\),故\(f(x)=\cos |x|\)是偶函数.
基本方法
【题型1】周期性
【典题1】 求下列函数的周期:
(1)\(y=\sin \left(2x+\dfrac{\pi}{3}\right)(x∈R)\); \(\qquad \qquad\)(2)\(y=\left|\sin x\right|(x∈R)\).
解析 (1)方法1 令\(z=2x+\dfrac{\pi}{3}\),
\(∵x∈R\),\(∴z∈R\),函数\(y=\sin z\)的最小正周期是\(2π\),就是说变量\(z\)只要且至少要增加到\(z+2π\),
函数\(y=\sin z(z∈R)\)的值才能重复取得,而\(z+2π=2x+\dfrac{\pi}{3}+2π=2(x+π)+\dfrac{\pi}{3}\),
\(∴\)自变量\(x\)只要且至少要增加到\(x+π\),函数值才能重复取得,
从而函数\(y=\sin \left(2x+\dfrac{\pi}{3}\right)(x∈R)\)的周期是\(π\).
方法2 \(y=\sin \left(2x+\dfrac{\pi}{3}\right)(x∈R)\)中,\(ω=2\), \(\therefore T=\dfrac{2 \pi}{|2|}=\pi\).
(2)作出\(y=|\sin x|\)的图象如图:
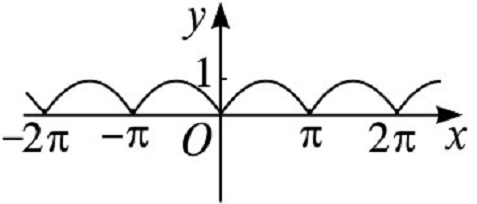
由图象易知\(y=|\sin x|\)的周期为\(π\).
点拨 求函数周期的方法:
1.定义法\(f(x+T)=f(x)\);
2.三角函数\(f(x)=A \sin (ωx+φ)\)或\(f(x)=A \cos (ωx+φ)\)的最小正周期 \(T=\dfrac{2 \pi}{|\omega|}\);
3.数形结合,注意函数图象的各种变换.
【典题2】 函数\(f(x)=\sin \left(ωx-\dfrac{\pi}{3}\right)\)在区间\(\left[0,2π\right]\)上至少存在\(5\)个不同的零点,则正整数\(ω\)的最小值为( )
A.\(2\) \(\qquad \qquad \qquad \qquad\) B.\(3\) \(\qquad \qquad \qquad \qquad\) C.\(4\) \(\qquad \qquad \qquad \qquad\) D.\(5\)
解析 函数\(f(x)=\sin \left(ωx-\dfrac{\pi}{3}\right)\)在区间\([0,2π]\)上至少存在\(5\)个不同的零点,
则 \(2 T+\dfrac{3 T}{4}<2 \pi\),整理得: \(\dfrac{11}{4} \cdot \dfrac{2 \pi}{\omega}<2 \pi\),解得: \(\omega>\dfrac{11}{4}\),
故选:\(B\).
【巩固练习】
1.下列函数中,周期为\(π\)的函数为( )
A.\(y=\sin \left(\dfrac{1}{4} x+\dfrac{\pi}{6}\right)\) \(\qquad \qquad \qquad \qquad\) B.\(y=\sin \left(\dfrac{1}{2} x+\dfrac{\pi}{3}\right)\)
C.\(y=\cos \left(2x-\dfrac{\pi}{3}\right)\) \(\qquad \qquad \qquad \qquad\) D.\(y=\cos \left(4x+\dfrac{\pi}{4}\right)\)
2.下列函数中,周期为\(\dfrac{\pi}{2}\)的是( )
A. \(y=\sin \dfrac{x}{2}\) \(\qquad \qquad \qquad\) B.\(y=\cos 2x\) \(\qquad \qquad \qquad\) C.\(y=|\sin 2x|\) \(\qquad \qquad \qquad\) D.\(y=\sin |x|\)
3.若函数\(y=2\sin \left(ωx+\dfrac{\pi}{4}\right)(ω>0)\)的周期为\(4π\),则\(ω=\)\(\underline{\quad \quad}\).
4.设函数\(f(x)=2\cos \left(\dfrac{1}{2} x-\dfrac{\pi}{3}\right)\),若对任意\(x∈R\)都有\(f(x_1)≤f(x)≤f(x_2)\)成立,则\(|x_1-x_2 |\)的最小值为\(\underline{\quad \quad}\).
参考答案
-
答案 \(C\)
解析 利用周期公式\(T=\dfrac{2\pi}{ω}\),可知\(C\)中函数周期\(T=\dfrac{2\pi}{2}=π\).故选\(C\). -
答案 \(C\)
解析 对于选项\(A\):函数 \(y=\sin \dfrac{x}{2}\)的最小正周期为\(4π\),故正确.
对于选项\(B\):函数的最小正周期为\(π\).故错误.
对于选项\(C\):函数的最小正周期为\(\dfrac{\pi}{2}\).故错误.
对于选项\(D\):函数不为周期函数,故错误.
故选:\(C\). -
答案 \(\dfrac{1}{2}\)
解析 由\(T=\dfrac{2\pi}{ω}\)得\(\dfrac{2\pi}{ω}=4π\),\(∴ω=\dfrac{1}{2}\). -
答案 \(2π\)
解析 函数 \(f(x)=2\cos \left(\dfrac{1}{2} x-\dfrac{\pi}{3}\right)\),若对于任意的\(x∈R\),都有\(f(x_1)≤f(x)≤f(x_2)\),
\(∴f(x_1)\)是函数的最小值,\(f(x_2)\)是函数的最大值,
\(|x_1-x_2 |\)的最小值就是函数的半周期 \(\dfrac{T}{2}=\dfrac{1}{2} \times \dfrac{2 \pi}{\frac{1}{2}}=2 \pi\).
【题型2】 奇偶性
【典题1】 判断下列函数的奇偶性:
(1)\(f(x)=\sin x\cdot\cos x\); \(\qquad \qquad\) (2) \(f(x)=\dfrac{\cos x}{1-\sin x}\); \(\qquad \qquad\) (3) \(f(x)=\sqrt{1-\cos x}+\sqrt{\cos x-1}\).
解析 (1)函数的定义域为\(R\),关于原点对称.
\(∵f(-x)=\sin (-x)\cos (-x)=-\sin x\cos x=-f(x)\),
\(∴f(x)=\sin x\cos x\)为奇函数.
(2)函数应满足\(1-\sin x≠0\),
\(∴\)函数的定义域为\(\{x∣x≠2kπ+\dfrac{\pi}{2},k∈Z\}\),显然定义域不关于原点对称,
\(∴f(x)=\dfrac{\cos x}{1-\sin x}\)为非奇非偶函数.
(3)由\(\left\{\begin{array}{l}
1-\cos x \geq 0 \\
\cos x-1 \geq 0
\end{array}\right.\)得\(\cos x=1\),
\(∴\)函数的定义域为\(\{x∣x=2kπ,k∈Z\}\),定义域关于原点对称.
当\(\cos x=1\)时,\(f(-x)=0\),\(f(x)=±f(-x)\).
\(∴f(x)=\sqrt{1-\cos x}+\sqrt{\cos x-1}\)既是奇函数又是偶函数.
点拨 判断函数奇偶性先确定定义域是否关于原点对称,再利用定义法、图象法或性质法判断.性质法:
奇+奇=奇,偶+偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇.
【典题2】 函数\(y=\sin \left(2x+\dfrac{\pi}{3}\right)\)的图象( )
A.关于点\(\left(\dfrac{\pi}{6} ,0\right)\)对称 \(\qquad \qquad \qquad \qquad\) B.关于点\(\left(\dfrac{\pi}{3} ,0\right)\)对称
C.关于直线\(x=\dfrac{\pi}{6}\)对称 \(\qquad \qquad \qquad \qquad\) D.关于直线\(x=\dfrac{\pi}{3}\)对称
解析 方法1 对于函数 \(y=\sin \left(2x+\dfrac{\pi}{3}\right)\),
(求出函数的所有对称轴和对称中心再判断)
令\(2x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+kπ\),则\(x=\dfrac{\pi}{12}+\dfrac{k\pi}{2}\) , 则函数的对称轴是\(x=\dfrac{\pi}{12}+\dfrac{k\pi}{2} (k∈N^*)\),
若\(\dfrac{\pi}{12}+\dfrac{k\pi}{2} =\dfrac{\pi}{6}\),解得\(k= \dfrac{1}{6}∉N^*\);若\(\dfrac{\pi}{12}+\dfrac{k\pi}{2} =\dfrac{\pi}{3}\),解得\(k=\dfrac{1}{2}∉N^*\),故排除\(C\) ,\(D\);
令\(2x+\dfrac{\pi}{3}=kπ\),则\(x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\) , 则函数的对称中心是\(\left(-\dfrac{\pi}{6}+\dfrac{k\pi}{2},0\right) (k∈N^*)\),
若\(-\dfrac{\pi}{6}+\dfrac{k\pi}{2}=\dfrac{\pi}{6}\),解得\(k= \dfrac{2}{3}∉N^*\),可排除\(A\);
若\(-\dfrac{\pi}{6}+\dfrac{k\pi}{2}=\dfrac{\pi}{3}\),解得\(k=1∈N^*\),故关于点\(\left(\dfrac{\pi}{3} ,0\right)\)对称.
故选:\(B\).
方法2 对于函数 \(y=\sin \left(2x+\dfrac{\pi}{3}\right)\),
当\(x=\dfrac{\pi}{6}\)时,\(2x+\dfrac{\pi}{3}=2\dfrac{\pi}{3}\),而\(\left(\dfrac{2\pi}{3} ,0\right)\)不是正弦函数\(y=\sin x\)的对称中心,故\(A\)错误;
当\(x=\dfrac{\pi}{3}\)时,\(2x+\dfrac{\pi}{3}=π\),而\((π,0)\)是正弦函数\(y=\sin x\)的对称中心,故\(B\)正确;
当\(x=\dfrac{\pi}{6}\)时,\(2x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}\),而\(x=\dfrac{2\pi}{3}\)不是正弦函数\(y=\sin x\)的对称轴,故\(C\)错误;
当\(x=\dfrac{\pi}{3}\)时,\(2x+\dfrac{\pi}{3}=π\),而\(x=π\)不是正弦函数\(y=\sin x\)的对称轴,故\(D\)错误;
故选:\(B\).
点拨 本题两种方法,
方法1是求出三角函数的全部对称轴或对称中心(此时把\(ωx+φ\)看成整体),再判断;
方法2是把问题转化正弦函数\(y=\sin x\)的性质判断;
对于三角函数\(f(x)=A\sin (ωx+φ)+B\)
① 若\(x=x_0\)是其对称轴,则\(ωx_0+φ\)是正弦函数\(y=\sin x\)的对称轴;
② 若\((x_0 ,B)\)是其对称中心,则\((ωx_0+φ ,B)\)满足函数\(y=A\sin x+B\)的对称中心.
对于三角函数\(f(x)=A\cos (ωx+φ)+B\)类似.
【典题3】 已知函数 \(f(x)=\cos \left(ωx+\dfrac{\pi}{3}\right)(ω>0)\)的一条对称轴为\(x=\dfrac{\pi}{3}\),一个对称中心为点\(\left(\dfrac{\pi}{12},0\right)\),则\(ω\)最小值\(\underline{\quad \quad}\) .
解析 由于函数的对称轴方程为\(x=\dfrac{\pi}{3}\),
所以\(\dfrac{\pi}{3} ω+\dfrac{\pi}{3}=k_1 π\),\((k∈Z)\),整理得\(ω=3k_1-1(k∈Z)\);
函数的一个对称中心为点 \(\left(\dfrac{\pi}{12},0\right)\),
所以\(\dfrac{\pi}{12}ω+\dfrac{\pi}{3}=k_2 π+\dfrac{\pi}{2}\),整理得\(ω=12k_2+2\),\((k∈Z)\),
由于\(ω>0\),
所以当\(k_1=1\)或\(k_2=0\)时,\(ω\)取到最小值为\(2\).
故答案为:\(2\).
【巩固练习】
1.函数\(f(x)=\sin (-x)\)的奇偶性是( )
A .奇函数 \(\qquad \qquad d \qquad\) B.偶函数 \(\qquad \qquad \qquad\) C.既是奇函数,又是偶函数 \(\qquad \qquad \qquad\) D.非奇非偶函数
2.在平面直角坐标系\(xOy\)中,函数\(y=2\sin \left(x-\dfrac{\pi}{6}\right)\)的图象( )
A. 关于直线\(x=\dfrac{\pi}{6}\)对称 \(\qquad \qquad \qquad\) B. 关于点\(\left(\dfrac{\pi}{6},0\right)\)对称
C. 关于直线\(x=-\dfrac{\pi}{6}\)对称 \(\qquad \qquad \qquad\) D. 关于点\(\left(-\dfrac{\pi}{6},0\right)\)对称
3.已知函数\(f(x)=\cos \left(\omega x+\dfrac{7}{8} \pi\right)(\omega>0)\)的图象关于点\(\left(\dfrac{\pi}{4},0\right)\)对称,则\(f(x)\)的最小正周期\(T\)的最大值为( )
A. \(\dfrac{2 \pi}{5}\) \(\qquad \qquad \qquad \qquad\) B. \(\dfrac{3 \pi}{5}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{4 \pi}{5}\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{6\pi}{5}\)
4.已知点\((2,0)\)为函数\(f(x)=2 \cos \left(\dfrac{\pi}{3} x+\varphi\right)\left(|\varphi|<\dfrac{\pi}{2}\right)\)图象的一个对称中心,则实数\(φ=\)( )
A.\(-\dfrac{\pi}{3}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{\pi}{6}\) \(\qquad \qquad \qquad \qquad\) C.\(\dfrac{\pi}{3}\) \(\qquad \qquad \qquad \qquad\) D.\(-\dfrac{\pi}{6}\)
5.已知直线\(x=x_1\),\(x=x_2\)分别是曲线 \(f(x)=2 \sin \left(x+\dfrac{\pi}{3}\right)\)与\(g(x)=-\cos x\)的对称轴,则\(f(x_1-x_2)=\) \(\underline{\quad \quad}\) .
6.已知直线\(x=\dfrac{\pi}{3}\)和\(x=\dfrac{5\pi}{6}\)是曲线\(y=\sin (ωx+φ)(ω>0)\)的相邻的两条对称轴,则满足条件的一个\(φ\)的值是\(\underline{\quad \quad}\).
7.若函数\(f(x)=4\cos (3x+φ)\left(|φ|<\dfrac{\pi}{2}\right)\)的图象关于直线\(x=\dfrac{11 \pi}{12}\)对称,且当\(x_1,x_2∈\left(-\dfrac{7 \pi}{12},-\dfrac{\pi}{12}\right)\),\(x_1≠x_2\)时,\(f(x_1 )=f(x_2 )\),则\(f(x_1+x_2 )=\) \(\underline{\quad \quad}\).
参考答案
-
答案 \(A\)
解析 \(∵f(x)=\sin (-x)=-\sin x\),
\(∴f(-x)=-\sin (-x)=\sin x=-f(x)\).
\(∴f(x)\)是奇函数. -
答案 \(B\)
解析 利用排除法和代入法求解,当\(x=\dfrac{\pi}{6}\)时,\(y=2\sin \left(x-\dfrac{\pi}{6}\right)=0\),故选:\(B\). -
答案 \(C\)
解析 函数\(f(x)=\cos \left(\omega x+\dfrac{7}{8} \pi\right)(\omega>0)\)的图象关于点\(\left(\dfrac{\pi}{4},0\right)\)对称,
故\(\dfrac{\pi}{4} \omega+\dfrac{7 \pi}{8}=k \pi+\dfrac{\pi}{2}(k \in Z)\),整理得: \(\omega=4 k-\dfrac{3}{2}(k \in Z)\),
当\(k=1\)时,\(ω=\dfrac{5}{2}\),
所以周期的最大值为 \(\dfrac{2 \pi}{\frac{5}{2}}=\dfrac{4 \pi}{5}\),故选\(C\). -
答案 \(D\)
解析 根据题意,得\(2 \cos \left(\dfrac{\pi}{3} \times 2+\varphi\right)=0\), \(\therefore \dfrac{2 \pi}{3}+\varphi=k \pi+\dfrac{\pi}{2}(k \in Z)\),
\(\thereforeφ=kπ-\dfrac{\pi}{6}(k∈Z)\),
又\(\because|\varphi|<\dfrac{\pi}{2}\),\(\therefore\)取\(k=0\),可得\(φ=-\dfrac{\pi}{6}\).
故选:\(D\). -
答案 \(±2\)
解析 由\(x+\dfrac{\pi}{3}=kπ+\dfrac{\pi}{2}\)得\(x=kπ+\dfrac{\pi}{6}\),即\(f(x)\)的对称轴为\(x=kπ+\dfrac{\pi}{6}\),\(k∈Z\),
\(y=-cox\)的对称轴为\(x=k_1 π\),\(k_1∈Z\),
\(\because\)直线\(x=x_1\),\(x=x_2\)分别是曲线\(f(x)\)与\(g(x)\)的对称轴,
\(\therefore x_1=kπ+\dfrac{\pi}{6}\),\(k∈Z\),\(x_2=k_1 π\),\(k_1∈Z\),
则\(x_1-x_2=kπ+\dfrac{\pi}{6}-k_1 π=(k-k_1)π+\dfrac{\pi}{6}\),\(k∈Z\),\(k_1∈Z\),
则\(f\left(x_1 x_2\right)=2 \sin \left[\left(k-k_1\right) \pi+\dfrac{\pi}{6}+\dfrac{\pi}{3}\right]=2 \sin \left[\left(k-k_1\right) \pi+\dfrac{\pi}{2}\right]\)\(=-2 \cos \left[\left(k-k_1\right) \pi\right]=\pm 2\). -
答案 \(-\dfrac{\pi}{6}\)
解析 直线\(x=\dfrac{\pi}{3}\)和\(x=\dfrac{5\pi}{6}\)是曲线\(y=\sin (ωx+φ)(ω>0)\)的相邻的两条对称轴,
故当 \(\dfrac{T}{2}=\dfrac{5 \pi}{6}-\dfrac{\pi}{3}=\dfrac{\pi}{2}\),
故\(T=π\),解得\(ω=2\),故\(f(x)=\sin (2x+φ)\),
当 \(x=\dfrac{\pi}{3}\)时, \(f\left(\dfrac{\pi}{3}\right)=\sin \left(\dfrac{2 \pi}{3}+\varphi\right)=\pm 1\),
故\(\dfrac{2\pi}{3}+φ=kπ+\dfrac{\pi}{2}\),整理得\(φ=kπ-\dfrac{\pi}{6}(k∈Z)\),
当\(k=0\)时,\(φ=-\dfrac{\pi}{6}\). -
答案 \(2 \sqrt{2}\)
解析 \(\because\)函数 \(f(x)=4\cos (3x+φ)\left(|φ|<\dfrac{\pi}{2}\right)\)的图象关于直线 \(x=\dfrac{11 \pi}{12}\)对称
\(\therefore 3 \times \dfrac{11 \pi}{12}+\varphi=k \pi\),\(k∈Z\),
\(\thereforeφ=\dfrac{\pi}{4}\),\(f(x)=4 \cos \left(3 x+\dfrac{\pi}{4}\right)\),
且当 \(x\in\left(-\dfrac{7 \pi}{12},-\dfrac{\pi}{12}\right)\)时,\(3x+\dfrac{\pi}{4}\in \left(-\dfrac{3\pi}{2},0\right)\),
当\(x_1,x_2∈\left(-\dfrac{7 \pi}{12},-\dfrac{\pi}{12}\right)\),\(x_1≠x_2\)时,\(f(x_1 )=f(x_2 )\),
则 \(f\left(x_1+x_2\right)=4 \cos \left[3\left(-\dfrac{5 \pi}{6}\right)+\dfrac{\pi}{4}\right]=4 \cos \left(-\dfrac{9 \pi}{4}\right)\)\(=4 \cos \left(-\dfrac{\pi}{4}\right)=4 \cos \dfrac{\pi}{4}=2 \sqrt{2}\).
分层练习
【A组---基础题】
1.函数 \(f(x)=\sqrt{3} \sin \left(\dfrac{x}{2}-\dfrac{\pi}{4}\right)\),\(x∈R\)的最小正周期为( )
A.\(\dfrac{\pi}{2}\) \(\qquad \qquad \qquad \qquad\) B.\(π\) \(\qquad \qquad \qquad \qquad\) C.\(2π\) \(\qquad \qquad \qquad \qquad\) D.\(4π\)
2.下列函数中周期 为\(\dfrac{\pi}{2}\),且为偶函数的是( )
A.\(y=\sin 4x\) \(\qquad \qquad\) B.\(y=\cos \dfrac{1}{4} x\) \(\qquad\qquad\) C.\(y=\sin \left(4x+\dfrac{\pi}{2}\right)\) \(\qquad \qquad\) D. \(y=\cos \left(\dfrac{1}{4} x-\dfrac{\pi}{2}\right)\)
3.若函数\(f(x)=\sin \dfrac{x+\varphi}{3}(\varphi \in[0,2 \pi])\)是偶函数,则\(φ=\)( )
A.\(\dfrac{\pi}{2}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{2\pi}{3}\) \(\qquad \qquad \qquad \qquad\) C.\(\dfrac{3\pi}{2}\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{5\pi}{3}\)
4.下列函数中,关于直线\(x=-\dfrac{\pi}{6}\)对称的是( )
A.\(y=\sin (x+\dfrac{\pi}{3})\) \(\qquad \qquad\) B.\(y=\sin (2x+\dfrac{\pi}{3})\) \(\qquad \qquad\) C.\(y=\cos (x+\dfrac{\pi}{3})\) \(\qquad\qquad\) D.\(y=\cos (2x+\dfrac{\pi}{3})\)
5.已知\(\left(\dfrac{\pi}{6},0 \right)\)为\(f(x)=\sin (-2x+φ)\left(|φ|<\dfrac{\pi}{2} \right)\)的一个对称中心,则\(f(x)\)的对称轴可能为( )
A. \(x=\dfrac{\pi}{2}\) \(\qquad \qquad \qquad \qquad\) B. \(x=\dfrac{2\pi}{3}\) \(\qquad \qquad \qquad \qquad\) C. \(x=-\dfrac{\pi}{3}\) \(\qquad \qquad \qquad \qquad\) D.\(x=-\dfrac{\pi}{12}\)
6.(多选)已知函数\(f(x)=\sin x\cos 2x\),下列结论错误的是( )
A.\(y=f(x)\)的图象关于\(x=\dfrac{\pi}{2}\)对称 \(\qquad \qquad\) B. \(y=f(x)\)的图象关于\((\dfrac{\pi}{2},0)\)对称 \(\qquad \qquad\)
C.\(y=f(x)\)的图象关于\(y\)轴对称 \(\qquad\qquad \qquad\) D. \(y=f(x)\)不是周期函数
7.函数\(f(x)=\left|\sin (x+\dfrac{\pi}{3})\right|\)的最小正周期是\(\underline{\quad \quad}\).
8.函数\(f(x)=2\cos (2x+θ)\)的图象关于原点对称,则\(θ\)的最大负值为\(\underline{\quad \quad}\) .
9.已知曲线 \(y=\sin \left(\omega x+\dfrac{\pi}{6}\right)\)关于\((-1,0)\)对称,则\(|ω|\)的最小值为 .
10.已知\(f(n)=\sin \dfrac{n\pi}{4}\),\(n∈Z\),则\(f(1)+f(2)+f(3)+⋯+f(2019)=\) \(\underline{\quad \quad}\).
11.已知函数 \(f(x)=\cos (2 x+\varphi)\left(|\varphi|<\dfrac{\pi}{2}\right)\)的图象关于直线 \(x=\dfrac{11 \pi}{10}\)对称,则\(φ=\)\(\underline{\quad \quad}\) .
12.已知函数 \(f(x)=\cos (3 x+\varphi)\left(-\dfrac{\pi}{2}<\varphi<\dfrac{\pi}{2}\right)\)图象关于直线 \(x=\dfrac{5 \pi}{18}\)对称,则函数\(f(x)\)在区间\([0,π]\)上零点的个数为\(\underline{\quad \quad}\) .
参考答案
-
答案 \(D\)
解析 易知 \(T=\dfrac{2 \pi}{\frac{1}{2}}=4 \pi\),故选\(D\). -
答案 \(C\)
解析 显然周期为\(\dfrac{\pi}{2}\)的有\(A\)和\(C\),又因为 \(y=\sin \left(4x+\dfrac{\pi}{2}\right)\)是偶函数,故选\(C\). -
答案 \(C\)
解析 \(\because f(x)=\sin \dfrac{x+\varphi}{3}\)是偶函数,
\(\therefore \sin \dfrac{\varphi}{3}=\pm 1\), \(\therefore \dfrac{\varphi}{3}=k \pi+\dfrac{\pi}{2}(k \in Z)\).
\(\thereforeφ=3kπ+\dfrac{3\pi}{2}(k∈Z)\).
又\(\because φ∈[0,2π]\),\(\therefore\)当\(k=0\)时,\(φ=\dfrac{3\pi}{2}\).故选\(C\). -
答案 \(D\)
解析 将\(x=-\dfrac{\pi}{6}\)代入\(y=\cos \left(2x+\dfrac{\pi}{3} \right)\),得函数值为\(1\),
故\(x=-\dfrac{\pi}{6}\)是\(y=\cos \left(2x+\dfrac{\pi}{3}\right)\)的一条对称轴,
故选:\(D\). -
答案 \(D\)
解析 因为\(\left(\dfrac{\pi}{6},0 \right)\)为\(f(x)=\sin \left(-2x+φ\right) \left(|φ|<\dfrac{\pi}{2}\right)\)的一个对称中心,
所以\(f \left(\dfrac{\pi}{6}\right)=0\),即\(\sin \left(-\dfrac{\pi}{3}+φ\right)=0\),\(\therefore-\dfrac{\pi}{3}+φ=kπ\),\(k∈Z\),
\(\thereforeφ=\dfrac{\pi}{3}+kπ\),\(k∈Z\),\(\therefore f(x)=\sin \left(-2 x+\dfrac{\pi}{3}+k \pi\right)\),\(k∈Z\)
由\(-2x+\dfrac{\pi}{3}+kπ=\dfrac{\pi}{2}+nπ\),\(k,n∈Z\),
得 \(x=-\dfrac{\pi}{12}+\dfrac{k-n}{2} \pi\),\(k,n∈Z\),
当\(k=n\)时,\(x=-\dfrac{\pi}{12}\). -
答案 \(BCD\)
解析 对于函数\(f(x)=\sin x\cos 2x\),
\(\because f(π-x)=\sin (π-x)\cos 2(π-x)=\sin x\cos 2x=f(x)\),
\(\therefore f(x)\)关于直线\(x=\dfrac{\pi}{2}\)对称,故\(A\)正确,\(B\)不正确.
根据\(f(-x)=-\sin x\cos 2x=-f(x)\),
故函数为奇函数,它的图象关于\(x\)轴对称,故排除\(C\).
\(\because f(x+2π)=\sin (2π+x)\cos 2(2π+x)=\sin x\cos 2x=f(x)\),
\(\therefore2π\)是函数\(y=f(x)\)的周期,故\(D\)错误.
故选:\(BCD\). -
答案 \(π\)
解析 对于 \(f(x)=\left|\sin (x+\dfrac{\pi}{3})\right|\),\(T=2π\),
函数 \(f(x)=\left|\sin (x+\dfrac{\pi}{3})\right|\)是函数\(y=\sin \left(x+\dfrac{\pi}{3}\right)\)的图象\(x\)轴上方的图象不动,将\(x\)轴下方的图象向上对折得到的,故 \(T^{\prime}=\dfrac{T}{2}=\pi\). -
答案 \(-\dfrac{\pi}{2}\)
解析 \(\because\)函数\(f(x)=2\cos (2x+θ)\)的图象关于原点对称,
\(\thereforeθ=kπ+\dfrac{\pi}{2}\),\(k∈Z\),
令\(k=-1\),可得\(θ\)的最大负值为\(-\dfrac{\pi}{2}\),
故答案为:\(-\dfrac{\pi}{2}\). -
答案 \(\dfrac{\pi}{6}\)
解析 因为曲线 \(y=\sin \left(\omega x+\dfrac{\pi}{6}\right)\)关于\((-1,0)\)对称,所以\(\sin (-ω+\dfrac{\pi}{6})=0\),
可得\(-ω+\dfrac{\pi}{6}=kπ\),\(k∈Z\),解得\(ω=\dfrac{\pi}{6}-kπ\),\(k∈Z\),则\(|ω|\)的最小值为\(\dfrac{\pi}{6}\). -
答案 \(1+\sqrt{2}\)
解析 \(\because f(n)=\sin \dfrac{n\pi}{4}\),\(n∈Z\),\(\therefore\)函数\(f(x)\)的最小正周期为 \(\dfrac{2 \pi}{\dfrac{\pi}{4}}=8\),
\(\because f(1)=\sin \dfrac{\pi}{4}=\dfrac{\sqrt{2}}{2}\), \(f(2)=\sin \dfrac{\pi}{2}=1\), \(f(3)=\sin \dfrac{3 \pi}{4}=\dfrac{\sqrt{2}}{2}\),\(f(4)=\sin π=0\), \(f(5)=\sin \dfrac{5 \pi}{4}=-\dfrac{\sqrt{2}}{2}\), \(f(6)=\sin \dfrac{3 \pi}{2}=-1\), \(f(7)=\sin \dfrac{7 \pi}{4}=-\dfrac{\sqrt{2}}{2}\),\(f(8)=\sin 2π=0\),
\(\therefore f(1)+f(2)+f(3)+⋯+f(8)=0\),
\(\therefore f(1)+f(2)+f(3)+⋯+f(2019)=252×0+f(1)+f(2)+f(3)\)
\(=0+\dfrac{\sqrt{2}}{2}+1+\dfrac{\sqrt{2}}{2}=1+\sqrt{2}\). -
答案 \(-\dfrac{\pi}{5}\)
解析 \(\because\)函数 \(f(x)=\cos (2 x+\varphi)\left(|\varphi|<\dfrac{\pi}{2}\right)\)的图象关于直线 \(x=\dfrac{11 \pi}{10}\)对称,
\(\therefore 2 \times \dfrac{11 \pi}{10}+\varphi=k \pi(k \in Z)\),
即\(φ=kπ-\dfrac{11 \pi}{5}(k∈Z)\),又\(|φ|<\dfrac{\pi}{2}\),
\(\therefore \varphi=-\dfrac{\pi}{5}\). -
答案 三
解析 \(\because\)函数\(f(x)=\cos (3 x+\varphi)\left(-\dfrac{\pi}{2}<\varphi<\dfrac{\pi}{2}\right)\)图象关于直线\(x=\dfrac{5 \pi}{18}\)对称
\(\therefore 3 \times \dfrac{5 \pi}{18}+\varphi=k \pi\),(\(y=\cos x\)的对称轴是\(x=kπ\))
\(\therefore φ=-\dfrac{5\pi}{6}+kπ\),\(k∈Z\),
由\(-\dfrac{\pi}{2}<φ<\dfrac{\pi}{2}\)知,\(k=1\)时,\(φ=\dfrac{\pi}{6}\),
故\(f(x)=\cos (3x+\dfrac{\pi}{6})\),
令\(f(x)=0\)得\(3x+\dfrac{\pi}{6}=\dfrac{\pi}{2}+kπ\),\(k∈Z\),\(\therefore x=\dfrac{\pi}{9}+\dfrac{k\pi}{3}\),\(k∈Z\).
因为\(x∈[0,π]\),所以\(k=0,1,2\)时, \(\varphi=\dfrac{\pi}{9}\), \(\dfrac{4 \pi}{9}\), \(\dfrac{7 \pi}{9}\)满足条件,
故零点有三个.
【B组---提高题】
1.\(f(x)=|\sin x|+|\cos x|\)的最小正周期是( )
A.\(\dfrac{\pi}{2}\) \(\qquad \qquad \qquad \qquad\) B.\(π\) \(\qquad \qquad \qquad \qquad\) C.\(2π\) \(\qquad \qquad \qquad \qquad\) D.\(3π\)
2.已知函数\(f(x)=\sin \left(ωx+\dfrac{\pi}{6}\right)(ω>0)\)的图象在\((0,π)\)上有且仅有两条对称轴,则\(ω\)的取值范围为( )
A. \(\left[1, \dfrac{3}{2}\right)\) \(\qquad \qquad \qquad\) B. \(\left(\dfrac{4}{3}, \dfrac{3}{2}\right)\) \(\qquad \qquad \qquad\) C. \(\left(\dfrac{4}{3}, \dfrac{7}{3}\right]\) \(\qquad \qquad \qquad\) D. \(\left[1, \dfrac{7}{3}\right]\)
3.已知\(f(x)=2\sin (ωx+φ)\left(ω>0,0<φ<\dfrac{\pi}{2}\right)\)的图象关于直线\(x=\dfrac{\pi}{6}\)对称,若存在\(x_1\),\(x_2∈R\),使得对于任意\(x\)都有\(f(x_1)≤f(x)≤f(x_2)\),且\(|x_1-x_2 |\)的最小值为\(\dfrac{\pi}{2}\),则\(φ\)等于( )
A.\(\dfrac{\pi}{12}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{\pi}{6}\) \(\qquad \qquad \qquad \qquad\) C.\(\dfrac{\pi}{4}\) \(\qquad \qquad \qquad \qquad\) D.\(\dfrac{\pi}{3}\)
4.(多选)已知函数\(f(x)=2\sin \left(2x-\dfrac{\pi}{6}\right)(x∈R)\),则下列命题正确的有( )
A. \(y=f(x)\)的图象关于直\(x=\dfrac{2\pi}{3}\)对称
B. \(y=f(x)\)的图象关于点\((\dfrac{\pi}{12},0)\)中心对称
C. \(y=f(x)\)的表达式可改写为\(y=2\cos \left(2x+\dfrac{\pi}{3}\right)\)
D.若 \(f(x_1 )=f(x_2 )=0\),则\(x_1-x_2=\dfrac{k\pi}{2}(k∈Z)\)
参考答案
-
答案 \(A\)
解析 \(f\left(x+\dfrac{\pi}{2}\right)=\left|\sin \left(x+\dfrac{\pi}{2}\right)\right|+\left|\cos \left(x+\dfrac{\pi}{2}\right)\right|=|\cos x|+|\sin x|=f(x)\),
故\(\dfrac{\pi}{2}\)是\(y=f(x)\)的周期,由选项可知选\(A\). -
答案 \(C\)
解析 令\(ωx+\dfrac{\pi}{6}=\dfrac{\pi}{2}\),\(\dfrac{3\pi}{2}\),\(\dfrac{5\pi}{2}\),解得\(x=\dfrac{\pi}{3ω}\),\(x=\dfrac{4\pi}{3ω}\),\(x=\dfrac{7\pi}{3ω}\),
分别为\(y=f(x)\)的\(y\)轴右侧由左往右最近的三条对称轴.
要满足图象在\((0,π)\)上有且仅有两条对称轴,
只需 \(\left\{\begin{array}{l} 0<\dfrac{\pi}{3 \omega}<\pi \\ 0<\dfrac{4 \pi}{3 \omega}<\pi \\ \dfrac{7 \pi}{3 \omega} \geq \pi \end{array}\right.\),解得 \(\dfrac{4}{3}<\omega \leq \dfrac{7}{3}\).
故选:\(C\). -
答案 \(B\)
解析 对于函数\(f(x)=2\sin (ωx+φ)\),
\(\because\) 对任意\(x∈R\),都有\(f(x_1)≤f(x)≤f(x_2)\),且\(|x_1-x_2 |\)的最小值为\(\dfrac{\pi}{2}\).
\(\therefore \dfrac{T}{2}=\dfrac{\pi}{2}\),则\(T=π\),
\(\therefore \omega=\dfrac{2 \pi}{T}=\dfrac{2 \pi}{\pi}=2\),可得\(f(x)=2\sin (2x+φ)\),
又\(\because f(x)=2\sin (ωx+φ)\)的图象关于直线\(x=\dfrac{\pi}{6}\)对称,
\(\therefore 2×\dfrac{\pi}{6}+φ=2kπ+\dfrac{\pi}{2}\),\(k∈Z\),可得\(φ=2kπ+\dfrac{\pi}{6}\),\(k∈Z\),
\(\because 0<φ<\dfrac{\pi}{2}\),\(\therefore φ=\dfrac{\pi}{6}\),
故选:\(B\). -
答案 \(BD\)
解析 函数\(f(x)=2\sin \left(2 x-\dfrac{\pi}{6}\right)(x\in R)\),
对于\(A\):当\(x=\dfrac{2\pi}{3}\)时,\(f\left(\dfrac{2\pi}{3}\right)=2\sin \left(\dfrac{8\pi}{6}-\dfrac{\pi}{6}\right)≠2\),故\(A\)错误;
对于\(B\):当\(x=\dfrac{\pi}{12}\)时,\(f\left(\dfrac{\pi}{12}\right)=2\sin 0=0\),故\(B\)正确;
对于\(C\):由于函数 \(f(x)=2 \sin \left(2 x-\dfrac{\pi}{6}\right)=2 \cos \left(\dfrac{\pi}{2}-2 x+\dfrac{\pi}{6}\right)\) \(=2 \cos \left(2 x-\dfrac{2 \pi}{3}\right)=-2 \cos \left(2 x+\dfrac{\pi}{3}\right)\),故\(C\)错误;
对于\(D\):由于\(f(x_1 )=f(x_2 )=0\),所以\(2\sin \left(2x_1-\dfrac{\pi}{6}\right)=0\),
整理得\(2x_1-\dfrac{\pi}{6}=k_1 π\),故\(x_1=\dfrac{k_1 π}{2}+\dfrac{\pi}{12} (k_1∈Z)\),同理 \(x_2=\dfrac{k_2 \pi}{2}+\dfrac{\pi}{12}\left(k_2 \in Z\right)\),
故\(x_1-x_2=\dfrac{(k_1-k_2 )\pi}{2} (k_1,k_2∈Z)\), 故 \(x_1-x_2=\dfrac{k\pi}{2}(k∈Z)\),故\(D\)正确;
故选\(BD\).
【C组---拓展题】
1.已知\(ω>0\),函数\(f(x)=\sin \left(ωx-\dfrac{\pi}{4}\right)\)的图象在区间\(\left(\dfrac{\pi}{2},π \right)\)上有且仅有一条对称轴,则实数\(ω\)的取值范围是\(\underline{\quad \quad}\).
2.关于函数 \(f(x)=\cos x+\dfrac{1}{\cos x}\) ,有如下四个命题:
①\(f(x)\)的图像关于\(y\)轴对称;\(\qquad \qquad \qquad \quad\) ②\(f(x)\)的图像关于原点对称;
③\(f(x)\)的图像关于直线\(x=\dfrac{\pi}{2}\)对称;\(\qquad \qquad\)④\(f(x)\)的图像关于点\(\left(\dfrac{\pi}{2},0 \right)\)对称.
其中所有真命题的序号是\(\underline{\quad \quad}\).
参考答案
-
答案 \(\left(\dfrac{3}{4}, \dfrac{3}{2}\right) \cup\left(\dfrac{7}{4}, \dfrac{11}{4}\right] \cup\left[\dfrac{7}{2}, \dfrac{15}{4}\right]\)
解析 函数数\(f(x)=\sin \left(ωx-\dfrac{\pi}{4} \right)\)的图象在区间\(\left(\dfrac{\pi}{2},π \right)\)上有且仅有一条对称轴,
根据正弦函数的对称轴性质,
可得 \(\omega \cdot \dfrac{\pi}{2}-\dfrac{\pi}{4}<k \pi+\dfrac{\pi}{2}<\omega \pi-\dfrac{\pi}{4} \Rightarrow \dfrac{4 k+3}{4}<\omega<\dfrac{4 k+3}{2}\),\(k∈z\),①
又因为:\(π-\dfrac{\pi}{2}≤T=\dfrac{2\pi}{ω}⇒ω≤4\);②
\(\because ω>0\);③
因为有且仅有一条对称轴;
所以还需满足:\(ωπ-\dfrac{\pi}{4}≤(k+1)π+\dfrac{\pi}{2}\) 且\((k-1)π-\dfrac{\pi}{2}≤ \dfrac{ω\pi}{2}-\dfrac{\pi}{4}\);
即 \(\dfrac{4 k-1}{2} \leq \omega \leq \dfrac{4 k+7}{4}\) ④
联立①②③④解得: \(\omega \in\left(\dfrac{3}{4}, \dfrac{3}{2}\right) \cup\left(\dfrac{7}{4}, \dfrac{11}{4}\right] \cup\left[\dfrac{7}{2}, \dfrac{15}{4}\right]\).
故答案为: \(\left(\dfrac{3}{4}, \dfrac{3}{2}\right) \cup\left(\dfrac{7}{4}, \dfrac{11}{4}\right] \cup\left[\dfrac{7}{2}, \dfrac{15}{4}\right]\). -
答案 ①④
解析 函数 \(f(x)=\cos x+\dfrac{1}{\cos x}\) ,
对于①,函数\(f(-x)=f(x)\),故函数为偶函数,
故\(f(x)\)的图像关于\(y\)轴对称,故①正确;
对于②,由于函数\(f(x)\)的图像关于\(y\)轴对称,
故函数\(f(x)\)的图象不关于原点对称,故②错误;
对于③,函数 \(f(\pi-x)=\cos (\pi-x)+\dfrac{1}{\cos (\pi-x)}=-\cos x-\dfrac{1}{\cos x} \neq f(x)\),
故函数\(f(x)\)的图像不关于\(x=\dfrac{\pi}{2}\)对称,故③错误;
对于④, \(f(\pi-x)=\cos (\pi-x)+\dfrac{1}{\cos (\pi-x)}=-\cos x-\dfrac{1}{\cos x}=-f(x)\),
故函数\(f(x)\)图像关于点\(\left(\dfrac{\pi}{2},0\right)\)对称,故④正确.
故答案为:①④.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号