5.3 诱导公式

 ${\color{Red}{欢迎到学科网下载资料学习 }}$  

【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019）
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

必修第一册同步巩固，难度2颗星！

基础知识

诱导公式

利用以上6组公式，最好结合图象，利用对称性和全等三角形进行理解消化.
(1) 公式(一) \(\sin ⁡(α+2kπ)=\sin ⁡α\);\(\cos (α+2kπ)=\cos α\) ;\(\tan (α+2kπ)=\tan α\).
由三角函数的定义易得.
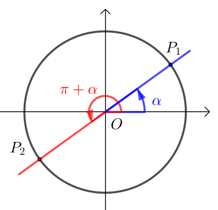
(2) 公式(二) \(\sin (π+α)=-\sin α\);\(\cos (π+α)=-\cos α\); \(\tan (π+α)=\tan α\).
证明 如下图，\(α\)的终边与单位圆交于\(P_1 (x ,y)\)，则\(π+α\)的终边与单位圆交于\(P_2 (x ,y)\)，
显然\(P_2\)与\(P_1\)关于原点对称，则\(P_2 (-x ,-y)\).
由三角函数的定义，可知\(\sin α=y\),\(\cos α=x\), \(\tan \alpha=\dfrac{y}{x}\);
\(\sin ⁡(π+α)=-y\),\(\cos ⁡(π+α)=-x\),\(\tan ⁡(π+α)=\dfrac{y}{x}\)；
故\(\sin (π+α)=-\sin α\) ; \(\cos (π+α)=-\cos α\) ; \(\tan (π+α)=\tan α\).

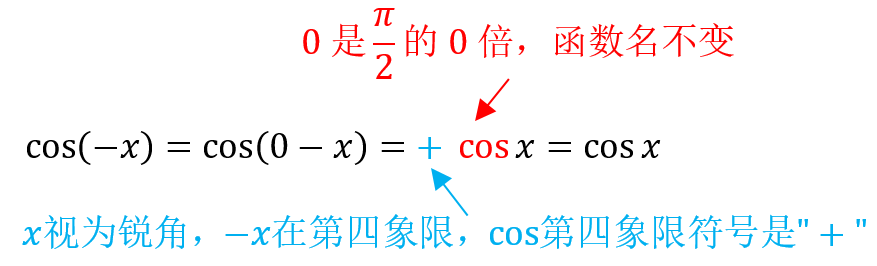
(3) 公式(三) \(\sin (-α)=-\sin α\) ; \(\cos (-α)=\cos α\) ;\(\tan (-α)=-\tan α\).
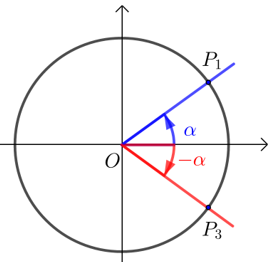若\(P_1 (x ,y)\)，则\(P_3 (x ,-y)\).
(4) 公式(四) \(\sin (π-α)=\sin α\) ;\(\cos (π-α)=-\cos α\) ; \(\tan (π-α)=-\tan α\).
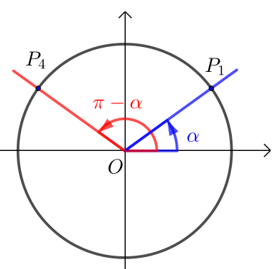若\(P_1 (x ,y)\)，则\(P_4 (-x ,y)\).
(5) 公式(五) \(\sin (\dfrac{\pi}{2} -α)=\cos α\) ; \(\cos (\dfrac{\pi}{2} -α)=\sin α\).
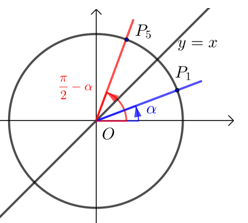若\(P_1 (x ,y)\)，则\(P_5 (y ,x)\).
(6) 公式(六) \(\sin (\dfrac{\pi}{2} +α)=\cos α\) ; \(\cos (\dfrac{\pi}{2} +α)=-\sin α\).
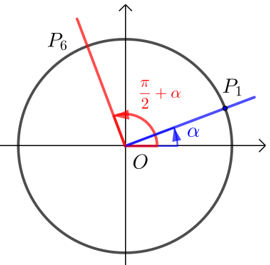若\(P_1 (x ,y)\)，则\(P_6 (-y ,x)\).
 

诱导公式口诀：奇变偶不变，符号看象限

(奇偶指的是\(\dfrac{\pi}{2} \cdot n+α\)中整数\(n\)是奇数还是偶数，看象限时把\(α\)看作锐角)
\(\qquad\) \(\sin \left(\frac{\pi}{2} \cdot n+\alpha\right)=\left\{\begin{array}{l} (-1)^{\frac{\pi}{2}} \sin \alpha, n \text { 为偶数 } \\ (-1)^{\frac{n+1}{2}} \cos \alpha, n \text { 为奇数 } \end{array}\right.\) \(\qquad \qquad\) \(\cos \left(\dfrac{\pi}{2} \cdot n+\alpha\right)=\left\{\begin{array}{l} (-1)^{\frac{n}{2}} \cos \alpha, n \text { 为偶数 } \\ (-1)^{\frac{n+1}{2}} \sin \alpha, n \text { 为奇数 } \end{array}\right.\)
 

【例】 利用诱导公式化简以下式子：(1) \(\sin (x+π)\)； (2) \(\cos (\dfrac{\pi}{2} -x)\)，(3) \(\sin (-x)\).
解析 (1)

(2)

(3)

 

常见结论

(1) \(A+B=π⇒\sin ⁡A=\sin ⁡B\)，\(\cos ⁡A=-\cos ⁡B\)；
(2) \(A+B=\dfrac{\pi}{2} ⇒\sin ⁡A=\cos ⁡B\).
【例】 求\(\cos ⁡150°\)、 \(\sin ⁡120°\)的值.
解 \(\cos ⁡150°=-\cos ⁡30°=-\dfrac{\sqrt{3}}{2}\)，\(\sin ⁡120°=\sin ⁡60°=\dfrac{\sqrt{3}}{2}\).
 

基本方法

【题型1】求值与化简

【典题1】 求下列各三角函数值：
  (1)\(\sin ⁡(-945^∘ )\)；(2)\(\cos (-\dfrac{16\pi}{3} )\).
解析 (1) 方法1
\(\sin \left(-945^{\circ}\right)=-\sin 945^{\circ}=-\sin \left(225^{\circ}+2 \times 360^{\circ}\right)=-\sin 225^{\circ}\)
\(=-\sin ⁡(180^∘+45^∘ )=\sin ⁡45^∘=\dfrac{\sqrt{2}}{2}\)．
方法2 \(\sin ⁡(-945^∘ )=\sin ⁡(135^∘-3×360^∘ )=\sin ⁡135^∘\)\(=\sin ⁡(180^∘-45^∘ )=\sin ⁡45^∘=\dfrac{\sqrt{2}}{2}\)．
(2) 方法1 \(\cos \left(-\dfrac{16 \pi}{3}\right)=\cos \dfrac{16 \pi}{3}=\cos \left(\dfrac{4 \pi}{3}+4 \pi\right)=\cos \dfrac{4 \pi}{3}=\cos \left(\pi+\dfrac{\pi}{3}\right)=-\cos \dfrac{\pi}{3}=-\dfrac{1}{2}\)．
方法2 \(\cos \left(-\dfrac{16 \pi}{3}\right)=\cos \left(\dfrac{2 \pi}{3}-6 \pi\right)=\cos \dfrac{2 \pi}{3}=\cos \left(\pi-\dfrac{\pi}{3}\right)=-\cos \dfrac{\pi}{3}=-\dfrac{1}{2}\)．
点拨 角度负角化正角，大角化小角，小角化锐角.
 

【典题2】化简： \(\dfrac{\cos (\theta+4 \pi) \cdot \cos ^2(\theta+\pi) \cdot \sin ^2(\theta+3 \pi)}{\sin (\theta-4 \pi) \cdot \sin (5 \pi+\theta) \cdot \cos ^2(-\pi+\theta)}\).
解析 原式 \(=\dfrac{\cos \theta \cdot \cos ^2 \theta \cdot \sin ^2 \theta}{\sin \theta \cdot \sin (\pi+\theta) \cdot \cos ^2 \theta}=\dfrac{\cos ^3 \theta \cdot \sin ^2 \theta}{\sin \theta \cdot(-\sin \theta) \cdot \cos ^2 \theta}\)\(=\dfrac{\cos \theta \cdot \sin ^2 \theta}{-\sin ^2 \theta}=-\cos \theta\)．
 

【巩固练习】

1.若\(f(\cos x)=\cos 2x\)，则\(f(\sin 15°)=\)(　　)
 A．\(\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) B．\(\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad \qquad \qquad\) C．\(-\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) D．\(-\dfrac{\sqrt{3}}{2}\)
 

2.已知函数 \(f(x)=\cos \dfrac{x}{2}\)，则下列四个等式中成立的个数是\(\underline{\quad \quad}\)．
 ①\(f(2π-x)=f(x)\)；②\(f(2π+x)=f(x)\)；③\(f(-x)=-f(x)\)；④\(f(-x)=f(x)\)．
 

3.化简 \(\dfrac{\tan (\pi-\alpha) \cos \left(-\dfrac{\pi}{2}-\alpha\right) \cos (6 \pi-\alpha)}{\sin \left(\dfrac{\pi}{2}-\alpha\right) \cos \left(\dfrac{3 \pi}{2}-\alpha\right)}=\) \(\underline{\quad \quad}\).
 

4.化简 \(\dfrac{\cos \left(90^{\circ}-\alpha\right)}{\sin \left(270^{\circ}+\alpha\right)} \cdot \sin \left(180^{\circ}-\alpha\right) \cdot \cos \left(360^{\circ}-\alpha\right)=\) \(\underline{\quad \quad}\).
 

5.化简： \(\sin \left(2 n \pi+\dfrac{2 \pi}{3}\right) \cos \left(n \pi+\dfrac{4 \pi}{3}\right)(n \in \mathrm{Z})\)．
 
 

参考答案

1. 答案 \(D\)
   解析 \(f(\sin ⁡15^∘ )=f(\cos ⁡75^∘ )=\cos 150^∘=\cos (180^∘-30^∘ )\)\(=-\cos 30^∘=-\dfrac{\sqrt{3}}{2}\)．

2. 答案 \(1\)
   解析 \(f(2 \pi-x)=\cos \dfrac{2 \pi-x}{2}=\cos \left(\pi-\dfrac{x}{2}\right)=-\cos \dfrac{x}{2}=-f(x)\)，①不成立；
   \(f(2 \pi+x)=\cos \dfrac{2 \pi+x}{2}=\cos \left(\pi+\dfrac{x}{2}\right)=-\cos \dfrac{x}{2}=-f(x)\)，②不成立；
   \(f(-x)=\cos \left(-\dfrac{x}{2}\right)=\cos \dfrac{x}{2}=f(x)\)，③不成立；④成立．

3. 答案 \(-\tan α\)
   解析 原式 \(=\dfrac{-\tan \alpha \cos \left(\dfrac{\pi}{2}+\alpha\right) \cos (-\alpha)}{\cos \alpha \cos \left[\pi+\left(\dfrac{\pi}{2}-\alpha\right)\right]}=\dfrac{\tan \alpha \cdot \sin \alpha \cdot \cos \alpha}{-\cos \alpha \cdot \cos \left(\dfrac{\pi}{2}-\alpha\right)}=-\dfrac{\tan \alpha \cdot \sin \alpha}{\sin \alpha}=-\tan \alpha\)．

4. 答案 \(-\sin ^2 α\)
   解析 原式 \(=\dfrac{\sin \alpha}{-\cos \alpha} \cdot \sin \alpha \cdot \cos \alpha=-\sin ^2 \alpha\)．

5. 答案 \(\dfrac{\sqrt{3}}{4}\)或 \(-\dfrac{\sqrt{3}}{4}\)
   解析 (1)当\(n\)为奇数时，
   原式 \(=\sin \dfrac{2}{3} \pi \cdot\left(-\cos \dfrac{4}{3} \pi\right)=\sin \left(\pi-\dfrac{\pi}{3}\right) \cdot\left[-\cos \left(\pi+\dfrac{\pi}{3}\right)\right]\)\(=\sin \dfrac{\pi}{3} \cdot \cos \dfrac{\pi}{3}=\dfrac{\sqrt{3}}{2} \times \dfrac{1}{2}=\dfrac{\sqrt{3}}{4}\)．
   (2)当n为偶数时，
   原式 \(=\sin \dfrac{2}{3} \pi \cdot \cos \dfrac{4}{3} \pi=\sin \left(\pi-\dfrac{\pi}{3}\right) \cdot \cos \left(\pi+\dfrac{\pi}{3}\right)\)\(=\sin \dfrac{\pi}{3} \cdot\left(-\cos \dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2} \times\left(-\dfrac{1}{2}\right)=-\dfrac{\sqrt{3}}{4}\)．
    

【题型2】诱导公式的应用

【典题1】 已知\(\cos ⁡(α-75^∘ )=-\dfrac{1}{3}\)，且\(α\)为第四象限角，求\(\sin (105°+α)\)的值．
解析 \(∵\cos ⁡(α-75^∘ )=-\dfrac{1}{3}<0\)，且\(α\)为第四象限角，
\(∴α-75°\)是第三象限角．
\(\therefore \sin \left(\alpha-75^{\circ}\right)=-\sqrt{1-\cos ^2\left(\alpha-75^{\circ}\right)}=-\sqrt{1-\left(-\dfrac{1}{3}\right)^2}=-\dfrac{2 \sqrt{2}}{3}\)．
\(\therefore \sin \left(105^{\circ}+\alpha\right)=\sin \left[180^{\circ}+\left(\alpha-75^{\circ}\right)\right]=-\sin \left(\alpha-75^{\circ}\right)=\dfrac{2 \sqrt{2}}{3}\)．
点拨
1.注意已知角\(α-75^∘\)与所求角\(105°+α\)之间的关系，比如它们的和或差、倍数的和差是否为特殊值( \(\dfrac{\pi}{3}\),\(π\)等).
2.由诱导公式可知：\(A+B=π⇒\sin ⁡A=\sin ⁡B\)，\(\cos ⁡A=-\cos ⁡B\)；\(A+B=\dfrac{\pi}{2} ⇒\sin ⁡A=\cos ⁡B\).
 

【典题2】已知\(α∈(\dfrac{\pi}{2} ,π)\)，且\(\sin (π-α)+\cos (2π+α)=\dfrac{\sqrt{2}}{3}\)．求值：
  (1)\(\sin α-\cos α\)．\(\qquad \qquad\) (2)\(\tan α\)．
解析 已知\(α∈(\dfrac{\pi}{2} ,π)\)，且\(\sin (π-α)+\cos (2π+α)=\dfrac{\sqrt{2}}{3}\)，即\(\sin α+\cos α=\dfrac{\sqrt{2}}{3}\)，
平方可得\(1+2\sin α\cos α=\dfrac{2}{9}\)，即\(2\sin α\cos α=-\dfrac{7}{9}\)．
\(\therefore \sin \alpha-\cos \alpha=\sqrt{(\sin \alpha-\cos \alpha)^2}=\sqrt{1-2 \sin \alpha \cos \alpha}=\dfrac{4}{3}\)．
(2) \(\because \sin \alpha+\cos \alpha=\dfrac{\sqrt{2}}{3}\)， \(\sin \alpha-\cos \alpha=\dfrac{4}{3}\)， \(\therefore \sin \alpha=\dfrac{4+\sqrt{2}}{6}\)， \(\cos \alpha=\dfrac{\sqrt{2}-4}{6}\)，
\(\therefore \tan \alpha=\dfrac{\sin \alpha}{\cos \alpha}=\dfrac{4+\sqrt{2}}{\sqrt{2}-4}=-\dfrac{9+4 \sqrt{2}}{7}\)．
 

【典题3】证明 \(\dfrac{\sin \left(\alpha+\dfrac{3 \pi}{2}\right) \sin \left(\dfrac{3 \pi}{2}-\alpha\right) \cdot \tan ^2(-\alpha) \cdot \tan (\pi-\alpha)}{\cos \left(\dfrac{\pi}{2}-\alpha\right) \cos \left(\dfrac{\pi}{2}+\alpha\right)}=\tan \alpha\).
证明 左边 \(=\dfrac{-\cos \alpha \cdot(-\cos \alpha) \tan ^2 \alpha \cdot(-\tan \alpha)}{\sin \alpha \cdot(-\sin \alpha)}=\dfrac{\tan ^2 \alpha \tan \alpha}{\tan ^2 \alpha}=\tan \alpha=\)右边．
\(∴\)原式成立．
 

【巩固练习】

1.已知\(α∈(0,π)\)，且\(\cos ⁡(π+α)=-\dfrac{\sqrt{3}}{2}\)，则\(\sin ⁡α=\) (　　)
  A. \(\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) B. \(-\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad \qquad \qquad\) D. \(-\dfrac{\sqrt{3}}{2}\)
 

2.若 \(\cos \left(\dfrac{\pi}{6}+\alpha\right)=-\dfrac{1}{3}\)，那么 \(\sin \left(\dfrac{2 \pi}{3}+\alpha\right)\)的值为(　　)
 A．\(-\dfrac{1}{3}\) \(\qquad \qquad \qquad \qquad\) B．\(\dfrac{1}{3}\) \(\qquad \qquad \qquad \qquad\) C．\(-\dfrac{2 \sqrt{2}}{3}\) \(\qquad \qquad \qquad \qquad\) D．\(\dfrac{2 \sqrt{2}}{3}\)
 

3.已知 \(\sin \left(\dfrac{\pi}{3}-\alpha\right)=\dfrac{1}{2}\)，求 \(\cos \left(\dfrac{\pi}{6}+\alpha\right)=\) \(\underline{\quad \quad}\)．
 
 

4.证明： \(\dfrac{\sin \left(\dfrac{\pi}{2}-\alpha\right) \cos \left(\dfrac{\pi}{2}+\alpha\right)}{\cos (\pi+\alpha)}-\dfrac{\sin (2 \pi-\alpha) \cos \left(\dfrac{\pi}{2}-\alpha\right)}{\sin (\pi-\alpha)}=2 \sin \alpha\).
 
 

5.已知函数 \(f(\alpha)=\dfrac{\sin \left(\alpha-\dfrac{\pi}{2}\right) \cos \left(\dfrac{3 \pi}{2}+\alpha\right) \tan (2 \pi-\alpha)}{\tan (\alpha+\pi) \sin (\alpha+\pi)}\).
(1)化简\(f(α)\)；
(2)若 \(f(\alpha) \cdot f\left(\alpha+\dfrac{\pi}{2}\right)=-\dfrac{1}{8}\)，且 \(\dfrac{\pi}{4} \leq \alpha \leq \dfrac{\pi}{2}\)，求 \(f(\alpha)+f\left(\alpha+\dfrac{\pi}{2}\right)\)；
(3)若 \(f\left(\alpha+\dfrac{\pi}{2}\right)=2 f(\alpha)\)，求 \(f(\alpha) \cdot f\left(\alpha+\dfrac{\pi}{2}\right)\).
 
 

参考答案

1. 答案 \(A\)
   解析 因为\(α∈(0,π)\)，且\(\cos ⁡(π+α)=-\cos ⁡α=-\dfrac{\sqrt{3}}{2}\)，可得\(\cos ⁡α=\dfrac{\sqrt{3}}{2}\)，
   所以可得\(\sin ⁡α=\sqrt{1-\cos ^2⁡α}=\dfrac{1}{2}\)，故选\(A\).

2. 答案 \(A\)
   解析 \(\sin \left(\dfrac{2 \pi}{3}+\alpha\right)=\sin \left[\dfrac{\pi}{2}+\left(\dfrac{\pi}{6}+\alpha\right)\right]=\cos \left(\dfrac{\pi}{6}+\alpha\right)=-\dfrac{1}{3}\)．

3. 答案 \(\dfrac{1}{2}\)
   解析 \(\cos \left(\dfrac{\pi}{6}+\alpha\right)=\cos \left[\dfrac{\pi}{2}-\left(\dfrac{\pi}{3}-\alpha\right)\right]=\sin \left(\dfrac{\pi}{3}-\alpha\right)=\dfrac{1}{2}\)．

4. 证明 左边 \(=\dfrac{\cos \alpha(-\sin \alpha)}{-\cos \alpha}-\dfrac{\sin (-\alpha) \sin \alpha}{\sin \alpha}=\sin \alpha-(-\sin \alpha)=2 \sin \alpha=\)右边，所以原式成立．

5. 答案 (1) \(-\cos α\) \(\qquad\) (2) \(-\dfrac{\sqrt{3}}{2}\) \(\qquad\) (3) \(\dfrac{2}{5}\)
   解析 (1) \(f(\alpha)=\dfrac{(-\cos \alpha) \sin \alpha(-\tan \alpha)}{\tan \alpha(-\sin \alpha)}=-\cos \alpha\)；
   (2) \(f\left(\alpha+\dfrac{\pi}{2}\right)=-\cos \left(\alpha+\dfrac{\pi}{2}\right)=\sin \alpha\)，
   因为 \(f(\alpha) \cdot f\left(\alpha+\dfrac{\pi}{2}\right)=-\dfrac{1}{8}\)，所以 \(\cos \alpha \cdot \sin \alpha=\dfrac{1}{8}\)，
   可得 \((\sin \alpha-\cos \alpha)^2=\dfrac{3}{4}\)，结合 \(\dfrac{\pi}{4} \leq \alpha \leq \dfrac{\pi}{2}\),\(\cos α>\sin α\)，
   所以 \(f(\alpha)+f\left(\alpha+\dfrac{\pi}{2}\right)=\sin \alpha-\cos \alpha=-\dfrac{\sqrt{3}}{2}\)，
   (3) 若\(f(α+\dfrac{\pi}{2})=2f(α)\)，则\(\sin ⁡α=-2 \cos ⁡α\)，代入\(\sin ^2⁡α+\cos ^2⁡α=1\)，
   解得 \(\cos ^2 \alpha=\dfrac{1}{5}\)，
   所以 \(f(\alpha) \cdot f\left(\alpha+\dfrac{\pi}{2}\right)=-\sin \alpha \cos \alpha=2 \cos ^2 \alpha=\dfrac{2}{5}\).
    

分层练习

【A组---基础题】

1.\(\cos 300°=\)(　　)
  A．\(-\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad \qquad \qquad\) B．\(-\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) C．\(\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) D．\(\dfrac{\sqrt{3}}{2}\)
 

2.已知\(f(x)=\sin x\)，下列式子成立的是(　　)
 A．\(f(x+π)=\sin x\) \(\qquad\) B．\(f(2π-x)=\sin x\) \(\qquad\) C．\(f(x-\dfrac{\pi}{2})=-\cos x\) \(\qquad\) D．\(f(π-x)=-f(x)\)
 

3.设\(\tan (5π+α)=m\)，则 \(\dfrac{\sin (\alpha-3 \pi)+\cos (\pi-\alpha)}{\sin (-\alpha)-\cos (\pi+\alpha)}\)的值为(　　)
 A． \(\dfrac{m+1}{m-1}\) \(\qquad \qquad \qquad \qquad\) B． \(\dfrac{m-1}{m+1}\) \(\qquad \qquad \qquad \qquad\) C．\(－1\) \(\qquad \qquad \qquad \qquad\) D．\(1\)
 

4.若 \(\text { isin }\left(\alpha+\dfrac{3 \pi}{2}\right)=\dfrac{3}{5}\)，且\(α\)是第三象限角, 则 \(\cos \left(\alpha+\dfrac{2021 \pi}{2}\right)=\) (　　)
  A. \(\dfrac{3}{5}\) \(\qquad \qquad \qquad \qquad\) B. \(-\dfrac{3}{5}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{4}{5}\) \(\qquad \qquad \qquad \qquad\) D. \(-\dfrac{4}{5}\)
 

5.已知 \(\sin \left(\alpha-\dfrac{\pi}{4}\right)=\dfrac{1}{3}\)，则 \(\cos \left(\dfrac{\pi}{4}+\alpha\right)\)的值等于(　　)
 A．\(\dfrac{2 \sqrt{2}}{3}\) \(\qquad \qquad \qquad \qquad\) B．\(-\dfrac{2 \sqrt{2}}{3}\) \(\qquad \qquad \qquad \qquad\) C．\(\dfrac{1}{3}\) \(\qquad \qquad \qquad \qquad\) D．\(-\dfrac{1}{3}\)
 

6.已知\(\cos α=\dfrac{1}{5}\)，且\(α\)为第四象限角，那么 \(\cos \left(\alpha+\dfrac{\pi}{2}\right)=\) \(\underline{\quad \quad}\)\(\underline{\quad \quad}\).
 

7.化简 \(\sin (\pi+\alpha) \cos \left(\dfrac{3 \pi}{2}+\alpha\right)+\sin \left(\dfrac{\pi}{2}+\alpha\right) \cos (\pi+\alpha)=\) \(\underline{\quad \quad}\).
 
 
8.若 \(\sin (3 \pi+\theta)=\dfrac{1}{4}\)，求 \(\dfrac{\cos (\pi+\theta)}{\cos (-\pi+\theta)[\cos (\pi+\theta)-1]}-\dfrac{\cos (\theta-2 \pi)}{\cos (\theta+2 \pi) \cos (\theta+\pi)+\cos (-\theta)}\)的值．
 
 

9.已知 \(\cos \left(\dfrac{\pi}{6}-\alpha\right)=\dfrac{\sqrt{3}}{3}\)，求 \(\cos \left(\dfrac{5 \pi}{6}+\alpha\right)-\sin ^2\left(\alpha-\dfrac{\pi}{6}\right)\)的值．
 
 

10.已知 \(\sin (\alpha+\pi)=\dfrac{4}{5}\)，且\(\sin α \cdot \cos α<0\)，求 \(\dfrac{2 \sin (\alpha-\pi)+3 \tan (3 \pi-\alpha)}{4 \cos (\alpha-3 \pi)}\)的值．
 
 
 

参考答案

1. 答案 \(C\)

2. 答案 \(C\)

3. 答案 \(A\)

4. 答案 \(C\)
   解析 \(\because \sin \left(\alpha+\dfrac{3 \pi}{2}\right)=-\cos \alpha=\dfrac{3}{5}\)， \(\therefore \cos \alpha=-\dfrac{3}{5}\)，
   又\(α\)是第三象限角， \(\therefore \sin \alpha=-\sqrt{1-\cos ^2 \alpha}=-\dfrac{4}{5}\)，
   \(\therefore \cos \left(\alpha+\dfrac{2021 \pi}{2}\right)=-\sin \alpha=\dfrac{4}{5}\).
   故选\(C\).

5. 答案 \(D\)
   解析 \(\because \dfrac{\pi}{4}+\alpha-\left(\alpha-\dfrac{\pi}{4}\right)=\dfrac{\pi}{2}\)，
   \(\therefore \cos \left(\dfrac{\pi}{4}+\alpha\right)=\cos \left[\dfrac{\pi}{2}+\left(\alpha-\dfrac{\pi}{4}\right)\right]=-\sin \left(\alpha-\dfrac{\pi}{4}\right)=-\dfrac{1}{3}\)．故选\(D\)．

6. 答案 \(\dfrac{2 \sqrt{6}}{5}\)
   解析 \(∵α\)为第四象限 角， \(\therefore \sin \alpha=-\sqrt{1-\cos ^2 \alpha}=-\dfrac{2 \sqrt{6}}{5}\)，
   从而 \(\cos \left(\alpha+\dfrac{\pi}{2}\right)=-\sin \alpha=\dfrac{2 \sqrt{6}}{5}\)．

7. 答案 \(-1\)
   解析 原式\(=-\sin α·\sin α-\cos α·\cos α=-1\)．

8. 答案 \(-32\)
   解析 \(\because \sin (3 \pi+\theta)=\dfrac{1}{4}\)， \(\therefore \sin (\pi+\theta)=\dfrac{1}{4}\)．
   \(\therefore \sin (\theta)=-\dfrac{1}{4}\)．
   \(\therefore \dfrac{\cos (\pi+\theta)}{\cos (-\pi+\theta)[\cos (\pi+\theta)-1]}-\dfrac{\cos (\theta-2 \pi)}{\cos (\theta+2 \pi) \cos (\theta+\pi)+\cos (-\theta)}\)
   \(=\dfrac{\cos \theta}{\cos (\pi-\theta)(1+\cos \theta)}-\dfrac{\cos \theta}{\cos \theta-\cos ^2 \theta}\)
   \(=\dfrac{-1}{1+\cos \theta}-\dfrac{1}{1-\cos \theta}=-\dfrac{2}{1-\cos ^2 \theta}=-\dfrac{2}{\sin ^2 \theta}=-32\)．

9. 答案 \(-\dfrac{2+\sqrt{3}}{3}\)
   解析 \(\cos \left(\dfrac{5 \pi}{6}+\alpha\right)=\cos \left[\pi-\left(\dfrac{\pi}{6}-\alpha\right)\right]=-\cos \left(\dfrac{\pi}{6}-\alpha\right)=-\dfrac{\sqrt{3}}{3}\)，
   而 \(\sin ^2\left(\alpha-\dfrac{\pi}{6}\right)=1-\cos ^2\left(\dfrac{\pi}{6}-\alpha\right)=1-\dfrac{1}{3}=\dfrac{2}{3}\)，
   \(∴\)原式 \(=\dfrac{-\sqrt{3}}{3}-\dfrac{2}{3}=-\dfrac{2+\sqrt{3}}{3}\)．

10. 答案 \(-\dfrac{7}{3}\)
    解析 \(\because \sin (\alpha+\pi)=\dfrac{4}{5}\)， \(\therefore \sin \alpha=-\dfrac{4}{5}\)．
    又\(\sin α\cos ⁡α<0\)，\(∴\cos α>0\)， \(\cos \alpha=\sqrt{1-\sin ^2 \alpha}=\dfrac{3}{5}\)，
    \(\therefore \tan \alpha=-\dfrac{4}{3}\)．
    原式 \(=\dfrac{-2 \sin \alpha-3 \tan \alpha}{-4 \cos \alpha}=\dfrac{2 \times\left(-\dfrac{4}{5}\right)+3 \times\left(-\dfrac{4}{3}\right)}{4 \times \dfrac{3}{5}}=-\dfrac{7}{3}\)．

 

【B组---提高题】

1.设 \(f(n)=\cos \left(\dfrac{n \pi}{2}+\dfrac{\pi}{4}\right)\)，则\(f(1)+f(2)+f(3)+⋯+f(2018)\)等于\(\underline{\quad \quad}\)．
 

2.已知 \(g(\theta)=\dfrac{\cos \left(-\theta-\dfrac{\pi}{2}\right) \cdot \sin \left(\dfrac{7 \pi}{2}+\theta\right)}{\sin (2 \pi-\theta)}\)．
(1)化简\(g(θ)\)；
(2)若 \(g\left(\dfrac{\pi}{3}+\theta\right)=\dfrac{1}{3}\), \(\theta \in\left(\dfrac{\pi}{6}, \dfrac{7 \pi}{6}\right)\)，求 \(g\left(\dfrac{5 \pi}{6}+\theta\right)\)的值；
(3)若 \(g\left(\dfrac{3}{2} \pi-\theta\right)-g(\theta)=\dfrac{1}{3}\) , \(\theta \in\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)\)，求 \(g(\theta)-g\left(\dfrac{\pi}{2}-\theta\right)\)的值．
 
 

参考答案

1. 答案 \(- \sqrt{2}\)
   解析 \(\because f(n+4)=\cos \left[\dfrac{(n+4) \pi}{2}+\dfrac{\pi}{4}\right]=\cos \left(\dfrac{n \pi}{2}+\dfrac{\pi}{4}\right)\) ,
   \(∴f(n)\)是以\(4\)为周期的函数，
   又 \(f(1)=-\dfrac{\sqrt{2}}{2}\) , \(f(2)=-\dfrac{\sqrt{2}}{2}\), \(f(3)=\dfrac{\sqrt{2}}{2}\), \(f(4)=\dfrac{\sqrt{2}}{2}\) ,
   \(∴f(1)+f(2)+f(3)+⋯+f(2018)\)
   \(=504[f(1)+f(2)+f(3)+f(4)]+f(1)+f(2)=- \sqrt{2}\)．

2. 答案 (1)\(g(θ)=-\cos θ\)； (2) \(\dfrac{2 \sqrt{2}}{3}\)或\(-\dfrac{2 \sqrt{2}}{3}\)； (3) \(\dfrac{\sqrt{17}}{3}\)
   解析 (1) \(g(\theta)=\dfrac{\cos \left(\theta+\dfrac{\pi}{2}\right) \sin \left(4 \pi-\dfrac{\pi}{2}+\theta\right)}{\sin (-\theta)}=\dfrac{-\sin \theta(-\cos \theta)}{-\sin \theta}=-\cos \theta\)；
   (2)\(∵ \theta \in\left(\dfrac{\pi}{6}, \dfrac{7 \pi}{6}\right)\)， \(\therefore \dfrac{\pi}{3}+\theta \in\left(\dfrac{\pi}{2}, \dfrac{3 \pi}{2}\right)\)，
   \(\because g\left(\dfrac{\pi}{3}+\theta\right)=-\cos \left(\dfrac{\pi}{3}+\theta\right)=\dfrac{1}{3}\) ，即 \(\cos \left(\dfrac{\pi}{3}+\theta\right)=-\dfrac{1}{3}\)；
   \(\therefore g\left(\dfrac{5 \pi}{6}+\theta\right)=-\cos \left(\dfrac{5 \pi}{6}+\theta\right)=-\cos \left(\dfrac{\pi}{2}+\dfrac{\pi}{3}+\theta\right)=\sin \left(\dfrac{\pi}{3}+\theta\right)\)；
   \(∴\)当 \(\dfrac{\pi}{3}+\theta \in\left(\dfrac{\pi}{2}, \pi\right)\)时，
   \(g\left(\dfrac{5 \pi}{6}+\theta\right)=\sin \left(\dfrac{\pi}{3}+\theta\right)=\sqrt{1-\cos ^2\left(\dfrac{\pi}{3}+\theta\right)}=\dfrac{2 \sqrt{2}}{3}\)；
   当 \(\dfrac{\pi}{3}+\theta \in\left(\pi, \dfrac{3 \pi}{2}\right)\)，
   \(g\left(\dfrac{5 \pi}{6}+\theta\right)=\sin \left(\dfrac{\pi}{3}+\theta\right)=-\sqrt{1-\cos ^2\left(\dfrac{\pi}{3}+\theta\right)}=-\dfrac{2 \sqrt{2}}{3}\)；
   (3) \(g(\theta)-g\left(\dfrac{\pi}{2}-\theta\right)=-\cos \theta+\cos \left(\dfrac{\pi}{2}-\theta\right)=\sin \theta-\cos \theta\)
   由 \(g\left(\dfrac{3}{2} \pi-\theta\right)-g(\theta)=\dfrac{1}{3}\)，得 \(-\cos \left(\dfrac{3}{2} \pi-\theta\right)+\cos \theta=\dfrac{1}{3}\)，
   整理得 \(\sin \theta+\cos \theta=\dfrac{1}{3}\)，
   两边平方得： \((\sin \theta+\cos \theta)^2=1+2 \sin \theta \cos \theta=\dfrac{1}{9}\)，即 \(2 \sin \theta \cos \theta=-\dfrac{8}{9}<0\)，
   \(\therefore(\sin \theta-\cos \theta)^2=1-2 \sin \theta \cos \theta=\dfrac{17}{9} \Rightarrow \sin \theta-\cos \theta=\pm \dfrac{\sqrt{17}}{3}\)，
   \(\because \theta \in\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)\)，
   \(∴\cos θ>0\) ,\(\sin θ<0\)，即\(\sin θ-\cos θ <0\)，
   则 \(g(\theta)-g\left(\dfrac{\pi}{2}-\theta\right)=\dfrac{\sqrt{17}}{3}\)．
    

【C组---拓展题】

1. \(\sin ^2 1^{\circ}+\sin ^2 2^{\circ}+\sin ^2 3^{\circ}+\cdots+\sin ^2 89^{\circ}=\)\(\underline{\quad \quad}\).
    
    

参考答案

1. 答案 \(\dfrac{89}{2}\)
   解析 设 \(S=\sin ^2 1^{\circ}+\sin ^2 2^{\circ}+\sin ^2 3^{\circ}+\cdots+\sin ^2 89^{\circ}=\) ①
   又 \(\because \mathrm{S}=\sin ^2 89^{\circ}+\sin ^2 88^{\circ}+\sin ^2 87^{\circ}+\cdots+\sin ^2 1^{\circ}\)
   \(=\cos ^2 1^{\circ}+\cos ^2 2^{\circ}+\cos ^2 3^{\circ}+\cdots+\cos ^2 89^{\circ}\) ②
   由①+②得 \(2S=89\)，则 \(S=\dfrac{89}{2}\)．