5.2.2 同角三角函数的基本关系

${\color{Red}{欢迎到学科网下载资料学习 }}$  

【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019）
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

必修第一册同步巩固，难度2颗星！

基础知识

同角三角函数基本关系式

\[\sin ^2 α+\cos ^2 α=1 \]

\[\tan \alpha=\dfrac{\sin \alpha}{\cos \alpha} \]

解释
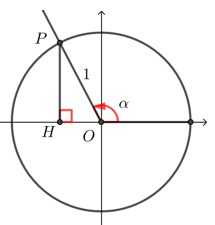
由三角函数的定义，如下图，\(α\)的终边与单位圆交于点\(P(x,y)\)，
可知\(\sin α=y\)，\(\cos α=x\)， \(\tan \alpha=\dfrac{y}{x}=(x \neq 0)\).
过点\(P\)作\(PH⊥x\)轴，在\(Rt∆PHO\)中，\(OH^2+PH^2=OP^2=1\)，
因此\(x^2+y^2=1\)，即\(\sin ^2 α+\cos ^2 α=1\)，
当\(α≠π/2+kπ(k∈Z)\)时， \(\tan \alpha=\dfrac{y}{x}=\dfrac{\sin \alpha}{\cos \alpha}\).

 

拓展

\(\qquad\) \((\sin α+\cos α)^2=1+2 \sin α \cdot \cos α\)；\(\qquad \qquad\) \((\sin α-\cos α)^2=1-2 \sin α \cdot \cos α\).
 

基本方法

【题型1】利用三角函数基本关系式求值

【典题1】 已知\(α∈(0,π)\)，\(\tan α=-2\)，则\(\cos α=\) \(\underline{\quad \quad}\).
解析 方法1 \(∵\tan α=-2\)， \(\therefore \dfrac{\sin \alpha}{\cos \alpha}=-2\)，即\(\sin α=-2\cos α\)，
又 \(\sin ^2 \alpha+\cos ^2 \alpha=1 \Rightarrow \cos \alpha=\pm \dfrac{\sqrt{5}}{5}\)，
\(∵α∈(0，π)\)，且\(\tan α=-2<0\)，
\(∴α\)为第二象限角，\(∴\cos α<0\)，
\(∴\cos α=-\dfrac{\sqrt{5}}{5}\).
方法2 \(∵\tan α=-2\)，构造直角三角形\(Rt△ABC\)如下图，

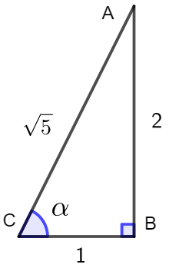
在直角三角形中， \(\cos \alpha=\dfrac{B C}{A C}=\dfrac{1}{\sqrt{5}}=\dfrac{\sqrt{5}}{5}\)，
\(∵α∈(0，π)\)，且\(\tan α=-2<0\)，
\(∴α\)为第二象限角，
\(∴\cos α<0\)， \(∴\cos α=-\dfrac{\sqrt{5}}{5}\).
点拨
① 若知\(\sin α\)、\(\cos α\)、\(\tan α\)三者中一个的值，可求另外两个的值，即“知一得二”；
② 在非解答题中用方法二解题速度更快些，只是要多留意三角函数的符号.
 

【典题2】 已知\(\tan α=-2\)，求下列各式的值：
  (1) \(\dfrac{4 \sin \alpha-2 \cos \alpha}{5 \cos \alpha+3 \sin \alpha}\)；   (2) \(\dfrac{1}{4} \sin ^2 \alpha+\dfrac{2}{5} \cos ^2 \alpha\).
解析 方法1 由\(\tan α=-2\)，得\(\sin α=-2\cos α\)．
(1) \(\dfrac{4 \sin \alpha-2 \cos \alpha}{5 \cos \alpha+3 \sin \alpha}=\dfrac{-8 \cos \alpha-2 \cos \alpha}{5 \cos \alpha-6 \cos \alpha}=10\)．
(2) \(\dfrac{1}{4} \sin ^2 \alpha+\dfrac{2}{5} \cos ^2 \alpha=\dfrac{\dfrac{1}{4} \sin ^2 \alpha+\dfrac{2}{5} \cos ^2 \alpha}{\sin ^2 \alpha+\cos ^2 \alpha}=\dfrac{\cos ^2 \alpha+\dfrac{2}{5} \cos ^2 \alpha}{4 \cos ^2 \alpha+\cos ^2 \alpha}=\dfrac{7}{25}\)．
方法2 \(∵\tan α=-2\)，\(∴\cos α≠0\)．
(1) \(\dfrac{4 \sin \alpha-2 \cos \alpha}{5 \cos \alpha+3 \sin \alpha}=\dfrac{4 \tan \alpha-2}{5+3 \tan \alpha}=\dfrac{4 \times(-2)-2}{5+3 \times(-2)}=10\)．
(2) \(\dfrac{1}{4} \sin ^2 \alpha+\dfrac{2}{5} \cos ^2 \alpha=\dfrac{\dfrac{1}{4} \sin ^2 \alpha+\dfrac{2}{5} \cos ^2 \alpha}{\sin ^2 \alpha+\cos ^2 \alpha}=\dfrac{\dfrac{1}{\tan ^2 \alpha+\frac{2}{5}}}{\tan ^2 \alpha+1}=\dfrac{7}{25}\)．
点拨 方法2中当分式\(\dfrac{f(x)}{g(x)}\)中\(f(x)\)、\(g(x)\)关于\(\cos α\)、\(\sin α\)的“齐次化式”，分子分母同除以\(\cos α\)或\(\sin α\).
第(2)问中巧妙的使用了\(\sin ^2 α+\cos ^2 α=1\).
 

【典题3】 已知 \(\sin \alpha+\cos \alpha=-\dfrac{1}{5}\)．
  (1)求\(\sin α\cdot \cos α\)的值；
  (2)若\(\dfrac{π}{2}<α<π\)，求\(\dfrac{1}{\sin \alpha}-\dfrac{1}{\cos (2 \pi+\alpha)}\)的值．
解析 (1)\(∵\sin \alpha+\cos \alpha=-\dfrac{1}{5}\) ①， \(\therefore(\sin \alpha+\cos \alpha)^2=\dfrac{1}{25}\)，
即\(1+2 \sin \alpha \cos \alpha=\dfrac{1}{25}\)， \(\therefore \sin \alpha \cdot \cos \alpha=-\dfrac{12}{25}\) ，
(2)由(1)得，\((\sin \alpha-\cos \alpha)^2=1-2 \sin \alpha \cos \alpha=\dfrac{49}{25}\)，
又 \(\dfrac{π}{2}<α<π\)，\(∴\sin α-\cos α>0\)，
\(\therefore \sin \alpha-\cos \alpha=\dfrac{7}{5}\) ②．
\(\therefore \dfrac{1}{\sin \alpha}-\dfrac{1}{\cos (2 \pi+\alpha)}=\dfrac{1}{\sin \alpha}-\dfrac{1}{\cos \alpha}=\dfrac{\cos \alpha-\sin \alpha}{\sin \alpha \cos \alpha}=\dfrac{35}{12}\) .
点拨
① \((\sin α+\cos α)^2=1+2 \sin α \cdot \cos α\)； \((\sin α-\cos α)^2=1-2 \sin α \cdot \cos α\).
②\(\sin θ+\cos θ\)、\(\sin θ-\cos θ\)、\(\sin θ\cos θ\)也是“知一得二”.
 

【巩固练习】

1.已知\(α\)是第四象限角， \(\cos \alpha=\dfrac{12}{13}\)，则\(\sin α\)等于(　　)
 A． \(\dfrac{5}{13}\) \(\qquad \qquad \qquad \qquad\) B． \(-\dfrac{5}{13}\) \(\qquad \qquad \qquad \qquad\) C． \(\dfrac{5}{12}\) \(\qquad \qquad \qquad \qquad\) D． \(-\dfrac{5}{12}\)
 

2.已知\(\alpha=-\dfrac{1}{2}\)，则\(\dfrac{2 \sin \alpha \cos \alpha}{\sin ^2 \alpha-\cos ^2 \alpha}\)的值是(　　)
 A． \(\dfrac{4}{3}\) \(\qquad \qquad \qquad \qquad\) B．\(3\) \(\qquad \qquad \qquad \qquad\) C． \(-\dfrac{4}{3}\) \(\qquad \qquad \qquad \qquad\) D．\(-3\)
 

3.如果角\(θ\)满足\(\sin \theta+\cos \theta=\sqrt{2}\)，那么\(\tan \theta+\dfrac{1}{\tan \theta}\)的值是(　　)
  A.\(-1\) \(\qquad \qquad \qquad \qquad\) B．\(-2\) \(\qquad \qquad \qquad \qquad\) C．\(1\) \(\qquad \qquad \qquad \qquad\) D．\(2\)
 

4.若\(\alpha \in\left(\dfrac{\pi}{2}, \pi\right)\)，且\(\cos ^2 \alpha-\sin \alpha=\dfrac{1}{4}\)，则\(\tan α\)的值等于(　　)
 A． \(-\dfrac{\sqrt{3}}{3}\) \(\qquad \qquad \qquad \qquad\) B． \(\dfrac{\sqrt{3}}{3}\) \(\qquad \qquad \qquad \qquad\) C． \(\sqrt{3}\) \(\qquad \qquad \qquad \qquad\) D． \(-\sqrt{3}\)
 

5.已知\(\tan \alpha=\dfrac{4}{3}\)，且\(α\)是第三象限角，求\(\sin α\)，\(\cos α\)的值．
 
 

6.已知\(\sin θ\)、\(\cos θ\)是关于\(x\)的方程 \(x^2-2 \sqrt{2} a x+a=0\)的两个根．
(1)求实数\(a\)的值；(2)若\(θ∈\left(-\dfrac{\pi}{2},0\right)\)，求\(\sin θ-\cos θ\)的值．
 
 
 

参考答案

1. 答案 \(B\)
   解析 \(∵α\)是第四象限角，
   \(\therefore \sin \alpha=-\sqrt{1-\cos ^2 \alpha}=-\sqrt{1-\left(\dfrac{12}{13}\right)^2}=-\dfrac{5}{13}\)．

2. 答案 \(A\)
   解析 原式 \(=\dfrac{2 \tan \alpha}{\tan ^2 \alpha-1}=\dfrac{2 \times\left(-\frac{1}{2}\right)}{\left(-\frac{1}{2}\right)^2-1}=\dfrac{4}{3}\)．

3. 答案 \(D\)
   解析 \(\because \sin \theta+\cos \theta=\sqrt{2}\)，
   \(\therefore 1+2 \sin \theta \cos \theta=2\)，即 \(\sin \theta \cos \theta=\dfrac{1}{2}\)，
   那么 \(\tan \theta+\dfrac{1}{\tan \theta}=\dfrac{\sin \theta}{\cos \theta}+\dfrac{\cos \theta}{\sin \theta}=\dfrac{1}{\sin \theta \cos \theta}=2\)，
   故选：\(D\)．

4. 答案 \(A\)
   解析 \(∵\cos ^2 \alpha-\sin \alpha=\dfrac{1}{4}\)，\(∴4(1-\sin ^2⁡α )-4\sin α-1=0\)，
   即\(A\)\(4 \sin ^2⁡α+4\sin α－3=0\)，\(∴\)解得 \(\sin \alpha=\dfrac{1}{2}\)或 \(\sin \alpha=-\dfrac{3}{2}\)(舍)．
   \(∵\alpha \in\left(\dfrac{\pi}{2}, \pi\right)\)， \(\therefore \alpha=\dfrac{5 \pi}{6}\)， \(\therefore \tan \alpha=\tan \dfrac{5 \pi}{6}=-\dfrac{\sqrt{3}}{3}\)．
   故选：\(A\)．

5. 答案 \(\cos \alpha=-\dfrac{3}{5}\)， \(\sin \alpha=-\dfrac{4}{5}\)．
   解析 由 \(\tan \alpha=\dfrac{\sin \alpha}{\cos \alpha}=\dfrac{4}{3}\)得\(\sin α=\dfrac{4}{3} \cos α\)．①
   又\(\sin ^2 α+\cos ^2 α=1\)，②
   由①②得 \(\dfrac{16}{9} \cos ^2 \alpha+\cos ^2 \alpha=1\)，即 \(\cos ^2 \alpha=\dfrac{9}{25}\)．
   \(∵α\)在第三象限，
   \(\therefore \cos \alpha=-\dfrac{3}{5}\)， \(\sin \alpha=\dfrac{4}{3} \cos \alpha=-\dfrac{4}{5}\)．

6. 答案 (1) \(a=-\dfrac{1}{4}\)或 \(\dfrac{1}{2}\)；(2) \(-\dfrac{\sqrt{6}}{2}\).
   解析 (1)\(∵\sin θ\)、\(\cos θ\)是关于\(x\)的方程 \(x^2-2 \sqrt{2} a x+a=0\)的两个根，
   \(\therefore \sin \theta+\cos \theta=2 \sqrt{2} a\) ①，\(\sin θ\cos θ=a\) ②，
   \(△=b^2-4ac=8a^2-4a≥0\)，即\(a≤0\)或\(a≥\dfrac{1}{2}\)，
   \(∴(\sin θ+\cos θ)^2=1+2\sin θ\cos θ=1+2a=8a^2\)，
   即\(8a^2-2a-1=0\)，解得\(a=-\dfrac{1}{4}\)或 \(\dfrac{1}{2}\)．
   (2)\(∵θ∈\left(-\dfrac{\pi}{2},0 \right)\)，
   \(∴\sin θ<0\)，\(\cos θ>0\)，可得\(\sin θ\cos θ=a<0\)，由(1)可得\(a=-\dfrac{1}{4}\)，
   \(∴\sin θ\cos θ=-\dfrac{1}{4}\)，
   \(∴(\sin θ-\cos θ)^2=1-2\sin θ\cos θ=1+\dfrac{1}{2}=\dfrac{3}{2}\)，
   又\(\sin θ-\cos θ<0\)，\(∴ \sin θ-\cos θ=-\dfrac{\sqrt{6}}{2}\).
   (注意判断\(\sin θ－\cos θ\)的正负)

 

【题型2】三角函数式的化简

【典题1】 化简下列各式：
  (1) \(\dfrac{\sqrt{1-2 \sin 130^{\circ} \cos 130^{\circ}}}{\sin 130^{\circ}+\sqrt{1-\sin ^2 130^{\circ}}}\)；
  (2) \(\sin ^2 \alpha \cdot \tan \alpha+2 \sin \alpha \cdot \cos \alpha+\dfrac{\cos ^2 \alpha}{\tan \alpha}\).
解析 (1)原式 \(=\dfrac{\sqrt{\sin ^2 130^{\circ}-2 \sin 130^{\circ} \cos 130^{\circ}+\cos ^2 130^{\circ}}}{\sin 130^{\circ}+\sqrt{\cos ^2 130^{\circ}}}\)
\(=\dfrac{\left|\sin 130^{\circ}-\cos 130^{\circ}\right|}{\sin 130^{\circ}+\left|\cos 130^{\circ}\right|}=\dfrac{\sin 130^{\circ}-\cos 130^{\circ}}{\sin 130^{\circ}-\cos 130^{\circ}}=1\)．
(2)原式 \(=\sin ^2 \alpha \cdot \dfrac{\sin \alpha}{\cos \alpha}+2 \sin \alpha \cos \alpha+\cos ^2 \alpha \cdot \dfrac{\cos \alpha}{\sin \alpha}\)
\(=\dfrac{\sin ^4 \alpha+2 \sin ^2 \alpha \cos ^2 \alpha+\cos ^4 \alpha}{\cos \alpha \sin \alpha}\)\(=\dfrac{\left(\sin ^2 \alpha+\cos ^2 \alpha\right)^2}{\sin \alpha \cos \alpha}=\dfrac{1}{\sin \alpha \cos \alpha}\)．
点拨 遇到正切一般化为正弦与余弦，"切化弦"的方法.
 

【巩固练习】

1.若角\(α\)的终边在第二象限，则\(\dfrac{\sin \alpha}{\sqrt{1-\sin ^2 \alpha}}+\dfrac{\sqrt{1-\cos ^2 \alpha}}{\cos \alpha}\) 的值等于(　　)
 A．\(2\) \(\qquad \qquad \qquad \qquad\) B．\(-2\) \(\qquad \qquad \qquad \qquad\) C．\(0\) \(\qquad \qquad \qquad \qquad\) D．\(-2\)或\(2\)
 

参考答案

1. 答案 \(C\)
   解析 \(∵α\)是第二象限角，
   \(∴\sin α>0\)，\(\cos α<0\)．
   \(\therefore \dfrac{\sin \alpha}{\sqrt{1-\sin ^2 \alpha}}+\dfrac{\sqrt{1-\cos ^2 \alpha}}{\cos \alpha}=\dfrac{\sin \alpha}{|\cos \alpha|}+\dfrac{|\sin \alpha|}{\cos \alpha}=-\tan \alpha+\tan \alpha=0\)．
    

【题型3】三角恒等式的证明

【典题1】 求证： \(\dfrac{1-2 \sin 2 x \cos 2 x}{\cos ^2 2 x-\sin ^2 2 x}=\dfrac{1-\tan 2 x}{1+\tan 2 x}\).
证明 左边 \(=\dfrac{\cos ^2 2 x+\sin ^2 2 x-2 \sin 2 x \cos 2 x}{\cos ^2 2 x-\sin ^2 2 x}=\dfrac{(\cos 2 x-\sin 2 x)^2}{(\cos 2 x-\sin 2 x)(\cos 2 x+\sin 2 x)}\)
\(=\dfrac{\cos 2 x-\sin 2 x}{\cos 2 x+\sin 2 x}=\dfrac{1-\tan 2 x}{1+\tan 2 x}=\)右边，
所以原式成立．
 

【巩固练习】

1.求证： \(2(1-\sin \alpha)(1+\cos \alpha)=(1-\sin \alpha+\cos \alpha)^2\).

参考答案

1. 证明 右边\(=[(1-\sin α)+\cos α]^2\)
   \(=(1-\sin ⁡α)^2 +\cos ^2⁡α+2 \cos ⁡α(1-\sin ⁡α )\)
   \(=1-2\sin α+\sin ^2 α+\cos ^2 α+2\cos α(1-\sin α)\)
   \(=2-2\sin α+2\cos α(1-\sin α)\)
   \(=2(1-\sin α)(1+\cos α)=\)左边，
   所以原式成立．

 

分层练习

【A组---基础题】

1.已知\(\cos α=-\dfrac{12}{13}\)，\(α∈(π,2π)\)，则\(\tan α=\) (　　)
 A． \(\dfrac{12}{5}\) \(\qquad \qquad \qquad \qquad\) B． \(\dfrac{5}{12}\) \(\qquad \qquad \qquad \qquad\) C． \(-\dfrac{5}{12}\) \(\qquad \qquad \qquad \qquad\) D． \(-\dfrac{12}{5}\)
 

2.已知\(\tan \alpha=\dfrac{3}{4}\)，则\(\dfrac{\sin \alpha-2 \cos \alpha}{2 \sin \alpha+\cos \alpha}=\)(　　)
 A．\(-2\) \(\qquad \qquad \qquad \qquad\) B．\(2\) \(\qquad \qquad \qquad \qquad\) C．\(-\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) D． \(\dfrac{1}{2}\)
 

3.如果角\(θ\)满足\(\sin θ+\cos θ=\sqrt{2}\)，那么\(\tan \theta+\dfrac{1}{\tan \theta}\)的值是(　　)
 A．\(-1\) \(\qquad \qquad \qquad \qquad\) B．\(-2\) \(\qquad \qquad \qquad \qquad\) C．\(1\) \(\qquad \qquad \qquad \qquad\) D．\(2\)
 

4.已知角\(α\)是锐角，若\(\sin α\),\(\cos α\)是关于\(x\)的方程\(x^2+mx+n=0\)的两个实数根，则实数\(m\)和\(n\)一定满足(　　)
 A．\(m^2-4n=0\) \(\qquad \qquad\) B．\(m^2=2n+1\) \(\qquad \qquad\) C．\(m+n+1≤0\) \(\qquad \qquad\) D．\(mn>0\)
 

5.已知\(α\)是第三象限角，\(4\sin ^2 α-3\sin α\cos α-5\cos ^2 α=1\)，则\(\tan α=\)(　　)
 A．\(-1\)或\(2\) \(\qquad \qquad \qquad \qquad\) B． \(\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) C．\(1\) \(\qquad \qquad \qquad \qquad\) D．\(2\)
 

6.已知\(α∈(π,\dfrac{3\pi}{2})\)，\(\tan α=2\)，则\(\cos α=\) \(\underline{\quad \quad}\).
 

7.已知\(\sin α+\cos α=\dfrac{1}{5}\)，则\(\sin α\cos α=\) \(\underline{\quad \quad}\)．
 

8.若\(\sin α=\dfrac{\sqrt{5}}{5}\)，则\(\sin ^4 α-\cos ^4 α=\) \(\underline{\quad \quad}\).
 

9.已知\(α\)为第二象限角，则\(\dfrac{2 \sin \alpha}{\sqrt{1-\cos ^2 \alpha}}+\cos \alpha \sqrt{1+\tan ^2 \alpha}\)的值是\(\underline{\quad \quad}\)．
 

10.已知\(\tan \theta+\dfrac{1}{\tan \theta}=3\)，求\(\tan ^2 \theta+(\sin \theta-\cos \theta)^2+\dfrac{1}{\tan ^2 \theta}\)的值．
 
 
 

参考答案

1. 答案 \(B\)
   解析 \(∵\cos α=-\dfrac{12}{13}\)，\(α∈(π,2π)\)，则\(α∈(π,\dfrac{3\pi}{2})\)，\(∴\sin α<0\)．
   又\(\sin ^2 α+\cos ^2 α=1\)，
   \(\therefore \sin ^2 \alpha=1-\cos ^2 \alpha=\dfrac{25}{169}\)，
   \(\therefore \sin \alpha=-\dfrac{5}{13}\)， \(\therefore \tan \alpha=\dfrac{\sin \alpha}{\cos \alpha}=\dfrac{5}{12}\)．

2. 答案 \(C\)
   解析 \(∵\tan \alpha=\dfrac{3}{4}\) ， \(\therefore \dfrac{\sin \alpha-2 \cos \alpha}{2 \sin \alpha+\cos \alpha}=\dfrac{\tan \alpha-2}{2 \tan \alpha+1}=-\dfrac{1}{2}\)．故选：\(C\)．

3. 答案 \(D\)
   解析 \(∵\sin θ+\cos θ=\sqrt{2}\)，\(∴1+2\sin θ\cos θ=2\)，即\(\sin θ\cos θ= \dfrac{1}{2}\)，
   那么 \(\tan \theta+\dfrac{1}{\tan \theta}=\dfrac{\sin \theta}{\cos \theta}+\dfrac{\cos \theta}{\sin \theta}=\dfrac{1}{\sin \theta \cos \theta}=2\)，
   故选：\(D\)．

4. 答案 \(B\)
   解析 由题可得\(\sin α+\cos α=-m\)，\(\sin α\cos α=n\)，
   因为\(1=\sin ^2 α+\cos ^2 α=(\sin α+\cos α)^2-2\sin α\cos α=m^2-2n\)，
   \(∴m^2=2n+1\)，
   故选：\(B\)．

5. 答案 \(D\)
   解析 由\(4\sin ^2 α-3\sin α\cos α-5\cos ^2 α=1\)
   可得 \(\dfrac{4 \sin ^2 \alpha-3 \sin \alpha \cos \alpha-5 \cos ^2 \alpha}{\sin ^2 \alpha+\cos ^2 \alpha}=1\)．
   分子，分母同时除以\(\cos ^2⁡α\)，得 \(\dfrac{4 \tan ^2 \alpha-3 \tan \alpha-5}{\tan ^2 \alpha+1}=1\)，
   解得\(\tan α=-1\)或\(\tan α=2\)．
   又\(∵α\)是第三象限角，
   \(∴\tan α>0\)．\(∴\tan α=2\)．

6. 答案 \(-\dfrac{\sqrt{5}}{5}\)
   解析 \(∵α∈\left(π,\dfrac{3\pi}{2}\right)\)，\(\tan α=2\)，
   \(∴\cos α<0\)， \(\dfrac{\sin \alpha}{\cos \alpha}=2\)．
   又\(\sin ^2 α+\cos ^2 α=1\)，
   \(∴5 \cos ^2⁡α=1\)，\(∴\cos α=-\dfrac{\sqrt{5}}{5}\)．

7. 答案 \(-\dfrac{12}{25}\)
   解析 \(∵\sin α+\cos α=\dfrac{1}{5}\)，
   \(∴\)两边平方可得：\(\sin ^2 α+\cos ^2 α+2\sin α\cos α=\dfrac{1}{25}\)，
   \(∴1+2\sin α\cos α=\dfrac{1}{25}\)，则\(\sin α\cos α=-\dfrac{12}{25}\)．

8. 答案 \(-\dfrac{3}{5}\)
   解析 \(\sin ^4⁡α-\cos ^4⁡α=(\sin ^2⁡α+\cos ^2⁡α )(\sin ^2⁡α-\cos ^2⁡α )\)
   \(=\sin ^2⁡α-\cos ^2⁡α=\sin ^2⁡α-(1-\sin ^2⁡α )\)
   \(=2 \sin ^2 \alpha-1=2 \times\left(\dfrac{\sqrt{5}}{5}\right)^2-1=-\dfrac{3}{5}\)．

9. 答案 \(1\)
   解析 \(∵α\)为第二象限角，\(\cos α<0\)，
   \(\therefore \dfrac{2 \sin \alpha}{\sqrt{1-\cos ^2 \alpha}}+\cos \alpha \sqrt{1+\tan ^2 \alpha}=\dfrac{2 \sin \alpha}{\sin \alpha}+\cos \alpha \sqrt{\dfrac{1}{\cos ^2 \alpha}}\)\(=2+\cos \alpha\left|\dfrac{1}{\cos \alpha}\right|=2-1=1\)．
   故答案为：\(1\)．

10. 答案 \(\dfrac{22}{3}\)
    解析 由已知得 \(\dfrac{\sin \theta}{\cos \theta}+\dfrac{\cos \theta}{\sin \theta}=3\)，
    \(\therefore \dfrac{\sin ^2 \theta+\cos ^2 \theta}{\sin \theta \cos \theta}=3\), \(\therefore \sin \theta \cos \theta=\dfrac{1}{3}\)．
    \(∴\)原式 \(=\left(\tan \theta+\dfrac{1}{\tan \theta}\right)^2-2+(1-2 \sin \theta \cos \theta)=3^2-2+1-\dfrac{2}{3}=\dfrac{22}{3}\)．

 

【B组---提高题】

1.已知 \(\dfrac{1-\cos x+\sin x}{1+\cos x+\sin x}=-2\)，则\(\tan ⁡x\)的值为\(\underline{\quad \quad}\).
 

2.已知\(3\sin α+4\cos α=5\)，求\(\tan α\).
 
 

3.已知\(0<x<π\)，\(\sin x+\cos x=\dfrac{1}{4}\)．
①求\(\sin x-\cos x\)的值；②求\(\sin ^3⁡x+\cos ^3⁡x\)的值．
 
 
 

参考答案

1. 答案 \(\dfrac{4}{3}\)
   解析 由条件，得\(1-\cos x+\sin x=-2-2\cos x-2\sin x\)，
   整理得：\(3\sin x+\cos x=-3\)，
   即 \(\cos x=-3\sin x-3\) ①，
   代入\(\sin ^2 x+\cos ^2 x=1\)中，得\(\sin ^2 x+(-3\sin x-3)^2=1\)，
   整理得：\(5\sin ^2 x+9\sin x+4=0\)，即\((\sin x+1)(5\sin x+4)=0\)，
   解得\(\sin x=-1\)(舍)或\(\sin x=-\dfrac{4}{5}\)，
   把 \(\sin x=-\dfrac{4}{5}\)，代入①，得\(\cos x=-\dfrac{3}{5}\)，所以\(\tan x=\dfrac{4}{3}\)．

2. 答案 \(\dfrac{3}{4}\)
   解析 方法1解方程组法
   由\(\left\{\begin{array}{c} 3 \sin \alpha+4 \cos \alpha=5 \\ \sin ^2 \alpha+\cos ^2 \alpha=1 \end{array}\right.\)得\(25 \sin ^2⁡α-30\sin α+9=0\)，
   解得\(\sin α=\dfrac{3}{5}\)，
   \(∴\cos α=\dfrac{4}{5}\) , \(∴\tan α=\dfrac{3}{4}\).
   方法2 “对偶式”法
   设\(4\sin α-3\cos α=x\)，等式两边平方得\(16 \sin ^2⁡α-24\sin α\cos α+9 \cos ^2⁡α=x^2\) ①
   将\(3\sin α+4\cos α=5\)两边平方，得\(9 \sin ^2⁡α+24\sin α\cos α+16 \cos ^2⁡α=25\) ②
   由①+②得，\(25=x^2+25\)，解得\(x=0\)，
   \(∴4\sin α-3\cos α=0\), \(∴4\sin α=3\cos α\), \(∴\tan α=\dfrac{3}{4}\).
   方法3 “弦化切”法
   将\(3\sin α+4\cos α=5\)两边平方，得\(9 \sin ^2⁡α+24\sin α\cos α+16 \cos ^2⁡α=25\)
   即\(\dfrac{9 \sin ^2 \alpha+24 \sin \alpha \cos \alpha+16 \cos ^2 \alpha}{\sin ^2 \alpha+\cos ^2 \alpha}=25\)，
   即 \(\dfrac{9 \tan ^2 \alpha+24 \tan \alpha+16}{\tan ^2 \alpha+1}=25\)，解得 \(\tan α=\dfrac{3}{4}\).

3. 答案 ① \(\dfrac{\sqrt{31}}{4}\); ② \(\dfrac{47}{128}\)．
   解析 已知\(0<x<π\)， \(\sin x+\cos x=\dfrac{1}{4}\)．
   所以 \((\sin x+\cos x)^2=\dfrac{1}{16}\)，解得 \(\sin x \cos x=-\dfrac{15}{32}\)，
   所以\(\dfrac{\pi}{2}<x<π\)．
   ① \(\sin x-\cos x=|\sin x-\cos x|=\sqrt{(\sin x+\cos x)^2-4 \sin x \cos x}\)
   \(=\sqrt{\dfrac{1}{16}-4 \times\left(-\dfrac{15}{32}\right)}=\dfrac{\sqrt{31}}{4}\)．
   ② \(\sin ^3 x+\cos ^3 x=(\sin x+\cos x)\left(\sin ^2 x-\sin x \cos x+\cos ^2 x\right)\)\(=\dfrac{1}{4} \times\left(1+\dfrac{15}{32}\right)=\dfrac{47}{128}\)．
    

【C组---拓展题】

1.已知函数\(y=\cos ^2⁡x+a\sin ⁡x-a^2+2a+5\)有最大值\(2\)，求实数\(a\)的值．
 
 
 

参考答案

1. 答案 \(a=-\dfrac{4}{3}\)或 \(a=\dfrac{3+\sqrt{21}}{2}\)．
   解析 \(y=-\sin ^2⁡x+a\sin ⁡x-a^2+2a+6\)，令\(\sin ⁡x=t\),\(t∈[-1,1]\)，
   则\(y=-t^2+at-a^2+2a+6\)，对称轴为\(t=\dfrac{a}{2}\)，
   当\(\dfrac{a}{2}<-1\)，即\(a<-2\)时，\([-1,1]\)是函数\(y\)的递减区间， \(y_{\max }=\left.y\right|_{t=-1}=-a^2+a+5=2 \text {, }\)，
   得 \(a^2-a-3=0\), \(a=\dfrac{1 \pm \sqrt{13}}{2}\)与\(a<-2\)矛盾；
   当\(\dfrac{a}{2}>1\)，即\(a>2\)时，\([-1,1]\)是函数\(y\)的递增区间， \(y_{\max }=\left.y\right|_{t=-1}=-a^2+a+5=2\)，
   得\(a^2-3a-3=0\), \(a=\dfrac{3 \pm \sqrt{21}}{2}\)，
   而\(a>2\)，即 \(a=\dfrac{3 + \sqrt{21}}{2}\)；
   当\(-1≤\dfrac{a}{2}≤1\) ，即\(-2≤a≤2\)时， \(y_{\max }=\left.y\right|_{t=\dfrac{a}{2}}=-\dfrac{3}{4} a^2+2 a+6=2\)，
   得\(3a^2-8a-16=0\)，\(a=4\)或\(a=-\dfrac{4}{3}\)，
   而\(-2≤a≤2\)，即\(a=-\dfrac{4}{3}\)；
   \(∴a=-\dfrac{4}{3}\)或 \(a=\dfrac{3+\sqrt{21}}{2}\)．