5.1.1 任意角
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步巩固,难度2颗星!
基础知识
角的定义与分类
(1) 角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.
如下图,一条射线的端点是\(O\),从起始位置\(OA\)按逆时针旋转到终止位置\(OB\),
形成角\(α\),射线\(OA\) ,\(OB\)分别是角\(α\)的始边和终边.
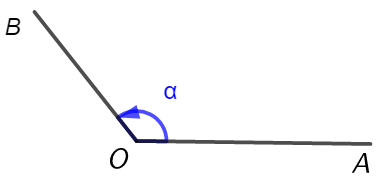
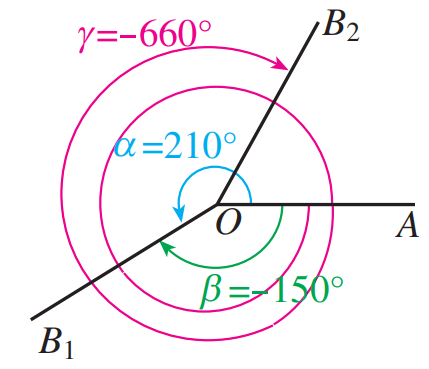
(2) 逆时针旋转为正角,顺时针旋转为负角,不旋转为零角.
如下图 \(α=210^{\circ}\) ,\(β=-150^{\circ}\),\(γ=-660^{\circ}\).
象限角的概念
(1) 角\(α\)的顶点与原点重合,角的始边与\(x\)轴的非负半轴重合,终边落在第几象限,则称\(α\)为第几象限角.
注 \(α\)终边落在坐标轴上,不能称\(α\)为象限角.
【例】 \(570^{\circ}\)、\(-350^{\circ}\)是第几象限角?
解析 \(570^{\circ}\)是第三象限角,\(-350^{\circ}\)是第一象限角.
(2) 角度的加减
角度的加减与实数的加减差不多.
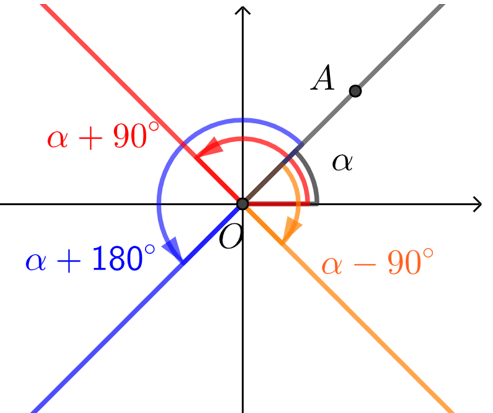
【例】 在直角坐标系中,\(α\)是个锐角,那\(α+90^{\circ}\)、\(α-90^{\circ}\)、\(α-180^{\circ}\)是第几象限角?
解析 \(α\)是锐角,则终边\(OA\)落在第一象限,
那\(α+90^{\circ}\)的终边把\(OA\)逆时针旋转\(90°\)落在第二象限,故\(α+90°\)是第二象限.
同理\(α-90^{\circ}\)是第四象限,\(α-180^{\circ}\)是第三象限.
终边相等的角
与角\(α\)终边相同的角的集合为\(\{β |β=α+k⋅ 360^∘ ,k∈ Z\}\).
注 表达式中的\(k∈ Z\)不能漏!
【例】 求与角\(30^{\circ}\)、\(-370^{\circ}\)终边相同的角的集合.
解析 与角\(30^{\circ}\)终边相同的角的集合为\(\{α |α=30°+k⋅ 360^∘ ,k∈ Z\}\);
与角\(-370^{\circ}\)终边相同的角的集合为\(\{α|α=-10°+k⋅ 360^∘,k∈ Z\}\).
基本方法
【题型1】角的概念
【典题1】从\(13:00\)到\(14:00\),时针转过的角为\(\underline{\quad \quad}\),分针转过的角为\(\underline{\quad \quad}\).
解析 从\(13:00\)到\(14:00\),经过一个小时,时针顺时针旋转\(30^{\circ}\),分针顺时针旋转\(360^{\circ}\),
结合负角的定义可知,时针转过的角为\(-30^{\circ}\),分针转过的角为\(-360^{\circ}\).
故答案为:\(-30^{\circ}\);\(-360^{\circ}\).
【典题2】下列命题:
①第一象限角是锐角;
②锐角都是第一象限角;
③第一象限角一定不是负角;
④第二象限角大于第一象限角;
⑤第二象限角是钝角;
⑥三角形内角是第一、第二象限的角;
⑦向左转体\(1\)周形成的角为\(360^{\circ}\).
其中是真命题的为\(\underline{\quad \quad}\) (把正确命题的序号都写上).
解析 ①\(390^{\circ}\)是第一象限角,可它不是锐角,所以①不正确;
②锐角是大于\(0^{\circ}\)且小于\(90^{\circ}\)的角,终边落在第一象限,故是第一象限角,所以②正确;
③\(-330^{\circ}\)是第一象限角,但它是负角,所以③不正确;
④\(120^{\circ}\)角是第二象限角,\(390^{\circ}\)角是第一象限角,显然\(390^{\circ}>120^{\circ}\),所以④不正确;
⑤\(480^{\circ}\)角是第二象限角,但它不是钝角,所以⑤不正确;
⑥\(90^{\circ}\)角可作三角形内角,但它既不是第一象限角,也不是第二象限角,所以⑥不正确;
⑦向左转体为逆时针旋转,所以转体\(1\)周形成的角为\(360^{\circ}\),所以⑦正确.
故填②⑦.
点拨 考核角的概念理解,判断假命题可举反例.
巩固练习
1.\(α\)是一个任意角,则\(α\)与\(-α\)的终边是( )
A.关于坐标原点对称 \(\qquad \qquad\) B.关于\(x\)轴对称 \(\qquad \qquad\) C.关于直线\(y=x\)对称 \(\qquad \qquad\) D.关于\(y\)轴对称
2.若\(α\)是第二象限角,则\(180^{\circ}-α\)是( )
A.第一象限角 \(\qquad \qquad \qquad\) B.第二象限角 \(\qquad \qquad \qquad\) C.第三象限角 \(\qquad \qquad \qquad\) D.第四象限角
3.下列说法正确的是( )
A.第二象限角大于第一象限角
B.不相等的角终边可以相同
C.若\(α\)是第二象限角,\(2α\)一定是第四象限角
D.终边在\(x\)轴正半轴上的角是零角
4.已知集合\(M=\{\)锐角\(\}\),\(N=\{\)小于\(90^∘\)的角\(\}\),\(P=\{\)第一象限的角\(\}\),下列说法:
①\(P⊆N\) , ② \(N∩P=M\) , ③ \(M⊆P\), ④\((M∪N)⊆P\).
其中正确的是\(\underline{\quad \quad}\).
参考答案
-
答案 \(B\)
-
答案 \(A\)
解析 不妨令\(\alpha=135^{\circ}\),则\(180^{\circ}-135^{\circ}=45^{\circ}\),为第一象限角,故选:\(A\). -
答案 \(B\)
解析 \(A\)选项,第一象限角\(390^{\circ}>120^{\circ}\),而\(120^{\circ}\)是第二象限角,∴该选项错误;\(B\)选项,\(360^{\circ}+30^{\circ}\)与\(30^{\circ}\)终边相等,但它们不相等,∴该选项正确;
\(C\)选项,若\(α\)是第二象限角,则\(360^{\circ} k+90^{\circ}<\alpha<360^{\circ} k+180^{\circ}(k \in Z)\),
\(\therefore 720^{\circ} k+180^{\circ}<2 \alpha<720^{\circ} k+360^{\circ}(k \in \boldsymbol{Z})\)是第三象限角或第四象限角或终边在\(y\)轴负半轴上的轴线角,
\(∴\)该选项错误;
\(D\)选项,\(360^{\circ}\)角的终边在\(x\)轴正半轴上,但不是零角,\(∴\)该选项错误.
故选:\(B\). -
答案 ③
解析 锐角的范围为\(0°<θ<90^∘\),小于\(90^∘\)角为\(θ<90^∘\)包含负角.
第一象限角为\(k\cdot 360^∘<θ<k\cdot360^∘+90^∘\),\(k∈Z\),
\(∴P\)与\(N\)之间没有包含的关系,故①错;
\(-300^{\circ} \in N \cap P\),但 \(-300^{\circ} \notin M\),故②错;
\(M∪N=N\),不一定包含于\(P\),故④错;③\(M⊆P\)对.
∴其中正确的是:③
【题型2】终边相同的角的问题
【典题1】 与\(-2014^{\circ}\)终边相同的最大负角是\(\underline{\quad \quad}\).
解析 \(∵-2014^{\circ}=-6×360^{\circ}+146^{\circ}\),
\(∴-2014^{\circ}\)终与\(146^{\circ}\)终边相同,
\(∴\)与\(-2014^{\circ}\)终边相同的角为\(\{α|146^{\circ}+k⋅360^{\circ}\}\),
当\(k=-1\),得到与\(-2014^{\circ}\)终边相同的最大负角\(146^{\circ}-360^{\circ}=-214^{\circ}\),
故答案为:\(-214^{\circ}\).
【典题2】写出角的终边在下图中阴影区域内角的集合(包括边界)

解析 (1) \(\{α| 45^∘ +k⋅360^∘≤α≤ 90^∘+k⋅360^∘,k∈ Z\}\)\(∪
\{α|180^∘+k⋅360^∘≤ α≤ 225^∘+k⋅360^∘,k∈ Z\}\);
(2) \(\{α | 90^∘+k⋅ 360≤α≤ 150^∘+k⋅ 360^∘,k∈ Z\}\)\(∪
\{α | 240^∘+k⋅ 360^∘≤α≤ 360^∘+k⋅ 360^∘,k∈ Z\}\);
(3) \(\{α|k⋅ 90^∘≤ α≤ 45^∘+k⋅ 90^∘,k∈ Z\}\).
巩固练习
1.与\(405^{\circ}\)角终边相同的角是( )
A.\(k·360^{\circ}-45^{\circ}\),\(k∈Z\) \(\qquad \qquad \qquad \qquad\) B.\(k·360^{\circ}±405^{\circ}\),\(k∈Z\) \(\qquad \qquad\)
C.\(k·360^{\circ}+45^{\circ}\),\(k∈Z\) \(\qquad \qquad \qquad \qquad\) D.\(k·180^{\circ}+45^{\circ}\),\(k∈Z\)
2.若角\(α\)与\(β\)的终边相同,则角\(α-β\)的终边( )
A.在\(x\)轴的非负半轴上 \(\qquad \qquad \qquad \qquad\) B.在\(x\)轴的非正半轴上
C.在\(y\)轴的非正半轴上 \(\qquad \qquad \qquad \qquad\) D.在\(y\)轴的非负半轴上
3.设角\(α\)和\(β\)的终边关于\(y\)轴对称,则有( )
A.\(α=90^{\circ}-β(k∈Z)\) \(\qquad \qquad \qquad \qquad\) B. \(\alpha=\left(2 k+\dfrac{1}{2}\right) \cdot 180^{\circ}-\beta(k \in \boldsymbol{Z})\)
C.\(α=360^{\circ}-β(k∈Z)\) \(\qquad \qquad \qquad \qquad\) D.\(α=(2k+1)\cdot 180^{\circ}-β(k∈Z)\)
4.用弧度制表示顶点在原点,始边重合于\(x\)轴的非负半轴,终边落在阴影部分内的角的集合(包括边界,如图所示).

参考答案
-
答案 \(C\)
解析 \(∵405^{\circ}=360^{\circ}+45^{\circ}\),是与\(45^{\circ}\)角终边相同的角,
即与\(405^{\circ}\)角终边相同的 角是\(k·360^{\circ}+45^{\circ}\),故选\(C\). -
答案 \(A\)
解析 由已知可得\(α=β+k·360^{\circ}(k∈Z)\),
\(∴α-β=k·360^{\circ}(k∈Z)\),\(∴α-β\)的终边在\(x\)轴的非负半轴上. -
答案 \(D\)
解析 由\(180^{\circ}-α\)与\(α\)的终边是关于\(y\)轴对称的两个角,
\(∴β\)与\(180^{\circ}-α\)的终边相同,即\(β=k\cdot360^{\circ}+(180^{\circ}-α)\)
\(∴α+β=α+k\cdot360^{\circ}+(180^{\circ}-α)=(2k+1)\cdot180^{\circ}\),\(k∈Z\);
\(∴α=(2k+1)\cdot180^{\circ}-β\),\(k∈Z\).
故选:\(D\). -
答案 (1) \(\left\{a \mid k \cdot 360^{\circ}-30^{\circ} \leq a \leq k \cdot 360^{\circ}+75^{\circ}, k \in \mathbf{Z}\right\}\);
(2) \(\left\{a \mid k \cdot 180^{\circ}+30^{\circ} \leq a \leq k \cdot 180^{\circ}+90^{\circ}, k \in \mathbf{Z}\right\}\).
【题型3】象限角
【典题1】 若\(α\)是第三象限的角,则\(\dfrac{\alpha}{3}\)可能是第\(\underline{\quad \quad}\)象限角.
解析 方法1 不等式法
\(∵α\)是第三象限角,即\(k \cdot 360^{\circ}+180^{\circ}<\alpha<k \cdot 360^{\circ}+270^{\circ}\) ,\(k∈Z\).
\(k \cdot 120^{\circ}+60^{\circ} \leq \dfrac{\alpha}{3} \leq k \cdot 120^{\circ}+90^{\circ}\),(以下对\(k\)被\(3\)除的余数分类讨论)
当\(k=3n\) ,\(n∈Z\)时,\(\dfrac{\alpha}{3} \in\left(n \cdot 360^{\circ}+60^{\circ}, n \cdot 360^{\circ}+90^{\circ}\right)\),\(\dfrac{\alpha}{3}\)为第一象限角;
当\(k=3n+1\) ,\(n∈Z\)时, \(\dfrac{\alpha}{3} \in\left(n \cdot 360^{\circ}+180^{\circ}, n \cdot 360^{\circ}+210^{\circ}\right)\), \(\dfrac{\alpha}{3}\)为第三象限角.
当\(k=3n+2\) ,\(n∈Z\)时, \(\dfrac{\alpha}{3} \in\left(n \cdot 360^{\circ}+300^{\circ}, n \cdot 360^{\circ}+330^{\circ}\right)\), \(\dfrac{\alpha}{3}\)为第四象限角.
所以\(\dfrac{\alpha}{3}\)可能是第一、三、四象限角.
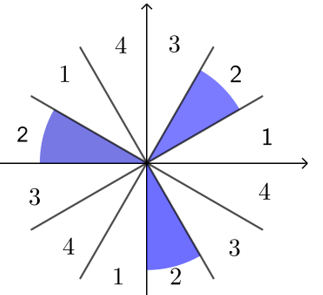
方法2 八卦图法
先把直角坐标系每个象限平均分成\(3\)份,从\(x\)轴正半轴上方各区域标上\(1、2、3、4\),找到标有\(α\)所在象限
数字\(“3”\)所在的区域,该区域在哪个象限,则\(\dfrac{\alpha}{3}\)的终边就在哪个象限.
故\(\dfrac{\alpha}{3}\)可能是第一、三、四象限角.
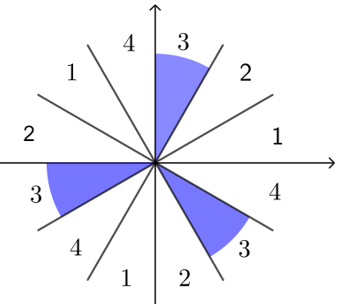
点拨
1 方法\(1\)中令\(k=3n\)、\(3n+1\)、\(3n+2\) ,\(n∈Z\),是从\(3\)的余数\(“0、1、2”\)角度思考,故也可令\(k=0\)、\(1\)、\(2\).
2 方法\(2\)中的解题套路
判断\(\dfrac{\alpha}{n}\)的象限
① 每个象限平分\(n\)份;② 从\(x\)轴上方逆时针开始标数;③ 找到\(α\)所在象限数字.
例:判断\(\dfrac{\alpha}{3}\)的象限(\(α\)是第二象限的角)
① 每个象限平分\(3\)份; ② 从\(x\)轴上方逆时针开始标数; ③ 找到\(α\)所在象限数字\(“2”\).
巩固练习
1.\(-870°\)的终边在第几象限( )
A.一 \(\qquad \qquad \qquad \qquad\) B.二 \(\qquad \qquad \qquad \qquad\) C.三 \(\qquad \qquad \qquad \qquad\) D.四
2.已知\(α\)是第二象限角,则\(\dfrac{\alpha}{2}\)是( )
A.锐角 \(\qquad \qquad\) B.第一象限角 \(\qquad \qquad\) C.第一、三象限角 \(\qquad \qquad\) D.第二、四象限角
3.若\(α\)是第三象限角,判断\(2α\),\(\dfrac{\alpha}{3}\)和\(180^{\circ}-α\)是第几象限角.
参考答案
-
答案 \(C\)
解析 因为\(-870^{\circ}=-2×360^{\circ}-150^{\circ}\).\(-150^{\circ}\)是第三象限角. -
答案 \(C\)
解析 \(∵α\)是第二象限角,所以\(90^{\circ}+k \cdot 360^{\circ}<\alpha<180^{\circ}+k \cdot 360^{\circ}\),\(k∈Z\),
\(\therefore 45^{\circ}+k \cdot 180^{\circ}<\dfrac{\alpha}{2}<90^{\circ}+k \cdot 180^{\circ}\),\(k∈Z\),
\(∴\dfrac{\alpha}{2}\)是第一象限或第三象限角,
故选:\(C\). -
答案 \(2α\)是第一、二象限角,或终边在\(y\)轴的非负半轴上的角;
\(\dfrac{\alpha}{3}\)为第一或第三或第四象限角;\(180^{\circ}-α\)是第四象限角
解析 \(∵α\)是第三象限角,
\(∴180^{\circ}+k·360^{\circ}<α<270^{\circ}+k·360^{\circ}(k∈Z)\),
(1)\(360^{\circ}+2k·360^{\circ}<2α<540^{\circ}+2k·360^{\circ}(k∈Z)\),
即\((2k+1)·360^{\circ}<2α<180^{\circ}+(2k+1)·360^{\circ}(k∈Z)\),
则\(2α\)是第一、二象限角,或终边在\(y\)轴的非负半轴上的角.
(2) \(60^{\circ}+k \cdot 120^{\circ}<\dfrac{\alpha}{3}<90^{\circ}+k \cdot 120^{\circ}(k \in Z)\),
当\(k=3m(m∈Z)\)时 ,\(\dfrac{\alpha}{3}\)为第一象限角;
当\(k=3m+1(m∈Z)\)时,\(\dfrac{\alpha}{3}\)为第三象限角;
当\(k=3m+2(m∈Z)\)时,\(\dfrac{\alpha}{3}\)为第四象限角.
所以\(\dfrac{\alpha}{3}\)为第一或第三或第四象限角.
(3)\(-270^{\circ}+k·360^{\circ}<-α<-180^{\circ}+k·360^{\circ}(k∈Z)\),
则\(-90^{\circ}+k·360^{\circ}<180^{\circ}-α<k·360^{\circ}(k∈Z)\).
所以\(180^{\circ}-α\)是第四象限角.
分层练习
【A组---基础题】
1.手表时针走过\(2\)小时,转过的角度为( )
A. \(60^{\circ}\) \(\qquad \qquad \qquad \qquad\) B.\(-60^{\circ}\) \(\qquad \qquad \qquad \qquad\) C. \(30^{\circ}\) \(\qquad \qquad \qquad \qquad\) D.\(-30^{\circ}\)
2.下列说法正确的是( )
A.终边相同的角相等 \(\qquad \qquad \qquad \qquad \qquad\) B.相等的角终边相同
C.小于\(90^{\circ}\)的角是锐角 \(\qquad \qquad \qquad \qquad\) D.第一象限的角是正角
3.下列叙述正确的是( )
A.第一或第二象限的角都可作为三角形的内角 \(\qquad \qquad\) B.始边相同而终边不同的角一定不相等
C.第四象限角一定是负角 \(\qquad \qquad \qquad \qquad \qquad \qquad\) D.钝角比第三象限角小
4.下列各角中与角\(390^{\circ}\)终边相同的是( )
A.\(k\cdot180^{\circ}+30^{\circ}\),\(k∈Z\) \(\qquad \qquad \qquad \qquad \qquad\) B.\(k\cdot360^{\circ}+30^{\circ}\),\(k∈Z\)
C.\(k\cdot180^{\circ}-30^{\circ}\),\(k∈Z\) \(\qquad \qquad \qquad \qquad \qquad\) D.\(k\cdot360^{\circ}-30^{\circ}\),\(k∈Z\)
5.下列命题正确的是( )
A.\(-330^{\circ}\)与\(330^{\circ}\)都是第四象限角 \(\qquad \qquad\) B.\(45^{\circ}\)角是按顺时针方向旋转形成的
C.钝角都是第二象限角 \(\qquad \qquad \qquad \qquad \qquad\) D.小于\(90^{\circ}\)的角都是锐角
6.已知\(α\)是锐角,那么\(2α\)是( )
A.第一象限角 \(\qquad \qquad\) B.第二象限角 \(\qquad \qquad\) C.小于\(180°\)的正角 \(\qquad \qquad\) D.不大于直角的正角
7.若集合\(M=\{x|x=k·90^{\circ}+45^{\circ},k∈Z\}\),\(N=\{x|x=k·45^{\circ}+90^{\circ},k∈Z\}\),则\(M\)\(\underline{\quad \quad}\) \(N\) (填\(“⊆”\)或\(“⊇”\))
8.在\(0°~360°\)范围内:与\(-1000°\)角终边相同的最小正角是\(\underline{\quad \quad}\),是第\(\underline{\quad \quad}\)象限角.
9.写出与\(15^{\circ}\)角终边相同的角的集合,并求该集合中适合不等式\(-1080^{\circ}≤β<720^{\circ}\)的元素\(β\).
10.已知角\(α=2012^{\circ}\).
(1)把\(α\)改写成\(k·360^{\circ}+β(k∈Z,0^{\circ}≤β<360^{\circ})\)的形式,并指出它是第几象限角;
(2)求\(θ\),使\(θ\)与\(α\)终边相同,且\(-360°≤θ<720°\).
11.如图所示,试分别表示出终边落在阴影区域内的角.

参考答案
-
答案 \(B\)
-
答案 \(B\)
解析 终边相同的角相差周角的整数倍,\(A\)不正确;相等的角终边一定相同;
所以\(B\)正确;小于\(90°\)的角是锐角可以是负角;第一象限的角是正角,也可以是负角.故选:\(B\). -
答案 \(D\)
解析 \(-330°\)角是第一象限角,但不能作为三角形的内角,故\(A\)错;
\(280^{\circ}\)角是第四象限角,它是正角,故\(C\)错;\(-100^{\circ}\)角是第三象限角,它比钝角小,故\(D\)错. -
答案 \(B\)
解析 \(∵390^{\circ}=360^{\circ}+30^{\circ}\),\(∴\)与\(390^{\circ}\)终边相同的是\(k\cdot360^{\circ}+30^{\circ}\),\(k∈Z\).故选:\(B\). -
答案 \(C\)
解析 对于\(A\),\(-330^{\circ}\)是第一象限角,故\(A\)排除;
对于\(B\),\(45^{\circ}\)角是正角,按逆时针旋转形成的,故排除\(B\);
对于\(D\),\(-60^{\circ}\)角是小于\(90^{\circ}\)的角,但它不是锐角,故排除\(D\).
综上,此题应选\(C\). -
答案 \(C\)
解析 \(∵α\)是锐角,即 \(0<\alpha<90^{\circ}\),\(∴0<2α<180^{\circ}\),
\(2α\)是小于\(180^{\circ}\)的正角,故选:\(C\). -
答案 \(⊆\)
解析 \(M=\{x|x=k·90^{\circ}+45^{\circ},k∈Z\}=\{x|x=4 5^{\circ}·(2k+1),k∈Z\}\),
\(N=\{x|x=k·45^{\circ}+90^{\circ},k∈Z\}=\{x|x=45^{\circ}·(k+2),k∈Z \}\),
\(∵k∈Z\),\(∴k+2∈Z\)且\(2k+1\)为奇数,\(∴M⊆N\). -
答案 \(80°\),一
解析 \(-1 000^{\circ}=-3×36^{\circ}+80^{\circ}\),
\(∴\)与\(-1 000^{\circ}\)角终边相同的最小正角是\(80^{\circ}\),为第一象限角. -
答案 \(\{β|β=15^{\circ}+k·360^{\circ},k∈Z\}\),\(-1 065^{\circ}\),\(-705^{\circ}\),\(-345^{\circ}\),\(15^{\circ}\),\(375^{\circ}\).
解析 与\(15^{\circ}\)角终边相同的角的集合为\(\{β|β=15^{\circ}+k·360^{\circ},k∈Z\}\).
由\(-1080^{\circ}≤15^{\circ}+k·360^{\circ}<720^{\circ}\),得到\(-1095^{\circ}≤k·360^{\circ}<705^{\circ}\).
又\(k∈Z\),\(∴k\)可取\(-3,-2,-1,0,1\).
相应的\(β\)的值分别为\(-1 065^{\circ}\),\(-705^{\circ}\),\(-345^{\circ}\),\(15^{\circ}\),\(375^{\circ}\).
\(∴\)满足条件的角\(β\)的度数有\(-1 065^{\circ}\),\(-705^{\circ}\),\(-345^{\circ}\),\(15^{\circ}\),\(375^{\circ}\). -
答案 (1) \(α=5×360^{\circ}+212^{\circ}\),第三象限角;(2)\(-148^{\circ}\),\(212^{\circ}\),\(572^{\circ}\)
解析 (1)用\(2012^{\circ}\)除以\(360^{\circ}\)商为\(5\),
余数为\(212^{\circ}\).\(∴k=5\).
\(∴α=5×360^{\circ}+212^{\circ}\).
\(∴α\)为第三象限角.
(2)与\(2012^{\circ}\)终边相同的角为\(k·360^{\circ}+2012^{\circ}(k∈Z)\),
令\(-360^{\circ}≤k·360^{\circ}+2012^{\circ}<720^{\circ}(k∈Z)\),
解得\(-\dfrac{593}{90} \leq k<-\dfrac{323}{90}(k \in \mathrm{Z})\),\(∴k=-6\),\(-5\),\(-4\).
将\(k\)的值代入\(k·360^{\circ}+2012^{\circ}\)中,得角\(θ\)的值为\(-148^{\circ}\),\(212^{\circ}\),\(572^{\circ}\). -
答案 (1) \(\{α|45^{\circ}+k·360^{\circ}≤α≤210^{\circ}+k·360^{\circ},k∈Z\}\)
(2) \(\{α|-45^{\circ}+k·360^{\circ}≤α≤45^{\circ}+k·360^{\circ},k∈Z\}\)
解析 在图(1)中,\(0^{\circ}~360^{\circ}\)范围内的终边落在 指定区域的角\(α\)满足\(45^{\circ}≤α≤210^{\circ}\),
故满足条件的角的集合为\(\{α|45^{\circ}+k·360^{\circ}≤α≤210^{\circ}+k·360^{\circ},k∈Z\}\).
在图(2)中,\(0^{\circ}~ 360^{\circ}\)范围内的终边落在指定区域的角\(α\)满足\(0^{\circ}≤α≤45^{\circ}\)或\(315^{\circ}≤α≤360^{\circ}\),
转化为\(-180^{\circ}~180^{\circ}\)范围内,终边落在指定区域的角\(α\)满足\(-45^{\circ}≤α≤45^{\circ}\),
故满足条件的角的集合为\(\{α|-45^{\circ}+k·360^{\circ}≤α≤45^{\circ}+k·360^{\circ},k∈Z\}\).
【B组---提高题】
1.设集合\(A=\left\{\alpha \mid \alpha=90^{\circ}+k \cdot 180^{\circ}, k \in Z\right\} \cup\left\{\alpha \mid \alpha=k \cdot 180^{\circ}, k \in Z\right\}\),集合\(B=\left\{\beta \mid \beta=k \cdot 90^{\circ}, k \in Z\right\}\),则( )
A. \(A⊆B\) \(\qquad \qquad \qquad \qquad\) B.\(B⊆A\) \(\qquad \qquad \qquad \qquad\) C. \(A∩B=0\) \(\qquad \qquad \qquad \qquad\) D.\(A=B\)
2.已知\(α=60^{\circ}\),回答下列问题.
(1)写出所有与\(α\)终边相同的角;
(2)写出在\((-720^{\circ},360^{\circ})\)内与\(α\)终边相同的角;
(3)若角\(β\)与\(α\)终边相同,则\(\dfrac{\beta}{2}\)是第几象限的角?
参考答案
-
答案 \(D\)
解析 由于\(A=\left\{\alpha \mid \alpha=90^{\circ}+k \cdot 180^{\circ}, k \in Z\right\} \cup\left\{\alpha \mid \alpha=k \cdot 180^{\circ}, k \in Z\right\}\)\(=\left\{\alpha \mid \alpha=(2 k+1) \cdot 90^{\circ}, k \in Z\right\} \cup\left\{\alpha \mid \alpha=2 k \cdot 90^{\circ}, k \in Z\right\}\)\(=\left\{\alpha \mid \alpha=k \cdot 90^{\circ}, k \in Z\right\} =\left\{\beta \mid \beta=k \cdot 90^{\circ}, k \in Z\right\}=B\),
故选:\(D\). -
答案 (1) \(\{θ∣θ=k·360^{\circ}+60^{\circ},k∈Z\}\) (2) \(-660^{\circ},-300^{\circ}, 60^{\circ}\). (3) 第一、三象限角
解析 (1)所有与\(α\)终边相同的角可表示为\(\{θ∣θ=k·360^{\circ}+60^{\circ},k∈Z\}\).
(2)由(1)令\(-720^{\circ}<k·360^{\circ}+60^{\circ}<360^{\circ}(k∈Z)\),则有 \(-\dfrac{13}{6}<k<\dfrac{5}{6}\),
\(∵k∈Z\),\(∴\)取\(k=-2、-1、0\).
故在\((-720^{\circ},360^{\circ})\)内与\(α\)终边相同的角是\(-660^{\circ},-300^{\circ}, 60^{\circ}\).
(3)由(1)有\(β=k·360^{\circ}+60^{\circ}(k∈Z)\),则\(\dfrac{\beta}{2}=k\cdot180^{\circ}+30^{\circ}(k∈Z)\).
\(∴\dfrac{\beta}{2}\)是第一、三象限的角.
【C组---拓展题】
1.我们知道当\(12\)点时,闹钟的\(3\)个指针完全重合,请说出除了\(12\)点外,是否还有其他时间,\(3\)针完全重合.
如有请举出;若无,给出理由.
参考答案
- 答案 不可能
解析 每小时时针、分针旋转一次,速度为时针\(0.5^{\circ} / \min\),分针\(6^{\circ} / \min\),相差\(5.5^{\circ} / \min\),
故在\(n\)时\(00\)分至\((n+1)\)时\(00\)分之间,时针和分针完全重合的时刻为\(n\)时\(\dfrac{60 n}{11}\)分,它们是:
1时5分27.27秒 \(\qquad\) 2时10分54.54秒 \(\qquad\) 3时16分21.82秒 \(\qquad\) 4时21分49.09秒
5时27分16.36秒 \(\qquad\) 6时32分43.64秒 \(\qquad\) 7时38分10.91秒 \(\qquad\) 8时43分38.18秒
9时49分5.45秒 \(\qquad\) 10时54分32.73秒 \(\qquad\) 12时00分00秒
这些时刻里除了\(12\)时外,“分”和“秒“的值相差都很大,分针和秒针显然不可能重合.所以仅在\(12\)时三针重合.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号