3.3.2 抛物线的简单几何性质(2)
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高二数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性必修第一册同步巩固,难度3颗星!
基础知识
直线与抛物线的位置关系
设直线\(l:Ax+By+C=0\),抛物线\(C:f(x,y)=0\),把两者方程联立得到方程组,消元\(y\)(或\(x\))得到一个关于\(x\)(或\(y\))的方程\(ax^2+bx+c=0\)(或\(ay^2+by+c=0\)).
① 当\(a≠0\)时,
\(∆>0⇔\)方程有两个不同的实数解,即直线与抛物线有两个交点\(⇔\)相交;
\(∆=0⇔\)方程有两个相同的实数解,即直线与抛物线有一个交点\(⇔\)相切;
\(∆<0⇔\)方程无实数解,即直线与抛物线无交点\(⇔\)相离.
② 当\(a=0\),\(b≠0\)时,即得到一个一次方程,则直线\(l\)与抛物线\(C\)相交,且只有一个交点,直线\(l\)与抛物线的对称轴的位置关系是平行.
【例】直线\(y=kx+2\)与抛物线\(y^2=8x\)只有一个公共点,则\(k\)的值为\(\underline{\quad \quad}\) .
解析 联立 \(\left\{\begin{array}{l}
y=k x+2 \\
y^2=8 x
\end{array}\right.\)得\((kx+2)^2-8x=0\).
整理得\(k^2 x^2+(4k-8)x+4=0\).
当\(k=0\)时,方程变为\(-8x+4=0\),只有一解,这时直线与抛物线只有一个公共点;
当\(k≠0\)时,由\(Δ=0\)得 \((4k-8)^2-16k^2=0\),解得\(k=1\).
综上,\(k=0\)或\(1\).
直线与抛物线的弦长公式
(1)直线\(y=kx+b\)与抛物线相交于\(A(x_1,y_1 )\),\(B(x_2,y_2)\),则
\(A B=\sqrt{1+k^2} \cdot\left|x_1-x_2\right|=\sqrt{1+k^2} \cdot \sqrt{\left(x_1+x_2\right)^2-4 x_1 x_2}=\sqrt{1+k^2} \cdot \dfrac{\sqrt{\Delta}}{|a|}\)
或
\(A B=\sqrt{1+\dfrac{1}{k^2}} \cdot\left|y_1-y_2\right|=\sqrt{1+\dfrac{1}{k^2}} \cdot \sqrt{\left(y_1+y_2\right)^2-4 y_1 y_2}=\sqrt{1+\dfrac{1}{k^2}} \cdot \dfrac{\sqrt{\Delta}}{|a|}\),
(\(∆=b^2-4ac\),注意对公式推导的理解,其本质是两点距离公式)
(2) 抛物线\(y^2=2px(p>0)\)的焦点弦长 \(|A B|=x_1+x_2+p=\dfrac{2 p}{\sin ^2 \theta}\) ,
\(θ\)为弦\(AB\)所在直线的倾斜角.(其他形式的抛物线类似)
抛物线常见的结论
(选学内容,证明可见另一专题《圆锥曲线常见二级结论》)
点\(F\)是抛物线\(y^2=2px(p>0)\)的焦点,过焦点的直线与抛物线交于\(A\)、\(B\),点\(A\)、\(B\)在准线上的投影分别是\(A_1\) 、\(B_1\),有如下结论
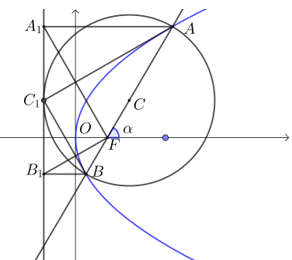
(1) \(x_1 x_2=\dfrac{p^2}{4}\), \(y_1 y_2=-p^2\);
(2) \(A\)、\(O\)、\(B_1\)三点共线;\(B\)、\(O\)、\(A_1\)三点共线;
(3) \(AC_1\) 垂直平分\(A_1 F\);\(BC_1\)垂直平分\(B_1 F\);
(4) \(AB=x_1+x_2+p\);
(5) 以\(AB\)为直径的圆与准线\(l\)相切;
(6) \(∠AC_1 B=90^∘\),\(∠A_1 FB_1=90^∘\);
(7) \(A F=\dfrac{p}{1-\cos \alpha}\), \(B F=\dfrac{p}{1+\cos \alpha}\); \(A B=\dfrac{2 p}{\sin ^2 \alpha}\) ; \(\dfrac{1}{A F}+\dfrac{1}{B F}=\dfrac{2}{p}\);
(8) \(S_{\triangle A O B}=\dfrac{p^2}{2 \sin \alpha} ; \quad \dfrac{S_{\triangle A O B}^2}{A B}=\left(\dfrac{p}{2}\right)^3\);
(9) 切线方程\(y_0 y=p(x+x_0)\).
基本方法
【题型1】直线与抛物线的位置关系
【典题1】 已知抛物线\(C:y^2=2px(p>0)\)过点\(A(1,-2)\).
(1)求抛物线\(C\)的方程,并求其准线方程;
(2)是否存在平行于\(OA\)(\(O\)为坐标原点)的直线\(l\),使得直线\(l\)与抛物线\(C\)有公共点,且直线\(OA\)与\(l\)的距离等于\(\dfrac{\sqrt{5}}{5}\)?若存在,求出直线\(l\)的方程;若不存在,说明理由.
解析 (1)将\((1,-2)\)代入\(y^2=2px\),得 \((-2)^2=2p·1\),\(∴p=2\).
故所求的抛物线\(C\)的方程为\(y^2=4x\),其准线方程为\(x=-1\).
(2)假设存在符合题意的直线\(l\),其方程为\(y=-2x+t\).
由 \(\left\{\begin{array}{l}
y=-2 x+t \\
y^2=4 x
\end{array}\right.\)得\(y^2+2y-2t=0\).
\(∵\)直线\(l\)与抛物线\(C\)有公共点,
\(∴Δ=4+8t≥0\),解得 \(t \geq-\dfrac{1}{2}\).
另一方面,由直线\(OA\)与\(l\)的距离 \(d=\dfrac{\sqrt{5}}{5}\),可得\(\dfrac{|t|}{\sqrt{5}}=\dfrac{1}{\sqrt{5}}\),解得\(t=±1\).
\(\because-1 \notin\left[-\dfrac{1}{2},+\infty\right)\), \(1 \in\left[-\dfrac{1}{2},+\infty\right)\),
\(∴\)符合题意的直线\(l\)存在,其方程为\(2x+y-1=0\).
巩固练习
1.过点\((2,4)\)作直线与抛物线\(y^2=8x\)只有一个公共点,这样的直线有\(\underline{\quad \quad}\)条.
2.已知抛物线\(C\)的方程为 \(x^2=\dfrac{1}{2} y\),过点\(A(0,-1)\)和点\(B(t,3)\)的直线与抛物线\(C\)没有公共点,则实数\(t\)的取值范围是\(\underline{\quad \quad}\) .
参考答案
- 答案 \(2\)
解析 点\((2,4)\)在抛物线\(y^2=8x\)上,由图易得满足题意的直线有\(2\)条. - 答案 \((-\infty,-\sqrt{2}) \cup(\sqrt{2},+\infty)\)
解析 如图,设过\(A\)的直线方程为\(y=kx-1\),与抛物线方程联立得 \(x^2-\dfrac{1}{2} k x+\dfrac{1}{2}=0\),
\(\triangle=\dfrac{1}{4} k^2-2=0\), \(k=\pm 2 \sqrt{2}\),求得过\(A\)的抛物线的切线与\(y=3\)的交点为 \((\pm \sqrt{2}, 3)\),
则当过点\(A(0,-1)\)和点\(B(t,3)\)的直线与抛物线\(C\)没有公共点,
实数\(t\)的取值范围是 \((-\infty,-\sqrt{2}) \cup(\sqrt{2},+\infty)\).
【题型2】弦长问题
【典题1】 过抛物线\(x^2=2py(p>0)\)的焦点作斜率为\(1\)的直线与该抛物线交于\(A\),\(B\)两点,\(A\),\(B\)在\(x\)轴上的正射影分别为\(D\),\(C\).若梯形\(ABCD\)的面积为 \(12 \sqrt{2}\),则\(AB=\)\(\underline{\quad \quad}\).
解析 如图,抛物线焦点为 \(\left(0, \dfrac{p}{2}\right)\),

设\(A(x_1,y_1 )\),\(B(x_2,y_2 )\),直线\(A B: y-\dfrac{p}{2}=x\),即 \(y=x+\dfrac{p}{2}\).
联立\(x_2=2py\),得 \(\left\{\begin{array}{l}
y=x+\dfrac{p}{2} \\
x^2=2 p y
\end{array}\right.\)消去\(y\)得 \(x^2-2px-p^2=0\),
\(∴x_1+x_2=2p\),\(x_1 x_2=-p^2\),
\(\therefore|A D|+|B C|=y_1+y_2=x_1+\dfrac{p}{2}+x_2+\dfrac{p}{2}=2 p+p=3 p\),
\(|C D|=\left|x_1-x_2\right|=\sqrt{\left(x_1+x_2\right)^2-4 x_1 x_2}=2 \sqrt{2} p\).
由 \(S_{\text {梯形 } A B C D}=\dfrac{1}{2}(|A D|+|B C|) \cdot|C D|=\dfrac{1}{2} \cdot 3 p \cdot 2 \sqrt{2} p=12 \sqrt{2}\),解得\(p=2\).
则\(AB=y_1+y_2+p=4p=8\).
点拨 对于焦点弦的弦长,可不用弦长公式 \(d=\sqrt{1+k^2} \cdot\left|x_1-x_2\right|\),用抛物线定义\(AB=y_1+y_2+p\)更好些.
【典题2】 已知抛物线\(y^2=6x\)的弦\(AB\)经过点\(P(4,2)\),且\(OA⊥OB\)(\(O\)为坐标原点),求弦\(AB\)的长.
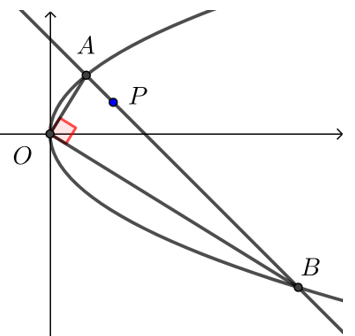
解析 依题意可设直线\(AB\)方程为\(x=my+n\),
因为过点\(P(4,2)\),所以\(n=2-4m\),
联立方程 \(\left\{\begin{array}{c}
x=m y+n \\
y^2=6 x
\end{array}\right.\)得 \(y^2-6my-6n=0\),
设\(A(x_1,y_1)\),\(B(x_2,y_2)\),
则\(y_1+y_2=6m\),\(y_1 y_2=-6n\),
因为\(OA⊥OB\),所以 \(\overrightarrow{O A} \cdot \overrightarrow{O B}=0\),
而 \(\overrightarrow{O A} \cdot \overrightarrow{O B}=x_1 x_2+y_1 y_2=\left(m y_1+n\right)\left(m y_2+n\right)+y_1 y_2\)
\(=(1+m^2 ) y_1 y_2+mn(y_1+y_2 )+n^2=n^2-6n\),
所以\(n^2-6n=0\),解得\(n=6\)或\(n=0\)(舍去),
则\(m=-1\),
所以 \(A B=\sqrt{1+\dfrac{1}{k^2}} \cdot\left|y_1-y_2\right|=\sqrt{1+m^2} \cdot \sqrt{\left(y_1+y_2\right)^2-4 y_1 y_2}\)
\(=\sqrt{1+m^2} \cdot \sqrt{36 m^2+24 n}=\sqrt{2} \cdot \sqrt{180}=6 \sqrt{10}\).
点拨
1.本题解法很多,直线\(AB\)方程的设定需要注意
① 直线\(AB\)方程设为\(x=my+n\),不设为\(y=kx+b\);
首先明白 \(n=\dfrac{1}{k}\),当直线\(AB\)垂直\(x\)轴,\(k\)不存在;当直线\(AB\)垂直\(y\)轴,\(k=0\),则\(m\)不存在;
本题中直线\(AB\)不可能垂直\(y\)轴,否则与抛物线没有两个交点,故直线设\(x=my+n\)不需要分类讨论,而设为\(y=kx+b\)需要讨论\(k\)是否存在;
② 直线\(AB\)过点\(P(4,2)\),不设为\(x=m(y-2)+4\),不代入点\(P(4,2)\)设为\(x=my+n\),这可简化计算,您可尝试下,感受更深刻些;
2 对于垂直关系\(OA⊥OB\),可有 \(k_{O A} \cdot k_{O B}=-1\), \(\overrightarrow{O A} \cdot \overrightarrow{O B}=0\),勾股定理等想法.
巩固练习
1.已知直线\(l\)经过抛物线\(y^2=6x\)的焦点\(F\),且与抛物线相交于\(A\),\(B\)两点.
(1)若直线\(l\)的倾斜角为\(60°\),求\(|AB|\)的值;
(2)若\(|AB|=9\),求线段\(AB\)的中点\(M\)到准线的距离.
2.设离心率为\(3\),实轴长为\(1\)的双曲线 \(E: \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>b>0)\)的左焦点为\(F\),顶点在原点的抛物线\(C\)的准线经过点\(F\),且抛物线\(C\)的焦点在\(x\)轴上.
(1)求抛物线\(C\)的方程;
(2)若直线\(l\)与抛物线\(C\)交于不同的两点\(M\),\(N\),且满足\(OM⊥ON\),求\(|MN|\)的最小值.
参考答案
-
答案 (1) \(8\) (2) \(\dfrac{9}{2}\)
解析 (1)因为直线\(l\)的倾斜角为\(60°\),所以其斜率 \(k=\tan 60^{\circ}=\sqrt{3}\).

又 \(F\left(\dfrac{3}{2}, 0\right)\),所以直线\(l\)的方程为 \(y=\sqrt{3}\left(x-\dfrac{3}{2}\right)\),
联立 \(\left\{\begin{array}{l} y^2=6 x \\ y=\sqrt{3}\left(x-\dfrac{3}{2}\right) \end{array}\right.\),消去\(y\)得 \(x^2-5 x+\dfrac{9}{4}=0\).
设\(A(x_1,y_1 )\),\(B(x_2,y_2 )\),则\(x_1+x_2=5\),
而 \(|A B|=|A F|+|B F|=x_1+\dfrac{p}{2}+x_2+\dfrac{p}{2}=x_1+x_2+p\),
所以\(|AB|=5+3=8\).
(2)设\(A(x_1,y_1 )\),\(B(x_2,y_2 )\),由抛物线定义知
\(|AB|=|AF|+|BF|=x_1+x_2+p=x_1+x_2+3\),
所以\(x_1+x_2=6\),于是线段\(AB\)的中点\(M\)的横坐标是\(3\).
又准线方程是 \(x=-\dfrac{3}{2}\),
所以\(M\)到准线的距离为 \(3+\dfrac{3}{2}=\dfrac{9}{2}\). -
答案 (1) \(y^2=6x\) (2) \(12\)
解析 (1)离心率为\(3\),实轴长为\(1\),即 \(e=\dfrac{c}{a}=3\), \(a=\dfrac{1}{2}\),
可得 \(c=\dfrac{3}{2}\), \(F\left(-\dfrac{3}{2}, 0\right)\),
可设抛物线的方程为\(y^2=2px\),\(p>0\),
可得 \(\dfrac{p}{2}=\dfrac{3}{2}\),即\(p=3\),
可得抛物线的方程为\(y^2=6x\);
(2)设直线\(l\)的方程为\(x=my+t\),设点\(M(x_1,y_1)\)、\(N(x_2,y_2)\),
则 \(x_1=\dfrac{y_1^2}{6}\),\(x_2=\dfrac{y_2^2}{6}\)
将直线\(l\)的方程与抛物线\(C\)的方程联立 \(\left\{\begin{array}{l} x=m y+t \\ y^2=6 x \end{array}\right.\),得 \(y^2-6my-6t=0\),
由韦达定理得\(y_1+y_2=6m\),\(y_1 y_2=-6t\),
\(∵OM⊥ON\), \(\therefore k_{O M} \cdot k_{O N}=\dfrac{6}{y_1} \cdot \dfrac{6}{y_2}=-\dfrac{36}{6 t}=-1\),即\(t=6\),
由\(△=36m^2+24×6>0\)恒成立,
则 \(|M N|=\sqrt{1+m^2} \sqrt{\left(y_1+y_2\right)^2-4 y_1 y_2}=\sqrt{1+m^2} \cdot \sqrt{36 m^2+144}\)
\(=6 \sqrt{\left(1+m^2\right)\left(4+m^2\right)} \geq 12\),
当且仅当\(m=0\)时,\(|MN|\)取得最小值\(12\).
【题型3】综合题型
【典题1】 已知抛物线\(C:y^2=2px(p>0)\),焦点为\(F\),准线为\(l\),抛物线\(C\)上一点\(A\)的横坐标为\(3\),且点\(A\)到焦点的距离为\(4\).
(1)求抛物线的方程;
(2)设过点\(P(6,0)\)的直线\(l\)与抛物线交于\(A\),\(B\)两点,若以\(AB\)为直径的圆过点\(F\),求直线\(l\)的方程.

解析 (1)抛物线\(y^2=2px(p>0)\)的准线方程为 \(x=-\dfrac{p}{2}\),
由抛物线\(C\)上一点\(A\)的横坐标为\(3\),
根据抛物线的定义可知, \(3+\dfrac{p}{2}=4\),解得\(p=2\),
所以抛物线\(C\)的方程是\(y^2=4x\);
(2)由题意可知,直线\(l\)不垂直于\(y\)轴,
可设直线\(l:x=my+6\),
则由 \(\left\{\begin{array}{l}
y^2=4 x \\
x=m y+6
\end{array}\right.\)可得 \(y^2-4my-24=0\),
设\(A(x_1,y_1)\),\(B(x_2,y_2\)),则\(y_1+y_2=4m\),\(y_1 y_2=-24\),
因为以\(AB\)为直径的圆过点\(F\),所以\(FA⊥FB\),即 \(\overrightarrow{F A} \cdot \overrightarrow{F B}=0\),
可得 \((x_1-1)(x_2-1)+y_1 y_2=0\),
即\((my_1+5)(my_2+5)+y_1 y_2=0\)
\(⇒(1+m^2 ) y_1 y_2+5m(y_1+y_2 )+25=0\)
\(⇒-24(1+m^2 )+20m^2+25=0\)
\(⇒1-4m^2=0\),
解得 \(m=\pm \dfrac{1}{2}\),
所以直线 \(l: x=\pm \dfrac{1}{2} y+6\),
即\(l:2x+y-12=0\)或\(2x-y-12=0\).
【典题2】 已知抛物线\(Γ:y^2=2px(p>0)\)的焦点为\(F\),\(P\)是抛物线\(Γ\)上一点,且在第一象限,满足 \(\overrightarrow{FP}=(2,2 \sqrt{3})\),
(1)求抛物线\(Γ\)的方程;
(2)已知经过点\(A(3,-2)\)的直线交抛物线\(Γ\)于\(M\),\(N\)两点,经过定点\(B(3,-6)\)和\(M\)的直线与抛物线\(Γ\)交于另一点\(L\),问直线\(NL\)是否恒过定点,如果过定点,求出该定点,否则说明理由.
解析 (1)由抛物线的方程可得焦点 \(F\left(\dfrac{p}{2}, 0\right)\),满足 \(\overrightarrow{F P}=(2,2 \sqrt{3})\)的\(P\)的坐标为 \(\left(2+\dfrac{p}{2}, 2 \sqrt{3}\right)\),\(P\)在抛物线上,所以 \((2 \sqrt{3})^2=2 p\left(2+\dfrac{p}{2}\right)\),\(p>0\),解得\(p=2\),
所以抛物线的方程为:\(y^2=4x\);
(2)设\(M(x_0,y_0 )\),\(N(x_1,y_1 )\),\(L(x_2,y_2 )\),则 \(y_1^2=4 x_1\),\(y_2^2=4 x_2\)
直线\(MN\)的斜率 \(k_{M N}=\dfrac{y_1-y_0}{x_1-x_0}=\dfrac{y_1-y_0}{\dfrac{y_1^2-y_0^2}{4}}=\dfrac{4}{y_1+y_0}\),
则直线\(MN\)的方程为: \(y-y_0=\dfrac{4}{y_1+y_0}\left(x-\dfrac{y_0^2}{4}\right)\),即\(y=\dfrac{4 x+y_0 y_1}{y_0+y_1}\) ①,
同理可得直线\(ML\)的方程整理可得 \(y=\dfrac{4 x+y_0 y_2}{y_0+y_2}\)②,
将\(A(3,-2)\),\(B(3,-6)\)分别代入①,②的方程可得 \(\left\{\begin{array}{l}
-2=\dfrac{12+y_0 y_1}{y_0+y_1} \\
-6=\dfrac{12+y_0 y_2}{y_0+y_2}
\end{array}\right.\),消\(y_0\)可得\(y_1 y_2=12\),
易知直线 \(k_{N L}=\dfrac{4}{y_1+y_2}\),则直线\(NL\)的方程为: \(y-y_1=\dfrac{4}{y_1+y_2}\left(x-\dfrac{y_1^2}{4}\right)\),
即 \(y=\dfrac{4}{y_1+y_2} x+\dfrac{y_1 y_2}{y_1+y_2}\),故 \(y=\dfrac{4}{y_1+y_2} x+\dfrac{12}{y_1+y_2}\),
所以 \(y=\dfrac{4}{y_1+y_2}(x+3)\),
因此直线\(NL\)恒过定点\((-3,0)\).
巩固练习
1.已知直线 \(l: \sqrt{3} x-y-\sqrt{3}=0\)过抛物线\(C:y^2=2px\)的焦点\(F\),且与抛物线\(C\)交于点\(A\)、\(B\)两点,过\(A\)、\(B\)两点分别作抛物线准线的垂线,垂足分别为\(M\)、\(N\),则下列说法错误的是( )
A.抛物线的方程为\(y^2=4x\) \(\qquad\) B.线段\(AB\)的长度为 \(\dfrac{16}{3}\) \(\qquad\) C.\(∠MFN=90°\) \(\qquad\) D.线段\(AB\)的中点到\(y\)轴的距离为 \(\dfrac{8}{3}\)
2.已知直线\(y=kx+m(k<0)\)与抛物线\(C:y^2=8x\)及其准线分别交于\(A\),\(B\)两点,\(F\)为抛物线的焦点,若 \(2 \overrightarrow{F A}=\overrightarrow{A B}\),则\(m\)等于( )
A. \(\sqrt{3}\) \(\qquad \qquad\) B. \(2\sqrt{3}\) \(\qquad \qquad\) C. \(2\sqrt{2}\) \(\qquad \qquad\) D. \(2\sqrt{6}\)
3.已知直线\(l:kx-y-k=0(k∈R)\)与抛物线 \(C: y^2=2 p x\left(p>\dfrac{1}{2}\right)\)相交于\(A\),\(B\)两点,\(O\)为坐标原点,则\(△AOB\)为( )
A.锐角三角形 \(\qquad \qquad\) B.直角三角形 \(\qquad \qquad\) C.钝角三角形 \(\qquad \qquad\) D.不确定
4.已知抛物线\(y^2=2px(p>0)\)上的点\(T(3,t)\)到焦点\(F\)的距离为\(4\).
(1)求\(t\),\(p\)的值;
(2)设抛物线的准线与\(x\)轴的交点为\(M\),是否存在过点\(M\)的直线\(l\)交抛物线于\(A\),\(B\)两点(点\(B\)在点\(A\)的右侧),使得直线\(AF\)与直线\(OB\)垂直?若存在,求出\(△AFB\)的面积,若不存在,请说明理由.
参考答案
- 答案 \(D\)
解析 直线 \(l: \sqrt{3} x-y-\sqrt{3}=0\)经过点\(F(1,0)\),
可得\(p=2\),即抛物线\(C:y^2=4x\),准线方程为\(x=-1\),
联立直线 \(\sqrt{3} x-y-\sqrt{3}=0\)和抛物线\(C:y^2=4x\),
可得\(3x^2-10x+3=0\),
可得 \(A(3,2 \sqrt{3})\), \(B\left(\dfrac{1}{3},-\dfrac{2 \sqrt{3}}{3}\right)\),
即有 \(|A B|=\sqrt{\left(3-\dfrac{1}{3}\right)^2+\left(2 \sqrt{3}+\dfrac{2 \sqrt{3}}{3}\right)^2}=\dfrac{16}{3}\),
由 \(M(-1,2 \sqrt{3})\), \(N\left(-1,-\dfrac{2 \sqrt{3}}{3}\right)\), \(F(1,0)\)
可得 \(k_{N F} \cdot k_{M F}=\dfrac{\dfrac{2 \sqrt{3}}{3}}{2} \cdot \dfrac{2 \sqrt{3}}{-2}=-1\),则\(MF⊥NF\)即\(∠MFN=90°\),
线段\(AB\)的中点为 \(\left(\dfrac{5}{3}, \dfrac{4 \sqrt{3}}{3}\right)\),则线段\(AB\)的中点到\(y\)轴的距离为 \(\dfrac{5}{3}\),
综上可得\(A\),\(B\),\(C\)正确,\(D\)错误.
故选:\(D\). - 答案 \(B\)
解析 因为 \(2 \overrightarrow{F A}=\overrightarrow{A B}\),所以点\(A\),\(B\),\(F\)共线,
所以直线\(y=kx+m\)经过抛物线\(y^2=8x\)的焦点\(F(2,0)\),
所以\(2k+m=0\),\(m=-2k\)
因为抛物线的准线为\(x=-2\),
所以 \(\left\{\begin{array}{l} x=-2 \\ y=k x+m \end{array}\right.\)得\(B(-2,-2k+m)\),即\(B(-2,-4k)\)
因为 \(2 \overrightarrow{F A}=\overrightarrow{A B}\),所以 \(2\left(x_A-2, y_A\right)=\left(-2-x_A,-4 k-y_A\right)\),
所以 \(\left\{\begin{array}{l} 2 x_A-4=-2-x_A \\ 2 y_A=-4 k-y_A \end{array}\right.\),解得 \(\left\{\begin{array}{l} x_A=\dfrac{2}{3} \\ y_A=\dfrac{-4 k}{3} \end{array}\right.\),
将点\(A\)的坐标代入抛物线方程得: \(\left(-\dfrac{4 k}{3}\right)^2=8 \times \dfrac{2}{3}\),解得 \(k=-\sqrt{3}(k<0)\),
所以 \(m=-2 k=-2(-\sqrt{3})=2 \sqrt{3}\).
故选:\(B\). - 答案 \(C\)
解析 设\(A(x_1,y_1)\),\(B(x_2,y_2)\),则 \(y_1^2=2 p x_1\),\(y_2^2=2 p x_2\)
联立直线\(l:kx-y-k=0(k∈R)\)与抛物线 \(C: y^2=2 p x\left(p>\dfrac{1}{2}\right)\),
可得\((kx-k)^2=2px\),即为 \(k^2 x^2-(2k^2+2p)x+k^2=0\),
则 \(△=(2k^2+2p)^2-4k^4=4p^2+8pk^2>0\),\(x_1 x_2=1\),
则 \((y_1 y_2 )^2=4p^2 x_1 x_2=4p^2\),
由于直线\(l\)恒过定点\((1,0)\),且与抛物线有两个交点,可得\(y_1 y_2<0\),
则\(y_1 y_2=-2p\),
则 \(\overrightarrow{O A} \cdot \overrightarrow{O B}=x_1 x_2+y_1 y_2=1-2 p\),
由 \(p>\dfrac{1}{2}\),可得\(1-2p<0\),
可得 \(\overrightarrow{O A} \cdot \overrightarrow{O B}<0\),即\(∠AOB\)为钝角,则\(△AOB\)为钝角三角形.
故选:\(C\). - 答案 (1) \(p=2, t \pm 2 \sqrt{3}\) (2) \(\dfrac{8 \sqrt{5}}{5}\)
解析 (1)由题意及抛物线的定义得 \(3+\dfrac{p}{2}=4\),则\(p=2\),
\(∴\)抛物线的方程为\(y^2=4x\),
又\(∵\)点\(T\)在抛物线上,故\(t^2=4×3\),解得 \(t=\pm 2 \sqrt{3}\).
(2)由(1)易得\(M(-1,0)\),\(F(1,0)\).
设\(A(x_1,y_1 )\),\(B(x_2,y_2 )\)假设存在直线\(l\)满足题意,设其方程为\(x=my-1(m≠0)\),
将其代入 \(y^2=4x\)得 \(y^2-4my+4=0\),所以 \(\left\{\begin{array}{l} y_1+y_2=4 m \\ y_1 y_2=4 \end{array}\right.\),
由\(Δ=16m^2-16>0\),得\(m>1\)或\(m<-1\).
又直线\(AF\)与直线\(OB\)垂直,
易知直线\(AF\)与直线\(OB\)的斜率都存在,所以 \(k_{A F} \cdot k_{O B}=-1\),
即 \(\dfrac{y_1}{x_1-1} \cdot \dfrac{y_2}{x_2}=-1\),
所以 \(\dfrac{y_1 y_2}{x_2\left(x_1-1\right)}=\dfrac{4}{\left(m y_2-1\right)\left(m y_1-2\right)}=\dfrac{4}{2-m y_2}=-1\)
故 \(y_1=\dfrac{2 m}{3}\), \(y_2=\dfrac{6}{m}\).
又\(y_2^2-4my_2+4=0\),解得 \(m=\pm \dfrac{3 \sqrt{5}}{5}\),满足\(Δ>0\),
所以满足条件的直线\(l\)的方程为 \(5 x \pm 3 \sqrt{5}+5=0\).
此时 \(|A B|=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}=\sqrt{1+m^2}\),
又点F到直线\(l\)的距离 \(d=\dfrac{|5+5|}{\sqrt{5^2+(\pm 3 \sqrt{5})^2}}=\dfrac{10}{\sqrt{70}}\),
所以\(△AFB\)的面积 \(S=\dfrac{1}{2}|A B| \cdot d=\dfrac{1}{2} \times \dfrac{8 \sqrt{14}}{5} \times \dfrac{10}{\sqrt{70}}=\dfrac{8 \sqrt{5}}{5}\).
分层练习
【A组---基础题】
1.设抛物线\(y^2=8x\)的焦点为\(F\),准线为\(l\),\(P\)为抛物线上一点,\(PA⊥l\),\(A\)为垂足,如果直线\(AF\)的斜率为 \(-\sqrt{3}\),那么\(|PF|=\)( )
A. \(4 \sqrt{3}\) \(\qquad \qquad\) B.\(8\) \(\qquad \qquad\) C. \(8 \sqrt{3}\) \(\qquad \qquad\) D.\(16\)
2.已知点\(P\)在直线\(y=x-1\)上,点\(Q\)在曲线\(x^2=2y\)上,则\(|PQ|\)的最小值为( )
A. \(\dfrac{1}{4}\) \(\qquad \qquad\) B. \(\dfrac{1}{8}\) \(\qquad \qquad\) C. \(\dfrac{\sqrt{2}}{2}\) \(\qquad \qquad\) D. \(\dfrac{\sqrt{2}}{4}\)
3.直线\(y=kx-2\)与抛物线\(y^2=8x\)交于\(A\),\(B\)两点,且\(AB\)中点的横坐标为\(2\),则\(k\)的值为( )
A.\(-1\) \(\qquad \qquad\) B.\(2\) \(\qquad \qquad\) C.\(2\)或\(-1\) \(\qquad \qquad\) D.\(4\)
4.设抛物线\(C:x^2=4y\)的焦点为\(F\),准线为\(l\),过点\(F\)的直线交抛物线\(C\)于\(M\),\(N\)两点,交\(l\)于点\(P\),且 \(\overrightarrow{P F}=\overrightarrow{F M}\),则\(|MN|=\) ( )

A.\(2\) \(\qquad \qquad\) B. \(\dfrac{8}{3}\) \(\qquad \qquad\) C.\(5\) \(\qquad \qquad\) D. \(\dfrac{16}{3}\)
5.过抛物线\(y^2=6x\)的焦点\(F\)的直线\(l\)与抛物线交于\(A\),\(B\)两点,线段\(AB\)的中点\(M\)在直线\(y=1\)上,\(O\)为坐标原点,则\(△AOB\)的面积为( )
A. \(\dfrac{3 \sqrt{10}}{2}\) \(\qquad \qquad\) B. \(4 \sqrt{5}\) \(\qquad \qquad\) C. \(\dfrac{9 \sqrt{2}}{2}\) \(\qquad \qquad\) D.\(9\)
6.已知点\(A(1,2)\)在抛物线\(C:y^2=4x\)上,过点\(A\)作两条直线分别交抛物线于点\(D\),\(E\),直线\(AD\),\(AE\)的斜率分别为 \(k_{A D}\), \(k_{A E}\).若直线\(DE\)过点\((-1,-2)\),则 \(k_{A D} \cdot k_{A E}=\)( )
A.\(4\) \(\qquad \qquad\) B.\(3\) \(\qquad \qquad\) C.\(2\) \(\qquad \qquad\) D.\(1\)
7.过抛物线\(y^2=2px(p>0)\)的焦点\(F\)作一条直线交抛物线于\(A\),\(B\)两点,求 \(\dfrac{1}{|A F|}+\dfrac{1}{|B F|}\)的值.
8.已知双曲线 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)\)的一条渐近线方程为 \(y=\dfrac{\sqrt{3}}{3} x\),点 \((2 \sqrt{3}, 1)\)在双曲线上,抛物线\(y^2=2px(p>0)\)的焦点\(F\)与双曲线的右焦点重合.
(1)求双曲线和抛物线的标准方程;
(2)过点\(F\)做互相垂直的直线\(l_1\),\(l_2\),设\(l_1\)与抛物线的交点为\(A\),\(B\),\(l_2\)与抛物线的交点为\(D\),\(E\),求\(|AB|+|DE|\)的最小值.
9.如图,过抛物线\(y^2=4x\)的焦点\(F\)任作直线\(l\),与抛物线交于\(A\),\(B\)两点,\(AB\)与\(x\)轴不垂直,且点\(A\)位于\(x\)轴上方.\(AB\)的垂直平分线与\(x\)轴交于\(D\)点.
(1)若 \(\overrightarrow{A F}=2 \overrightarrow{F B}\),求\(AB\)所在的直线方程;
(2)求证: \(\dfrac{|A B|}{|D F|}\)为定值.

参考答案
-
答案 \(B\)
解析 如图,直线\(AF\)的方程为 \(y=-\sqrt{3}(x-2)\),与准线方程\(x=-2\)联立得 \(A(-2,4 \sqrt{3})\).

设 \(P\left(x_0, 4 \sqrt{3}\right)\),代入抛物线\(y^2=8x\),得\(8x_0=48\),\(∴x_0=6\).
\(∴|PF|=x_0+2=8\). -
答案 \(D\)
解析 设与直线\(y=x-1\)平行且与抛物线相切的直线为\(y=x+b\),
则\(|PQ|\)的最小值即为两直线间的距离,
所以 \(\left\{\begin{array}{l} y=x+b \\ x^2=2 y \end{array}\right.\),消去\(y\),得\(x^2-2x-2b=0\),\(△=4+8b=0\),
\(\therefore b=-\dfrac{1}{2}\),进而可得直线 \(y=x-\dfrac{1}{2}\)与抛物线交点为 \(\left(1, \dfrac{1}{2}\right)\),
交点到直线\(x-y-1=0\)的距离为 \(\dfrac{\left|1-\dfrac{1}{2}-1\right|}{\sqrt{2}}=\dfrac{\sqrt{2}}{4}\).
故选:\(D\). -
答案 \(B\)
解析 \(∵\)直线\(y=kx-2\)与抛物线\(y^2=8x\)交于两点,\(∴k≠0\).
由 \(\left\{\begin{array}{l} y=k x-2 \\ y^2=8 x \end{array}\right.\)消去\(y\),得 \(k^2 x^2-4kx-8x+4=0\),
\(\therefore x_1+x_2=\dfrac{4 k+8}{k^2}\).
而\(AB\)中点的横坐标为\(2\),
\(\therefore \dfrac{4 k+8}{k^2}=4\),解得\(k=-1\)或\(k=2\).
而当\(k=-1\)时,方程\(k^2 x^2-4kx-8x+4=0\)只有一个解,
即\(A\),\(B\)两点重合,\(∴k≠-1\). -
答案 \(D\)
解析 如图,过点\(M\)做\(MD\)垂直于准线\(l\),由抛物线定义得\(MF=MD\),
因为 \(\overrightarrow{P F}=\overrightarrow{F M}\),所以\(PM=2MD\),所以\(∠DPM=30^∘\)
则直线\(MN\)方程为 \(x=\sqrt{3}(y-1)\),
联立 \(\left\{\begin{array}{l} x=\sqrt{3}(y-1) \\ x^2=4 y \end{array}\right.\)消去\(x\)得 \(3y^2-10y+3=0\),
设\(M(x_1,y_1 )\),\(N(x_2,y_2 )\),所以 \(y_1+y_2=\dfrac{10}{3}\),
得 \(|M N|=y_1+y_2+2=\dfrac{10}{3}+2=\dfrac{16}{3}\).
故选:\(D\).

-
答案 \(A\)
解析 由抛物线\(y^2=6x\),得焦点坐标为 \(\left(\dfrac{3}{2}, 0\right)\),
设直线\(AB\)的方程为 \(x=t y+\dfrac{3}{2}\),点\(A(x_1,y_1 )\),\(B(x_2,y_2 )\),线段\(AB\)的中点为\(M\),
联立 \(\left\{\begin{array}{l} x=t y+\dfrac{3}{2} \\ y^2=6 x \end{array}\right.\)消去\(x\)得 \(y^2-6ty-9=0\),
\(∴y_1+y_2=6t\),\(y_1 y_2=-9\),由 \(y_M=\dfrac{y_1+y_2}{2}=3 t=1\),得 \(t=\dfrac{1}{3}\),
\(\therefore S_{\triangle A O B}=\dfrac{1}{2}|O F| \cdot\left|y_1-y_2\right|=\dfrac{1}{2} \times \dfrac{3}{2} \times \sqrt{\left(y_1+y_2\right)^2-4 y_1 y_2}\)
\(=\dfrac{1}{2} \times \dfrac{3}{2} \times \sqrt{4-4 \times(-9)}=\dfrac{3 \sqrt{10}}{2}\).
故选:\(A\). -
答案 \(C\)
解析 设\(F(-1,-2)\),过\(F\)点直线\(DE\)方程为:\(y+2=k(x+1)\),
联立 \(\left\{\begin{array}{l} y^2=4 x \\ y+2=k(x+1) \end{array}\right.\),消去\(x\)、整理得: \(ky^2-4y+4k-8=0\),
由题意及韦达定理可得: \(y_1+y_2=\dfrac{4}{k}\), \(y_1 y_2=\dfrac{4 k-8}{k}\),
\(\therefore x_1+x_2=\dfrac{y_1+y_2+4-2 k}{k}=\dfrac{4+4 k-2 k^2}{k^2}\),
\(x_1 x_2=\dfrac{\left(y_1+2-k\right)\left(y_2+2-k\right)}{k^2}=\dfrac{4-4 k+k^2}{k^2}\) ,
\(\therefore k_{A D} k_{A E}=\dfrac{y_1-2}{x_1-1} \cdot \dfrac{y_2-2}{x_2-1}=\dfrac{y_1 y_2-2\left(y_1+y_2\right)+4}{x_1 x_2-\left(x_1+x_2\right)+1}\)\(=\dfrac{\dfrac{4 k-8}{k}-2 \cdot \dfrac{4}{k}+4}{\dfrac{4-4 k+k^2}{k^2}-\dfrac{4+4 k-2 k^2}{k^2}+1}=2\),
故选:\(C\). -
答案 \(\dfrac{2}{p}\)
解析 已知抛物线的焦点 \(F\left(\dfrac{p}{2}, 0\right)\),

设\(A\),\(B\)两点的坐标分别为\((x_1,y_1 )\),\((x_2,y_2 )\).
对于直线\(AB\),分两种情况考虑:
(1)若直线\(AB\)的倾斜角为\(90°\),
则有\(|AF|=|BF|=p\),所以 \(\dfrac{1}{|A F|}+\dfrac{1}{|B F|}=\dfrac{2}{p}\);
(2)若直线\(AB\)的倾斜角不等于\(90°\),
设直线\(AB\)的方程为 \(y=k\left(x-\dfrac{p}{2}\right)\),
与抛物线方程联立并消去\(y\),整理得 \(k^2 x^2-\left(k^2+2\right) p x+\dfrac{k^2 p^2}{4}=0\),
由韦达定理得, \(x_1+x_2=\dfrac{\left(k^2+2\right) p}{k^2}\), \(x_1 x_2=\dfrac{p^2}{4}\).
另一方面,由抛物线定义得 \(|A F|=x_1+\dfrac{p}{2}\), \(|B F|=x_2+\dfrac{p}{2}\).
于是 \(\dfrac{1}{|A F|}+\dfrac{1}{|B F|}=\dfrac{1}{x_1+\dfrac{p}{2}}+\dfrac{1}{x_2+\dfrac{p}{2}}=\dfrac{x_1+x_2+p}{x_1 x_2+\dfrac{p}{2}\left(x_1+x_2\right)+\dfrac{p^2}{4}}\)\(=\dfrac{\dfrac{\left(k^2+2\right) p}{k^2}+p}{\dfrac{p^2}{4}+\dfrac{p}{2} \cdot \dfrac{\left(k^2+2\right) p}{k^2}+\dfrac{p^2}{4}}=\dfrac{2}{p}\). -
答案 (1) \(y^2=8 \sqrt{3} x\) (2) \(32 \sqrt{3}\)
解析 (1)由题意可得 \(\dfrac{b}{a}=\dfrac{\sqrt{3}}{3}\),即\(a= \sqrt{3} b\),
所以双曲线方程为 \(x^2-3y^2=3b^2\),
将点\((2 \sqrt{3} ,1)\)代入双曲线方程,可得\(b^2=3\),
所以双曲线的标准方程为 \(\dfrac{x^2}{9}-\dfrac{y^2}{3}=1,\),
\(c^2=a^2+b^2=12\),所以 \(\dfrac{p}{2}=c=2 \sqrt{3}\),
所以抛物线的方程为\(y^2=8 \sqrt{3} x\).
(2)由题意知 \(F(2 \sqrt{3}, 0)\),\(l_1\),\(l_2\)与坐标轴不平行,
设直线\(l_1\)的方程为 \(y=k(x-2 \sqrt{3})\),
\(\left\{\begin{array}{l} y=k(x-2 \sqrt{3}) \\ y^2=8 \sqrt{3} x \end{array}\right.\),整理可得 \(k^2 x^2-\left(4 \sqrt{3} k^2+8 \sqrt{3}\right) x+12 k^2=0\),
\(△>0\)恒成立, \(\therefore \chi_A+\chi_B=\dfrac{4 \sqrt{3} k^2+8 \sqrt{3}}{k^2}\) ,
因为直线\(l_1\),\(l_2\)互相垂直,可设直线\(l_2\)的方程为 \(y=-\dfrac{1}{k}(x-2 \sqrt{3})\),
同理可得 \(x_D+x_E=8 \sqrt{3} k^2+4 \sqrt{3}\),
\(|A B|+|D E|=x_A+x_B+x_D+x_E+2 p\)
\(=\dfrac{4 \sqrt{3} k^2+8 \sqrt{3}}{k^2}+8 \sqrt{3} k^2+4 \sqrt{3}+8 \sqrt{3}\)
\(=16 \sqrt{3}+8 \sqrt{3}\left(k^2+\dfrac{1}{k^2}\right) \geq 32 \sqrt{3}\).
当且仅当\(k=±1\)时取等号,所以\(|AB|+|DE|\)的最小值为 \(32 \sqrt{3}\). -
答案 (1) \(2 \sqrt{2} x-y-2 \sqrt{2}=0\) (2)略
解析 (1)直线\(l\)的斜率不为\(0\),可得\(F(1,0)\),
设直线\(l:x=ty+1\),\(A(x_1,y_1)\),\(B(x_2,y_2)\),由\(A\)在\(x\)轴上方,
所以\(y_1>0\),\(y_2<0\),
由 \(\left\{\begin{array}{l} x=t y+1 \\ y^2=4 x \end{array}\right.\)可得 \(y^2-4ty-4=0\),
所以\(y_1+y_2=4t\),\(y_1 y_2=-4\),
因为 \(\overrightarrow{A F}=2 \overrightarrow{F B}\),可得\((1-x_1,-y_1)=2(x_2-1,y_2)\),所以\(-y_1=2y_2\),
由 \(\left\{\begin{array}{l} y_1+y_2=4 t \\ -y_1=2 y_2 \end{array}\right.\)可得\(y_1=8t\),\(y_2=-4t\),代入\(y_1 y_2=-4\),
因为\(y_1>0\),所以\(t>0\),解得 \(t=\dfrac{1}{2 \sqrt{2}}\),
所以\(AB\)所在直线方程为 \(2 \sqrt{2} x-y-2 \sqrt{2}=0\);
(2)证明:设\(AB\)的中点为\(N(x_N,y_N)\),
所以 \(y_N=\dfrac{y_1+y_2}{2}=2 t\), \(x_N=2 t^2+1\),即 \(N(2t^2+1,2t)\),
所以\(AB\)的中垂线\(l':y-2t=-t(x-2t^2-1)\),
所以 \(D(2t^2+3,0)\),则 \(|D F|=\left|2 t^2+3-1\right|=2 t^2+2\),
又 \(|A B|=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}=\sqrt{\left(t y_1-t y_2\right)^2+\left(y_1-y_2\right)^2}\)
\(=\sqrt{1+t^2} \cdot \sqrt{\left(y_1+y_2\right)^2-4 y_1 y_2}=\sqrt{1+t^2} \cdot \sqrt{16 t^2+16}=4 t^2+4\),
所以 \(\dfrac{|A B|}{|D F|}=\dfrac{4 t^2+4}{2 t^2+2}=2\)为定值.
【B组---提高题】
1.已知抛物线\(C:y^2=2px(p>0)\),\(F\)为\(C\)的焦点,过焦点\(F\)且倾斜角为\(α\)的直线\(l\)与\(C\)交于\(A(x_1,y_1)\)、\(B(x_2,y_2)\)两点,则下面陈述不正确的为( )
A. \(x_1 x_2+y_1 y_2=-\dfrac{3}{4} p^2\) \(\qquad\) B. \(|A B|=\dfrac{2 p}{\sin ^2 \alpha}\) \(\qquad\) C. \(\dfrac{1}{|A F|}+\dfrac{1}{|B F|}=\dfrac{2}{p}\) \(\qquad\) D.记原点为\(O\),则 \(S_{\triangle A O B}=\dfrac{p^2}{\sin \alpha}\)
2.已知\(F\)为抛物线\(C:y^2=2px(p>0)\)的焦点,\(K\)为\(C\)的准线与\(x\)轴的交点,点\(P\)在抛物线\(C\)上,设\(∠KPF=α\),\(∠PKF=β\),\(∠PFK=θ\),有以下\(3\)个结论:
①\(β\)的最大值是 \(\dfrac{\pi}{4}\);② \(\tan \beta=\sin \theta\);③存在点\(P\),满足\(α=2β\).
其中正确结论的序号是\(\underline{\quad \quad}\) .
3.已知抛物线方程\(y^2=4x\),\(F\)为焦点,\(P\)为抛物线准线上一点,\(Q\)为线段\(PF\)与抛物线的交点,定义: \(d(P)=\dfrac{|P F|}{|F Q|}\).
(1)当 \(P\left(-1,-\dfrac{8}{3}\right)\)时,求\(d(P)\);
(2)证明:存在常数\(a\),使得\(2d(P)=|PF|+a\);
(3)\(P_1\),\(P_2\),\(P_3\)为抛物线准线上三点,且\(|P_1 P_2 |=|P_2 P_3 |\),判断\(d(P_1)+d(P_3)\)与\(2d(P_2\))的关系.
参考答案
-
答案 \(D\)
解析 设直线l方程为 \(x=m y+\dfrac{p}{2}\),
联立方程组 \(\left\{\begin{array}{l} y^2=2 p x \\ x=m y+\dfrac{p}{2} \end{array}\right.\),消去\(x\)可得: \(y^2-2pmy-p^2=0\),
\(∴y_1+y_2=2pm\),\(y_1 y_2=-p^2\),
\(\therefore x_1 x_2=\left(m y_1+\dfrac{p}{2}\right)\left(m y_2+\dfrac{p}{2}\right)=m^2 y_1 y_2+\dfrac{m p}{2}\left(y_1+y_2\right)+\dfrac{p^2}{4}\)
\(=-m^2 p^2+m^2 p^2+\dfrac{p^2}{4}=\dfrac{p^2}{4}\),
\(\therefore x_1 x_2+y_1 y_2=-\dfrac{3 p^2}{4}\),故\(A\)正确;
由抛物线性质知 \(|AB|=x_1+x_2+p=m(y_1+y_2 )+2p=2m^2 p+2p=2p(m^2+1)\),
当\(m=0\)时, \(\alpha=\dfrac{\pi}{2}\),显然 \(|A B|=2 p=\dfrac{2 p}{\sin ^2 \alpha}\),
当\(m≠0\)时, \(\tan \alpha=\dfrac{1}{m}\),故 \(m^2+1=\dfrac{\cos ^2 \alpha}{\sin ^2 \alpha}+1=\dfrac{1}{\sin ^2 \alpha}\),
于是 \(|A B|=\dfrac{2 p}{\sin ^2 \alpha}\),故\(B\)正确;
\(\dfrac{1}{|A F|}+\dfrac{1}{|B F|}=\dfrac{1}{x_1+\dfrac{p}{2}}+\dfrac{1}{x_2+\dfrac{p}{2}}=\dfrac{x_1+x_2+p}{x_1 x_2+\dfrac{p}{2}\left(x_1+x_2\right)+\dfrac{p^2}{4}}\)\(=\dfrac{x_1+x_2+p}{\dfrac{p}{2}\left(x_1+x_2+p\right)}=\dfrac{2}{p}\),
故\(C\)正确;
\(S_{\triangle A O B}=\dfrac{1}{2} \times \dfrac{p}{2} \times\left|y_1-y_2\right|=\dfrac{p}{4} \sqrt{\left(y_1+y_2\right)^2-4 y_1 y_2}=\dfrac{p}{4} \times \sqrt{4 p^2 m^2+4 p^2}=\dfrac{p^2 \sqrt{m^2+1}}{2}\)
显然当\(m≠0\)时, \(S_{\triangle A O B}=\dfrac{p^2}{2 \sin \alpha}\),故\(D\)错误.
故选:\(D\). -
答案 ①②③
解析 ①设点\(P(m,n)\),则\(n^2=2pm\)(1),
当直线\(PK\)与抛物线相切时,可使\(β\)取得最大值.
可设直线\(PK\)方程为 \(y=k\left(x+\dfrac{p}{2}\right)\),
由 \(\left\{\begin{array}{c} y=k\left(x+\dfrac{p}{2}\right) \\ y^2=2 p x \end{array}\right.\),得 \(k^2 x^2+\left(k^2 p-2 p\right) x+\dfrac{p^2 k^2}{4}=0\),
则 \(\Delta=\left(k^2 p-2 p\right)^2-4 k^2 \cdot \dfrac{p^2 k^2}{4}=0 \Rightarrow k^2=1 \Rightarrow k=\pm 1\),
\(∵β\)是锐角, \(\therefore \tan \beta=k=1 \Rightarrow \beta=\dfrac{\pi}{4}\),故①正确

②过\(P\)作\(PQ⊥x\)轴于点\(Q\),在\(Rt△PQK\)中, \(\tan \beta=\dfrac{P Q}{K Q}=\dfrac{n}{m+\dfrac{p}{2}}\),
在\(Rt△PQF\)中, \(\sin \theta=\sin \angle P F Q=\dfrac{P Q}{P F}=\dfrac{n}{m+\dfrac{p}{2}}\),
\(\therefore \tan \beta=\sin \theta\),即②正确;
③在\(△PKF\)中,由正弦定理知, \(\dfrac{P F}{\sin \beta}=\dfrac{K F}{\sin \alpha}\),
若\(α=2β\),则 \(\dfrac{m+\dfrac{p}{2}}{\sin \beta}=\dfrac{p}{2 \sin \beta \cos \beta}\),解得 \(m=\dfrac{p}{2}\left(\dfrac{1}{\cos \beta}-1\right)\),
\(\therefore n^2=2 p m=p^2\left(\dfrac{1}{\cos \beta}-1\right)\),
故存在点\(P\)符合题意,即③正确.
故答案为:①②③. -
答案 (1) \(\dfrac{8}{3}\) (2) 略 (3) \(d(P_1)+d(P_3)>2d(P_2)\)
解析 (1)抛物线方程\(y^2=4x\)的焦点\(F(1,0)\), \(P\left(-1,-\dfrac{8}{3}\right)\),
\(k_{P F}=\dfrac{\dfrac{8}{3}}{2}=\dfrac{4}{3}\),\(PF\)的方程为 \(y=\dfrac{4}{3}(x-1)\),
代入抛物线的方程,解得 \(x_Q=\dfrac{1}{4}\),
抛物线的准线方程为\(x=-1\),可得 \(|P F|=\sqrt{2^2+\dfrac{64}{9}}=\dfrac{10}{3}\),
\(|Q F|=\dfrac{1}{4}+1=\dfrac{5}{4}\), \(d(P)=\dfrac{|P F|}{|Q F|}=\dfrac{8}{3}\);
(2)证明:当\(P(-1,0)\)时,\(a=2d(P)-|PF|=2×2-2=2\),
设\(P(-1,y_P)\),\(y_P>0\),\(PF:x=my+1\),则\(my_P=-2\),
联立\(x=my+1\)和\(y^2=4x\),
可得 \(y^2-4 m y-4=0\),\(y_Q=\dfrac{4 m+\sqrt{16 m^2+16}}{2}=2 m+2 \sqrt{1+m^2}\)
\(2 d(P)-|P F|=2 \dfrac{y_P}{y_Q}-\sqrt{1+m^2} y_P=2 \cdot \dfrac{-2}{m\left(2 m+2 \sqrt{1+m^2}\right)}+\dfrac{2 \sqrt{1+m^2}}{m}\)
\(=-2 \cdot \dfrac{\sqrt{1+m^2}-m}{m}+\dfrac{2 \sqrt{1+m^2}}{m}=2\),
则存在常数\(a\),使得\(2d(P)=|PF|+a\);
另解: \(d(P)=\dfrac{|P F|}{|F Q|}=\dfrac{|P Q|+|F Q|}{|F Q|}=1+\dfrac{|P Q|}{|F Q|}=1+\dfrac{|P Q|}{t}=1+\dfrac{|P F|}{2}\),
可得\(2d(P)=|PF|+2\).
(3)设\(P_1 (-1,y_1)\),\(P_2 (-1,y_2)\),\(P_3 (-1,y_3)\),则
\(2[d(P_1 )+d(P_3 )]-4d(P_2 )=|P_1 F|+|P_3 F|-2|P_2 F|\)
\(=\sqrt{4+y_1^2}+\sqrt{4+y_3{ }^2}-2 \sqrt{4+y_2{ }^2}\)
\(=\sqrt{4+y_1^2}+\sqrt{4+y_3^2}-2 \sqrt{\left(\dfrac{y_1+y_3}{2}\right)^2+4}\)
\(=\sqrt{4+y_1^2}+\sqrt{4+y_3{ }^2}-\sqrt{\left(y_1+y_3\right)^2+16}\)
由 \(\left(\sqrt{4+y_1^2}+\sqrt{4+y_3^2}\right)^2-\left[\left(y_1+y_3\right)^2+16\right]=2 \sqrt{4+y_1^2} \sqrt{4+y_3^2}-2 y_1 y_3-8\),
\(\left(4+y_1^2\right)\left(4+y_3^2\right)-\left(y_1 y_3+4\right)^2=4\left(y_1^2+y_3^2\right)-8 y_1 y_3=4\left(y_1-y_3\right)^2>0\)
则\(d(P_1)+d(P_3)>2d(P_2)\).

【C组---拓展题】
1.已知抛物线\(y^2=2px(p>0)\)的焦点\(为F(4,0)\),过\(F\)作直线\(l\)交抛物线于\(M\),\(N\)两点,则\(p=\)\(\underline{\quad \quad}\), \(\dfrac{|N F|}{9}-\dfrac{4}{|M F|}\)的最小值为\(\underline{\quad \quad}\).
2.如图,椭圆 \(C_1: \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)\)的左、右焦点分别为\(F_1\),\(F_2\),离心率为 \(\dfrac{\sqrt{3}}{2}\),过抛物线 \(C_2:x^2=4by\)焦点\(F\)的直线交抛物线于\(M\),\(N\)两点,当 \(|M F|=\dfrac{7}{4} \mid\)时,\(M\)点在\(x\)轴上的射影为\(F_1\),连接\(NO\),\(MO\)并延长分别交\(C_1\)于\(A\),\(B\)两点,连接\(AB\),\(ΔOMN\)与\(ΔOAB\)的面积分别记为 \(S_{\triangle O M N}\), \(S_{\triangle O A B}\),设 \(\lambda=\dfrac{s_{\triangle O M N}}{s_{\triangle O A B}}\) .
(1)求椭圆\(C_1\)和抛物线\(C_2\)的方程;
(2)设\(ON\),\(OM\)所在直线的斜率为 \(k_{O M}\), \(k_{O N}\),求证 \(k_{O M} \cdot k_{O N}\)为定值;
(3)求\(λ\)的取值范围.

参考答案
-
答案 \(8\), \(\dfrac{1}{3}\)
解析 抛物线\(y^2=2px\)的焦点\(F\),因为\(F(4,0)\),
\(\therefore \dfrac{p}{2}=4 \Rightarrow p=8 \Rightarrow y^2=16 x\);
当直线\(l\)的斜率不存在时,直线\(l\)为\(x=4\),
由 \(\left\{\begin{array}{l} x=4 \\ y^2=16 x \end{array}\right.\),可得\(M(4,8)\),\(N(4,-8)\),
\(∴|MF|=|NF|=8\),
\(\therefore \dfrac{|N F|}{9}-\dfrac{4}{|M F|}=\dfrac{8}{9}-\dfrac{4}{8}=\dfrac{7}{18}\);
当直线\(l\)的斜率存在时,设过点\(F\)作直线\(l\)的方程为\(y=k(x-4)\),
不妨设\(M(x_1,y_1 )\),\(N(x_2,y_2 )\),
由 \(\left\{\begin{array}{l} y^2=16 x \\ y=k(x-4) \end{array}\right.\),消\(y\)可得 \(k^2 x-(16+8k^2 )x+16k^2=0\),
\(\therefore x_1+x_2=8+\dfrac{16}{k^2}\) ,\(x_1 x_2=16\),
\(\therefore|M F|=x_1+\dfrac{p}{2}=x_1+4\), \(|N F|=x_2+\dfrac{p}{2}=x_2+4\)
\(\therefore \dfrac{1}{N F}+\dfrac{1}{M F}=\dfrac{1}{x_1+4}+\dfrac{1}{x_2+4}=\dfrac{x_1+x_2+8}{x_1 x_2+4\left(x_1+x_2\right)+16}\)
\(=\dfrac{16+\frac{16}{k^2}}{16+4\left(8+\frac{16}{k^2}\right)+16}=\dfrac{1}{4}\).
\(\therefore \dfrac{|N F|}{9}-\dfrac{4}{|M F|}=\dfrac{N F}{9}-4\left(\dfrac{1}{4}-\dfrac{1}{|N F|}\right)=\dfrac{|N F|}{9}+\dfrac{4}{|N F|}-1\)
\(\geq 2 \sqrt{\dfrac{4}{9}}-1=\dfrac{1}{3}\).
(当且仅当\(|NF|=6\)时等号成立).
故答案为:\(8\), \(\dfrac{1}{3}\). -
答案 (1) \(C_1: \quad \dfrac{x^2}{4}+y^2=1, \quad C_2: \quad x^2=4 y\) (2) \(-\dfrac{1}{4}\) (3)\([2,+∞)\)
解析 (1)由抛物线定义可得 \(M\left(-c, \dfrac{7}{4}-b\right)\),
\(∵\)点\(M\)在抛物线 \(x^2=4 b y\)上, \(\therefore c^2=4 b\left(\dfrac{7}{4}-b\right)\),即 \(c^2=7b-4b^2\) ①
又由 \(\dfrac{c}{a}=\dfrac{\sqrt{3}}{2}\),得 \(c^2=3b^2\)将上式代入①,得 \(7b^2=7b\)解得\(b=1\),
\(\therefore c=\sqrt{3}\),\(∴a=2\),
所以曲线\(C_1\)的方程为 \(\dfrac{x^2}{4}+y^2=1\),曲线\(C_2\)的方程为\(x^2=4y\).
(2)证明:设直线\(MN\)的方程为\(y=kx+1\),
由 \(\left\{\begin{array}{l} y=k x+1 \\ x^2=4 y \end{array}\right.\)消去\(y\)整理得 \(x^2-4kx-4=0\),
设\(M(x_1,y_1 )\),\(N(x_2,y_2 )\).则\(x_1 x_2=-4\),
设 \(k_{O N}=m\), \(k_{O M}=m^{\prime}\),则 \(m m^{\prime}=\dfrac{y_2}{x_2} \cdot \dfrac{y_1}{x_1}=\dfrac{1}{16} x_1 x_2=-\dfrac{1}{4}\),
(3)由(2),可得 \(m^{\prime}=-\dfrac{1}{4 m}\),②
设直线\(ON\)的方程为\(y=mx(m>0)\),由 \(\left\{\begin{array}{l} y=m x \\ x^2=4 y \end{array}\right.\),解得\(x_N=4m\),
所以 \(| O N|=\sqrt{1+m^2}| x_N \mid=4 m \sqrt{1+m^2}\),
由②可知,用 \(-\dfrac{1}{4 m}\)代替\(m\),可得 \(|O M|=\sqrt{1+\left(-\dfrac{1}{4 m}\right)^2}\left|x_M\right|=\dfrac{1}{m} \sqrt{1+\dfrac{1}{16 m^2}}\),
由 \(\left\{\begin{array}{l} y=m x \\ \dfrac{x^2}{4}+y^2=1 \end{array}\right.\),解得 \(x_A=\dfrac{2}{\sqrt{4 m^2+1}}\),
所以 \(|O A|=\sqrt{1+m^2}\left|x_A\right|=\dfrac{2 \sqrt{1+m^2}}{\sqrt{4 m^2+1}}\),
用 \(-\dfrac{1}{4 m}\)代替\(m\),可得 \(|O B|=\sqrt{1+\dfrac{1}{16 m^2}}\left|x_B\right|=\dfrac{\sqrt[2]{1+\frac{1}{16 m^2}}}{\sqrt{\frac{1}{4 m^2}+1}}\),
所以 \(\lambda=\dfrac{S_{\triangle O M N}}{S_{\triangle O A B}}=\dfrac{|O N| \cdot|O M|}{|O A| \cdot|O B|}=\dfrac{4 m \sqrt{1+m^2} \cdot \dfrac{1}{m} \sqrt{1+\frac{1}{16 m^2}}}{\dfrac{2 \sqrt{1+m^2}}{\sqrt{4 m^2+1}} \cdot \dfrac{\sqrt{1+\dfrac{1}{16 m^2}}}{\sqrt{\frac{1}{4 m^2}+1}}}\)
\(=\sqrt{4 m^2+1} \cdot \sqrt{\dfrac{1}{4 m^2}+1}=\sqrt{4 m^2+2+\dfrac{1}{4 m^2}}=2 m+\dfrac{1}{2 m} \geq 2\),
当且仅当 \(m=\dfrac{1}{2}\)时等号成立.
所以\(λ\)的取值范围为\([2,+∞)\).

