3.3.1 抛物线及其标准方程
【基础过关系列】2022-2023 学年高二数学上学期同步知识点剖析精品讲义 (人教 A 版 2019)
选择性必修第一册同步巩固,难度 2 颗星!
基础知识
抛物线的定义
平面内与一个定点 F 和一条定直线 的距离相等的点的轨迹称为抛物线,定点 称为抛物线的焦点,定直线 称为抛物线的准线.
如图, 在抛物线上,.

抛物线的标准方程
| 标准方程 | ||||
| 图形 | 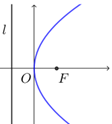
| 
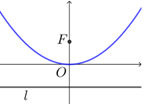
| 
| 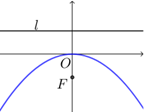 |
| 焦点 | ||||
| 准线方程 |
解释
(1) 求解焦点在 轴正半轴上的抛物线方程
取经过点 且垂直于直线 的直线为 轴,垂足为 ,并使原点与线段 的中点重合,建立平面直角坐标系 ,
设 ,那么焦点 的坐标为 ,准线 的方程为 ,
设 是抛物线上任意一点,点 到准线 的距离为 ,由抛物线的定义,
因为 ,所以 ,
化简得 .

(2) 涉及抛物线,先看一次项的取值范围确定开口方向,比如 中一次项 则该抛物线开口向左;再确定 值、焦点和准线位置.
可想象下抛物线是鱼缸里的一条鱼,焦点是它眼睛,准线是鱼缸玻璃壁 .
【例】 画出以下抛物线的图象,写出相应的焦点坐标和准线方程.
(1); (2) ;(3);(4) ;
解析
| 方程 | ||||
|---|---|---|---|---|
| 图象 |  |
 |
 |
 |
| 焦点坐标 | ||||
| 准线方程 |
基本方法
【题型1】抛物线的定义
【典题 1】 若点 到点 的距离比它到直线 的距离少 ,求动点 的轨迹的形状.
解析 点 到点 的距离比它到直线 的距离少 ,即 ,
点 到直线 的距离和它到点 的距离相等,即 ,

根据抛物线的定义可得点 的轨迹是以点 为焦点,以直线 为准线的抛物线.
【典题 2】与圆 外切,且与直线 相切的动圆圆心 的轨迹方程是 .
解析 由圆 可得:圆心 ,半径 .
设所求动圆圆心为 ,过点 作 直线 , 为垂足.
因为圆 与圆 外切,则 ,可得 .

过点 作 直线 , 为垂足,则 ,
即点 的轨迹是到定点 的距离和到直线 的距离相等的点的集合.
由抛物线的定义可知:
点 的轨迹是抛物线,定点 为焦点,定直线 是准线.
抛物线的方程为:.
与圆 外切,且与直线 相切的动圆圆心的轨迹方程是 .
巩固练习
1. 已知定点 和直线 ,则到定点 的距离和到定直线 的距离相等的点的轨迹为 ( )
A.椭圆 B.双曲线 C.抛物线 D.直线
2. 动点 到点 的距离比它到直线 的距离大 ,则动点 的轨迹是 ( )
A.椭圆 B.双曲线 C.双曲线的一支 D.抛物线
3. 一个动圆的圆心在抛物线 上,且动圆恒与直线 相切,则动圆必过定点 ( )
A. B. C.(2,0) D.
参考答案
- 答案
解析 因为定点 在直线 上,
所以到定点 的距离和到定直线 的距离相等的点的轨迹是直线,
就是经过定点 与直线 垂直的直线.
故选:. - 答案
解析 动点 到点 的距离比它到直线 的距离大 ,
将直线 向左平移 个单位,得到直线 ,
可得点 到点 的距离等于它到直线 的距离.
因此点 的轨迹是以 为焦点、 为准线的抛物线,
设抛物线的方程为 ,可得 ,得 ,
抛物线的方程为 ,即为点 的轨迹方程.
故选:. - 答案
解析 抛物线 的准线方程为 ,
由题可知动圆的圆心在 上,且恒与抛物线的准线相切,
由定义可知,动圆恒过抛物线的焦点 ,
故选:.
【题型2】求抛物线的标准方程
【典题 1】抛物线 的准线经过椭圆 的右焦点,则抛物线的焦点到准线的距离为 .
解析 椭圆 的右焦点 ,
抛物线 的准线经过椭圆 的右焦点,
可得 ,解得 ,
则抛物线的焦点到准线的距离为 .
点拨 抛物线的焦点与准线均与 有关.
【典题 2】根据下列条件,求抛物线的标准方程.
(1) 焦点坐标为 ;(2) 准线方程为 ;(3) 过点 .
解析 (1)∵抛物线的焦点坐标为 (-2,0),
,则 ,且抛物线的开口向左,故抛物线方程为 ;
(2)∵抛物线准线方程为 ,
,则 ,且抛物线的开口向上,故抛物线方程为 ;
(3) 抛物线过点 ,
可设抛物线方程为 或 ,
把点 代入 ,得 ,故抛物线方程为 ;
代入 ,得 ,故抛物线方程为 .
∴所求抛物线方程为 或 .
点拨
1. 求抛物线方程的方法主要是定义法和待定系数法;
2. 明确了抛物线的焦点或准线的位置,可确定抛物线的开口方向,其标准方程便可设定.
巩固练习
1. 抛物线 的焦点到其准线的距离是 ( )
A. B. C. D.
2. 焦点在 轴的正半轴上,且焦点到准线的距离为 的抛物线的标准方程是 ( )
A. B. C. D.
3. 已知抛物线的准线方程为 ,则此抛物线的标准方程为 ( )
A. B. C. D.
4. 已知圆 与抛物线 的准线相切,则 .
5. 若抛物线 的焦点与双曲线 的右顶点重合,则 .
6. 抛物线 上一点 的纵坐标为 ,该点到准线的距离为 ,则抛物线方程为 .
参考答案
- 答案
解析 由抛物线 的方程可得 ,所以 ,
焦点到其准线的距离是 ,
故选:. - 答案
解析 由题意可设抛物线方程为 ,
且 ,则抛物线方程为 ,
故选:. - 答案
解析 因为抛物线的准线方程为 ,
所以设抛物线方程为 ,
则 ,得 ,
所以抛物线方程为
故选:. - 答案
解析 圆 的圆心为 ,半径为 ,
抛物线 的准线为 .由 ,得 或 (舍). - 答案
解析 双曲线 的右顶点坐标为 ,
抛物线 的焦点与双曲线 的右顶点重合,
, . - 答案 或
解析 由于抛物线的准线方程是 ,而点 到准线的距离为 ,
所以 点的横坐标是 ,于是 ,
代入方程得 ,解得 或 ,
故方程为 或 .
分层练习
【A组---基础题】
1. 如图,在正方体 中, 是侧面 上的一个动点,若点 到直线 与直线 的距离相等,则动点 的轨迹是下列哪种曲线的一部分 ( )

A.直线 B.圆 C.双曲线 D.抛物线
2. 已知点 到点 的距离比它到直线 的距离小 ,则点 的轨迹方程为 ( )
A. B. C. D.
3. 若抛物线 的焦点与椭圆 的左焦点重合,则 的值为 ( )
A. B. C. D.
4. 抛物线 上一点 到 轴的距离为 ,则点 到抛物线焦点 的距离为 ( )
A. B. C. D.
5. 已知点 为抛物线 上的点,且点 到抛物线 的焦点 的距离为 ,则 .
6. 点 与点 的距离比它到直线 的距离小 ,则点 的轨迹方程是 .
7. 抛物线 上的一点 到焦点的距离为 ,则点 的纵坐标是 .
参考答案
- 答案
解析 由正方体的性质知, 平面 ,
所以点 到直线 的距离与到点 的距离相等,
又点 到直线 与直线 的距离相等,
所以点 到直线 与到点 的距离相等,
根据抛物线的定义,可得动点 的轨迹是抛物线.
故选:. - 答案
解析 由题意,点 到点 的距离等于它到直线 的距离,
可得点 的轨迹是以 为焦点, 为准线的抛物线,
则点 的轨迹方程为 ,
故选:. - 答案
解析 抛物线 的焦点坐标为
椭圆 , ,
,
椭圆的左焦点坐标为
抛物线 的焦点与椭圆 的左焦点重合,
,
故选:. - 答案
解析 由抛物线的方程可得焦点 ,准线方程为:,
设 ,由题意可得 ,由 到 轴的距离为 可得 ,所以 ,
再由抛物线的性质到焦点的距离等于到准线的距离,
所以点 到抛物线焦点 的距离为 ,
故选:. - 答案
解析 抛物线 的焦点为 ,准线为 ,
因为点 为抛物线 上的点,且点 到抛物线 的焦点 的距离为 ,
所以 ,得 . - 答案
解析 依题意可知:点 与点 的距离比它到直线 的距离小 ,
转化为点 与点 的距离与它到直线 的距离相等,
满足抛物线的定义,所以 $P=My^2=16x$. - 答案
解析 根据抛物线的定义可知 到焦点的距离为 ,则其到准线距离也为 .
又 抛物线的准线为 ,
点的纵坐标为 .
【B组---提高题】
1. 如图,正方体 的棱长为 ,点 是平面 上的动点,点 在棱 上,且 ,且动点 到直线 的距离与点 到点 的距离的平方差为 ,则动点 的轨迹是 ( )

A.圆 B.抛物线 C.双曲线 D.直线
2. 已知点 在以原点为圆心的单位圆上运动,则点 的轨迹是 ( )
A.圆 B.抛物线 C.椭圆 D.双曲线
3. 已知抛物线的顶点在原点,焦点 在 轴正半轴 上.若抛物线上一动点 到 , 两点距离之和的最小值为 ,且 为抛物线内一点,求抛物线方程.
参考答案
-
答案
解析 如图所示:正方体 中,作 , 为垂足,则 面 ,

过点 作 ,
则 面 , 即为点 到直线 的距离,由题意可得 .
又已知 ,
,即 到点 的距离等于 到 的距离,
根据抛物线的定义可得,点 的轨迹是抛物线,
故选:. -
答案
解析 设 ,则 ,
, .
点 的轨迹是抛物线.
故选:. -
答案
解析 设所求的抛物线方程为 ,
其焦点为 ,准线 .
如图所示,若 点在 “抛物线所包含的区域之内”,
过点 作准线的垂线,垂足为 ,

由抛物线定义可知 .
当 在同一条直线上时,
取最小值 ,解得 ,
故所求的抛物线方程为 .
【C组---拓展题】
1. 若动点 满足 ,则 点的轨迹应为 ( )
A.椭圆 B.抛物线 C.双曲线 D.圆
- 已知抛物线 的焦点为 ,点 是抛物线 上的一点,以 为圆心的圆交直线 于 , 两点 (点 在点 的上方),若 ,则抛物线 的方程是 .
参考答案
- 答案
解析 动点 满足 ,
可知:动点 到定点 与到定直线 的距离相等,其中定点不在定直线上.
因此 点的轨迹应为抛物线.
故选:. - 答案
解析 画出图形如右图所示,作 ,垂足为 ,

由题意得点 在抛物线上,则 ,①
由抛物线的性质,可知 ,
因为 ,所以 ,
所以 ,解得 ,②
由①②解得 (舍去) 或 .
故抛物线 的方程为 .




【推荐】编程新体验,更懂你的 AI,立即体验豆包 MarsCode 编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下 AI 助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客 6.5 折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 在鹅厂做java开发是什么体验
· 百万级群聊的设计实践
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战
· 永远不要相信用户的输入:从 SQL 注入攻防看输入验证的重要性
· 全网最简单!3分钟用满血DeepSeek R1开发一款AI智能客服,零代码轻松接入微信、公众号、小程