3.2.2 双曲线的简单几何性质(2)
${\color{Red}{欢迎到学科网下载资料学习 }}$
【基础过关系列】2022-2023 学年高二数学上学期同步知识点剖析精品讲义 (人教 A 版 2019)
跟贵哥学数学,soeasy!跟贵哥学数学,soeasy!
选择性必修第一册同步巩固,难度 3 颗星!
基础知识
直线与双曲线的位置关系
设直线 l:Ax+By+C=0l:Ax+By+C=0,双曲线 C:f(x,y)=0C:f(x,y)=0,把两者方程联立得到方程组,消元 y(y( 或 x)x) 得到一个关于 x(x( 或 y)y) 的方程 ax2+bx+c=0ax2+bx+c=0(或 ay2+by+c=0ay2+by+c=0).
① 当 a≠0a≠0 时,
∆>0⇔Δ>0⇔ 方程有两个不同的实数解,即直线与双曲线有两个交点 ⇔⇔ 相交;
∆=0⇔Δ=0⇔ 方程有两个相同的实数解,即直线与双曲线有一个交点 ⇔⇔ 相切;
∆<0⇔Δ<0⇔ 方程无实数解,即直线与双曲线无交点 ⇔⇔ 相离.
② 当 a=0a=0,b≠0b≠0 时,即得到一个一次方程,则只有一个交点,此时直线 ll 与双曲线的渐 * 线 * 行.
直线与圆锥曲线的弦长公式
(1) 直线 y=kx+by=kx+b 与双曲线相交于 A(x1,y1)A(x1,y1),B(x2,y2)B(x2,y2),则
AB=√1+k2⋅|x1−x2|=√1+k2⋅√(x1+x2)2−4x1x2=√1+k2⋅√Δ|a|AB=√1+k2⋅|x1−x2|=√1+k2⋅√(x1+x2)2−4x1x2=√1+k2⋅√Δ|a|
或
AB=√1+1k2⋅|y1−y2|=√1+1k2⋅√(y1+y2)2−4y1y2=√1+1k2⋅√Δ|a|AB=√1+1k2⋅|y1−y2|=√1+1k2⋅√(y1+y2)2−4y1y2=√1+1k2⋅√Δ|a|,
(∆=b2−4acΔ=b2−4ac,注意对公式推导的理解,其本质是两点距离公式)
中点弦
① 涉及到中点弦问题可用点差法求解,在处理双曲线的中点弦问题要注意检验!
② “点差法” 的常见题型:求中点弦方程、求 (过定点、* 行弦) 弦中点轨迹、垂直 * 分线问题.
双曲线常见的结论
(选学内容,证明可见另一专题《圆锥曲线常见二级结论》)
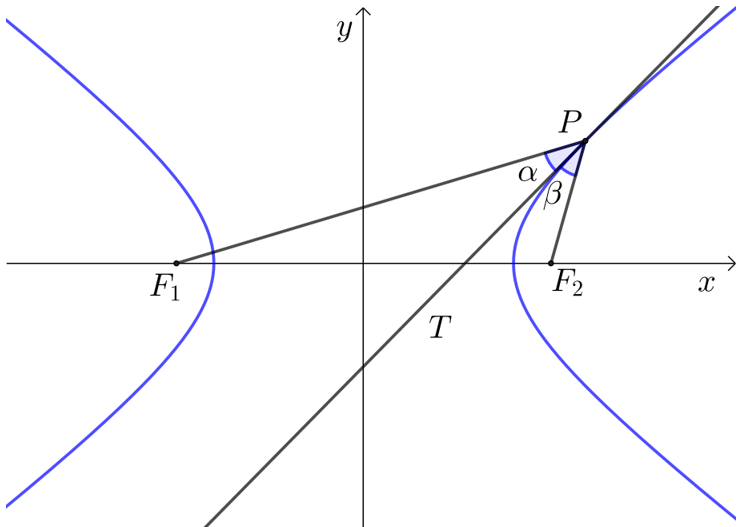
(1) 双曲线点 PP 处的切线 PTPT* 分 △PF1F2△PF1F2 在点 PP 处的内角.
(2) 双曲线 x2a2−y2b2=1(a>0,b>0)x2a2−y2b2=1(a>0,b>0) 的焦半径公式:
当 M(x0,y0)M(x0,y0) 在右支上时, MF1=ex0+aMF1=ex0+a, MF2=ex0−aMF2=ex0−a.
当 M(x0,y0)M(x0,y0) 在左支上时, MF1=−ex0+aMF1=−ex0+a, MF2=−ex0−aMF2=−ex0−a.
(3) ABAB 是双曲线 x2a2−y2b2=1(a>0,b>0)x2a2−y2b2=1(a>0,b>0) 的不 * 行于对称轴的弦, M(x0,y0)M(x0,y0) 为 ABAB 的中点,
则 kOM⋅kAB=b2a2kOM⋅kAB=b2a2,即 kAB=b2x0a2y0kAB=b2x0a2y0.
(4) 已知双曲线 x2a2−y2b2=1(a>0,b>0)x2a2−y2b2=1(a>0,b>0),OO 为坐标原点,PP、QQ 为双曲线上两动点,且 OP⊥OQOP⊥OQ.
(i) 1OP2+1OQ2=1a2−1b21OP2+1OQ2=1a2−1b2 ; (ii) OP2+OQ2OP2+OQ2 的最小值为 4a2b2b2−a24a2b2b2−a2(或 4a2b2a2−b24a2b2a2−b2).
(5) 若 P0(x0,y0)P0(x0,y0) 在双曲线 x2a2−y2b2=1(a>0,b>0)x2a2−y2b2=1(a>0,b>0) 上,则过 P0P0 的双曲线的切线方程是 x0xa2−y0yb2=1x0xa2−y0yb2=1.
(6) 过双曲线 x2a2−y2b2=1(a>0,b>0)x2a2−y2b2=1(a>0,b>0) 上任意一点 PP(不是其顶点) 作椭圆切线 PAPA,则有 kPA⋅kOP=e2−1kPA⋅kOP=e2−1 .
(7) 过直线 mx+ny=1(m≠0)mx+ny=1(m≠0) 且在双曲线 x2a2−y2b2=1(a>0,b>0)x2a2−y2b2=1(a>0,b>0) 外一点 MM 向双曲线引两条切线,切点分别为 AA,BB,
则直线 ABAB 必过定点 N(ma2,nb2)N(ma2,nb2).
基本方法
【题型1】直线与双曲线的位置关系与弦长问题
【典题 1】已知双曲线 x2−y24=1x2−y24=1,过点 P(1,1)P(1,1) 的直线 ll 与双曲线只有一个公共点,求直线 ll 的方程.
解析 方法 1 代数法
(1) 当直线 ll 的斜率不存在时,直线 ll 的方程为 x=1x=1,与双曲线 x2−y24=1x2−y24=1 只有一个交点,满足题意;
(2) 当直线 ll 的斜率存在时,设直线 ll 方程为 y=k(x−1)+1y=k(x−1)+1,
联立方程得 {y=k(x−1)+1x2−y24=1 得 (4−k2)x2+(2k2−2k)x−k2+2k−5=0(∗),
(i) 当 4−k2=0 时,k=±2,方程 (∗) 变成 4x−5=0 或 12x−13=0,方程只有一个根,
即直线 l 与双曲线只有一个交点,满足题意,
此时直线 l 的方程为 2x−y−1=0 或 2x+y−3=0;
(ii) 当 4−k2≠0,即 k≠±2 时,要满足题意则要 △=0,解得 k=52,
此时直线方程为 y=52x−32,即 5x−2y−3=0.
综上所述,直线 l 的方程为 x=1 或 2x−y−1=0 或 2x+y−3=0 或 5x−2y−3=0.
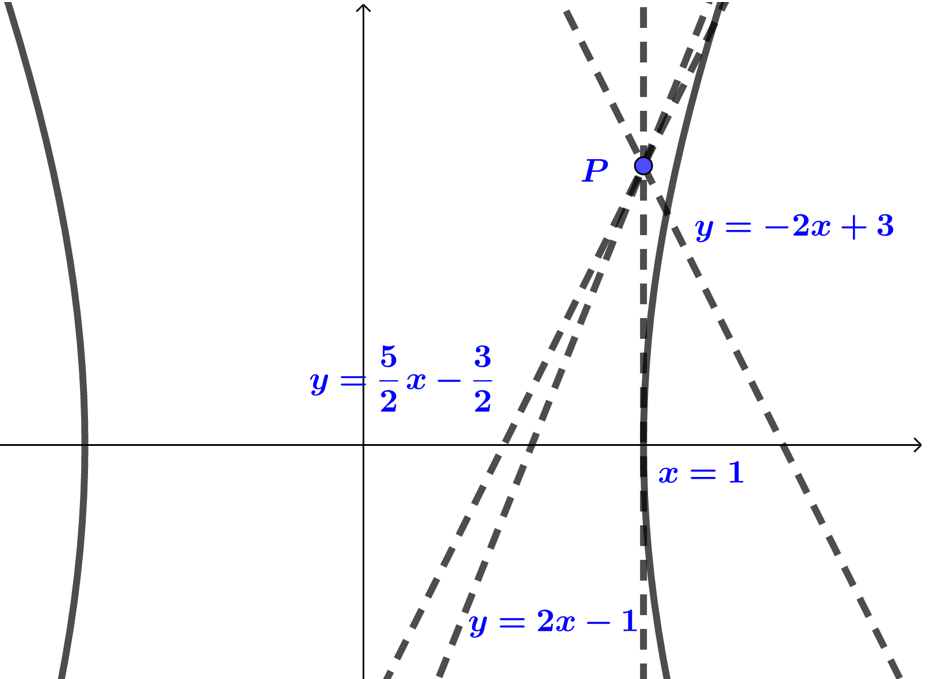
方法 2 几何法
双曲线 x2−y24=1 的渐 * 线方程为 y=±2x,
(1) 直线 l:x=1 与双曲线只有一个公共点;
(2) 直线 l* 行于渐 * 线 y=±2x 时,直线 l 与双曲线只有一个公共点,
方程为 y−1=±2(x-1),即 2x−y−1=0 或 2x+y−3=0;
(3) 直线 l 不 * 行于渐 * 线 y=±2x 时,设过 P 的直线方程为 y−1=k(x−1),(k≠±2)
由 {y=k(x−1)+1x2−y24=1 得 (4−k2)x2+(2k2−2k)x−k2+2k−5=0,
只有一个交点,即 △=0,解得 k=52,
此时直线方程为 y=52x−32,即 5x−2y−3=0.
故直线 l 的方程为 x=1 或 2x−y−1=0 或 2x+y−3=0 或 5x−2y−3=0.
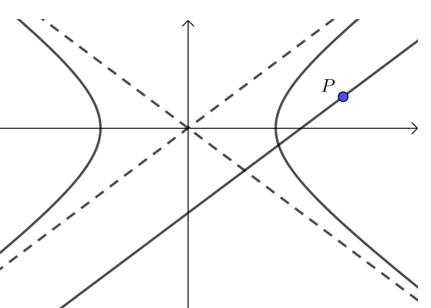
点拨 从几何的角度看,直线与双曲线 x2a2−y2b2=1(a>0,b>0) 的位置关系与渐 * 线 y=bax 有关,
(1) 当点 P 在双曲线上或内,
当 k=ba 或 k=−ba 时,只有 1 个交点;当 k≠±ba 时,只有 2 个交点;
(2) 当点 P 在双曲线外,
当 k=ba 或 k=−ba 时,只有 0 或 1 个交点;
当 k>ba 或 k<−ba 时,只有 0 或 2 个交点;
当 0<k<ba 或 −ba<k<0 时,只有 2 个交点.
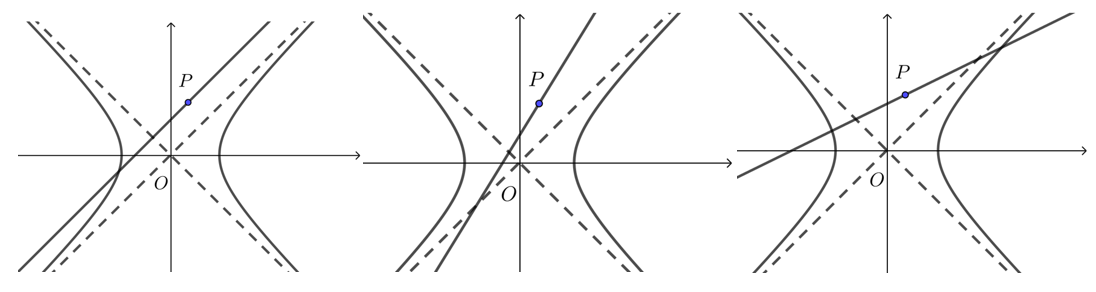
做题时注意特殊情况:斜率 k 不存在的直线.
【典题 2】已知双曲线 x2a2−y2b2=1(a>0,b>0) 的离心率为 2,焦点到渐 * 线的距离等于 √3,,过右焦点 F2 的直线 l 交双曲线于 A、B 两点,F1 为左焦点.
(1) 求双曲线的方程;
(2) 若 △F1AB 的面积等于 6√2,求直线 l 的方程.
解析 (1)∵ 双曲线 x2a2−y2b2=1(a>0,b>0) 的渐 * 线方程为 bx±ay=0,
∴ 双曲线焦点 (±c,0) 到渐 * 线的距离为 |bc|√b2+a2=b=√3,
又 ∵ 双曲线离心率 e=ca=2
∴c=2a,* 方得 c2=a2+b2=a2+3=4a2,解得 a=1,
因此双曲线的方程为 x2−y23=1.
(2) 方法 1 设 A(x1,y1),B(x2,y2),
当直线 l 的斜率不存在,则直线 l 的方程 x=2,此时易得 S△F1AB=12≠6√2,
故可设直线 l 的方程为 y=k(x−2)
由 {y=k(x−2)x2−y23=1,消元得 (k2−3)x2−4k2x+4k2+3=0,
∵ 有两个交点, ∴k≠±√3,且 x1+x2=4k2k2−3, x1x2=4k2+3k2−3,
∴|AB|=√1+k2⋅√(x1+x2)2−4x1x2=√1+k2⋅6√k2+1k2−3=6(k2+1)k2−3,
∵F1(−2,0) 到直线 l 的距离为: d=4|k|√1+k2,
∴△F1AB 的面积 S=12⋅d⋅|AB|=12⋅4|k|√1+k2⋅6(k2+1)k2−3=12|k|⋅√k2+1k2−3=6√2,
∴k4+8k2−9=0,解得 k=±1,
∴ 所以直线 l 的方程为 y=±(x−2).
方法 2 设 A(x1,y1),B(x2,y2),
同方法 1 可得: k≠±√3,且 x1+x2=4k2k2−3, x1x2=4k2+3k2−3,
∴y1−y2=k(x1−x2),
∴△F1AB 的面积 S=12|F1F2||y1−y2|=2|k||x1−x2|=2|k|√(4k2)2−4(k2−3)(4k2+3)|k2−3|=12|k|√k2+1|k2−3|=6√2,
两边去分母并且 * 方整理,得 k4+8k2−9=0,解之得 k2=1,
∴k=±1,得直线 l 的方程为 y=±(x-2).
点拨
1. 过一定点设直线方程为 y=kx+m,但要注意斜率是否存在,也设直线方程为 x=ty+m;
2. 求三角形面积可以用 S△=12⋅AB⋅d_,_其中 AB 为弦长,d 为 F2 到直线 AB 的距离;或用 S△=12|F1F2||y1−y2|.
巩固练习
1. 双曲线 x2−y2=1 与直线 x−y=1 交点的个数为 ( )
A.0 B.1 C.2 D.4
2. 已知双曲线 x212−y24=1 的右焦点为 F,若过点 F 的直线与双曲线的右支有且只有一个交点,则该直线斜率的取值范围是 ( )
A. (−√33,√33) B. (−√3,√3) C. [−√33,√33] D. [−√3,√3]
3. 已知双曲线 C:x2a2−y2b2=1(a>0,b>0) 的离心率为 √5,虚轴长为 4.
(1) 求双曲线的标准方程;
(2) 过点 (0,1),倾斜角为 45° 的直线 l 与双曲线 C 相交于 A、B 两点,O 为坐标原点,求 ∆OAB 的面积.
4. 已知双曲线 C:x2a2−y2b2=1(a>0,b>0) 的右焦点 F(2,0),一条渐 * 线的倾斜角为 30∘.
(1) 求双曲线 C 的方程;
(2) 经过点 F 的直线与双曲线的右支交于 A,B 两点,与 y 轴交于 P 点,点 P 关于原点的对称点为点 Q,求证: S△QAB>4√33.
参考答案
- 答案 B
解析 联立方程可得 {x2−y2=1x−y=1,消 y 可得 x2−(x−1)2=1,
即 2x−1=1,故 x=1,
故方程组有且只有一组解,
故双曲线 x2−y2=1 与直线 x−y=1 有且只有一个交点;
故选:B. - 答案 C
解析 渐 * 线方程 y=±√33x,
当过焦点的两条直线与两条渐 * 线 * 行时,
这两条直线与双曲线右支分别只有一个交点 (因为双曲线正在与渐 * 线无限接 * 中),
那么在斜率是 [−√33,√33] 两条直线之间的所有直线中,
都与双曲线右支只有一个交点.
此直线的斜率的取值范围 [−√33,√33].
故选:C. - 答案 (1) x2−y24=1 (2) 43
解析 (1) 依题意可得 {ca=√52b=4c2=a2+b2 ,解得 a=1,b=2, c=√5,
∴ 双曲线的标准方程为 x2−y24=1.
(2) 直线 l 的方程为 y=x+1,
设 A(x1,y1),B(x2,y2),
由 {y=x+1x2−y24=1 可得 3x2−2x−5=0,
由韦达定理可得 x1+x2=23,x1x2=−53
即 |AB|=√1+k2⋅√(x1+x2)2−4x1x2=√2⋅√49+203=8√23
原点到直线 l 的距离为 d=√22,
于是 S△OAB=12⋅|AB|⋅d=12⋅8√23⋅√22=43,
∴∆OAB 的面积为 43. - 答案 (1) x23−y2=1 (2) 略
解析 (1) 由题意得 c=2, ba=tan30∘=√33,c2=a2+b2
解得 a2=3,b2=1
所以双曲线 C 的方程为 x23−y2=1.
(2) 证明:由题意知直线的斜率存在,设直线方程为 y=k(x−2),得 P(0,−2k),Q(0,2k),
设 A(x1,y1),B(x2,y2),
联立 {x23−y2=1y=k(x−2),整理可得 (3k2−1)x2−12k2x+12k2+3=0,
x1+x2=12k23k2−1, x1⋅x2=12k2+33k2−1,
所以 S△QAB=|S△QPB−S△QPA|=12|PQ‖x1−x2|=2|k||x1−x2|
所以 S2△QAB=4k2[(x1+x2)2−4x1x2]=4k2[(12k23k2−1)2−4(12k2+3)3k2−1]=48k2(k2+1)(3k2−1)2,
直线与双曲线右支有两个交点,
所以 x1+x2=12k23k2−1>0, x1⋅x2=12k2+33k2−1>0
所以 3k2>1,
设 t=3k2−1>0,
S2△QAB=48(t+1)3⋅(t+13+1)t2=163(4t2+5t+1)=643(1t+58)2−3>643×2564−3=163,
所以 S△QAB>4√33.
【题型2】直线与双曲线的综合题型
【典题 1】 动点 M(x,y) 与定点 F(4,0) 的距离和 M 到定直线 l:x=94 的距离的比是常数 43,求动点 M 的轨迹,
解析 如图,设 d 是点 M 直线 l:x=94 的距离,
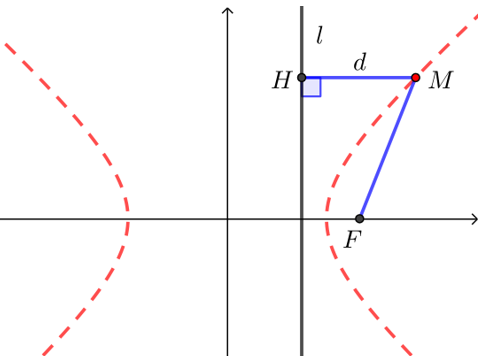
根据题意,得 √(x−4)2+y2|x−94|=43,化简得 7x2−9y2=63,即 x29−y27=1,
所以动点 M 的轨迹是焦点在 x 轴上,实轴长为 6、虚轴长为 2√7 的双曲线.
点拨 这是双曲线的第二定义,其中直线 l:x=94 叫做准线,距离之比 43 为双曲线离心率.
【典题 2】已知双曲线 x2a2−y2b2=1(a>0,b>0) 渐 * 线方程为 y=±√3x,O 为坐标原点,点 M(−√3,√3) 在双曲线上.
(1) 求双曲线的方程;
(2) 已知 P,Q 为双曲线上不同两点,点 O 在以 PQ 为直径的圆上,求 1|OP|2+1|OQ|2 的值.
解析 (1)∵x2a2−y2b2=1(a>0,b>0) 渐 * 线方程为 y=±√3x,
∴ 设双曲线方程为 (y+√3x)(y−√3x)=λ,λ≠0,即 y2-3x2=λ,
∵O 为坐标原点,点 M(−√3,√3) 在双曲线上,
∴(√3)2−3(−√3)2=λ,解得 λ=−6,
∴ 双曲线方程为 y2−3x2=−6,即 x22−y26=1,
(2)∵ 直线 l 与双曲线交于 P、Q 两点,以弦 PQ 为直径的圆经过原点 O,
∴OP⊥OQ,
设直线 OP 的方程为 y=kx,(k≠0)
代入 λx2−y26=1 中,得 {x2=63−k2y2=6k23−k2,
∴|OP|2=x2+y2=6(k2+1)3−k2,同理,得 |OQ|2=6(k2+1)3k2−1,
∴1|OP|2+1|OQ|2=13 .
点拨 这是定值问题,引入变量表示所求量,最后确定所求值与变量无关,这是常见解题思路。比如本题用 k 表示 |OP|2 与 |OQ|2,最后通过运算确定 1|OP|2+1|OQ|2 的值与 k 无关.
【典题 3】已知双曲线 C 过点 (4,√3),且渐 * 线方程为 y=±12x,直线 l 与曲线 C 交于点 M、N 两点.
(1) 求双曲线 C 的方程;
(2) 若直线 l 过点 (1,0),问在 x 轴上是否存在定点 Q,使得 →QM⋅→QN 为常数?若存在,求出点坐标及此常数的值;若不存在,说明理由.
解析 (1) 因为双曲线 C 过点 (4,√3),且渐 * 线方程为 y=±12x,
所以 {16a2−3b2=1ba=12,解得 b2=1,a2=4
所以双曲线的方程为 x24−y2=1.
(2) 设直线 l 的方程为 x=my+1,设定点 Q(t,0),
联立方程组 {x24−y2=1x=my+1,消 x 可得 (m2−4)y2+2my−3=0,
所以 m2−4≠0,且 △=4m2+12(m2-4)>0,解得 m2>3 且 m2≠4.
设 M(x1,y1),N(x2,y2),
所以 y1+y2=−2mm2−4, y1y2=−3m2−4,
所以 x1+x2=m(y1+y2)+2=−2m2m2−4+2=−8m2−4
x1x2=(my1+1)(my2+1)=m2y1y2+m(y1+y2)+1
=−3m2−4−2mm2−4+1=−4m2+4m2−4=−4−20m2−4
所以 →QM⋅→QN=(x1−t,y1)(x2−t,y2)=(x1−t)(x2−t,)+y1y2
=x1x2−t(x1+x2)+y1y2=x1x2−t(x1+x2)+t2+y1y2
=−4−20m2−4+t⋅8m2−4−3m2−4+t2
=−4+t2+8t−23m2−4 为常数,与 m 无关,
所以 8t−23=0,解得 t=238,
此时 →QM⋅→QN=27364.
点拨 这是定点问题,先设元 (设定点坐标) 再根据已知条件求出其元的值,从而确定定点.
巩固练习
1. 双曲线 E:x2a2−y2b2=1(a>0,b>0) 被斜率为 4 的直线截得的弦 AB 的中点为 (2,1),则双曲线 E 的离心率为 ( )
A. √2 B. √3 C.2 D. √5
2. 已知双曲线 x2a2−y2b2=1(a>0,b>0) 的渐 * 线为 y=±√3x,过右焦点 F 的直线 l 与双曲线交于 A,B 两点且 →AF=3→FB,则直线 l 的斜率为 ( )
A. ±√3 B. ±√15 C.±1 D. ±√5
3. 已知双曲线 Γ:x2a2−y2b2=1(a>0,b>0),O 为坐标原点.
(1) 若 Γ 为等轴双曲线,且 Γ 的右焦点 F 到点 O 的距离为 2,求 Γ 的方程;
(2) a=√2, b=√3,设斜率为 1 的直线 l 交 Γ 于 P、Q 两点,且 OP⊥OQ,若 l 与圆 x2+y2=r2(r>0) 相切,求 r 的值.
4. 已知双曲线的方程 C:2x2−y2=1.
(1) 求点 P(0,1) 到双曲线 C 上点的距离的最小值;
(2) 已知圆 M:x2+y2=1 的切线 l(直线 l 的斜率存在) 与双曲线 C 交于 A、B 两点,那么 ∠AOB 是否为定值?如果是,求出定值;如果不是,请说明理由.
参考答案
- 答案 B
解析 设 A(x1,y1),B(x2,y2) 代入双曲线方程作差有 (x1−x1)(x1+x2)a2=(y1−y2)(y1+y2)b2,
双曲线 E:x2a2−y2b2=1(a>0,b>0) 被斜率为 4 的直线截得的弦 AB 的中点为 (2,1),
所以 x1+x2=4,y1+y2=2,
有 b2a2=(y1−y2)(y1+y2)(x1−x2)(x1+x2)=2,所以 c2a2=3, e=√3,
故选:B. - 答案
解析 双曲线 x2a2−y2b2=1(a>0,b>0) 的渐 * 线为 y=±√3x,可得 b=√3a,c=2a,
双曲线的方程即为 3x2−y2=3a2,
由 →AF=3→FB,可得 A,F,B 三点共线,且 A,B 均在双曲线的右支上,
设 A,B 的纵坐标分别为 y1,y2,可得 −y1=3y2,①
可设直线 l 的方程为 x=my+c,即 x=my+2a,
联立双曲线的方程 3x2−y2=3a2,可得 (3m2−1)y2+12amy+9a2=0,
可得 y1+y2=−12am3m2−1, y1y2=9a23m2−1,②
联立①②可得 −3⋅36a2m2(3m2−1)2=9a23m2−1,
化为 15m2=1,解得 m=±√1515,
则直线 l 的斜率为 ±√15.
故选:B. - 答案 (1) x22−y22=1 (2) √6
解析 (1)Γ 为等轴双曲线,可得 a=b,
由 Γ 的右焦点 F(c,0) 到点 O 的距离为 2,可得 c=2,即 a2+b2=4,
解得 a=b=√2,
则双曲线的方程为 x22−y22=1;
(2) 由题意可得 Γ:x22−y23=1,,设直线 l:y=x+m,P(x1,y1),Q(x2,y2),
将直线方程代入双曲线方程,并化简得 x2−4mx−(2m2+6)=0,
则 △=16m2−4(2m2+6)>0,解得 m>√3 或 m<−√3,
且 x1+x2=4m,x1x2=−2m2−6,(∗)
∵OP⊥OQ,
∴x1x2+y1y2=x1x2+(x1+m)(x2+m)=2x1x2+m(x1+x2)+m2=0,
将 (∗) 代入,得 m2=12,
∴m=±2√3,
又直线 l 与圆相切,可得 r=d=|m|√2=√6. - 答案 (1) √306 (2) 90°
解析 (1) 设 Q(a,b) 为双曲线上的点,则 2a2−b2=1,
则 |PQ|=√a2+(b−1)2=√32b2−2b+32=√32(b−23)2+56,
当 b=23 时 |PQ| 最小,且为 √306,
所以点 P(0,1) 到双曲线 C 上点的距离的最小值为 √306;
(2) 设直线 l 的方程为 y=kx+t,
由直线 l 与圆相切,可得 d=|t|√1+k2=1,即 t2=1+k2,
设 A(x1,y1),B(x2,y2),联立 {y=kx+t2x2−y2=1,
可得 (2−k2)x2−2ktx−t2−1=0,
则 2−k2≠0, x1+x2=2kt2−k2,x1x2=−t2+12−k2=−2+k22−k2
所以 y1y2=(kx1+t)(kx2+t)=k2x1x2+kt(x1+x2)+t2
=−k2t2−k2+2k2t2+2t2−k2t22−k2=2t2−k22−k2=2+k22−k2,
所以 →OA⋅→OB=x1x2+y1y2=−2+k22−k2+2+k22−k2=0,
所以 ∠AOB 为定值 90°.
分层练习
【A组---基础题】
1. 直线 y=kx(k>0) 与双曲线 x22−y26=1 没有交点,则 k 的取值范围为 ( )
A. [√33,+∞) B.(2,+∞) C. [√3,+∞) D. (0,√3)
2. 过双曲线 x23−y2=1 的右焦点 F,作倾斜角为 60° 的直线 l, 交双曲线的渐 * 线于点 A、B,O 为坐标原点,则 △OAB 的面积为 ( )
A. √3 B.3 C. 3√32 D.6
3. 已知倾斜角为 π4 的直线与双曲线 C:x2a2−y2b2=1(a>0,b>0) 相交于 A,B 两点,M(4,2) 是弦 AB 的中点,则双曲线的离心率为 _ .
4. 已知曲线 C:x2−y2=1 及直线 l:y=kx−1.且直线 l 与双曲线 C 有两个不同的交点 A,B.
(1) 求实数 k 的取值范围;
(2)O 是坐标原点,且 △AOB 的面积为 √2,求实数 k 的值.
5. 已知双曲线 C:x2a2−y2b2=1(a>0,b>0) 的焦距为 2√5,且过点 A(2√2,−1),直线 l 与曲线 C 右支相切 (切点不为右项点),且 l 分别交双曲线 C 的两条渐 * 线与 M,N 两点,O 为坐标原点.
(1) 求双曲线 C 的方程;
(2) 求证:△MON 面积为定值,并求出该定值.

6. 已知 F1(−2,0),F2(2,0),点 P 满足 |PF1|−|PF2|=2,记点 P 的轨迹为 E.
(1) 求轨迹 E 的方程;
(2) 若直线 l 过点 F2 且与轨迹 E 交于 P、Q 两点.无论直线 l 绕点 F2 怎样转动,在 x 轴上总存在定点 M(m,0),使 MP⊥MQ 恒成立,求实数 m 的值.
参考答案
-
答案 C
解析 双曲线 x22−y26=1 的渐 * 线方程为: y=±√3x,
根据双曲线的性质可知直线 y=kx(k>0) 与双曲线 x22−y26=1 没有交点,满足 k≥√3.
故选:C. -
答案 C
解析 不妨设点 A 在第一象限,点 B 在第四象限,因为 ∠OFB=60°,
双曲线 x23−y2=1 的渐 * 线方程 y=±√33x,
所以 ∠AOF=30°,所以 ∠FOB=30°,
所以 ∠OBA=∠OBF=90°,所以 |OB|=|OF|cos30∘=√3.
又 ∠AOB=60°,则 ∠OAB=30°,所以 |OA|=2|OB|=2√3,所以 |AB|=3,
从而 △OAB 的面积为: 12⋅|OA||OB|sin60∘=3√32.
故选:C.

-
答案 √62
解析 设 A、B 的坐标分别为 (x1,y1),(x2,y2),
则 {x21a2−y21b2=1x22a2−y22b2=1,两式相减,整理得, y1−y2x1−x2=b2(x1+x2)a2(y1+y2),
∵ 直线 AB 的倾斜角为 π4,且弦 AB 的中点为 M(4,2),
∴tanπ4=b2×4a2×2,得 b2a2=12,
∴ 离心率 e=√c2a2=√1+b2a2=√1+12=√62. -
答案 (1) {k∣−√2<k<√2, 且 k≠±1} (2) ±√62
解析 (1) 设 A(x1,y1),B(x2,y2),
联立 {y=kx−1x2−y2=1,整理可得 (1−k2)x2+2kx−2=0,
当 {1−k2≠0Δ=4k2−4(1−k2)(−2)>0 时,直线 l 与双曲线由两个不同的交点,
即 {k≠1 且 k≠−1−√2<k<√2,
所以 k 的取值范围为 {k∣−√2<k<√2, 且 k≠±1};
(2) 由 (1) 可知 x1+x2=−2k1−k2, x1x2=−21−k2,
所以弦长 |AB|=√1+k2⋅√(x1+x2)2−4x1x2=√1+k2⋅√4k2(1−k2)2−4⋅−21−k2
=√1+k2⋅√8−4k2|1−k2| ,
原点 O 到直线 AB 的距离 d=1√1+k2,
所以 S△AOB=12⋅|AB|⋅d=12⋅√1+k2⋅√8−4k2|1−k2|⋅1√1+k2=√2−k2(1−k2)2,
由题意 √2=√2−k2(1−k2)2,解得: k=±√62 符合题意,
所以实数 k 的值为 ±√62.

-
答案 (1) x24−y2=1 (2) 2
解析 (1) 设双曲线的焦距为 2c,由题意可得 {2c=2√5c2=a2+b28a2−1b2=1,解得 a2=4,b2=1
所以双曲线的方程为 x24−y2=1;
(2) 证明:设直线 l 的方程:y=kx+m,直线与曲线的右支相切 (切点表示右顶点)
则 {y=kx+mx24−y2=1,整理可得: (4k2−1)x2+8kmx+4m2+4=0,
△=64k2m2−4(4k2−1)(4m2+4)=0,可得 4k2=m2+1,①
设直线 l 与 x 轴交于一点 D,则 OD=−mk,
S△OMN=S△MOD+S△NOD=12|OD||yM−yN|=−m2k|k||xM−xN|,
双曲线的渐 * 线的方程为 y=±12x,
联立 {y=12xy=kx+m,可得 M(2m1−2k,m1−2k),
同理可得 N(−2m1+2k,m1+2k),
则 S△MON=−m2k|k||2m1−2k+2m1+2k|=−m2k|k||4m1−4k2|,
由①及直线 l 与曲线 C 右支相切,m 与 k 异号,
则 S△MON=2. -
答案 (1) x2−y23=1(x≥1) (2) −1
解析 (1) 由 |PF1|−|PF2|=2<|F1F2| 知,点 P 的轨迹 E 是以 F1、F2 为焦点的双曲线右支,
由 c=2,2a=2, ∴b2=3,故轨迹 E 的方程为 x2−y23=1(x≥1).
(2) 当直线 l 的斜率存在时,设直线方程为 y=k(x-2),P(x1,y1),Q(x2,y2),
与双曲线方程联立消 y 得 (k2−3)x2-4k2x+4k2+3=0,
∴{k2−3≠0Δ>0x1+x2=4k2k2−3>0x1⋅x2=4k2+3k2−3>0,解得 k2>3.
∵→MP⋅→MQ=(x1−m)(x2−m)+y1y2
=(x1−m)(x2−m)+k2(x1−2)(x2−2)
=(k2+1)x1x2−(2k2+m)(x1+x2)+m2+4k2
=(k2+1)(4k2+3)k2−3−4k2(2k2+m)k2−3+m2+4k2
=3−(4m+5)k2k2−3+m2.
∵MP⊥MQ, ∴→MP⋅→MQ=0,
故得 3(1−m2)+k2(m2−4m−5)=0 对任意的 k2>3 恒成立,
∴{1−m2=0m2−4m−5=0,解得 m=−1.
∴ 当 m=-1 时,MP⊥MQ.
当直线 l 的斜率不存在时,由 P(2,3),Q(2,-3) 及 M(−1,0) 知结论也成立,
综上,当 m=−1 时,MP⊥MQ.

【B组---提高题】
1. 已知 F1,F2 为双曲线 C:x2−y2b2=1(b>0) 的左、右焦点,过 F2 作垂直于 x 轴的垂线,在 x 轴上方交双曲线 C 于点 M,且 ∠MF1F2=30°.
(1) 求双曲线 C 的两条渐 * 线的夹角 θ 的正切值;
(2) 过点 F2 的直线 l 和双曲线 C 的右支交于 A,B 两点,求 △AF1B 的面积最小值;
(3) 过双曲线 C 上任意一点 Q 分别作该双曲线两条渐 * 线的 * 行线,它们分别交两条渐 * 线于 Q1,Q2 两点,求 * 行四边形 OQ1QQ2 的面积.
参考答案
- 答案 (1) 2√2 (2) 4√3 (3) √22
解析 (1) 双曲线 C:x2−y2b2=1(b>0) 的 a=1, c=√1+b2,
可令 x=c,解得 y=b√c2−1=b2,设 M(c,b2),
由 ∠MF1F2=30°,可得 b2=2ctan30∘=2√33√1+b2,解得 b=√2,
则双曲线的方程为 x2−y22=1,
可得双曲线的方程为 y=±√2x,
即有 tanθ=|√2+√21−√2×√2|=2√2,
(2) 当直线 AB 的斜率不存在,可得 A(√3,2),B(√3,−2),
可得 △AF1B 的面积为 12×2√3×4=4√3;
直线 AB 的斜率存在,设过点 F2 的直线 l 设为 y=k(x−√3),
联立双曲线方程 2x2−y2=2,
可得 (2−k2)x2+2√3k2x−3k2−2=0,设 A(x1,y1),B(x2,y2),
又 x1+x2=−2√3k22−k2>0, x1x2=−3k2+22−k2>0,可得 k2>2,
可得 △AF1B 的面积为 S=12⋅2c⋅|y1−y2|=√3⋅|k(x1−x2)|
=√3⋅|k|⋅√(−2√3k22−k2)2+4⋅3k2+22−k2=√3|k|⋅4√1+k2k2−2,
设 t=k2−2(t>0),可得 S=4√3⋅√(2+t)(3+t)t=4√3⋅√1+5t+6t2>4√3,
综上可得 △AF1B 的面积的最小值为 4√3;
(3) 设 Q(m,n),可得 2m2−n2=2,
双曲线的渐 * 线方程为 y=±√2x,
Q 到直线 y=√2x 的距离为 d=|√2m−n|√3,
由 * 行于直线 y=−√2x 的直线 y=−√2(x−m)+n,
联立直线 y=√2x,可得 Q2(n+√2m2√2,n+√2m2),
|OQ2|=√64|n+√2m|,
即有行四边形 OQ1QQ2 的面积为
d⋅|OQ2|=√64|n+√2m|⋅|√2m−n|√3=√24⋅|2m2−n2|=√24⋅2=√22.
【C组---拓展题】
1. 在 * 面直角坐标系 xOy 中,已知点 F1(−√17,0), F2(√17,0),点 M 满足 |MF1|−|MF2|=2.记 M 的轨迹为 C.
(1) 求 C 的方程;
(2) 设点 T 在直线 x=12 上,过 T 的两条直线分别交 C 于 A,B 两点和 P,Q 两点,且 |TA|⋅|TB|=|TP|⋅|TQ|,求直线 AB 的斜率与直线 PQ 的斜率之和.
参考答案
- 答案 (1) x2−y216=1(x≥1) (2) 0
解析 (1) 由双曲线的定义可知,M 的轨迹 C 是双曲线的右支,
设 C 的方程为 x2a2−y2b2=1(a>0,b>0),x≥1,
根据题意 {c=√172a=2c2=a2+b2,解得 {a=1b=4c=√17,
∴C 的方程为 x2−y216=1(x≥1);
(2)(法一) 设 T(12,m),直线 AB 的参数方程为 {x=12+tcosθy=m+tsinθ,
将其代入 C 的方程并整理可得,
(16cos2θ−sin2θ)t2+(16cosθ−2msinθ)t−(m2+12)=0,
由参数的几何意义可知,|TA|=t1,|TB|=t2,则 t1t2=m2+12sin2θ−16cos2θ=m2+121−17cos2θ,
设直线 PQ 的参数方程为 {x=12+λcosβy=m+λsinβ, |TP|=λ1,|TQ|=λ2,
同理可得, λ1λ2=m2+121−17cos2β,
依题意, m2+121−17cos2θ=m2+121−17cos2β,则 cos2θ=cos2β,
又 θ≠β,故 cosθ=−cosβ,则 cosθ+cosβ=0,
即直线 AB 的斜率与直线 PQ 的斜率之和为 0.
(法二) 设 T(12,t),直线 AB 的方程为 y=k1(x−12)+t,
A(x1,y1),B(x2,y2),设 12<x1<x2,
将直线 AB 方程代入 C 的方程化简并整理可得
(16−k21)x2+(k21−2tk1)x−14k21+k1t−t2−16=0,
由韦达定理有, x1+x2=k21−2k1tk21−16, x1x2=−14k21+k1t−t2−1616−k21,
又由 A(x1,k1x1−12k1+t), T(12,t) 可得 ∣AT∣=√1+k21(x1−12),
同理可得 |BT|=√1+k21(x2−12),
∴|AT||BT|=(1+k21)(x1−12)(x2−12)=(1+k12)(t2+12)k12−16,
设直线 PQ 的方程为 y=k2(x−12)+t,P(x3,y3),Q(x4,y4),设 12<x3<x4,
同理可得 |PT||QT|=(1+k22)(t2+12)k22−16,
又 |AT||BT|=|PT||QT|,则 1+k21k21−16=1+k22k22−16,化简可得 k21=k22,
又 k1≠k2,则 k1=﹣k2,即 k1+k2=0,即直线 AB 的斜率与直线 PQ 的斜率之和为 0.




【推荐】国内首个 AI IDE,深度理解中文开发场景,立即下载体验 Trae
【推荐】编程新体验,更懂你的 AI,立即体验豆包 MarsCode 编程助手
【推荐】抖音旗下 AI 助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具