直线系与圆系方程
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高二数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性必修第一册同步巩固,难度2颗星!
基础知识
直线系方程
(1) 过点\((x_0 ,y_0)\)的直线系方程为\(A(x-x_0 )+B(y-y_0 )=0\)(其中\(A\) ,\(B\)不全为零)
(2) 平行于直线\(Ax+By+C=0\)的直线系方程\(Ax+By+C_0=0(C≠C_0)\);
(3) 垂直于直线\(Ax+By+C=0\)的直线系方程\(Bx-Ay+C_0=0\);
(4) 过两条已知直线\(l_1:A_1 x+B_1 y+C_1=0\)和\(l_2:A_2 x+B_2 y+C_2=0\)交点的直线系方程
\(A_1 x+B_1 y+C_1+λ(A_2 x+B_2 y+C_2 )=0\)
(\(λ∈R\) , 这个直线系下不包括直线\(l_2:A_2 x+B_2 y+C_2=0\),解题时注意检验\(l_2\)是否满足题意)
【例】写出与直线\(x-2y+1=0\)平行、垂直的直线系方程.
解析 与直线\(x-2y+1=0\)平行的直线系方程分别为\(x-2y+m=0\),
与直线\(x-2y+1=0\)垂直的直线系方程分别为\(2x+y+m=0\).
圆系方程
(1) 以\((a ,b)\)为圆心的同心圆圆系方程: \((x-a)^2+(y-b)^2=λ(λ>0)\);
(2) 与圆 \(x^2+y^2+Dx+Ey+F=0\)同心圆的圆系方程为 \(x^2+y^2+Dx+Ey+λ=0\);
(3) 过直线\(Ax+By+C=0\)与圆 \(x^2+y^2+Dx+Ey+F=0\)交点的圆系方程为 \(x^2+y^2+Dx+Ey+F+λ(Ax+By+C)=0(λ∈R)\);
(4) 过两圆 \(C_1:x^2+y^2+D_1 x+E_1 y+F_1=0\), \(C_2:x^2+y^2+D_2 x+E_2 y+F_2=0\)交点的圆系方程为 \(x^2+y^2+D_1 x+E_1 y+F_1+λ(x^2+y^2+D_2 x+E_2 y+F_2 )=0\)
(\(λ≠-1\) , 此圆系不含 \(C_2:x^2+y^2+D_2 x+E_2 y+F_2=0\))
特别地,当\(λ=-1\)时,上述方程为一次方程.
两圆相交时,表示公共弦方程;两圆相切时,表示公切线方程.
【例】直线\(l:x-2y+1=0\),圆 \(C_1:x^2+y^2+2x-2y+1=0\),圆 \(C_2:x^2+y^2+x+y=0\),写出过直线\(l\)与圆\(C_1\)交点的圆系方程,过圆\(C_1\)与圆\(C_2\)交点的曲线方程,过圆\(C_1\)与圆\(C_2\)交点的公共弦方程.
解析 过直线\(l\)与圆\(C_1\)交点的圆系方程为 \(x^2+y^2+2x-2y+1+λ(x-2y+1)=0\),
化简为 \(x^2+y^2+(2+λ)x-(2+2λ)y+1+λ=0\);
过圆\(C_1\)与圆\(C_2\)交点的曲线方程 \(x^2+y^2+2x-2y+1+λ(x^2+y^2+x+y)=0\),
化简为\((1+λ) x^2+(1+λ) y^2+(2+λ)x+(λ-2)y+1=0\),
令\(λ=-1\),得过圆\(C_1\)与圆\(C_2\)交点的公共弦方程\(x-3y+1=0\).
过圆上一点的切线方程
过圆上一点\(P(x_0 ,y_0)\)作圆 \(\odot M:(x-a)^2+(y-b)^2=r^2\)的切线\(l\)方程为\((x_0-a)(x-a)+(y_0-b)(y-b)=r^2\).
证明 向量法 向量 \(\overrightarrow{P M}=\left(a-x_{0}, b-y_{0}\right)\),设切线上任意一点\(B(x ,y)\),
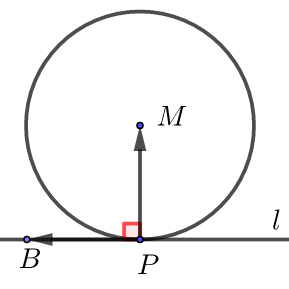
\(∵l⊥PM\), \(\therefore \overrightarrow{P M} \perp \overrightarrow{P B}\),即 \(\overrightarrow{P M} \cdot \overrightarrow{P B}=0\),
\(∴(a-x_0 ,b-y_0 )(x-x_0 ,y-y_0 )=0\)
\(⇒(a-x_0)(x-x_0)+(b-y_0)(y-y_0)=0\)
即切线\(l\)方程为\((a-x_0)(x-x_0)+(b-y_0)(y-y_0)=0\).
\(∵(a-x_0 )(x-x_0 )+(b-y_0 )(y-y_0 )=0\)
\(⇒(a-x_0 )(x-a+a-x_0 )+(b-y_0 )(y-b+b-y_0 )=0\)
\(⇒(a-x_0 )(x-a)+(a-x_0 )^2+(b-y_0 )(y-y_0 )+(b-y_0 )^2=0\)
\(⇒(a-x_0 )(x-a)+(b-y_0 )(y-y_0 )+r^2=0\)
\(⇒(x_0-a)(x-a)+(y_0-b)(y-b)=r^2\)
\(∴\)切线\(l\)方程也可以写成\((x_0-a)(x-a)+(y_0-b)(y-b)=r^2\).
【例】 求过点\((1,-2)\)作圆 \((x+2)^2+(y+1)^2=1\)的切线方程.
解析 切线方程为\((1+2)(x+2)+(-2+1)(y+1)=1\),化简为\(3x-y+4=0\).
基本方法
【题型一】直线系方程
【典题1】求过两条直线\(y=2x+3\)与\(3x-y+2=0\)的交点,且分别满足下列条件的直线方程:
(1)斜率为 \(-\dfrac{1}{2}\);\(\qquad\) (2)过点\(P(2,3)\);\(\qquad\) (3)平行于直线\(3x+y=1\).
解析 直线\(y=2x+3\)与\(3x-y+2=0\)的交点为\((1,5)\),
方法一
(1)当斜率为 \(-\dfrac{1}{2}\)时,由直线的点斜式方程得:直线方程为 \(y-5=-\dfrac{1}{2}(x-1)\).
直线方程为\(x+2y-11=0\).
(2)过点\(P(2,3)\)时,由两点式得: \(y-5=\dfrac{3-5}{2-1}(x-1)\)即为\(y=-2x+7\).
直线方程为\(2x+y-7=0\).
(3)平行于直线\(3x+y=1\)时,得直线斜率为\(k=-3\),直线方程为\(y-5=-3(x-1)\),
即直线方程为\(3x+y-8=0\).
方法二
由直线系方程可设所求直线为\(2x+3-y+λ(3x-y+2)=0\)
(1) \(2x+3-y+λ(3x-y+2)=0\)\(⇒(2+3λ)x-(λ+1)y+2λ+3=0\)
直线的斜率为 \(-\dfrac{1}{2}\)时, \(\dfrac{2+3 \lambda}{\lambda+1}=-\dfrac{1}{2}\),解得 \(\lambda=-\dfrac{5}{7}\),
故所求直线方程为\(x+2y-11=0\).
(2) 过点\(P(2,3)\)时,代入方程得 \(4+5 \lambda=0 \Rightarrow \lambda=-\dfrac{4}{5}\),
故所求直线方程为\(2x+y-7=0\).
(3) 平行于直线\(3x+y=1\)时, \(\dfrac{2+3 \lambda}{\lambda+1}=-3\),解得 \(\lambda=-\dfrac{5}{6}\),
故所求直线方程为\(3x+y-8=0\).
点拨 此题是直线系问题,从本题来看,用直线系方程的方法求解对于一般的解法也没有优势,这里只是拓展大家的思路.
巩固练习
1.求过两直线\(x-2y+4=0\)和\(x+y-2=0\)的交点\(P\),且分别满足下列条件的直线\(l\)的方程.
(1)过点\((2 ,1)\);$\qquad $ (2)和直线\(3x-4y+5=0\)垂直.
参考答案
- 答案 (1)\(x+2y-4=0\) (2)\(4x+3y-6=0\)
解析 由 \(\left\{\begin{array}{l} x-2 y+4=0 \\ x+y-2=0 \end{array}\right.\) 解得 \(\left\{\begin{array}{l} x=0 \\ y=2 \end{array}\right.\),\(∴P(0 ,2)\).
(1)设过点\(P\)的直线方程为\(x-2y+4+λ(x+y-2)=0\),
\(∵\)过点\((2 ,1)\),\(∴2-2+4+λ=0⇒λ=-4\),
故所求直线方程为\(x-2y+4-4(x+y-2)=0⇒x+2y-4=0\).
(2) 设所求直线为\(4x+3y+λ=0\),
\(∵\)过点\(P(0 ,2)\),\(∴0+6+λ=0⇒λ=-6\),
故所求直线方程为\(4x+3y-6=0\).
【题型2】过圆上一点的切线方程
【典题1】求过点\(P(-1 ,4)\),圆 \((x-2)^2+(y-3)^2=1\)的切线\(l\)的方程.
解析 方法一
当直线\(l\)斜率不存在时,方程为\(x=-1\),显然不是切线,
故可设切线方程为\(y=k(x+1)+4\),
\(∵\)直线\(l\)与圆相切,\(∴\)圆心\((2 ,3)\)到直线\(l\)的距离等于半径\(1\),
故 \(\dfrac{|3 k+1|}{\sqrt{1+k^{2}}}=1\),解得\(k=0\)或 \(-\dfrac{3}{4}\),
故所求直线\(l\)的方程为\(y=4\)或\(3x+4y-13=0\).
方法二
如方法一,设切线方程为\(y=k(x+1)+4\),
由 \(\left\{\begin{array}{c}
y=k(x+1)+4 \\
(x-2)^{2}+(y-3)^{2}=1
\end{array}\right.\)得 \((1+k^2 ) x^2+(2k^2+2k-4)x+k^2+2k-4=0\)
其判别式 \(∆=(2k^2+2k-4)^2-4(1+k^2 )(k^2+2k-4)=0\), 解得\(k=0\)或 \(-\dfrac{3}{4}\),
故所求直线\(l\)的方程为\(y=4\)或\(3x+4y-13=0\).
方法三
因为切线过点\(P(-1 ,4)\),
故可设所求直线的方程为\(A(x+1)+B(y-4)=0\)(其中\(A\) ,\(B\)不全为零),
\(∵\)直线\(l\)与圆相切,
\(∴\)圆心\((2 ,3)\)到直线\(l\)的距离等于半径\(1\),故 \(\dfrac{|3 A-B|}{\sqrt{A^{2}+B^{2}}}=1\)
整理,得\(A(4A-3B)=0\),即\(A=0\)(这时\(B≠0\))或 \(A=\dfrac{3}{4}, B \neq 0\).
故所求直线l的方程为\(y=4\)或\(3x+4y-13=0\).
点拨 本题的方法很多,这里利用了直线系方程,过点\((x_0 ,y_0)\)的直线系方程为\(A(x-x_0 )+B(y-y_0 )=0\)(其中\(A\) ,\(B\)不全为零) , 它比起斜截式\(y=kx+b\)的设法好在不用对\(k\)的存在进行讨论.
巩固练习
1.求过点\(P(1 ,3)\)且与圆 \((x+1)^2+y^2=4\)的相切的直线\(l\)的方程.
2.求过点 \(P(0, \sqrt{3})\)且与圆 \((x+1)^2+y^2=4\)的相切的直线\(l\)的方程.
参考答案
-
答案 \(x=1\)或\(5x+12y+31=0\)
解析 因为切线过点\(P(1 ,3)\),
故设所求直线的方程为\(A(x-1)+B(y-3)=0\)(其中\(A\) ,\(B\)不全为零),
\(∵\)直线\(l\)与圆相切,
\(∴\)圆心\((-1 ,0)\)到直线\(l\)的距离等于半径\(2\),
故 \(\dfrac{|-2 A-3 B|}{\sqrt{A^{2}+B^{2}}}=2\),
整理得\(B(5B+12A)=0\),即\(B=0\)(这时\(A≠0\))或 \(A=-\dfrac{5}{12}, B \neq 0\),
故所求直线\(l\)的方程为\(x=1\)或\(5x+12y+31=0\). -
答案 \(x+\sqrt{3} y-3=0\)
解析 易发现点\(P(0,\sqrt{3})\)在圆 \((x+1)^2+y^2=4\)上,
故直线\(l\)的方程为\((0+1)(x+1)+\sqrt{3}y=4\),化简得\(x+\sqrt{3}y-3=0\),
即所求直线\(l\)的方程为\(x+\sqrt{3} y-3=0\).
【题型3】圆系方程
【典题1】经过直线\(2x-y+3=0\)与圆 \(x^2+y^2+2x-4y+1=0\)的两个交点,且面积最小的圆的方程是\(\underline{\quad \quad}\).
解析 方法一
(面积最小的圆是以两个交点为直径的圆)
\(∵\)圆 \(x^2+y^2+2x-4y+1=0\)的方程可化为 \((x+1)^2+(y-2)^2=4\).
\(∴\)圆心坐标为\((-1 ,2)\),半径为\(r=2\);
\(∴\)圆心到直线\(2x-y+3=0\)的距离为 \(d=\dfrac{1}{\sqrt{5}}\),
设直线\(2x-y+3=0\)和圆 \(x^2+y^2+2x-4y+1=0\)的交点为\(A\) ,\(B\),
则 \(|A B|=2 \sqrt{r^{2}-d^{2}}=2 \sqrt{4-\dfrac{1}{5}}=\dfrac{2 \sqrt{19}}{\sqrt{5}}\),
\(∴\)过点\(A\),\(B\)的最小圆半径为 \(\dfrac{\sqrt{19}}{\sqrt{5}}\),
联立 \(\left\{\begin{array}{l}
2 x-y+3=0 \\
x^{2}+y^{2}+2 x-4 y+1=0
\end{array}\right.\)得\(5x^2+6x-2=0\),
故 \(x_{1}+x_{2}=-\dfrac{6}{5}\),
则圆心的横坐标为: \(\dfrac{1}{2}\left(x_{1}+x_{2}\right)=-\dfrac{3}{5}\),纵坐标为 \(2 \times\left(-\dfrac{3}{5}\right)+3=\dfrac{9}{5}\),
\(∴\)最小圆的圆心为 \(\left(-\dfrac{3}{5}, \dfrac{9}{5}\right)\),
\(∴\)最小圆的方程为 \(\left(x+\dfrac{3}{5}\right)^{2}+\left(y-\dfrac{9}{5}\right)^{2}=\dfrac{19}{5}\).
方法二
依题意,
可设过点\(A\)、\(B\)两点圆的方程为 \(x^2+y^2+2x-4y+1+λ(2x-y+3)=0\),
(利用圆系方程把满足题意的所有圆表示出来,再用代数的方法求面积最小的圆)
整理得 \((x+\lambda+1)^{2}+\left(y-\dfrac{4+\lambda}{2}\right)^{2}=\dfrac{5}{4} \lambda^{2}+\lambda+4\)
若要使得圆的面积最小,则只需半径最小,即 \(\dfrac{5}{4} \lambda^{2}+\lambda+4\)取到最小值,
而 \(\text { i } \dfrac{5}{4} \lambda^{2}+\lambda+4=\dfrac{5}{4}\left(\lambda+\dfrac{2}{5}\right)^{2}+\dfrac{19}{5} \geq \dfrac{19}{5}\),当 \(\lambda=-\dfrac{2}{5}\)时取到最小值,
此时圆的方程为 \(\left(x+\dfrac{3}{5}\right)^{2}+\left(y-\dfrac{9}{5}\right)^{2}=\dfrac{19}{5}\).
点拨 本题是过直线与圆交点的圆系问题.方法一可以说是从几何的角度得出思路求解,而方法二算是“代数法”,略显简洁些.
【典题2】 已知圆 \(C_1:x^2+y^2=10\)与圆 \(C_2:x^2+y^2+2x+2y-14=0\).
(1)求证:圆\(C_1\)与圆\(C_2\)相交;
(2)求两圆公共弦所在直线的方程;
(3)求经过两圆交点,且圆心在直线\(x+y-6=0\)上的圆的方程.
解析 (1)证明:(圆心距\(C_1 C_2∈(R-r ,R+r)⇔\)两圆相交)
圆 \(C_2:x^2+y^2+2x+2y-14=0\)化为标准方程为 \((x+1)^2+(y+1)^2=16\)
\(∴C_2 (-1 ,-1)\),\(r=4\)
\(∵\)圆 \(C_1:x^2+y^2=10\)的圆心坐标为\((0 ,0)\),半径为 \(R=\sqrt{10}\)
\(\therefore\left|C_{1} C_{2}\right|=\sqrt{2}\),
\(\because 4-\sqrt{10}<\sqrt{2}<4+\sqrt{10}\),\(∴\)两圆相交;
(2)(两圆方程相减所得方程即是公共弦所在直线方程)
将两圆方程相减,可得\(2x+2y-4=0\),
即两圆公共弦所在直线的方程为\(x+y-2=0\);
(3) 方法一
(先求出两个交点,再求圆心与半径得圆的方程,思路很直接)
由 \(\left\{\begin{array}{c}
x^{2}+y^{2}+2 x+2 y-14=0 \\
x^{2}+y^{2}=10
\end{array}\right.\)解得 \(\left\{\begin{array}{c}
x=3 \\
y=-1
\end{array}\right.\)或 \(\left\{\begin{array}{c}
x=-1 \\
y=3
\end{array}\right.\),(这里还是有些计算量的)
则交点为\(A(3 ,-1)\) ,\(B(-1 ,3)\),
\(∵\)圆心在直线\(x+y-6=0\)上,设圆心为\(P(6-n ,n)\),
则\(AP=BP\),解得\(n=3\),
故圆心\(P(3 ,3)\),半径\(r=AP=4\),
\(∴\)所求圆的方程为 \((x-3)^2+(y-3)^2=16\).
方法二
设所求圆的方程为 \(x^2+y^2+2x+2y-14+λ(x^2+y^2-10)=0(λ≠-1)\)
即\((1+λ) x^2+(1+λ) y^2+2x+2y-14-10λ=0\)
\(∴\)圆心坐标为 \(\left(-\dfrac{1}{1+\lambda},-\dfrac{1}{1+\lambda}\right)\)
代入直线\(x+y-6=0\)可得: \(-\dfrac{1}{1+\lambda}-\dfrac{1}{1+\lambda}-6=0\), \(\therefore \lambda=-\dfrac{4}{3}\)
\(∴\)所求圆的方程为 \(x^2+y^2-6x-6y+2=0\).
点拨 此题是过圆与圆交点的圆系问题.
① 两圆之间的位置关系看圆心距\(O_1 O_2\)与两圆半径\(R\)与\(r\)之间的关系;
② 过两圆 \(C_1:x^2+y^2+D_1 x+E_1 y+F_1=0\), \(C_2:x^2+y^2+D_2 x+E_2 y+F_2=0\)交点的圆系方程为 \(x^2+y^2+D_1 x+E_1 y+F_1+λ(x^2+y^2+D_2 x+E_2 y+F_2 )=0\)
(\(λ≠-1\) , 此圆系不含 \(C_2:x^2+y^2+D_2 x+E_2 y+F_2=0\))
特别地,当\(λ=-1\)(即两圆方程相减)时,上述方程为一次方程.
两圆相交时,表示公共弦方程;两圆相切时,表示公切线方程.
③ 方法的选取在于思考难度、计算量、严谨性性等.
巩固练习
1.求经过原点,且过圆 \(x^2+y^2+8x-6y+21=0\)和直线\(x-y+7=0\)的两个交点的圆的方程.
2.求经过圆 \(x^2+y^2+8x-6y+21=0\)与直线\(x-y+5=0\)的交点且在\(y\)轴上的弦长为 \(2 \sqrt{33}\)的圆的方程.
3.求经过两圆 \(x^2+y^2+6x-4=0\)和 \(x^2+y^2+6y-28=0\)的交点,并且圆心在直线\(x-y-4=0\)上的圆的方程.
4.已知圆 \(C_1:x^2+y^2-3x-3y+3=0\),圆 \(C_2:x^2+y^2-2x-2y=0\).
(1)求两圆的公共弦所在的直线方程及公共弦长.
(2)求过两圆交点且面积最小的圆的方程.
参考答案
- 答案 \(x^2+y^2+5x-3y=0\)
解析 (1)设圆的方程为 \(x^2+y^2+8x-6y+21+λ(x-y+7)=0\),
代入\((0,0)\),可得\(21+7λ=0\),\(∴λ=-3\),
\(∴\)圆的方程为 \(x^2+y^2+8x-6y+21-3(x-y+5)=0\),
即 \(x^2+y^2+5x-3y=0\). - 答案 \(x^2+y^2-2x+4y-29=0\)或 \(x^2+y^2+26x-24y+111=0\)
解析 设所求的圆的方程为 \((x^2+y^2+8x-6y+21)+k(x-y+5)=0\),且与\(y\)轴的交点坐标为\(y_1\)、\(y_2\),
令\(x=0\)得 \((y^2-6y+21)+k(-y+5)=0\),化简得 \(y^2-(k+6)y+21+5k=0\),
\(∴y_1+y_2=k+6\),\(y_1⋅y_2=5k+21\),
由 \(\left|y_{1}-y_{2}\right|=2 \sqrt{33}\)两边平方得\((y_1+y_2)^2-4y_1⋅y_2=132\),
\(∴(k+6)^2-4(5k+21)=132\),化简得\(k^2-8k-180=0\),
解得\(k=-10\)或\(k=18\),
\(∴\)所求圆的方程为 \((x^2+y^2+8x-6y+21)-10(x-y+5)=0\),
或 \((x^2+y^2+8x-6y+21)+18(x-y+5)=0\),
\(∴\)所求圆的方程为 \(x^2+y^2-2x+4y-29=0\)或 \(x^2+y^2+26x-24y+111=0\). - 答案 \(x^2+y^2-x+7y-32=0\)
解析 设经过两圆 \(x^2+y^2+6x-4=0\)和 \(x^2+y^2+6y-28=0\)的交点的圆的方程,
为 \((x^2+y^2+6x-4)+λ(x^2+y^2+6y-28)=0\),
即 \(x^{2}+y^{2}+\dfrac{6}{1+\lambda} x+\dfrac{6 \lambda}{1+\lambda} y-\dfrac{4+28 \lambda}{1+\lambda}=0\),
则它的圆心坐标为 \(\left(-\dfrac{3}{1+\lambda},-\dfrac{3 \lambda}{1+\lambda}\right)\).
再根据圆心在直线\(x-y-4=0\)上,可得 \(-\dfrac{3}{1+\lambda}+\dfrac{3 \lambda}{1+\lambda}-4=0\),解得\(λ=-7\),
故所求的圆的方程为 \(x^2+y^2-x+7y-32=0\). - 答案 (1) \(x+y-3=0, \sqrt{6}\) (2) \(\left(x-\dfrac{3}{2}\right)^{2}+\left(y-\dfrac{3}{2}\right)^{2}=\dfrac{3}{2}\)
解析 (1)设两圆的交点为\(A(x_1,y_1)\),\(B(x_2,y_2)\),
则\(A\)、\(B\)两点的坐标是圆 \(C_1:x^2+y^2-3x-3y+3=0\),圆 \(C_2:x^2+y^2-2x-2y=0\),联立方程组的解,
两方程相减得:\(x+y-3=0\),
\(∵A\)、\(B\)两点的坐标都满足该方程,\(∴x+y-3=0\)为所求.
将圆\(C_2\)的方程化为标准形式, \((x-1)^2+(y-1)^2=2\),
\(∴\)圆心\(C_2 (1,1)\),半径 \(r=\sqrt{2}\).
圆心\(C_2\)到直线\(AB\)的距离 \(d=\dfrac{|1+1-3|}{\sqrt{2}}=\dfrac{1}{\sqrt{2}}\), \(|A B|=\sqrt{6}\).
即两圆的公共弦长为 \(\sqrt{6}\).
(2) \(C_{1}\left(\dfrac{3}{2}, \dfrac{3}{2}\right)\),\(C_2 (1,1)\),直线\(C_1 C_2\)方程:\(x-y=0\).
\(\left\{\begin{array}{l} x-y=0 \\ x+y-3=0 \end{array}\right.\),交点为 \(\left(\dfrac{3}{2}, \dfrac{3}{2}\right)\),
即为圆的圆心,半径 \(r=\sqrt{\dfrac{3}{2}}\),
所以圆的方程是: \(\left(x-\dfrac{3}{2}\right)^{2}+\left(y-\dfrac{3}{2}\right)^{2}=\dfrac{3}{2}\).
分层练习
【A组---基础题】
1.求经过原点且经过以下两条直线的交点的直线的方程:\(l_1:x-2y+2=0\),\(l_2:2x-y-2=0\);
2.已知直线\(x+2y=0\)与圆 \(x^2+y^2-2x=0\)的交点为\(A\)、\(B\),
(1)求弦长AB;\(\qquad\) (2)求过A、B两点且面积最小的圆的方程.
3.求圆心在直线\(3x+4y-1=0\)上,且过两圆 \(x^2+y^2-x+y-2=0\)与 \(x^2+y^2=5\)交点的圆的方程.
4.过圆 \(x^2+y^2=4\)内一点\(A(1 ,1)\)作一弦交圆于\(B\)、\(C\)两点,过点\(B\)、\(C\)作圆的切线\(PB\)、\(PC\),求点\(P\)的轨迹方程.
5.已知点\(M(2,-2)\),圆 \(O:x^2+y^2=3\)(\(O\)为坐标原点).
(1)求经过\(M\),以及圆\(O\)与圆 \(x^2+y^2+3x=0\)交点的圆的方程;
(2)过点\(M\)向圆\(O\)引两条切线,切点分别为\(A\),\(B\),求直线\(AB\)的方程.
6.已知圆\(C\)的圆心在\(x\)轴的正半轴上,半径为\(2\),且被直线\(l:4x-3y-3=0\)截得的弦长为2√3.
(1)圆\(C\)的方程;
(2)设\(P\)是直线\(x+y+4=0\)上动点,过点\(P\)作圆\(C\)的切线\(PA\),切点为\(A\),证明:经过\(A\),\(P\) ,\(C\)三点的圆必过定点,并求所有定点坐标.
参考答案
-
答案 \(y=x\)
解析 方法一 方程组 \(\left\{\begin{array}{l} x-2 y+2=0 \\ 2 x-y-2=0 \end{array}\right.\)得 \(\left\{\begin{array}{l} x=2 \\ y=2 \end{array}\right.\)
所以\(l_1\)与\(l_2\)的交点是\((2,2)\).
设经过原点的直线方程为\(y=kx\),把点\((2,2)\)的坐标代入以上方程,得\(k=1\),
所以所求直线方程为\(y=x\).
方法二 过直线\(l_1\)与\(l_2\)的交点的直线可设为\(x-2y+2+λ(2x-y-2)=0\)
因为过原点,故\(2-2λ=0⇒λ=1\),
则所求直线方程为\(y=x\). -
答案 (1) \(\dfrac{4}{5} \sqrt{5}\) (2) \(\left(x-\dfrac{4}{5}\right)^{2}+\left(y+\dfrac{2}{5}\right)^{2}=\dfrac{4}{5}\)
解析 (1)设\(A(x_1,y_1)\),\(B(x_2,y_2)\),则
直线\(x+2y=0\)与圆 \(x^2+y^2-2x=0\)联立,消去\(x\),可得\(5y^2+4y=0\),
\(\therefore y_{1}=0\), \(y_{2}=-\dfrac{4}{5}\),
\(∴\left\{\begin{array}{l} x_{1}=0 \\ y_{1}=0 \end{array}\right.\), \(\left\{\begin{array}{l} x_{2}=\dfrac{8}{5} \\ y_{2}=-\dfrac{4}{5} \end{array}\right.\),
\(\therefore|A B|=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}=\dfrac{4}{5} \sqrt{5}\).
(2)所求圆的圆心为\(AB\)中点 \(C\left(\dfrac{4}{5},-\dfrac{2}{5}\right)\),
所求面积最小的圆的方程是 \(\left(x-\dfrac{4}{5}\right)^{2}+\left(y+\dfrac{2}{5}\right)^{2}=\dfrac{4}{5}\). -
答案 \(x^2+y^2+2x-2y-11=0\)
解析 设所求圆的方程为 \((x^2+y^2-x+y-2)+m(x^2+y^2-5)=0\).
整理得\((1+m) x^2+(1+m) y^2-x+y-2-5m=0\).
圆心坐标为 \(\left(\dfrac{1}{2(1+m)},-\dfrac{1}{2(1+m)}\right)\)代入\(3x+4y-1=0\)得 \(m=-\dfrac{3}{2}\),
\(∴\)所求圆的方程为 \(x^2+y^2+2x-2y-11=0\). -
答案 \(x+y=4\)
解析 设\(B(x_1,y_1)\),\(C(x_2,y_2)\),\(P(x_0,y_0)\),
则过圆 \(x^2+y^2=4\)上的\(B\),\(C\)点的切线方程分别为:
\(xx_1+yy_1=4\),\(xx_2+yy_2=4\),\(P\)点在切线上;
\(∴x_0 x_1+y_0 y_1=4\),\(x_0 x_2+y_0 y_2=4\);
\(∴\)直线\(BC\)的方程为:\(xx_0+yy_0=4\);
直线\(BC\)过点\(A(1,1)\);
\(∴x_0+y_0=4\);
\(∴\)点\(P\)的轨迹方程为\(x+y=4\).
故答案为:\(x+y=4\). -
答案 (1) \(3x^2+3y^2-5x-14=0\) (2) \(2x-2y=3\).
解析 (1)设圆的方程为 \(x^2+y^2+3x+λ(x^2+y^2-3)=0\),因为点\(M(2,-2)\)在圆上,
所以 \(\lambda=-\dfrac{14}{5}\),所求圆的方程是 \(3x^2+3y^2-5x-14=0\);
(2)以\(MO\)为直径的圆\(C\)的方程为 \(x^2+y^2-2x+2y=0\),
则由圆系方程可知圆\(C\)与圆\(O\)方程相减即得直线\(AB\)方程为是\(2x-2y=3\).
若切点弦的公式可直接得到\(2x-2y=3\). -
答案 (1) \((x-2)^2+y^2=4\) (2)\((-1 ,-3)\)和\((2 ,0)\)
解析 (1)设圆\(C\)的圆心为\((a,0)\),则圆心到直线l的距离 \(d=\dfrac{|4 a-3|}{5}\).
由题意可得, \(d^{2}+(\sqrt{3})^{2}=r^{2}\),
即 \(\dfrac{(4 a-3)^{2}}{25}+3=4\),解得\(a=2\)或 \(a=-\dfrac{1}{2}\)(舍).
\(∴\)圆\(C\)的方程为 \((x-2)^2+y^2=4\);
(2)证明:\(∵P\)是直线\(x+y+4=0\)上的点,\(∴P(m,-m-4)\).
\(∵PA\)为圆的切线,
\(∴PA⊥AC\),即过\(A\),\(B\),\(C\)三点的圆是以\(PC\)为直径的圆.
设圆上任意一点\(Q(x,y)\),则 \(\overrightarrow{P Q} \cdot \overrightarrow{C Q}=0\).
\(\because \overrightarrow{P Q}=(x-m, y+m+4)\), \(\overrightarrow{C Q}=(x-2, y)\),
\(\therefore \overrightarrow{P Q} \cdot \overrightarrow{C Q}=(x-m)(x-2)+y(y+m+4)=0\),
即 \(x^2+y^2-2x+4y+m(-x+y+2)=0\).
故 \(\left\{\begin{array}{l} x^{2}+y^{2}-2 x+4 y=0 \\ -x+y+2=0 \end{array}\right.\),解得 \(\left\{\begin{array}{l} x=-1 \\ y=-3 \end{array}\right.\)或 \(\left\{\begin{array}{l} x=2 \\ y=0 \end{array}\right.\).
因此经过\(A\),\(P\) ,\(C\)三点的圆必过定点\((-1,-3)\)和\((2,0)\).
【B组---提高题】
1.已知圆 \(C:x^2+y^2=1\),直线\(l:x+y+2=0\),\(P\)为直线\(l\)上的动点,过点\(P\)作圆\(C\)的两条切线,切点分别为\(A\),\(B\),则直线\(AB\)过定点( )
A. \(\left(-\dfrac{1}{2},-\dfrac{1}{2}\right)\) \(\qquad \qquad\) B.\((-1,-1)\) \(\qquad \qquad\) C. \(\left(-\dfrac{1}{2}, \dfrac{1}{2}\right)\) \(\qquad \qquad\) D. \(\left(\dfrac{1}{2},-\dfrac{1}{2}\right)\)
2.已知圆\(C\)的方程为 \((x+2)^2+y^2=4\),点\(M\)在圆\(C\)上运动,点\(N\)的坐标是\((2,0)\).
(1)若线段\(MN\)的中点形成的轨迹为\(G\),求轨迹\(G\)的方程;
(2)点\(P\)在直线\(x=8\)上,过\(P\)点引轨迹\(G\)的两条切线\(PA\)、\(PB\),切点为\(A\)、\(B\),求证:直线\(AB\)恒过定点.
参考答案
-
答案 \(A\)
解析 根据题意,\(P\)为直线\(l:x+y+2=0\)上的动点,设\(P\)的坐标为\((t,-2-t)\),
过点\(P\)作圆\(C\)的两条切线,切点分别为\(A\),\(B\),则\(PA⊥AC\),\(PB⊥BC\),
则点\(A\)、\(B\)在以\(PC\)为直径的圆上,
又由\(C(0,0)\),\(P(t,-2-t)\),
则以\(PC\)为直径的圆的方程为\(x(x-t)+y(y+2+t)=0\),
变形可得: \(x^2+y^2-tx+(t+2)y=0\),
则有 \(\left\{\begin{array}{l} x^{2}+y^{2}=1 \\ x^{2}+y^{2}-t x+(t+2) y=0 \end{array}\right.\),
联立可得:\(1-tx+(t+2)y=0\),
变形可得:\(1+2y-t(x-y)=0\),
即直线\(AB\)的方程为\(1+2y-t(x-y)=0\),
变形可得:\(1+2y-t(x-y)=0\),
则有 \(\left\{\begin{array}{l} 1+2 y=0 \\ x-y=0 \end{array}\right.\),解可得 \(\left\{\begin{array}{l} x=-\dfrac{1}{2} \\ y=-\dfrac{1}{2} \end{array}\right.\),
故直线\(AB\)过定点 \(\left(-\dfrac{1}{2},-\dfrac{1}{2}\right)\),
故选:\(A\). -
答案 (1) \(x^2+y^2=1\) (2) \(\left(\dfrac{1}{8}, 0\right)\)
解析 (1)设线段\(MN\)的中点\((x,y)\),则\(M(2x-2,2y)\)
\(∵NM\)在圆 \((x+2)^2+y^2=4\)上运动
\(∴(2x-2+2)^2+(2y)^2=4\),
即 \(x^2+y^2=1\)①;
(2)连接\(OA\),\(OB\),
\(∵PA\),\(PB\)是圆\(C\)的两条切线,
\(∴OA⊥AP\),\(OB⊥BP\),
\(∴A,B\)在以\(OP\)为直径的圆上,
设点\(P\)的坐标为\((8,b)\),\(b∈R\),
则线段\(OP\)的中点坐标为 \(\left(4, \dfrac{b}{2}\right)\)
\(∴\)以\(OP\)为直径的圆方程化简得: \(x^2+y^2-8x-by=0\),\(b∈R\),②
\(∵AB\)为两圆的公共弦,
\(∴\)①\(-\)②得:直线\(AB\)的方程为\(8x+by=1\),\(b∈R\),
即 \(8\left(x-\dfrac{1}{8}\right)+b y=0\),
则直线\(AB\)恒过定点 \(\left(\dfrac{1}{8}, 0\right)\).

【C组---拓展题】
1.已知直线\(l:y=kx-2\),\(M(-2 ,0)\) ,\(N(-1 ,0)\),\(O\)为坐标原点,动点\(Q\)满足 \(\dfrac{|Q M|}{|Q N|}=\sqrt{2}\),动点\(Q\)的轨迹为曲线\(C\).
(1)求曲线\(C\)的方程;
(2)若直线\(l\)与圆 \(O:x^2+y^2=2\)交于不同的两点\(A\) ,\(B\),当\(\angle A O B=\dfrac{\pi}{2}\)时,求\(k\)的值;
(3)若 \(k=\dfrac{1}{2}\),\(P\)是直线\(l\)上的动点,过点\(P\)作曲线\(C\)的两条切线\(PC\)、\(PD\),切点为\(C\)、\(D\),探究:直线\(CD\)是否过定点.
参考答案
- 答案 (1) \(x^2+y^2=2\) (2) \(\pm \sqrt{3}\) (3) \(\left(\dfrac{1}{2},-1\right)\)
解析 (1)设点\(Q(x ,y)\),依题意知 \(\dfrac{|Q M|}{|Q N|}=\dfrac{\sqrt{(x+2)^{2}+y^{2}}}{\sqrt{(x+1)^{2}+y^{2}}}=\sqrt{2}\),
整理得 \(x^2+y^2=2\),
\(∴\)曲线\(C\)的方程为 \(x^2+y^2=2\);
(2)\(∵\)点\(O\)为圆心, \(\angle A O B=\dfrac{\pi}{2}\),
\(∴\)点\(O\)到\(l\)的距离 \(d=\dfrac{\sqrt{2}}{2} r\),
\(\therefore \dfrac{2}{\sqrt{k^{2}+1}}=\dfrac{\sqrt{2}}{2} \cdot \sqrt{2} \Rightarrow k=\pm \sqrt{3}\);
(3)由题意可知:\(O\)、\(P\)、\(C\)、\(D\)四点共圆且在以\(OP\)为直径的圆上,
(对角互补的四边形的四顶点共圆)
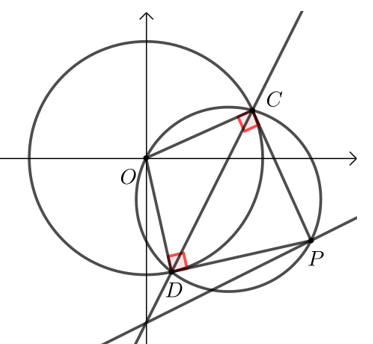
设 \(P\left(t, \dfrac{1}{2} t-2\right)\),则圆心 \(\left(\dfrac{t}{2}, \dfrac{t}{4}-1\right)\),半径 \(\sqrt{\dfrac{t^{2}}{4}+\left(\dfrac{t}{4}-1\right)^{2}}\)
得 \(\left(x-\dfrac{t}{2}\right)^{2}+\left(y-\dfrac{t}{4}+1\right)^{2}=\dfrac{\mathrm{t}^{2}}{4}+\left(\dfrac{t}{4}-1\right)^{2}\)
即 \(x^{2}-t x+y^{2}-\left(\dfrac{1}{2} t-2\right) y=0\)
又\(C\)、\(D\)在圆 \(O:x^2+y^2=2\)上
\(\therefore l_{C D}: t x+\left(\dfrac{1}{2} t-2\right) y-2=0\)即 \(\left(x+\dfrac{y}{2}\right) t-2 y-2=0\)
(直线\(CD\)是两圆的公共弦所在直线,故两圆方程相减便得其方程)
由 \(\left\{\begin{array}{l} x+\dfrac{y}{2}=0 \\ 2 y+2=0 \end{array}\right.\)得 \(\left\{\begin{array}{l} x=\dfrac{1}{2} \\ y=-1 \end{array}\right.\),
\(∴\)直线\(CD\)过定点 \(\left(\dfrac{1}{2},-1\right)\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号