2.5.2 圆与圆的位置关系
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高二数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性必修第一册同步巩固,难度2颗星!
基础知识
圆与圆的位置关系
1 在同一个平面内,两个不等的圆的位置关系共有五种:外离、外切、相交、内切、内含.
圆心距:两圆圆心的距离叫做圆心距.
2 设两圆\(⊙O_1\)与圆\(⊙O_2\)的圆心距为\(O_1 O_2=d\),半径分别为\(r\),\(R(r<R)\),则有
| 位置关系 | 交点个数 | 关系式 | 图示 |
|---|---|---|---|
| 外离 | 没有公共点 | \(d>R+r\) |  |
| 外切 | 有唯一的公共点 | \(d=R+r\) |  |
| 相交 | 有两个公共点 | \(R-r<d<R+r\) |  |
| 内切 | 有唯一的公共点 | \(d=R-r\) |  |
| 内含 | 没有公共点 | \(0≤d<R-r\) |  |
注 当两圆相切时分为两种情况:外切和内切.
判断两个圆位置关系的方法
1 几何法
通过判断圆心距与两个圆半径之间的关系从而确定两个圆的位置关系.
2 代数法
设由两圆的方程组成的方程组为 \(\left\{\begin{array}{l}
x^{2}+y^{2}+D_{1} x+E_{1} y+F_{1}=0 \\
x^{2}+y^{2}+D_{2} x+E_{2} y+F_{2}=0
\end{array}\right.\),
由此方程组得:有两组不同的实数解则两圆相交;有两组相同的实数解则两圆相切;无实数解则两圆相离.
【例】判断圆 \(⊙O_1:x^2+y^2=1\)与 \(⊙O_2:x^2+y^2-2x-4y+1=0\)的位置关系.
解析 几何法
圆 \(x^2+y^2=1\)圆心\(O_1 (0,0)\),半径\(r=1\),
\(⊙O_2:x^2+y^2-2x-4y+1=0⟹(x-1)^2+(y-2)^2=4\)圆心\(O_2 (1,2)\),半径\(r=2\),
则圆心距 \(O_{1} O_{2}=\sqrt{(1-0)^{2}+(2-0)^{2}}=\sqrt{5}\),\(R-r=3\),\(R-r=1\),
则\(R-r<O_1 O_2<R-r\),故两个圆相交.
代数法
联立方程 \(\left\{\begin{array}{c}
x^{2}+y^{2}=1 \\
x^{2}+y^{2}-2 x-4 y+1=0
\end{array}\right.\)得\(5y^2-4y=0\),显然方程组有两个实数解,
故两个圆相交.
两圆的公共弦方程
(1) 两圆 \(C_1:x^2+y^2+D_1 x+E_1 y+F_1=0\), \(C_2:x^2+y^2+D_2 x+E_2 y+F_2=0\)相交,交点为\(A\),\(B\),
则线段\(AB\)为两圆的公共弦;
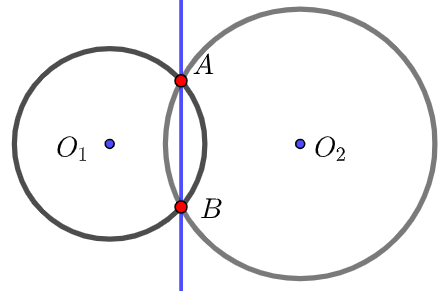
(2) 若两圆 \(C_1:x^2+y^2+D_1 x+E_1 y+F_1=0\), \(C_2:x^2+y^2+D_2 x+E_2 y+F_2=0\)相交于\(A\),\(B\)两点,
则直线\(AB\)的方程为\((D_1-D_2 )x+(E_1-E_2 )y+F_1-F_2=0\).
证明 设点\(A(x_1,y_1)\),\(B(x_2,y_2)\),
因为点\(A\)在两圆上,
所以 \(x_1^2+y_1^2+D_1 x_1+E_1 y_1+F_1=0\),且 \(x_1^2+y_1^2+D_2 x_1+E_2 y_1+F_2=0\),
两等式相减得\((D_1-D_2 ) x_1+(E_1-E_2 ) y_1+F_1-F_2=0 \quad (1)\),
同理可得\((D_1-D_2 ) x_2+(E_1-E_2 ) y_2+F_1-F_2=0 \quad (2)\),
由(1),(2)可知点\(A\),\(B\)均在直线\((D_1-D_2 )x+(E_1-E_2 )y+F_1-F_2=0\),
即直线\(AB\)的方程为\((D_1-D_2 )x+(E_1-E_2 )y+F_1-F_2=0\).
【例】若圆 \(x^2+y^2=1\)与 \(x^2+y^2+2x-2y=0\)相交于\(A\),\(B\)两点,求直线\(AB\)的方程.
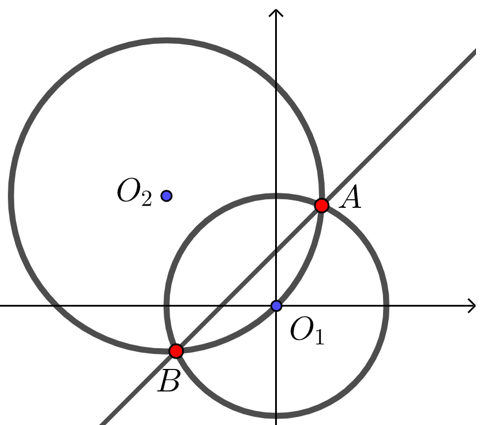
解析 两圆相减: \(x^2+y^2+2x-2y-(x^2+y^2 )=0-1\),化简得\(2x-2y+1=0\),
即直线\(AB\)的方程为\(2x-2y+1=0\).
基本方法
【题型1】两圆的位置关系
【典题1】 已知圆 \(C_1:x^2+y^2-2ax-2y+a^2-15=0\),圆 \(C_2:x^2+y^2-4ax-2y+4a^2=0(a>0)\).试求\(a\)为何值时两圆\(C_1\),\(C_2\)的位置关系为:
(1)相切; \(\qquad\) (2)相交;\(\qquad\) (3)外离; \(\qquad\) (4)内含.
解析 圆\(C_1\),\(C_2\)的方程,经配方后可得: \(C_1:(x-a)^2+(y-1)^2=16\),\(C_2:(x-2a)^2+(y-1)^2=1\),
\(∴\)圆心\(C_1 (a,1)\),\(C_2 (2a,1)\),半径\(r_1=4\),\(r_2=1\).
\(\therefore\left|C_{1} C_{2}\right|=\sqrt{(a-2 a)^{2}+(1-1)^{2}}=a\).
(1)当\(|C_1 C_2 |=r_1+r_2=5\),即\(a=5\)时,两圆外切,
当\(|C_1 C_2 |=r_1-r_2=3\),即\(a=3\)时,两圆内切.
(2)当\(3<|C_1 C_2 |<5\),即\(3<a<5\)时,两圆相交.
(3)当\(|C_1 C_2 |>5\),即\(a>5\)时,两圆外离.
(4)当\(|C_1 C_2 |<3\),即\(a<3\)时,两圆内含.
巩固练习
1.已知圆\(A\),圆\(B\)相切,圆心距为\(10 cm\),其中圆\(A\)的半径为\(4 cm\),则圆\(B\)的半径为\(\underline{\quad \quad}\) .
2.圆 \((x+2)^2+y^2=4\)与圆 \((x-2)^2+(y-1)^2=9\)的位置关系为\(\underline{\quad \quad}\).
3.两圆 \(x^2+y^2=1\)和 \((x-1)^2+(y-a)^2=4\)相切,则实数\(a\)的值\(\underline{\quad \quad}\).
4.已知点\(O(0,0)\),\(M(1,0)\),且圆 \(C:(x-5)^2+(y-4)^2=r^2 (r>0)\)上至少存在一点\(P\),使得\(|P O|=\sqrt{2}|P M|\),则\(r\)的最小值是\(\underline{\quad \quad}\).
参考答案
- 答案 \(6cm\)或\(14cm\)
解析 设圆\(B\)的半径为\(rcm\),
因为圆\(A\)、圆\(B\)相切,圆心距为\(10cm\),
①当圆\(A\)与圆\(B\)外切时,则\(r+4=10\),解得\(r=6\);
②当圆\(A\)与圆\(B\)内切时,则\(|r-4|=10\),解得\(r=14\).
故圆B半径为\(6cm\)或\(14cm\). - 答案 相交
解析 圆 \((x+2)^2+y^2=4\)的圆心\(C_1(-2,0)\),半径\(r=2\).
圆 \((x-2)^2+(y-1)^2=9\)的圆心\(C_2(2,1)\),半径\(R=3\),
两圆的圆心距离\(d=\sqrt{(-2-2)^{2}+(0-1)^{2}}=\sqrt{17}\),
\(R+r=5\),\(R-r=1\),\(R+r>d>R-r\),
所以两圆相交. - 答案 \(a=\pm 2 \sqrt{2}\)或\(a=0\)
解析 两圆圆心距为 \(\sqrt{a^{2}+1}\),因为两圆相切,
所以 \(\sqrt{a^{2}+1}=2+1\)或 \(\sqrt{a^{2}+1}=2-1\),
即 \(\sqrt{a^{2}+1}=3\)或 \(\sqrt{a^{2}+1}=1\).所以 \(a=\pm 2 \sqrt{2}\)或\(a=0\). - 答案 \(5-\sqrt{2}\)
解析 设\(P(x,y)\),
\(∵|PO|=\sqrt{2}|PM|\),
\(∴x^2+y^2=2(x-1)^2+2y^2\),即 \((x-2)^2+y^2=2\),
圆心距 \(=\sqrt{(5-2)^{2}+(4-0)^{2}}=r+\sqrt{2}\),
\(∴r\)的最小值是\(5-\sqrt{2}\).
【题型2】两圆公共弦问题
【典题1】 已知圆 \(C_1:x^2+y^2+6x-4=0\)和圆 \(C_2:x^2+y^2+6y-28=0\).
(1)求两圆公共弦所在直线的方程;
(2)求经过两圆交点且圆心在直线\(x-y-4=0\)上的圆的方程.
解析 (1)设两圆交点为\(A(x_1,y_1 )\),\(B(x_2,y_2 )\),
则\(A\),\(B\)两点坐标是方程组 \(\left\{\begin{array}{l}
x^{2}+y^{2}+6 x-4=0 \quad (1)\\
x^{2}+y^{2}+6 y-28=0 \quad (2)
\end{array}\right.\)的解.
①\(-\)②得\(x-y+4=0\).
\(∵A,B\)两点坐标都满足此方程,
\(∴x-y+4=0\)即为两圆公共弦所在直线的方程.
(2)方法一:解方程组 \(\left\{\begin{array}{l}
x^{2}+y^{2}+6 x-4=0 \\
x^{2}+y^{2}+6 y-28=0
\end{array}\right.\)两圆的交点\(A(-1,3)\),\(B(-6,-2)\).
设所求圆的圆心为\((a,b)\),因圆心在直线\(x-y-4=0\)上,
故\(b=a-4\).
则 \(\sqrt{(a+1)^{2}+(a-4-3)^{2}}=\sqrt{(a+6)^{2}+(a-4+2)^{2}}\),解得 \(a=\dfrac{1}{2}\),
故圆心为 \(\left(\dfrac{1}{2},-\dfrac{7}{2}\right)\),半径为 \(\sqrt{\dfrac{89}{2}}\).
故圆的方程为 \(\left(x-\dfrac{1}{2}\right)^{2}+\left(y+\dfrac{7}{2}\right)^{2}=\dfrac{89}{2}\),
即 \(x^2+y^2-x+7y-32=0\).
方法二:设所求圆的方程为 \(x^2+y^2+6x-4+λ(x^2+y^2+6y-28)=0(λ≠-1)\),
其圆心为 \(\left(-\dfrac{3}{1+\lambda},-\dfrac{3 \lambda}{1+\lambda}\right)\),代入\(x-y-4=0\),解得\(λ=-7\).
故所求圆的方程为 \(x^2+y^2-x+7y-32=0\).
点拨 过两圆 \(C_1:x^2+y^2+D_1 x+E_1 y+F_1=0\), \(C_2:x^2+y^2+D_2 x+E_2 y+F_2=0\)交点的圆系方程为 \(x^2+y^2+D_1 x+E_1 y+F_1+λ(x^2+y^2+D_2 x+E_2 y+F_2 )=0\)
(\(λ≠-1\), 此圆系不含 \(C_2:x^2+y^2+D_2 x+E_2 y+F_2=0\))
特别地,当\(λ=-1\)时,上述方程为一次方程.
两圆相交时,表示公共弦方程;两圆相切时,表示公切线方程.
巩固练习
1.(多选)已知圆 \(C_1:x^2+y^2=1\),圆 \(C_2:(x-3)^2+(y+4)^2=r^2 (r>0)\),则( )
A.若圆\(C_1\)与圆\(C_2\)无公共点,则\(0<r<4\)
B.当\(r=5\)时,两圆公共弦长所在直线方程为\(6x-8y-1=0\)
C.当\(r=2\)时,\(P\)、\(Q\)分别是圆\(C_1\)与圆\(C_2\)上的点,则\(|PQ|\)的取值范围为\([2,8]\)
D.当\(0<r<4\)时,过直线\(6x-8y+r^2-26=0\)上任意一点分别作圆\(C_1\)、圆\(C_2\)切线,则切线长相等
2.圆 \(x^2+y^2-2x-5=0\)和圆 \(x^2+y^2+2x-4y-4=0\)的交点为\(A\),\(B\),则线段\(AB\)的垂直平分线的方程为\(\underline{\quad \quad}\).
3.如图所示,在圆\(O\)上任取\(C\)点为圆心,作一圆\(C\)与圆\(O\)的直径\(AB\)相切于\(D\),圆\(C\)与圆\(O\)交于\(E\),\(F\),且\(EF\)与\(CD\)相交于\(H\).

求证:\(EF\)平分\(CD\).
参考答案
-
答案 \(BCD\)
解析 圆 \(C_1:x^2+y^2=1\),其圆心为\((0,0)\),半径为\(1\),
圆 \(C_2:(x-3)^2+(y+4)^2=r^2 (r>0)\),其圆心为\((3,4)\),半径为\(r\).
对于\(A\),两圆的圆心距 \(\left|C_{1} C_{2}\right|=\sqrt{9+16}=5\),
若圆\(C_1\)与圆\(C_2\)无公共点,即两圆内含或外离,
必有\(r+1<5\)或\(r-1>5\),即\(0<r<4\)或\(r>6\),故\(A\)错误;
对于\(B\),当\(r=5\)时,圆 \(C_2:(x-3)^2+(y+4)^2=25\),
联立圆\(C_1\)和圆\(C_2\)的方程可得\(6x-8y-1=0\),
即两圆公共弦长所在直线方程为\(6x-8y-1=0\),\(B\)正确;
对于\(C\),当\(r=2\)时,圆 \(C_2:(x-3)^2+(y+4)^2=r^2\),
\(P\)、\(Q\)分别是圆\(C_1\)与圆\(C_2\)上的点,
则\(|PQ|\)的最小值为\(|C_1 C_2 |-2-1=2\),最大值为\(|C_1 C_2 |+2+1=8\),
即\(|PQ|\)的取值范围为\([2,8]\),故\(C\)正确;
对于\(D\),当\(0<r<4\)时,两圆外离,
过\(P(x_0,y_0)\)引两圆\(C_1\),\(C_2\)的切线分别为\(PA\),\(PB\),
由\(|PA|=|PB|\),得 \(\left|P C_{1}\right|^{2}-1=\left|P C_{2}\right|^{2}-r^{2}\),
即 \(x_{0}^{2}+y_{0}^{2}-1=\left(x_{0}-3\right)^{2}+\left(y_{0}+4\right)^{2}-r^{2}\),
整理得: \(6x_0-8y_0+r^2-26=0,\),
可得过直线\(6x-8y+r^2-26=0\)上任意一点分别作圆\(C_1\)、圆\(C_2\)切线,则切线长相等,
故\(D\)正确.
故选:\(BCD\). -
答案 \(x+y-1=0\)
解析 \(∵\)圆 \(x^2+y^2-2x-5=0\)的圆心\(M(1,0)\),
圆 \(x^2+y^2+2x-4y-4=0\)的圆心\(N(-1,2)\),
又\(∵\)圆 \(x^2+y^2-2x-5=0\)和圆 \(x^2+y^2+2x-4y-4=0\)的交点为\(A\),\(B\),
\(∴\)线段\(AB\)的垂直平分线是\(MN\)所在的直线,
\(∴MN\)的方程为: \(\dfrac{y-0}{2-0}=\dfrac{x-1}{-1-1}\),即\(x+y-1=0\). -
证明 以\(AB\)所在直线为\(x\)轴,\(O\)为坐标原点建立平面直角坐标系.

如图,设\(|AB|=2r\),\(D(a,0)\),
则 \(|C D|=\sqrt{r^{2}-a^{2}}\), \(\therefore C\left(a, \sqrt{r^{2}-a^{2}}\right)\).
\(∴\)圆 \(O:x^2+y^2=r^2\),圆 \(C:(x-a)^{2}+\left(y-\sqrt{r^{2}-a^{2}}\right)^{2}=r^{2}-a^{2}\).
两方程作差得直线\(E F\)的方程为 \(2 a x+2 \sqrt{r^{2}-a^{2} y}=r^{2}+a^{2}\).
令\(x=a\),得 \(y=\dfrac{1}{2} \sqrt{r^{2}-a^{2}}\),
\(\therefore H\left(a, \dfrac{1}{2} \sqrt{r^{2}-a^{2}}\right)\),即\(H\)为\(CD\)的中点.
\(∴EF\)平分\(CD\).
分层练习
【A组---基础题】
1.圆 \(O_1:x^2+y^2=2\)和圆 \(O_2:x^2+y^2+4y+3=0\)的位置关系是( )
A.相离 \(\qquad \qquad\) B.外切 \(\qquad \qquad\) C.内切 \(\qquad \qquad\)D.相交
2.设\(r>0\),两圆 \((x-1)^2+(y+3)^2=r^2\)与 \(x^2+y^2=16\)的位置关系不可能是( )
A.相切 \(\qquad \qquad\) B.相交 \(\qquad \qquad\) C.内切和内含 \(\qquad \qquad\) D.外切和外离
3.(多选)点\(P\)在圆 \(C_1:x^2+y^2=1\)上,点\(Q\)在圆 \(C_2:x^2+y^2-6x+8y+24=0\)上,则( )
A.\(|PQ|\)的最小值为\(0\)
B.\(|PQ|\)的最大值为\(7\)
C.两个圆心所在的直线斜率为 \(-\dfrac{4}{3}\)
D.两个圆相交弦所在直线的方程为\(6x-8y-25=0\)
4.圆 \(C_1:x^2+y^2+4x-4y-5=0\),圆 \(C_2:x^2+y^2-8x+4y+7=0\)的公切线条数是\(\underline{\quad \quad}\).
5.以\((3,-4)\)为圆心,且与圆 \(x^2+y^2=64\)内切的圆的方程是\(\underline{\quad \quad}\).
6.已知点\(A(-1,0)\),\(B(1,2)\),圆 \(C:(x-a)^2+y^2=25(a>0)\)上存在唯一的点\(P\),使 \(PA^2+PB^2=12\),则实数\(a\)的值是\(\underline{\quad \quad}\).
7.半径为\(3\)的圆与\(x\)轴相切,且与圆 \(x^2+(y-1)^2=1\)外切,求此圆的方程.
8.求与圆 \(C:x^2+y^2-2x=0\)外切且与直线 \(l: x+\sqrt{3} y=0\)相切于点\(M(3,-\sqrt{3} )\)的圆的方程.
9.已知圆 \(C_1:x^2+y^2+2x-6y+1=0\),圆 \(C_2:x^2+y^2-4x+2y-11=0\).求两圆的公共弦所在直线的方程及公共弦长.
参考答案
-
答案 \(D\)
解析 圆 \(x^2+y^2=2\)的圆心\((0,0)\),半径为 \(R=\sqrt{2}\),
圆 \(x^2+y^2+4y+3=0\)化为标准方程得: \(x^2+(y+2)^2=1\),
故圆心坐标\((0,-2)\),半径为\(r=1\),
\(∵\)圆心之间的距离\(d=2\),\(R+r=1+\sqrt{2}>2\),\(R-r=\sqrt{2}-1<2\)
\(∴R-r<d<R+r\),
则两圆的位置关系是相交.
故选:\(D\). -
答案 \(D\)
解析 圆 \((x-1)^2+(y+3)^2=r^2\)与 \(x^2+y^2=16\),
所以两圆的圆心分别为\((1,-3)\),\((0,0)\),半径分别为\(r\),\(4\),
则两圆的圆心距为 \(\sqrt{(1-0)^{2}+(-3-0)^{2}}=\sqrt{10}\),
因为\(r>0\),
所以 \(r+4>\sqrt{10}\),
则两圆不可能是外切和相离.
故选:\(D\). -
答案 \(BC\)
解析 根据题意,圆 \(C_1:x^2+y^2=1\),其圆心\(C_1 (0,0)\),半径\(R=1\),
圆 \(C_2:x^2+y^2-6x+8y+24=0\),其圆心\(C_2 (3,-4)\),半径\(r=1\),
圆心距 \(\left|C_{1} C_{2}\right|=\sqrt{16+9}=5\),
则\(|PO|\)的最小值为\(|C_1 C_2 |-R-r=3\),最大值为\(|C_1 C_2|+R+r=7\),
故\(A\)错误,\(B\)正确;
对于\(C\),圆心\(C_1 (0,0)\),圆心\(C_2 (3,-4)\),
则两个圆心所在的直线斜率 \(k=\dfrac{-4-0}{3-0}=-\dfrac{4}{3}\),\(C\)错误,
对于\(D\),两圆圆心距\(|C_1 C_2 |=5\),有\(|C_1 C_2 |>R+r=2\),
两圆外切,不存在公共弦,\(D\)错误.
故选:\(BC\). -
答案 \(3\)
解析 圆 \(C_{1}:(x+2)^{2}+(y-2)^{2}=13\),圆 \(C_2:(x-4)^2+(y+2)^2=13\),
因此两圆的圆心坐标分别为\(C_1 (-2,2)\),\(C_2 (4,-2)\),两圆的半径 \(r_{1}=r_{2}=\sqrt{13}\).
圆心距 \(\left|C_{1} C_{2}\right|=\sqrt{(-2-4)^{2}+(2+2)^{2}}=2 \sqrt{13}=r_{1}+r_{2}\),
\(∴\)两圆外切,有\(3\)条公切线. -
答案 \((x-3)^2+(y+4)^2=9\)或 \((x-3)^2+(y+4)^2=169\)
解析 设所求的圆的方程为 \((x-3)^2+(y+4)^2=r^2,r>0\),
则由题意可得 \(\sqrt{9+16}=|8-r|\),求得\(r=3\),或\(r=13\),
故所求的圆的方程为 \((x-3)^2+(y+4)^2=9\)或 \((x-3)^2+(y+4)^2=169\),
故答案为: \((x-3)^2+(y+4)^2=9\)或 \((x-3)^2+(y+4)^2=169\). -
答案 \(\pm 4 \sqrt{3}\)或 \(\pm 2 \sqrt{2}\)
解析 设\(P(x,y)\),则 \(PA^2=(x+1)^2+(y-0)^2=x^2+y^2+2x+1\),
\(P B^{2}=(x-1)^{2}+(y-2)^{2}=x^{2}+y^{2}-2 x-4 y+5\),
\(∵PA^2+PB^2=12\),
\(∴x^2+y^2-2y-3=0\),即 \(x^2+(y-1)^2=4\);
\(∴P\)点轨迹方程为 \(x^2+(y-1)^2=4\).
又圆\(C\)上存在唯一的点P符合题意,
\(∴\)两圆相切,
\(\therefore \sqrt{a^{2}+1}=7\)或 \(\sqrt{a^{2}+1}=3\),解得 \(a=\pm 4 \sqrt{3}\)或 \(a=\pm 2 \sqrt{2}\),
\(∴\)实数\(a\)的值为 \(\pm 4 \sqrt{3}\)或 \(\pm 2 \sqrt{2}\). -
答案 \((x \pm 2 \sqrt{3})^{2}+(y-3)^{2}=9\)或 \(x^{2}+(y+3)^{2}=9\)
解析 因为所求圆的半径为\(3\)且与\(x\)轴相切,
所以设圆心坐标为\((a,-3)\)或\((a,3)\).
又因为所求圆与圆 \(x^2+(y-1)^2=1\)外切,
所以 \(\sqrt{a^{2}+4}=4\)或 \(\sqrt{a^{2}+16}=4\),即 \(a=\pm 2 \sqrt{3}\)或\(a=0\).
所以所求圆的方程为 \((x \pm 2 \sqrt{3})^{2}+(y-3)^{2}=9\)或 \(x^{2}+(y+3)^{2}=9\). -
答案 \((x-4)^2+y^2=4\)
解析 圆\(C\)的方程可化为 \((x-1)^2+y^2=1\),圆心\(C(1,0)\),半径为\(1\).
设所求圆的方程为 \((x-a)^2+(y-b)^2=r^2 (r>0)\),
由题意可得 \(\left\{\begin{array}{l} \sqrt{(a-1)^{2}+b^{2}}=r+1 \\ \dfrac{b+\sqrt{3}}{a-3} \times\left(-\dfrac{\sqrt{3}}{3}\right)=-1 \\ \dfrac{|a+\sqrt{3} b|}{2}=r \end{array}\right.\),解得\(\left\{\begin{array}{l} a=4 \\ b=0 \\ r=2 \end{array}\right.\),
所以所求圆的方程为 \((x-4)^2+y^2=4\). -
答案 \(\dfrac{24}{5}\)
解析 联立方程组 \(\left\{\begin{array}{l} x^{2}+y^{2}+2 x-6 y+1=0 \quad (1) \\ x^{2}+y^{2}-4 x+2 y-11=0 \quad (2) \end{array}\right.\)
①-②得\(3x-4y+6=0\).
\(∴3x-4y+6=0\)即为两圆公共弦所在直线的方程.
易知圆\(C_1\)的圆 心\((-1,3)\),半径\(r=3\).
又\(C_1\)到直线\(AB\)的距离为 \(d=\dfrac{|-1 \times 3-4 \times 3+6|}{\sqrt{3^{2}+4^{2}}}=\dfrac{9}{5}\),
\(\therefore|A B|=2 \sqrt{r^{2}-d^{2}}=2 \sqrt{3^{2}-\left(\dfrac{9}{5}\right)^{2}}=\dfrac{24}{5}\),
即两圆的公共弦长为\(\dfrac{24}{5}\).
【B组---提高题】
1.(多选)已知点\(Q(4,0)\),过圆 \((x-4)^2+y^2=16\)上的一动点\(P\)作圆 \((x-4)^2+y^2=4\)的两条切线\(PA\)、\(PB\),切点分别为\(A\)、\(B\),两个切点\(A\)、\(B\)之间的线段\(AB\)称为切点弦.则下列结论正确的是( )
A.\(PQ⊥AB\) \(\qquad \qquad\) B. \(|P A|=2 \sqrt{3}\) \(\qquad \qquad\) C.\(|AB|=3\) \(\qquad \qquad\) D.四边形\(APBQ\)的面积为\(4\sqrt{3}\)
2.如图,设圆 \(C_1:(x-5)^2+(y+2)^2=4\),圆 \(C_2:(x-7)^2+(y+1)^2=25\),点\(A\)、\(B\)分别是圆\(C_1\),\(C_2\)上的动点,\(P\)为直线\(y=x\)上的动点,则\(|PA|+|PB|\)的最小值为\(\underline{\quad \quad}\) .

参考答案
- 答案 \(ABD\)
解析 因为\(Q(4,0)\)为两已知圆的圆心,由几何性质可知\(|PA|=|PB|\),\(|QA|=|QB|\),
所以\(PQ⊥AB\),故\(A\)正确;
因为\(|PQ|=4\),\(|AQ|=|BQ|=2\),
所以 \(|P B|=|P A|=\sqrt{|Q P|^{2}-|Q A|^{2}}=2 \sqrt{3}\),故\(B\)正确;
因为 \(\sin \angle A P Q=\dfrac{|A Q|}{|P Q|}=\dfrac{1}{2}\),
又\(∠APQ\)为锐角,所以\(∠APQ=30°\),同理可得\(∠BPQ=30°\),
所以\(∠APB=60°\),则\(△APB\)为等边三角形,所以\(|AB|=2\sqrt{3}\),
\(S_{\triangle A P B Q}=2 S_{\triangle A P Q}=|P A| \cdot|A Q|=4 \sqrt{3}\),故\(C\)错误,\(D\)正确,
故选:\(ABD\). - 答案 \(3 \sqrt{13}-7\)
解析 依题意可知圆\(C_1\)的圆心\((5,-2)\),\(r=2\),圆\(C_2\)的圆心\((7,-1)\),\(R=5\),如图所示:

对于直线\(y=x\)上的任一点\(P\),由图象可知,要使\(|PA|+|PB|\)的得最小值,
则问题可转化为求\(|PC_1 |+|PC_2 |-R-r=|PC_1 |+|PC_2 |-7\)的最小值,
即可看作直线\(y=x\)上一点到两定点距离之和的最小值减去\(7\),
由平面几何的知识易知当\(C_1\)关于直线\(y=x\)对称的点为 \(C_1^′(-2,5)\),
与\(P\)、\(C_2\)共线时,\(|PC_1 |+|PC_2 |\)的最小值,
取得最小值,即直线\(y=x\)上一点到两定点距离之和取得最小值为 \(\left|C C_{2}\right|=3 \sqrt{13}\),
\(∴|PA|+|PB|\)的最小值 \(\left[=\left|P C_{1}\right|+\left|P C_{2}\right|-7=3 \sqrt{13}-7\right.\).
【C组---拓展题】
1.两圆 \(x^2+y^2+2ax+2ay+2a^2-1=0\)和 \(x^2+y^2+2bx+2by+2b^2-2=0\)的公共弦中,最长的弦等于\(\underline{\quad \quad}\).
参考答案
- 答案 \(2\)
解析 将两圆方程相减得公共弦所在直线方程: \((2a-2b)x+(2a-2b)y+2a^2-2b^2+1=0\),
\(x^2+y^2+2ax+2ay+2a^2-1=0\)化为标准方程为 \((x+a)^2+(y+a)^2=1\),
其圆心为\((-a,-a)\),半径为\(1\),
圆心到公共弦所在直线的距离为 \(d=\dfrac{\left|(2 a-2 b)(-a) \times 2+2 a^{2}-2 b^{2}+1\right|}{2 \sqrt{2}|a-b|}=\dfrac{\left|1-2(a-b)^{2}\right|}{2 \sqrt{2}|a-b|}\)
所以公共弦长为 \(2 \sqrt{1-d^{2}}=2 \sqrt{1-\left(\dfrac{1-2(a-b)^{2}}{2 \sqrt{2}|a-b|}\right)^{2}}\)\(=2 \sqrt{1-\left(\dfrac{(a-b)^{2}}{2}+\dfrac{1}{8(a-b)^{2}}-\dfrac{1}{2}\right)}\)
\(\leq 2 \sqrt{1-\left(2 \sqrt{\dfrac{1}{16}}-\dfrac{1}{2}\right)}=2\),
故答案为:\(2\).


