2.2.3 直线的一般式方程
${\color{Red}{欢迎到学科网下载资料学习 }}$
【基础过关系列】2022-2023学年高二数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性必修第一册同步巩固,难度2颗星!
基础知识
直线的一般式方程
关于\(x,y\)的二元一次方程\(Ax+By+C=0\)(其中\(A,B\)不同时为\(0\))叫做直线的一般式方程,简称一般式.
解释
① 任何一直线都可以表示为一个关于\(x,y\)的二元一次方程;
② 对于任意一个二元一次方程\(Ax+By+C=0\)(其中\(A,B\)不同时为\(0\))也可以表示一条直线.
当\(B=0\)时,方程变形为 \(x=-\dfrac{C}{A}\),它表示过点 \(\left(-\dfrac{C}{A}, 0\right)\),且垂直\(x\)轴的直线;
当\(B≠0\)时,方程变形为 \(y=-\dfrac{A}{B} x-\dfrac{C}{B}\),它表示 \(\left(0,-\dfrac{C}{B}\right)\),斜率为 \(-\dfrac{A}{B}\)的直线.
③ 一般式\(Ax+By+C=0\)的直线一方向向量为 \(\vec{n}=(B,-A)\),斜率 \(k=-\dfrac{A}{B}(B \neq 0)\).
【例】把直线\(l\)的一般式方程\(2x-3y+6=0\)化为斜截式,求出直线\(l\)的斜率及其在\(x\)轴与\(y\)轴的截距,并画出图形.
解析 直线方程化为斜截式为 \(y=\dfrac{2}{3} x+2\),直线斜率为\(\dfrac{2}{3}\),直线\(y\)轴的截距为\(2\);
令\(y=0\)得\(x=-3\),故直线在\(x\)轴的截距为\(-3\),
其图形如下图

两直线的位置关系
| 直线位置关系 | ||
|---|---|---|
| 直线方程 | \(l_1:y=k_1x+b_1\) \(l_2:y=k_2 x+b_2\) |
\(l_1:A_1 x+B_1 y+C_1=0\) \(l_2:A_2 x+B_2 y+C_2=0\) |
| 重合 | \(k_1=k_2\)且\(b_1=b_2\) | \(\dfrac{A_{1}}{A_{2}}=\dfrac{B_{1}}{B_{2}}=\dfrac{C_{1}}{C_{2}}\left(A_{2} B_{2} C_{2} \neq 0\right)\) |
| 相交 | \(k_1≠k_2\) | \(\dfrac{A_{1}}{A_{2}} \neq \dfrac{B_{1}}{B_{2}}\left(A_{2} B_{2} \neq 0\right)\) |
| 平行 | \(k_1=k_2\)且\(b_1≠b_2\) | \(\dfrac{A_{1}}{A_{2}}=\dfrac{B_{1}}{B_{2}} \neq \dfrac{C_{1}}{C_{2}}\left(A_{2} B_{2} C_{2} \neq 0\right)\) |
| 垂直 | \(k_1\cdot k_2=-1\) | \(A_{1} A_{2}+B_{1} B_{2}=0\) |
【例】已知直线\(l_1:2x-y-6=0\)与直线\(l_2:6x-ay+4=0\),
(1) 若\(l_1//l_2\),求\(a\)值; (2)若\(l_1⊥l_2\),求\(a\)值.
解析 (1) 若\(l_1//l_2\),由 \(\dfrac{6}{2}=\dfrac{-a}{-1}\)解得\(a=3\);
(2) 若\(l_1⊥l_2\),由\(2×6+(-1)×(-a)=0\)解得\(a=-12\).
方向向量与直线的参数方程 (选学内容)
直线的参数方程 \(\left\{\begin{array}{l}
x=x_{0}+m t \\
y=y_{0}+n t
\end{array}\right.\) (\(t\)为参数) ,
其表示过点\((x_0,y_0)\)且斜率 \(k=\dfrac{n}{m}(m \neq 0)\)的直线.
解释
① 证明 设直线\(l\)经过点\(P_0 (x_0,y_0 )\), \(\vec{v}=(m, n)\)是它的一个方向向量,\(P(x,y)\)是直线\(l\)上任意一点,
则向量 \(\overrightarrow{P_{0} P}\)与\(\vec{v}\)共线,则 \(\overrightarrow{P_{0} P}=t \vec{v}\),即\((x-x_0,y-y_0 )=t(m,n)\),所以 \(\left\{\begin{array}{l}
x=x_{0}+m t \\
y=y_{0}+n t
\end{array}\right.\).
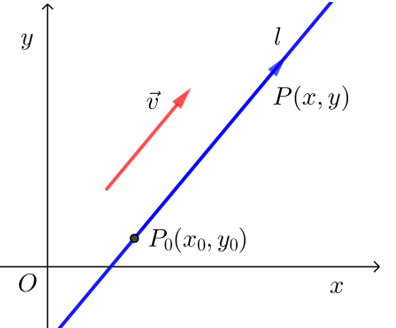
② 参数方程中的\((m,n)\)的几何意义是直线的方向向量,即 \(k=\dfrac{n}{m}(m \neq 0)\).
③ 标准式参数方程
若直线的参数方程 \(\left\{\begin{array}{l}
x=x_{0}+m t \\
y=y_{0}+n t
\end{array}\right.\)(\(t\)为参数)中\(m,n\)满足 \(m^2+n^2=1\),可称为标准式参数方程,
则参数\(t\)是以定点\(P_0 (x_0,y_0 )\)为起点,点\(P(x,y)\)为终点的有向线段\(P_0 P\)的数量,
又称为点\(P\)与点\(P_0\)间的有向距离.
根据\(t\)的几何意义,有以下结论.
(i)设\(A、B\)是直线上任意两点,它们对应的参数分别为\(t_A\)和\(t_B\),
则 \(|A B|=\left|t_{B}-t_{A}\right|=\sqrt{\left(t_{B}-t_{A}\right)^{2}-4 t_{A} \cdot t_{B}}\).
(ii)线段\(AB\)的中点所对应的参数值等于 \(\dfrac{t_{A}+t_{B}}{2}\).
(直线参数方程的应用要学到圆的方程才发挥它的威力)
【例】直线的参数方程 \(\left\{\begin{array}{l}
x=1+3 t \\
y=2+4 t
\end{array}\right.\)化为直角坐标系方程,它是直线标准式参数方程么?若不是,把其化为标准式.
解析 直线的参数方程 \(\left\{\begin{array}{l}
x=1+3 t \\
y=2+4 t
\end{array}\right.\),它表示过点\((1,2)\)且斜率 \(k=\dfrac{4}{3}\)的直线,
化为直角坐标系方程为 \(y-2=\dfrac{4}{3}(x-1)\),即\(4x-3y+2=0\);
直线的参数方程 \(\left\{\begin{array}{l}
x=1+3 t \\
y=2+4 t
\end{array}\right.\),不是直线标准式参数方程,化为标准式 \(\left\{\begin{array}{l}
x=1+\dfrac{3}{5} t \\
y=2+\dfrac{4}{5} t
\end{array}\right.\).
基本方法
【题型1】一般式方程
【典题1】 根据下列条件分别写出直线的方程,并化为一般式方程.
(1) 斜率是 \(\sqrt{3}\),且经过点\(A(5,3)\);
(2) 斜率为\(4\),在\(y\)轴上的截距为\(-2\);
(3) 经过\(A(-1,5)\),\(B(2,-1)\)两点;
(4) 在\(x,y\)轴上的截距分别是\(-3\),\(-1\).
解析 (1)由点斜式方程可知,
所求直线方程为\(y-3=\sqrt{3}(x-5)\),化为一般式 为 \(\sqrt{3} x-y+3-5 \sqrt{3}=0\).
(2)由斜截式方程可知,所求直线方程为\(y=4x-2\),
化为一般式为\(4x-y-2=0\).
(3)由两点式方程可知,所求直线方程为 \(\dfrac{y-5}{-1-5}=\dfrac{x-(-1)}{2-(-1)}\).
化为一般式方程为\(2x+y-3=0\).
(4)由截距式方程可得,所求直线方程为 \(\dfrac{x}{-3}+\dfrac{y}{-1}=1\),化成一般式方程为\(x+3y+3=0\).
【典题2】设直线\(l\)的方程是\(x+By-4=0\)倾斜角为\(α\).若 \(\dfrac{\pi}{6}<\alpha<\dfrac{3 \pi}{4}\),则\(B\)的取值范围是\(\underline{\quad \quad}\) .
解析 \(∵\)直线\(l\)的方程是\(x+By-4=0\)倾斜角为\(α\),
则 \(\alpha=\dfrac{\pi}{2}\)时,斜率\(\tanα\)不存在,\(B=0\);
当 \(\alpha \neq \dfrac{\pi}{2}\)时, \(\tan \alpha=\dfrac{1}{-B}\).
若 \(\dfrac{\pi}{6}<\alpha<\dfrac{\pi}{2}\),则 \(\tan \alpha=\dfrac{1}{-B}>\dfrac{\sqrt{3}}{3}\),求得\(-\sqrt{3}<B<0\).
若 \(\dfrac{\pi}{2}<\alpha<\dfrac{3 \pi}{4}\),则 \(-\dfrac{1}{B}<-1\),\(∴0<B<1\).
综上可得,\(B\)的取值范围为\((-\sqrt{3},0)∪(0,1)\),或\(\{0\}\),
即\(B\)的范围为\((-\sqrt{3},1)\),
【典题3】 已知直线\(l:(2+m)x+(1-2m)y+4-3m=0\).
(1)求证:不论\(m\)为何实数,直线恒过一定点\(M\);
(2)过定点\(M\)作一条直线\(l_1\),使夹在两坐标轴之间的线段被\(M\)点平分,求直线\(l_1\)的方程.
(3)若直线\(l\)与两坐标轴的负半轴围成的三角形面积最小,求\(l\)的方程.
解析 (1)直线\(l:(2+m)x+(1-2m)y+4-3m=0\).
化为:\(m(x-2y-3)+2x+y+4=0\),
联立\(\left\{\begin{array}{l}
x-2 y-3=0 \\
2 x+y+4=0
\end{array}\right.\),解得 \(x=-1,y=-2\).
可得:不论\(m\)为何实数,直线恒过一定点\(M(-1,-2)\).
(2)设直线\(l_1\)与两条坐标轴分别相交于\(A(a,0)\),\(B(0,b)\).
线段\(AB\)的中点为\(M(-1,-2)\),则\(M(-1,-2)\),\(b=-4\).
\(∴\)直线\(l_1\)的方程为\(\dfrac{x}{-2}+\dfrac{y}{-4}=1\),可得:\(2x+y+4=0\).
(3)设直线\(l\)与两条坐标轴分别相交于\(A(a,0)\),\(B(0,b)\).
可得方程为\(\dfrac{x}{a}+\dfrac{y}{b}=1\), 把点\(M(-1,-2)\)代入可得:\(\dfrac{-1}{a}+\dfrac{-2}{b}=1\),
\(\therefore 1 \geq 2 \sqrt{\dfrac{-1}{a} \cdot \dfrac{-2}{b}}\),化为:\(ab≥8\),当且仅当\(b=2a=-4\)时取等号.
可得:直线\(l\)与两坐标轴的负半轴围成的三角形面积最小,\(S=\dfrac{1}{2}(-a)(-b)=4\).
则的方程为\(\dfrac{x}{-2}+\dfrac{y}{-4}=1\),可得:\(2x+y+4=0\).
巩固练习
1.(多选)下列有关直线\(l:x+my-1=0(m∈R)\)的说法中不正确的是( )
A.直线\(l\)的斜率为\(-m\) \(\qquad \qquad\) B.直线\(l\)的斜率为 \(-\dfrac{1}{m}\)
C.直线\(l\)过定点\((0,1)\) \(\qquad \qquad\) D.直线\(l\)过定点\((1,0)\)
2.(多选)已知直线\(l:(a^2+a+1)x-y+1=0\),其中\(a∈R\),下列说法正确的是( )
A.当\(a=-1\)时,直线\(l\)与直线\(x+y=0\)垂直
B.若直线\(l\)与直线\(x-y=0\)平行,则\(a=0\)
C.直线\(l\)过定点\((0,1)\)
D.当\(a=0\)时,直线\(l\)在两坐标轴上的截距相等
3.直线\(x+(a^2+1)y-1=0\)的倾斜角的取值范围是\(\underline{\quad \quad}\).
4.已知直线方程为\((2+λ)x+(1-2λ)y+4-3λ=0\).
(1)求证不论\(λ\)取何实数值,此直线必过定点;
(2)过这定点引一直线,使它夹在两坐标轴间的线段被这点平分,求这条直线方程.
参考答案
- 答案 \(ABC\)
解析 当\(m≠0\)时,直线\(l\)的方程可变为 \(y=-\dfrac{1}{m}(x-1)\),其斜率为 \(-\dfrac{1}{m}\),过定点\((1,0)\),
当\(m=0\)时,直线\(l\)的方程变为\(x=1\),其斜率不存在,过点\((1,0)\),
故\(AB\)不正确,\(D\)正确,
将点\((0,1)\)代入直线方程得\(m-1=0\),
故只有当\(m=1\)时直线才会过点\((0,1)\),即\(C\)不正确,
故选:\(ABC\). - 答案 \(AC\)
解析 直线\(l:(a^2+a+1)x-y+1=0\),
对于\(A\),当\(a=-1\)时,直线l的斜率\(k_1=1\),直线\(x+y=1\)的斜率为\(-1\),直线\(l\)与直线\(x+y=0\)垂直,故\(A\)正确;
对于\(B\),若直线\(l\)与直线\(x-y=0\)平行,则\(a^2+a+1=1\),解得\(a=0\)或\(a=-1\),故\(B\)错误;
对于\(C\),无论\(a\)取何值,当\(x=0\)时,\(y=1\),\(∴\)直线\(l\)过定点\((0,1)\),故\(C\)正确;
对于\(D\),当\(a=0\)时,直线\(l:x-y+1=0\)在\(x\)轴上的截距为\(-1\),在\(y\)轴上的截距为\(1\),
当\(a=0\)时,直线\(l\)在两坐标轴上的截距不相等,故\(D\)错误.
故选:\(AC\). - 答案 \(\left[\dfrac{3 \pi}{4}, \pi\right)\)
解析 直线 \(x+(a^2+1)y-1=0\)可化为 \(y=-\dfrac{1}{a^{2}+1} x+\dfrac{1}{a^{2}+1}\);
且直线的斜率为 \(k=-\dfrac{1}{a^{2}+1}\),
由\(a^2+1≥1\),所以\(0<\dfrac{1}{a^{2}+1}≤1\),
所以 \(-1 \leq-\dfrac{1}{a^{2}+1}<0\),
所以\(-1≤\tanθ<0\),
又\(θ∈[0,π)\),
所以直线的倾斜角\(θ\)的取值范围是 \(\left[\dfrac{3 \pi}{4}, \pi\right)\). - 证明 (1)直线方程为\((2+λ)x+(1-2λ)y+4-3λ=0\)可化为:
\(∵λ(x-2y-3)+2x+y+4=0\),
\(∴\)由 \(\left\{\begin{array}{l} x-2 y-3=0 \\ 2 x+y+4=0 \end{array}\right.\)得 \(\left\{\begin{array}{l} x=-1 \\ y=-2 \end{array}\right.\),
\(∴\)直线\(l\)恒过定点\(M(-1,-2)\).
(2)当斜率不存在时,不合题意;
当斜率存在时,设所求直线\(l_1\)的方程为\(y+2=k(x+1)\),
直线\(l_1\)与\(x\)轴、\(y\)轴交于\(A、B\)两点,则 \(A\left(\dfrac{2}{k}-1,0\right)\),\(B(0,k-2)\).
\(∵AB\)的中点为\(M\),
\(\therefore\left\{\begin{array}{l} \dfrac{2}{k}-1=-2 \\ k-2=-4 \end{array}\right.\),解得\(k=-2\).
\(∴\)所求直线\(l_1\)的方程为\(y+2=-2(x+1)\),即:\(2x+y+4=0\).
所求直线\(l_1\)的方程为\(2x+y+4=0\).
【题型2】直线的位置关系
【典题1】 求满足下列条件的直线\(l\)的方程:
(1)与直线\(3x+4y-12=0\)平行,且与直线\(2x+3y+6=0\)在\(y\)轴上的截距相同;
(2)与直线\(x+2y-1=0\)垂直,且与直线\(x+2y-4=0\)在\(x\)轴上的截距相同.
解析 (1)由\(3x+4y-12=0\),得 \(y=-\dfrac{3}{4} x+3\).
\(∵\)直线\(l\)与该直线平行,
\(∴\)直线\(l\)的斜率为 \(-\dfrac{3}{4}\).
由\(2x+3y+6=0\),得 \(y=-\dfrac{2}{3} x-2\).
\(∵\)直线\(l\)与直线\(2x+3y+6=0\)在\(y\)轴上的截距相同,
\(∴\)直线\(l\)在\(y\)轴上的截距为\(-2\).
\(∴\)直线\(l\)的方程为 \(y=-\dfrac{3}{4} x-2\),即\(3x+4y+8=0\).
(2)\(∵\)直线\(l\)与直线\(x+2y-1=0\)垂直,
\(∴\)直线\(l\)的斜率为\(2\).
由\(x+2y -4=0\),得 \(\dfrac{x}{4}+\dfrac{y}{2}=1\).
∵直线\(l\)与直线\(x+2y-4=0\)在\(x\)轴上的截距相同,
\(∴\)直线经过点\((4,0)\).
\(∴\)直线\(l\)的方程为\(y=2(x-4)\),即\(2x-y-8=0\).
巩固练习
1.若直线\(x+2ay-1=0\)与\((a-1)x-ay+1=0\)平行,则\(a\) 的值为( )
A.\(\dfrac{1}{2}\) \(\qquad \qquad\) B.\(\dfrac{1}{2}\)或\(0\) \(\qquad \qquad\) C.\(0\) \(\qquad \qquad\) D.\(-2\)
2.经过点\(A(2,1)\),且与直线\(2x+y-10=0\)垂直的直线\(l\)的方程为\(\underline{\quad \quad}\).
3.(1)已知直线\(l_1:2x+(m+1)y+4=0\)与直线\(l_2:mx+3y-2=0\)平行,求\(m\)的值.
(2)当\(a\)为何值时,直线\(l_1:(a+2)x+(1-a)y-1=0\)与直线\(l_2:(a-1)x+(2a+3)y+2=0\)互相垂直?
(3)求与直线\(3x+4y+1=0\)平行且过点\((1,2)\)的直线\(l\)的方程.
参考答案
- 答案 \(B\)
解析 当\(a=0\)时,两直线平行;当\(a≠0\)时,由 \(\dfrac{1}{a-1}=\dfrac{2 a}{-a}\)解得 \(a=\dfrac{1}{2}\),故选\(B\). - 答案 \(x-2y=0\).
解析 与\(2x+y-10=0\)垂直的直线\(l\)为\(x-2y+c=0\),
又过点\(A(2,1)\),则\(2-2+c=0\),即\(c=0\),即直线方程为\(x-2y=0\). - 答案 (1) \(2\)或\(-3\) (2) \(a=1\)或\(a=-1\) (3)\(3x+4y-11=0\)
解析 (1)由\(2×3-m(m+1)=0\),得\(m=-3\)或\(m=2\).
当\(m=-3\)时,\(l_1:x-y+2=0\),\(l_2:3x-3y+2=0\),
显然\(l_1\)与\(l_2\)不重合,\(∴l_1∥l_2\).
同理当\(m=2\)时,\(l_1:2x+3y+4=0\),\(l_2:2x+3y-2=0\),\(l_1\)与\(l_2\)不重合,\(l_1∥l_2\),
\(∴m\)的值为\(2\)或\(-3\).
(2)由直线\(l_1⊥l_2\),
\(∴(a+2)(a-1)+(1-a)(2a+3)=0\),解得\(a=±1\).
故当\(a=1\)或\(a=-1\)时,直线\(l_1⊥l_2\).
(3)设与直线\(3x+4y+1=0\)平行的直线\(l\)的方程为\(3x+4y+m=0\).
\(∵l\)经过点\((1,2)\),\(∴3×1+4×2+m=0\),解得\(m=-11\).
\(∴\)所求直线方程为\(3x+4y-11=0\).
【题型3】直线的参数方程(选学内容)
【典题1】 已知直线\(l\)经过点\(M(-1,2)\),且倾斜角为 \(\dfrac{\pi}{6}\),则直线\(l\)的一个参数方程为(其中\(t\)为参数) ( )
A. \(\left\{\begin{array}{l}
x=-1+\dfrac{1}{2} t \\
y=2+\dfrac{\sqrt{3}}{2} t
\end{array}\right.\) \(\qquad \qquad\) B. \(\left\{\begin{array}{l}
x=-1+\dfrac{\sqrt{3}}{2} t \\
y=2+\dfrac{1}{2} t
\end{array}\right.\) \(\qquad \qquad\)
C. \(\left\{\begin{array}{l}
x=2+\dfrac{1}{2} t \\
y=-1+\dfrac{\sqrt{3}}{2} t
\end{array}\right.\) \(\qquad \qquad\) D. \(\left\{\begin{array}{l}
x=2+\dfrac{\sqrt{3}}{2} t \\
y=-1+\dfrac{1}{2} t
\end{array}\right.\)
解析 \(∵\)直线\(l\)经过点\(M(-1,2)\),且倾斜角为 \(\dfrac{\pi}{6}\),
\(\therefore k=\dfrac{\sqrt{3}}{3}\),即直线的方向向量为\((3,\sqrt{3})\)
则直线l的一个参数方程为(其中\(t\)为参数)即 \(\left\{\begin{array}{l}
x=-1+\dfrac{\sqrt{3}}{2} t \\
y=2+\dfrac{1}{2} t
\end{array}\right.\).
故选:\(B\).
【典题2】已知直线 \(\left\{\begin{array}{l}
x=3+4 t \\
y=-4+3 t
\end{array}\right.\)(\(t\)为参数),下列命题中错误的是( )
A.直线经过点\((7,-1)\) \(\qquad \qquad\) B.直线的斜率为 \(\dfrac{3}{4}\)
C.直线不过第二象限 \(\qquad \qquad\) D.\(|t|\)是定点\(M_0 (3,-4)\)到该直线上对应点\(M\)的距离
解析 根据题意, \(\left\{\begin{array}{l}
x=3+4 t \\
y=-4+3 t
\end{array}\right.\)(\(t\)为参数),
依次分析选项:
对于\(A\)、令\(3+4t=7\)解得\(t=1\),\(y=-4+3t=-1\),故直线经过点\((7,-1)\),\(A\)正确;
对于\(B\)、直线的方向向量为\((4,3)\),其斜率\(k=\dfrac{3}{4}\),\(B\)正确;
对于\(C\)、直线过定点\((3,-4)\), 且斜率 \(k=\dfrac{3}{4}\),故直线不经过第二象限,\(C\)正确;
对于\(D\)、直线 \(\left\{\begin{array}{l}
x=3+4 t \\
y=-4+3 t
\end{array}\right.\)(\(t\)为参数),不是标准式,故\(D\)错误,化为标准式 \(\left\{\begin{array}{l}
x=3+\dfrac{4}{5} t^{\prime} \\
y=-4+\dfrac{3}{5} t^{\prime}
\end{array}\right.\)
\(|t'|=|5t|\)才是定点\(M_0 (3,-4)\)到该直线上对应点\(M\)的距离;
故选:\(D\).
巩固练习
1.以\(t\)为参数的方程 \(\left\{\begin{array}{l}
x=1-\dfrac{1}{2} t \\
y=-2+\dfrac{\sqrt{3}}{2} t
\end{array}\right.\)(\(t\)为参数)表示( )
A.过点\((1,-2)\)且倾斜角为 \(\dfrac{\pi}{3}\)的直线
B.过点\((-1,2)\)且倾斜角为 \(\dfrac{\pi}{3}\)的直线
C.过点\((1,-2)\)且倾斜角为 \(\dfrac{2\pi}{3}\)的直线
D.过点\((-1,2)\)且倾斜角为 \(\dfrac{2\pi}{3}\)的直线
2.下列直线中,与曲线 \(C:\left\{\begin{array}{l}
x=1+2 t \\
y=-2+4 t
\end{array}\right.\)(\(t\)为参数)没有公共点的是( )
A.\(2x+y=0\) \(\qquad \qquad\) B.\(2x+y-4=0\) \(\qquad \qquad\) C.\(2x-y=0\) \(\qquad \qquad\) D.\(2x-y-4=0\)
3.下列点不在直线 \(\left\{\begin{array}{l}
x=-1+\dfrac{\sqrt{2}}{2} t \\
y=2+\dfrac{\sqrt{2}}{2} t
\end{array}\right.\)(\(t\)为参数)上的是( )
A.\((-1,2)\) \(\qquad \qquad\) B.\((-3,2)\) \(\qquad \qquad\) C.\((1,4)\) \(\qquad \qquad\) D.\((2,5)\)
4.若直线\(l\)的参数方程为 \(\left\{\begin{array}{l}
x=-2+3 t \\
y=3-4 t
\end{array}\right.\)(\(t\)为参数),则直线\(l\)的倾斜角的余弦值为\(\underline{\quad \quad}\) .
5.曲线 \(\left\{\begin{array}{l}
x=-2+5 t \\
y=1-2 t
\end{array}\right.\)(\(t\)为参数)与\(x\)轴的交点是\(\underline{\quad \quad}\).
参考答案
- 答案 \(C\)
解析 根据题意,以\(t\)为参数的方程 \(\left\{\begin{array}{l} x=1-\dfrac{1}{2} t \\ y=-2+\dfrac{\sqrt{3}}{2} t \end{array}\right.\)的直线斜率为 \(k=-\sqrt{3}\),
表示为过点\((1,-2)\)且倾斜角为 \(\dfrac{2\pi}{3}\)的直线,故选:\(C\). - 答案 \(C\)
解析 曲线\(C:\left\{\begin{array}{l} x=1+2 t \\ y=-2+4 t \end{array}\right.\)(\(t\)为参数)的斜率\(k=2\),且过\((1,-2)\),
其直角坐标方程为\(2x-y-4=0\),
选项中斜率为\(2\)的直线为\(C\),\(D\),而\(D\)与曲线\(C\)重合,有无数个公共点,排除.
故选:\(C\). - 答案 \(B\)
解析 直线 \(\left\{\begin{array}{l} x=-1+\dfrac{\sqrt{2}}{2} t \\ y=2+\dfrac{\sqrt{2}}{2} t \end{array}\right.\)(\(t\)为参数),转换为直角坐标方程为\(x-y+3=0\).
由于\(ACD\)三个坐标满足该方程,故该点在直线上,点\(B\)的坐标不满足该直线方程,
故选:\(B\). - 答案 \(-\dfrac{3}{5}\)
解析 设直线\(l\)的倾斜角为\(α\),由题意, \(\tan \alpha=-\dfrac{4}{3}\), \(\therefore \cos \alpha=-\dfrac{3}{5}\). - 答案 \((\dfrac{1}{2},0)\)
解析 \(∵\)直线的参数方程 \(\left\{\begin{array}{l} x=-2+5 t \\ y=1-2 t \end{array}\right.\)(\(t\)为参数),令\(y=1-2t=0\),可得 \(t=\dfrac{1}{2}\),
把 \(t=\dfrac{1}{2}\)代入\(x=-2+5t\),可得 \(x=-2+5 \times \dfrac{1}{2}=\dfrac{1}{2}\).
\(∴\)直线与\(x\)轴的交点坐标为\((\dfrac{1}{2},0)\).
分层练习
【A组---基础题】
1.直线\(3x-5y-15=0\)在\(x\)轴和\(y\)轴上的截距分别为( )
A.\(5,3\) \(\qquad \qquad\) B.\(-5,- 3\) \(\qquad \qquad\) C.\(5,-3\) \(\qquad \qquad\) D.\(-5,3\)
2.下列四条直线,其倾斜角最大的是( )
A.\(x+2y+3=0\) \(\qquad \qquad\) B.\(2x-y+1=0\) \(\qquad \qquad\) C.\(x+y+1=0\) \(\qquad \qquad\) D.\(x+1=0\)
3.直线\(2x-y+2=0\)与直线\(ax+2y-5=0\)平行,则实数\(a\)的值是( )
A.\(4\) \(\qquad \qquad\) B.\(-4\) \(\qquad \qquad\) C.\(2\) \(\qquad \qquad\) D.\(-2\)
4.直线\(l\)绕它与\(x\)轴的交点逆时针旋转\(\dfrac{\pi}{3}\),得到直线\(\sqrt{3} x+y-3=0\),则直线\(l\)的直线方程( )
A.\(x-\sqrt{3} y-1=0\) \(\qquad \qquad\) B.\(\sqrt{3} x-y-3=0\) \(\qquad \qquad\) C.\(x+\sqrt{3} y-1=0\) \(\qquad \qquad\) D.\(\sqrt{3} x-y-1=0\)
5.(多选)下列说法中,正确的有( )
A.过点\(P(1,2)\)且在\(x、y\)轴截距相等的直线方程为\(x+y-3=0\)
B.直线\(y=3x-2\)在\(y\)轴上的截距为\(-2\)
C.直线\(x- \sqrt{3} y+1=0\)的倾斜角为\(60°\)
D.过点\((5,4)\)并且倾斜角为\(90°\)的直线方程为\(x-5=0\)
6.若直线\(ax-y+3=0\)与直线\(ax+4y-2=0\)垂直,则实数\(a\)的值为\(\underline{\quad \quad}\).
7.经过点\(A(3,2)\),且与直线\(2x+3y-16=0\)垂直的直线\(l\)的方程为\(\underline{\quad \quad}\).
8.已知直线\((a-2)y=(3a-1)x-1\),为使这条直线不经过第二象限,则实数\(a\)的范围是\(\underline{\quad \quad}\).
9.已知方程 \((m^2-2m-3)x+(2m^2+m-1)y+6-2m=0(m∈R)\).
(1)当\(m\)为何实数时,方程表示的直线斜率不存在?求出这时的直线方程;
(2)已知方程表示的直线\(l\)在\(x\)轴上的截距为\(-3\),求实数\(m\)的值;
(3)若方程表示的直线\(l\)的倾斜角是\(45^∘\),求实数\(m\)的值.
10.已知直线方程为\((2+2m)x+(1-m)y+4=0\).
(1)该直线是否过定点?如果存在,请求出该点坐标,如果不存在,说明你的理由;
(2)当\(m\)在什么范围时,该直线与两坐标轴负半轴均相交?
参考答案
-
答案 \(C\)
解析 直线\(3x-5y-15=0\)可化为 \(\dfrac{x}{5}+\dfrac{y}{-3}=1\),
则直线在\(x\)轴和\(y\)轴上的截距分别为\(5,-3\) ,
故选\(C\). -
答案 \(A\)
解析 根据题意,依次分析选项:
对于\(A\)、\(x+2y+3=0\),其斜率 \(k_{1}=-\dfrac{1}{2}\),倾斜角\(θ_1\)为钝角,
对于\(B\)、\(2x-y+1=0\),其斜率\(k_2=2\),倾斜角\(θ_2\)为锐角,
对于\(C\)、\(x+y+1=0\),其斜率\(k_3=-1\),倾斜角\(θ_3\)为\(135°\),
对于\(D\)、\(x+1=0\),倾斜角\(θ_4\)为\(90°\),
而\(k_1>k_3\),故\(θ_1>θ_3\),
故选:\(A\). -
答案 \(B\)
解析 由 \(\dfrac{2}{a}=\dfrac{-1}{2}\)解得\(a=-4\),故选\(B\). -
答案 \(B\)
解析 直线直线\(\sqrt{3} x+y-3=0\)的斜率等于\(-\sqrt{3}\),设倾斜角等于\(θ\),即\(θ=\dfrac{2\pi}{3}\),
绕它与\(x\)轴的交点\((\sqrt{3} ,0)\)逆时针旋转 \(\dfrac{\pi}{3}\),
所得到的直线的倾斜角等于\(θ-\dfrac{\pi}{3}\),
故所求直线的斜率为\(\tan(\dfrac{2\pi}{3}-\dfrac{\pi}{3})=\sqrt{3}\),
故所求的直线方程为\(y-0=\sqrt{3} (x-\sqrt{3})\),即\(\sqrt{3} x-y-3=0\),
故选:\(B\). -
答案 \(BD\)
解析 \(∵\)过点P\((1,2)\)且在\(x、y\)轴截距相等的直线方程为\(x+y-3=0\),或者\(y=2x\),故\(A\)错误;
\(∵\)直线\(y=3x-2\)在\(y\)轴上的截距为\(-2\),故\(B\)正确;
由于直线 \(x- \sqrt{3} y+1=0\)的斜率为 \(\dfrac{\sqrt{3}}{3}\),故它的倾斜角为\(30°\),故\(C\)错误;
\(∵\)过点\((5,4)\)并且倾斜角为\(90°\)的直线方程为\(x-5=0\),故\(D\)正确,
故选:\(BD\). -
答案 \(2\)或\(-2\)
解析 由\(a^2+(-1)×4=0\)解得\(a=±2\),故填\(2\)或\(-2\). -
答案 \(3x-2y-5=0\)
解析 与直线\(2x+3y-16=0\)垂直的直线\(l\)的方程为\(3x-2y+c=0\),
又经过点\(A(3,2)\),则\(9-4+c=0\),即\(c=-5\),
即直线方程为\(3x-2y-5=0\). -
答案 \([2,+∞)\)
解析 若\(a-2=0\),即\(a=2\)时,直线方程可化为 \(x=\dfrac{1}{5}\),
此时直线不经过第二象限,满足条件;
若\(a-2≠0\),直线方程可化为 \(y=\dfrac{3 a-1}{a-2} x-\dfrac{1}{a-2}\),此时若直线不经过第二象限,
则 \(\dfrac{3 a-1}{a-2} \geq 0\), \(\dfrac{1}{a-2} \geq 0\),解得\(a>2\)
综上满足条件的实数\(a\)的范围是\([2,+∞)\)
故答案为:\([2,+∞)\). -
答案 (1) \(m=\dfrac{1}{2}\) (2) \(m=-\dfrac{5}{3}\) (3) \(m=\dfrac{4}{3}\)
解析 (1)斜率不存在,即\(2m^2+m-1=0\),解得 \(m=\dfrac{1}{2}\);
(2)依题意,有 \(\dfrac{2 m-6}{m^{2}-2 m-3}=-3\),解得 \(m=-\dfrac{5}{3}\);
(3)依题意有 \(-\dfrac{m^{2}-2 m-3}{2 m^{2}+m-1}=1\),解得 \(m=\dfrac{4}{3}\). -
答案 (1) \((-1,-2)\) (2) \((-1,1)\)
解析 (1)该直线过定点\((-1,-2)\),
直线方程为\((2+2m)x+(1-m)y+4=0\),
可化为\((2x-y)m+(2x+y+4)=0\),
对任意\(m\)都成立,则 \(\left\{\begin{array}{l} 2 x-y=0 \\ 2 x+y+4=0 \end{array}\right.\),解得 \(\left\{\begin{array}{l} x=-1 \\ y=-2 \end{array}\right.\),
所以直线恒过定点\((-1,-2)\);
(2)\(∵\)方程为\((2+2m)x+(1-m)y+4=0\),
\(∴\)令\(x=0\),则 \(y=-\dfrac{4}{1-m}\),令\(y=0\), \(x=-\dfrac{4}{2+2 m}\)
\(∵\)直线分别与\(x\)轴,\(y\)轴的负半轴都相交,
\(\therefore\left\{\begin{array}{l} -\dfrac{4}{1-m}<0 \\ -\dfrac{4}{2+2 m}<0 \end{array}\right.\),解得\(-1<m<1\),
则\(m\)的取值范围是\((-1,1)\).
【B组---提高题】
1.直线\(x+y\cosθ-5=0\)的倾斜角\(α\)的取值范围是\(\underline{\quad \quad}\).
2.如图所示,在平面直角坐标系\(xOy\)中,已知点\(A(0,2)\),\(B(-2,0)\),\(C(1,0)\),分别以\(AB\),\(AC\)为边向外作正方形\(ABEF\)与\(ACGH\),则点\(H\)的坐标为 ,直线\(FH\)的一般式方程为\(\underline{\quad \quad}\)

3.已知直线\(l:kx-y+2k+1=0\),\(k∈R\).
(1)当\(k\)变化时,直线\(l\)恒过一定点\(P\),求点\(P\)的坐标;
(2)若直线\(l\)交\(x\)轴负半轴于点\(A\),交\(y\)轴正半轴于点\(B\), \(O\)为坐标原点,设\(△AOB\)的面积为\(S\),求\(S\)的最小值.
参考答案
-
答案 \(\left[\dfrac{\pi}{4}, \dfrac{3 \pi}{4}\right]\)
解析 若\(\cosθ=0\),则直线方程为\(x=5\),即倾斜角 \(\alpha=\dfrac{\pi}{2}\);
若\(\alpha=\dfrac{\pi}{2}\),则直线方程为 \(y=-\dfrac{1}{\cos \theta} x+\dfrac{5}{\cos \theta}\),
即 \(\tan \alpha=-\dfrac{1}{\cos \theta}\),
\(\because \cos \theta \in[-1,0) \cup(0,1]\), \(\therefore-\dfrac{1}{\cos \theta} \leq-1\)或 \(-\dfrac{1}{\cos \theta} \geq 1\),
即\(\tanα≤-1\)或\(\tanα≥1\),
解得 \(\alpha \in\left[\dfrac{\pi}{4}, \dfrac{\pi}{2}\right) \cup\left(\dfrac{\pi}{2}, \dfrac{3 \pi}{4}\right]\),
综上可得 \(\alpha \in\left[\dfrac{\pi}{4}, \dfrac{3 \pi}{4}\right]\). -
答案 \(x+4y-14=0\)
解析 分别过\(H\)、\(F\)作\(y\)轴的垂线,垂足分别为\(M\)、\(N\),
\(∵\)四边形\(ACGH\)为正方形,
\(∴Rt△AHM≌Rt△CAO\),可得\(AM=OC\),\(MH=OA\),
\(∵A(0,2)\),\(C(1,0)\),
\(∴MH=OA=2\),\(AM=OC=1\),可得\(OM=OA+AM=3\),
由此可得\(H\)坐标为\((2,3)\),同理得到\(F(-2,4)\),
\(∴\)直线\(FH\)的斜率为 \(k=\dfrac{4-3}{-2-2}=-\dfrac{1}{4}\),
可得直线\(FH\)的方程为\(y-3=-\dfrac{1}{4}(x-2)\),化简得\(x+4y-14=0\).
故答案为:\(x+4y-14=0\).

-
答案 (1) \(P(-2,1)\) (2)\(4\)
解析 (1)由直线\(l:kx-y+2k+1=0\),\(k∈R\).
变形为:\(k(x+2)-y+1=0\),
令 \(\left\{\begin{array}{l} x+2=0 \\ -y+1=0 \end{array}\right.\),解得\(x=-2,y=1\).
(2)直线\(l\)交\(x\)轴负半轴于点 \(A\left(-\dfrac{2 k+1}{k}, 0\right)\),交\(y\)轴正半轴于点\(B(0,2k+1)\),
则 \(\left\{\begin{array}{l} -\dfrac{2 k+1}{k}<0 \\ 2 k+1>0 \end{array}\right.\),\(k≠0\),解得\(k>0\).
设\(△AOB\)的面积为 \(S=\dfrac{1}{2} \times \dfrac{2 k+1}{k} \cdot(2 k+1)=\dfrac{1}{2}\left(4 k+\dfrac{1}{k}+4\right)\)\(\geqslant \dfrac{1}{2}\left(2 \sqrt{4 k \cdot \dfrac{1}{k}}+4\right)=4\),
当且仅当 \(k=\dfrac{1}{2}\)时取等号.
\(∴S\)的最小值为\(4\).
【C组---拓展题】
1.如图,将一块等腰直角三角板\(ABO\)置于平面直角坐标系中,已知\(AB=OB=1\),\(AB⊥OB\),点 \(P\left(\dfrac{1}{2}, \dfrac{1}{4}\right)\)是三角板内一点,现因三角板中部分(\(△POB\)内部,不含边界)受损坏,要把损坏的部分锯掉,可用经过\(P\)的任意一直线\(MN\)将其锯成\(△AMN\).
(1)求直线\(MN\)的斜率的取值范围;
(2)若\(P\)点满足 \(\overrightarrow{M P}=\dfrac{1}{3} \overrightarrow{P N}\),这样的直线\(MN\)是否存在,如不存在,请说明理由;若存在,求出此时直线\(MN\)的方程;
(3)如何确定直线\(MN\)的斜率,才能使锯成的\(△AMN\)的面积取得最大值和最小值?并求出最值.

参考答案
- 答案 (1) \(\left[-\dfrac{1}{2}, \dfrac{1}{2}\right]\) (2) \(x+2y-1=0\) (3) \(k=-\dfrac{1}{2}\)时 \(S_{\Delta \max }=\dfrac{1}{3}\);\(k=\dfrac{1}{2}\)时 \(S_{\Delta \min }=\dfrac{1}{4}\).
解析
(1) (根据观察图象易得 \(k_{P A} \leq k_{M N} \leq k_{P B} \Rightarrow-\dfrac{1}{2} \leq k \leq \dfrac{1}{2}\),但也可以设直线\(MN\)的方程,从而求出点\(M、N\)的坐标,从而由点\(M、N\)的限制求出 \(k_{M N}\)的范围)
依题意,得\(MN\)的方程为 \(y-\dfrac{1}{4}=k\left(x-\dfrac{1}{2}\right)\),即 \(y=k x-\dfrac{2 k-1}{4}\),
因为\(AB⊥OB\),\(|AB|=|OB|=1\),
所以直线\(OA\)的方程为\(y=x\),直线\(AB\)的方程为\(x=1\),
联立 \(\left\{\begin{array}{l} y-\dfrac{1}{4}=k\left(x-\dfrac{1}{2}\right) \\ y=x \end{array}\right.\),得 \(M\left(\dfrac{2 k-1}{4(k-1)}, \dfrac{2 k-1}{4(k-1)}\right)\),
联立 \(\left\{\begin{array}{l} y-\dfrac{1}{4}=k\left(x-\dfrac{1}{2}\right) \\ x=1 \end{array}\right.\),得 \(N\left(1, \dfrac{2 k+1}{4}\right)\),
所以 \(\left\{\begin{array}{l} 0 \leq \dfrac{2 k-1}{4(k-1)} \leq 1 \\ 0 \leq \dfrac{2 k+1}{4} \leq 1 \end{array}\right.\),解得 \(-\dfrac{1}{2} \leq k \leq \dfrac{1}{2}\).
所以\(k\)的取值范围为 \(\left[-\dfrac{1}{2}, \dfrac{1}{2}\right]\).
(得到\(M、N\)的坐标,便于求解第二、三问)
(2) 若 \(\overrightarrow{M P}=\dfrac{1}{3} \overrightarrow{P N}\),可得 \(\dfrac{1}{2}-\dfrac{2 k-1}{4(k-1)}=\dfrac{1}{3}\left(1-\dfrac{1}{2}\right)\),解得 \(k=-\dfrac{1}{2}\),
所以直线\(MN\)的方程为 \(y-\dfrac{1}{4}=-\dfrac{1}{2}\left(x-\dfrac{1}{2}\right)\),
整理得\(x+2y-1=0\).
(3)在\(△AMN\)中,由(1)知,
\(S_{\triangle A M N}=\dfrac{1}{2} \cdot|A N| \cdot h=\dfrac{1}{2}\left[1-\dfrac{2 k+1}{4}\right]\left[1-\dfrac{2 k-1}{4(k-1)}\right]\)\(=\dfrac{1}{32}\left[4(1-k)+\dfrac{1}{1-k}+4\right]\),
设 \(t=1-k \in\left[\dfrac{1}{2}, \dfrac{3}{2}\right]\),
则 \(f(t)=4 t+\dfrac{1}{t}\),
因为\(f(t)\)在 \(\left[\dfrac{1}{2}, \dfrac{3}{2}\right]\)是单调递增,(利用对勾函数的性质易得)
所以当 \(t=\dfrac{3}{2}\)时, \(f(t)=\dfrac{20}{3}\),
即当 \(1-k=\dfrac{3}{2}\),即\(k=-\dfrac{1}{2}\)时, \(S_{\max }=\dfrac{1}{32}\left[\dfrac{20}{3}+4\right]=\dfrac{1}{3}\),
当 \(t=\dfrac{1}{2}\)时,\(f(t)=4\),
即当 \(1-k=\dfrac{1}{2}\),即 \(k=\dfrac{1}{2}\)时,\(S_{\min }=\dfrac{1}{32}[4+4]=\dfrac{1}{4}\),
所以 \(k=-\dfrac{1}{2}\)时 \(S_{\Delta \max }=\dfrac{1}{3}\);_ _\(k=\dfrac{1}{2}\)时 \(S_{\Delta \min }=\dfrac{1}{4}\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号