2.2.2 直线的两点式方程
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高二数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性必修第一册同步巩固,难度2颗星!
基础知识
直线的两点式方程
经过两点\(P_1 (x_1,y_1 )\),\(P_2 (x_2,y_2 )\)(其中\(x_1≠x_2,y_1≠y_2\))的直线的方程是 \(\dfrac{y-y_{1}}{y_{2}-y_{1}}=\dfrac{x-x_{1}}{x_{2}-x_{1}}\),我们把它叫做直线的两点式方程,简称两点式.
解释
① 证明:当\(x_1≠x_2\)时,经过两点\(P_1 (x_1,y_1 )\),\(P_2 (x_2,y_2 )\)的直线斜率 \(k=\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}\),
再取点\(P_1 (x_1,y_1 )\),由点斜式可得 \(y-y_{1}=\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}\left(x-x_{1}\right)\);
当\(y_1≠y_2\)时,可得 \(\dfrac{y-y_{1}}{y_{2}-y_{1}}=\dfrac{x-x_{1}}{x_{2}-x_{1}}\).
② 在\(P_1 (x_1,y_1 )\),\(P_2 (x_2,y_2 )\)中,如果\(x_1=x_2\)或\(y_1=y_2\),则直线\(P_1 P_2\)没有两点式;
③ 两点式从代数的角度明确了”两点确定一直线”的事实.
【例】 利用两点式求过点\(A(0,1)\)和\(B(1,2)\)的直线方程.
解析 直线方程为 \(\dfrac{y-1}{2-1}=\dfrac{x-0}{1-0}\),化简为\(y=x+1\).
直线的截距式方程
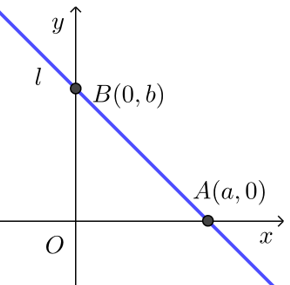
我们把 \(\dfrac{x}{a}+\dfrac{y}{b}=1\)(其中\(a\),\(b\)分别是直线在\(x\)轴、\(y\)轴上的截距且\(a≠0,b≠0\))叫做直线的截距式方程,简称截距式.
解释
① 证明:因为直线\(l\)与\(x\)轴的交点为\(A(a,0)\),与\(y\)轴的交点为\(B(0,b)\),
由两点式可得 \(\dfrac{y-0}{b-0}=\dfrac{x-a}{0-a}\),即 \(\dfrac{x}{a}+\dfrac{y}{b}=1\).
② 使用截距式的前提是直线\(x\)轴、\(y\)轴上的截距均不为\(0\).
【例】 求经过点\(A(0,2)\)和\(B(-1,0)\)的直线方程.
解析 直线的截距式方程为 \(\dfrac{x}{-1}+\dfrac{y}{2}=1\),化简为\(y=2x+2\).
基本方法
【题型1】直线的两点式与截距式
【典题1】 已知\(△ABC\)的三个顶点\(A(1,1)\),\(B(-2,-1)\),\(C(3,-3)\),求\(△ABC\)三条边所在的直线方程和\(AB\)边的中线所在直线的方程.
解析 由两点式方程,得直线\(AB\)的方程是 \(\dfrac{y-1}{-1-1}=\dfrac{x-1}{-2-1}\)
整理,得\(2x-3y+1=0\).
直线\(BC\)的方程是 \(\dfrac{y+1}{-3-(-1)}=\dfrac{x+2}{3-(-2)}\),
整理,得\(2x+5y+9=0\),
直线\(AC\)的方程是 \(\dfrac{y-1}{-3-1}=\dfrac{x-1}{3-1}\),整理,得\(2x+y-3=0\).
设\(AB\)的中点\(D(x,y)\),则 \(x=\dfrac{1-2}{2}=-\dfrac{1}{2}\), \(y=\dfrac{1-1}{2}=0\),
\(∴\)点\(D\)的坐标为 \(\left(-\dfrac{1}{2}, 0\right)\).
\(∴\)直线\(CD\)的方程为 \(\dfrac{y-0}{-3-0}=\dfrac{x+\dfrac{1}{2}}{3-\left(-\dfrac{1}{2}\right)}\),
整理,得\(6x+7y+3=0\).
因此\(△ABC\)三边\(AB\),\(BC\),\(AC\)及中线\(CD\)所在的直线方程分别是
\(2x-3y+1=0\),\(2x+5y+9=0\),\(2x+y-3=0\),\(6x+7y+3=0\).
【典题2】已知直线\(l\)经过点\((2,1)\),且在两坐标轴上的截距相等,求直线\(l\)的方程.
解析 方法一 设直线\(l\)在两坐标轴上的截距均为\(a\),
若\(a≠0\),则l的方程可设为 \(\dfrac{x}{a}+\dfrac{y}{a}=1\).
又\(∵l\)过点\((2,1)\),代入 \(\dfrac{x}{a}+\dfrac{y}{a}=1\),得\(a=3\),
∴直线\(l\)的方程为 \(\dfrac{x}{3}+\dfrac{y}{3}=1\),即\(x+y-3=0\).
若\(a=0\)时,\(l\)过点\((0,0)\)与\((2,1)\),
\(∴l\)的斜率 \(k=\dfrac{1}{2}\),
\(∴\)直线\(l\)的方程为\(y=\dfrac{1}{2} x\),即\(x-2y=0\).
\(∴\)直线\(l\)的方程为\(x+y-3=0\)或\(x-2y=0\).
方法二 由题意可知直线\(l\)的斜率存在且不为\(0\).
设过点\(A(2,1)\)的直线方程为\(y-1=k(x-2)(k≠0)\).
令\(x=0\),则\(y=1-2k\);
令\(y=0\),则 \(x=2-\dfrac{1}{k}\).
由已知条件,得 \(1-2 k=2-\dfrac{1}{k}\),解得\(k=-1\)或\(k=\dfrac{1}{2}\).
\(∴\)所求直线的方程为\(x+y-3=0\)或\(x-2y=0\).
巩固练习
1.直线经过点\((-2,0)\)和\((0,3)\),则直线的方程为( )
A. \(\dfrac{x}{2}+\dfrac{y}{3}=1\) \(\qquad \qquad\) B. \(\dfrac{x}{-2}+\dfrac{y}{3}=1\) \(\qquad \qquad\) C. \(\dfrac{x}{-2}+\dfrac{y}{-3}=1\) \(\qquad \qquad\) D. \(\dfrac{x}{2}+\dfrac{y}{-3}=1\)
2.过两点\((5,0)\),\((2,-5)\)的直线的方程是( )
A.\(5 x+3y-25=0\) \(\qquad \qquad\) B.\(5x-3y-25= 0\) \(\qquad \qquad\) C.\(3x-5y-25=0\) \(\qquad \qquad\) D.\(5x-3y+25= 0\)
3.梯形\(ABCD\)四个顶点坐标分别为\(A(-5,1)\),\(B(1,-3)\),\(C(4, 1)\),\(D(1,3)\).求该梯形中位线所在直线的方程.
4.已知直线\(l\)与\(x\)轴,\(y\)轴分别交于\(A\),\(B\)两点,且线段\(AB\)的中点为\(P(4,1)\),求直线\(l\)的方程.
5.求过点\(P(2,3)\)且在\(x\)轴上的截距是在\(y\)轴上截距的\(2\)倍的直线方程.
参考答案
-
答案 \(B\)
-
答案 \(B\)
解析 由两点式得 \(\dfrac{y-0}{x-5}=\dfrac{0+5}{5-2}\),化简得\(5x-3y-25= 0\),故选\(B\). -
答案 \(2x+3y-2=0\)
解析 \(\because k_{A B}=-\dfrac{2}{3}\), \(k_{C D}=-\dfrac{2}{3}\), \(∴AB∥CD\)
又\(AD\)中点\(M(-2,2)\),\(BC\)中 点 \(N\left(\dfrac{5}{2},-1\right)\),
由直线的两点式方程得梯形的中位线\(MN\)所在直线方程为 \(\dfrac{y-2}{-1-2}=\dfrac{x+2}{\dfrac{5}{2}+2}\),
化简得\(2x+3y-2=0\). -
答案 \(x+4y-8=0\)
解析 由题意可设\(A(x,0)\),\(B(0,y)\),
由中点坐标公式可得 \(\left\{\begin{array}{l} \dfrac{x+0}{2}=4 \\ \dfrac{0+y}{2}=1 \end{array}\right.\)解得 \(\left\{\begin{array}{l} x=8 \\ y=2 \end{array}\right.\)
\(∴A(8,0)\),\(B(0,2)\).
由直线方程的截距式得l方程为 \(\dfrac{x}{8}+\dfrac{y}{2}=1\),即\(x+4y-8=0\). -
答案 \(x+2y-8=0\)或\(3x-2y=0\)
解析 方法一:设直线在\(y\)轴上的截距为\(b\),则在\(x\)轴上的截距为\(2b\).
若\(b=0\),则直线过\((0,0)\)与\((2,3)\)点,则其方程为\(3x-2y=0\).
若\(b≠0\),则设其方程为 \(\dfrac{x}{2 b}+\dfrac{y}{b}=1 \text {, }\),又\(∵\)过点\((2,3)\),
\(\therefore \dfrac{2}{2 b}+\dfrac{3}{b}=1\),即\(b=4\).
\(\therefore \dfrac{x}{8}+\dfrac{y}{4}=1\),即\(x+2y-8=0\).
综上,所求直线方程为\(3x-2y=0\)或\(x+2y-8=0\).
方法二:由题意知直线的斜率存在且不为\(0\).
设过点\(P\)的直线方程为\(y-3=k(x-2)\).
由\(x=0\)得\(y=3-2k\);由\(y=0\)得 \(x=2-\dfrac{3}{k}\).
由已知条件,得 \(2-\dfrac{3}{k}=2(3-2 k)\),解得 \(k=-\dfrac{1}{2}\)或 \(k=\dfrac{3}{2}\).
所以所求直线方程为\(3x-2y=0\)或\(x+2y-8=0\).
【题型2】综合练习
【典题1】 过点\(P(2,1)\)作直线\(l\)分别与\(x,y\)轴正半轴交于\(A\)、\(B\)两点.
(1)当\(△AOB\)面积最小时,求直线\(l\)的方程;
(2)当\(|OA|+|OB|\)取最小值时,求直线\(l\)的方程.
解析 设\(A(a,0)\),\(B(0,b)(a,b>0)\).
(1)设直线方程为 \(\dfrac{x}{a}+\dfrac{y}{b}=1\),
代入\(P(2,1)\)得 \(\dfrac{2}{a}+\dfrac{1}{b}=1 \geqslant 2 \sqrt{\dfrac{2}{a b}}\),
得\(ab⩾8\),从而 \(S_{\triangle A O B}=\dfrac{1}{2} a b \geqslant 4\),此时 \(\dfrac{2}{a}=\dfrac{1}{b}, k=-\dfrac{b}{a}=-\dfrac{1}{2}\)
\(∴\)方程为\(x+2y-4=0\).
(2) \(a+b=(a+b)\left(\dfrac{2}{a}+\dfrac{1}{b}=1\right)=3+\dfrac{a}{b}+\dfrac{2 b}{a} \geqslant 3+2 \sqrt{2}\),
此时 \(\dfrac{a}{b}=\dfrac{2 b}{a}\), \(k=-\dfrac{b}{a}=-\dfrac{\sqrt{2}}{2}\).
\(∴\)方程为 \(x+\sqrt{2} y-2-\sqrt{2}=0\).
巩固练习
1.若直线过点\((1,1)\)且与两坐标轴所围成的三角形的面积为\(2\),则这样的直线有( )
A.\(1\)条 \(\qquad \qquad\) B.\(2\)条 \(\qquad \qquad\) C.\(3\)条 \(\qquad \qquad\) D.\(4\)条
2.过点\(M(2,1)\)作直线\(l\),分别交\(x\)轴、\(y\)轴的正半轴于点\(A\),\(B\),若\(△ABO\)的面积\(S\)最小,试求直线\(l\)的方程.
参考答案
- 答案 \(C\)
解析 设直线\(l\)的截距式为 \(\dfrac{x}{a}+\dfrac{y}{b}=1\),
\(∵\)直线\(l\)经过点\((1,1)\),且与两坐标轴所围成的三角形的面积为\(2\),
\(\therefore\left\{\begin{array}{l} \dfrac{1}{a}+\dfrac{1}{b}=1 \\ \dfrac{1}{2}|a b|=2 \end{array}\right.\),
解得\(a=b=2\),或 \(a=2+2 \sqrt{2}, b=2-2 \sqrt{2}\),或 \(a=2-2 \sqrt{2}, b=2+2 \sqrt{2}\)
直线\(l\)的条数为\(3\).
故选:\(C\). - 答案 \(x+2y-4=0\)
解析 设\(A(a,0)\),\(B(0,b),(a,b>0)\),
则直线\(l\)的方程为 \(\dfrac{x}{a}+\dfrac{y}{b}=1\),
又\(∵M(2,1)\)在直线\(l\)上, \(\therefore \dfrac{2}{a}+\dfrac{1}{b}=1\)
又 \(\because 1=\dfrac{2}{a}+\dfrac{1}{b} \geqslant 2 \sqrt{\dfrac{2}{a b}}\),\(∴ab⩾8\),
\(\therefore S=\dfrac{1}{2} a b \geqslant 4\),等号当且仅当,即\(a=4,b=2\)时成立,
\(∴\)直线\(l\)的方程为: \(\dfrac{x}{4}+\dfrac{y}{2}=1\),即\(x+2y-4=0\).
分层练习
【A组---基础题】
1.直线 \(\dfrac{x}{a^{2}}-\dfrac{y}{b^{2}}=1(a b \neq 0)\)在\(y\)轴上的截距是( )
A.\(a^2\) \(\qquad \qquad\) B.\(-b^2\) \(\qquad \qquad\) C.\(|a|\) \(\qquad \qquad\) D.\(b^2\)
2.过点\(P_1 (-2,0)\),\(P_2 (1,3)\)的直线方程是( )
A.\(y=-x+1\) \(\qquad \qquad\) B.\(y=-3x-6\) \(\qquad \qquad\) C.\(y=x+2\) \(\qquad \qquad\) D.\(y=-x-2\)
3.过点\((-2,0)\)且在两坐标轴上的截距之差为\(3\)的直线方程是( )
A. \(\dfrac{x}{-2}+y=1\) \(\qquad \qquad \qquad\qquad\) B. \(\dfrac{x}{-2}+\dfrac{y}{-5}=1\)
C. \(\dfrac{x}{-2}+\dfrac{y}{-1}=1\) \(\qquad \qquad \qquad\qquad\) D.\(\dfrac{x}{-2}+y=1\)或\(\dfrac{x}{-2}+\dfrac{y}{-5}=1\)
4.直线 \(\dfrac{x}{5}-\dfrac{y}{3}=1\)与坐标轴围成的三角形的面积为\(\underline{\quad \quad}\).
5.经过点\(A(-2,3)\),且在两坐标轴上的截距之和为\(2\)的直线的方程为\(\underline{\quad \quad}\).
6.已知点\(P(b,a)\),直线 \(\dfrac{x}{a}+\dfrac{y}{b}=1(a≠b)\)与\(x\)轴、\(y\)轴分别交于\(A\)、\(B\)两点.设直线\(PA\)、\(PB\)、\(AB\)的斜率分别为\(k_1\),\(k_2\),\(k_3\).
(1)当\(a=2\),\(b=1\)时,求\(k_1 k_2 k_3\)的值;
(2)求证:不论\(a,b\)为何实数,\(k_1 k_2 k_3\)的值都为定值.
参考答案
- 答案 \(B\)
- 答案 \(C\)
解析 由两点式可得 \(\dfrac{y-0}{x+2}=\dfrac{3-0}{1+2}\),化简得\(y=x+2\),故选\(C\). - 答案 \(D\)
解析 过点\((-2,0)\)即直线在\(x\)轴上的截距为\(-2\),
又直线在两坐标轴上的截距之差为\(3\),则直线在\(x\)轴上的截距为\(-5\)或\(1\),
所以直线方程为\(\dfrac{x}{-2}+y=1\)或\(\dfrac{x}{-2}+\dfrac{y}{-5}=1\),故选\(D\). - 答案 \(\dfrac{15}{2}\)
解析 直线 \(\dfrac{x}{5}-\dfrac{y}{3}=1\)与坐标轴的交点坐标为:
当\(x=0\)时,\(y=-3\),即\(A(0,-3)\);当\(y=0\)时,\(x=5\),即\(B(5,0)\);
故 \(S_{\triangle A O B}=\dfrac{1}{2} \times 3 \times 5=\dfrac{15}{2}\).
故答案为: \(\dfrac{15}{2}\) - 答案 \(y=-x+1\)或 \(y=\dfrac{3}{2} x+6\)
解析 由题意可得设直线\(l\)的方程为 \(\dfrac{x}{a}+\dfrac{y}{b}=1\),
\(∵\)直线\(l\)过点\(P(-2,3)\), \(\therefore-\dfrac{2}{a}+\dfrac{3}{2-a}=1\),
又\(a+b=2\),解得:\(a=1\)或\(a=-4\),
\(∴\)直线l的方程为\(y=-x+1\)或 \(y=\dfrac{3}{2} x+6\).
故答案为:\(y=-x+1\)或 \(y=\dfrac{3}{2} x+6\). - 答案 (1) \(1\) (2)略
解析 (1)当\(a=2\),\(b=1\)时,\(A(2,0)\),\(B(0,1)\),\(P(1,2)\)
\(\therefore k_{1}=\dfrac{0-2}{2-1}=-2\), \(k_{2}=\dfrac{1-2}{0-1}=1\), \(k_{3}=\dfrac{0-1}{2-0}=-\dfrac{1}{2}\),
\(∴k_1 k_2 k_3=1\).
(2)可得\(A(a,0)\),\(B(0,b)\),\(P(b,a)\),
\(\therefore k_{1}=\dfrac{0-a}{a-b}=\dfrac{-a}{a-b}\), \(k_{2}=\dfrac{b-a}{0-b}=\dfrac{b-a}{-b}\), \(k_{3}=\dfrac{0-b}{a-0}=\dfrac{-b}{a}\)
\(\therefore k_{1} k_{2} k_{3}=\dfrac{-a}{a-b} \cdot \dfrac{b-a}{-b} \cdot \dfrac{-b}{a}=1\),
\(∴\)不论\(a,b\)为何实数,\(k_1 k_2 k_3\)的值都为定值\(1\).
【B组---提高题】
1.已知直线\(l\)与\(x\)轴,\(y\)轴分别交于\(A\),\(B\)两点,且线段\(AB\)的中点为\(P(4,1)\),求直线\(l\)的方程.
2.过点\(P(2,4)\)作直线\(l\)分别与\(x,y\)轴正半轴交于\(A\)、\(B\)两点.
(1)当\(△AOB\)面积最小时,求直线\(l\)的方程;
(2)当\(|OA|+|OB|\)取最小值时,求直线\(l\)的方程.
参考答案
-
答案 \(x+4y-8=0\)
解析 由题意可设\(A(x,0)\),\(B(0,y)\),
由中点坐标公式可得 \(\left\{\begin{array}{l} \dfrac{x+0}{2}=4 \\ \dfrac{0+y}{2}=1 \end{array}\right.\)解得 \(\left\{\begin{array}{l} x=8 \\ y=2 \end{array}\right.\)
\(∴A(8,0)\),\(B(0,2)\).
由直线方程的截距式得\(l\)方程为 \(\dfrac{x}{8}+\dfrac{y}{2}=1\),即\(x+4y-8=0\). -
答案 (1)\(y=-2x+8\) (2) \(y=-\sqrt{2} x+2 \sqrt{2}+4\)
解析 设\(A(a,0)\),\(B(0,b)(a,b>0)\).
(1)设直线方程为 \(\dfrac{x}{a}+\dfrac{y}{b}=1\),
代入\(P(2,1)\)得 \(\dfrac{2}{a}+\dfrac{4}{b}=1 \geqslant 4 \sqrt{\dfrac{2}{a b}}\),
得\(ab⩾32\),从而 \(S_{\triangle A O B}=\dfrac{1}{2} a b \geqslant 16\),此时 \(\dfrac{2}{a}=\dfrac{4}{b}\), \(k=-\dfrac{b}{a}=-2\)
\(∴\)方程为\(y-4=-2(x-2)\),即\(y=-2x+8\).
(2)\(a+b=(a+b)\left(\dfrac{2}{a}+\dfrac{4}{b}\right)=6+\dfrac{4 a}{b}+\dfrac{2 b}{a} \geqslant 6+4 \sqrt{2}\),
此时 \(\dfrac{4 a}{b}=\dfrac{2 b}{a}\), \(k=-\dfrac{b}{a}=-\sqrt{2}\).
\(∴\)方程为 \(y-4=-\sqrt{2}(x-2)\),即 \(y=-\sqrt{2} x+2 \sqrt{2}+4\).
【C组---拓展题】
1.直线\(l\)通过点\(P(1,3)\)且与两坐标轴的正半轴交于\(A\),\(B\)两点.
(1)直线\(l\)与两坐标轴所围成的三角形面积为\(6\),求直线\(l\)的方程;
(2)求\(OA+OB\)的最小值;
(3)求\(PA⋅PB\)的最小值.
参考答案
- 答案 (1) \(3x+y-6=0\) (2) \(4+2 \sqrt{3}\) (3) \(6\)
解析 (1)设直线l的方程为\(y-3=k(x-1)(k<0)\),
由\(x=0\),得\(y=3-k\),由\(y=0\),得 \(x=1-\dfrac{3}{k}\)
\(\therefore S_{\triangle A O B}=\dfrac{1}{2}(3-k)\left(1-\dfrac{3}{k}\right)=6\),解得\(k=-3\)
\(∴\)直线\(l\)的方程为\(3x+y-6=0\);
(2) \(O A+O B=3-k+1-\dfrac{3}{k}=4+(-k)+\left(-\dfrac{3}{k}\right)\)\(\geqslant 4+2 \sqrt{-k \cdot\left(-\dfrac{3}{k}\right)}=4+2 \sqrt{3}\).
当且仅当 \(-k=-\dfrac{3}{k}\),即 \(k=-\sqrt{3}\)时上式“\(=\)”成立;
(3)设直线\(l\)在\(x,y\)轴上的截距分别为\(a,b\),
则 \((P A \cdot P B)^{2}=\left[(a-1)^{2}+9\right]\left[(b-3)^{2}+1\right]\)
\(=\left[(a-1)^{2}+9\right]\left[\dfrac{9}{(a-1)^{2}}+1\right]=18+(a-1)^{2}+\dfrac{81}{(a-1)^{2}}\)\(\geqslant 18+2 \sqrt{81}=36\).
当且仅当\(a=4\)时上式取等号.
\(∴PA⋅PB\)的最小值为\(6\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号