2.1.2 两条直线平行与垂直的判定
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高二数学上学期同步知识点剖析精品讲义(人教A版2019）
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)
选择性必修第一册同步巩固，难度2颗星！
基础知识
两直线平行
1 对于斜率分别为\(k_1\)，\(k_2\)的两条直线\(l_1\) ,\(l_2\)，有\(l_1//l_2⇔k_1=k_2\).
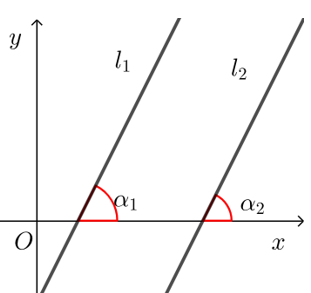
解释
① 证明：若\(l_1//l_2\)，则\(l_1\)与\(l_2\)的倾斜角\(α_1\)与\(α_2\)相等，则 \(\tan \alpha_{1}=\tan \alpha_{2}\)，即\(k_1=k_2\).
因此若\(l_1//l_2\)，则\(k_1=k_2\)；反之\(k_1=k_2\)时， \(\tan \alpha_{1}=\tan \alpha_{2}\)，
由倾斜角范围\(α∈[0,π)\)及正切函数的单调性可知\(α_1=α_2\)，因此\(l_1//l_2\).
② 当\(α_1=α_2=90°\)时，直线的斜率不存在，此时\(l_1//l_2\).
③ 若存在斜率的两直线\(l_1\),\(l_2\)重合，此时仍然有\(k_1=k_2\).
故可用斜率相等证明三点共线时.
【例1】两条不重合直线\(l_1\),\(l_2\)斜率\(k_1=k_2\)是\(l_1// l_2\)的\(\underline{\quad \quad}\)条件.
解析 若直线\(l_1\),\(l_2\)斜率\(k_1=k_2\)，则\(l_1// l_2\)；故\(k_1=k_2\)是\(l_1// l_2\)的充分条件；
若\(l_1// l_2\)，不一定有\(k_1=k_2\)，因为两直线可能垂直\(x\)轴而不存在斜率，
故\(k_1=k_2\)是\(l_1// l_2\)的不必要条件；
故填充分不必要条件.
【例2】已知\(A(2,2)\)，\(B(4,0)\)，\(C(0,4)\)，求证：\(A,B,C\)三点共线.
解析 直线\(AB\)的斜率 \(k_{A B}=\dfrac{0-2}{4-2}=-1\)，直线\(AC\)的斜率 \(k_{A C}=\dfrac{4-2}{0-2}=-1\)，
\(\therefore k_{A B}=k_{A C}\)．
\(∵\)直线\(AB\)与直线\(AC\)的倾斜角相同且过同一点\(A\)，
\(∴\)直线\(AB\)与直线\(AC\)为同一直线．
故\(A,B,C\)三点共线．
两直线垂直
对于斜率分别为\(k_1\)，\(k_2\)的两条直线\(l_1\) ,\(l_2\)，有\(l_1⊥ l_2⇔k_1⋅ k_2=-1\).
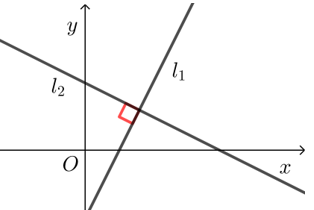
解释
① 证明：直线\(l_1\) ,\(l_2\)的方向向量分别是 \(\vec{a}=\left(1, k_{1}\right)\)， \(\vec{b}=\left(1, k_{2}\right)\)，于是
\(l_{1} \perp l_{2} \Leftrightarrow \vec{a} \perp \vec{b} \Leftrightarrow \vec{a} \cdot \vec{b}=0 \Leftrightarrow 1 \times 1+k_{1} k_{2}=0\)，即\(k_1⋅ k_2=-1\)；
② 当直线\(l_1\) 或\(l_2\)的倾斜角为\(90°\)时，若\(l_1⊥ l_2\)，则另一条直线的倾斜角为\(0°\)；反之亦然.
【例1】两条直线\(l_1\),\(,l_2\)斜率\(k_1⋅ k_2=-1\)是\(l_1⊥ l_2\)的\(\underline{\quad \quad}\)条件.
解析 若直线\(l_1\) ,\(l_2\)存在斜率，且\(k_1⋅ k_2=-1\)，则\(l_1⊥ l_2\)；故\(k_1⋅ k_2=-1\)是\(l_1⊥ l_2\)的充分条件；
若\(l_1⊥ l_2\)，不一定有\(k_1⋅ k_2=-1\)，因为若两直线倾斜角分别为\(90°\)和\(0°\)，它们依然相互垂直，
但由于一直线不存在斜率，则不存在\(k_1⋅ k_2=-1\)，
故\(k_1⋅ k_2=-1\)是\(l_1⊥ l_2\)的不必要条件；
故填充分不必要条件.
基本方法
【题型1】两条直线位置关系的判断
【典题1】 判断下列各小题中的直线\(l_1\)与\(l_2\)是否平行：
(1) \(l_1\)经过点\(A(－1,－2)\)，\(B(2,1)\)，\(l_2\)经过点\(M(3,4)\)，\(N(－1,－1)\)；
(2) \(l_1\)的斜率为\(1\)，\(l_2\)经过点\(A(1,1)\)，\(B(2,2)\)；
(3) \(l_1\)经过点\(A(0,1)\)，\(B(1,0)\)，\(l_2\)经过点\(M(－1,3)\)，\(N(2,0)\)；
(4) \(l_1\)经过点\(A(－3,2)\)，\(B(－3,10)\)，\(l_2\)经过点\(M(5,－2)\)，\(N(5,5)\)．
解析 (1) \(k_{1}=\dfrac{1-(-2)}{2-(-1)}=1\), \(k_{2}=\dfrac{-1-4}{-1-3}=\dfrac{5}{4}\)，\(k_1≠k_2\)，\(l_1\)与\(l_2\)不平行．
(2) \(k_1=1\), \(k_{2}=\dfrac{2-1}{2-1}=1\)，\(k_1=k_2\)，\(∴l_1∥l_2\)或\(l_1\)与\(l_2\)重合．
(3) \(k_{1}=\dfrac{0-1}{1-0}=-1\), \(k_{2}=\dfrac{0-3}{2-(-1)}=-1\)，则有\(k_1=k_2\)．
又 \(k_{A M}=\dfrac{3-1}{-1-0}=-2 \neq-1\)，
\(∴A ,B,M\)不共线．故\(l_1∥l_2\)．
(4)由已知点的坐标，得\(l_1\)与\(l_2\)均与\(x\)轴垂直且不重合，故有\(l_1∥l_2\)．
点拨 两斜率相等还要主要两直线是否会重合.
【典题2】直线\(l_1\)过点\((2m,1)\)，\((-3,m)\)，直线\(l_2\)过点\((m,m)\)，\((1,-2)\)，若\(l_1\)与\(l_2\)垂直，求实数\(m\)的值．
解析 ①当两直线斜率都存在，即 \(m \neq-\dfrac{3}{2}\)且\(m≠1\)时，有 \(k_{1}=\dfrac{1-m}{2 m+3}\), \(k_{2}=\dfrac{m+2}{m-1}\)．
\(∵\)两直线互相垂直， \(\therefore \dfrac{1-m}{2 m+3} \cdot \dfrac{m+2}{m-1}=-1\)．\(∴m=-1\)．
②当\(m=1\)时，\(k_1=0\)，\(k_2\)不存在，此时亦有两直线垂直．
当\(2m=-3\)即 \(m=-\dfrac{3}{2}\)时，\(k_1\)不存在， \(k_{2}=\dfrac{m+2}{m-1}=\dfrac{-\dfrac{3}{2}+2}{-\dfrac{3}{2}-1}=-\dfrac{1}{5}\)，\(l_1\)与\(l_2\)不垂直．
综上\(m=±1\)．
点拨 求斜率时是否会存在；判断直线位置关系时，也要注意直线是否存在斜率.
巩固练习
1.若\(l_1\)与\(l_2\)为两条不重合的直线，它们的倾斜角分别为\(a_1\),\(a_2\)，斜率分别为\(k_1\),\(k_2\)，则下列命题
(1)若\(l_1∥l_2\)，则斜率\(k_1=k_2\)； \(\qquad \qquad\) (2)若斜率\(k_1=k_2\)，则\(l_1∥l_2\)；
(3)若\(l_1∥l_2\)，则倾斜角\(a_1=a_2\)； \(\qquad \qquad\) (4)若倾斜角\(a_1=a_2\)，则\(l_1∥l_2\)；
其中正确命题的个数是( )
A．\(1\) \(\qquad \qquad\) B．\(2\) \(\qquad \qquad\) C．\(3\) \(\qquad \qquad\) D．\(4\)
2.如果直线\(l_1\)的斜率为\(a\)，\(l_1⊥l_2\)，则直线\(l_2\)的斜率为( )
A． \(\dfrac{1}{a}\) \(\qquad \qquad\) B．\(a\) \(\qquad \qquad\) C． \(-\dfrac{1}{a}\) \(\qquad \qquad\) D． \(-\dfrac{1}{a}\)或不存在
3.已知过\(A(-2,m)\)和\(B(m,4)\)的直线与斜率为\(-2\)的直线平行，则\(m\)的值是( )
A．\(-8\) \(\qquad \qquad\) B．\(0\) \(\qquad \qquad\) C．\(2\) \(\qquad \qquad\) D．\(10\)
4.若直线\(l\)经过点\((a－2,－1)\)和\((－a－2,1)\)，且与斜率为 \(-\dfrac{2}{3}\)的直线垂直，则实数\(a\)的值是( )
A． \(-\dfrac{2}{3}\) \(\qquad \qquad\) B． \(-\dfrac{3}{2}\) \(\qquad \qquad\) C． \(\dfrac{2}{3}\) \(\qquad \qquad\) D． \(\dfrac{3}{2}\)
5.直线\(l_1\)的斜率为\(2\)，\(l_1∥l_2\)，直线\(l_2\)过点\(( -1,1)\)且与\(y\)轴交于点\(P\)，则\(P\)点坐标为\(\underline{\quad \quad}\) .
6.已知\(A(1,－1)\)，\(B(2,2)\)，\(C(3,0)\)三点，且有一点\(D\)满足\(CD⊥AB\)，\(CB∥AD\)，则\(D\)点的坐标为\(\underline{\quad \quad}\).
参考答案
-
答案 \(D\)
解析 (1)由于斜率都存在，若\(l_1∥l_2\)，则\(k_1=k_2\)，此命题正确；
(2)因为两直线的斜率相等即斜率\(k_1=k_2\)，得到倾斜角的正切值相等即\(\tan a_1=\tan a_2\)，
即可得到\(a_1=a_2\)，所以\(l_1∥l_2\)，此命题正确；
(3)因为\(l_1∥l_2\)，根据两直线平行，得到\(a_1=a_2\)，此命题正确；
(4)因为两直线的倾斜角\(a_1=a_2\)，根据同位角相等，得到\(l_1∥l_2\)，此命题正确；
所以正确的命题个数是\(4\)．
故选：\(D\)． -
答案 \(D\)
解析 当\(a=0\)时，直线\(l_2\)的斜率不存在，当\(a≠0\)时，直线\(l_2\)的斜率为 \(-\dfrac{1}{a}\)，故选\(D\). -
答案 \(A\)
解析 由 \(k_{A B}=\dfrac{m-4}{-2-m}=-2\)解得\(m=-8\). -
答案 \(A\)
解析 依题意得直线l的斜率 \(k=\dfrac{3}{2}\)，由 \(\dfrac{3}{2}=\dfrac{1-(-1)}{-a-2-(a-2)}\)，解得 \(a=-\dfrac{2}{3}\). -
答案 \((0,3)\)
解析 因为直线\(l_1\)的斜率为\(2\)，\(l_1∥l_2\)，所以直线\(l_2\)的斜率也等于\(2\)，
设点\(P(0,m)\),
又直线\(l_2\)过点\(( -1,1)\)，则 \(\dfrac{m-1}{0-(-1)}=2\)，解得\(m=3\),
得到直线\(l_2\)与\(y\)轴交于点\(P\)为\((0,3)\)． -
答案 \((0,1)\)
解析 \(k_{A B}=\dfrac{2-(-1)}{2-1}=3\) ，\(k_{C B}=\dfrac{2-0}{2-3}=-2\)．
\(∵CD⊥AB\)，\(CB∥AD\)，\(∴CD\)与\(AD\)的斜率 都存在．
设\(D\)点坐标为\((x,y)\)，则 \(k_{C D}=\dfrac{y}{x-3}\), \(k_{A D}=\dfrac{y+1}{x-1}\)．
解方程组 \(\left\{\begin{array}{l} \dfrac{y}{x-3}=-\dfrac{1}{3} \\ \dfrac{y+1}{x-1}=-2 \end{array}\right.\)得 \(\left\{\begin{array}{l} x=0 \\ y=1 \end{array}\right.\)，
\(∴\)点\(D\)坐标为\((0,1)\)．
【题型2】两直线平行与垂直的综合应用
【典题1】 顺次连接\(A(-4 ,3)\)、\(B(2 ,5)\)、\(C(6 ,3)\)、\(D(-3 ,0)\)，所组成的图形是( )
A．平行四边形 \(\qquad \qquad\) B．直角梯形 \(\qquad \qquad\) C．等腰梯形\(\qquad \qquad\) D．以上都不对
解析 (要判断四边形形状，需要判断各边的位置关系，可从直线斜率入手)
\(AB\)的斜率为 \(\dfrac{5-3}{2+4}=\dfrac{1}{3}\)，\(CD\)的斜率为 \(\dfrac{3-0}{6+3}=\dfrac{1}{3}\)，
则\(k_{AB}=k_{CD}\)，故\(AB||CD\)；
由\(AD\)的斜率为 \(\dfrac{3-0}{-4+3}=-3\)得 \(k_{A D} \cdot k_{A B}=-1\)，则\(AB⊥AD\)；
由\(BC\)的斜率为 \(\dfrac{5-3}{2-6}=-\dfrac{1}{2}\)得 \(k_{A D} \neq k_{B C}\)，则\(AD\)与\(BC\)不平行，
故四边形为直角梯形，故选\(B\)．
【典题2】已知正方形\(ABCD\)的边长为\(4\)，若\(E\)是\(BC\)的中点，\(F\)是\(CD\)的中点，试建立坐标系，求证：\(BF⊥AE\)．
证明 建立平面直角坐标系，如图所示，
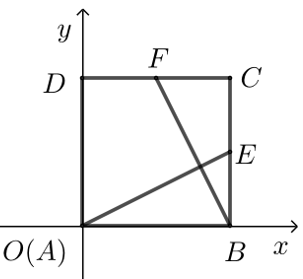
则\(B(4,0)\),\(E(4,2)\),\(F(2,4)\),\(A(0,0)\)，
所以斜率 \(k_{A E}=\dfrac{2}{4}=\dfrac{1}{2}\), \(k_{B F}=\dfrac{4-0}{2-4}=-2\)．
又 \(k_{A E} \cdot k_{B F}=\dfrac{1}{2} \times(-2)=-1\)，所以\(BF⊥AE\)．
巩固练习
1.已知\(A(－1,1)\)，\(B(2,－1)\)，\(C(1,4)\)，则\(△ABC\)是( )
A．锐角三角形
B．钝角三角形
C．以\(A\)点为直角顶点的直 角三角形
D．以\(B\)点为直角顶点的直角三角形
2.已知\(A(-1,2)\)，\(B(3,3)\)，\(C(2,-3)\)，\(D(-2,-4)\)四点，若顺次连接\(A,B,C,D\)四点，试判定四边形\(ABCD\)的形状．
参考答案
- 答案 \(C\)
解析 \(k_{A B}=\dfrac{1-(-1)}{-1-2}=-\dfrac{2}{3}\), \(k_{A C}=\dfrac{4-1}{1-(-1)}=\dfrac{3}{2}\)，
\(\therefore k_{A B} \cdot k_{A C}=-1\)．\(∴AB⊥AC\)．\(∴∠A\)是直角． - 答案 平行四边形
解析 由斜率公式可得
\(k_{A B}=\dfrac{3-2}{3-(-1)}=\dfrac{1}{4}\) , \(k_{C D}=\dfrac{-3-(-4)}{2-(-2)}=\dfrac{1}{4}\),
\(k_{A D}=\dfrac{2-(-4)}{-1-(-2)}=6\), \(k_{B C}=\dfrac{3-(-3)}{3-2}=6\),
\(∴k_{A B} = k_{CD}\)， \(k_{A D} = k_{B C}\)，
\(∴AB∥CD\),\(AD∥BC\)．，且\(𝐴𝐵\)与\(𝐶𝐷\)，\(𝐴𝐷\)与\(𝐵𝐶\)不重合，
故四边形\(𝐴𝐵𝐶𝐷\)为平行四边形．
分层练习
【A组---基础题】
1.下列说 法中正确的是( )
A．平行的两条直线的斜率一定存在且相等
B．平行的两条直线的倾斜角一定相等
C．垂直的两直线的斜率之积为\(－1\)
D．只有斜率相等的两条直线才一定平行
2.已知直线\(l_1\)经过点\(A(－2,5)\)，\(B(3,5)\)，直线\(l_2\)经过点\(M(2,4)\)，\(N(2,－4)\)，则直线\(l_1\)与\(l_2\)的关系是( )
A．\(l_1∥l_2\) \(\qquad \qquad\) B．\(l_1⊥l_2\) \(\qquad \qquad\) C．重合 \(\qquad \qquad\)D．以上都不对
3.两直线的斜率分别是方程\(x^2+2013x-1=0\)的两根，那么这两直线的位置关系是( )
A．垂直\(\qquad \qquad\) B．斜交\(\qquad \qquad\) C．平行 \(\qquad \qquad\) D．重合
4.已知直线\(l_1\)经过两点\((－1,－2)\)，\((－1,4)\)，直线\(l_2\)经过两点\((2,1)\)，\((x,6)\)，且\(l_1∥l_2\)，则\(x\)等于( )
A．\(2\) \(\qquad \qquad\) B．\(－2\) \(\qquad \qquad\) C． \(4\) \(\qquad \qquad\) D．\(1\)
5.顺次连接\(A(-4,3)\)、\(B(2,5)\)、\(C(6,3)\)、\(D(-3,0)\)，所组成的图形是( )
A．平行四边形 \(\qquad \qquad\) B．直角梯形 \(\qquad \qquad\) C．等腰梯形 \(\qquad \qquad\) D．以上都不对
6.(多选)已知点\(A(-4,2)\),\(B(6,-4)\),\(C(12,6)\),\(D(2,12)\)，那么下面四个结论中正确的是( )
A．\(AB∥CD\) \(\qquad \qquad\) B．\(AB⊥CD\) \(\qquad \qquad\)C．\(AC∥BD\) \(\qquad \qquad\) D．\(AC⊥BD\)
7.已知\(△ABC\)的三个顶点的坐标分别为\(A(－1,0)\)，\(B(2,0)\)，\(C(2,3)\)，则\(AB\)边上的高所在直线的斜率\(\underline{\quad \quad}\)， \(BC\)边上的高所在直线的斜率为\(\underline{\quad \quad}\) ．
8.已知直线\(l_1\)的倾斜角为\(45°\)，直线\(l_2∥l_1\)，且\(l_2\)过点\(A(-2,-1)\)和\(B(3,a)\)，则\(a\)的值为\(\underline{\quad \quad}\)．
9.在直角梯形\(ABCD\)中，已知\(A(-5,-10)\)，\(B(15,0)\)，\(C(5,10)\)，\(AD\)是腰且垂直两底，求顶点的坐标．
10.如图，在\(△ABC\)中，点\(A\)的坐标为\((－1,1)\)，点\(B\)坐标为\((4,6)\)，点\(C\)在\(x\)轴上，线段\(AB\)与\(y\)轴相交于点\(D\)，且\(AB⊥CD\)．
(1)求点\(C\)的坐标；(2)求\(△ABC\)的面积．
参考答案
- 答案 \(B\)
- 答案 \(B\)
- 答案 \(A\)
解析 设两直线的斜率分别为\(k_1\),\(k_2\)，\(k_1\),\(k_2\)是方程\(x^2+2013x-1=0\)的两根，
利用根与系数的关系得：\(k_1 k_2=-1\)，
\(∴\)两直线的位置关系是垂直．
故选：\(A\)． - 答案 \(A\)
- 答案 \(B\)
解析 \(AB\)的斜率为 \(\dfrac{5-3}{2+4}=\dfrac{1}{3}\)，\(CD\)的斜率为 \(\dfrac{3-0}{6+3}=\dfrac{1}{3}\) ，
故 \(AB//CD\)．\(AD\)的斜率为 \(\dfrac{3-0}{-4+3}=-3\)，
\(∴AB⊥AD\),\(BC\)的斜率为 \(\dfrac{5-3}{2-6}=-\dfrac{1}{2}\)，
故\(AD\)与\(BC\)不平行，故四边形为直角梯形，故选 \(B\)． - 答案 \(AD\)
解析 易知\(A,B,C,D\)四点不共线，
\(\because k_{A B}=\dfrac{-4-2}{6-(-4)}=-\dfrac{3}{5}\)， \(k_{C D}=\dfrac{12-6}{2-12}=-\dfrac{3}{5}\)， \(k_{B D}=\dfrac{12-(-4)}{2-6}=-4\)， \(k_{A C}=\dfrac{6-2}{12-(-4)}=\dfrac{1}{4}\)
\(\therefore k_{A B}=k_{C D}\)， \(k_{A C} \cdot k_{B D}=-1\)，
\(∴AB∥CD\)，\(AC⊥BD\)，
故选：\(AD\)． - 答案 不存在 \(0\)
- 答案 \(4\)
解析 \(k_1=tan45°=1\)， \(k_{2}=\dfrac{a-(-1)}{3-(-2)}=\dfrac{a+1}{5}\)，
\(∵l_2∥l_1\)， \(\therefore k_{1}=k_{2} \Rightarrow \dfrac{a+1}{5}=1\)，解得\(a=4\). - 答案 \(D(-11,2)\)
解析 设\(D(x,y)\)，则\(∵DC//AB\)， \(\therefore \dfrac{y-10}{x-5}=\dfrac{0+10}{15+5}\)，
又\(∵DA⊥AB\)， \(\therefore \dfrac{y+10}{x+5} \cdot \dfrac{0+10}{15+5}=-1\)
由以上方程组解得：\(x=-11\),\(y=2\)．
\(∴D(-11,2)\)． - 答案 (1) \((2,0)\) (2) \(10\)
解析 (1)\(∵\)在\(△ABC\)中，点\(A\)的坐标为\((－1,1)\)，
点\(B\)坐标为\((4,6)\)，点\(C\)在\(x\)轴上，线段\(AB\)与\(y\)轴相交于点\(D\)，
\(∴\)直线\(AB\)的斜率为 \(k_{A B}=\dfrac{6-1}{4+1}=1\)，
设直线\(AB\)的方程为\(y=x+b\)，
代入点\((－1,1)\)可得直线\(AB\)的方程为\(y=x+2\)，\(∴D(0,2)\)，
\(∵AB⊥CD\)， \(\therefore k_{A B} \cdot k_{C D}=-1\)， \(\therefore k_{C D}=-1\)，
\(∴\)直线\(CD\)的直线方程为\(y=-x+2\)，
令\(y=0\)，得\(x=2\)，
\(∴\)点\(C\)的坐标为\((2,0)\)．
(2)由(1)得 \(|A B|=\sqrt{5^{2}+5^{2}}=5 \sqrt{2}\)， \(|C D|=\sqrt{2^{2}+2^{2}}=2 \sqrt{2}\)，
\(∴△ABC\)的面积 \(S=\dfrac{1}{2} \times|A B| \times|C D|=\dfrac{1}{2} \times 5 \sqrt{2} \times 2 \sqrt{2}=10\)．
【B组---提高题】
1.已知平行四边形的三个顶点\(A(-2,1)\),\(B(-1,3)\),\(C(3,4)\)，则第四个顶点\(D\)的坐标为\(\underline{\quad \quad}\)．
2.已知点\(A(1,2)\)，\(B(3,1)\)，则线段\(AB\)的垂直平分线的方程为\(\underline{\quad \quad}\).
参考答案
-
答案 \((2,2)\)或\((-6,0)\)或\((4,6)\)
解析 若构成的平行四边形为\(ABCD_1\)，即\(AC\)为一条对角线，
设\(D_1 (x,y)\)，
则由\(AC\)中点也是\(BD_1\)中点，可得 \(\left\{\begin{array}{l} \dfrac{-2+3}{2}=\dfrac{x-1}{2} \\ \dfrac{1+4}{2}=\dfrac{y+3}{2} \end{array}\right.\)，
解得 \(\left\{\begin{array}{l} x=2 \\ y=2 \end{array},\right.\)，\(∴D_1 (2,2)\)．
同理可得，若构成以\(AB\)为对角线的平行四边形\(ACBD_2\)，
则\(D_2 (-6,0)\)；以\(D_2 (-6,0)\)为对角线的平行四边形\(ACD_3 B\)，则\(D_3 (4,6)\)，
\(∴\)第四个顶点\(D\)的坐标为：\((2,2)\)或\((-6,0)\)或\((4,6)\)． -
答案 \(y=2 x-\dfrac{5}{2}\)
解析 \(k_{A B}=\dfrac{2-1}{1-3}=-\dfrac{1}{2}\)，所以线段\(AB\)的垂直平分线的斜率为\(2\)，
可设直线方程为\(y=2x+m\)，又过\(AB\)的中点 \(\left(2, \dfrac{3}{2}\right)\)，
所以 \(\dfrac{3}{2}=4+m\)，解得 \(m=-\dfrac{5}{2}\)，所以所求直线方程为 \(y=2 x-\dfrac{5}{2}\).
【C组---拓展题】
1.如图，在平面直角坐标系\(xoy\)中，设三角形\(ABC\)的顶点分别为\(A(0,a)\),\(B(b,0)\),\(C(c,0)\)，点\(P(0,p)\)在线段\(AO\)上的一点(异于端点)，这里\(a,b,c,p\)均为非零实数，设直线\(BP\)，\(CP\)分别与边\(AC\),\(AB\)交于点\(E\),\(F\)．
(1)若\(BE⊥AC\)，求证\(CF⊥AB\)；
(2)若\(O\)、\(E\)分别是\(BC\)、\(AC\)的中点，求证\(F\)也是\(AB\)的中点．
参考答案
- 证明 (1)根据点\(B(b,0)\)和点\(P\)的坐标\((0,p)\)写出直线\(BP\)的斜率为 \(-\dfrac{p}{b}\)，
由点\(A(0,a)\)和\(C(c,0)\)写出直线AC的斜率为 \(-\dfrac{a}{c}\)
因为\(BE⊥AC\)，所以 \(\left(-\dfrac{p}{b}\right)\left(-\dfrac{a}{c}\right)=-1\)，即\(pa=-bc\)
而由\(C(c,0)\)和\(P(0,p)\)斜率为 \(-\dfrac{p}{c}\)，由\(A(0,a)\)和\(B(b,0)\)斜率为 \(-\dfrac{a}{b}\)，
则斜率之积为 \(\left(-\dfrac{p}{c}\right)\left(-\dfrac{a}{b}\right)=\dfrac{p a}{b c}=\dfrac{p a}{-p a}=-1\)，所以\(CF⊥AB\)；
(2)因为\(O\)为线段\(BC\)的中点，且\(PO⊥BC\)，
所以\(OP\)为线段\(BC\)的垂直平分线，
\(∴BP|=|CP∣\)，且\(|AB|=|AC|\)，
\(∴∠PBO=∠PCO\)，且\(∠ABC=∠ACB\)，
\(∴∠ABP=∠ACP\)，
又\(∠FPB=∠EPC\)，\(∴△BPF≅△CPE\)，\(∴|BF|=|CE|\)，
又\(E\)是线段\(AC\)的中点，所以 \(|C E|=\dfrac{1}{2}|A C| .\),
则\(|BF|=\dfrac{1}{2}|AB|\)，所以\(F\)为线段\(AB\)的中点．
