1.4.2(2) 用空间向量研究平面间的夹角

\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高二数学上学期同步知识点剖析精品讲义(人教A版2019）
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

选择性必修第一册同步巩固，难度2颗星！

基础知识

二面角

二面角的平面角是指在二面角\(α-l-β\)的棱上任取一点\(O\)，分别在两个半平面内作射线\(AO⊥ l\)，\(BO⊥ l\)，则\(∠AOB\)为二面角\(α-l-β\)的平面角，二面角的取值范围是\([0 ,π]\).
如图：

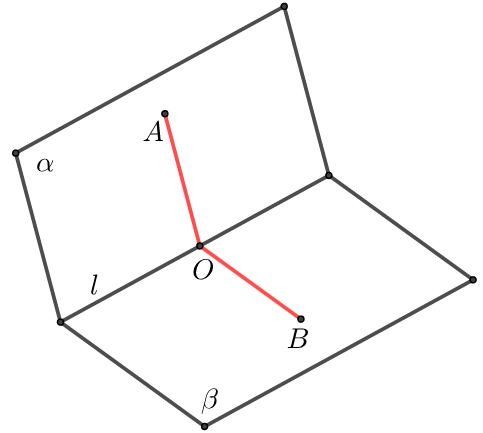
平面α与平面β的夹角

平面\(α\)与平面\(β\)相交，形成四个二面角，我们把这四个二面角不大于\(90^o\)的二面角称为平面\(α\)与平面\(β\)的夹角.

空间向量求平面α与平面β的夹角

求法：设平面\(α\)与平面\(β\)的法向量分别为\(\vec{m}\) ,\(\vec{n}\)，
再设\(\vec{m}\),\(\vec{n}\)的夹角为\(φ\)，平面\(α\)与平面\(β\)的平面角为\(θ\)，则\(θ\)为\(φ\)或\(π-φ\) ，

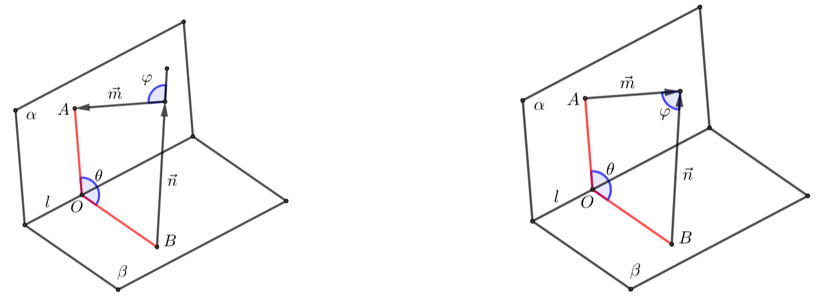
则 \(\cos \theta=|\cos \varphi|=\left|\dfrac{\vec{m} \cdot \vec{n}}{|\vec{m}||\vec{n}|}\right|=\dfrac{|\vec{m} \cdot \vec{n}|}{|\vec{m}||\vec{n}|}\) .
(与线面所成角的情况一样，均由法向量的方向导致两种情况的出现)

【例1】在正方体\(ABCD-A'B'C'D'\)中，易得平面\(ACD'\)与平面\(ABC\)的法向量分别是 \(\overrightarrow{D B^{\prime}}\)、 \(\overrightarrow{B B^{\prime}}\)，其夹角是\(φ\)，二面角\(D'-AC-B\)为θ，平面\(ACD'\)与平面\(ABC\)的夹角\(α\)，判断三个角之间的关系！

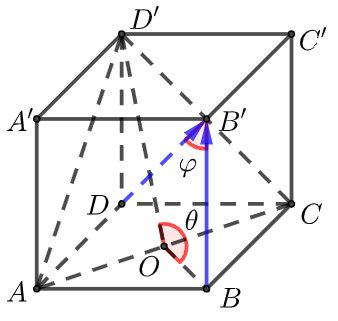
解析两个法向量的 \(\overrightarrow{D B^{\prime}}\)、 \(\overrightarrow{B B^{\prime}}\)的夹角\(φ=∠DB'B\)，二面角\(D'-AC-B\)为\(θ=∠D'OB\)是个钝角，则平面\(ACD'\)与平面\(ABC\)的夹角\(α=π-θ\)，而\(φ=π-θ\).所以三角关系是\(α=φ=π-θ\).

【例2】两平面的法向量分别为 \(\vec{m}=(0,1,0)\), \(\vec{n}=(0,1,1)\)，则两平面的夹角为\(\underline{\quad \quad}\) .
解析两平面的法向量分别为 \(\vec{m}=(0,1,0)\), \(\vec{n}=(0,1,1)\)，
所以 \(\cos \langle\vec{m}, \vec{n}\rangle=\dfrac{\vec{m} \cdot \vec{n}}{|\vec{n}||\vec{m}|}=\dfrac{1}{1 \times \sqrt{2}}=\dfrac{\sqrt{2}}{2}\)，则两平面的夹角为\(45^∘\)．

基本方法

【题型1】求平面间的夹角

【典题1】 正方体\(ABCD-A_1 B_1 C_1 D_1\)的棱长为\(1\)，点\(E\),\(F\)分别为\(CD\),\(DD_1\)的中点，求平面\(AED\)与平面\(AEF\)夹角的余弦值．

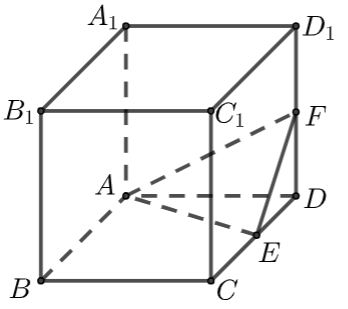
解析因为\(ABCD-A_1 B_1 C_1 D_1\)是正方体，
以\(A\)为原点，\(AB\)为\(x\)轴，\(AD\)为\(y\)轴，\(AA_1\)为\(z\)轴，建立空间直角坐标系，

依题意得\(A(0,0,0)\)， \(F\left(0,1, \dfrac{1}{2}\right)\)， \(E\left(\dfrac{1}{2}, 1,0\right)\)， \(\overrightarrow{A E}=\left(\dfrac{1}{2}, 1,0\right)\)， \(\overrightarrow{A F}=\left(0,1, \dfrac{1}{2}\right)\)，
设平面\(AEF\)的法向量\(\vec{n}=(x,y,z)\)，
则 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{A E}=\dfrac{1}{2} x+y=0 \\ \vec{n} \cdot \overrightarrow{A F}=y+\dfrac{1}{2} z=0 \end{array}\right.\)，取\(y=-1\)，得 \(\vec{n}=(2,-1,2)\)，
易知平面\(ADE\)的法向量\(\vec{m}=(0,0,1)\)，
设平面\(AED\)与平面\(AEF\)的夹角为\(θ\)，则 \(\cos \theta=\dfrac{|\vec{n} \cdot \vec{m}|}{|\vec{n}| \cdot|\vec{m}|}=\dfrac{2}{3}\)，
所以平面\(AED\)与平面\(AEF\)夹角的余弦值为 \(\dfrac{2}{3}\)．

【典题2】如图，四边形\(ABCD\)是边长为\(3\)的菱形，\(DE⊥\)平面\(ABCD\)，\(AB⊥AD\)，\(AF∥DE\)，\(DE=3AF\)．
(1)求证：\(AC⊥\)平面\(BDE\)；
(2)若\(BE\)与平面\(ABCD\)所成角为\(60°\)，求平面\(FBE\)与平面\(DEB\)夹角的正弦值．

解析 (1)证明：因为\(DE⊥\)平面\(ABCD\)，\(AC⊂\)平面\(ABCD\)，
所以\(DE⊥AC\)．
因为四边形\(ABCD\)是菱形，所以\(AC⊥BD\)．
又因为\(BD∩DE=D\)，\(BD⊂\)平面\(BDE\)，\(DE⊂\)平面\(BDE\)，
所以\(AC⊥\)平面\(BDE\)．
(2)据题设知\(DA\)、\(DC\)、\(DE\)两两互相垂直．
以\(DA\)、\(DC\)、\(DE\)分别为\(x\)轴，\(y\)轴，\(z\)轴建立空间直角坐标系\(D－xyz\)，如图所示，

因为\(BE\)与平面\(ABCD\)所成角为\(60°\)，即\(∠DBE\)，所以 \(\dfrac{D E}{B E}=\sqrt{3}\)，
又\(AD=3\)，\(DE=3AF\)，
所以 \(D E=3 \sqrt{6}\)， \(A F=\sqrt{6}\)，
所以\(A(3,0,0)\)，\(B(3,3,0)\)， \(F(3,0, \sqrt{6})\)， \(E(0,0,3 \sqrt{6})\)，\(C(0,3,0)\)，
所以 \(\overrightarrow{B F}=(0,-3, \sqrt{6})\)， \(\overrightarrow{E F}=(3,0,-2 \sqrt{6})\)，
设平面\(FBE\)的一个法向量\(\vec{m}=(x,y,z)\)，
则 \(\left\{\begin{array}{l} \vec{m} \cdot \overrightarrow{B F}=-3 y+\sqrt{6} z=0 \\ \vec{m} \cdot \overrightarrow{E F}=3 x-2 \sqrt{6} z=0 \end{array}\right.\)，令 \(z=\sqrt{6}\)，得 \(\vec{m}=(4,2, \sqrt{6})\)．
因为\(AC⊥\)平面\(DEB\)，所以 \(\overrightarrow{C A}\)为平面DEB的一个法向量，且 \(\overrightarrow{C A}=(3,-3,0)\)，
所以 \(\cos \langle\vec{m}, \overrightarrow{C A}\rangle=\dfrac{\vec{m} \cdot \overrightarrow{C A}}{|\vec{m}| \cdot|\overrightarrow{C A}|}=\dfrac{6}{\sqrt{26} \cdot \sqrt{18}}=\dfrac{\sqrt{13}}{13}\)，
所以 \(\sin \langle\vec{m}, \overrightarrow{C A}\rangle=\sqrt{1-\left(\dfrac{\sqrt{13}}{13}\right)^{2}}=\dfrac{2 \sqrt{39}}{13}\)．
所以平面\(FBE\)与平面\(DEB\)夹角的正弦值为 \(\dfrac{2 \sqrt{39}}{13}\)．

巩固练习

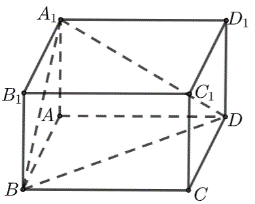
1如图，在长方体\(ABCD-A_1 B_1 C_1 D_1\)中，已知 \(A D=\sqrt{6}\), \(A B=\sqrt{3}\), \(A A_{1}=\sqrt{2}\)，求平面\(A_1 BD\)与平面\(ABCD\)夹角的大小和二面角\(A_1-BD-C\)的大小．

2如图，四棱锥\(P－ABCD\)中，底面\(ABCD\)为矩形，\(PA⊥\)平面\(ABCD\)，\(E\)为\(PD\)的中点．
(1)证明：\(PB∥\)平面\(AEC\)；
(2)若\(AB=1\)，\(AD=2\)，\(AP=2\)，求平面\(AEC\)与平面\(DAE\)夹角的余弦值．

3 如图，四边形\(ABCD\)为菱形，\(DE⊥\)平面\(ABCD\)，\(FC⊥\)平面\(ABCD\)，\(DE=2FC\)，\(∠DAB=60^∘\)，\(DE=DC=2\)．
(1)设\(BE\)的中点为\(H\)，证明：\(FH⊥\)平面\(EDB\)；
(2)求二面角\(A-EB-D\)的平面角的正弦值．

参考答案

答案平面\(A_1 BD\)与平面\(ABCD\)夹角为\(45^∘\)，二面角\(A_1-BD-C\)为\(135^∘\).
解析以\(A\)为原点，\(AB\)为\(x\)轴，\(AD\)为\(y\)轴，\(AA_1\)为\(z\)轴，建立空间直角坐标系，
\(A_{1}(0,0, \sqrt{2})\), \(B(\sqrt{3}, 0,0)\), \(D(0, \sqrt{6}, 0)\)，
\(\overrightarrow{A_{1} B}=(\sqrt{3}, 0,-\sqrt{2})\), \(\overrightarrow{A_{1} D}=(0, \sqrt{6},-\sqrt{2})\)，
设平面\(A_1 BD\)的法向量\(\vec{n}=(x,y,z)\)，
则 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{A_{1} B}=\sqrt{3} x-\sqrt{2} z=0 \\ \vec{n} \cdot \overrightarrow{A_{1} D}=\sqrt{6} y-\sqrt{2} z=0 \end{array}\right.\)，取 \(x=\sqrt{2}\)，得 \(\vec{n}=(\sqrt{2}, 1, \sqrt{3})\)，
易知平面\(ABCD\)的法向量\(\vec{m}=(0,0,1)\)，
设平面\(A_1 BD\)与平面\(ABCD\)夹角为\(θ\)，
则 \(\cos \theta=\dfrac{|\vec{m} \cdot \vec{n}|}{|\vec{m}| \cdot|\vec{n}|}=\dfrac{\sqrt{3}}{\sqrt{2+1+3}}=\dfrac{\sqrt{2}}{2}\)，\(∴θ=45^∘\)．
\(∴\)平面\(A_1 BD\)与平面\(ABCD\)夹角为\(45^∘\)，二面角\(A_1-BD-C\)为\(135^∘\).
答案 (1) 略 (2) \(\dfrac{\sqrt{6}}{3}\)
解析 (1)证明：连接\(BD\)，设\(BD∩AC=O\)，连接\(EO\)，
\(∵E\)是\(PD\)的中点，\(O\)为\(BD\)的中点，\(∴EO∥PB\)，
又\(∵EO⊂\)平面\(AEC\)，\(PB⊄\)平面\(AEC\)，
\(∴PB∥\)平面\(AEC\)；
(2)以\(A\)为坐标原点，分别以\(AB\)，\(AD\)，\(AP\)所在直线为\(x,y,z\)轴建立空间直角坐标系．

则\(D(0,2,0)\)，\(E(0,1,1)\)，\(C(1,2,0)\)， \(\overrightarrow{A E}=(0,1,1)\)， \(\overrightarrow{A C}=(1,2,0)\)，
设\(\vec{n}=(x,y,z)\)为平面\(AEC\)的一个法向量，
则 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{A C}=x+2 y=0 \\ \vec{n} \cdot \overrightarrow{A E}=y+z=0 \end{array}\right.\)，取\(z=1\)，则\(\vec{n}=(2,-1,1)\)，
又平面\(DAE\)的一个法向量为\(\vec{m}=(1,0,0)\)．
\(\cos <\vec{m}, \vec{n}>=\dfrac{\vec{m} \cdot \vec{n}}{|\vec{m}| \cdot|\vec{n}|}=\dfrac{2}{\sqrt{6}}=\dfrac{\sqrt{6}}{3}\)．
则平面\(AEC\)与平面\(DAE\)夹角的余弦值为 \(\dfrac{\sqrt{6}}{3}\)．
答案 (1) 略 (2) \(\dfrac{\sqrt{42}}{7}\)
解析 (1)证明：连接\(AC\)交\(BD\)于点\(O\)，连接\(HO\)．
\(∵\)四边形\(ABCD\)为菱形，点\(H\)是\(EB\)的中点，
所以\(OH\)为\(△BDE\)的中位线．
所以\(OH//DE\)， \(O H=\dfrac{1}{2} D E\)，而\(FC//DE\)，\(FC=\dfrac{1}{2} DE\)，
所以\(OH//FC\),\(OH=FC\)，
\(∴\)四边形\(CFHO\)为平行四边形，\(∴FH//CO\)，
\(∵DE⊥\)平面\(ABCD\)，\(CO⊂\)平面\(ABCD\)，
\(∴DE⊥CO\)．
又\(∵CO⊥BD\),\(ED\cap BD=D\)，
\(∴CO⊥\)平面\(EDB\)，
\(∴FH⊥\)平面\(EDB\)
(2)解：因为\(OB,OC,OH\)两两垂直，
故以点\(O\)为坐标原点，分别 \(\overrightarrow{O B}, \overrightarrow{O C}, \overrightarrow{O H}\)的方向为\(x\)轴，\(y\)轴，\(z\)轴的正方向，
建立如图所示的空间直角坐标系\(O-xyz\)．

由题意得 \(A(0,-\sqrt{3}, 0)\),\(C(0,\sqrt{3},0)\),\(B(1,0,0)\),\(E(-1,0,2)\)，
则 \(\overrightarrow{E B}=(2,0,-2)\), \(\overrightarrow{A B}=(1, \sqrt{3}, 0)\), \(\overrightarrow{B C}=(-1, \sqrt{3}, 0)\)．
设平面\(AEB\)的一个法向量为\(\vec{m}=(x,y,z)\)，
则 \(\left\{\begin{array}{l} \vec{m} \cdot \overrightarrow{E B}=2 x-2 z=0 \\ \vec{m} \cdot \overrightarrow{A B}=x+\sqrt{3} y=0 \end{array}\right.\)，取 \(\vec{m}=(3,-\sqrt{3}, 3)\)，
由第(1)问可知\(OC⊥\)平面\(DEB\)，
故平面\(DEB\)的一个法向量为\(\vec{n}=(0,1,0)\)，
所以 \(\cos \langle\vec{m}, \vec{n}\rangle=\dfrac{\vec{m} \cdot \vec{n}}{|\vec{m}| \cdot|\vec{n}|}=\dfrac{3 \times 0+(-\sqrt{3}) \times 1+3 \times 0}{\sqrt{9+3+9} \times \sqrt{0+1+0}}=-\dfrac{\sqrt{7}}{7}\)，
设二面角\(A-EB-D\)的平面角为\(θ\)，
则 \(\sin \theta=\sqrt{1-\cos ^{2}<\vec{m}, \vec{n}>}=\dfrac{\sqrt{42}}{7}\)．

【题型2】空间角问题的综合题

【典题1】 如图，在四棱锥\(P－ABCD\)中，平面\(PAB⊥\)平面\(ABCD\)，\(AD∥BC\)，\(AB⊥AD\)，\(AB⊥PA\)，点\(E\)为\(BC\)上一点且\(BC=2AB=2AD=4BE\)．
(1)求证：平面\(PED⊥\)平面\(PAC\)；
(2)若直线\(PE\)与平面\(PAC\)所成的角的正弦值为 \(\dfrac{\sqrt{5}}{5}\)，求二面角\(A－PC－D\)的余弦值．

解析 (1)证明：\(∵\)平面\(PAB⊥\)平面\(ABCD\)，平面\(PAB∩\)平面\(ABCD=AB\)，\(AB⊥PA\)，
\(∴PA⊥\)平面\(ABCD\)，又\(AB⊥AD\)．
分别以\(AB\)、\(AD\)、\(AP\)为\(x\)轴、\(y\)轴、\(z\)轴，建立空间直角坐标系\(o－xyz\)，
可得\(A(0,0,0)\)，\(D(0,2,0)\)，\(E(2,1,0)\)，\(C(2,4,0)\)，\(P(0,0,λ)(λ>0)\)．
\(\therefore \overrightarrow{A C}=(2,4,0)\)， \(\overrightarrow{A P}=(0,0, \lambda)\)， \(\overrightarrow{D E}=(2,-1,0)\)．
由 \(\overrightarrow{D E} \cdot \overrightarrow{A C}=4-4+0=0\)， \(\overrightarrow{D E} \cdot \overrightarrow{A P}=0\)，
\(∴DE⊥AC\)且\(DE⊥AP\)，
\(∵AC\)、\(AP\)是平面\(PAC\)内的相交直线，\(∴ED⊥\)平面\(PAC\)．
\(∵ED⊂\)平面\(PED\)，
\(∴\)平面\(PED⊥\)平面\(PAC\)；
(2)解：由(1)得平面\(PAC\)的一个法向量是 \(\overrightarrow{D E}=(2,-1,0)\)，而 \(\overrightarrow{P E}=(2,1,-\lambda)\)．
设直线\(PE\)与平面\(PAC\)所成的角为\(θ\)，
则 \(|\sin \theta=| \cos <\overrightarrow{P E}, \overrightarrow{D E}>\mid=\dfrac{|\overrightarrow{P E} \cdot \overrightarrow{D E}|}{|\overrightarrow{P E}| \cdot|\overrightarrow{D E}|}=\dfrac{|4-1|}{\sqrt{5} \cdot \sqrt{5+\lambda^{2}}}=\dfrac{\sqrt{5}}{5}\)，解得\(λ=±2\)．
\(∵λ>0\)，
\(∴λ=2\)，可得\(P\)的坐标为\((0,0,2)\)．
设平面\(PCD\)的一个法向量为\(\vec{n}=(x,y,z)\)，
\(\overrightarrow{D C}==(2,2,0)\)， \(\overrightarrow{D P}=(0,-2,2)\)，
由 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{D C}=2 x+2 y=0 \\ \vec{n} \cdot \overrightarrow{D P}=-2 y+2 z=0 \end{array}\right.\)，令\(x=1\)，得\(\vec{n}=(1,－1,－1)\)．
\(\therefore \cos <\vec{n}, \overrightarrow{D E}>=\dfrac{\vec{n} \cdot \overrightarrow{D E}}{|\vec{n}| \cdot|\overrightarrow{D E}|}=\dfrac{\sqrt{15}}{5}\)．
由图形可得二面角\(A－PC－D\)的平面角是锐角，
\(∴\)二面角\(A－PC－D\)的平面角的余弦值为 \(\dfrac{\sqrt{15}}{5}\)．

巩固练习

1如图．正四面体\(ABCD\)的顶点\(A\)，\(B\)，\(C\)分别在两两垂直的三条射线\(Ox\)，\(Oy\)，\(Oz\)上，则在下列命题中，错误的为(　　)

A．\(O－ABC\)是正三棱锥 \(\qquad \qquad \qquad \qquad\) B．二面角\(D－OB－A\)的平面角为 \(\dfrac{\pi}{3}\)
C．直线\(AD\)与直线\(OB\)所成角为 \(\dfrac{\pi}{4}\) \(\qquad \qquad\) D．直线\(OD⊥\)平面\(ABC\)

2 四棱锥\(P－ABCD\)中，\(PA⊥\)平面\(ABCD\)，四边形\(ABCD\)是矩形，且\(PA=AB=2\)，\(AD=3\)，\(E\)是线段\(BC\)上的动点，\(F\)是线段\(PE\)的中点．
(Ⅰ)求证：\(PB⊥\)平面\(ADF\)；
(Ⅱ)若直线\(DE\)与平面\(ADF\)所成角为\(30°\)，
(1)求线段\(CE\)的长；(2)求二面角\(P－ED－A\)的余弦值．

参考答案

答案 \(B\)
解析正四面体\(ABCD\)的顶点\(A\)，\(B\)，\(C\)分别在两两垂直的三条射线\(Ox\)，\(Oy\)，\(Oz\)上，
在\(A\)中，\(∵AC=AB=BC\)，\(OA=OB=OC\)，
\(∴O－ABC\)是正三棱锥，故\(A\)正确；
在\(B\)中，设\(OB=1\)，则\(A(1,0,0)\)，\(B(0,1,0)\)，\(D(1,1,1)\)，\(O(0,0,0)\)，
\(\overrightarrow{O D}=(1,1,1)\)， \(\overrightarrow{O B}=(0,1,0)\)，
设平面\(OBD\)的法向量\(\vec{m}=(x,y,z)\)，
则 \(\left\{\begin{array}{l} \vec{m} \cdot \overrightarrow{O B}=y=0 \\ \vec{m} \cdot \overrightarrow{O D}=x+y+z=0 \end{array}\right.\)，取\(x=1\)，得\(\vec{m}=(1,0,－1)\)，
而平面\(OAB\)的法向量\(\vec{n}=(0,0,1)\)，
\(\cos \langle\vec{m}, \vec{n}\rangle=\dfrac{\vec{m} \cdot \vec{n}}{|\vec{m}| \cdot|\vec{n}|}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)，
二面角\(D－OB－A\)的平面角为 \(\dfrac{\pi}{4}\)，故\(B\)错误；
在\(C\)中，设\(OB=1\)，则\(A(1,0,0)\)，\(B(0,1,0)\)，\(D(1,1,1)\)，\(O(0,0,0)\)，
\(\overrightarrow{A D}=(0,1,1)\)， \(\overrightarrow{A D}=(0,1,1), \quad \overrightarrow{O B}=(0,1,0)\)，
\(\cos <\overrightarrow{A D}, \overrightarrow{O B}>=\dfrac{|\overrightarrow{A D} \cdot \overrightarrow{O B}|}{|\overrightarrow{A D}| \cdot|\overrightarrow{O B}|}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)，
\(∴\)直线\(AD\)与直线\(OB\)所成角为 \(\dfrac{\pi}{4}\)，故\(C\)正确；
在\(D\)中，设\(OB=1\)，则\(A(1,0,0)\)，\(B(0,1,0)\)，\(D(1,1,1)\)，\(O(0,0,0)\)，\(C(0,0,1)\)，
\(\overrightarrow{O D}=(1,1,1)\)， \(\overrightarrow{A B}=(-1,1,0)\)， \(\overrightarrow{A C}=(-1,0,1)\)，
\(\overrightarrow{O D} \cdot \overrightarrow{A B}=0\)， \(\overrightarrow{O D} \cdot \overrightarrow{A C}=0\)，\(∴OD⊥AB\)，\(OD⊥AC\)，
\(∵AB∩AC=A\)，\(∴\)直线\(OD⊥\)平面\(ABC\)，故\(D\)正确．
故选：\(B\)．
答案 (Ⅰ) 略 (Ⅱ)(1)略 (2) \(\dfrac{3 \sqrt{17}}{17}\)
解析 (Ⅰ)证明：依题意，以点\(A\)为原点建立空间直角坐标系(如图)，

可得\(A(0,0,0)\)，\(B(2,0,0)\)，\(C(2,3,0)\)，\(D(0,3,0)\)，\(E(2,y,0)\)，\(F(1,\dfrac{m}{2},1)\)，\(P(0,0,2)\)．
\(\overrightarrow{P B}=(2,0,-2)\)， \(\overrightarrow{A D}=(0,3,0)\)， \(\overrightarrow{A F}=\left(1, \dfrac{m}{2}, 1\right)\)，
\(\overrightarrow{P B} \cdot \overrightarrow{A D}=0\)， \(\overrightarrow{P B} \cdot \overrightarrow{A F}=0\)，
即\(PB⊥AD\)，\(PB⊥AF\)，\(AF∩AD=A\)，所以\(PB⊥\)平面\(ADF\)．
(Ⅱ)解：(1)设\(\vec{n}=(x,y,z)\)为平面\(ADF\)的法向量，
则 \(\left\{\begin{array}{l} \overrightarrow{A D} \cdot \vec{n}=3 y=0 \\ \overrightarrow{A F} \cdot \vec{n}=x+\dfrac{m}{2} y+z=0 \end{array}\right.\)，
不妨令\(v\)，可得\(\vec{n}=(1,0,-1)\)为平面\(ADF\)的一个法向量，
向量 \(\overrightarrow{D E}=(2, y-3,0)\)
\(∵\)直线\(DE\)与平面\(ADF\)所成角为\(30°\)，于是有 \(\cos \langle\vec{n} \cdot \overrightarrow{D E}\rangle=\dfrac{\vec{n} \cdot \overrightarrow{D E}}{|\vec{n}| \cdot|\overrightarrow{D E}|}=\dfrac{1}{2}\)，
所以 \(\dfrac{1 \times 2+0 \times(y-3)+0 \times(-1)}{\sqrt{1+0+1} \cdot \sqrt{2^{2}+(y-3)^{2}+0}}=\dfrac{1}{2}\)，得\(y=1\)，\(y=5\)(舍)
\(E(2,1,0)\)，\(C(2,3,0)\)，线段\(CE\)的长为\(2\)．
(2)设\(\vec{n}=(a,b,c)\)为平面\(PED\)的法向量，
\(\overrightarrow{P E}==(2,1,-2)\)， \(\overrightarrow{P D}=(0,3,-2)\)
则 \(\left\{\begin{array}{l} \overrightarrow{P E} \cdot \vec{m}=2 a+y-2 c=0 \\ \overrightarrow{P D} \cdot \vec{m}=3 b-2 c=0 \end{array}\right.\)，
不妨令\(a=2\)，可得\(\vec{n}=(2,2,3)\)为平面\(ADF\)的一个法向量，
又 \(\overrightarrow{A P}=(0,0,2)\)为平面\(ADE\)的一个法向量，
\(∴\)二面角\(P－ED－A\)的余弦值为 \(\cos <\vec{n}, \overrightarrow{A P}>=\dfrac{\vec{n} \cdot \overrightarrow{A P}}{\vec{n} \cdot \overrightarrow{A P}}=\dfrac{3 \sqrt{17}}{17}\)．

分层练习

【A组---基础题】

1 平面\(α\)，\(β\)的法向量分别是 \(\overrightarrow{n_{1}}=(1,1,1)\)， \(\overrightarrow{n_{2}}=(-1,0,-1)\)，则平面\(α\)，\(β\)所成角的正弦值是(　　)
A. \(\dfrac{\sqrt{3}}{3}\) \(\qquad \qquad\) B. \(\dfrac{1}{2}\) \(\qquad \qquad\) C. \(\dfrac{\sqrt{6}}{3}\) \(\qquad \qquad\) D. \(\dfrac{\sqrt{2}}{2}\)

2 在正方体\(ABCD－A_1 B_1 C_1 D_1\)中，平面\(A_1 BD\)与平面\(ABCD\)所成二面角的正弦值为(　　)
A． \(\dfrac{\sqrt{3}}{2}\)\(\qquad \qquad\) B． \(\dfrac{\sqrt{2}}{2}\) \(\qquad \qquad\) C． \(\dfrac{\sqrt{6}}{3}\) \(\qquad \qquad\) D． \(\dfrac{1}{3}\)

3 若面\(α\)的法向量\(\vec{n}=(1,λ,1)\)，面\(β\)的法向量\(\vec{m}=(2,-1,-2)\)，两面夹角的正弦值为 \(\dfrac{\sqrt{34}}{6}\)，则\(λ=\underline{\quad \quad}\)．

4 如图，在三棱柱\(ABC-A_1 B_1 C_1\)中，\(AB\),\(AC\),\(AA_1\)两两互相垂直，\(AB=AC=AA_1\)，\(M\),\(N\)分别是侧棱\(BB_1\)，\(CC_1\)上的点，平面\(AMN\)与平面\(ABC\)夹角为 \(\dfrac{\pi}{6}\)，则当\(|B_1 M|\)最小时\(∠AMB=\underline{\quad \quad}\).

5 如图，在棱长为\(2\)的正方体\(ABCD-A_1 B_1 C_1 D_1\)中，点\(E\)是棱\(D_1 D\)的中点，点\(F\)在棱\(B_1 B\)上，且满足\(B_1 F=2FB\)．
(1)求证：\(A_1 C_1⊥D_1 D\)；
(2)求平面\(AEF\)与平面\(AA_1 D_1 D\)所成锐二面角的余弦值．

6 如图，四棱锥\(P-ABCD\)的底面是正方形，\(PD⊥\)底面\(ABCD\)，\(PD=DC\)，\(E\)是\(PC\)的中点．
(1)证明：平面\(PAB⊥\)平面\(PAD\)；(2)求二面角\(P-AB-D\)的大小．

7 如图，在四棱锥\(P－ABCD\)中，底面\(ABCD\)是边长为\(2\)的菱形，\(∠ABC=60°\)，\(△PAB\)为正三角形， \(P C=\sqrt{6}\)，\(E\)为线段\(AB\)的中点．
(1)证明：\(PE⊥\)平面\(ABCD\)；
(2)若 \(3 \overrightarrow{P M}=\overrightarrow{P D}\)，求二面角\(M－EC－D\)的大小．

8 如图，菱形\(ABCD\)中\(∠BAD=60^∘\)，把\(△BDC\)沿\(BD\)折起，使得点\(C\)至\(P\)处．
(1)证明：平面\(PAC⊥\)平面\(ABCD\)；
(2)若\(PA\)与平面\(ABD\)所成角的余弦值为 \(\dfrac{\sqrt{3}}{3}\)，求二面角\(B-PA-D\)的余弦值．

参考答案

答案 \(A\)
解析设向量 \(\overrightarrow{n_{1}}=(1,1,1)\)， \(\overrightarrow{n_{2}}=(-1,0,-1)\)所成角为\(θ\)，
则 \(\cos \theta=\dfrac{\overrightarrow{n_{1}} \cdot \overrightarrow{n_{2}}}{\left|\overrightarrow{n_{1}}\right|\left|\overrightarrow{n_{2}}\right|}=\dfrac{-2}{\sqrt{3} \sqrt{2}}=-\dfrac{2}{\sqrt{6}}\)，
\(\therefore \sin \theta=\sqrt{1-\dfrac{2}{3}}=\dfrac{\sqrt{3}}{3}\)，故选：\(A\)．
答案 \(C\)
解析以\(D\)为原点，\(DA\)为\(x\)轴，\(DC\)为\(y\)轴，\(DD_1\)为\(z\)轴，建立空间直角坐标系，
设正方体\(ABCD－A_1 B_1 C_1 D_1\)中棱长为\(1\)，
则\(A_1 (1,0,1)\)，\(B(1,1,0)\)，\(D(0,0,0)\)， \(\overrightarrow{D A}_{1}=(1,0,1)\)， \(\overrightarrow{D B}=(1,1,0)\)，
设平面\(A_1 BD\)的法向量\(\vec{n}=(x,y,z)\)，
则 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{D A_{1}}=x+z=0 \\ \vec{n} \cdot \overrightarrow{D B}=x+y=0 \end{array}\right.\)，取\(x=1\)，得\(\vec{n}=(1,－1,－1)\)，
平面\(ABCD\)的法向量\(\vec{m}=(0,0,1)\)，
设平面\(A_1 BD\)与平面\(ABCD\)所成二面角的平面角为\(α\)，
则 \(\cos \alpha=\dfrac{|\vec{m} \cdot \vec{n}|}{|\vec{m}| \cdot|\vec{n}|}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)，
\(\therefore \sin \alpha=\sqrt{1-\left(\dfrac{\sqrt{3}}{3}\right)^{2}}=\dfrac{\sqrt{6}}{3}\)．
\(∴\)平面\(A_1 BD\)与平面\(ABCD\)所成二面角的正弦值为 \(\dfrac{\sqrt{6}}{3}\)．
故选：\(C\)．
答案 \(\pm \sqrt{2}\)
解析设面\(α\)与面\(β\)的夹角为\(θ\)，
则 \(|\cos \theta=| \cos <\vec{n}, \vec{m}>|=| \dfrac{-\lambda}{\sqrt{2+\lambda^{2}} \cdot \sqrt{9}} \mid=\dfrac{|\lambda|}{3 \sqrt{2+\lambda^{2}}}\)，
所以 \(\sin 2 \theta=1-\cos 2 \theta=1-\dfrac{\lambda^{2}}{9\left(2+\lambda^{2}\right)}=\dfrac{34}{36}\)，解得 \(\lambda=\pm \sqrt{2}\)．
答案 \(\dfrac{\pi}{3}\)
解析以点\(A\)为坐标原点，建立空间直角坐标系如图所示，

设\(CN=b\)，\(BM=a\)，
则\(N(0,1,b)\),\(M(1,0,a)\),\(A(0,0,0)\),\(B(1,0,0)\)，
所以 \(\overrightarrow{A M}=(1,0, a)\), \(\overrightarrow{A N}=(0,1, b)\)，
设平面\(AMN\)的法向量为\(\vec{n}=(x,y,z)\)，
则 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{A M}=x+a z=0 \\ \vec{n} \cdot \overrightarrow{A N}=y+b z=0 \end{array}\right.\)，令\(z=1\)，则\(\vec{n}=(-a,-b,1)\)，
平面\(ABC\)的法向量为\(\vec{m}=(0,0,1)\)，
因为平面\(AMN\)与平面\(ABC\)夹角为 \(\dfrac{\pi}{6}\)，
所以 \(\cos <\vec{m}, \vec{n}>=\dfrac{|\vec{m} \cdot \vec{n}|}{|\vec{m}||\vec{n}|}=\dfrac{1}{\sqrt{a^{2}+b^{2}+1}}=\dfrac{\sqrt{3}}{2}\)，
化简可得\(3a^2+3b^2=1\)，
当\(|B_1 M|\)最小时，则\(b=0\), \(B M=a=\dfrac{\sqrt{3}}{3}\)，
所以 \(\tan \angle A M B=\dfrac{A B}{B M}=\dfrac{1}{\dfrac{\sqrt{3}}{3}}=\sqrt{3}\)，
则 \(\angle A M B=\dfrac{\pi}{3}\)．
答案 (1)略 (2) \(\dfrac{2}{7}\)
解析证明：(1)\(∵\)在正方体\(ABCD-A_1 B_1 C_1 D_1\)中，\(D_1 D⊥\)平面\(A_1 B_1 C_1 D_1\)，\(A_1 C_1⊂\)平面\(A_1 B_1 C_1 D_1\)，
\(∴A_1 C_1⊥D_1 D\)．
(2)如图，以\(D\)为原点，\(DA\)，\(DC\)，\(DD_1\)分别为\(x，y，z\)轴，建立空间直角坐标系，

则\(A(2,0,0)\),\(E(0,0,1)\), \(, F\left(2,2, \dfrac{2}{3}\right)\),\(B(2,2,0)\)，
\(\therefore \overrightarrow{A E}=(-2,0,1)\), \(\overrightarrow{A F}=\left(0,2, \dfrac{2}{3}\right)\),\(\overrightarrow{A B}=(0,2,0)\)
设\(\vec{n}=(x,y,z)\)是平面\(AEF\)的一个法向量，
则 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{A E}=-2 x+z=0 \\ \vec{n} \cdot \overrightarrow{A F}=2 y+\dfrac{2}{3} z=0 \end{array}\right.\)，取\(z=6\)，得\(\vec{n}=(3,-2,6)\)，
\(∵AB⊥\)平面\(AA_1 D_1 D\)，
\(: \overrightarrow{A B}=(0,2,0)\)是平面\(AA_1 D_1 D\)的一个法向量，
\(\therefore \cos <\overrightarrow{A B}, \vec{n}>=\dfrac{\overrightarrow{A B} \cdot \vec{n}}{|\overrightarrow{A B}| \cdot|\vec{n}|}=\dfrac{-4}{2 \sqrt{49}}=-\dfrac{2}{7}\)，
\(∴\)平面\(AEF\)与平面\(AA_1 D_1 D\)所成锐二面角的余弦值为 \(\dfrac{2}{7}\).
答案 (1)略 (2)\(45^∘\)
解析证明：(1)\(∵\)四棱锥\(P-ABCD\)的底面是正方形，\(PD⊥\)底面\(ABCD\)，\(PD=DC\)，\(E\)是\(PC\)的中点．
\(∴AB⊥AD\),\(AB⊥PD\)，
又\(AD\cap PD=D\)，\(∴AB⊥\)平面\(PAD\)，
\(∵AB⊂\)平面\(PAB\)，\(∴\)平面\(PAB⊥\)平面\(PAD\)．
解：(2)以\(D\)为原点，\(DA\)为\(x\)轴，\(DC\)为\(y\)轴，\(DP\)为\(z\)轴，建立空间直角坐标系，
设\(PD=DC=AD=2\)，
则\(A(2,0,0)\)，\(P(0,0,2)\)，\(D(0,0,0)\)，\(B(2,2,0)\)，
\(\overrightarrow{A P}=(-2,0,2)\), \(\overrightarrow{A B}=(0,2,0)\)，
设平面 \(PAB\)的法向量\(\vec{n}=(x,y,z)\)，
则 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{A P}=-2 x+2 z=0 \\ \vec{n} \cdot \overrightarrow{A B}=2 y=0 \end{array}\right.\)，取\(x=1\)，得 \(\vec{n}=(1,0,1)\)，
平面\(ABD\)的法向量 \(\vec{m}=\left( 0, 0, 1\right)\)，
设二面角\(P-AB-D\)的大小为\(θ\)，
则 \(\cos \theta=\dfrac{|\vec{m} \cdot \vec{n}|}{|\vec{m}| \cdot|\vec{n}|}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)，\(θ=45^∘\)，
\(∴\)二面角\(P-AB-D\)的大小为\(45^∘\)．
答案 (1)略 (2)\(60°\)
解析 (1)证明：连接\(CE\)，
\(∵△PAB\)是边长为\(2\)的正三角形，且\(E\)是\(AB\)中点， \(\therefore P E=\sqrt{3}\)
又\(∵ABCD\)是边长为\(2\)的菱形，\(∠ABC=60°\)，
\(∴△ABC\)是正三角形，\(CE=\sqrt{3}\)，
又\(∵PC=\sqrt{6}\)，\(∴PC^2=PE^2+CE^2\)，即\(PE⊥CE\)，
又\(PE⊥AB\)，\(CE∩AB=E\)，
\(∴PE⊥\)平面\(ABCD\)．
(2)解：由(1)可得：以\(E\)为原点，分别以 \(\overrightarrow{E B}, \overrightarrow{E C}, \overrightarrow{E P}\)为\(x,y,z\)轴的正方向，建立空间直角坐标系\(E－xyz\)，
则\(E(0,0,0)\)，\(B(1,0,0)\)，\(P(0,0,\sqrt{3})\)，\(C(0,\sqrt{3},0)\)，\(D(-2,\sqrt{3},0)\)．
设点\(M\)坐标为\((x,y,z)\)，由 \(3 \overrightarrow{P M}=\overrightarrow{P D}\)，得 \(3(x, y, z-\sqrt{3})=(-2, \sqrt{3},-\sqrt{3})\)，
\(\therefore M\left(-\dfrac{2}{3}, \dfrac{\sqrt{3}}{3}, \dfrac{2 \sqrt{3}}{3}\right)\)，
\(\therefore \overrightarrow{E M}=\left(-\dfrac{2}{3}, \dfrac{\sqrt{3}}{3}, \dfrac{2 \sqrt{3}}{3}\right)\)，\(\overrightarrow{E C}=(0, \sqrt{3}, 0)\)，
设平面\(CEM\)的法向量为\(\vec{n}=(x,y,z)\)，
则 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{E M}=-\dfrac{2}{3} x+\dfrac{\sqrt{3}}{3} y+\dfrac{2 \sqrt{3}}{3} z=0 \\ \vec{n} \cdot \overrightarrow{E C}=\sqrt{3} y=0 \end{array}\right.\)，取\(z=1\)，解得 \(\vec{m}=(\sqrt{3}, 0,1)\)．
\(∵PE⊥\)平面\(ABCD\)，\(∴\)平面\(ABCD\)的法向量 \(\vec{m}=(0,0,1)\)，
\(\therefore|\cos <\vec{n}, \vec{m}>|=\dfrac{|\vec{n} \cdot \vec{m}|}{|\vec{n}| \cdot|\vec{m}|}=\dfrac{1}{2}\)，
\(∴\)二面角\(M－EC－D\)的大小为\(60°\)．
答案 (1)略 (2) \(\dfrac{1}{3}\)
解析 (1)证明：设\(AC\cap BD\)于\(O\)，连接\(PO\)，
在菱形\(ABCD\)中，\(O\)为\(BD\)的中点，且\(BD⊥AC\)，
\(∵PB=PD\)，\(∴BD⊥PO\)，
\(∴PO∩AC=O\)，\(∴BD⊥\)平面\(PAC\) ，
\(∵BD⊂\)平面\(ABCD\)，
\(∴\)平面\(PAC⊥\)平面\(ABCD\)；
(2)在平面\(PAC\)内，作\(OM⊥AC\)，以\(O\)为坐标原点，\(OA,OB,OM\)为\(x,y,z\)轴，建立空间直角坐标系，如图，

设\(PB=PD=AB=AD=2\)，则\(OA=OP=\sqrt{3}\)，\(OR=1\)，
由(1)知平面\(PAC⊥\)平面\(ABCD\)，
\(∴∠PAO\)是\(PA\)与平面\(ABCD\)所成角，
\(\therefore \cos \angle P A O=\dfrac{\sqrt{3}}{3}\)，可得 \(P\left(\dfrac{\sqrt{3}}{3}, 0, \dfrac{2 \sqrt{6}}{3}\right)\)，
由\(A(\sqrt{3},0,0)\),\(B(0,1,0)\),\(D(0,-1,0)\)，
\(\therefore \overrightarrow{A D}=(-\sqrt{3},-1,0)\), \(\overrightarrow{A B}=(-\sqrt{3}, 1,0)\), \(\overrightarrow{A P}=\left(-\dfrac{2 \sqrt{3}}{3}, 0, \dfrac{2 \sqrt{6}}{3}\right),\)，
设平面\(PAB\)的法向量为\(\vec{m}=(x,y,z)\)，
则 \(\left\{\begin{array}{l} \vec{m} \cdot \overrightarrow{A B}=-\sqrt{3} x+y=0 \\ \vec{m} \cdot \overrightarrow{A P}=-\dfrac{2 \sqrt{3}}{3} x+\dfrac{2 \sqrt{6}}{3} z=0 \end{array}\right.\)，取\(z=1\)，得 \(\vec{m}=(\sqrt{2}, \sqrt{6}, 1)\)，
设平面\(PAD\)的法向量为\(\vec{n}=(a,b,c)\)，
则 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{A D}=-\sqrt{3} a-b=0 \\ \vec{n} \cdot \overrightarrow{A P}=-\dfrac{2 \sqrt{3}}{3} a+\dfrac{2 \sqrt{6}}{3} c=0 \end{array}\right.\)，取\(c=1\)，得 \(\vec{n}=(\sqrt{2},-\sqrt{6}, 1)\)，
\(\therefore \cos \langle\vec{m}, \vec{n}\rangle=\dfrac{\vec{m} \cdot \vec{n}}{|\vec{m}| \cdot|\vec{n}|}=\dfrac{2-6+1}{\sqrt{2+6+1} \cdot \sqrt{2+6+1}}=-\dfrac{1}{3}\)，
由图知二面角\(B-PA-D\)为锐角，故其余弦值为 \(\dfrac{1}{3}\)．

【B组---提高题】

1 如图，三棱锥\(V－ABC\)的侧棱长都相等，底面\(ABC\)与侧面\(VAC\)都是以\(AC\)为斜边的等腰直角三角形，\(E\)为线段\(AC\)的中点，\(F\)为直线\(AB\)上的动点，若平面\(VEF\)与平面\(VBC\)所成锐二面角的平面角为\(θ\)，则\(\cosθ\)的最大值是(　　)

A． \(\dfrac{\sqrt{3}}{3}\) \(\qquad \qquad\) B． \(\dfrac{2}{3}\) \(\qquad \qquad\) C． \(\dfrac{\sqrt{5}}{3}\) \(\qquad \qquad\) D． \(\dfrac{\sqrt{6}}{3}\)

2 在底面为锐角三角形的直三棱柱\(ABC－A_1 B_1 C_1\)中，\(D\)是棱\(BC\)的中点，记直线\(B_1 D\)与直线\(AC\)所成角为\(θ_1\)，直线\(B_1 D\)与平面\(A_1 B_1 C_1\)所成角为\(θ_2\)，二面角\(C_1－A_1 B_1－D\)的平面角为\(θ_3\)，则(　　)
A．\(θ_2<θ_1,θ_2<θ_3\) \(\qquad \qquad\) B．\(θ_2>θ_1,θ_2<θ_3\) \(\qquad \qquad\) C．\(θ_2<θ_1,θ_2>θ_3\) \(\qquad \qquad\) D．\(θ_2>θ_1,θ_2>θ_3\)

3如图所示，在等边\(△ABC\)中，\(AB=6\)，\(M\),\(N\)分别是\(AB\),\(AC\)上的点，且\(AM=AN=4\)，\(E\)是\(BC\)的中点，\(AE\)交\(MN\)于点\(F\)．以\(MN\)为折痕把\(△AMN\)折起，使点\(A\)到达点\(P\)的位置\((0<∠PFE<π)\)，连接\(PB,PE,PC\)．

(1)证明：\(MN⊥PE\)；
(2)设点\(P\)在平面\(ABC\)内的射影为点\(Q\)，若二面角\(P-MN-B\)的大小为 \(\dfrac{2}{3} \pi\)，求直线\(QC\)与平面\(PBC\)所成角的正弦值．

参考答案

答案 \(D\)
解析由底面\(ABC\)与侧面\(VAC\)都是以\(AC\)为斜边的等腰直角三角形，
得\(Rt△ABC≌Rt△AVC\)，\(∴VA=VC=BA=BC\)．
设\(VA=VC=BA=BC=2\)，
由\(E\)为线段\(AC\)的中点，可得 \(V E=E B=\sqrt{2}\)．
由\(VE^2+BE^2=VB^2\)，可得\(VE⊥EB\)．
以\(E\)为坐标原点，分别以\(EB\),\(EC\),\(EV\)所在直线为\(x,y,z\)轴建立空间直角坐标系．
则\(C(0,\sqrt{2},0)\)，\(B(\sqrt{2},0,0)\)，\(V(0,0,\sqrt{2})\)，设\(F(x,x-\sqrt{2},0)\)，
\(\overrightarrow{V C}=(0, \sqrt{2},-\sqrt{2})\)， \(\overrightarrow{V B}=(\sqrt{2}, 0,-\sqrt{2})\)，
\(\overrightarrow{E V}=(0,0, \sqrt{2})\)， \(\overrightarrow{V F}=(x, x-\sqrt{2},-\sqrt{2})\)．
设平面\(VBC\)的一个法向量为\(\vec{m}=(x,y,z)\)，
由 \(\left\{\begin{array}{l} \vec{m} \cdot \overrightarrow{V C}=\sqrt{2} y-\sqrt{2} z=0 \\ \vec{m} \cdot \overrightarrow{V B}=\sqrt{2} x-\sqrt{2} z=0 \end{array}\right.\)，取\(x=1\)，得\(\vec{m}=(1,1,1)\)；
设平面\(VEF\)的一个法向量为\(\vec{n}=(x_1,y_1,z_1)\)，
由 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{E V}=\sqrt{2} z_{1}=0 \\ \vec{n} \cdot \overrightarrow{V F}=x \cdot x_{1}+(x-\sqrt{2}) y_{1}-\sqrt{2} z_{1}=0 \end{array}\right.\)，取\(y_1=1\)，得 \(\vec{n}=\left(\dfrac{\sqrt{2}}{x}-1,1,0\right)\)．
平面\(VEF\)与平面\(VBC\)所成锐二面角的平面角为\(θ\)，
则 \(\cos \theta=\dfrac{\vec{m} \cdot \vec{n}}{|\vec{m}| \cdot|\vec{n}|}=\dfrac{\dfrac{\sqrt{2}}{x}}{\sqrt{3} \cdot \sqrt{\dfrac{2}{x^{2}}-\dfrac{2 \sqrt{2}}{x}+2}}=\dfrac{\sqrt{2}}{\sqrt{6 x^{2}-6 \sqrt{2} x+6}}\)．
令 \(f(x)=6 x^{2}-6 \sqrt{2} x+6=6\left(x-\dfrac{\sqrt{2}}{2}\right)^{2}+3\)．
当 \(x=\dfrac{\sqrt{2}}{2}\)时， \(f(x)_{\min }=3\)．\(∴\cosθ\)的最大值为 \(\dfrac{\sqrt{2}}{\sqrt{3}}=\dfrac{\sqrt{6}}{3}\)．
故选：\(D\)．
答案 \(A\)
解析由选项可知，角\(θ_1\)与\(θ_2\)，\(θ_2\)与\(θ_3\)的大小确定，且三棱柱的底面为锐角三角形．
\(∴\)设三棱柱\(ABC－A_1 B_1 C_1\)是棱长为\(2\)的正三棱柱，取\(D\)是\(BC\)中点，
以\(A\)为原点，在平面\(ABC\)中，过\(A\)作\(AC\)的垂线为\(x\)轴，\(AC\)为\(y\)轴，\(AA_1\)为\(z\)轴，建立空间直角坐标系，
则\(A(0,0,0)\)，\(A_1 (0,0,2)\)， \(B_{1}(\sqrt{3}, 1,2)\)，\(C(0,2,0)\)， \(D\left(\dfrac{\sqrt{3}}{2}, \dfrac{3}{2}, 0\right)\)，
\(\overrightarrow{A C}=(0,2,0)\)， \(\overrightarrow{B_{1} D}=\left(-\dfrac{\sqrt{3}}{2}, \dfrac{1}{2},-2\right)\)， \(\overrightarrow{A_{1} B_{1}}=(\sqrt{3}, 1,0)\)，
\(∵\)直线\(B_1 D\)与直线\(AC\)所成的角为\(θ_1\)，
\(\therefore \cos \theta_{1}=\dfrac{\left|\overrightarrow{B_{1} D} \cdot \overrightarrow{A C}\right|}{\left|\overrightarrow{B_{1} D}\right| \cdot|\overrightarrow{A C}|}=\dfrac{2 \times \dfrac{1}{2}}{2 \cdot \sqrt{5}}=\dfrac{\sqrt{5}}{10}\)，
\(∵\)直线\(B_1 D\)与平面\(A_1 B_1 C_1\)所成的角为\(θ_2\)，平面\(A_1 B_1 C_1\)的法向量\(\vec{n}=(0,0,1)\)，
\(\therefore \sin \theta_{2}=\dfrac{\left|\overrightarrow{B_{1} D} \cdot \vec{n}\right|}{\left|\overrightarrow{B_{1} D}\right| \cdot|\vec{n}|}=\dfrac{|-2|}{\sqrt{5} \cdot 1}=\dfrac{2}{\sqrt{5}}\)，
\(\therefore \cos \theta_{2}=\sqrt{1-\left(\dfrac{2}{\sqrt{5}}\right)^{2}}=\dfrac{\sqrt{5}}{5}\)，
设平面\(A_1 B_1 D\)的法向量\(\vec{m}=(x,y,z)\)，
由 \(\left\{\begin{array}{l} \vec{m} \cdot \overrightarrow{A_{1} B_{1}}=\sqrt{3} x+y=0 \\ \vec{m} \cdot \overrightarrow{B_{1} D}=-\dfrac{\sqrt{3}}{2} x+\dfrac{1}{2} y-2 z=0 \end{array}\right.\)，取\(x=\sqrt{3}\)，得 \(\vec{m}=\left(\sqrt{3},-3,-\dfrac{3}{2}\right)\)，
\(∵\)二面角\(C_1－A_1 B_1－D\)的平面角为\(θ_3\)，
\(\therefore \cos \theta_{3}=\dfrac{|\vec{m} \cdot \vec{n}|}{|\vec{m}| \cdot|\vec{n}|}=\dfrac{\dfrac{3}{2}}{\sqrt{\dfrac{57}{4}} \cdot 1}=\dfrac{\sqrt{57}}{19}\)．
且\(θ_1，θ_2\)与\(θ_3\)均为锐角，结合余弦函数在 \(\left[0, \dfrac{\pi}{2}\right]\)上为减函数，则\(θ_2<θ_1,θ_2<θ_3\)，
故选：\(A\)．
答案 (1)略 (2) \(\dfrac{2 \sqrt{3}}{7}\)
解析 (1)证明：因为\(△ABC\)是等边三角形，\(E\)是\(BC\)的中点，所以\(AE⊥BC\)，
因为\(AM=AN=4\)，所以\(MN//BC\)，所以\(MN⊥AE\)，
可得\(MN⊥PF\),\(MN⊥FE\)，
又\(PF\cap FE=F\)，所以\(MN⊥\)平面\(PFE\)，
又\(PE⊂\)平面\(PFE\)，所以\(MN⊥PE\)．
(2)解：因为\(MN⊥PF\),\(MN⊥FE\)，
所以二面角\(P-MN-B\)的平面角为\(∠PFE\)，
所以\(∠PFE=\dfrac{2}{3} \pi\)，可得\(∠PFA=\dfrac{1}{3} \pi\)，
由第(1)问知，\(MN⊥\)平面\(PFE\)，\(MN⊂\)平面\(ABC\)，
所以平面\(ABC⊥\)平面\(PFE\)，
又因为平面\(PFE∩\)平面\(ABC=AE\)，
所以点\(P\)在平面\(ABC\)内的射影\(Q\)在\(AE\)上，
因为 \(P F=2 \sqrt{3}\)，所以 \(Q F=\sqrt{3}\),\(PQ=3\)，
过\(F\)作直线\(l//PQ\)交\(PE\)于点\(K\)，以\(F\)为坐标原点，
以 \(\overrightarrow{F M}, \overrightarrow{F E}, \overrightarrow{F K}\)的方向分别为\(x,y,z\)轴的正方向，
建立如图所示的空间直角坐标系，

\(P(0,-\sqrt{3},3)\),\(C(-3,\sqrt{3},0)\),\(E(0,\sqrt{3},0)\),\(Q(0,-\sqrt{3},0)\)，
\(\overrightarrow{Q C}=(-3,2 \sqrt{3}, 0)\) ，\(\overrightarrow{P C}=(-3,2 \sqrt{3},-3)\), \(\overrightarrow{P E}=(0,2 \sqrt{3},-3)\)，
设平面\(PBC\)的法向量为\(\vec{n}=(x,y,z)\)，
则 \(\left\{\begin{array}{c} \vec{n} \cdot \overrightarrow{P C}=-3 x+2 \sqrt{3} y-3 z=0 \\ \vec{n} \cdot \overrightarrow{P E}=2 \sqrt{3} y-3 z=0 \end{array}\right.\)，令\(z=2\)，可得 \(\vec{n}=(0, \sqrt{3}, 2)\)，
所以 \(\cos \langle\overrightarrow{Q C}, \vec{n}\rangle=\dfrac{6}{\sqrt{7} \times \sqrt{21}}=\dfrac{2 \sqrt{3}}{7}\)，
所以直线\(QC\)与平面\(PBC\)所成角的正弦值为 \(\dfrac{2 \sqrt{3}}{7}\)．

【C组---拓展题】

1 如图所示，在正三棱台\(ABC－A_1 B_1 C_1\)中， \(A B=3 A A_{1}=\dfrac{3}{2} A_{1} B_{1}=3\)，记侧面\(ABB_1 A_1\)与底面\(ABC\)，侧面\(ABB_1 A_1\)与侧面\(BCC_1 B_1\)，以及侧面\(ABB_1 A_1\)与截面\(A_1 BC\)所成的锐二面角的平面角分别为\(α,β,γ\)，则(　　)

A．\(γ<β=α\) \(\qquad \qquad\) B．\(β=α<γ\) \(\qquad \qquad\) C．\(β<α<γ\)\(\qquad \qquad\) D．\(α<β<γ\)

2 如图，在圆锥\(SO\)中，\(A\)，\(B\)是\(⊙O\)上的动点，\(BB'\)是\(⊙O\)的直径，\(M\)，\(N\)是\(SB\)的两个三等分点，\(∠AOB=θ(0<θ<π)\)，记二面角\(N－OA－B\)，\(M－AB'－B\)的平面角分别为\(α\)，\(β\)，若\(α≤β\)，则\(θ\)的最大值是(　　)

A． \(\dfrac{5 \pi}{6}\) \(\qquad \qquad\) B． \(\dfrac{2 \pi}{3}\) \(\qquad \qquad\) C． \(\dfrac{\pi}{2}\) \(\qquad \qquad\) D． \(\dfrac{\pi}{4}\)

3折纸与数学有着千丝万缕的联系，吸引了人们的广泛兴趣．因\(A4\)纸的长宽比 \(\sqrt{2}: 1\)称为白银分割比例，故\(A4\)纸有一个白银矩形的美称．现有一张如图\(1\)所示的\(A4\)纸\(EFCH\)，\(EF：EH=\sqrt{2}: 1\)．\(A,B,C,D\)分别为\(EF\),\(FG\),\(GH\),\(HE\)的中点，将其按折痕\(AB\)，\(BC\)，\(CD\),\(DA\),\(AC\)折起(如图\(2\))，使得\(E,F,G,H\)四点重合，重合后的点记为\(S\)，折得到一个如图\(3\)所示的三棱锥\(D－ABC\)．记\(O\)为\(AC\)的中点，在\(△SOB\)中，\(SP\)为\(BO\)边上的高．
(1)求证：\(SP∥\)平面\(ACD\)；
(2)若\(M,N\)分别是棱\(AB\),\(BC\)上的动点，且\(AM=BN\)．当三棱锥\(B－DMN\)的体积最大时，求平面\(DAB\)与平面\(DMN\)所成锐二面角的余弦值．

参考答案

答案 \(B\)
解析如图，设底面三角形\(ABC\)的外心为\(O\)，
以\(O\)为坐标原点，以\(OB\)所在直线为\(x\)轴，以过\(O\)平行于\(AC\)的直线为\(y\)轴，以过\(O\)垂直于底面\(ABC\)的直线为z轴建立空间直角坐标系，

\(∵A B=3 A A_{1}=\dfrac{3}{2} A_{1} B_{1}=3\)，
\(\therefore B(\sqrt{3}, 0,0)\)， \(B_{1}\left(\dfrac{2 \sqrt{3}}{3}, 0, \dfrac{\sqrt{6}}{3}\right)\)， \(C\left(-\dfrac{\sqrt{3}}{2}, \dfrac{3}{2}, 0\right)\)， \(A_{1}\left(-\dfrac{\sqrt{3}}{3},-1, \dfrac{\sqrt{6}}{3}\right)\)，
\(\overrightarrow{B B}_{1}==\left(-\dfrac{\sqrt{3}}{3}, 0, \dfrac{\sqrt{6}}{3}\right)\)， \(\overrightarrow{B A_{1}}=\left(-\dfrac{4 \sqrt{3}}{3},-1, \dfrac{\sqrt{6}}{3}\right)\)， \(\overrightarrow{B C}==\left(-\dfrac{3 \sqrt{3}}{2}, \dfrac{3}{2}, 0\right)\)，
设平面\(ABB_1 A_1\)的一个法向量为\(\vec{n}=(x,y,z)\)，
由 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{B B}_{1}=-\dfrac{\sqrt{3}}{3} x+\dfrac{\sqrt{6}}{3} z=0 \\ \vec{n} \cdot \overrightarrow{B A_{1}}=-\dfrac{4 \sqrt{3}}{3} x-y+\dfrac{\sqrt{6}}{3} z=0 \end{array}\right.\)，取\(x=\sqrt{2}\)，得 \(\vec{n}=(\sqrt{2},-\sqrt{6}, 1)\)；
平面\(ABC\)的一个法向量为\(\vec{α}=(0,0,1)\)；
设平面\(BCC_1 B_1\)的一个法向量为\(\vec{β} =(x_1,y_1,z_1)\)，
由 \(\left\{\begin{array}{l} \vec{\beta} \cdot \overrightarrow{B B_{1}}=-\dfrac{\sqrt{3}}{3} x_{1}+\dfrac{\sqrt{6}}{3} z_{1}=0 \\ \vec{\beta} \cdot \overrightarrow{B C}=-\dfrac{3 \sqrt{3}}{2} x_{1}+\dfrac{3}{2} y_{1}=0 \end{array}\right.\)，取 \(x_{1}=\sqrt{2}\)，得 \(\vec{\beta}=(\sqrt{2}, \sqrt{6}, 1)\)；
设平面\(A_1 BC\)的一个法向量为 \(\vec{\gamma}=\left(x_{2}, y_{2}, z_{2}\right)\)，
由 \(\left\{\begin{array}{l} \vec{\gamma} \cdot \overrightarrow{B A_{1}}=-\dfrac{4 \sqrt{3}}{3} x_{2}-y_{2}+\dfrac{\sqrt{6}}{3} z_{2}=0 \\ \vec{\gamma} \cdot \overrightarrow{B C}=-\dfrac{3 \sqrt{3}}{2} x_{2}+\dfrac{3}{2} y_{2}=0 \end{array}\right.\)，取 \(y_{2}=\sqrt{3}\)，得 \(\vec{\gamma}=\left(1, \sqrt{3}, \dfrac{7 \sqrt{2}}{2}\right)\)．
\(\therefore \cos \alpha=|\cos <\vec{n}, \vec{\alpha}>|=\left|\dfrac{\vec{n} \cdot \vec{\alpha}}{|\vec{n}||\vec{\alpha}|}\right|=\dfrac{1}{3 \times 1}=\dfrac{1}{3},\)，
\(\cos \beta=|\cos <\vec{n}, \vec{\beta}>|=\left|\dfrac{\vec{n} \cdot \vec{\beta}}{|\vec{n}||\vec{\beta}|}\right|=\dfrac{|2-6+1|}{3 \times 3}=\dfrac{1}{3}\)；
\(\cos \gamma=|\cos <\vec{n}, \vec{\gamma}>|=\left|\dfrac{\vec{n} \cdot \vec{\gamma}}{|\vec{n}| \vec{\gamma} \mid}\right|=\dfrac{\left|\sqrt{2}-3 \sqrt{2}+\dfrac{7 \sqrt{2}}{2}\right|}{3 \times \dfrac{\sqrt{114}}{2}}=\dfrac{\sqrt{57}}{57}\)．
\(\because \cos \alpha=\cos \beta>\cos \gamma\)，且余弦函数在 \(\left(0, \dfrac{\pi}{2}\right)\)上为减函数，
\(∴β=α<γ\)．
故选：\(B\)．
答案 \(B\)
解析设底面圆的半径为\(r\)，\(OS=a\)，以\(B'B\)所在直线为\(x\)轴，以垂直于\(B'B\)所在直线为\(y\)轴，以\(OS\)所在直线为\(z\)轴建立空间直角坐标系．
则由\(∠AOB=θ(0<θ<π)\)，可得：\(O(0,0,0)\)，\(B(r,0,0)\)，\(S(0,0,a)\)， \(A(r \cos \theta, r \sin \theta, 0)\)， \(B^{\prime}(-r, 0,0)\)，
\(∵M,N\)是\(SB\)的两个三等分点，
\(\therefore M\left(\dfrac{r}{3}, 0, \dfrac{2 a}{3}\right)\), \(N\left(\dfrac{2 r}{3}, 0, \dfrac{a}{3}\right)\)，
\(\therefore \overrightarrow{O A}=(r \cos \theta, r \sin \theta, 0)\)， \(\overrightarrow{O N}=\left(\dfrac{2 r}{3}, 0, \dfrac{a}{3}\right)\)，
设平面\(NOA\)的一个法向量为\(\vec{m} =(x_1,y_1,z_1)\)，
由 \(\left\{\begin{array}{l} \vec{m} \cdot \overrightarrow{O A}=x_{1} r \cos \theta+y_{1} r \sin \theta=0 \\ \vec{m} \cdot \overrightarrow{O N}=\dfrac{2 x_{1} r}{3}+\dfrac{a z_{1}}{3}=0 \end{array}\right.\)，取\(x_1=1\)，得 \(\vec{m}=\left(1,-\dfrac{\cos \theta}{\sin \theta},-\dfrac{2 r}{a}\right)\)；
平面\(OAB\)的一个法向量为\(\vec{n} =(0,0,1)\)．
由图可知，\(N－OA－B\)的平面角\(α\)为锐二面角， \(\therefore \cos \alpha=\dfrac{|\vec{m} \cdot \vec{n}|}{|\vec{m}| \cdot|\vec{n}|}=\dfrac{\left|\dfrac{2 r}{a}\right|}{\sqrt{1+\dfrac{\cos ^{2} \theta}{\sin ^{2} \theta}+\dfrac{4 r^{2}}{a^{2}}}}\)；
设平面\(B'AM\)的一个法向量为\(\vec{k} =(x_2,y_2,z_2)\)，
\(\overrightarrow{B^{\prime} A}=(r+r \cos \theta, r \sin \theta, 0)\)， \(\overrightarrow{A M}=\left(\dfrac{r}{3}-r \cos \theta,-r \sin \theta, \dfrac{2 a}{3}\right)\)．
由 \(\left\{\begin{array}{l} \vec{k} \cdot \overrightarrow{B^{\prime}} A=x_{2} r+x_{2} r \cos \theta+y_{2} r \sin \theta=0 \\ \vec{k} \cdot \overrightarrow{A M}=\dfrac{x_{2} r}{3}-x_{2} r \cos \theta-y_{2} r \sin \theta+\dfrac{2 a z_{2}}{3}=0 \end{array}\right.\)，
取\(x_2=1\)，得 \(\vec{k}=\left(1, \dfrac{-1-\cos \theta}{\sin \theta},-\dfrac{2 r}{a}\right)\)；
平面\(AB'B\)的一个法向量为\(\vec{h} =(0,0,1)\)，
由题意可知，\(M－AB'－B\)的平面角β为锐二面角，
\(\therefore \cos \beta=\dfrac{|\vec{k} \cdot \vec{h}|}{|\vec{k}| \cdot|\vec{h}|}=\dfrac{\left|\dfrac{2 r}{a}\right|}{\sqrt{1+\left(\dfrac{-1-\cos \theta}{\sin \theta}\right)^{2}+\dfrac{4 r^{2}}{a^{2}}}}\)．
由二面角的范围可知\(0≤α≤β≤π\)．
即 \(\dfrac{\left|\dfrac{2 r}{a}\right|}{\sqrt{1+\dfrac{\cos ^{2} \theta}{\sin ^{2} \theta}+\dfrac{4 r^{2}}{a^{2}}}} \geq \dfrac{\left|\dfrac{2 r}{a}\right|}{\sqrt{1+\left(\dfrac{-1-\cos \theta}{\sin \theta}\right)^{2}+\dfrac{4 r^{2}}{a^{2}}}}\)，
化简可得 \(\cos \theta \leq-\dfrac{1}{2}\)，且\(0<θ<π\)，则 \(0<\theta \leq \dfrac{2 \pi}{3}\)．
\(∴θ\)的最大值是 \(\dfrac{2 \pi}{3}\)．
故选：\(B\)．
答案 (1)略 (2) \(\dfrac{3 \sqrt{5}}{10}\)
解析 (1)证明：连接\(DO\)．设\(EH=4a\)，则 \(E F=4 \sqrt{2} a\)，翻折后的\(BD=DE+FB=4a\)．
在\(△SAC\)中，\(SA=SC=2\sqrt{2} a\)，\(AC=4a\)，\(O\)为\(AC\)的中点，
\(∴SO=2a\)．
又\(∵\)在\(△SOB\)中，\(BS=2a\)，\(SP⊥BO\)，
\(∴P\)为\(BO\)的中点，
\(∴SP∥DO\)．
\(∵SP⊄\)平面\(ACD\)，\(DO⊂\)平面\(ACD\)，
\(∴SP∥\)平面\(ACD\)．
(2)解： \(\because V_{B-D M N}=V_{D-B M N}\)且三棱锥\(D－BMN\)的高为定值，
\(\therefore S_{\triangle B M N}\)最大时，三棱锥\(B－DMN\)的体积取得最大值．
设\(AM=BN=x(0≤x≤2\sqrt{3} a)\)，
\(\therefore S_{\triangle B M N}=\dfrac{1}{2} B M \cdot B N \cdot \sin \angle M B N=\dfrac{1}{2} x(2 \sqrt{3} a-x) \sin \angle M B N\)
\(=\dfrac{1}{2}\left[-(x-\sqrt{3} a)^{2}+3 a^{2}\right] \sin \angle M B N\)
又 \(\because \sin \angle M B N\)为定值．
\(∴\)当 \(x=\sqrt{3} a\)时， \(S_{\triangle B M N}\)最大，即三棱锥\(B－DMN\)的体积最大．
此时\(M\)，\(N\)分别是\(AB\)，\(BC\)上的中点，
由(1)可得\(SP∥DO\)，\(SP⊥BO\)，\(∴DO⊥BO\)．
\(∵DA=DC\)，\(BA=BC\)，\(∴DO⊥AC\)，\(BO⊥AC\)．
以\(O\)为坐标原点， \(\overrightarrow{O A}, \overrightarrow{O B}, \overrightarrow{O D}\)分别为\(x，y，z\)轴的正方向建立空间直角坐标系\(O-xyz\)，
则\(A(2a,0,0)\),\(B(0,2\sqrt{2} a,0)\),\(C(-2a,0,0)\),\(D(0,0,2\sqrt{2}a)\),\(M(a,\sqrt{2}a,0)\)，
\(N=(-a,\sqrt{2} a,0)\)， \(\overrightarrow{D M}=(a, \sqrt{2} a,-2 \sqrt{2} a)\)， \(\overrightarrow{N M}=(2 a, 0,0,)\)， \(\overrightarrow{D A}=(2 a, 0,-2 \sqrt{2} a)\)， \(\overrightarrow{A B}=(-2 a, 2 \sqrt{2} a, 0)\)．
设平面\(DMN\)的一个法向量为 \(\overrightarrow{n_{1}}=\left(x_{1}, y_{1}, z_{1}\right)\)．
\(\therefore\left\{\begin{array}{l} \overrightarrow{n_{1}} \cdot \overrightarrow{D M}=0 \\ \overrightarrow{n_{1}} \cdot N M=0 \end{array}\right.\)，
\(\therefore\left\{\begin{array}{l} a x_{1}+\sqrt{2} a y_{1}-2 \sqrt{2} a z_{1}=0 \\ 2 a x_{1}=0 \end{array}\right.\),取\(z_1=1\)，则\(y_1=2\)，\(x_1=0\)，
\(∴\)平面\(DMN\)的一个法向量为 \(\overrightarrow{n_{1}}=(0,2,1)\)．
设平面\(DAB\)的一个法向量为 \(\overrightarrow{n_{2}}=\left(x_{2}, y_{2}, z_{2}\right)\)．
\(\therefore\left\{\begin{array}{l} \overrightarrow{n_{2}} \cdot \overrightarrow{D A}=0 \\ \overrightarrow{n_{2}} \cdot \overrightarrow{A B}=0 \end{array}\right.\)，
\(\therefore\left\{\begin{array}{l} 2 a x_{2}+2 \sqrt{2} a z_{2}=0 \\ -2 a x_{2}+2 \sqrt{2} a y_{2}=0 \end{array}\right.\)取 \(x_{2}=\sqrt{2}\)，则\(y_2=z_2=1\)，
\(∴\)平面\(DAB\)的一个法向量为 \(\overrightarrow{n_{2}}=(\sqrt{2}, 1,1)\)．
则 \(\cos <\overrightarrow{n_{1}}, \overrightarrow{n_{2}}>=\dfrac{\overrightarrow{n_{1}} \cdot \overrightarrow{n_{2}}}{\left|\overrightarrow{n_{1}}\right| \cdot\left|\overrightarrow{n_{2}}\right|}=\dfrac{3 \sqrt{5}}{10}\)．
所以平面\(DAB\)与平面\(DMN\)所成锐二面角的余弦值为 \(\dfrac{3 \sqrt{5}}{10}\)．