1.4.1(2) 用空间向量研究直线、平面的平行
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
【基础过关系列】2022-2023学年高二数学上学期同步知识点剖析精品讲义(人教A版2019)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性必修第一册同步巩固,难度2颗星!
基础知识
线线平行
设直线\(l_1\),\(l_2\)的方向向量分别是\(\vec{a}\),\(\vec{b}\),则要证明\(l_1 || l_2\),只需证明\(\vec{a}|| \vec{b}\),即 \(\vec{a}=k \vec{b}(k \in R)\).
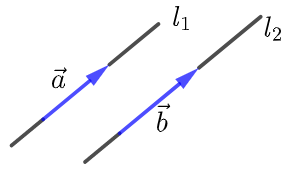
线面平行
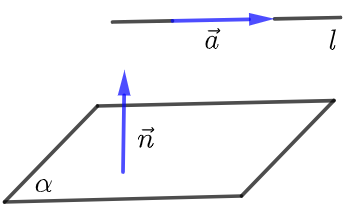
设直线\(l\) 的方向向量是\(\vec{a}\),平面\(α\)的法向量是\(\vec{n}\),且\(l⊄α\),
则要证明\(l||α\),只需证明\(\vec{a}⊥ \vec{n}\),即\(\vec{a}⋅ \vec{n}=0\).
【例】\(\vec{u}=(2,2,-1)\)是平面\(α\)的法向量,\(\vec{a}=(-3,4, 2)\)是直线\(l\)的方向向量,则直线\(l\)与\(α\)的位置关系是 ( )
A.\(l//α\) \(\qquad \qquad\) B.\(l⊥α\) \(\qquad \qquad\) C.\(l⊂α\) \(\qquad \qquad\) D.\(l⊂α\)或\(l//α\)
解 \(\vec{u}\cdot \vec{a}=-6+8-2=0\),\(∴\vec{u}⊥\vec{a}\).\(∴l⊂α\)或\(l//α\).故选:\(D\)
面面平行
若平面\(α\) 的法向量为 \(\overrightarrow{n_{1}}\),平面\(β\)的法向量为 \(\overrightarrow{n_{2}}\),要证\(α||β\) ,只需证 \(\overrightarrow{n_{1}} \| \overrightarrow{n_{2}}\),即证 \(\overrightarrow{n_{1}}=\lambda \overrightarrow{n_{2}}\).
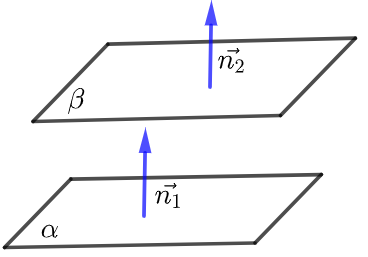
【例】若两个不同平面\(α\),\(β\)的法向量分别为 \(\vec{u}=(1,2,-1)\), \(\vec{v}=(-3,-6,3)\),则 ( )
A.\(α//β\) \(\qquad \qquad\) B.\(α⊥β\) \(\qquad \qquad\) C.\(α,β\)相交但不垂直 \(\qquad \qquad\) D.以上均不正确
解 \(\because \vec{v}=-3 \vec{u}\), \(\therefore \vec{v} / / \vec{u}\).故\(α//β\).故选:\(A\).
基本方法
【典题1】如图,在长方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(AD=AA_1=2\),\(AB=6\),\(E\),\(F\)分别为\(A_1 D_1\),\(D_1 C_1\)的中点.分别以\(DA\)、\(DC\)、\(DD_1\)所在直线为\(x\)轴、\(y\)轴、\(z\)轴建立空间直角坐标系\(D-xyz\).
(1)求点\(E,F\)的坐标;(2)求证:\(EF//\)平面\(ACD_1\).

解析 (1)解:由题意,\(AD=AA_1=2\),\(AB=6\),\(E,F\)分别为\(A_1 D_1\),\(D_1 C_1\)的中点
\(∴E(1,0,2)\),\(F(0,3,2)\).
(2)证明:\(∵A(2,0,0)\),\(C(0,6,0)\), \(\therefore \overrightarrow{A C}=(-2,6,0)\),
\(∵E(1,0,2)\),\(F(0,3,2)\), \(\therefore \overrightarrow{E F}=(-1,3,0)\)
\(\therefore \overrightarrow{A C}=2 \overrightarrow{E F}\),\(∴AC//EF\)
\(∵EF⊂\)面\(ACD_1\),\(AC⊂\)平面\(ACD_1\),
\(∴EF//\)平面\(ACD_1\).
【典题2】 如图,在直三棱柱\(ABC-A_1 B_1 C_1\)中,\(A_1 B_1=A_1 C_1\),\(F\)为\(B_1 C_1\)的中点,\(D\),\(E\)分别是棱\(BC\),\(CC_1\)上的点,且\(AD⊥BC\).
(1) 求证:直线\(A_1 F∥\)平面\(ADE\);
(2) 若\(∆ABC\)是正三角形,\(E\)为\(C_1 C\)中点,能否在线段\(B_1 B\)上找一点\(N\),使得\(A_1 N∥\)平面\(ADE\)?若存在,确定该点位置;若不存在,说明理由.

解析 (1)证明:在直三棱柱\(ABC-A_1 B_1 C_1\)中,
\(∵AB=AC\),\(AD⊥BC\),\(∴D\)是\(BC\)的中点,
又\(∵F\)为\(B_1 C_1\)的中点 \(∴DF//AA_1\),
\(∴\)四边形\(DFA_1 A\)是平行四边形,\(∴A_1 F∥AD\),
\(∵A_1 F⊄\)平面\(ADE\),\(AD⊂\)平面\(ADE\),\(∴A_1 F∥\)平面\(ADE\).
(2)在直线\(B_1 B\)上找一点\(N\),使得\(A_1 N∥\)平面\(ADE\),证明如下:
在直三棱柱\(ABC-A_1 B_1 C_1\)中,\(∵DF//AA_1\) \(∴DF⊥AD\),\(DF⊥DC\)
又\(∵AD⊥BC\) \(∴DA\),\(DC\),\(DF\)两两垂直,
以\(D\)为原点,\(DA\)为\(x\)轴,\(DC\)为\(y\)轴,\(DF\)为\(z\)轴,建立空间直角坐标系,
设\(A_1 B_1=2\),\(AA_1=2t\),
\(∵N\)在线段\(B_1 B\)上,设\(BN=λBB_1\),\(0≤λ≤1\),则\(N(0,-1,2λt)\),
则\(A(\sqrt{3}, 0,0)\),\(D(0,0,0)\),\(E(0,1,t)\),\(B(0,-1,0)\),\(B_1 (0,-1,2t)\),\(A_1 (\sqrt{3},0,2t)\),
\(\overrightarrow{D A}=(\sqrt{3}, 0,0)\), \(\overrightarrow{D E}=(0,1, t)\), \(\overrightarrow{A_{1} N}=(-\sqrt{3}, \quad-1,(2 \lambda-2) t)\),
设平面\(ADE\)的法向量\(\vec{n}=(x,y,z)\),
则 \(\left\{\begin{array}{l}
\vec{n} \cdot \overrightarrow{D A}=\sqrt{3} x=0 \\
\vec{n} \cdot \overrightarrow{D E}=y+t z=0
\end{array}\right.\),取\(z=1\),得\(\vec{n}=(0,-t,1)\),
\(∵A_1 N∥\)平面\(ADE\), \(\therefore \overrightarrow{A_{1}} N \cdot \vec{n}=0+t+(2 \lambda-2) t=0\),解得 \(\lambda=\dfrac{1}{2}\),
\(∴\)在直线\(B_1 B\)上存在一点\(N\),且 \(B N=\dfrac{1}{2} B B_{1}\),使得\(A_1 N∥\)平面\(ADE\).

【典题3】 证明“平面与平面平行的判定定理”:若一个平面内两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图,\(a⊂β\),\(b⊂β\),\(a∩b=P\),\(a//α\),\(b//α\),求证:\(α//β\).

证明 如图,取平面\(α\)的法向量\(\vec{n}\),直线\(a,b\)的方向向量\(\vec{u}\),\(\vec{v}\),
因为\(a//α\),\(b//α\),所以\(\vec{n}\cdot \vec{u}=0\),\(\vec{n}\cdot \vec{v}=0\),
因为\(a⊂β\),\(b⊂β\),\(a∩b=P\),
所以对任意点\(Q∈β\),存在\(x,y∈R\),使得 \(\overrightarrow{P Q}=x \vec{u}+y \vec{v}\),
从而 \(\vec{n} \cdot \overrightarrow{P Q}=\vec{n} \cdot(x \vec{u}+y \vec{v})=x \vec{n} \cdot \vec{u}+y \vec{n} \cdot \vec{v}=0\),
所以向量 \(\vec{n}\)也是平面β的法向量,故\(α//β\).
【典题4】 如图,在长方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(AB=3\),\(AA_1=4\),\(AD=5\).
求证:平面\(A_1 BD//\)平面\(B_1 D_1 C\).

证明 如图,证明如图,以\(D\)为坐标原点,分别以\(DA\),\(DC\),\(DD_1\)所在直线为\(x\)轴,\(y\)轴,\(z\)轴,建立空间直角坐标系\(D-xyz\),
则\(D(0,0,0)\),\(A_1 (5,0,4)\),\(B(5,3,0)\),\(D_1 (0,0,4)\),\(B_1 (5,3,4)\),\(C(0,3,0)\),
\(\therefore \overrightarrow{A_{1} D}=(-5,0,-4)\), \(\overrightarrow{A_{1} B}=(0,3,-4)\), \(\overrightarrow{D_{1} C}=(0,3,-4)\), \(\overrightarrow{B_{1} C}=(-5,0,-4)\),
设平面\(A_1 BD\)的一个法向量为\(\vec{m}=(x,y,z)\),
则 \(\left\{\begin{array}{l}
\vec{m} \perp \overrightarrow{A_{1} D} \\
\vec{m} \perp \overrightarrow{A_{1} B}
\end{array}\right.\),即 \(\left\{\begin{array}{l}
\vec{m} \cdot \overrightarrow{A_{1} D}=-5 x-4 z=0 \\
\vec{m} \cdot \overrightarrow{A_{1} B}=3 y-4 z=0
\end{array}\right.\),
取\(z=1\),得 \(x=-\dfrac{4}{5}, y=\dfrac{4}{3}\),则 \(\vec{m}=\left(-\dfrac{4}{5}, \dfrac{4}{3}, 1\right)\),
设平面\(B_1 D_1 C\)的一个法向量为\(\vec{n}=(a,b,c)\),
则 \(\left\{\begin{array}{l}
\vec{n} \cdot \overrightarrow{\bar{D}_{1} C}=0 \\
\vec{n} \cdot \overrightarrow{B_{1} C}=0
\end{array}\right.\),得 \(\vec{n}=\left(-\dfrac{4}{5}, \dfrac{4}{3}, 1\right)\),
\(∵\vec{m}//\vec{n}\),\(∴\)平面\(A_1 BD//\)平面\(B_1 D_1 C\).

巩固练习
1已知\(\vec{u}=(1,2,1)\)是直线\(l\)的方向向量,\(\vec{v}=(2,y,2)\)为平面\(α\)的法向量,若\(l//α\),则\(y\)的值为\(\underline{\quad \quad}\).
2 设平面\(α\)的法向量为\(\vec{a}=(x,1,-2)\),平面\(β\)的法向量为\(\vec{b}=(1,x,x-3)\),若\(α//β\),则 \(x\)的值为\(\underline{\quad \quad}\).
3 如图,在正方体\(ABCD-A'B'C'D'\)中,\(E\),\(F\)分别是面\(AB'\),面\(A'C'\)的中心,求证:\(EF//\)平面\(ACD'\).

4 已知正方体\(ABCD-A_1 B_1 C_1 D_1\)的棱长为\(2\),\(E\),\(F\)分别是\(BB_1\),\(DD_1\)的中点,求证:
(1) \(FC_1//\)平面\(ADE\);(2)平面\(ADE∥\)平面\(B_1 C_1 F\).
参考答案
-
答案 \(-2\)
解析 \(\vec{u}=(1,2,1)\)是直线\(l\)的方向向量,\(\vec{v}=(2,y,2)\)为平面\(α\)的法向量,\(l//α\),
\(∴\vec{u}⊥\vec{v}\),\(∴\vec{u}\cdot \vec{v}=1×2+2y+1×2=0\),解得\(y=-2\). -
答案 \(1\)
解析 设平面\(α\)的法向量为\(\vec{a}=(x,1,-2)\),平面\(β\)的法向量为\(\vec{b}=(1,x,x-3)\),
若\(α//β\),则\(\vec{a}//\vec{b}\), \(\therefore \dfrac{x}{1}=\dfrac{1}{x}=\dfrac{-2}{x-3}\),解得\(x=1\). -
证明 如图所示,建立空间直角坐标系,

设正方体的边长为\(1\),则 \(E\left(1, \dfrac{1}{2}, \dfrac{1}{2}\right)\), \(F\left(\dfrac{1}{2}, \dfrac{1}{2}, 1\right)\), \(A(1,0,0)\),\(C(0,1,0)\),\(D' (0,0,1)\),\(D(0,0,0)\),\(B'(1,1,1)\),
\(\therefore \overrightarrow{E F}=\left(-\dfrac{1}{2}, 0, \dfrac{1}{2}\right)\), \(\overrightarrow{A C}=(-1,1,0)\), \(\overrightarrow{O D}=(0,-1,1)\), \(\overrightarrow{D B}=(1,1,1)\),
\(∴\)设平面\(ACD'\)的法向量为\(\vec{n}=(x,y,z)\),
\(\therefore\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{A C}=0 \\ \vec{n} \cdot \overrightarrow{C D^{\prime}}=0 \end{array}\right.\),取\(x=1\),则\(y=1\),\(z=1\),\(∴\vec{n}=(1.1.1)\),
\(\therefore \overrightarrow{E F} \cdot \vec{n}=\left(-\dfrac{1}{2}, 0, \dfrac{1}{2}\right) \cdot(1,1,1)=0\),
\(∴EF//\)平面\(ACD'\). -
证明 如图所示建立空间直角坐标系\(D-xyz\),

则有\(D(0,0,0)\),\(A(2,0,0)\),\(C(0,2,0)\),\(C_1 (0,2,2)\),\(E(2,2,1)\),\(F(0,0,1)\),\(B_1 (2,2,2)\),
所以 \(\overrightarrow{F C}_{1}=(0,2,1), \overrightarrow{D A}=(2,0,0), \overrightarrow{A E}=(0,2,1)\).
(1)设 \(\vec{n}_{1}=\left(x_{1}, y_{1}, z_{1}\right)\)是平面\(ADE\)的法向量,
则 \(\overrightarrow{n_{1}} \perp \overrightarrow{D A}\), \(\overrightarrow{n_{1}} \perp \overrightarrow{A E}\),
即 \(\left\{\begin{array} { l } { \vec { n _ { 1 } } \cdot \vec { D A } = 2 x _ { 1 } } \\ { \vec { n _ { 1 } } \cdot \vec { A E } = 2 y _ { 1 } + z _ { 1 } } \end{array} \Rightarrow \left\{\begin{array}{l} x_{1}=0 \\ z_{1}=-2 y_{1} \end{array}\right.\right.\),令\(z_1=2⇒y_1=-1\),
所以 \(\overrightarrow{n_{1}}=(0,-1,2)\),
因为 \(\overrightarrow{n_{1}} \cdot \overrightarrow{F C_{1}}=-2+2=0\),所以 \(\overrightarrow{n_{1}} \perp \overrightarrow{F C_{1}}\),
又因为\(FC_1⊄\)平面\(ADE\),
即\(FC_1∥\)平面\(ADE\).
(2)因为 \(\overrightarrow{C_{1} B_{1}}=(2,0,0)\),设 \(\overrightarrow{n_{2}}=\left(x_{2}, y_{2}, z_{2}\right)\)是平面\(B_1 C_1 F\)的一个法向量.
由 \(\vec{n}_{2} \perp \overrightarrow{F C_{1}}\), \(\vec{n}_{2} \perp \overrightarrow{C_{1} B_{1}}\),得 \(\left\{\begin{array} { l } { \vec { n _ { 2 } } \cdot \vec { F C _ { 1 } } = 2 y _ { 2 } + z _ { 2 } = 0 } \\ { \vec { n _ { 2 } } \cdot \vec { C _ { 1 } B _ { 1 } } = 2 x _ { 2 } = 0 } \end{array} \Rightarrow \left\{\begin{array}{l} x_{2}=0 \\ z_{2}=-2 y_{2} \end{array}\right.\right.\).
令\(z_2=2⇒y_2=-1\),所以\(\overrightarrow{n_{2}}=(0,-1,2)\),
所以 \(\overrightarrow{n_{1}}=\overrightarrow{n_{2}}\),所以平面\(ADE∥\)平面\(B_1 C_1 F\).
分层练习
【A组---基础题】
1 已知直线\(l\)的方向向量\(\vec{a}=(-2,3,1)\),平面\(α\)的一个法向量为\(\vec{e}=(4,0,8)\),则直线\(l\)与平面\(α\)的位置关系是( )
A.平行 \(\qquad \qquad\) B.垂直\(\qquad \qquad\) C.在平面内 \(\qquad \qquad\) D.平行或在平面内
2 已知\(\vec{u}=(1,2,1)\)是直线\(l\)的方向向量,\(\vec{v}=(2,y,2)\)为平面\(α\)的法向量,若\(l//α\),则\(y\)的值为( )
A.\(-2\) \(\qquad \qquad\) B.\(-\dfrac{1}{2}\) \(\qquad \qquad\) C.4 \(\qquad \qquad\) D. \(\dfrac{1}{4}\)
3 已知平面\(α,β\)的法向量分别为 \(\overrightarrow{n_{1}}=(x, 1,-1)\), \(\overrightarrow{n_{2}}=(6, y, 3)\),且\(α//β\),则\(x+y=\) \(\underline{\quad \quad}\) .
4用向量方法证明“直线与平面平行的判定定理”:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
已知:直线\(l\),\(m\)和平面\(α\),其中\(l⊄α\),\(m⊂α\),\(l//m\),
求证:\(l//α\).
5 在正方体\(ABCD-A_1 B_1 C_1 D_1\),\(E\)是棱\(DD_1\)的中点.在棱\(C_1 D_1\)上是否存在一点\(F\),使\(B_1 F//\)平面\(A_1 BE\)?证明你的结论.
6 如图,在四棱锥\(P-ABCD\)中,\(PA⊥\)平面\(ABCD\),\(PB\)与底面所成的角为\(45°\),底面\(ABCD\)为直角梯形,\(∠ABC=∠BAD=90^∘\), \(P A=B C=\dfrac{1}{2} A D=1\),问在棱\(PD\)上是否存在一点\(E\),使\(CE∥\)平面\(PAB\)?若存在,求出\(E\)点的位置;若不存在,请说明理由.

7 如图所示,在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(E,F,G,H\)分别是\(BC\),\(CC_1\),\(C_1 D_1\),\(A_1 A\)的中点,
求证:(1)\(BF//HD_1\);(2)\(EG//\)平面\(BB_1 D_1 D\);(3)平面\(BDF//\)平面\(B_1 D_1 H\).

参考答案
-
答案 \(D\)
解析 直线\(l\) 的方向向量\(\vec{a}=(-2,3,1)\),平面\(α\)的一个法向量为\(\vec{e}=(4,0,8)\),
则\(\vec{a}⋅\vec{e}=-8+0+8=0\),
\(∴\)直线\(l\)与平面\(α\)的位置关系是平行或在平面内.
故选:\(D\). -
答案 \(A\)
解析 \(\vec{u}=(1,2,1)\)是直线\(l\)的方向向量,\(\vec{v}=(2,y,2)\)为平面\(α\)的法向量,\(l//α\),
\(∴\vec{u}⊥\vec{v}\),\(∴\vec{u}\cdot ⋅\vec{v}=1×2+2y+1×2=0\),解得\(y=-2\).
故选:\(A\). -
答案 \(-5\)
解析 \(∵\)平面\(α,β\)的法向量分别为 \(\overrightarrow{n_{1}}=(x, 1,-1)\), \(\overrightarrow{n_{2}}=(6, y, 3)\),且\(α//β\),
\(\therefore \overrightarrow{n_{1}} / / \overrightarrow{n_{2}}\), \(\therefore \dfrac{6}{x}=\dfrac{y}{1}=\dfrac{3}{-1}\),解得\(x=-2\),\(y=-3\),
\(∴x+y=-5\). -
证明 设直线\(l\),\(m\)的方向向量分别为\(\vec{a}\),\(\vec{b}\),平面\(α\)的法向量为\(\vec{u}\),
\(∵l//m\),\(∴\vec{a}=k\vec{b}\),\(k∈R\),
\(∵\)平面\(α\)的法向量为\(\vec{u}\),\(∴\vec{u}⊥α\),
\(∵m⊂α\), 直线\(m\)的方向向量分别为\(\vec{b}\),
\(\therefore \vec{u} \perp \vec{b}\), \(\therefore \vec{u} \cdot \vec{b}=0\),
\(\therefore \vec{u} \cdot \vec{a}=\vec{u} \cdot(k \vec{b})=k \vec{u} \cdot \vec{b}=0\), \(\therefore \vec{u} \perp \vec{a}\),
\(∵l⊄α\),\(∴l//α\). -
证明 以\(A\)为坐标原点,如图建立坐标系,

设正方形的棱长为\(2\),则\(B(2,0,0)\),\(E(0,2,1)\),\(A_1 (0,0,2)\),\(B_1 (2,0,2)\),
\(\therefore \overrightarrow{B E}=(-2,2,1)\), \(\overrightarrow{B A_{1}}=(-2,0,2)\),
设面\(BEA_1\)的法向量为\(\vec{m}=(x,y,z)\),
则 \(\vec{m} \cdot \overrightarrow{B E}=-2 x+2 y+z=0\)且 \(\vec{m} \cdot \overrightarrow{B A_{1}}=2 x+2 z=0\),
取\(x=1\),则\(z=-1\), \(y=\dfrac{3}{2}\), \(\therefore \vec{m}=\left(1, \dfrac{3}{2},-1\right)\)
假设在棱\(C_1 D_1\)上存在一点\(F\),使\(B_1 F//\)平面\(A_1 BE\),
设\(F(x_0,2,2)(0⩽x_0⩽2)\),则\(BF=(x_0-2,2,2)\),
则 \(\vec{m} \cdot B F=1 \times\left(x_{0}-2\right)+\dfrac{3}{2} \times 2+(-1) \times 2=0\),解得\(x_0=1\),
\(∴\)当\(F\)为\(C_1 D_1\)中点时,\(B_1 F//\)平面\(A_1 BE\). -
答案 存在点\(E\),当点\(E\)是\(PD\)的中点时,\(CE∥\)平面\(PAB\).
解析 存在点\(E\)使\(CE∥\)平面\(PAB\).
以\(A\)为坐标原点,分别以\(AB,AD,AP\)所在直线为\(x\)轴,\(y\)轴,\(z\)轴建立空间直角坐标系\(Axyz\),

\(∴P(0,0,1)\),\(C(1,1,0)\),\(D(0,2,0)\),
设\(E(0,y,z)\),则 \(\overrightarrow{P E}=(0, y, z-1)\), \(\overrightarrow{P D}=(0,2,-1)\),
\(\because \overrightarrow{P E} / / \overrightarrow{P D}\),\(∴y(-1)-2(z-1)=0\) ①;
\(\because \overrightarrow{A D}=(0,2,0)\)是平面\(PAB\)的法向量,
又 \(\overrightarrow{CE}=(-1, y-1, z)\),\(CE∥\)平面\(PAB\),
\(\therefore \overrightarrow{C E} \perp \overrightarrow{A D}\), \(∴(-1,y-1,z)⋅(0,2,0)=0\), \(∴y=1\),
代入①得 \(z=\dfrac{1}{2}\), \(∴E\)是\(PD\)的中点,
\(∴\)存在点\(E\),当点\(E\)是\(PD\)的中点时,\(CE∥\)平面\(PAB\). -
证明 设正方体棱长为\(1\),以\(DA,DC,DD_1\)所在直线为\(x,y,z\)轴建立空间直角坐标系.
(1)\(∵B(1,1,0)\), \(F\left(0,1, \dfrac{1}{2}\right)\), \(H\left(1,0, \dfrac{1}{2}\right)\),\(D_1 (0,0,1)\),
\(\therefore \overrightarrow{B F}=\left(-1,0, \dfrac{1}{2}\right)\), \(\overrightarrow{H D_{1}}=\left(-1,0, \dfrac{1}{2}\right)\),
\(\therefore \overrightarrow{B F} / / \overrightarrow{H D_{1}}\),\(∴BF//HD_1\).
(2) \(\because E\left(\dfrac{1}{2}, 1,0\right), G\left(0, \dfrac{1}{2}, 1\right)\), \(\therefore \overrightarrow{E G}=\left(-\dfrac{1}{2},-\dfrac{1}{2}, 1\right)\),
\(∵\)平面\(BB_1 D_1 D\)的一个法向量为 \(\overrightarrow{A C}=(-1,1,0)\), \(\therefore \overrightarrow{E G} \cdot \overrightarrow{A C}=0\),
\(\therefore \overrightarrow{E G} \perp \overrightarrow{A C}\),
\(∵EG\)不在平面\(BB_1 D_1 D\)内,\(∴EG//\)平面\(BB_1 D_1 D\).
(3)设平面\(BDF\)的一个法向量为 \(\overrightarrow{n_{1}}=\left(x_{1}, y_{1}, z_{1}\right)\),
平面\(B_1 D_1 H\)的一个法向量 \(\overrightarrow{n_{2}}=\left(x_{2}, y_{2}, z_{2}\right)\)
\(\therefore \overrightarrow{n_{1}} \perp \overrightarrow{D B}\), \(\overrightarrow{n_{1}} \perp \overrightarrow{D F}\), \(\overrightarrow{n_{2}} \perp \overrightarrow{D_{1} H}\),\(\overrightarrow{n_{2}} \perp \overrightarrow{D_{1} B_{1}}\)
\(\therefore\left\{\begin{array}{l} x_{1}+y_{1}=0 \\ y_{1}+\dfrac{1}{2} z_{1}=0 \end{array}\right.\),取 \(\text { 又 } \overrightarrow{n_{1}}=(1,-1,2)\);
\(\left\{\begin{array}{l} x_{2}-\dfrac{1}{2} z_{2}=0 \\ x_{2}+y_{2}=0 \end{array}\right.\),取 \(\overrightarrow{n_{2}}=(-1,1,-2)\),
\(\therefore \overrightarrow{n_{1}}=-\overrightarrow{n_{2}}\) ,\(∴\)平面\(BDF//\)平面\(B_1 D_1 H\).
【B组---提高题】
1 在三棱柱\(ABC-A_1 B_1 C_1\)中,侧棱垂直于底面,在底面\(ABC\)中\(∠ABC=90^∘\),\(D\)是\(BC\)上一点,且\(A_1 B//\)面\(AC_1 D,D_1\)为\(B_1 C_1\)的中点,求证:面\(A_1 BD_1∥\)面\(AC_1 D\).
参考答案
- 证明 以\(B\)点为原点,如图建立坐标系,

设\(AB=a\),\(BC=2b\),\(BB_1=c\),
则\(A(a,0,0)\),\(C_1 (0,2b,c)\),\(B_1 (0,0,c)\),\(A_1 (a,0,c)\),
\(∴D_1 (0,b,c)\),
设\(D(0,y_0,0)(0⩽y_0⩽2b)\),
\(\therefore \overrightarrow{A D}=\left(-a, y_{0}, 0\right)\), \(\overrightarrow{A C_{1}}=(-a, 2 b, c)\), \(\overrightarrow{B A_{1}}=(a, 0, c)\), \(\overrightarrow{B D_{1}}=(0, b, c)\),
设面\(AC_1 D\)的法向量为 \(\vec{m}=\left(x_{1}, y_{1}, z_{1}\right)\),
则 \(m \cdot \overrightarrow{A D}=-a x_{1}+y_{0} y_{1}=0\)且 \(m \cdot \overrightarrow{A C_{1}}=-a x_{1}+2 b y_{1}+c z_{1}=0\),
取\(y_1=a\),则\(x_1=y_0\), \(z_{1}=\dfrac{a y_{0}-2 a b}{c}\),则 \(\vec{m}=\left(y_{0}, a, \dfrac{a y_{0}-2 a b}{c}\right)\),
又\(∵A_1 B//\)面\(AC_1 D\),
\(\therefore \vec{m} \cdot \overrightarrow{B A_{1}}=a y_{0}+c \times \dfrac{a y_{0}-2 a b}{c}=0\),解得\(y_0=b\), \(\therefore \vec{m}=\left(b, a,-\dfrac{a b}{c}\right)\),
设面\(A_1 BD_1\)的法向量为 \(\overrightarrow{\mathrm{n}}=\left(x_{2}, y_{2}, z_{2}\right)\),
则 \(\overrightarrow{\mathrm{n}} \cdot \overrightarrow{B A_{1}}=a x_{2}+c z_{2}=0\)且 $\vec{n} \cdot \overrightarrow{B D_{1}}=b y_{2}+c z_{2}=0\(0, 取\)z_2=1$,则 \(x_{2}=-\dfrac{c}{a}\) ,\(y_{2}=-\dfrac{c}{b}\),则 \(n=\left(-\dfrac{c}{a},-\dfrac{c}{b}, 1\right)\),
\(\therefore \overrightarrow{\mathrm{n}}=-\dfrac{c}{a b} \vec{m}\), \(\therefore \vec{m} / / \overrightarrow{\mathrm{n}}\),
\(∴\)面\(A_1 BD_1//\)面\(AC_1 D\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号