3.1.2 函数的表示

${\color {Red}{欢迎到学科网下载资料学习 }}$
【基础过关系列】2022-2023 学年高一数学上学期同步知识点剖析精品讲义 (人教 A 版 2019）
${\color {Red}{ 跟贵哥学数学，so \quad easy！}}$

必修第一册同步巩固，难度 2 颗星！

基础知识

函数的表示方法

1 表格法

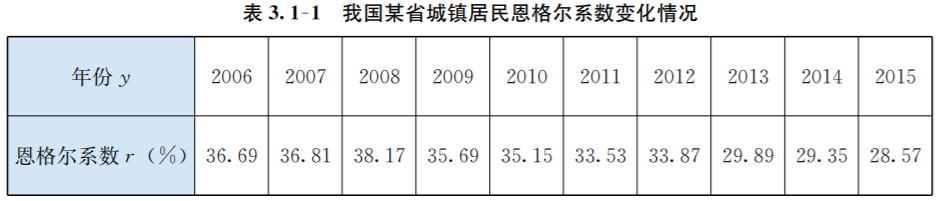
如上表，我们很容易看到 $y$ 与 $r$ 之间的函数关系.
在初中刚学画一次函数时，想了解其图像是一直线，第一步就是列表，其实就是用表格法表示一次函数.
 

【例】 描点法画函数 $y=x-2$ 的图像.
解析 列表

$x$	$-1$	$0$	$1$	$2$	$3$	$4$
$y$	$-3$	$-2$	$-1$	$0$	$1$	$2$

描点连线得

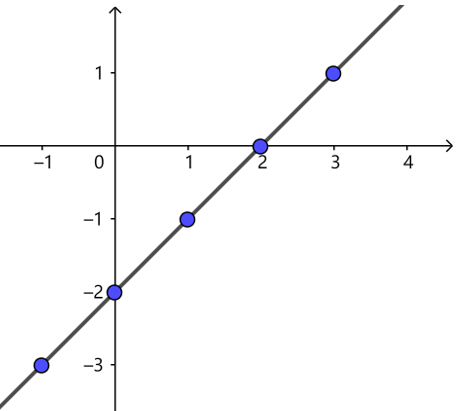
2 图像法

如上图，很清晰的看到某天空气质量指数$I$与时间$t$两个变量之间的关系，特别是其趋势. 数学中的“数形结合”也就是这回事，它是数学一大思想，在高中解题中识图和画图尤为重要.  

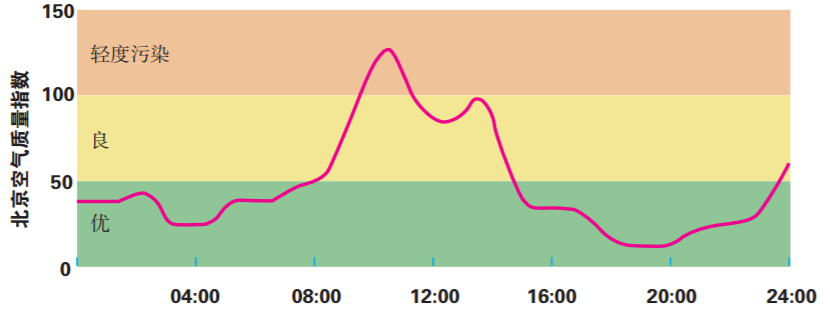
3 解析式
比如正方形周长 $C$ 与边长 $a$ 间的解析式为 $C=4a$，圆的面积 $S$ 与半径 $r$ 的解析式 $S=πr^2$ 等.

求函数解析式的方法
① 配凑法   ② 待定系数法   ③ 换元法   ④ 构造方程组法   ⑤ 代入法
 
【例】 购买某种饮料 $x$ 听，所需钱数是 $y$ 元．若每听 $2$ 元，试分别用解析法、列表法、图象法将 $y$ 表示成 $x(x \in\{1,2,3,4\})$ 的函数．
解析 解析法 $y=2x,x \in\{1,2,3,4\}$．
列表法

$x$	$1$	$2$	$3$	$4$
$y$	$2$	$4$	$6$	$8$

图象法

 

分段函数

定义：有些函数在其定义域中，对于自变量 $x$ 的不同取值范围，对应关系不同，这样的函数通常称为分段函数．
Eg $f(x)=|x|=\left\{\begin{array}{l} x, \quad x \geq 0 \\ -x, \quad x<0 \end{array}\right.$， $f (x)=(-1)^{x}=\left\{\begin {array}{l} -1, x \text { 为奇数 } \\ 1, x \in \text { 为偶数 } \end {array}(x \in \mathrm {N})\right.$.
 

【例】 湛江市自来水公司鼓励企业节约用水，按下表规定收取水费，

用水量	单价（元/吨）
不超过$40$吨的部分	$1.8$
超过$40$吨的部分	$2.2$

求用水量与水费之间的函数关系，并求用水 $30$ 吨和 $50$ 吨的水费.
解析 设用水量为 $x$ 吨，水费为 $y$ 元，
依题意知当 $x≤40$ 时，$y=1.8x$ 元；
当 $x>40$ 时，$y=2.2(x-40)+1.8×40=2.2x-16$ 元，
故用水量与水费之间的函数关系为 $f(x)=\left\{\begin{array}{l} 1.8 x, x \leq 40 \\ 2.2 x-1.6, x>40 \end{array}\right.$，
所以 $f(30)=54$，$f(50)=109.4$，即用水 $30$ 吨和 $50$ 吨的水费分别为 $54$ 元、$109.4$ 元.
 

基本方法

【题型1】求函数解析式

方法 1 待定系数法
【典题 1】 已知函数 $f(x)$ 是二次函数，若 $f(0)=0$, 且 $f(x+1)=f(x)+x+1$，求 $f(x)$ 的解析式．
解析 设 $f(x)=ax^2+bx+c(a≠0)$，
若 $f(0)=0$，且 $f(x+1)=f(x)+x+1$，
$∴c=0$ 且 $a(x+1)^2+b(x+1)+c=ax^2+bx+c+x+1$，
$\therefore\left\{\begin{array}{c} c=0 \\ 2 a+b=b+1 \\ a+b+c=c+1 \end{array},\right.$，解得 $\left\{\begin{array}{l} a=\dfrac{1}{2} \\ b=\dfrac{1}{2} \end{array}\right.$．
$\therefore f(x)=\dfrac{x^{2}+x}{2}$；
点拨 当若已知函数的类型，求其解析式时可用待定系数法.
 

方法 2 换元法
【典题 1】 已知 $f(\sqrt{x}+1)=x+2 \sqrt{x}$，求 $f(x+1)$.
解析 令 $t=\sqrt{x}+1$ ，则 $t≥1,x=(t-1)^2$，
$\because f(\sqrt{x}+1)=x+2 \sqrt{x}$
$∴ f(t)=(t-1)^2+2(t-1)=t^2-1 (t≥1)$ (若这里 $t$ 的范围不能忽略)
$∴ f(x)=x^2-1 (x≥1)$
$∴ f(x+1)=(x+1)^2-1=x^2+2x (x≥0)$
点拨 用换元法时注意新变量的取值范围.
 

方法 3 方程组法
【典题 1】 已知 $f(x)+3f(-x)=2x+1$，则 $f(x)$ 的解析式是 $\underline{\quad \quad}$．
解析 $∵f(x)+3f(-x)=2x+1$…①，
用 $-x$ 代替 $x$，得：$f(-x)+3f(x)=-2x+1$…②；
②×3－①得：$8f(x)=(-6x+3)-(2x+1)=-8x+2$，
$\therefore f(x)=-x+\dfrac{1}{4}$．
 

巩固练习

1. 已知 $f(\sqrt{x}+2)=x$，则有 (　　)
  A．$f(x)=(x-2)^2 (x≥0)$ $\qquad \qquad \qquad \qquad$B．$f(x)=(x-2)^2 (x≥2)$ $\qquad$
  C．$f(x)=(x+2)^2 (x≥0)$ $\qquad \qquad \qquad \qquad$D．$f(x)=(x+2)^2 (x≥2)$
 

2. 已知 $f(x-1)=x^2+3x-10$，则 $f(x)=0$ 的解集为 $\underline{\quad \quad}$.
 

3. 设 $f(x)$ 是一次函数，且 $f[ f(x) ]=4 x+3$，求 $f(x)$ 的解析式.
 

4.$f(x)$ 满足 $f(x)-2 f\left(\dfrac{1}{x}\right)=x$，求 $f(x)$ 的解析式.
 

参考答案

1. 答案 $B$
   解析 设 $\sqrt{x}+2=t$，$t≥2$，则 $x=(t-2)^2$，
   $∴f(t)=(t-2)^2$，$t≥2$，$∴f(x)=(x-2)^2(x≥2)$．
   故选：$B$．

2. 答案 $\{-6,1\}$
   解析 $∵f(x-1)=x^2+3x-10$，
   令 $x-1=t$，则 $x=t+1$，
   $∴f(t)=(t+1)^2+3(t+1)-10=t^2+5t-6$，
   $∴f(x)=x^2+5x-6$，
   由 $f(x)=0$，得 $x^2+5x-6=0$，解得 $x=-6$ 或 $x=1$，
   $∴f(x)=0$ 的解集为 $\{-6,1\}$．

3. 答案 $f(x)=2 x+1$ 或 $f(x)=-2 x+3$
   解析 设 $f(x)=ax+b(a≠ 0)$，
   则 $f[f(x)]=af(x)+b=a(ax+b)+b=a^2 x+ab+b$
   $\therefore\left\{\begin{array}{c} a^{2}=4 \\ a b+b=3 \end{array}\right.$ $\therefore\left\{\begin{array}{l} a=2 \\ b=1 \end{array}\right.$ 或 $\left\{\begin{array}{c} a=-2 \\ b=3 \end{array}\right.$.
   $∴ f(x)=2 x+1$ 或 $f(x)=-2 x+3$.

4. 答案 $f(x)=-\dfrac{x}{3}-\dfrac{2}{3 x}$
   解析 $\because f(x)-2 f\left(\dfrac{1}{x}\right)=x$ ①
   显然 $x≠0$, 将 $x$ 换成 $\dfrac{1}{x}$，得 $f\left(\dfrac{1}{x}\right)-2 f(x)=\dfrac{1}{x}$ ②
   解① ②联立的方程组，得 $f(x)=-\dfrac{x}{3}-\dfrac{2}{3 x}$.
    

【题型2】与分段函数有关问题

【典题 1】 已知函数 $f(x)=\left\{\begin{array}{lr} 3-x^{2} & (x>0) \\ 2 & (x=0) \\ 1-2 x & (x<0) \end{array}\right.$．
(1) 画出函数 $f(x)$ 图象；
(2) 求 $f(f(3))$，$f(a^2+1)(a∈R)$ 的值；
(3) 当 $f(x)≥2$ 时，求 $x$ 的取值范围．
解析 (1) 函数 $f(x)=\left\{\begin{array}{lr} 3-x^{2} & (x>0) \\ 2 & (x=0) \\ 1-2 x & (x<0) \end{array}\right.$ 的图象如图，

(2)$f(f(3))=f(-6)=13$， $f(a^2+1)=3-(a^2+1)^2=-a^4-2a^2+2$；
(3) 方法 1 由图象可知，当 $f(x)≥2$ 时， $x \leq-\dfrac{1}{2}$ 或 $x=0$ 或 $0<x≤1$．
方法 2 当 $x>0$ 时，$3-x^2≥2$，解得 $-1≤x≤1$，即 $0<x≤1$；
当 $x=0$ 时，满足 $f(x)≥2$，所以 $x=0$；
当 $x<0$ 时，$1-2x≥2$，解得 $x \leq-\dfrac{1}{2}$；
综上可得 $x$ 的取值范围是 $\{x \leq-\dfrac{1}{2}$ 或 $x=0$ 或 $0<x≤1\}$．
点拨 对于分段函数的赋值问题，特别要注意分类讨论.
 

【典题 2】 已知函数 $f(x)=\left\{\begin{array}{l} a x^{2}+2 x+1,(-2<x \leq 0) \\ a x-3,(x>0) \end{array}\right.$ 与 $x$ 轴有 $3$ 个交点，则实数 $a$ 的取值范围是 $\underline{\quad \quad}$．
解析① 当 $a=0$， $f(x)=\left\{\begin{array}{l} 2 x+1,(-2<x \leq 0) \\ -3,(x>0) \end{array}\right.$ 与 $x$ 轴有 $1$ 个交点，不满足题意；
② 当 $a<0$ 时，$y=ax-3,(x>0)$ 与 $x$ 轴没有交点，不可能满足题意；
③ 当 $a>0$ 时，$y=ax-3,(x>0)$ 与 $x$ 轴有 $1$ 个交点，
若要满足题意，则 $y=ax^2+2x+1$ 在 $(-2,0)$ 上与 $x$ 轴有 $2$ 个交点，
$\therefore\left\{\begin{array}{l} a>0 \\ a(-2)^{2}+2(-2)+1>0 \\ -2<-\dfrac{1}{a}<0 \\ \Delta=4-4 a>0 \end{array}\right.$，解得 $\dfrac{3}{4}<a<1$
故答案为 $\left(\dfrac{3}{4}, 1\right)$．
 

巩固练习

1. 设函数 $f(x)= \begin{cases}\dfrac{1}{2} x-1 & (x \geq 0) \\ \dfrac{1}{x} & (x<0)\end{cases}$，若 $f(a)=a$，则实数 $a$ 的值为 $\underline{\quad \quad}$．
 

2. 已知函数 $f(x)=\left\{\begin{array}{l} x^{2}-4, x \leq 0 \\ 2^{x}, x>0 \end{array}\right.$，则不等式 $f(x)≥4$ 的解集为 $\underline{\quad \quad}$．
 

3. 作下列各函数的图象．
(1) $y=\left\{\begin{array}{l} \dfrac{1}{x}, 0<x<1 \\ x, x \geq 1 \end{array}\right.$ $\qquad \qquad$ (2)$y=|x－1|$；
 
 
4. 求函数 $f(x)=\left\{\begin{array}{c} 2 x-x^{2},(0 \leq x \leq 3) \\ x^{2}+6 x,(-2 \leq x \leq 0) \end{array}\right.$ 的值域.
 
 
5. 已知函数 $f(x)=\left\{\begin{array}{l} x^{2}-6 x+6, x \geq 0 \\ 3 x+4, x<0 \end{array}\right.$，若互不相等的实数 $x_1 ,x_2 ,x_3$ 满足 $f(x_1)=f(x_2)=f(x_3)$，求 $x_1+x_2+x_3$ 的取值范围.
 
 
参考答案

1. 答案 $-1$
   解析 由题意知，$f(a)=a$；
   当 $a≥0$ 时，有 $\dfrac{1}{2} a-1=a$，解得 $a=－2$，(不满足条件，舍去)；
   当 $a<0$ 时，有 $\dfrac{1}{a}=a$，解得 $a=1$(不满足条件，舍去) 或 $a=－1$．
   所以实数 $a$ 的值是：$a=－1$．

2. 答案 $(-\infty,-2 \sqrt{2}] \cup[2,+\infty)$
   解析 $x≤0$ 时，$f(x)=x^2-4≥4$，解得 $x \geq 2 \sqrt{2}$ 或 $x \leq-2 \sqrt{2}$，
   因为 $x≤0$，故 $x \leq-2 \sqrt{2}$；
   $x>0$ 时，$f(x)=2^x≥4$，解得 $x≥2$，
   综上所述，不等式 $f(x)≥4$ 的解集为 $(-\infty,-2 \sqrt{2}] \cup[2,+\infty)$
   故答案为： $(-\infty,-2 \sqrt{2}] \cup[2,+\infty)$.

3. 解析 (1) 这个函数的图象由两部分组成：当 $0<x<1$ 时，为双曲线 $y=\dfrac{1}{x}$ 的一段；当 $x≥1$ 时，为直线 $y=x$ 的一段，如下图．
   
   (2) 方法一 所给函数可写成 $y= \begin{cases}x-1, & x \geq 1 \\ 1-x, & x<1\end{cases}$ 是端点为 $(1,0)$ 的两条射线，如下图．
   
   方法二 可以先画函数 $y=x－1$ 的图象，然后把其在 $x$ 轴下方的图象对称到上方．如图．
   

4. 答案 $[-8 ,1]$
   解析 $f(x)=2 x-x^2=-(x-1)^2+1$，开口向下，最大值为 $f(1)=1$,
   而 $f(0)=0 ,f(3)=-3$ ,
   $f(x)=x^2+6 x=(x+3)^2-9$, 开口向上，而 $f(-2)=-8 ,f(0)=0$，
   可得到函数图像如右图，易得函数值域为 $[-8 ,1]$.
   

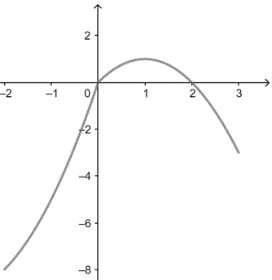
5. 答案 $\left(\dfrac{11}{3}, 6\right)$
   解析 函数 $f(x)=\left\{\begin{array}{l} x^{2}-6 x+6, x \geq 0 \\ 3 x+4, x<0 \end{array}\right.$ 的图象，如图，
   
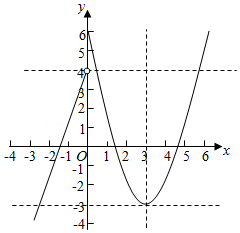
   不妨设 $x_1<x_2<x_3$，则 $x_2 ,x_3$ 关于直线 $x=3$ 对称，故 $x_2+x_3=6$，
   且 $x_1$ 满足 $-\dfrac{7}{3}<x_{1}<0$；
   则 $x_1+x_2+x_3$ 的取值范围是： $-\dfrac{7}{3}+6<x_{1}+x_{2}+x_{3}<0+6$；
   即 $x_{1}+x_{2}+x_{3} \in\left(\dfrac{11}{3}, 6\right)$．

 

【题型3】函数的简单应用

【典题 1】 如图所示的四个容器高度都相同，将水从容器顶部一个孔中以相同的速度注入其中，注满为止．用下面对应的图象显示该容器中水面的高度 $h$ 和时间 $t$ 之间的关系，其中不正确的有 (　　)

 A．$1$ 个　$\qquad \qquad$ 　B．$2$ 个　$\qquad \qquad$　C．$3$ 个 $\qquad \qquad$ 　D．$4$ 个
解析 对于一个选择题而言，求出每一个图中水面的高度 $h$ 和时间 $t$ 之间的函数关系式既无必要也不可能，因此可结合相应的两个图作定性分析，即充分利用数形结合．
对第一个图，不难得知水面高度的增加应是均匀的，因此不正确；
对于第二个图，随着时间的增加，越往上，增加同一个高度，需要的水越多，因此高度变化趋势愈加平缓，正确；
同理可分析第三个图、第四个图都是正确的．
故只有第一个图不正确，因此选 $A$．
 

【典题 2】 某产品生产厂家生产一种产品，每生产这种产品 $x$(百台)，其总成本为 $G(x)$(万元)，其中固定成本为 $42$ 万元，且每生产 $1$ 百台的生产成本为 $15$ 万元 (总成本 固定成本 生产成本)．销售收入 $R(x)$(万元) 满足 $R(x)=\left\{\begin{array}{l} -6 x^{2}+63 x, 0 \leqslant x \leqslant 5 \\ 165, x>5 \end{array}\right.$ 假定该产品产销平衡 (即生产的产品都能卖掉)，根据上述规律，完成下列问题：
(1) 写出利润函数 $y=f(x)$ 的解析式 (利润 = 销售收入 - 总成本)；
(2) 要使工厂有盈利，求产量 $x$ 的范围；
(3) 工厂生产多少台产品时，可使盈利最大？
解析 (1) 由题意得 $G(x)=42+15x$．
$\therefore f(x)=R(x)-G(x)=\left\{\begin{array}{l} -6 x^{2}+48 x-42,0 \leqslant x \leqslant 5 \\ 123-15 x, x>5 \end{array} .\right.$．
(2)①当 $0⩽x⩽5$ 时，由 $-6x^2+48x-42>0$ 得 $x^2-8x+7<0$，解得 $1<x<7$．
所以 $1<x⩽5$．
②当 $x>5$ 时，由 $123-15x>0$ 解得 $x<8.2$．所以 $5<x<8.2$．
综上得当 $1<x<8.2$ 时有 $y>0$．
所以当产量大于 $100$ 台，小于 $820$ 台时，能使工厂有盈利．
(3) 当 $x>5$ 时，函数 $f(x)$ 递减，$∴f(x)<f(5)=48$(万元)．
当 $0≤x≤5$ 时，函数 $f(x)=-6(x-4)^2+54$，
当 $x=4$ 时，$f(x)$ 有最大值为 $54$(万元)．
所以，当工厂生产 $400$ 台时，可使盈利最大为 $54$ 万元．
 

巩固练习

1. 某人去上班，先快速走，后中速走．如果 $y$ 表示该人离单位的距离，$x$ 表示出发后的时间，那么下列图象中符合此人走法的是 (　　)

 

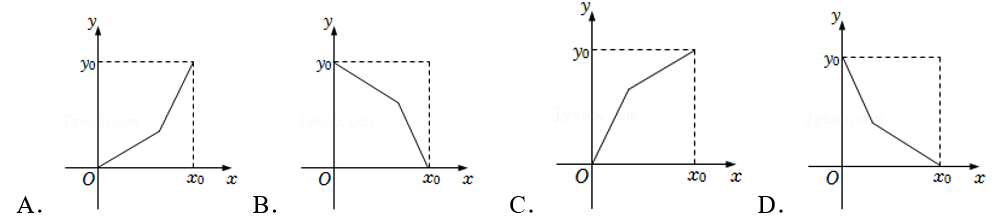
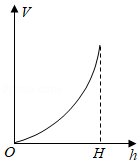
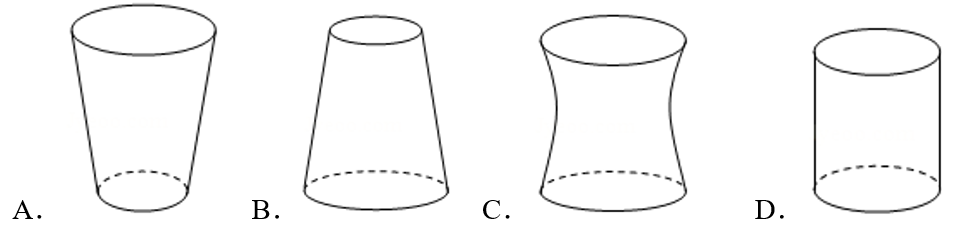
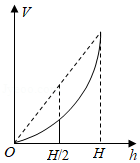
2. 如图，将水注入下面四种容器中，注满为止．如果注水量 $V$ 与水深 $h$ 的函数关系的图象如图所示，那么容器的形状是 (　　)

 

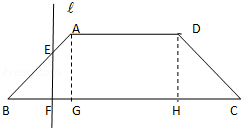
3. 如图，已知底角为 $45^∘$ 角的等腰梯形 $ABCD$，底边 $BC$ 长为 $7cm$，腰长为 2 $2 \sqrt{2} \mathrm{~cm}$，当一条垂直于底边 $BC$(垂足为 $F$) 的直线 把梯形 $ABCD$ 分成两部分，令 $BF=x$，求左边部分的面积 $y$ 关于 $x$ 的函数解析式，并画出图象．

 

参考答案

1. 答案 $D$
   解析 当 $x=0$ 时，距离学校最远，不可能是 $0$，排除 $A,C$，
   先快速走，距离学校的距离原来越近，而且变化速度较快，排除 $B$，
   故选：$D$．

2. 答案 $A$
   解析 根据题意，考虑当向高为 $H$ 的容器中注水为高为 $H$ 一半时，
   注水量 $V$ 与水深 $h$ 的函数关系．
   如图所示，此时注水量 $V$ 与容器容积关系是：$V<$ 容器的容积的一半．
   $A$ 选项符合题意；故选：$A$．
   

3. 解析 过 $A,D$ 分别作 $AG⊥BC$ 于 $G$，$DH⊥BC$ 于 $H$，
   $∵ABCD$ 是等腰梯形，底角 $45^∘$， $A B=2 \sqrt{2} \mathrm{~cm}$，
   $∴BG=AG=DH=HC=2cm$，又 $BC=7cm$，$∴AD=GH=3cm$，
   (1) 当点 $F$ 在 $BG$ 上，即 $x∈(0,2]$ 时， $y=\dfrac{1}{2} x^{2}$，
   (2) 当点 $F$ 在 $GH$ 上，即 $x∈(2,5]$ 时，$y=2+2(x-2)=2x-2$，
   (3) 当点 $F$ 在 $HC$ 上，即 $x∈(5,7)$ 时， $y=\dfrac{1}{2}(3+7) \times 2-\dfrac{1}{2}(x-7)^{2}=-\dfrac{1}{2}(x-7)^{2}+10$，
   $∴$ 函数的解析式为 $y=\left\{\begin{array}{l} \dfrac{1}{2} x^{2}, x \in(0,2] \\ 2 x-2, x \in(2,5] \\ -\dfrac{1}{2}(x-7)^{2}+10, x \in(5,7) \end{array}\right.$
   作图如下图：
   

分层练习

【A组---基础题】

1. 小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间，后为了赶时间加快速度行驶．与以上事件吻合得最好的图象是 　　
 A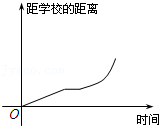． $\qquad \qquad \qquad \qquad \qquad\qquad$ B．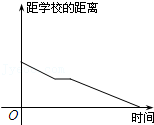
 C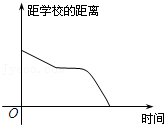． $\qquad \qquad \qquad \qquad \qquad\qquad$ D．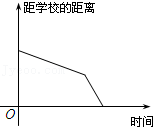

 

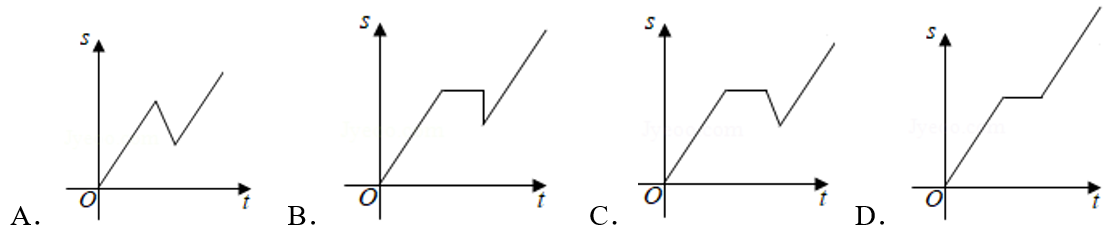
2. 某同学家门前有一笔直公路直通长城，星期天，他骑自行车匀速前往旅游，他先前进了 "$akm$" ，觉得有点累，就休息了一段时间，想想路途遥远，有些泄气，就沿原路返回骑了 $bkm⁡(b<a)$，当他记起诗句 “不到长城非好汉”，便调转车头继续前进．则该同学离起点的距离与时间的函数关系图象大致为

 

3. 已知函数 $f(2x+1)=5x-6$，且 $f(t)=9$，则 $t=$ (　　)
  A．$7$ $\qquad \qquad \qquad \qquad$ B．$5$ $\qquad \qquad \qquad \qquad$ C．$3$ $\qquad \qquad \qquad\qquad$ D．$4$
 

4. 已知函数 $f(x)$ 为一次函数，且 $f(3)=7,f(5)=-1$，则 $f(1)=$(　　)
  A．$15$ $\qquad \qquad \qquad \qquad$ B．$-15$ $\qquad \qquad \qquad \qquad$ C．$9$ $\qquad \qquad \qquad\qquad$ D．$-9$
 

5. 若 $f(\sqrt{x}+1)=x+\sqrt{x}$，则 $f(x)$ 的解析式为 (　　)
  A．$f(x)=x^2-x$ $\qquad \qquad \qquad \qquad \qquad \qquad$ B．$f(x)=x^2-x(x≥0)$
  C．$f(x)=x^2-x(x≥1)$ $\qquad \qquad \qquad \qquad\qquad$ D．$f(x)=x^2+x$
 

6. 已知 $f(x)=\left\{\begin{array}{l} 1, x \geq 0 \\ -1, x<0 \end{array}\right.$，则不等式 $x+(x+2)f(x+2)≤5$ 的解集是 $\underline{\quad \quad}$．
 

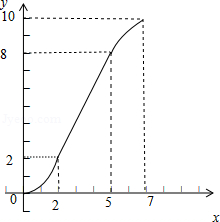
7. 若函数 $y＝f(x)$ 的图象如图所示，则其表达式 $f(x)$ 为 $\underline{\quad \quad}$．

 

8. 已知函数 $f(x)=\left\{\begin{array}{l} \dfrac{2}{x}, x<0 \\ -x, 0 \leqslant x<2 \\ \dfrac{1}{2} x-3, x \geqslant 2 \end{array}\right.$．
(1) 求 $f(0),f(f(2))$；(2) 若 $f(m)=-1$，求 $m$ 的值；(3) 作出函数 $f(x)$ 的图象．
 
 
 

9. 某产品生产厂家根据以往的生产销售经验得到下面有关销售的统计规律：每生产产品 $x$(百台)，其总成本为 $G(x)$ 万元，其中固定成本为 $2$ 万元，并且每生产 $100$ 台的生产成本为 $1$ 万元 (总成本 固定成本 生产成本)，销售收入 $R(x)$ 满足 $R(x)=\left\{\begin{array}{l} -0.4 x^{2}+4.2 x-0.8(0 \leq x \leq 5) \\ 10.2(x>5) \end{array}\right.$，假定该产品产销平衡，那么根据上述统计规律：
(1) 要使工厂有盈利，产品数量 $x$ 应控制在什么范围？
(2) 工厂生产多少台产品时盈利最大？此时每台产品售价为多少？
 
 
 

参考答案

1. 答案 $C$
   解析 考查四个选项，横坐标表示时间，纵坐标表示的是离开学校的距离，
   由此知，此函数图象一定是下降的，由此排除 $A$；
   再由小明骑车上学，开始时匀速行驶可得出图象开始一段是直线下降型，又途中因交通堵塞停留了一段时间，故此时有一段函数图象与 轴平行，由此排除 $D$，
   之后为了赶时间加快速度行驶，此一段时间段内函数图象下降的比较快，由此可确定 $C$ 正确，$B$ 不正确．故选：$C$．

2. 答案 $C$
   解析 根据他先前进了 "$akm$" ，得图象是一段上升的直线，
   由觉得有点累，就休息了一段时间，得图象是一段平行于 轴的直线，
   由想想路途遥远，有些泄气，就沿原路返回骑了 $bkm(b<a)$，得图象是一段下降的直线，
   由记起诗句 “不到长城非好汉”，便调转车头继续前进，得图象是一段上升的直线，
   综合，得图象是 $C$，故选：$C$．

3. 答案 $A$
   解析 $\because f(2 x+1)=5 x-6=\dfrac{5}{2}(2 x+1)-\dfrac{17}{2}$； $\therefore f(x)=\dfrac{5}{2} x-\dfrac{17}{2}$；
   $\therefore f(t)=\dfrac{5}{2} t-\dfrac{17}{2}=9$；解得 $t=7$．故选：$A$．

4. 答案 $A$
   解析 设 $f(x)=kx+b$，则 $\left\{\begin{array}{l} 3 k+b=7 \\ 5 k+b=-1 \end{array}\right.$，解得 $\left\{\begin{array}{l} k=-4 \\ b=19 \end{array}\right.$，
   $∴f(x)=-4x+19$，$∴f(1)=-4+19=15$．故选：$A$．

5. 答案 $C$
   解析 函数 $f(\sqrt{x}+1)=x+\sqrt{x}$，
   设 $\sqrt{x}+1=t$，则 $t≥1$， $\therefore \sqrt{x}=t-1$，
   $∴f(t)=(t-1)^2+(t-1)=t^2-t$，
   $∴f(x)=x^2-x，(x≥1)$．故选：$C$．

6. 答案 $\left\{x \mid x \leq \dfrac{3}{2}\right\}$
   解析 ①当 $x+2≥0$ 时，即 $x≥－2$，$f(x+2)=1$，
   由 $x+(x+2)f(x+2)≤5$ 可得 $x+x+2≤5$，
   $\therefore x \leq \dfrac{3}{2}$ 即 $-2 \leq x \leq \dfrac{3}{2}$，
   当 $x+2<0$ 即 $x<-2$ 时，$f(x+2)=-1$，
   由 $x+(x+2)f(x+2)≤5$ 可得 $x-(x+2)≤5$，即 $-2≤5$，$∴x<-2$，
   综上不等式的解集为 $\left\{x \mid x \leq \dfrac{3}{2}\right\}$.

7. 答案 $C$
   解析 $f(x)=\left\{\begin{array}{l} \dfrac{3}{2} x+3, x \in[-2,0) \\ -\dfrac{1}{2} x+3, x \in[0,2) \\ 2, x \in[2,4) \end{array}\right.$.

8. 答案 (1) $f(0)=0,f(f(2))=-1$ (2)$-2$ 或 $1$ 或 $4$ (3) 略
   解析 (1)$f(0)=0$, $f(2)=\dfrac{1}{2} \times 2-3=-2$， $\therefore f(f(2))=f(-2)=\dfrac{2}{-2}=-1$．
   (2) 当 $m<0$ 时， $f(m)=\dfrac{2}{m}=-1$，$∴m=-2$，
   当 $0⩽m<2$ 时，$f(m)=-m=-1$，$∴m=1$，
   当 $m⩾2$ 时， $f(m)=\dfrac{1}{2} m-3=-1$，$∴m=4$，
   综上所述，$m$ 的值为 $-2$ 或 $1$ 或 $4$．
   (3) 函数 $f(x)$ 的图象，如图所示，
   

9. 答案 (1) $f(x)=\left\{\begin{array}{l} -0.4 x^{2}+3.2 x-2.8,(0 \leq x \leq 5) \\ 8.2-x,(x>5) \end{array}\right.$ (2) $240$ 元 台
   解析 依题意，$G(x)=x+2$，设利润函数为 $f(x)$，则
   $f(x)=R(x)-G(x)=\left\{\begin{array}{l} -0.4 x^{2}+3.2 x-2.8,(0 \leq x \leq 5) \\ 8.2-x,(x>5) \end{array}\right.$
   (1) 要使工厂有盈利，即解不等式 $f(x)>0$，当 $0≤x≤5$ 时，
   解不等式 $-0.4x^2+3.2x-2.8>0$．即 $x^2-8x+7<0$．
   $∴1<x<7$,$∴1<x≤5$．
   当 $x>5$ 时，解不等式 $8.2-x>0，$ 得 $x<8.2$．
   $∴5<x<8.2$．
   综上，要使工厂盈利，$x$ 应满足 $1<x<8.2$，
   即产品应控制在大于 $100$ 台，小于 $820$ 台的范围内．
   (2)$0≤x≤5$ 时，$f(x)=-0.4(x-4)^2+3.6$，
   故当 $x=4$ 时，$f(x)$ 有最大值 $3.6$．
   而当 $x>5$ 时，$f(x)<8.2-5=3.2$
   所以，当工厂生产 $400$ 万台产品时，盈利最多．
   又 $x=4$ 时， $\dfrac{R(4)}{4}=240$(元 台)，
   故此时每台产品售价为 $240$(元 台)．
    
    

【B组---提高题】

1. 为庆祝深圳特区成立 $40$ 周年，2020 年 10 月 11 日深圳无人机精英赛总决赛在光明区举行，全市共 $39$ 支队伍参加．如图反映了某学校代表队制作的无人机载重飞行从某时刻开始 $15$ 分钟内的速度 $U(x)$(单位：米 分) 与时间 $x$(单位：分) 的关系．若定义 “速度差函数 “$u(x)$ 为无人机在时间段为 $[0,x]$ 内的最大速度与最小速度的差，则 的图象为

 A． $\qquad$ B．
$\qquad$
 C． $\qquad$ D．
 

2. 定义运算：$a \odot b=\left\{\begin{array}{l} a(a \leq b) \\ b(a>b) \end{array}\right.$ 如 $1⊙2=1$，则函数 $f(x)=2^x⊙2^{-x}$ 的值域为 (　　)
 A．$R$ $\qquad \qquad$ B．$(0，+∞)$ $\qquad \qquad$ C．$(0，1]$ $\qquad \qquad$ D．$[1，+∞)$
 

3. 若 $x∈R$，$f(x)$ 是 $y=2-x^2$，$y=x$ 这两个函数中的较小者，则 $f(x)$ 的最大值为 (　　)
 A．$2$　$\qquad \qquad$　B．$1$ $\qquad \qquad$ C．$－1$ $\qquad \qquad$ D．无最大值
 

4. 已知函数 $f(x)$ 满足：$2f(2x-1)+3f(1-2x)=6x$，求 $f(x)$ 的解析式．
 

5. 作出函数 $y＝|x+2|－|x－5|$ 的图象．
 

6. 某商品近一个月内 天) 预计日销量 $y=f(t)$(件) 与时间 $t$(天) 的关系如图 1 所示，单价 $y=g(t)$(万元 件) 与时间 $t$(天) 的函数关系如图 2 所示，($t$ 为整数)

(1) 试写出 $f(t)$ 与 $g(t)$ 的解析式；(2) 求此商品日销售额的最大值？
 

参考答案

1. 答案 $D$
   解析由题意可得，当 $x∈[0,6]$ 时，翼人做匀加速运动， $v(x)=80+\dfrac{40}{3} x$，
   “速度差函数” $u(x)=\dfrac{40}{3} x$．
   当 $x∈[6,10]$ 时，翼人做匀减速运动，速度 $v(x)$ 从 $160$ 开始下降，一直降到 $80$，$u(x)=160-80=80$．
   当 $x∈[10,12]$ 时，翼人做匀减速运动，$v(x)$ 从 $80$ 开始下降，$v(x)=180-10x$，$u(x)=160-(180-10x)=10x-20$．
   当 $x∈[12,15]$ 时，翼人做匀加速运动，“速度差函数”$u(x)=160-60=100$，
   结合所给的图象，故选：$D$．

2. 答案 $C$
   解析 $f(x)=2^{x} \odot 2^{-x}=\left\{\begin{array}{l} 2^{x}(x \leq 0) \\ 2^{-x}(x>0) \end{array}\right.$，
   $∴f(x)$ 在 $(－∞,0]$ 上是增函数，在 $(0,+∞)$ 上是减函数，
   $∴0<f(x)≤1$；故选：$C$．

3. 答案 $B$
   解析 由题目可获取的信息是：
   ①两个函数一个是二次函数，一个是一次函数；
   ②$f(x)$ 是两个函数中的较小者．
   解答此题可先画出两个函数的图象，然后找出 $f(x)$ 的图象，再求其最大值．
   在同一坐标系中画出函数 $y=2-x^2$，$y=x$ 的图象，
   如图，根据题意，坐标系中实线部分即为函数 $f(x)$ 的图象．
   
   故 $x=1$ 时， $f(x)_{\max }=1$，应选 $B$．

4. 答案 $f(x)=-3 x+\dfrac{3}{5}$
   解析 $2f(2x-1)+3f(1-2x)=6x$，
   令 $u=2x-1$，则 $2f(u)+3f(-u)=3u+3$，
   用 $-u$ 替换 $u$ 得：$2f(-u)+3f(u)=-3u+3$，
   消去 $f(-u)$ 可得 $5f(u)=-15u+3$，即 $f(u)=-3 u+\dfrac{3}{5}$， $\therefore f(x)=-3 x+\dfrac{3}{5}$．

5. 解析 $f(x)=\left\{\begin{array}{l} -7, x \in(-\infty,-2] \\ 2 x-3, x \in(-2,5] \\ 7, x \in(5,+\infty) \end{array}\right.$
   

6. 答案 (1) $f(t)=35-t(0≤t≤30,t∈Z)$， $g(t)=\left\{\begin{array}{l} \dfrac{1}{4} t+3,0 \leq t \leq 20, t \in Z \\ 20-\dfrac{3}{5} t, 20<t \leq 30, t \in Z \end{array}\right.$(2) $138$
   解析 (1)$f(t)$ 是一次函数，过两个点 $(30,5),(0,35)$
   $∴f(t)=35-t(0≤t≤30,t∈Z)$，
   $g(t)$ 是分段函数，当 $0≤t≤20$ 时，是一次函数，过两个点 $(20,8),(0,3)$，
   此时 $g(t)=\dfrac{1}{4} t+3$，
   当 $20<t≤30$ 时，是一次函数，过两个点 $(20,8),(30,2)$，此时 $g(t)=20-\dfrac{3}{5} t$
   $\therefore g(t)=\left\{\begin{array}{l} \dfrac{1}{4} t+3,0 \leq t \leq 20, t \in Z \\ 20-\dfrac{3}{5} t, 20<t \leq 30, t \in Z \end{array}\right.$
   (2) 设日销售额 $L(t)$ 是天数 t 的函数，则有
   $L(t)=f(t) \cdot g(t)=\left\{\begin{array}{l} (35-t)\left(\dfrac{1}{4} t+3\right), 0 \leq t \leq 20, t \in Z \\ (35-t)\left(20-\dfrac{3}{5} t\right), 20<t \leq 30, t \in Z \end{array}\right.$
   当 $0≤t≤20$ 时， $L(t)=\dfrac{1}{4}\left[-\left(t-\dfrac{23}{2}\right)^{2}+\dfrac{2209}{4}\right]$，
   当 $t=11$ 或 $12$ 时，$L(t)$ 最大值为 $138$ 万元．
   当 $20<t≤30$ 时， $L(t)=\dfrac{3 t^{2}-205 t+3500}{5}$ 在 $(20,30]$ 是减函数，
   故 $L(t)<L(20)=120$ 万元，
   $∵138>120$，$∴0≤t≤30$ 时，当 $t=11$ 或 $12$ 时，$L(t)$ 最大值为 $138$ 万元．
   答：第 $11$ 天与第 $12$ 天的日销售额最大，最大值为 $138$ 万元．

【C组---拓展题】

1. 某罐头加工厂库存芒果 $m(kg)$，今年又购进 $n(kg)$ 新芒果后，欲将芒果总量的三分之一用于加工为芒果罐头。被加工为头的新芒果最多为 $f_1 (kg)$，最少为 $f_2 (kg)$，则下列坐标图最能准确描述 $f_1,f_2$ 分别与 $n$ 的关系的是 ( )　
 A． $\qquad \qquad$ B． $\qquad \qquad$ C． $\qquad \qquad$ D．
 

2. 已知 $f(0)=1$，对于任意实数 $x,y$，等式 $f(x-y)=f(x)-y(2x-y+1)$，求 $f(x)$ 的解析式.
 

3. 已知函数 $y=x^2+x$ 与 $y=g(x)$ 与的图像关于 $(-2,3)$ 对称，求 $g(x)$ 的解析式.
 

4. 设函数 $f(x)=|x-1|+|x-2|$．
(1) 画出函数 $y=f(x)$ 的图象；
(2) 若不等式 $|a+b|+|a-b|≥|a|f(x)$，$(a≠0,a,b∈R)$ 恒成立，求实数 $x$ 的范围．
 
 

参考答案

1. 答案 $A$
   解析 要使得被加工为罐头的新芒果最少，尽量使用库存罐头，
   即当 $\dfrac{m+n}{3} \leqslant m, \quad n \leqslant 2 m$ 时 $f_2=0$，
   当 $n>2m$ 时， $f_{2}=\dfrac{m+n}{3}-m=\dfrac{n-2 m}{3}$，对照图象舍去 $C,D$．
   要使得被加工为罐头的新芒果最多，则尽量使用新芒果，
   即当 $\dfrac{m+n}{3} \leqslant n, n \geqslant \dfrac{m}{2}$ 时 $f_{1}=\dfrac{m+n}{3}$；当 $\dfrac{m+n}{3}>n, \quad n<\dfrac{m}{2}$ 时 $f_1=n$；
   $\because \dfrac{m}{2}<2 m$，故选：$A$．

2. 答案 $f(x)=x^2+x+1$
   解析 对于任意实数 $x、y$, 等式 $f(x-y)=f(x)-y(2x-y+1)$ 恒成立，
   不妨令 $x=0$, 则有 $f(-y)=f(0)-y(-y+1)=1+y(y-1)=y^2-y+1$
   再令 $-y=x$, 得函数解析式为：$f(x)=x^2+x+1$ .

3. 答案
   解析 设 $M(x,y)$ 为 $y=g(x)$ 上任一点，且 $M'(x',y')$ 为 $M(x,y)$ 关于点 $(-2,3)$ 的对称点
   则 $\left\{\begin{array}{l} \dfrac{x^{\prime}+x}{2}=-2 \\ \dfrac{y^{\prime}+y}{2}=3 \end{array}\right.$，解得： $\left\{\begin{array}{c} x^{\prime}=-x-4 \\ y^{\prime}=6-y \end{array}\right.$ .
   $∵$ 点 $M'(x',y')$ 在 $y=g(x)$ 上 $∴y'=x'^2+x'$
   把 $\left\{\begin{array}{c} x^{\prime}=-x-4 \\ y^{\prime}=6-y \end{array}\right.$，代入得：$6-y=(-x-4)^2+(-x-4)$，整理得 $y=-x^2-7 x-6$

4. 答案 (1) 略 (2) $\dfrac{1}{2} \leq x \leq \dfrac{5}{2}$
   解析 (1) $f(x)=\left\{\begin{array}{l} 2 x-3(x \geq 2) \\ 1(1<x<2) \\ 3-2 x(x \leq 1) \end{array}\right.$
   (2) 由 $|a+b|+|a-b|⩾|a|f(x)$ 得 $\dfrac{|a+b|+|a-b|}{|a|} \geq f(x)$，
   又因为 $\dfrac{|a+b|+|a-b|}{|a|} \geq \dfrac{|a+b+a-b|}{|a|}=2$，则有 $2≥f(x)$，
   解不等式 $2≥|x-1|+|x-2|$，得 $\dfrac{1}{2} \leq x \leq \dfrac{5}{2}$.