基础知识
函数的概念
1 概念 A 、 B A 、 B 是非空的数集,如果按照某个确定的对应关系 f f ,使对于集合 A A 中的任意一个数 x x ,在集合 B B 中都有唯一确定的数 f ( x ) f ( x ) 和它对应,那么就称 f : A → B f : A → B 为从集合 A A 到集合 B B 的一个函数.记作: y = f ( x ) , x ∈ A y = f ( x ) , x ∈ A x x x x A A 叫做函数的定义域;与 x x 的值相对应的 y y 值叫做函数值,函数值的集合 { f ( x ) | x ∈ A } { f ( x ) | x ∈ A } 叫做函数的值域.比如 15 k m / h 15 k m / h 的速度从大理去相距 180 k m 180 k m 的丽江,出发 t t 小时后行驶的路程是 s k m s k m ,则 s s 是 t t 的函数,记为 s = 12 t s = 12 t ,定义域是 { t | 0 ≤ t ≤ 12 } { t | 0 ≤ t ≤ 12 } ,值域为 { s | 0 ≤ s ≤ 180 } { s | 0 ≤ s ≤ 180 } .对集合 { t | 0 ≤ t ≤ 2 } { t | 0 ≤ t ≤ 2 } 中的任意一个实数,在集合 { s | 0 ≤ s ≤ 180 } { s | 0 ≤ s ≤ 180 } 中都有唯一的数 s = 12 t s = 12 t 和它对应.
对函数概念的理解 A , B A , B A , B A , B 只能是数集,即 A , B A , B 中的元素只能是实数;另一方面指出了定义域、值域都不能是空集. A , B A , B 间元素的对应可以是一对一、一对多,不能多对一,集合 B B 中的元素可以在集合 A A 没元素对应.
③ 函数定义中强调 “三性”:任意性、存在性、唯一性,即对于非空数集 A A 中的任意一个 (任意性) 元素 x x ,在非空数集 B B 中都有 (存在性) 唯一 (唯一性) 的元素 y y 与之对应.这 “三性” 只要有一个不满足,便不能构成函数.
定义域
① 概念 x x 的取值范围.求函数的定义域主要应考虑以下几点 f ( x ) f ( x ) 为整式,则其定义域为实数集 R R . f ( x ) f ( x ) 是分式,则其定义域是使分母不等于 0 0 的实数的集合. f ( x ) f ( x ) 为偶次根式,则其定义域是使根号内的式子大于或等于 0 0 的实数的集合. f ( x ) f ( x ) 是由几个部分的数学式子构成的,那么函数的定义域是使各部分都有意义的实数的集合,即交集.
【例】 f ( x ) = 1 x − 1 f ( x ) = 1 x − 1 f ( x ) = √ x − 2 f ( x ) = x − 2 答案 x ≠ 1 x ≠ 1 [ 2 , + ∞ ) [ 2 , + ∞ )
值域
① 概念 y y 的取值范围求值域的方法
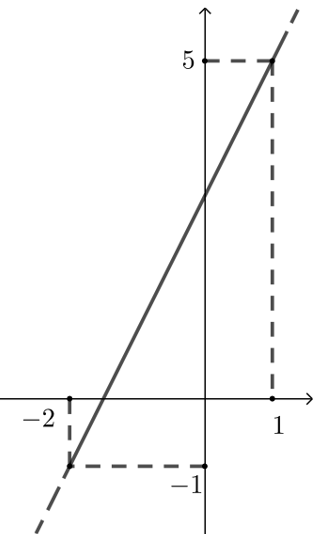
【例】 f ( x ) = 2 x + 3 , x ∈ { 1 , 2 , 3 } f ( x ) = 2 x + 3 , x ∈ { 1 , 2 , 3 } f ( x ) = 2 x + 3 , x ∈ ( − 2 , 1 ] f ( x ) = 2 x + 3 , x ∈ ( − 2 , 1 ] 解析 { 5 , 7 , 9 } { 5 , 7 , 9 } ; f ( x ) = 2 x + 3 f ( x ) = 2 x + 3 的图象.
由图象可知 f ( x ) = 2 x + 3 , x ∈ ( − 2 , 1 ] f ( x ) = 2 x + 3 , x ∈ ( − 2 , 1 ] 的值域为 ( - 2 , 5 ] ( - 2 , 5 ] .
区间
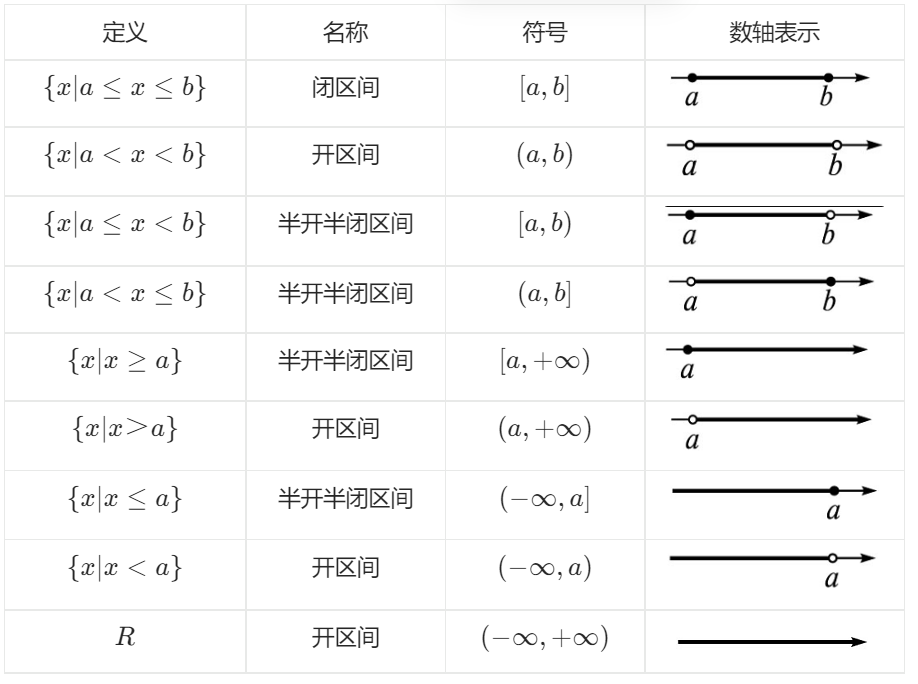
区间的几何表示如下表所示:
【例】 { x | x ≥ 2 } { x | x ≥ 2 } { x | x < 0 } { x | x < 0 } { x | − 2 < x ≤ 5 } { x | − 2 < x ≤ 5 } { x | 0 < x < 1 , { x | 0 < x < 1 , 2 ≤ x ≤ 4 } 2 ≤ x ≤ 4 } . 解析 [ 2 , + ∞ ) [ 2 , + ∞ ) ( - ∞ , 0 ) ( - ∞ , 0 ) ( − 2 , 5 ] ( − 2 , 5 ] ( 0 , 1 ) ∪ [ 2 , 4 ] ( 0 , 1 ) ∪ [ 2 , 4 ]
【练】 { x | x < 3 } { x | x < 3 } { x | x ≥ 0 } { x | x ≥ 0 } { x | − 2 ≤ x < 3 } { x | − 2 ≤ x < 3 } { x | x < 1 , { x | x < 1 , 2 ≤ x ≤ 4 } 2 ≤ x ≤ 4 } . 解析 ( − ∞ , 3 ) ( − ∞ , 3 ) [ 0 , + ∞ ) [ 0 , + ∞ ) [ − 2 , 3 ) [ − 2 , 3 ) ( − ∞ , 1 ) ∪ [ 2 , 4 ] ( − ∞ , 1 ) ∪ [ 2 , 4 ]
基本方法
【题型1】函数概念的理解
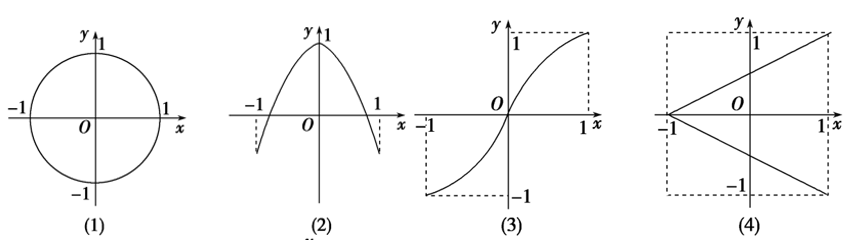
【典题 1】 x , y x , y 的对应关系,其中表示 y y 是 x x 的函数关系的有 – ––– – _ .
解析 x = a x = a ,则与函数的图象至多有一个交点,对于本题而言,当 - 1 ≤ a ≤ 1 - 1 ≤ a ≤ 1 时,直线 x = a x = a 与函数的图象仅有一个交点,当 a > 1 a > 1 或 a < - 1 a < - 1 时,直线 x = a x = a 与函数的图象没有交点.从而表示 y y 是 x x 的函数关系的有 (2)(3). 点拨 x x 是否对应唯一的 y y .
【典题 2】 y y 是 x x 的函数的是 ( )x 2 + y 2 = 1 x 2 + y 2 = 1 | x − 1 | + √ y 2 − 1 = 0 | x − 1 | + y 2 − 1 = 0 √ x − 1 + √ y − 1 = 1 x − 1 + y − 1 = 1 y = √ x − 2 + √ 1 − x y = x − 2 + 1 − x 解析 x 2 + y 2 = 1 x 2 + y 2 = 1 y = ± √ 1 − x 2 y = ± 1 − x 2 | x − 1 | + √ y 2 − 1 = 0 | x − 1 | + y 2 − 1 = 0 | x - 1 | = 0 | x - 1 | = 0 , √ y 2 − 1 = 0 y 2 − 1 = 0 x = 1 , y = ± 1 x = 1 , y = ± 1 ,所以②不是函数.√ x − 1 + √ y − 1 = 1 x − 1 + y − 1 = 1 y = ( 1 − √ x − 1 ) 2 + 1 y = ( 1 − x − 1 ) 2 + 1 y = √ x − 2 + √ 1 − x y = x − 2 + 1 − x { x − 2 ≥ 0 1 − x ≥ 0 { x − 2 ≥ 0 1 − x ≥ 0 { x ≥ 2 x ≤ 1 { x ≥ 2 x ≤ 1 C C
巩固练习
1. 下列四个图形中,不是以 x x 为自变量的函数的图象是 ( )
2. 函数 y = f ( x - 1 ) y = f ( x - 1 ) 与函数 y = f ( x + 1 ) y = f ( x + 1 ) ( )
3. 下列式子中 y y 是 x x 的函数的是 ( )x 2 + y 2 = 2 x 2 + y 2 = 2 √ x − 1 + √ y − 1 = 1 x − 1 + y − 1 = 1 y = √ x − 2 + √ 1 − x y = x − 2 + 1 − x y = ± √ x y = ± x
参考答案
答案 C C 解析 x x 都有唯一函数值与之对应,A 、 B 、 D A 、 B 、 D C C x x 而言,有两个不同的值与之对应,不符合函数定义.故选:C C 答案 D D 解析 y = f ( x - 1 ) y = f ( x - 1 ) 中 x - 1 x - 1 的范围与函数 y = f ( x + 1 ) y = f ( x + 1 ) 中 x + 1 x + 1 的范围相同,且两个函数具有相同的对应关系 f f ,故函数 y = f ( x - 1 ) y = f ( x - 1 ) 与函数 y = f ( x + 1 ) y = f ( x + 1 ) 具有相同的值域,D D 答案 B B 解析 B B ,满足函数的定义, C C : y = √ x − 2 + √ 1 − x y = x − 2 + 1 − x ∅ ∅ ,故不满足函数的定义, A A ,D D x = 1 x = 1 时,y y 2 2 个值相对应,故不满足函数的定义,故选:B B
【题型2】函数的定义域
【典题 1】 y = 3 1 − √ 2 − x y = 3 1 − 2 − x y = √ 2 x − 4 + ( x − 2 ) 0 x − 3 y = 2 x − 4 + ( x − 2 ) 0 x − 3 解析 { 2 − x ≥ 0 1 − √ 2 − x ≠ 0 ⇔ { x ≤ 2 x ≠ 1 ⇔ x ≤ 2 { 2 − x ≥ 0 1 − 2 − x ≠ 0 ⇔ { x ≤ 2 x ≠ 1 ⇔ x ≤ 2 x ≠ 1 x ≠ 1 , y = 3 1 − √ 2 − x y = 3 1 − 2 − x 的定义域为 ( − ∞ , 1 ) ∪ ( 1 , 2 ] ( − ∞ , 1 ) ∪ ( 1 , 2 ] .⎧ ⎪ ⎨ ⎪ ⎩ 2 x − 4 ≥ 0 x − 2 ≠ 0 x − 3 ≠ 0 { 2 x − 4 ≥ 0 x − 2 ≠ 0 x − 3 ≠ 0 x ≥ 2 x ≥ 2 且 x ≠ 2 x ≠ 2 且 x ≠ 3 x ≠ 3 , y = √ 2 x − 4 + ( x − 2 ) 0 x − 3 y = 2 x − 4 + ( x − 2 ) 0 x − 3 的定义域为 ( 2 , 3 ) ∪ ( 3 , + ∞ ) ( 2 , 3 ) ∪ ( 3 , + ∞ ) .
【典题 2】 f ( x − 1 ) f ( x − 1 ) 定义域为 [ 0 , 3 ] [ 0 , 3 ] ,求 f ( 2 x − 1 ) f ( 2 x − 1 ) 的定义域. 解析 ∵ 0 ≤ x ≤ 3 ∵ 0 ≤ x ≤ 3 ∴ − 1 ≤ x − 1 ≤ 2 ∴ − 1 ≤ x − 1 ≤ 2 ∴ − 1 ≤ 2 x − 1 ≤ 2 ∴ − 1 ≤ 2 x − 1 ≤ 2 ∴ 0 ≤ x ≤ 3 2 ∴ 0 ≤ x ≤ 3 2 f ( 2 x − 1 ) f ( 2 x − 1 ) 的定义域是 [ 0 , 3 2 ] [ 0 , 3 2 ] 点拨 f ( x − 1 ) f ( x − 1 ) 定义域为 [ 0 , 3 ] [ 0 , 3 ] ,求 f ( 2 t − 1 ) f ( 2 t − 1 ) 的定义域.” 好理解多了,f ( x − 1 ) f ( x − 1 ) [ 0 , 3 ] [ 0 , 3 ] ” 得到的是 “0 ≤ x ≤ 3 0 ≤ x ≤ 3 f ( 2 t − 1 ) f ( 2 t − 1 ) 的定义域” 指的就是求 t t 的范围.x − 1 x − 1 2 t − 1 2 t − 1 − 1 ≤ x − 1 ≤ 2 ⇒ − 1 ≤ 2 t − 1 ≤ 2 − 1 ≤ x − 1 ≤ 2 ⇒ − 1 ≤ 2 t − 1 ≤ 2
巩固练习
1. 函数 y = √ x − 4 | x | − 5 y = x − 4 | x | − 5 – ––– – _ .
2. 函数 f ( x ) = √ 1 − x + 1 x f ( x ) = 1 − x + 1 x – ––– – _ .
3. 函数 f ( x ) = √ − x 2 + 4 x + 12 + 1 x − 4 f ( x ) = − x 2 + 4 x + 12 + 1 x − 4 – ––– – _ .
4. 已知函数 f ( x ) f ( x ) 的定义域为 ( − 1 , 0 ) ( − 1 , 0 ) ,则函数 f ( 2 x − 2 ) f ( 2 x − 2 ) 的定义域为 – ––– – _ .
参考答案
答案 { x | 4 ≤ x < 5 { x | 4 ≤ x < 5 x > 5 } x > 5 } 解析 y = √ x − 4 | x | − 5 y = x − 4 | x | − 5 x x 须满足: { x − 4 ≥ 0 | x | − 5 ≠ 0 { x − 4 ≥ 0 | x | − 5 ≠ 0 x ∈ { x | 4 ≤ x < 5 x ∈ { x | 4 ≤ x < 5 或 x > 5 } x > 5 } y = √ x − 4 | x | − 5 y = x − 4 | x | − 5 { x | 4 ≤ x < 5 { x | 4 ≤ x < 5 或 x > 5 } x > 5 } . 答案 ( − ∞ , 0 ) ∪ ( 0 , 1 ] ( − ∞ , 0 ) ∪ ( 0 , 1 ] 解析 { 1 − x ≥ 0 x ≠ 0 { 1 − x ≥ 0 x ≠ 0 { x ≤ 1 x ≠ 0 { x ≤ 1 x ≠ 0 x ≤ 1 x ≤ 1 且 x ≠ 0 x ≠ 0 , ( − ∞ , 0 ) ∪ ( 0 , 1 ] ( − ∞ , 0 ) ∪ ( 0 , 1 ] . 答案 [ − 2 , 4 ) ∪ ( 4 , 6 ] [ − 2 , 4 ) ∪ ( 4 , 6 ] 解析 { − x 2 + 4 x + 12 ≥ 0 x − 4 ≠ 0 { − x 2 + 4 x + 12 ≥ 0 x − 4 ≠ 0 − 2 ≤ x ≤ 6 − 2 ≤ x ≤ 6 且 x ≠ 4 x ≠ 4 ;∴ f ( x ) ∴ f ( x ) [ − 2 , 4 ) ∪ ( 4 , 6 ] [ − 2 , 4 ) ∪ ( 4 , 6 ] 答案 ( 1 2 , 1 ) ( 1 2 , 1 ) 解析 ∵ f ( x ) ∵ f ( x ) ( − 1 , 0 ) ( − 1 , 0 ) ,∴ ∴ − 1 < 2 x − 2 < 0 − 1 < 2 x − 2 < 0 ,得 1 2 < x < 1 1 2 < x < 1 ∴ ∴ f ( 2 x − 2 ) f ( 2 x − 2 ) 的定义域为 ( 1 2 , 1 ) ( 1 2 , 1 )
【题型3】函数的解析式
【典题 1】 f ( x ) = 3 x 2 − 5 x + 2 f ( x ) = 3 x 2 − 5 x + 2 . f ( 3 ) f ( 3 ) , f ( − √ 2 ) f ( − 2 ) f ( a ) f ( a ) f ( a + 1 ) f ( a + 1 ) f ( x ) = 0 f ( x ) = 0 ,求 x x . 解析 f ( 3 ) = 3 × 3 2 − 5 × 3 + 2 = 14 f ( 3 ) = 3 × 3 2 − 5 × 3 + 2 = 14 f ( − √ 2 ) = 3 × ( − √ 2 ) 2 − 5 × ( − √ 2 ) + 2 = 8 + 5 √ 2 f ( − 2 ) = 3 × ( − 2 ) 2 − 5 × ( − 2 ) + 2 = 8 + 5 2 f ( a ) = 3 a 2 − 5 a + 2 f ( a ) = 3 a 2 − 5 a + 2 f ( a + 1 ) = 3 ( a + 1 ) 2 − 5 ( a + 1 ) + 2 = 3 a 2 + a f ( a + 1 ) = 3 ( a + 1 ) 2 − 5 ( a + 1 ) + 2 = 3 a 2 + a ∵ f ( x ) = 0 ∵ f ( x ) = 0 ∴ 3 x 2 − 5 x + 2 = 0 ∴ 3 x 2 − 5 x + 2 = 0 x = 1 x = 1 或 x = 2 3 x = 2 3
【典题 2】 f ( x ) = x , g ( x ) = 3 √ x 3 f ( x ) = x , g ( x ) = x 3 3 f ( x ) = √ x 2 , g ( x ) = | x | f ( x ) = x 2 , g ( x ) = | x | f ( x ) = x 2 - 3 x , g ( t ) = t 2 - 3 t f ( x ) = x 2 - 3 x , g ( t ) = t 2 - 3 t f ( x ) = x 2 − 4 x − 2 , g ( x ) = x + 2 f ( x ) = x 2 − 4 x − 2 , g ( x ) = x + 2 解析 A , B , C A , B , C D D g ( x ) = x + 2 g ( x ) = x + 2 的定义域是 R R , f ( x ) = x 2 − 4 x − 2 = x + 2 f ( x ) = x 2 − 4 x − 2 = x + 2 { x | x ≠ 2 } { x | x ≠ 2 } ,两个函数的定义域不相同,不是同一函数.D D 点拨
巩固练习
1. 已知函数 f ( x ) = 1 1 + x f ( x ) = 1 1 + x g ( x ) = x 2 + 2 g ( x ) = x 2 + 2 f ( g ( 2 ) ) = f ( g ( 2 ) ) = – ––– – _ g ( f ( 2 ) ) = g ( f ( 2 ) ) = – ––– – _
2. 函数 f ( x ) = x 1 + x 2 f ( x ) = x 1 + x 2 x ∈ ( - ∞ , 0 ) ∪ ( 0 , + ∞ ) x ∈ ( - ∞ , 0 ) ∪ ( 0 , + ∞ ) f ( x ) = f ( 1 x ) f ( x ) = f ( 1 x ) − f ( x ) = f ( 1 x ) − f ( x ) = f ( 1 x ) 1 f ( x ) = f ( 1 x ) 1 f ( x ) = f ( 1 x ) − 1 f ( x ) = f ( 1 x ) − 1 f ( x ) = f ( 1 x )
3. 下面各组函数中是同一函数的是 ( )y = √ − 2 x 3 y = − 2 x 3 y = x √ − 2 x y = x − 2 x y = ( √ x ) 2 y = ( x ) 2 y = | x | y = | x | f ( x ) = x 2 − 2 x − 1 f ( x ) = x 2 − 2 x − 1 g ( t ) = t 2 − 2 t − 1 g ( t ) = t 2 − 2 t − 1 y = √ x + 1 √ x − 1 y = x + 1 x − 1 y = √ ( x + 1 ) ( x − 1 ) y = ( x + 1 ) ( x − 1 )
4. 在下列四组函数中,f ( x ) f ( x ) g ( x ) g ( x ) 表示同一函数的是 ( )y = 1 , y = x x y = 1 , y = x x y = √ x − 1 ⋅ √ x + 1 , y = √ x 2 − 1 y = x − 1 ⋅ x + 1 , y = x 2 − 1 y = x , y = 3 √ x 3 y = x , y = x 3 3 y = | x | , y = ( √ x ) 2 y = | x | , y = ( x ) 2
参考答案
答案 1 7 , 19 9 1 7 , 19 9 解析 g ( 2 ) = 2 2 + 2 = 6 g ( 2 ) = 2 2 + 2 = 6 f ( g ( 2 ) ) = f ( 6 ) = 1 1 + 6 = 1 7 f ( g ( 2 ) ) = f ( 6 ) = 1 1 + 6 = 1 7 f ( 2 ) = 1 1 + 2 = 1 3 f ( 2 ) = 1 1 + 2 = 1 3 g ( f ( 2 ) ) = g ( 1 3 ) = ( 1 3 ) 2 + 2 = 19 9 g ( f ( 2 ) ) = g ( 1 3 ) = ( 1 3 ) 2 + 2 = 19 9 答案 A A 解析 f ( x ) = x 1 + x 2 f ( x ) = x 1 + x 2 ∴ f ( 1 x ) = 1 x 1 + ( 1 x ) 2 = x 1 + x 2 ∴ f ( 1 x ) = 1 x 1 + ( 1 x ) 2 = x 1 + x 2 ∴ f ( x ) = f ( 1 x ) ∴ f ( x ) = f ( 1 x ) A A 答案 C C 解析 A A .函数的定义域为 { x | x ≤ 0 } { x | x ≤ 0 } , y = √ − 2 x 3 = − x √ − 2 x y = − 2 x 3 = − x − 2 x B B y = ( √ x ) 2 = x y = ( x ) 2 = x { x | x ≥ 0 } { x | x ≥ 0 } ,函数的定义域不相同,不是同一函数C C D D { x + 1 ≥ 0 x − 1 ≥ 0 { x + 1 ≥ 0 x − 1 ≥ 0 { x ≥ − 1 x ≥ 1 { x ≥ − 1 x ≥ 1 x ≥ 1 x ≥ 1 , ( x + 1 ) ( x - 1 ) ≥ 0 ( x + 1 ) ( x - 1 ) ≥ 0 得 x ≥ 1 x ≥ 1 或 x ≤ - 1 x ≤ - 1 ,两个函数的定义域不相同,不是同一函数,故选:C C 答案 C C 解析 y = 1 y = 1 的定义域为 R R ,而函数 y = x x y = x x { x | x ≠ 0 } { x | x ≠ 0 } , A A .y = √ x − 1 ⋅ √ x + 1 y = x − 1 ⋅ x + 1 { x | x > 1 } { x | x > 1 } ,y = √ x 2 − 1 y = x 2 − 1 { x | 1 < x { x | 1 < x 或 x < - 1 } x < - 1 } , B B . y = x y = x 与函数 y = 3 √ x 3 y = x 3 3 y = | x | y = | x | 的定义域为 R R ,而函数 y = ( √ x ) 2 y = ( x ) 2 { x | x ≥ 0 } { x | x ≥ 0 } ,这两个函数的定义域不同,故不是同一个函数,故排除 D D .故选:C C
【题型4】函数的值域
【典题 1】 f ( x ) = 1 1 + x 2 f ( x ) = 1 1 + x 2 f ( x ) = x 2 − 4 x + 2 , x ∈ [ 1 , 4 ] f ( x ) = x 2 − 4 x + 2 , x ∈ [ 1 , 4 ] y = 2 x − 1 x + 1 ( x > 0 ) y = 2 x − 1 x + 1 ( x > 0 ) f ( x ) = x − 2 √ 1 − x + 1 f ( x ) = x − 2 1 − x + 1 解析 x ∈ R x ∈ R ,得 1 + x 2 ≥ 1 1 + x 2 ≥ 1 ,所以得 0 < 1 1 + x 2 ≤ 1 0 < 1 1 + x 2 ≤ 1 ( 0 , 1 ] ( 0 , 1 ] . f ( x ) = x 2 − 4 x + 2 f ( x ) = x 2 − 4 x + 2 ,开口向上,对称轴 x = 2 x = 2 , f ( x ) = x 2 − 4 x + 2 , x ∈ [ 1 , 4 ] f ( x ) = x 2 − 4 x + 2 , x ∈ [ 1 , 4 ] 如下,∴ ∴ f ( x ) = x 2 − 4 x + 2 f ( x ) = x 2 − 4 x + 2 在区间 [ 1 , 4 ] [ 1 , 4 ] 上的值域为 [ − 2 , 2 ] [ − 2 , 2 ] .y = 2 ( x + 1 ) − 3 x + 1 = 2 − 3 x + 1 y = 2 ( x + 1 ) − 3 x + 1 = 2 − 3 x + 1 ∵ x > 0 ∵ x > 0 ∴ x + 1 > 1 ∴ x + 1 > 1 ∴ 0 < 1 x + 1 < 1 ∴ 0 < 1 x + 1 < 1 ∴ − 1 < 2 − 3 x + 1 < 2 ∴ − 1 < 2 − 3 x + 1 < 2 ∴ ∴ y = 2 x − 1 x + 1 ( x > 0 ) y = 2 x − 1 x + 1 ( x > 0 ) ( − 1 , 2 ) ( − 1 , 2 ) .√ 1 − x = t 1 − x = t t ≥ 0 t ≥ 0 t t 的取值范围) x = 1 − t 2 x = 1 − t 2 ,y = 1 − t 2 − 2 t + 1 = − t 2 − 2 t + 2 y = 1 − t 2 − 2 t + 1 = − t 2 − 2 t + 2 [ 0 , + ∞ ) [ 0 , + ∞ ) 上的值域是 y ≤ 2 y ≤ 2 ,f ( x ) = x − 2 √ 1 − x + 1 f ( x ) = x − 2 1 − x + 1 ( - ∞ , 2 ] ( - ∞ , 2 ] . 点拨 y == a ⋅ g ( x ) + b c ⋅ g ( x ) + d y == a ⋅ g ( x ) + b c ⋅ g ( x ) + d y = x 2 + 1 4 x 2 − 2 , y = 3 ⋅ 2 x + 4 2 x − 1 y = x 2 + 1 4 x 2 − 2 , y = 3 ⋅ 2 x + 4 2 x − 1
巩固练习
1. 设 a > 0 a > 0 ,若函数 y = 8 x y = 8 x x ∈ [ a , 2 a ] x ∈ [ a , 2 a ] 时,y y [ a 4 , 2 ] [ a 4 , 2 ] ,则 a a 的值为 ( )2 2 4 4 6 6 8 8
2. 函数 f ( x ) = x 2 − 4 x ( − 1 ⩽ x ⩽ a ) f ( x ) = x 2 − 4 x ( − 1 ⩽ x ⩽ a ) 的值域为 [ − 4 , 5 ] [ − 4 , 5 ] ,则实数 a a 的取值范围为 – ––– – _ .
3. 函数 f ( x ) = x − 1 x + 3 ( x ≥ 1 ) f ( x ) = x − 1 x + 3 ( x ≥ 1 ) – ––– – _ .
4. 求函数 y = 2 x + √ 1 − 2 x y = 2 x + 1 − 2 x
参考答案
答案 B B 解析 ∵ a > 0 ∵ a > 0 y = 8 x y = 8 x x ∈ [ a , 2 a ] x ∈ [ a , 2 a ] 时,y y [ a 4 , 2 ] [ a 4 , 2 ] ,∴ ⎧ ⎪
⎪ ⎨ ⎪
⎪ ⎩ 8 a = 2 8 2 a = a 4 ∴ { 8 a = 2 8 2 a = a 4 a = 4 a = 4 .故选:B B 答案 [ 2 , 5 ] [ 2 , 5 ] 解析 f ( x ) = ( x − 2 ) 2 − 4 f ( x ) = ( x − 2 ) 2 − 4 x = 2 x = 2 ,由 ( x − 2 ) 2 − 4 = 5 ( x − 2 ) 2 − 4 = 5 ,得 x = 5 x = 5 或 x = − 1 x = − 1 ,∵ f ( − 1 ) = 5 ∵ f ( − 1 ) = 5 f ( 2 ) = − 4 f ( 2 ) = − 4 ∴ 2 ≤ a ≤ 5 ∴ 2 ≤ a ≤ 5 a a 的取值范围是 [ 2 , 5 ] [ 2 , 5 ] . 答案 [ 0 , 1 ) [ 0 , 1 ) 解析 f ( x ) = x + 3 − 4 x + 3 = x + 3 x + 3 − 4 x + 3 = 1 − 4 x + 3 f ( x ) = x + 3 − 4 x + 3 = x + 3 x + 3 − 4 x + 3 = 1 − 4 x + 3 x ≥ 1 x ≥ 1 时, 0 < 4 x + 3 ≤ 1 0 < 4 x + 3 ≤ 1 0 ≤ 1 − 4 x + 3 < 1 0 ≤ 1 − 4 x + 3 < 1 [ 0 , 1 ) [ 0 , 1 ) . 答案 ( − ∞ , 5 4 ] ( − ∞ , 5 4 ] 解析 t = √ 1 − 2 x ( t ≥ 0 ) t = 1 − 2 x ( t ≥ 0 ) x = 1 − t 2 2 x = 1 − t 2 2 ∴ y = − t 2 + t + 1 = − ( t − 1 2 ) 2 + 5 4 ∴ y = − t 2 + t + 1 = − ( t − 1 2 ) 2 + 5 4 ∵ ∵ t = 1 2 t = 1 2 x = 3 8 x = 3 8 y max = 5 4 y max = 5 4 ∴ ∴ y = 2 x + √ 1 − 2 x y = 2 x + 1 − 2 x ( − ∞ , 5 4 ] ( − ∞ , 5 4 ]
分层练习
【A组---基础题】
1. 下列图形中,不能表示以 x x 为自变量的函数图象的是 ( )
2. 下列变量 x x 与 y y 的关系式中,不能构成 y y 是 x x 的函数关系的是 ( )x − y = 1 x − y = 1 x 2 − y = 1 x 2 − y = 1 x − 2 y 2 = 1 x − 2 y 2 = 1 √ x − 2 y = 1 x − 2 y = 1
3. 函数 f ( x ) = x + 1 , x ∈ { − 1 , 1 , 2 } f ( x ) = x + 1 , x ∈ { − 1 , 1 , 2 } 的值域是 ( )0 , 2 , 3 0 , 2 , 3 0 ≤ y ≤ 3 0 ≤ y ≤ 3 { 0 , 2 , 3 } { 0 , 2 , 3 } [ 0 , 3 ] [ 0 , 3 ]
4. 下列各组函数中,表示同一函数的是 ( )f ( x ) = x 2 , g ( x ) = x 3 f ( x ) = x 2 , g ( x ) = x 3 f ( x ) = √ x 2 , g ( x ) = ( √ x ) 2 f ( x ) = x 2 , g ( x ) = ( x ) 2 f ( x ) = x 2 x , g ( x ) = x f ( x ) = x 2 x , g ( x ) = x f ( x ) = | x | f ( x ) = | x | g ( x ) = { x , x ≥ 0 − x , x < 0 g ( x ) = { x , x ≥ 0 − x , x < 0
5. 函数 f ( x ) = 2 x + √ 4 − x 2 x f ( x ) = 2 x + 4 − x 2 x – ––– – _ .
6. 若函数 y = f ( x ) y = f ( x ) 的定义域是 [ − 2 , 3 ] [ − 2 , 3 ] ,则函数 y = f ( x − 1 ) y = f ( x − 1 ) 的定义域是 – ––– – _ .
7. 已知函数 f ( x ) = 1 x 2 + 2 f ( x ) = 1 x 2 + 2 ,则 f ( x ) f ( x ) 的值域是 – ––– – _ .
8. 若函数 y = x 2 − 4 x − 4 y = x 2 − 4 x − 4 的定义域为 [ 0 , m ] [ 0 , m ] ,值域为 [ − 8 , − 4 ] [ − 8 , − 4 ] ,则 m m 的取值范围是 – ––– – _ .
9. 若函数 y = 2 x + 3 x + 2 y = 2 x + 3 x + 2 – ––– – _ .
10. 函数 y = x + √ 2 − x y = x + 2 − x 的值域为 – ––– – _ .
参考答案
答案 B B 解析 B B x > 0 x > 0 时,y y x x 对应,不满足函数 y y 的唯一性,A , C , D A , C , D B B
答案 C C 解析 A A x − y = 1 x − y = 1 得 y = x − 1 y = x − 1 是函数关系.B B x 2 − y = 1 x 2 − y = 1 y = x 2 − 1 y = x 2 − 1 是函数关系,C C x − 2 y 2 = 1 x − 2 y 2 = 1 ,得 y 2 = 1 2 ( x − 1 ) y 2 = 1 2 ( x − 1 ) y y 值不唯一,不是函数关系,D D √ x − 2 y = 1 x − 2 y = 1 y = 1 2 ( √ x − 1 ) y = 1 2 ( x − 1 ) C C
答案 C C 解析 ∵ f ( x ) = x + 1 , x ∈ { − 1 , 1 , 2 } ∵ f ( x ) = x + 1 , x ∈ { − 1 , 1 , 2 } ∴ ∴ x = − 1 x = − 1 时,f ( − 1 ) = 0 f ( − 1 ) = 0 x = 1 x = 1 时,f ( 1 ) = 2 f ( 1 ) = 2 x = 2 x = 2 时,f ( 2 ) = 3 f ( 2 ) = 3 ∴ ∴ f ( x ) = x + 1 , x ∈ { − 1 , 1 , 2 } f ( x ) = x + 1 , x ∈ { − 1 , 1 , 2 } 的值域是 { 0 , 2 , 3 } { 0 , 2 , 3 } ,故选:C C
答案 D D 解析 A A f ( x ) = x 2 , g ( x ) = x 3 f ( x ) = x 2 , g ( x ) = x 3 B B f ( x ) = √ x 2 , g ( x ) = ( √ x ) 2 f ( x ) = x 2 , g ( x ) = ( x ) 2 C C f ( x ) = x 2 x f ( x ) = x 2 x { x | x ≠ 0 } { x | x ≠ 0 } ,g ( x ) = x g ( x ) = x R R ,定义域不同,不是同一函数;D D f ( x ) = | x | = { x x ≥ 0 − x x < 0 f ( x ) = | x | = { x x ≥ 0 − x x < 0 g ( x ) = { x , x ≥ 0 − x , x < 0 g ( x ) = { x , x ≥ 0 − x , x < 0 D D
答案 [ − 2 , 0 ) ∪ ( 0 , 2 ] [ − 2 , 0 ) ∪ ( 0 , 2 ] 解析 f ( x ) f ( x ) 有意义,则 { 4 − x 2 ≥ 0 x ≠ 0 { 4 − x 2 ≥ 0 x ≠ 0 − 2 ≤ x ≤ 2 − 2 ≤ x ≤ 2 ,且 x ≠ 0 x ≠ 0 ;∴ f ( x ) ∴ f ( x ) [ − 2 , 0 ) ∪ ( 0 , 2 ] [ − 2 , 0 ) ∪ ( 0 , 2 ] .
答案 [ − 1 , 4 ] [ − 1 , 4 ] 解析 y = f ( x ) y = f ( x ) 的定义域是 [ − 2 , 3 ] [ − 2 , 3 ] ,∴ ∴ − 2 ≤ x − 1 ≤ 3 − 2 ≤ x − 1 ≤ 3 ,解得 − 1 ≤ x ≤ 4 − 1 ≤ x ≤ 4 .∴ ∴ y = f ( x − 1 ) y = f ( x − 1 ) 的定义域是 [ 1 , 4 ] [ 1 , 4 ] .
答案 ( 0 , 1 2 ] ( 0 , 1 2 ] 解析 ∵ x 2 + 2 ≥ 2 ∵ x 2 + 2 ≥ 2 ∴ 0 < 1 x 2 + 2 ≤ 1 2 ∴ 0 < 1 x 2 + 2 ≤ 1 2 ∴ f ( x ) ∴ f ( x ) ( 0 , 1 2 ] ( 0 , 1 2 ]
答案 [ 2 , 4 ] [ 2 , 4 ] 解析 y = x 2 − 4 x − 4 y = x 2 − 4 x − 4 的图象是开口向上,且以直线 x = 2 x = 2 为对称轴的抛物线∴ f ( 0 ) = f ( 4 ) = − 4 ∴ f ( 0 ) = f ( 4 ) = − 4 f ( 2 ) = − 8 f ( 2 ) = − 8 ∵ ∵ y = x 2 − 4 x − 4 y = x 2 − 4 x − 4 的定义域为 [ 0 , m ] [ 0 , m ] ,值域为 [ − 8 , − 4 ] [ − 8 , − 4 ] ,∴ 2 ≤ m ≤ 4 ∴ 2 ≤ m ≤ 4 m m 的取值范围是 [ 2 , 4 ] [ 2 , 4 ] .
答案 ( - ∞ , 2 ) ∪ ( 2 , + ∞ ) ( - ∞ , 2 ) ∪ ( 2 , + ∞ ) 解析 ∵ y = 2 − 1 x + 2 ∵ y = 2 − 1 x + 2 ∴ y ≠ 2 ∴ y ≠ 2 ∴ ∴ ( - ∞ , 2 ) ∪ ( 2 , + ∞ ) ( - ∞ , 2 ) ∪ ( 2 , + ∞ )
答案 ( − ∞ , 9 4 ] ( − ∞ , 9 4 ] 解析 y = x + √ 2 − x y = x + 2 − x t = √ 2 − x t = 2 − x t t 的值域为 [ 0 , + ∞ ) [ 0 , + ∞ ) ,可得:x = 2 - t 2 x = 2 - t 2 y = x + √ 2 − x y = x + 2 − x f ( t ) = 2 − t 2 + t f ( t ) = 2 − t 2 + t ,开口向下,对称轴 t = 1 2 t = 1 2 ∵ t ≥ 0 ∵ t ≥ 0 ∴ ∴ t = 1 2 t = 1 2 f ( t ) f ( t ) 取得最大值为 f ( 1 2 ) max = 9 4 f ( 1 2 ) max = 9 4 y = x + √ 2 − x y = x + 2 − x 9 4 9 4 ∴ ∴ y = x + √ 2 − x y = x + 2 − x ( − ∞ , 9 4 ] ( − ∞ , 9 4 ]
【B组---提高题】
1. 存在函数 f ( x ) f ( x ) 满足:对任意 x ∈ R x ∈ R 都有 ( )f ( | x | ) = x f ( | x | ) = x f ( | x | ) = x 2 + 2 x f ( | x | ) = x 2 + 2 x f ( | x + 1 | ) = x f ( | x + 1 | ) = x f ( | x + 1 | ) = x 2 + 2 x f ( | x + 1 | ) = x 2 + 2 x
2. 函数 y = √ 2 + x 1 − x + √ x 2 − x − 2 y = 2 + x 1 − x + x 2 − x − 2 [ − 2 , − 1 ] [ − 2 , − 1 ] [ − 2 , 1 ] [ − 2 , 1 ] [ 2 , + ∞ ) [ 2 , + ∞ ) ( − ∞ , 1 ) ∪ ( 1 , + ∞ ) ( − ∞ , 1 ) ∪ ( 1 , + ∞ )
3. 已知 f ( x + 1 ) = √ 1 − x 2 f ( x + 1 ) = 1 − x 2 f ( 2 x − 1 ) f ( 2 x − 1 ) 的定义域为 – ––– – _ .
4. 对于函数 f ( x ) = √ a x 2 + b x f ( x ) = a x 2 + b x b b ,使得 f ( x ) f ( x ) 的定义域和值域相同,则非零实数 a a 的值为 – ––– – _ .
5. 已知函数 f ( x ) = 4 x − 1 2 x − 1 f ( x ) = 4 x − 1 2 x − 1 f ( 1 2015 ) + f ( 2 2015 ) + ⋯ + f ( 2013 2015 ) + f ( 2014 2015 ) = f ( 1 2015 ) + f ( 2 2015 ) + ⋯ + f ( 2013 2015 ) + f ( 2014 2015 ) = – ––– – _
6. 已知函数 f ( x ) = 4 x − 6 x − 1 f ( x ) = 4 x − 6 x − 1 [ 2 , b ] ( b > 2 ) [ 2 , b ] ( b > 2 ) ,则实数 b b 的值为 – ––– – _ .
7. 求函数 y = 2 x 2 − x + 1 2 x − 1 ( x > 1 2 ) y = 2 x 2 − x + 1 2 x − 1 ( x > 1 2 )
8. 求函数 f ( x ) = x 2 + 4 x + 1 x 2 + 1 f ( x ) = x 2 + 4 x + 1 x 2 + 1
9. 求函数 f ( x ) = ( x 2 − 2 x − 3 ) ( x 2 − 2 x − 5 ) f ( x ) = ( x 2 − 2 x − 3 ) ( x 2 − 2 x − 5 )
参考答案
答案 D D 解析 A A 中,取 x = 1 x = 1 ,则 f ( 1 ) = 1 f ( 1 ) = 1 ,取 x = - 1 x = - 1 ,则 f ( 1 ) = - 1 f ( 1 ) = - 1 ,不成立; B B 中,令 | x | = t | x | = t ,t ≥ 0 t ≥ 0 x = ± t x = ± t x = 1 x = 1 ,则 f ( 1 ) = 3 f ( 1 ) = 3 ,取 x = - 1 x = - 1 ,则 f ( 1 ) = - 1 f ( 1 ) = - 1 ,不成立; C C 中,令 | x + 1 | = t | x + 1 | = t ,t ≥ 0 t ≥ 0 x 2 + 2 x = t 2 - 1 x 2 + 2 x = t 2 - 1 ∴ f ( t ) = t 2 - 1 ∴ f ( t ) = t 2 - 1 f ( x ) = x 2 - 1 f ( x ) = x 2 - 1 ,故 C C 不成立,D D D D 答案 A A 解析 ⎧ ⎨ ⎩ 2 + x 1 − x ≥ 0 ( 1 ) x 2 − x − 2 ≥ 0 ( 2 ) { 2 + x 1 − x ≥ 0 ( 1 ) x 2 − x − 2 ≥ 0 ( 2 ) - 2 ≤ x < 1 - 2 ≤ x < 1 x ≤ - 1 x ≤ - 1 x ≥ 2 x ≥ 2 .∴ ∴ y = √ 2 + x 1 − x + √ x 2 − x − 2 y = 2 + x 1 − x + x 2 − x − 2 [ - 2 , - 1 ] [ - 2 , - 1 ] .A A 答案 [ 1 2 , 3 2 ] [ 1 2 , 3 2 ] 解析 f ( x + 1 ) = √ 1 − x 2 f ( x + 1 ) = 1 − x 2 1 − x 2 ≥ 0 1 − x 2 ≥ 0 ,即 − 1 ≤ x ≤ 1 − 1 ≤ x ≤ 1 ,从而 0 ≤ x + 1 ≤ 2 0 ≤ x + 1 ≤ 2 , f ( x ) f ( x ) 的定义域为 [ 0 , 2 ] [ 0 , 2 ] , f ( 2 x − 1 ) f ( 2 x − 1 ) 的应满足 0 ≤ 2 x − 1 ≤ 2 0 ≤ 2 x − 1 ≤ 2 ,由此 1 2 ≤ x ≤ 3 2 1 2 ≤ x ≤ 3 2 答案 − 4 − 4 解析 f ( x ) = √ a x 2 + b x f ( x ) = a x 2 + b x a > 0 a > 0 ,由于 a x 2 + b x ≥ 0 a x 2 + b x ≥ 0 ,即 x ( a x + b ) ≥ 0 x ( a x + b ) ≥ 0 ,∴ ∴ b b ,f ( x ) f ( x ) D = ( − ∞ , − b a ] ∪ [ 0 , + ∞ ) D = ( − ∞ , − b a ] ∪ [ 0 , + ∞ ) f ( x ) f ( x ) 的值域 A ⊆ [ 0 , + ∞ ) A ⊆ [ 0 , + ∞ ) ,故 D ≠ A D ≠ A ,不合要求. a < 0 a < 0 ,对于正数 b b ,f ( x ) f ( x ) D = [ 0 , − b a ] D = [ 0 , − b a ] f ( x ) max = f ( − b 2 a ) = √ a × ( b 2 a ) 2 + b × ( − b 2 a ) = √ − b 2 4 a = b 2 √ 1 − a f ( x ) max = f ( − b 2 a ) = a × ( b 2 a ) 2 + b × ( − b 2 a ) = − b 2 4 a = b 2 1 − a A = [ 0 , b 2 √ 1 − a ] A = [ 0 , b 2 1 − a ] − b a = b 2 √ 1 − a − b a = b 2 1 − a b > 0 b > 0 ,解得:a = − 4 a = − 4 答案 4028 4028 解析 f ( x ) = 4 x − 1 2 x − 1 = 2 ( 2 x − 1 ) + 1 2 x − 1 = 2 + 1 2 x − 1 f ( x ) = 4 x − 1 2 x − 1 = 2 ( 2 x − 1 ) + 1 2 x − 1 = 2 + 1 2 x − 1 , f ( 1 − x ) = 2 + 1 2 ( 1 − x ) − 1 = 2 − 1 2 x − 1 f ( 1 − x ) = 2 + 1 2 ( 1 − x ) − 1 = 2 − 1 2 x − 1 f ( x ) + f ( 1 − x ) = 4 f ( x ) + f ( 1 − x ) = 4 f ( 1 2015 ) + f ( 2014 2015 ) = 4 ⋯ f ( 1007 2015 ) + f ( 1008 2015 ) = 4 f ( 1 2015 ) + f ( 2014 2015 ) = 4 ⋯ f ( 1007 2015 ) + f ( 1008 2015 ) = 4 f ( 1 2015 ) + f ( 2 2015 ) + ⋯ + f ( 2013 2015 ) + f ( 2014 2015 ) = 4 × 1007 = 4028 f ( 1 2015 ) + f ( 2 2015 ) + ⋯ + f ( 2013 2015 ) + f ( 2014 2015 ) = 4 × 1007 = 4028 答案 3 3 解析 f ( x ) = 4 x − 6 x − 1 = 4 ( x − 1 ) − 2 x − 1 = − 2 x − 1 + 4 f ( x ) = 4 x − 6 x − 1 = 4 ( x − 1 ) − 2 x − 1 = − 2 x − 1 + 4 f ( x ) = 4 x − 6 x − 1 f ( x ) = 4 x − 6 x − 1 [ 2 , b ] [ 2 , b ] 上为增函数,f ( x ) = 4 x − 6 x − 1 f ( x ) = 4 x − 6 x − 1 [ 2 , b ] ( b > 2 ) [ 2 , b ] ( b > 2 ) ,∴ f ( b ) = 4 b − 6 b − 1 = b ∴ f ( b ) = 4 b − 6 b − 1 = b b = 3 b = 3 3 3 答案 [ 1 2 + √ 2 , + ∞ ) [ 1 2 + 2 , + ∞ ) 解析 y = 2 x 2 − x + 1 2 x − 1 = x ( 2 x − 1 ) + 1 2 x − 1 = x + 1 2 x − 1 = x − 1 2 + 1 2 x − 1 + 1 2 y = 2 x 2 − x + 1 2 x − 1 = x ( 2 x − 1 ) + 1 2 x − 1 = x + 1 2 x − 1 = x − 1 2 + 1 2 x − 1 + 1 2 ∵ x > 1 2 ∵ x > 1 2 ∴ x − 1 2 > 0 ∴ x − 1 2 > 0 ∴ x − 1 2 + 1 2 x − 1 2 ≥ 2
⎷ ( x − 1 2 ) × 1 2 x − 1 2 = √ 2 ∴ x − 1 2 + 1 2 x − 1 2 ≥ 2 ( x − 1 2 ) × 1 2 x − 1 2 = 2 x − 1 2 = 1 2 x − 1 2 x − 1 2 = 1 2 x − 1 2 x = 1 + √ 2 2 x = 1 + 2 2 时等号成立, ∴ y ≥ √ 2 + 1 2 ∴ y ≥ 2 + 1 2 [ 1 2 + √ 2 , + ∞ ) [ 1 2 + 2 , + ∞ ) 答案 [ - 1 , 3 ] [ - 1 , 3 ] 解析 ∵ f ( x ) = x 2 + 4 x + 1 x 2 + 1 = x 2 + 1 x 2 + 1 + 4 x x 2 + 1 = 1 + 4 x x 2 + 1 ∵ f ( x ) = x 2 + 4 x + 1 x 2 + 1 = x 2 + 1 x 2 + 1 + 4 x x 2 + 1 = 1 + 4 x x 2 + 1 ∴ ∴ x = 0 x = 0 时,f ( x ) = 1 f ( x ) = 1 x > 0 x > 0 时, 4 x x 2 + 1 = 4 x + 1 x ≤ 4 2 √ x ⋅ 1 x = 2 4 x x 2 + 1 = 4 x + 1 x ≤ 4 2 x ⋅ 1 x = 2 x = 1 x = 1 时 “= = x < 0 x < 0 时,4 x x 2 + 1 = 4 x + 1 x = 4 − ( − x + 1 − x ) ≥ 4 − 2 √ ( − x ) ⋅ 1 − x = − 2 4 x x 2 + 1 = 4 x + 1 x = 4 − ( − x + 1 − x ) ≥ 4 − 2 ( − x ) ⋅ 1 − x = − 2 x = - 1 x = - 1 时取 “= = ∴ ∴ f ( x ) = x 2 + 4 x + 1 x 2 + 1 f ( x ) = x 2 + 4 x + 1 x 2 + 1 的值域为 [ - 1 , 3 ] [ - 1 , 3 ] . 答案 [ - 1 , + ∞ ) [ - 1 , + ∞ ) 解析 y = [ ( x − 1 ) 2 − 4 ] [ ( x − 1 ) 2 − 6 ] y = [ ( x − 1 ) 2 − 4 ] [ ( x − 1 ) 2 − 6 ] t = ( x − 1 ) 2 ≥ 0 t = ( x − 1 ) 2 ≥ 0 y = t 2 − 10 t + 24 = ( t − 5 ) 2 − 1 ≥ − 1 y = t 2 − 10 t + 24 = ( t − 5 ) 2 − 1 ≥ − 1 t = 5 t = 5 时取等号, y ≥ - 1 y ≥ - 1 .故函数的值域为 [ - 1 , + ∞ ) [ - 1 , + ∞ ) .
【C组---拓展题】
1. 函数 y = 1 a x 2 + 4 a x + 3 y = 1 a x 2 + 4 a x + 3 ( − ∞ , + ∞ ) ( − ∞ , + ∞ ) ,则实数 a a 的取值范围是 ( )( - ∞ , + ∞ ) ( - ∞ , + ∞ ) [ 0 , 3 4 ) [ 0 , 3 4 ) ( 3 4 , + ∞ ) ( 3 4 , + ∞ ) [ 0 , 3 4 ] [ 0 , 3 4 ]
2.(多选) 已知函数 f ( x ) = x 4 + 2 x 2 + a x 2 + 1 ( x ∈ R ) f ( x ) = x 4 + 2 x 2 + a x 2 + 1 ( x ∈ R ) [ m , + ∞ ) [ m , + ∞ ) ,则实数 a a 与实数 m m 的取值可能为 ( )a = 0 , m = 0 a = 0 , m = 0 a = 1 , m = 1 a = 1 , m = 1 a = 3 , m = 3 a = 3 , m = 3 a = √ 2 , m = √ 2 a = 2 , m = 2
3. 已知函数 f ( x ) = x 2 1 + x 2 f ( x ) = x 2 1 + x 2 f ( 2 ) f ( 2 ) 与 f ( 1 2 ) f ( 1 2 ) f ( 3 ) f ( 3 ) f ( 1 3 ) f ( 1 3 ) f ( x ) f ( x ) 与 ( 1 x ) ( 1 x ) f ( 1 ) + f ( 2 ) + f ( 3 ) + ⋯ + f ( 2013 ) + f ( 1 2 ) + f ( 1 3 ) + ⋯ + f ( 1 2013 ) f ( 1 ) + f ( 2 ) + f ( 3 ) + ⋯ + f ( 2013 ) + f ( 1 2 ) + f ( 1 3 ) + ⋯ + f ( 1 2013 )
参考答案
答案 B B 解析 f ( x ) f ( x ) ( - ∞ , + ∞ ) ( - ∞ , + ∞ ) ;∴ ∴ a x 2 + 4 a x + 3 > 0 a x 2 + 4 a x + 3 > 0 恒成立,或 a x 2 + 4 a x + 3 < 0 a x 2 + 4 a x + 3 < 0 恒成立;a = 0 a = 0 3 > 0 3 > 0 a ≠ 0 a ≠ 0 △= 16 a 2 − 12 a < 0 △= 16 a 2 − 12 a < 0 0 < a < 3 4 0 < a < 3 4 a a 的取值范围为 [ 0 , 3 4 ) [ 0 , 3 4 ) B B 答案 A B D A B D 解析 f ( x ) = x 2 ( x 2 + 1 ) + x 2 + 1 + a − 1 x 2 + 1 = x 2 + 1 + a − 1 x 2 + 1 f ( x ) = x 2 ( x 2 + 1 ) + x 2 + 1 + a − 1 x 2 + 1 = x 2 + 1 + a − 1 x 2 + 1 a - 1 = 0 a - 1 = 0 a = 1 a = 1 时,f ( x ) = x 2 + 1 ≥ 1 f ( x ) = x 2 + 1 ≥ 1 f ( x ) f ( x ) 的值域为 [ m , + ∞ ) [ m , + ∞ ) ,∴ m = 1 ∴ m = 1 0 < a - 1 ≤ 1 0 < a - 1 ≤ 1 1 < a ≤ 2 1 < a ≤ 2 时,函数 y = x + a − 1 x y = x + a − 1 x [ 1 , + ∞ ) [ 1 , + ∞ ) 上单调递增,∴ f ( x ) = x 2 + 1 + a − 1 x 2 + 1 ≥ 1 + a − 1 = a ∴ f ( x ) = x 2 + 1 + a − 1 x 2 + 1 ≥ 1 + a − 1 = a f ( x ) f ( x ) 的值域为 [ m , + ∞ ) [ m , + ∞ ) ,∴ m = a ∴ m = a ∴ a = √ 2 , m = √ 2 ∴ a = 2 , m = 2 a − 1 > 1 a − 1 > 1 a > 2 a > 2 时,y = x + a − 1 x y = x + a − 1 x 在 [ 1 , a - 1 ) 在 [ 1 , a - 1 ) ( a - 1 , + ∞ ) ( a - 1 , + ∞ ) 上单调递增,∴ f ( x ) = x 2 + 1 + a − 1 x 2 + 1 ≥ f ( a − 1 ) = a 2 − 2 a + 2 + a − 1 a 2 − 2 a + 2 ∴ f ( x ) = x 2 + 1 + a − 1 x 2 + 1 ≥ f ( a − 1 ) = a 2 − 2 a + 2 + a − 1 a 2 − 2 a + 2 ∴ m = a 2 − 2 a + 2 + a − 1 a 2 − 2 a + 2 ∴ m = a 2 − 2 a + 2 + a − 1 a 2 − 2 a + 2 ∴ a = 3 ∴ a = 3 m = 27 5 m = 27 5 a = 3 , m = 3 a = 3 , m = 3 错误;y = x − 1 x y = x − 1 x [ 1 , + ∞ ) [ 1 , + ∞ ) 上单调递增, f ( x ) = x 2 + 1 − 1 x 2 + 1 ≥ 0 f ( x ) = x 2 + 1 − 1 x 2 + 1 ≥ 0 ∴ m = 0 ∴ m = 0 A B D A B D 答案 f ( 2 ) = 4 5 , f ( 1 2 ) = 1 5 , f ( 3 ) = 9 10 , f ( 1 3 ) = 1 10 f ( 2 ) = 4 5 , f ( 1 2 ) = 1 5 , f ( 3 ) = 9 10 , f ( 1 3 ) = 1 10 f ( x ) + f ( 1 x ) = 1 f ( x ) + f ( 1 x ) = 1 4025 2 4025 2 解析 ∵ f ( x ) = x 2 1 + x 2 ∵ f ( x ) = x 2 1 + x 2 ∴ f ( 2 ) = 2 2 1 + 2 2 = 4 5 ∴ f ( 2 ) = 2 2 1 + 2 2 = 4 5 f ( 1 2 ) = ( 1 2 ) 2 1 + ( 1 2 ) 2 = 1 5 f ( 1 2 ) = ( 1 2 ) 2 1 + ( 1 2 ) 2 = 1 5 f ( 3 ) = 3 2 1 + 3 2 = 9 10 f ( 3 ) = 3 2 1 + 3 2 = 9 10 f ( 1 3 ) = ( 1 3 ) 2 1 + ( 1 3 ) 2 = 1 10 f ( 1 3 ) = ( 1 3 ) 2 1 + ( 1 3 ) 2 = 1 10 f ( x ) + f ( 1 x ) = 1 f ( x ) + f ( 1 x ) = 1 f ( x ) + f ( 1 x ) = x 2 1 + x 2 + ( 1 x ) 2 1 + ( 1 x ) 2 = x 2 1 + x 2 + 1 1 + x 2 = 1 f ( x ) + f ( 1 x ) = x 2 1 + x 2 + ( 1 x ) 2 1 + ( 1 x ) 2 = x 2 1 + x 2 + 1 1 + x 2 = 1 f ( 1 ) = 1 2 1 + 1 2 = 1 2 f ( 1 ) = 1 2 1 + 1 2 = 1 2 f ( 2 ) + f ( 1 2 ) = 1 , f ( 3 ) + f ( 1 3 ) = 1 , … , f ( 2013 ) + f ( 1 2013 ) = 1 f ( 2 ) + f ( 1 2 ) = 1 , f ( 3 ) + f ( 1 3 ) = 1 , … , f ( 2013 ) + f ( 1 2013 ) = 1 ∴ ∴ = 1 2 + 1 + 1 + 1 + ⋯ + 1 2012 个 = 2012 + 1 2 = 4025 2 = 1 2 + 1 + 1 + 1 + ⋯ + 1 ⏟ 2012 个 = 2012 + 1 2 = 4025 2

 B.
B. C.
C. D.
D.

 B.
B.  C.
C.  D.
D.





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· C#/.NET/.NET Core技术前沿周刊 | 第 29 期(2025年3.1-3.9)
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异