高一函数专题 抽象函数
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【高分突破系列】高一数学上学期同步知识点剖析精品讲义与分层练习]
(https://www.zxxk.com/docpack/2783085.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步拔高练习,难度3颗星!
模块导图

知识剖析
概念
我们把没有给出具体解析式的函数称为抽象函数,题目中往往只给出函数的特殊条件或特征.
常见抽象函数模型
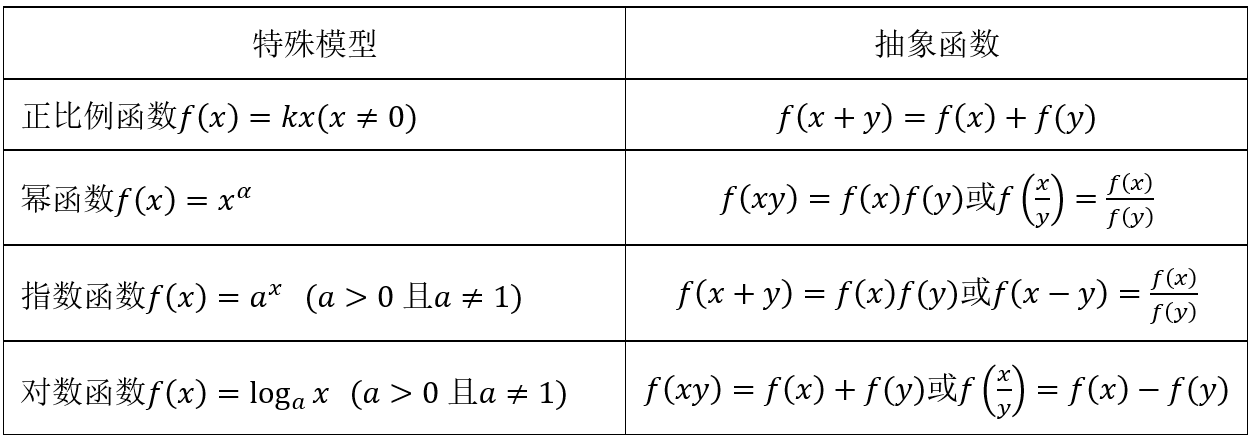
经典例题
【题型一】求值问题
【典题1】已知函数\(f(x)\)是定义在\((0 ,+∞)\)上的函数,且对任意\(x ,y∈(0 ,+∞)\),都有\(f(xy)=f(x)+f(y)\),\(f(2)=1\),求\(f(4) ,f(8)\).
【解析】\(∵\)对任意\(x,y∈(0 ,+∞)\),都有\(f(xy)=f(x)+f(y)\),\(f(2)=1\),
\(∴f(4)=f(2×2)=f(2)+f(2)=2\),\(f(8)=f(2×4)=f(2)+f(4)=3\).
【点拨】
① 对于抽象函数求值问题,可大胆取特殊值求解;
② 抽象函数\(f(xy)=f(x)+f(y)\)是对数函数\(f(x)=log_ax\)型,由\(f(2)=1\)可知\(f(x)=log_2x\),则易得\(f(4)=2\),\(f(8)=3\),作选填题可取.又如\(f(x+y)=f(x)f(y)\)且\(f(1)=2\),求\(f(3)\);由\(f(x+y)=f(x)f(y)\)可令\(f(x)=a^{x}\),又因\(f(1)=2\),得\(f(x)=2^{x}\),故易得\(f(3)=8\).
故要对常见抽象函数对应的函数模型比较熟悉.
【典题2】对任意实数\(x ,y\),均满足\(f(x+y^2 )=f(x)+2[f(y)]^2\)且\(f(1)≠0\),则\(f(2001)=\)_________.
【解析】令\(x=y=0\),得\(f(0)=0\),
令\(x=n\) ,\(y=1\),得\(f(n+1)=f(n)+2[f(1)]^2\)
令\(n=1\),得\(f(1)=f(0)+2 f[(1)]^{2}=2 f[(1)]^{2}\),
\(\therefore f(1)=\dfrac{1}{2}\),
\(\therefore f(n+1)-f(n)=\dfrac{1}{2}\),
\(\therefore f(n)=\dfrac{n}{2}\),即\(f(2001)=\dfrac{2001}{2}\).
【点拨】
① 常常需要赋予一些特殊值(如取\(x=0\)等)或特殊关系(如取\(y=x\),\(y=-x\)等),要观察等式方程的特点寻找目标,也要大胆下笔多些尝试找些规律;
② 比如本题中所求的\(f(2001)\)中自变量的取值\(2001\)较大,往往要从周期性或者函数的解析式的方向入手.
【题型二】单调性问题
【典题1】设函数\(y=f(x)\)是定义在\(R^+\)上的函数,并且满足下面三个条件
①对任意正数\(x ,y\),都有\(f(xy)=f(x)+f(y)\);②当\(x>1\)时,\(f(x)<0\);③\(f(3)=-1\).
(1)求\(f(1)\) ,\(f\left(\dfrac{1}{9}\right)\)的值;
(2)证明\(f(x)\)在\(R^+\)是减函数;
(3)如果不等式\(f(x)+f(2-x)<2\)成立,求\(x\)的取值范围.
【解析】(1)令\(x=y=1\),\(∴f(1)=f(1)+f(1)\),
\(∴f(1)=0\),
令\(x=y=3\),\(∴f(9)=f(3)+f(3)=-1-1=-2\),
且\(f(9)+f\left(\dfrac{1}{9}\right)=f(1)=0\) ,得\(f\left(\dfrac{1}{9}\right)=2\).
(2) \({\color{Red}{(利用函数单调性的定义证明) }}\)
取\(x_2>x_1>0\),则\(\dfrac{x_{2}}{x_{1}}>1\)
\(∴\)由②得\(f\left(\dfrac{x_{2}}{x_{1}}\right)<0\)
\(∵f(xy)=f(x)+f(y)\)
\(\therefore f\left(x_{2}\right)-f\left(x_{1}\right)=f\left(\dfrac{x_{2}}{x_{1}}\right)<0\)
\(∴f(x)\)在\(R^+\)上为减函数.
(3)由条件①得\(f[x(2-x)]<2\) , \({\color{Red}{ (凑项f(m)=2,再利用单调性求解) }}\)
由\(f\left(\dfrac{1}{9}\right)=2\)得\(f[x(2-x)]<f\left(\dfrac{1}{9}\right)\),
又\(∵f(x)\)在\(R^+\)上为减函数,\(\therefore x(2-x)>\dfrac{1}{9}\)
又\(∵x>0\),\(2-x>0\), \({\color{Red}{(注意函数定义域) }}\)
解得\(x\)的范围是\(\left(1-\dfrac{2 \sqrt{2}}{3}, 1+\dfrac{2 \sqrt{2}}{3}\right)\).
【点拨】
① 抽象函数的单调性常用单调性定义证明
(1) 任取\(x_1\) ,\(x_2∈D\),且\(x_1<x_2\);
(2) 作差\(f(x_1)-f(x_2)\)(根据题目给出的抽象函数特征来“"构造”" 出\(f(x_1)-f(x_2)\))
此步有时也会用作商法:判断\(\dfrac{f\left(x_{1}\right)}{f\left(x_{2}\right)}\)与\(1\)的大小;
(3) 变形;
(4) 定号(即判断差\(f(x_1 )-f(x_2)\)的正负);
(5) 下结论(指出函数f(x)在给定的区间\(D\)上的单调性).
② 在解不等式时,往往需要利用函数的单调性求解.
③ 抽象函数\(f(xy)=f(x)+f(y)\)符合对数函数\(f(x)=log_ax\)型,由\(f(3)=-1\)可知\(f(x)=\log _{\frac{1}{3}} x\),作选填题可用.
【题型三】奇偶性问题
【典题1】定义在\(R\)上的增函数\(y=f(x)\)对任意\(x ,y∈R\)都有\(f(x+y)=f(x)+f(y)\),则
(1)求\(f(0)\);
(2)证明:\(f(x)\)为奇函数;
(3)若\(f\left(k \cdot 3^{x}\right)+f\left(3^{x}-9^{x}-2\right)<0\)对任意\(x∈R\)恒成立,求实数\(k\)的取值范围.
【解析】(1)在\(f(x+y)=f(x)+f(y)\)中,
令\(x=y=0\)可得,\(f(0)=f(0)+f(0)\),则\(f(0)=0\),
(2) \({\color{Red}{(定义法证明函数奇偶性) }}\)
令\(y=-x\),得\(f(0)=f(x)+f(-x)\),
又\(f(0)=0\),则有\(0=f(x)+f(-x)\),
即可证得\(f(x)\)为奇函数;
(3)因为\(f(x)\)在\(R\)上是增函数,又由(2)知\(f(x)\)是奇函数,
\(f\left(k \cdot 3^{x}\right)<-f\left(3^{x}-9^{x}-2\right)=f\left(-3^{x}+9^{x}+2\right)\),
即有\(k \cdot 3^{x}<-3^{x}+9^{x}+2\),得\(k<3^{x}+\dfrac{2}{3^{x}}-1\) \({\color{Red}{(分离参数法) }}\)
又有\(3^{x}+\dfrac{2}{3^{x}}-1 \geq 2 \sqrt{2}-1\)(当\(x=\log _{3} \sqrt{2}\)时取到等号),
即\(3^{x}+\dfrac{2}{3^{x}}-1\)有最小值\(2 \sqrt{2}-1\),
所以要使\(f\left(k \cdot 3^{x}\right)+f\left(3^{x}-9^{x}-2\right)<0\)恒成立,只要使\(k<2 \sqrt{2}-1\)即可,
故\(k\)的取值范围是\((-\infty, 2 \sqrt{2}-1)\).
【点拨】
② 判断或证明抽象函数的奇偶性,从奇偶性的定义入手,判断\(f(-x)\)与\(f(x)\)的关系.
② 抽象函数\(f(x+y)=f(x)+f(y)\)是正比例函数\(f(x)=kx(x≠0\))型,由\(f(x)\)是增函数,可知\(k>0\),选填题可用.
【题型四】周期性问题
【典题1】奇函数\(f (x)\)定义在\(R\)上,且对常数\(T>0\),恒有\(f (x + T ) = f (x\)),则在区间\([0 ,2T]\)上,方程\(f (x) = 0\)根的个数最小值为 \(\underline{\quad \quad}\) .
【解析】\(∵\)函数\(f(x)\)是定义在\(R\)上的奇函数,
故\(f(0)=0\),
又\(∵f(x+T)=f(x)\),即周期为\(T\),
\(∴f(2T)=f(T)=f(0)=0\),
又由\(f\left(-\dfrac{T}{2}\right)=f\left(-\dfrac{T}{2}+T\right)=f\left(\dfrac{T}{2}\right)\),且\(f\left(-\dfrac{T}{2}\right)=-f\left(\dfrac{T}{2}\right)\)
\(\therefore f\left(\dfrac{T}{2}\right)=0\),\(\therefore f\left(\dfrac{3 T}{2}\right)=f\left(\dfrac{T}{2}\right)=0\),
故在区间\([0 ,2T]\),方程\(f(x)=0\)根有\(x=0, \dfrac{T}{2}, T, \dfrac{3 T}{2}, 2 T\),
个数最小值是\(5\)个,
【点拨】抽象函数的周期性常与奇偶性,对称性放在一起,记住有关周期性和对称性的结论,做题时常画图像更容易找到思路.
巩固练习
1 (★★)\(f(x)\)的定义域为\((0 ,+∞)\),对任意正实数\(x ,y\)都有\(f(xy)=f(x)+f(y)\) 且\(f(4)=2\),则\(f(\sqrt{2})=\)\(\underline{\quad \quad}\) .
2 (★★★)已知\(f(x)\)是定义在\(R\)上的偶函数,对任意\(x∈R\)都有\((f(x+2)-1)^{2}=2 f(x)-f^{2}(x)\),则\(f(2019)=\)\(\underline{\quad \quad}\) .
3 (★★)\(f(x)\)是定义在\(R\)上的以\(3\)为周期的奇函数,且\(f(2)=0\),则方程\(f(x)=0\)在区间\([-6 ,6]\)内解的个数的最小值是\(\underline{\quad \quad}\) .
4 (★★★)已知定义在\((-∞ ,0)∪(0 ,+∞)\)上的函数\(f(x)\)满足
①对任意\(x ,y∈(-∞ ,0)∪(0 ,+∞)\),都有\(f(xy)=f(x)+f(y)\);
②当\(x>1\)时,\(f(x)>0\)且\(f(2)=1\);
(1)试判断函数\(f(x)\)的奇偶性;
(2)判断函数\(f(x)\)在区间\([-4 ,0)∪(0 ,-4]\)上的最大值;
(3)求不等式\(f(3x-2)+f(x)≥4\)的解集.
5 (★★★)已知定义在\((0 ,+∞)\)的函数\(f(x)\),对任意的\(x、y∈(0 ,+∞)\),都有\(f(xy)=f(x)+f(y)\),且当\(0<x<1\)时,\(f(x)>0\).
(1)证明:当\(x>1\)时,\(f(x)<0\);
(2)判断函数\(f(x)\)的单调性并加以证明;
(3)如果对任意的\(x、y∈(0 ,+∞)\),\(f\left(x^{2}+y^{2}\right) \leq f(a)+f(x y)\)恒成立,求实数\(a\)的取值范围.
6 (★★★)定义在\(R\)上的单调增函数\(f(x)\)满足:对任意\(x ,y∈R\)都有\(f(x+y)=f(x)+f(y)\)成立
(1)求\(f(0)\)的值;
(2)求证:\(f(x)\)为奇函数;
(3)若\(f\left(1+2^{x}\right)+f\left(t \cdot 3^{x}\right)>0\)对\(x∈(-∞ ,1]\)恒成立,求\(t\)的取值范围.
挑战学霸
已知\(f(x)\)是定义在\(R\)上不恒为\(0\)的函数,满足对任意\(x ,y∈R\),\(f(x+y)=f(x)+f(y)\),\(f(xy)=f(x)f(y)\).
(1)求\(f(x)\)的零点;
(2)判断\(f(x)\)的奇偶性和单调性,并说明理由;
(3)①当\(x∈Z\)时,求f(x)的解析式;②当\(x∈R\)时,求\(f(x)\)的解析式.
参考答案
- 【答案】\(\dfrac{1}{2}\)
【解析】取\(x=y=2\),得\(f(4)=f(2)+f(2)⇔ f(2)=1\);
取\(x=y=\sqrt{2}\),得\(f(2)=f(\sqrt{2})+f(\sqrt{2}) \Leftrightarrow f(\sqrt{2})=\dfrac{1}{2}\); - 【答案】\(1 \pm \dfrac{\sqrt{2}}{2}\)
【解析】根据题意,\(f(x)\)为偶函数且\(f(x)\)满足\((f(x+2)-1)^{2}=2 f(x)-f^{2}(x)\),
变形可得\([f(x+2)-1]^{2}+\left[f^{2}(x)-2 f(x)+1\right]=1\),
即\([f(x+2)-1]^{2}+[f(x)-1]^{2}=1\),
令\(x=-1\)可得\([f(-1)-1]^{2}+[f(1)-1]^{2}=1\),即\(2[f(1)-1]^2=1\),
解可得:\(f(1)=f(-1)=1 \pm \dfrac{\sqrt{2}}{2}\),
又由\(f(x)\)满足\([f(x+2)-1]^{2}+[f(x)-1]^{2}=1\),
则有\([f(x+4)-1]^{2}+[f(x+2)-1]^{2}=1\),
联立可得:\([f(x+4)-1]^{2}=[f(x)-1]^{2}\),
变形可得:\(f(x+4)=f(x)\)或\(f(x+4)+f(x)=2\),
若\(f(x+4)=f(x)\),则有\(f(2019)=f(-1+505 \times 4)=f(-1)=1 \pm \dfrac{\sqrt{2}}{2}\),
此时有\(f(2019)=1 \pm \dfrac{\sqrt{2}}{2}\),
若\(f(x+4)+f(x)=2\),即\(f(x+4)=2-f(x)\),
则有\(f(x+8)=2-f(x+4)=f(x)\),则有\(f(2019)=f(3+2016)=f(3)\),
则\(f(3)=2-f(-1)=1 \pm \dfrac{\sqrt{2}}{2}\),
综合可得:\(f(2019)=1 \pm \dfrac{\sqrt{2}}{2}\). - 【答案】\(13\)
【解析】\(∵f(x)\)是定义在\(R\)上的以\(3\)为周期的奇函数,
\(∴f(x+3)=f(x)\),且\(f(-x)=-f(x)\),
则\(f(0)=0\),则\(f(3)=f(6)=f(-6)=f(0)=0\),\(f(-3)=-f(3)=0\),
\(∵f(2)=0\),\(∴f(5)=f(-1)=f(-4)=0\),\(f(-5)=0\),
\(f(1)=0\),\(f(4)=0\),\(f(-2)=0\),
方程的解可能为\(0,3,6,-6,-3,2,5,\)\(-5,-2,-1,1,4,-4\)共\(13\)个,
故选:\(D\). - 【答案】\((1)\)偶函数 \((2)2\) \((3)x≤-2\)或\(x \geq \dfrac{8}{3}\)
【解析】\((1)∵f(xy)=f(x)+f(y)\);
令\(x=y=a\),则\(f(a^2)=f(a)+f(a)=2f(a)\),
令\(x=y=-a\),则\(f(a^2)=f(-a)+f(-a)=2f(-a)\),
即\(f(a)=f(-a)\),
故函数\(f(x)\)是偶函数,
(2)任取\(0<x_1<x_2\),则\(x_2-x_1>0\),
\(∵f(xy)=f(x)+f(y)\);
\(∴f(xy)-f(x)=f(y)\);
\(\therefore f\left(x_{2}\right)-f\left(x_{1}\right)=f\left(\dfrac{x_{2}}{x_{1}}\right)\)
\(\because \dfrac{x_{2}}{x_{1}}>1\),\(x>1\)时,\(f(x)>0\),
\(\therefore f\left(x_{2}\right)-f\left(x_{1}\right)=f\left(\dfrac{x_{2}}{x_{1}}\right)>0\),
得到\(f(x_1)<f(x_2)\),
\(∴f(x)\)为\((0,+∞)\)上的增函数.
故函数\(f(x)\)在区间\((0,-4]\)上的最大值为\(f(4)=f(2)+f(2)=2\),
又由函数\(f(x)\)是偶函数,
\(∴\)函数\(f(x)\)在区间\([-4,0)\)上的最大值也为\(2\),
故函数\(f(x)\)在区间\([-4,0)∪(0,-4]\)上的最大值为\(2\);
(3)由(2)得\(f(4)=2\),则\(f(16)=f(6)+f(6)=4\),
故不等式\(f(3x-2)+f(x)≥4\)可化为:\(f[(3x-2)x]≥f(16)\),
由(2)中结论可得:\(|(3x-2)x|≥16\),
即\((3x-2)x≥16\)或\((3x-2)x≤-16\),
解得\(x≤-2\)或\(x \geq \dfrac{8}{3}\) - 【答案】\((1)\) 略 \((2)\)减函数,函数单调性定义证明 \((3) (0 ,2]\)
【解析】\((1)∵f(xy)=f(x)+f(y)\),
令\(x=y=1\),则\(f(1)=f(1)+f(1)\),所以\(f(1)=0\),
再令\(y=\dfrac{1}{x}\),则\(f(1)=f(x)+f\left(\dfrac{1}{x}\right)=0\),
当\(x>1\)时,\(0<\dfrac{1}{x}<1\).
\(\because f\left(\dfrac{1}{x}\right)>0\).\(\therefore f(x)=-f\left(\dfrac{1}{x}\right)<0\)
(2)任取\(x_1\),\(x_2∈(0,+∞)\),且\(x_1<x_2\),则\(f\left(x_{2}\right)-f\left(x_{1}\right)=f\left(\dfrac{x_{2}}{x_{1}}\right)\)
\(∵x_1<x_2\),所以\(\dfrac{x_{2}}{x_{1}}>1\),则\(f\left(\dfrac{x_{2}}{x_{1}}\right)<0\),\(f(x_2)<f(x_1)\),
\(∴f(x)\)在\((0,+∞)\)上是减函数,
(3)\(f\left(x^{2}+y^{2}\right) \leq f(a)+f(x y)\)恒成立,
\(\therefore f\left(x^{2}+y^{2}\right) \leq f(a x y)\)恒成立,
\(∵f(x)\)在\((0,+∞)\)上是减函数,
\(\therefore x^{2}+y^{2} \geq a x y\),
\(\therefore 0<a \leq \dfrac{x^{2}+y^{2}}{x y}=\dfrac{y}{x}+\dfrac{x}{y} \geq 2\),当且仅当\(x=y\)取等号,
\(∴\)实数\(a\)的取值范围\((0,2]\) - 【答案】\((1) 0\) \((2)\)略,定义证明 \((3) t>-1\)
【解析】(1)令\(x=y=0\),则\(f(0)=f(0)+f(0)\),\(∴f(0)=0\).
(2)令\(y=-x\),则\(f(0)=f(x)+f(-x)\),
\(∵f(0)=0\),\(∴f(-x)=-f(x)\),
\(∴f(x)\)为奇函数.
(3)\(\because f\left(t \cdot 3^{x}\right)>-f\left(1+2^{x}\right)\),\(\therefore f\left(t \cdot 3^{x}\right)>f\left(-1-2^{x}\right)\),\(\therefore t \cdot 3^{x}>-1-2^{x}\)
\(\therefore t>-\left(\dfrac{1}{3}\right)^{x}-\left(\dfrac{2}{3}\right)^{x}\)恒成立,
而\(-\left(\dfrac{1}{3}\right)^{x}-\left(\dfrac{2}{3}\right)^{x}\)单调递增,\(\therefore-\left(\dfrac{1}{3}\right)^{x}-\left(\dfrac{2}{3}\right)^{x} \leq-1\)
从而\(t>-1\).
【挑战学霸】
【解析】(1)记\(f(x+y)=f(x)+f(y)\) ①,\(f(xy)=f(x)f(y)\) ②
在①中取\(y=0\)得\(f(0)=0\).若存在\(x≠0\),使得\(f(x)=0\),则对任意\(y∈R\),
\(f(y)=f\left(x \cdot \dfrac{y}{x}\right)=f(x) f\left(\dfrac{y}{x}\right)=0\),与\(f(x)\)不恒为\(0\)矛盾.
所以\(x≠0\)时,\(f(x)≠0\),
所以函数的零点是\(0\).
(2)在①中取\(y=-x\)得\(f(x)+f(-x)=f(0)=0\),即\(f(-x)=-f(x)\),
所以\(f(x)\)是奇函数.
\(x ,y∈R\), \(y>x\)时,\(f(y)-f(x)=f(y)+f(-x)=f(y-x)=(f(\sqrt{y-x}))^{2}>0\),
可得\(f(y)>f(x)\).
所以函数\(f(x)\)在\(R\)上递增.
(3)①由\(f(xy)=f(x)f(y)\)中取\(x ,y=1\)得\(f(1)=f^2 (1)\).
因为\(f(1)≠0\),所以\(f(1)=1\),
对任意正整数\(n\),由①得\(f(n)=\underbrace{f(1)+\cdots+f(1)}_{n 个}=n \times 1=n\),
\(f(-n)=-f(n)=-n\),
又因为\(f(0)=0\),所以\(x∈N\)时,\(f(x)=x\);
对任意有理数\(\dfrac{m}{n}\left(m \in \boldsymbol{N}^{*}, \quad n \in \boldsymbol{N}^{*}\right)\),由①,
\(f(m)=f\left(n \cdot \dfrac{m}{n}\right)=\underbrace{f\left(\dfrac{m}{n}\right)+\cdots+f\left(\dfrac{m}{n}\right)=n f\left(\dfrac{m}{n}\right)}_{n \text { 个 }}\) ,
所以\(f\left(\dfrac{m}{n}\right)=\dfrac{f(m)}{n}=\dfrac{m}{n}\),即对一切\(x∈Z\) ,\(f(x)=x\).
②若存在\(x∈R\),使得\(f(x)≠x\),
不妨设\(f(x)>x\)(否则以\(-f(-x)\)代替\(f(x)\),\(-x\)代替\(x\)即可),
则存在有理数\(\alpha\),使得\(x<\alpha<f(x)\)
(例如可取\(n=\left[\dfrac{1}{f(x)-x}\right]+1\),\(m=[nx]+1\),\(\alpha=\dfrac{m}{n}\)).
\(x<\alpha\)但\(f(x)>\alpha=f(\alpha)\),与\(f(x)\)的递增性矛盾.
所以\(x∈R\)时,\(f(x)=x\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号