专题立体几何之所成角

\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】高一数学下学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)

适合必修第二册同步拔高练习、高三专题练习，难度3颗星！

模块导图

知识剖析

异面直线所成的角

1 范围
异面直线所成角的范围： \((0^∘ ,90^∘]\)；

2 作异面直线所成的角
平移法.
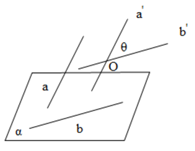
如图,在空间任取一点\(O\),过O作\(a^{\prime} / / a\) ,\(b^{\prime} / / b\),则\(a^{\prime}\) ,\(b^{\prime}\)所成的\(θ\)角为异面直线\(a\) ,\(b\)所成的角.特别地,找异面直线所成的角时,经常把一条异面直线平移到另一条异面直线的特殊点(如线段中点,端点等)上,形成异面直线所成的角.

线面所成的角

1 定义
如下图，平面的一条斜线(直线\(l\))和它在平面上的射影(\(AO\))所成的角，叫做这条直线和这个平面所成的角.

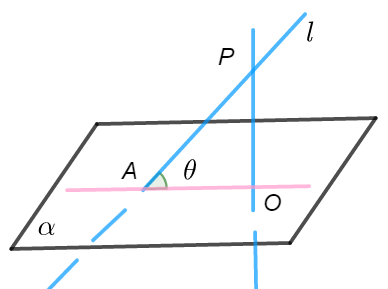
一条直线垂直平面，则\(θ=90^°\)；一条直线和平面平行或在平面内，则\(θ=0^°\).

2 范围
线面所成角的范围： \([0^∘ ,90^∘]\)

二面角

1 定义
从一条直线出发的两个半平面所组成的图形叫做二面角.
在二面角的棱\(l\)上任取一点\(O\),以点\(O\)为垂足,在半平面\(α\)和\(β\)内分别作垂直于棱\(l\)的射线\(OA\)和\(OB\),则射线\(OA\)和\(OB\)构成的\(∠AOB\)叫做二面角的平面角.

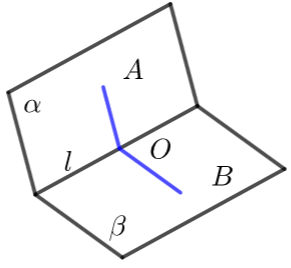
2 范围
二面角的范围： \([0^° ,180^°]\).

经典例题

【题型一】异面直线所成的角

【典题1】如图,正方体\(ABCD—A_1 B_1 C_1 D_1\)中，点\(E\),\(F\)分别是\(AA_1\),\(AD\)的中点，则\(CD_1\)与\(EF\)所成角为 (　　)

A．\(0°\) \(\qquad \qquad \qquad \qquad\)B．\(45°\) \(\qquad \qquad \qquad \qquad\) C．\(60°\)\(\qquad \qquad \qquad \qquad\) D．\(90°\)
【解析】连结\(A_1 D\)、\(BD\)、\(A_1 B\),
\(∵\)正方体\(ABCD—A_1 B_1 C_1 D_1\)中,点\(E\) ,\(F\)分别是\(AA_1\),\(AD\)的，\(EF∥A_1 D\),
\(∵A_1 B∥D_1 C\)，\(∴∠DA_1 B\)是\(CD_1\)与\(EF\)所成角,
\(∵A_1 D=A_1 B=BD\) ,\(∴∠DA_1 B=60°\)．
\(∴CD_1\)与\(EF\)所成角为\(60°\)．
故选 \(C\)．

【点拨】
① 找异面直线所成的角,主要是把两条异面直线通过平移使得它们共面,可平移一条直线也可以同时平移两条直线；
② 平移时常利用中位线、平行四边形的性质；

【典题2】如图所示,在棱长为\(2\)的正方体\(ABCD—A_1 B_1 C_1 D_1\)中,\(O\)是底面\(ABCD\)的中心,\(E\)、\(F\)分别是\(CC_1\) ,\(AD\)的中点,那么异面直线\(OE\)和\(FD_1\)所成角的余弦值等于\(\underline{\quad \quad}\)．

【解析】取\(BC\)的中点\(G\)．连接\(GC_1\),则\(GC_1∥FD_1\),再取\(GC\)的中点\(H\),连接\(HE\)、\(OH\),

\(∵E\)是\(CC_1\)的中点,\(∴GC_1∥EH\),\(∴∠OEH\)为异面直线所成的角．
在\(△OEH\)中,\(O E=\sqrt{3}\),\(H E=\dfrac{\sqrt{5}}{2}\),\(O H=\dfrac{\sqrt{5}}{2}\)．
由余弦定理,可得\(\cos \angle O E H=\dfrac{O E^{2}+E H^{2}-O H^{2}}{2 O E \cdot E H}=\dfrac{3}{2 \cdot \sqrt{3} \cdot \frac{\sqrt{5}}{2}}=\dfrac{\sqrt{15}}{5}\)．
故答案为 \(\dfrac{\sqrt{15}}{5}\).
【点拨】本题利用平移法找到异面直线所成的角(\(∠OEH\))后,确定含有该角的三角形(\(△OEH\)),利用解三角形的方法(正弦定理,余弦定理等)把所求角\(∠OEH\)最终求出来.

【典题3】如图,已知\(P\)是平行四边形\(ABCD\)所在平面外一点,\(M\),\(N\)分别是\(AB\) ,\(PC\)的中点．
(1)求证：\(MN∥\)平面\(PAD\)；
(2)若\(MN=BC=4\) ,\(P A=4 \sqrt{3}\),求异面直线\(PA\)与\(MN\)所成的角的大小．

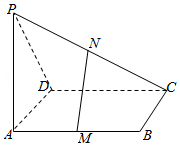
【解析】(1)证明：取\(PD\)中点\(Q\),连\(AQ\)、\(QN\),

则\(AM∥QN\),且\(AM=QN\),
\(∴\)四边形\(AMNQ\)为平行四边形
\(∴MN∥AQ\)
又\(∵AQ\)在平面\(PAD\)内,\(MN\)不在平面\(PAD\)内
\(∴MN∥\)面\(PAD\)；
(2)解
\({\color{Red}{方法一 }}\) \(∵MN∥AQ\)
\(∴∠PAQ\)即为异面直线\(PA\)与\(MN\)所成的角
\(∵MN=BC=4\) ,\(P A=4 \sqrt{3}\),
\(∴AQ=4\),
设\(PQ=x\),根据余弦定理可知\(\cos \angle A Q D+\cos \angle A Q P=0\)
即\(\dfrac{16+x^{2}-48}{8 x}+\dfrac{16+x^{2}-16}{8 x}=0\),解得\(x=4\)
在三角形\(AQP\)中,\(AQ=PQ=4\) ,\(A P=4 \sqrt{3}\)
\(\therefore \cos \angle P A Q=\dfrac{48+16-16}{2 \times 4 \times 4 \sqrt{3}}=\dfrac{\sqrt{3}}{2}\),即\(∠PAQ=30°\)
\(∴\)异面直线\(PA\)与\(MN\)所成的角的大小为\(30°\)
\({\color{Red}{方法二 }}\) 过点\(A\)作\(AH⊥PD\)交\(PD\)于\(H\),如图

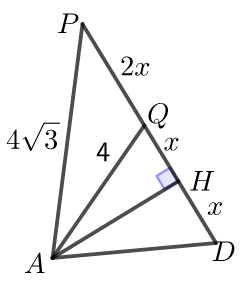
\(∵MN=BC=4\),\(∴H\)是\(QD\)的中点
设\(HD=x\),则\(QH=x\),\(PQ=2x\),
在\(Rt△AQD\)和\(Rt△APH\)
利用勾股定理可得\(AH^2=16-x^2=48-9x^2\),解得\(x=2\)
\(\therefore \cos \angle P A Q=\dfrac{P H}{A P}=\dfrac{6}{4 \sqrt{3}}=\dfrac{\sqrt{3}}{2}\),即\(∠PAQ=30°\)
\(∴\)异面直线\(PA\)与\(MN\)所成的角的大小为\(30°\)
【点拨】本题中所成角\(∠PAQ\)找到后,无法在一个三角形里求出,此时把问题转化为平面几何问题, 再利用解三角形的方法进行求解.

【题型二】线面所成的角

【典题1】如图,直角梯形\(ABCD\)与等腰直角三角形\(ABE\)所在的平面互相垂直．\(AB∥CD\),\(AB⊥BC\),\(AB=2CD=2BC\),\(EA⊥EB\)．
(1)求证：\(AB⊥DE\)；
(2)求直线\(EC\)与平面\(ABE\)所成角的正弦值．

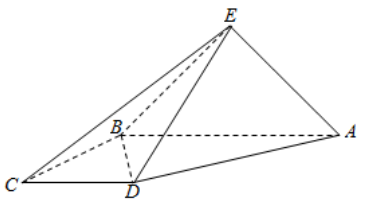
【解析】(1)证明：取\(AB\)中点\(O\),连接\(EO\),\(DO\)．
\(∵EB=EA\),\(∴EO⊥AB\)．
\(∵\)四边形\(ABCD\)为直角梯形,\(AB=2CD=2BC\),\(AB⊥BC\),
\(∴\)四边形\(OBCD\)为正方形,\(∴AB⊥OD\)．
又\(∵EO∩OD=O\),\(∴AB⊥\)平面\(EOD\)．
\(∴AB⊥ED\)．
(2)\(∵\)平面\(ABE⊥\)平面\(ABCD\),且\(AB⊥BC\),
\(∴BC⊥\)平面\(ABE\)．
则\(∠CEB\)为直线\(EC\)与平面\(ABE\)所成的角．
设\(BC=a\),则\(AB=2a\),\(B E=\sqrt{2} a\),
\(\therefore C E=\sqrt{3} a\),
在直角三角形\(CBE\)中,\(\sin \angle C E B=\dfrac{C B}{C E}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)．
即直线\(EC\)与平面\(ABE\)所成角的正弦值为\(\dfrac{\sqrt{3}}{3}\)．
【点拨】本题中的“直线\(EC\)与平面\(ABE\)所成的角”是根据线面角的定义直接在题目原图上找到的,在含所求角\(∠CEB\)的直角三角形\(CBE\)中求出角度！

【典题2】如图,四边形\(ABCD\)为正方形,\(PA⊥\)平面\(ABCD\),且\(AB=4\),\(PA=3\),点\(A\)在\(PD\)上的射影为\(G\)点,\(E\)点在\(AB\)边上,平面\(PEC⊥\)平面\(PDC\)．
(1)求证：\(AG∥\)平面\(PEC\)；
(2)求\(BE\)的长；
(3)求直线\(AG\)与平面\(PCA\)所成角的余弦值．

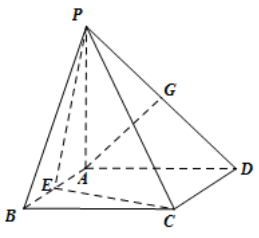
【解析】(1)证明：\(∵CD⊥AD\),\(CD⊥PA\)
\(∴CD⊥\)平面\(PAD\) \(∴CD⊥AG\),
又\(PD⊥AG\)
\(∴AG⊥\)平面\(PCD\)
作\(EF⊥PC\)于\(F\),因面\(PEC⊥\)面\(PCD\)
\(∴EF⊥\)平面\(PCD\)
\(∴EF∥AG\),又\(AG⊄\)面\(PEC\),\(EF⊂\)面\(PEC\),
\(∴AG∥\)平面\(PEC\)
(2)由(1)知\(A\)、\(E\)、\(F\)、\(G\)四点共面,又\(AE∥CD\)
\(∴AE∥\)平面\(PCD\)
\(∴AE∥GF\)
\(∴\)四边形\(AEFG\)为平行四边形,\(∴AE=GF\)
\(∵PA=3\),\(AD=AB=4\) \(\therefore P D=5\)，\(A G=\dfrac{12}{5}\)
在\(Rt△PAGP\)中，\(P G^{2}=P A^{2}-A G^{2}=\dfrac{81}{25}\)
\(\therefore P G=\dfrac{9}{5}\)
又\(\dfrac{G F}{C D}=\dfrac{P G}{P D}\) \(\therefore G F=\dfrac{36}{25}\)
\(\therefore A E=\dfrac{36}{25}\),故\(B E=\dfrac{64}{25}\)
(3)\(∵EF∥AG\),所以\(AG\)与平面\(PAC\)所成角等于\(EF\)与平面\(PAC\)所成的角,
过\(E\)作\(EO⊥AC\)于\(O\)点,易知\(EO⊥\)平面\(PAC\),又\(EF⊥PC\),

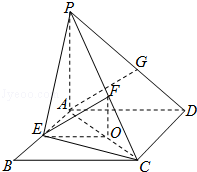
\(∴OF\)是\(EF\)在平面\(PAC\)内的射影
\(∴∠EFO\)即为\(EF\)与平面\(PAC\)所成的角
\(E O=A E \sin 45^{\circ}=\dfrac{36}{25} \times \dfrac{\sqrt{2}}{2}=\dfrac{18 \sqrt{2}}{25}\),
又\(E F=A G=\dfrac{12}{5}\),
\(\therefore \sin \angle E F O=\dfrac{E O}{E F}=\dfrac{18 \sqrt{2}}{25} \times \dfrac{5}{12}=\dfrac{3 \sqrt{2}}{10}\)
故\(\cos \angle E F O=\sqrt{1-\sin ^{2} \angle E F O}=\dfrac{\sqrt{82}}{10}\)
所以\(AG\)与平面\(PAC\)所成角的余弦值等于\(\dfrac{\sqrt{82}}{10}\).
【点拨】
① 若在题目中不能直接找到所求线面角,则可用“作高法”确定所求角,
比如下图中,求直线\(AP\)与平面\(α\)所成的角,具体步骤如下：

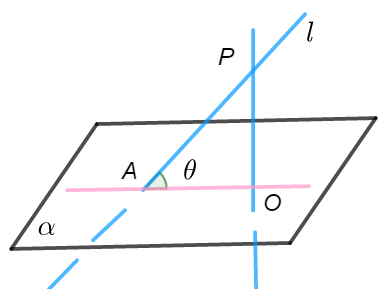
(1) 如图,过点\(P\)作平面\(α\)的高\(PO\),垂足为\(O\),则\(AO\)是线段\(AP\)在平面\(α\)上的投影；
(2) 找到所求角\(θ\)；
(3) 求解三角形\(APO\)进而求角\(θ\).
(此方法关键在于找到垂足\(O\)的位置,证明到\(PO⊥\)平面\(α\),如本题中\(EO⊥\)平面\(PAC\)的证明)
② 本题若直接求“\(AG\)与平面\(PAC\)所成角”,过点\(G\)做高有些难度,则由\(EF∥AG\),能把“\(AG\)与平面\(PAC\)所成角”转化为“\(EF\)与平面\(PAC\)所成的角”,这方法称为“间接法”吧.

【典题3】如图,正四棱锥\(S－ABCD\)中,\(SA=AB=2\),\(E\),\(F\),\(G\)分别为\(BC\),\(SC\),\(CD\)的中点．设\(P\)为线段\(FG\)上任意一点．
(Ⅰ)求证：\(EP⊥AC\)；
(Ⅱ)当\(P\)为线段\(FG\)的中点时,求直线\(BP\)与平面\(EFG\)所成角的余弦值．

【解析】证明：(Ⅰ)连接\(AC\)交\(BD\)于\(O\),
\(∵S－ABCD\)是正四棱锥,\(∴ SO⊥\)平面\(ABCD\),\(∴SO⊥AC\),
又\(∵AC⊥BD\),\(SO∩BD=O\),\(∴AC⊥\)平面\(SBD\),\(∴AC⊥SD\),
\(∵F\),\(G\)分别为\(SC\),\(CD\)的中点,\(∴SD∥FG\),
\(∴AC⊥GF\),
同理\(AC⊥EF\),\(∴AC⊥\)平面\(GEF\),
又\(∵PE⊂\)平面\(GEF\),\(∴EP⊥AC\)．
(Ⅱ) \({\color{Red}{ 方法一}}\) 过\(B\)作\(BH⊥GE\)于点\(H\),连接\(PH\),
\(∵BD⊥AC\),\(BD∥GF\),\(∴BH∥AC\),
由(Ⅰ)知：\(AC⊥\)平面\(GEF\),\(∴BH⊥\)平面\(GEF\),
\(∴∠BPH\)就是直线\(BP\)与平面\(EFG\)所成的角,
\(∵SA=AB=2\),
\(∴\)在\(Rt△BHP\)中,解得\(B H=\dfrac{\sqrt{2}}{2}\),\(P H=\dfrac{\sqrt{13}}{2}\),\(P B=\dfrac{\sqrt{15}}{2}\),
\({\color{Red}{(易知△BHE是等腰直角三角形,又由斜边BE=1,\therefore B H=\dfrac{\sqrt{2}}{2}；在三角形PGH中,P G=\dfrac{1}{2},G H=\dfrac{3 \sqrt{2}}{2},}}\)
\({\color{Red}{\angle P G H=\dfrac{\pi}{4},用余弦定理可得P H=\dfrac{\sqrt{13}}{2}) }}\)
则\(\cos \angle B P H=\dfrac{P H}{P B}=\dfrac{\sqrt{195}}{15}\),
故直线\(BP\)与平面\(EFG\)所成角的余弦值为\(\sqrt{\dfrac{195}{15}}\).

\({\color{Red}{ 方法二 }}\)
设过点\(B\)作平面\(EFG\)的垂直,垂直为\(T\),
则\(∠BPT\)就是直线\(BP\)与平面\(EFG\)所成的角,\(BT\)是点\(B\)到平面\(PGE\)的距离,
由已知条件可求\(GF=EF=1\),\(G E=\sqrt{2}\),则\(∠GFE=90^°\),
\(\therefore S_{\triangle P E G}=\dfrac{1}{2} S_{\triangle G F E}=\dfrac{1}{2} \times \dfrac{1}{2}=\dfrac{1}{4}\),
由于\(P、F\)是中点,易得点\(P\)到平面\(ABCD\)的距离\(h_{1}=\dfrac{1}{4} S O=\dfrac{\sqrt{2}}{4}\),
而\(S_{\triangle G E B}=\dfrac{1}{2} S_{\triangle G C B}=\dfrac{1}{2} \times 1=\dfrac{1}{2}\),
对于三棱锥\(P-GEB\),
由\(V_{B-P E G}=V_{P-G E B} \Rightarrow \dfrac{1}{3} \times B T \times S_{\triangle P E G}=\dfrac{1}{3} \times h_{1} \times S_{\triangle G E B}\)\(\Rightarrow \dfrac{1}{12} B T=\dfrac{\sqrt{2}}{24} \Rightarrow B T=\dfrac{\sqrt{2}}{2}\),
在正四棱锥\(S－ABCD\)中可求\(P B=\dfrac{\sqrt{15}}{2}\),
\({\color{Red}{(方法较多,提示过点P作平面ABCD的PI) }}\)
\(\therefore \sin \angle B P T=\dfrac{B T}{B P}=\dfrac{\sqrt{30}}{15}\)
\(\therefore \cos \angle B P T=\sqrt{1-\sin \angle B P T}=\dfrac{\sqrt{195}}{15}\)
故直线\(BP\)与平面\(EFG\)所成角的余弦值为\(\sqrt{\dfrac{195}{15}}\).
【点拨】
① 本题第二问中方法一就是用“做高法”,计算量有些大；方法二是觉得垂足\(H\)的位置难确定,可设点\(B\)到平面\(EFG\)的投影为\(T\)(即垂足),再用“等积法”求高\(BT\),则\(\sin \angle B P T=\dfrac{B T}{B P}\),可求所求角\(∠BPT\),这种方法称为“等积法”；
② 思考：上一题试试用“等积法”！

【题型三】二面角

【典题1】如图,在棱长为\(a\)的正方体\(ABCD－A_1 B_1 C_1 D_1\)中,\(AC\)与\(BD\)相交于点\(O\)．求二面角\(A_1－BD－A\)的正切值．

【解析】在正方体中\(BD⊥\)平面\(A_1 ACC_1\)，
\(∴AO⊥BD\),\(A_1 O⊥BD\)，
\(∴\)二面角\(A_1－BD－A\)的平面角为\(∠A_1 OA\)

由题中的条件求出：\(A O=\dfrac{\sqrt{2}}{2} a\) ,\(AA_1=a\)
\(\therefore \tan \angle A_{1} O A=\dfrac{a}{\dfrac{\sqrt{2}}{2} a}=\sqrt{2}\),
所以二面角\(A_1－BD－A\)的正切值为\(\sqrt{2}\)．
【点拨】本题根据二面角的定义找到二面角二面角\(A_1－BD－A\)的平面角为\(∠A_1 OA\),再在三角形\(AOA_1\)内用解三角形的方法求解角\(∠A_1 OA\).

【典题2】如图,四棱锥\(P－ABCD\)中,底面\(ABCD\)为矩形,\(PA⊥\)底面\(ABCD\),\(P A=A B=\sqrt{6}\),点\(E\)是棱\(PB\)的中点．
(1)求直线\(AD\)与平面\(PBC\)的距离；
(2)若\(A D=\sqrt{3}\),求二面角\(A－EC－D\)的平面角的余弦值．

【解析】(1)在矩形\(ABCD\)中,\(AD∥BC\),从而\(AD∥\)平面\(PBC\),
故直线\(AD\)与平面\(PBC\)的距离为点\(A\)到平面\(PBC\)的距离,
因\(PA⊥\)底面\(ABCD\),
\(故PA⊥AB\),可得\(△PAB\)为等腰直角三角形,
又点\(E\)是棱\(PB\)的中点,
故\(AE⊥PB\),
\(∵BC⊥AB\),\(BC⊥PA\), \(∴BC⊥\)平面\(PAB\)
\(∴BC⊥AE\),从而\(AE⊥\)平面\(PBC\),
故\(AE\)之长即为直线\(AD\)与平面\(PBC\)的距离,
在\(Rt△PAB\)中,\(P A=A B=\sqrt{6}\),
所以\(A E=\dfrac{1}{2} P B=\dfrac{1}{2} \sqrt{P A^{2}+A B^{2}}=\sqrt{3}\)
(2)过点\(D\)作\(DF⊥CE\)于\(F\),过点\(F\)做\(FG⊥CE\),交\(AC\)于\(G\),连接\(DG\),

则\(∠DFG\)为所求的二面角的平面角．
由(1)知\(BC⊥AE\),又\(AD∥BC\),得\(AD⊥AE\),
从而\(D E=\sqrt{A E^{2}+A D^{2}}=\sqrt{6}\)
在\(Rt△CBE\)中,\(C E=\sqrt{B E^{2}+B C^{2}}=\sqrt{6}\),
由\(C D=\sqrt{6}\),
所以\(△CDE\)为等边三角形,
故\(F\)为\(CE\)的中点,且\(D F=C D \cdot \sin \dfrac{\pi}{3}=\dfrac{3 \sqrt{2}}{2}\)
因为\(AE⊥\)平面\(PBC\),
故\(AE⊥CE\),又\(FG⊥CE\),知\(FG∥AE\)．
\(∴G\)点为\(AC\)的中点，\(F G=\dfrac{1}{2} A E=\dfrac{\sqrt{3}}{2}\)
则在\(Rt△ADC\)中,\(D G=\dfrac{1}{2} \sqrt{A D^{2}+C D^{2}}=\dfrac{3}{2}\),
所以\(\cos \angle D F G=\dfrac{D F^{2}+F G^{2}-D G^{2}}{2 D F \cdot F G}=\dfrac{\sqrt{6}}{3}\)
【点拨】若在题目中不能直接得到所求二面角,就需要构造出二面角,
比如本题求二面角\(A－EC－D\),解题具体步骤如下

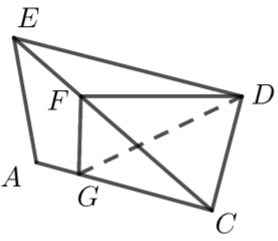
(1) 过点\(D\)作\(DF⊥EC\),过点\(F\)作\(FG⊥EC\)交\(AC\)于点\(D\),则二面角\(∠DFG\)为所求的二面角的平面角；
(2) 确定含角\(∠DFG\)的三角形\(DFG\),利用解三角形的方法求出角\(∠DFG\),常见的是求出三角形三边再用余弦定理.

【典题3】如图,已知三棱锥\(P－ABC\),\(PA⊥\)平面\(ABC\),\(∠ACB=90°\),\(∠BAC=60°\),\(PA=AC\),\(M\)为\(PB\)的中点．
(1)求证：\(PC⊥BC\)．
(2)求二面角\(M－AC－B\)的大小．

【解析】(1)证明：由\(PA⊥\)平面\(ABC\),\(∴PA⊥BC\),
又因为\(∠ACB=90°\),即\(BC⊥AC\)．
\(∴BC⊥\)面\(PAC\), \(∴PC⊥BC\)．
(2)取\(AB\)中点\(O\),连结\(MO\)，过\(O\)作\(HO⊥AC\)于\(H\),连结\(MH\),

\(∵M\)是\(PB\)的中点,\(∴MO∥PA\),
又\(∵PA⊥\)面\(ABC\),\(∴MO⊥\)面\(ABC\)．
\(∴∠MHO\)为二面角\(M－AC－B\)的平面角．
设\(AC=2\),则\(B C=2 \sqrt{3}\),\(MO=1\),\(O H=\sqrt{3}\),
在\(Rt△MHO\)中,\(\tan \angle M H O=\dfrac{M O}{H O}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)．
二面角\(M－AC－B\)的大小为\(30^∘\)．
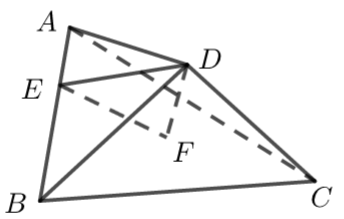
【点拨】求二面角也可以转化为线面角,比如求二面角\(D－AB－C\),解题思路如下过点\(D\)作\(DE⊥AB\),则二面角\(D－AB－C\)等于直线\(ED\)与平面\(ABC\)所成的角或其补角,若过点\(D\)作\(DF⊥\)平面\(ABC\),则二面角\(D－AB－C\)是锐角,等于角\(∠DEF\)；二面角\(D－AB－C\)是钝角,等于角\(∠DEF\)的补角.

巩固练习

1(★)在正方体\(ABCD﹣A'B'C'D'\)中,点\(P\)在线段\(AD'\)上运动,则异面直线\(CP\)与\(BA'\)所成的角\(θ\)的取值范围是 (　　)

A. \(0<\theta<\dfrac{\pi}{2}\) \(\qquad \qquad\)B. \(0<\theta \leq \dfrac{\pi}{2}\) \(\qquad \qquad\)C. \(0 \leq \theta \leq \dfrac{\pi}{3}\) \(\qquad \qquad\)D. \(0<\theta \leq \dfrac{\pi}{3}\)

2(★★)如图所示的几何体,是将高为\(2\)、底面半径为\(1\)的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体．\(O_1\),\(O_2\),\(O_2'\)分别为\(AB\) ,\(BC\),\(DE\)的中点,\(F\)为弧\(AB\)的中点,\(G\)为弧\(BC\)的中点．则异面直线\(AF\)与\(GO_2'\)所成的角的余弦值为\(\underline{\quad \quad}\)．

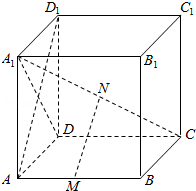
3(★★)如图所示,在正方体\(ABCD－A_1 B_1 C_1 D_1\)中,\(M\)是\(AB\)上一点,\(N\)是\(A_1 C\)的中点,\(MN⊥\)平面\(A_1 DC\)．
(1)求证：\(AD_1⊥\)平面\(A_1 DC\)；
(2)求\(MN\)与平面\(ABCD\)所成的角．

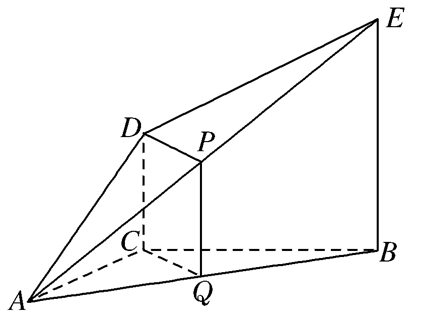
4(★★★)如图,\(DC⊥\)平面\(ABC\),\(EB∥DC\),\(AC=BC=EB=2DC=2\),\(∠ACB=120°\),\(P\) ,\(Q\)分别为\(AE\),\(AB\)的中点．
(1)证明：\(PQ∥\)平面\(ACD\)；
(2)求\(AD\)与平面\(ABE\)所成角的正弦值．

5(★★★)四棱锥\(P－ABCD\)中,\(PA⊥\)平面\(ABCD\),四边形\(ABCD\)为菱形,\(∠ADC=60°\),\(PA=AD=2\),\(E\)为\(AD\)的中点．
(1)求证：平面\(PCE⊥\)平面\(PAD\)；
(2)求\(PC\)与平面\(PAD\)所成的角的正切值；
(3)求二面角\(A－PD－C\)的正弦值．

6(★★★)如图,\(AB\)是圆\(O\)的直径,点\(C\)是圆\(O\)上异于\(A\) \(,B\)的点,直线\(PC⊥\)平面\(ABC\),\(E\) ,\(F\)分别是\(PA\),\(PC\)的中点．
(1)记平面\(BEF\)与平面\(ABC\)的交线为\(l\),试判断直线\(l\)平面\(PAC\)的位置关系,并加以证明；
(2)设\(PC=2AB=4\),求二面角\(E－l－C\)大小的取值范围．

参考答案

【答案】\(D\)
【解析】\(∵A_1 B∥D_1 C\)，\(∴CP\)与\(A_1 B\)成角可化为\(CP\)与\(D_1 C\)成角．
\(∵△AD_1 C\)是正三角形可知当\(P\)与\(A\)重合时成角为\(\dfrac{\pi}{3}\)，
\(∵P\)不能与\(D_1\)重合因为此时\(D_1 C\)与\(A_1 B\)平行而不是异面直线，
\(\therefore 0<\theta \leq \dfrac{\pi}{3}\)．
故选 \(D\)．
【答案】\(\dfrac{\sqrt{10}}{10}\)
【解析】如图，连接\(AF\)、\(FB\)、\(BG\)、\(GC\)，
\(∵F\)为半圆弧\(AFB\)的中点，\(G\)为半圆弧\(BGC\)的中点，
由圆的性质可知，\(G\)、\(B\)、\(F\)三点共线，且\(AF=CG\)，\(FB=GB\)，\(AB=BC\)，
\(\therefore \triangle A F B \cong \triangle C G B\)，\(∴AF∥CG\)，则\(∠CGO_2'\)即为所求的角或其补角，
又\(∵\)半径为\(1\)，高为\(2\)，且\(△AFB\)，\(△CGB\)都是等腰\(Rt△\)，
\(\therefore C G=\sqrt{2}\)，\(C O_{2}^{\prime}=G O_{2}^{\prime}=\sqrt{1+2^{2}}=\sqrt{5}\)，
\(∴\)在\(△CGO_2'\)中，\(\cos \angle C G O_{2}^{\prime}=\dfrac{\sqrt{5}^{2}+\sqrt{2}^{2}-\sqrt{5}^{2}}{2 \sqrt{2} \cdot \sqrt{5}}=\dfrac{\sqrt{10}}{10}\)，
即异面直线\(AF\)与\(GO_2'\)所成的角余弦值\(\dfrac{\sqrt{10}}{10}\)．
故答案为\(\dfrac{\sqrt{10}}{10}\)．
【答案】(1) 见解析 \(\text { (2) } \dfrac{\pi}{4}\)
【解析】(1)证明：由\(A B C D-A_{1} B_{1} C_{1} D_{1}\)为正方体，得\(CD⊥\)平面\(A D D_{1} A_{1}\)，\(A D_{1} \subset\)平面\(A D D_{1} A_{1}\)
\(\therefore C D \perp A D_{1}\)，
又\(A D_{1} \perp A_{1} D\)，且\(A_{1} D \cap C D=D\)，
\(\therefore A D_{1} \perp\)平面\(A_{1} D C\)；
(2)解：\(∵MN⊥\)平面\(A_{1} D C\)，
又由(1)知\(A D_{1} \perp\)平面\(A_{1} D C\)，
\(\therefore M N / / A D_{1}\)，
\(\therefore A D_{1}\)与平面\(ABCD\)所成的角，就是\(MN\)与平面\(ABCD\)所成的角，
\(\because D_{1} D \perp\)平面\(ABCD\)，
\(\therefore \angle D_{1} A D\)即为\(A D_{1}\)与平面\(ABCD\)所成的角，
由正方体可知\(\angle D_{1} A D=\dfrac{\pi}{4}\)，
\(∴MN\)与平面\(ABCD\)所成的角为\(\dfrac{\pi}{4}\)．
【答案】(1) 见解析 \(\text { (2) } \dfrac{\sqrt{5}}{5}\)
【解析】(1)证明：因为\(P\)，\(Q\)分别为\(AE\)，\(AB\)的中点，所以\(PQ∥EB\).
又\(DC∥EB\)，因此\(PQ∥DC\)，
又\(P Q \not \subset\)平面\(ACD\)，从而\(PQ∥\)平面\(ACD\).

(2)如图，连接\(CQ\)，\(DP\)，因为\(Q\)为\(AB\)的中点，且\(AC＝BC\)，所以\(CQ⊥AB\).
因为\(DC⊥\)平面\(ABC\)，\(EB∥DC\)，所以\(EB⊥\)平面\(ABC\)，
因此\(CQ⊥EB\). 故\(CQ⊥\)平面\(ABE\).
由(1)有\(PQ∥DC\)，又\(P Q=\dfrac{1}{2} E B=D C\)，所以四边形\(CQPD\)为平行四边形，
故\(DP∥CQ\)，因此\(DP⊥\)平面\(ABE\)，\(∠DAP\)为\(AD\)和平面\(ABE\)所成的角，
在\(Rt△DPA\)中，\(A D=\sqrt{5}\)，\(DP＝1\)，\(\sin \angle D A P=\dfrac{\sqrt{5}}{5}\)，
即\(AD\)与平面\(ABE\)所成角的正弦值为\(\dfrac{\sqrt{5}}{5}\)。
【答案】(1) 见解析 \((2) \dfrac{\sqrt{15}}{5} \qquad (3) \dfrac{\sqrt{42}}{7}\)
【解析】(1)证明：\(∵\)四边形\(ABCD\)为菱形，\(∴DA=DC\)，
\(∵∠ADC=60°\)，\(∴△ADC\)为等边三角形，\(∴CA=CD\)，
在\(△ADC\)中，\(E\)是\(AD\)中点，\(∴CE⊥AD\)，
\(∵PA⊥\)平面\(ABCD\)，\(CE⊂\)平面\(ABCD\)，\(∴CE⊥PA\)，
\(∵PA∩AD=A\)，\(PA⊂\)平面\(PAD\)，\(AD⊂\)平面\(PAD\)，
\(∴EC⊥\)平面\(PAD\)，
\(∵CE⊂\)平面\(PCE\)，\(∴\)平面\(PCE⊥\)平面\(PAD\)．
(2)解：\(∵EC⊥\)平面\(PAD\)，\(∴\)斜线\(PC\)在平面内的射影为\(PE\)，
即\(∠CPE\)是\(PC\)与平面\(PAD\)所成角的平面角，
\(∵PA⊥\)平面\(ABCD\)，\(AD⊂\)平面\(ABCD\)，\(∴PA⊥AD\)，
在\(Rt△PAE\)中，\(P E=\sqrt{P A^{2}+A E^{2}}=\sqrt{5}\)，
在\(Rt△CED\)中，\(C E=\sqrt{C D^{2}-E D^{2}}=\sqrt{3}\)，
\(∵EC⊥\)平面\(PAD\)，\(PE⊂\)平面\(PAD\)，\(∴EC⊥PE\)，
在\(Rt△CEP\)中，\(\tan \angle C P E=\dfrac{C E}{P E}=\dfrac{\sqrt{15}}{5}\)，
\(∴PC\)与平面\(PAD\)所成角的正切值为\(\dfrac{\sqrt{15}}{5}\)．
(3)解：在平面\(PAD\)中，过点\(E\)作\(EM⊥PD\)，垂足为\(M\)，连结\(CM\)，
\(∵EC⊥\)平面\(PAD\)，\(PD⊂\)平面\(PAD\)，\(∴EC⊥PD\)，
\(∵EM∩CM=M\)，\(∴PD⊥\)平面\(EMC\)，\(∴PD⊥CM\)，
\(∴∠EMC\)是二面角\(A－PD－C\)的平面角，
在\(Rt△EMD\)中，\(ED=1\)，\(∠ADP=45°\)，\(\therefore E M=M D=\dfrac{\sqrt{2}}{2}\)，
在\(Rt△CMD\)中，\(M D=\dfrac{\sqrt{2}}{2}\)，\(CD=2\)，\(\therefore C M=\sqrt{C D^{2}-M D^{2}}=\dfrac{\sqrt{14}}{2}\)，
在\(△EMC\)中，\(E C=\sqrt{3}\)，
由余弦定理得\(\cos \angle E M C=\dfrac{M E^{2}+M C^{2}-E C^{2}}{2 M E \cdot M C}=\dfrac{\dfrac{1}{2}+\dfrac{7}{2}-3}{2 \times \dfrac{\sqrt{2}}{2} \times \dfrac{\sqrt{14}}{2}}=\dfrac{1}{\sqrt{7}}\)，
\(∴\)二面角\(A－PD－C\)的正弦值为\(\dfrac{\sqrt{42}}{7}\)．
【答案】(1) 平行，证明见解析 \(\text { (2) }\left(\dfrac{\pi}{4}, \dfrac{\pi}{2}\right)\)
【解析】(1)证明：直线\(l∥\)平面\(PAC\)．证明如下：
连接\(EF\)，\(∵E，F\)分别是\(PA\)，\(PC\)的中点，\(∴EF∥AC\)．
又\(EF⊄\)平面\(ABC\)，\(AC⊂\)平面\(ABC\)，\(∴EF∥\)平面\(ABC\)．
而\(EF⊂\)平面\(BEF\)，且平面\(BEF∩\)平面\(ABC=l\)，\(∴EF∥l\)．
\(∵l⊄\)平面\(PAC\)，\(EF⊂\)平面\(PAC\)，
\(∴\)直线\(l∥\)平面\(PAC\)；
(2)解：由(1)知，\(l∥AC\)．
\(∵AB\)是\(⊙O\)的直径，\(∴AC⊥BC\)，于是\(l⊥BC\)．
已知\(PC⊥\)平面\(ABC\)，而\(l⊂\)平面\(ABC\)，\(∴PC⊥l\)．
而\(PC∩BC=C\)，\(∴l⊥\)平面\(PBC\)．
\(∵BF⊂\)平面\(PBC\)，\(∴l⊥BF\)．
故\(∠CBF\)就是二面角\(E－l－C\)的平面角．
\(∵PC=2AB=4\)，\(∴AB=2\)，\(CF=2\)．
在\(Rt△BCF\)中，\(\tan \angle C B F=\dfrac{C F}{B C}=\dfrac{2}{B C}\)，
\(∵0＜BC＜2\)，\(\therefore \tan \angle C B F=\dfrac{C F}{B C}=\dfrac{2}{B C} \in(1,+\infty)\)．
则\(\angle C B F \in\left(\dfrac{\pi}{4}, \dfrac{\pi}{2}\right)\)．
故二面角\(E－l－C\)大小的取值范围是\(\left(\dfrac{\pi}{4}, \dfrac{\pi}{2}\right)\)．