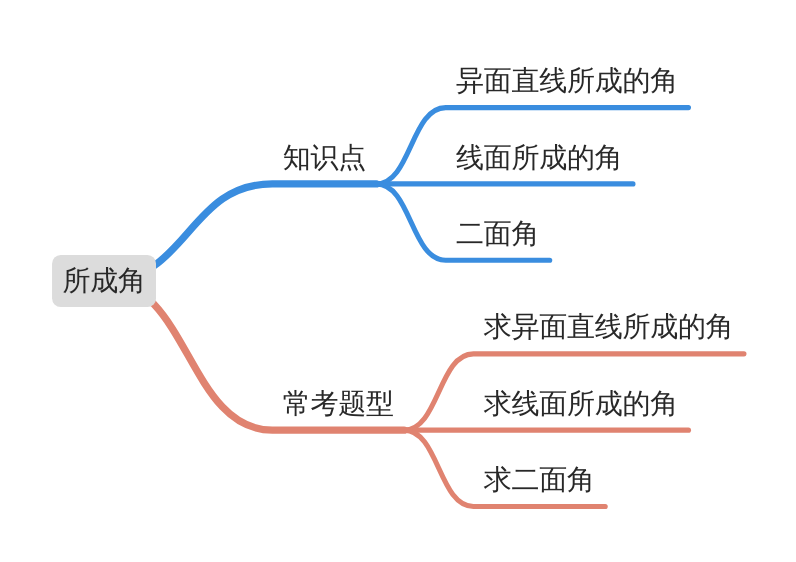
专题 关于球的外接与内切问题
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高一数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
适合必修第二册同步拔高练习、高三专题练习,难度4颗星!
模块导图
题型一 构造长方体求解
知识剖析
情况1 墙角模型
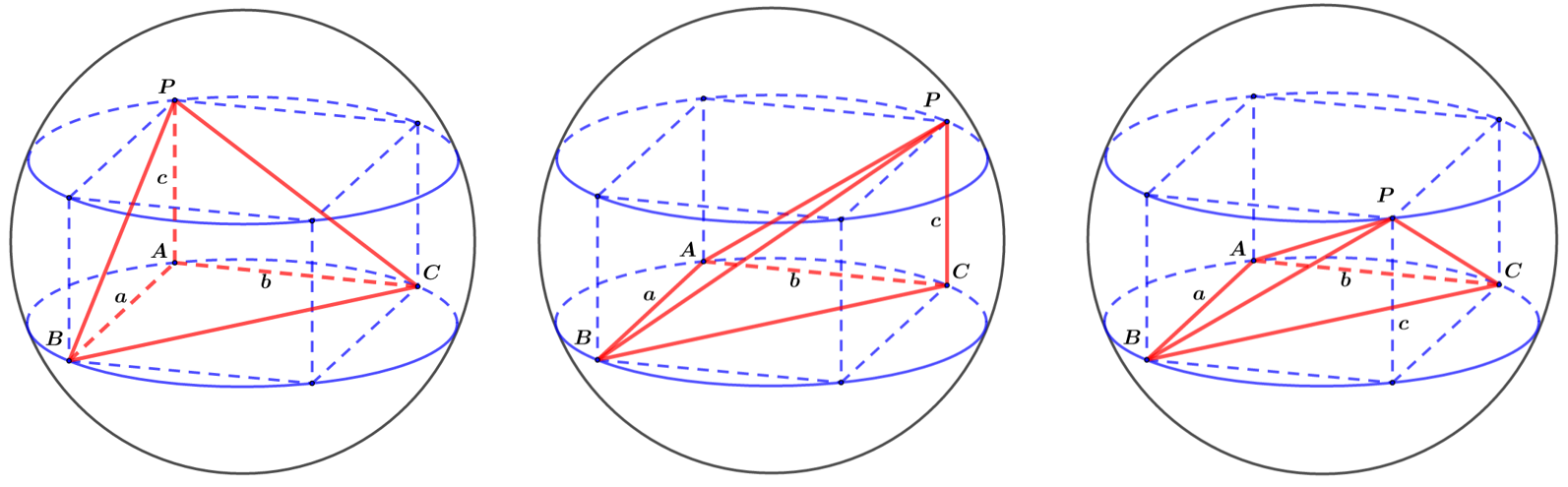
遇到以上四种三棱锥(有三条两两垂直的直线),均可构造长方体求解外接球半径\(R\);
求解外接球半径步骤
① 确定球心\(O\)的位置:外接球的球心是长方体的体对角线的中点;
② 求半径\(R\):长方体的体对角线即外接球直径,
则\((2 R)^{2}=a^{2}+b^{2}+c^{2} \Rightarrow R=\dfrac{\sqrt{a^{2}+b^{2}+c^{2}}}{2}\).
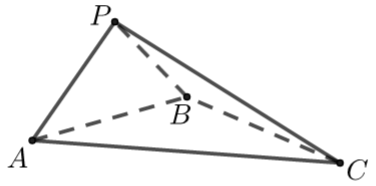
情况2 对棱相等的三棱锥
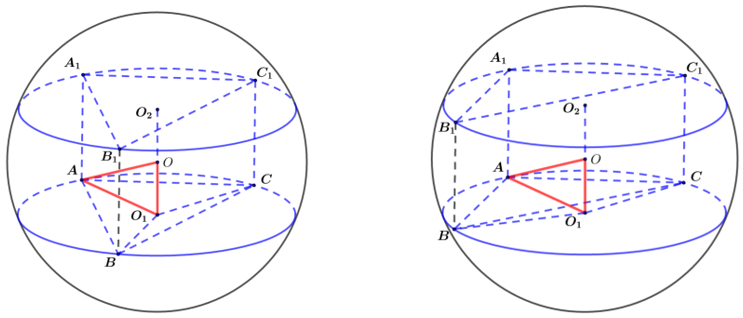
若三棱锥(即四面体)中,已知三组对棱分别相等(\(AD=BC=x\) ,\(AB=CD=y\),\(AC=BD=z\)),求外接球半径.
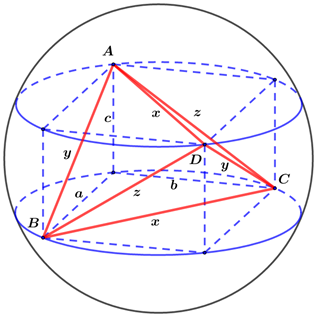
求解外接球半径步骤
① 确定球心\(O\)的位置:如上图构造一个长方体,标出三组互为异面直线的对棱;
② 求半径\(R\):
设长方体的长宽高分别为\(a\) ,\(b\) ,\(c\),\(AD=BC=x\) ,\(AB=CD=y\) ,\(AC=BD=z\),列方程组
\(\left\{\begin{array}{l}
a^{2}+b^{2}=x^{2} \\
b^{2}+c^{2}=y^{2} \\
c^{2}+a^{2}=z^{2}
\end{array} \Rightarrow(2 R)^{2}=a^{2}+b^{2}+c^{2}=\dfrac{x^{2}+y^{2}+z^{2}}{2}\right.\)
求出\(R\).
经典例题
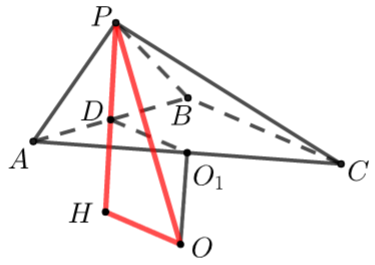
【典题1】如图,在三棱锥\(A-BCD\)中,\(BD⊥\)平面\(ADC\),\(BD=1\),\(AB=2\),\(BC=3\),\(A C=\sqrt{11}\),则三棱锥\(A-BCD\)外接球的体积为\(\underline{\quad \quad}\).
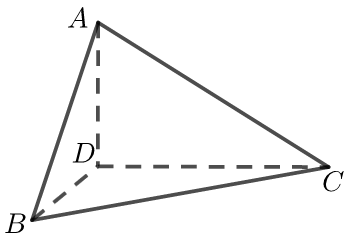
【解析】由\(BD=1\),\(AB=2\),\(BC=3\),\(A C=\sqrt{11}\),\(BD⊥\)平面\(ADC\),
\(\therefore A D=\sqrt{3}\),\(C D=2 \sqrt{2}\),\(A C=\sqrt{11}\),由勾股定理逆定理可知\(AD⊥CD\),
此时三棱锥中\(AD\)、\(BD\)、\(CD\)三直线两两垂直,
可知如图,三棱锥\(A-BCD\)是长方体的一个角,
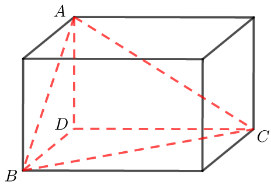
外接球的直径是长方体的体对角线,
所以三棱锥\(A-BCD\)外接球的半径为\(\dfrac{1}{2} \sqrt{1^{2}+(2 \sqrt{2})^{2}+(\sqrt{3})^{2}}=\sqrt{3}\).
所以外接球的体积\(V=\dfrac{4 \pi}{3} \times(\sqrt{3})^{3}=4 \sqrt{3} \pi\).
【点拨】
① 三棱锥中存在三条两两垂直的棱,可构造长方体进行求解外接球问题;
② 求解过程中要注意利用解三角形的方法求解各线段长度及其它们的位置关系,例如利用勾股定理逆定理证明线线垂直.
【典题2】如图,在三棱锥\(P-ABC\)中,\(PA⊥\)平面\(ABC\),\(AB⊥BC\),\(AD⊥BP\),\(PA=AC\),若三棱锥\(P-ABC\)外接球表面积为\(8π\),则三棱锥\(P-ACD\)体积的最大值为\(\underline{\quad \quad}\).

【解析】设\(AB=a\),\(BC=b\),由三棱锥\(P-ABC\)外接球表面积为\(8π\),得外接球的半径为\(\sqrt{2}\),
又\(PA⊥\)平面\(ABC\),得\(AB⊥BC\),
此时三棱锥中\(PA\)、\(AB\)、\(BC\)三直线两两垂直,
则如下图,三棱锥\(P-ABC\)是长方体的一个“角”,
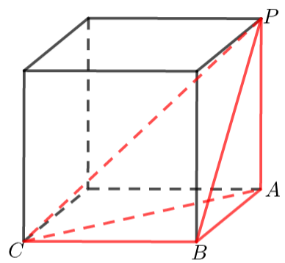
外接球的半径即为长方体的体对角线,
\(∴(2R)^2=AB^2+BC^2+AP^2=AC^2+AP^2=2AP^2\),得\(AP=2\),
\(∴a^2+b^2=4\).
\(∵PA⊥\)平面\(ABC\),\(AD⊥BP\),
\(\therefore P B=\sqrt{4+a^{2}}\),\(B D=\dfrac{a^{2}}{\sqrt{4+a^{2}}}\), \({\color{Red}{(此处用到了射影定理) }}\)
过\(D\)作\(DE⊥AB\),垂足为\(E\),则\(DE⊥\)平面\(ABC\),

\(∴DE∥PA\),可得\(\dfrac{D E}{P A}=\dfrac{B D}{P B}\),则\(D E=\dfrac{2 a^{2}}{4+a^{2}}\).
\(\therefore V_{P-A C D}=V_{P-A B C}-V_{D-A B C}=\dfrac{1}{3} S_{\triangle A B C} \cdot(P A-D E)\) \({\color{Red}{ (利用了割补法求体积) }}\)
\(=\dfrac{1}{6} a b \cdot\left(2-\dfrac{2 a^{2}}{4+a^{2}}\right)=\dfrac{4 a b}{3\left(4+a^{2}\right)}=\dfrac{4 a b}{3\left(2 a^{2}+b^{2}\right)}\)\(=\dfrac{4}{3\left(\dfrac{2 a}{b}+\dfrac{b}{a}\right)} \leq \dfrac{4}{6 \sqrt{2}}=\dfrac{\sqrt{2}}{3}\).
当且仅当\(\dfrac{2 a}{b}=\dfrac{b}{a}\),即\(a=\dfrac{2 \sqrt{3}}{3}\),\(b=\dfrac{2 \sqrt{6}}{3}\)时,等号成立.
\(∴\)三棱锥\(P-ACD\)体积的最大值为\(\dfrac{\sqrt{2}}{3}\).
【点拨】
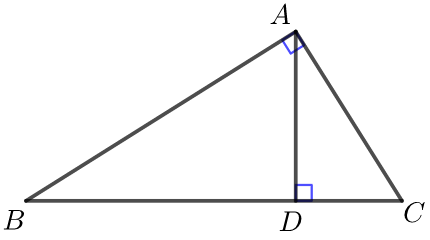
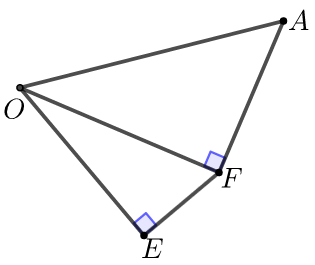
① 射影定理,如下图,已知\(Rt∆ABC\),\(AD⊥BC\),则\(D A^{2}=D B \cdot D C\),\(B A^{2}=B D \cdot B C\),\(C A^{2}=C D \cdot C B\).
② 求体积也可以用等积法\(V_{P-A C D}=V_{D-P A C}\).
【典题3】在三棱锥\(S-ABC\)中,\(SA=BC=5\),\(S B=A C=\sqrt{17}\),\(S C=A B=\sqrt{10}\),则该三棱锥外接球的表面积为 ( )
A.\(20π\) \(\qquad \qquad \qquad \qquad\) B.\(25π\) \(\qquad \qquad \qquad \qquad\) C.\(26π\) \(\qquad \qquad \qquad \qquad\) D.\(34π\)
【解析】由题意可将该三棱锥放在长方体中,
可得长方体的过同一个顶点的三个相邻的面的对角线分别为\(5\),\(\sqrt{17}\),\(\sqrt{10}\),
设长方体的长,宽,高分别为\(a ,b ,c\) ,
则\(\left\{\begin{array}{l}
a^{2}+b^{2}=5^{2}=25 \\
b^{2}+c^{2}=(\sqrt{17})^{2}=17 \\
a^{2}+c^{2}=(\sqrt{10})^{2}=10
\end{array}\right.\),
设三棱锥外接球的半径为\(R\),则\((2R)^2=a^2+b^2+c^2=26\),
外接球的表面积\(S=4πR^2=26π\),故选:\(C\).
【点拨】对棱相等的三棱锥的外接球问题可通过构造长方体求解.
巩固练习
1(★★)已知各顶点都在同一球面上的正四棱柱的高为\(4\),体积为\(16\),则这个球的表面积是\(\underline{\quad \quad}\).
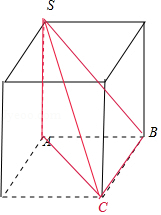
2(★★)设\(S\),\(A\),\(B\),\(C\)是球\(O\)表面上的四点,\(SA⊥\)平面\(ABC\),\(AB⊥BC\),\(S A=A B=\sqrt{2}\),\(BC=2\),则球\(O\)的表面积等于\(\underline{\quad \quad}\).
3(★★)在边长为\(4\)的正方形\(ABCD\)中,\(E\),\(F\)分别为\(AB\),\(BC\)的中点.将\(△AED\),\(△CFD\),\(△BEF\)分别沿\(DE\),\(DF\),\(EF\)折起,使\(A\),\(C\),\(B\)三点重合于\(A'\),则三棱锥\(A'-EFD\)的外接球表面积为\(\underline{\quad \quad}\).
4(★★)在三棱锥\(A-BCD\)中,\(AB=CD=2\),\(AD=BC=3\),\(AC=BD=4\),则三棱锥\(A-BCD\)外接球的表面积为\(\underline{\quad \quad}\).
5(★★)三棱锥\(A-BCD\),其中\(AB=CD=5\),\(AD=BC=7\),\(AC=BD=6\),则该三棱锥外接球的表面积为\(\underline{\quad \quad}\).
参考答案
-
【答案】\(24π\)
【解析】\(∵V=a^2 h=16\) \(∴a=2\),
由\((2R)^2=a^2+a^2+h^2=24⇒4R^2=24\)
\(∴S=4πR^2=24π\). -
【答案】\(8π\)
【解析】由题意将此三棱锥放在长方体中,因为\(AB⊥BC\),\(A B=\sqrt{2}\),\(BC=2\),
可得长方体的过同一个顶点的三条棱分别为:\(\sqrt{2}, 2, \sqrt{2}\),
而长方体的对角线的长度等于其外接球的直径\(2R\),
所以\((2 R)^{2}=2 \times(\sqrt{2})^{2}+2^{2}=8\),
所以外接球的表面积\(S=4πR2=8π\),
-
【答案】\(24π\)
【解析】在正方形\(ABCD\)中,\(∠A\)、\(∠B\)、\(∠C\)均为直角,
\(∴\)在三棱锥\(A′-DEF\)中,\(A′D\),\(A′E\),\(A′F\)三条线段两两垂直,
以\(A′D\),\(A′E\),\(A′F\)为棱构造长方体,
则长方体的外接球就是三棱锥\(A′-EFD\)的外接球,
正方形\(ABCD\)边长为\(4\),由题意\(A′E=A′F=2\),\(A′D=4\),
\(∴\)三棱锥\(A′-EFD\)外接球的半径\(r=\dfrac{\sqrt{A \prime E^{2}+A \prime F^{2}+A \prime D^{2}}}{2}=\sqrt{6}\),
\(∴\)三棱锥\(A′-EFD\)外接球的表面积为\(S=4 \pi \times(\sqrt{6})^{2}=24 \pi\).

-
【答案】\(\dfrac{29}{2} \pi\)
【解析】设补形为长方体,三个长度为三对面的对角线长,设长宽高分别为\(a,b,c\),
则\(a^2+b^2=9\),\(b^2+c^2=4\),\(c^2+a^2=16\)
\(\therefore 2\left(a^{2}+b^{2}+c^{2}\right)=29 \Rightarrow a^{2}+b^{2}+c^{2}=\dfrac{29}{2}\)\(\Rightarrow 4 R^{2}=\dfrac{29}{2} \Rightarrow S=\dfrac{29}{2} \pi\). -
【答案】\(55π\)
【解析】设补形为长方体,三个长度为三对面的对角线长,设长宽高分别为\(a,b,c\),
\(∴2(a^2+b^2+c^2 )=110⇒a^2+b^2+c^2=55\)\(⇒4R^2=55⇒S=55π\)
题型二 汉堡模型
知识剖析
预备知识
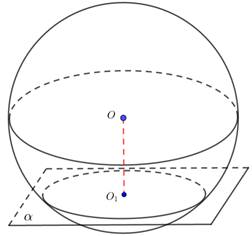
球体的截面都是圆,设某个不过球心的小圆圆心为\(O_1\),则球心\(O\)在过\(O_1\)且垂直平面\(α\)的直线上(即\(OO_1⊥α\)).
模型参考图像(棱柱以三棱柱为例)
模型条件:棱柱外接球问题
求解外接球半径步骤
① 确定球心\(O\)的位置:\(O_1\)是柱体底面所在的球体截面圆心,则\(OO_1⊥\)平面\(ABC\),由于柱体和外接球组合的几何体的对称性,则线段\(O_1 O_2\)的中点是球心\(O\);
② 算出小圆\(O_1\)的半径\(AO_1\),\(O O_{1}=\dfrac{1}{2} A A_{1}\);
③ 求半径\(R\):由勾股定理可得\(R=\sqrt{O_{1} A^{2}+O_{1} O^{2}}\).
经典例题
【典题1】已知三棱柱\(ABC-A_1 B_1 C_1\)的六个顶点都在同一球面上,且\(AA_1⊥\)底面\(ABC\),\(△ABC\)是等边三角形,\(AA_1=2\),\(AB=3\),则该球的表面积为( )
A.\(8π\) \(\qquad \qquad \qquad \qquad\) B.\(12π\) \(\qquad \qquad \qquad \qquad\) C.\(16π\) \(\qquad \qquad \qquad \qquad\) D.\(20π\)
【解析】如图,

由题意可知,三棱柱\(ABC-A_1 B_1 C_1\)为正三棱柱,底面边长\(AB=3\),高\(AA_1=2\).
在底面等边三角形\(ABC\)中,设其外心为\(O\),\(D\)为\(BC\)的中点,
则\(A O=\dfrac{2}{3} A D=\dfrac{2}{3} \sqrt{3^{2}-\left(\dfrac{3}{2}\right)^{2}}=\sqrt{3}\)
\({\color{Red}{(此处由2 r=\dfrac{A B}{\sin \angle C}=\dfrac{3}{\sin 60^{\circ}}=2 \sqrt{3} \Rightarrow A O=r=\sqrt{3}更容易些) }}\)
设上底面中心为\(O_1\),\(∵OO_1⊥\)平面\(ABC\),
\(∴\)三棱柱外接球的球心\(G\)必在直线\(OO_1\)
又由图像的对称性,可知三棱柱外接球的球心\(G\)为\(OO_1\)的中点,
连接\(GA\),则\(GA^2=AO^2+AG^2=3+1=4\).
\(∴\)该球的表面积为\(4π×4=16π\).故选:\(C\).
【点拨】
① 直棱柱的外接球问题属于“汉堡模型”.
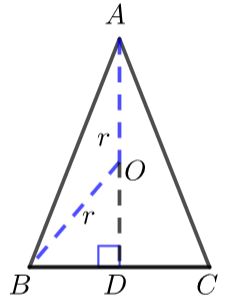
② 常见三角形的外接圆半径\(r\)
(1)等腰三角形\(r^2=(AD-r)^2+BD^2\)
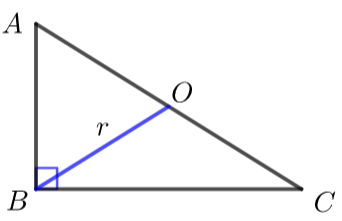
(2)直角三角形\(r=\dfrac{A C}{2}\)
(3)等边三角形 \(r=\dfrac{\sqrt{3}}{3} a\)
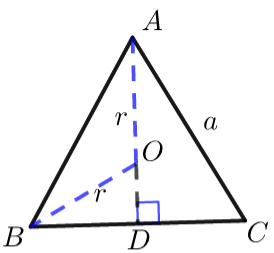
(4) 利用正弦定理可求任一三角形外接圆的半径\(\dfrac{a}{\sin A}=2 r\).
③ 柱体是四棱柱、五棱柱呢?常见情况如下,长方形、正六边形的外接圆圆心是对角线的中点.
【典题2】已知直三棱柱\(ABC-A_1 B_1 C_1\)的六个顶点都在球\(O\)的球面上,\(AB=AC=1\),\(B C=\sqrt{3}\),\(AA_1=2\),则球\(O\)的表面积为( )
A.\(4π\) \(\qquad \qquad \qquad \qquad\) B.\(8π\) \(\qquad \qquad \qquad \qquad\) C.\(12π\) \(\qquad \qquad \qquad \qquad\) D.\(16π\)
【解析】\(∵ AB=AC=1\),\(B C=\sqrt{3}\),
\(∴\)由余弦定理可得\(\cos \angle B A C=\dfrac{1+1-3}{2 \times 1 \times 1}=-\dfrac{1}{2}\),
\(\therefore \sin \angle B A C=\dfrac{\sqrt{3}}{2}\),
设\(△ABC\)的外接圆的半径为\(r\),
则\(2 r=\dfrac{B C}{\sin \angle B A C}=\dfrac{\sqrt{3}}{\dfrac{\sqrt{3}}{2}}=2\),所以\(r=1\),
设外接球的半径为\(R\),则\(R^{2}=\left(\dfrac{A A_{1}}{2}\right)^{2}+r^{2}=\left(\dfrac{2}{2}\right)^{2}+1^{2}=2\),
所以外接球的表面积\(S=4πR^2=8π\),
故选:\(B\).
【点拨】底面三角形\(∆ABC\)三边都已知,则三角形是确定的,则利用解三角形的方法便可求出其外接圆的半径.
巩固练习
1(★★)一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为\(\dfrac{9}{8}\),底面周长为\(3\),则这个球的体积为\(\underline{\quad \quad}\).
2(★★)在直三棱柱\(ABC-A_1 B_1 C_1\)中,\(AB=4\),\(AC=6\),\(\angle B A C=\dfrac{\pi}{3}\) ,\(AA_1=4\) , 则直三棱柱\(ABC-A_1 B_1 C_1\)的外接球的表面积为\(\underline{\quad \quad}\).
3(★★)直三棱柱\(ABC-A_1 B_1 C_1\)的各顶点都在同一球面上,若\(AB=AC=AA_1=2\) ,\(∠BAC=120^°\),则此球的表面积等于\(\underline{\quad \quad}\).
参考答案
- 【答案】\(\dfrac{4 \pi}{3}\)
【解析】设正六边形边长为\(a\),正六棱柱的高为\(h\),底面外接圆的关径为\(r\),则\(a=\dfrac{1}{2}\),
底面积为\(S=6 \cdot \dfrac{\sqrt{3}}{4} \cdot\left(\dfrac{1}{2}\right)^{2}=\dfrac{3 \sqrt{3}}{8}\),\(V=S h=\dfrac{3 \sqrt{3}}{8}=\dfrac{9}{8} \Rightarrow h=\sqrt{3}\),
\(\therefore R^{2}=\left(\dfrac{\sqrt{3}}{2}\right)^{2}+\left(\dfrac{1}{2}\right)^{2}=1 \Rightarrow R=1\),球的体积为\(V=\dfrac{4 \pi}{3}\). - 【答案】\(\dfrac{160}{3} \pi\)
【解析】\(B C^{2}=16+36-2 \cdot 4 \cdot 6 \cdot \dfrac{1}{2}=28\),所以\(B C=2 \sqrt{7}\)
\(2 r=\dfrac{2 \sqrt{7}}{\dfrac{\sqrt{3}}{2}}=\dfrac{4 \sqrt{7}}{\sqrt{3}} \Rightarrow r=\dfrac{2 \sqrt{7}}{\sqrt{3}}, \quad R^{2}=r^{2}+\left(\dfrac{A A_{1}}{2}\right)^{2}=\dfrac{40}{3}\),
所以\(S=\dfrac{160}{3} \pi\). - 【答案】\(20π\)
【解析】在\(∆ABC\)中,因为\(AB=AC=AA_1=2\) ,\(∠BAC=120^°\),可得\(B C=2 \sqrt{3}\),
由正弦定理可得\(∆ABC\)外接圆的半径\(r=2\),
设圆心为\(O'\),球心为\(O\),在\(Rt∆OBO'\)中,易得球半径\(R=\sqrt{5}\),
故此球的表面积为\(4πR^2=20π\).
题型三 垂面模型(一条直线垂直于一个平面)
知识剖析
情况1 模型参考图像(以三棱锥为例)
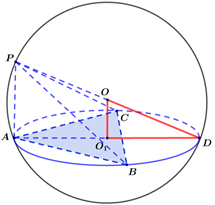
模型条件:三棱锥\(P-ABC\)中\(PA⊥\)平面\(ABC\)
解题步骤
① 确定球心\(O\)的位置:\(O_1\)是\(△ABC\)的外心,
则\(OO_1⊥\)平面\(ABC\)且\(O O_{1}=\dfrac{P A}{2}\);
② 由正弦定理\(\dfrac{a}{\sin A}=2 r\)算出小圆\(O_1\)的半径\(AO_1=r\);
③ 求半径\(R\):由勾股定理\(R=\sqrt{\left(\dfrac{P A}{2}\right)^{2}+r^{2}}\).
情况2
预备知识:\(P\)的射影是\(∆ABC\)的外心\(⇔\)三棱锥\(P-ABC\)的三条侧棱相等
模型参考图像模型参考图像(以三棱锥为例)
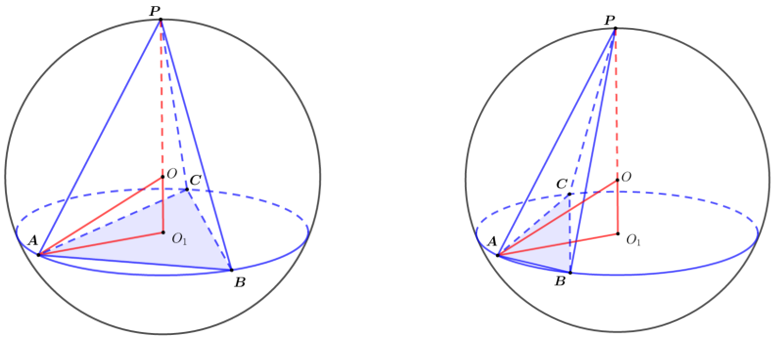
模型条件:三棱锥\(P-ABC\)中\(P\)的射影是\(△ABC\)的外心\(O_1\).
解题步骤
① 确定球心\(O\)的位置: 取\(△ABC\)的外心\(O_1\),因为\(P\)的射影是\(△ABC\)的外心\(O_1\),则球心在直线\(PO_1\)上;
② 由正弦定理\(\dfrac{a}{\sin A}=2 r\)算出小圆\(O_1\)的半径\(AO_1=r\),算出棱锥的高\(PO_{1}\);
③ 求半径\(R\):\(OA^2=O_1 A^2+O_1 O^2⇒R^2=(h-R)^2+r^2\),解出\(R\).
若是如下图的三棱锥(球心在锥体的下方),方法类似.
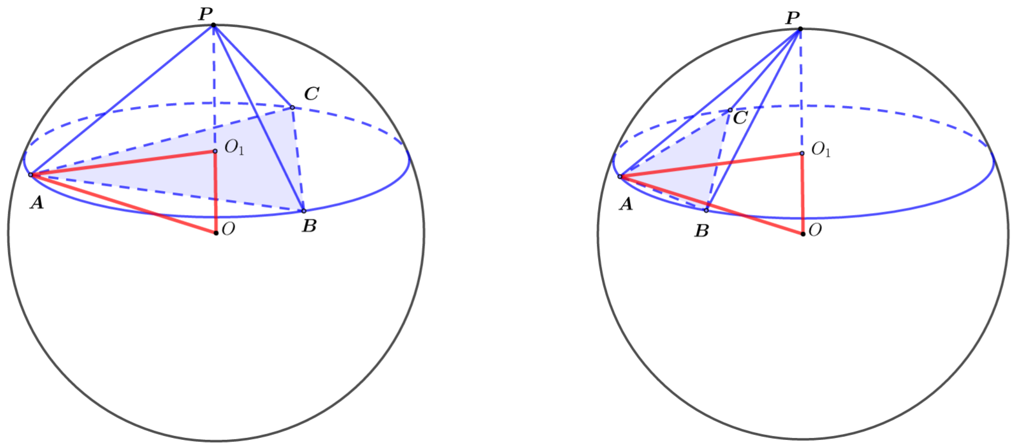
情况3
模型参考图像
(以三棱锥为例,其中\(O\)是球心,\(O_1\)是三角形\(ABC\)的外接圆圆心,\(PD⊥\)平面\(ABC\))
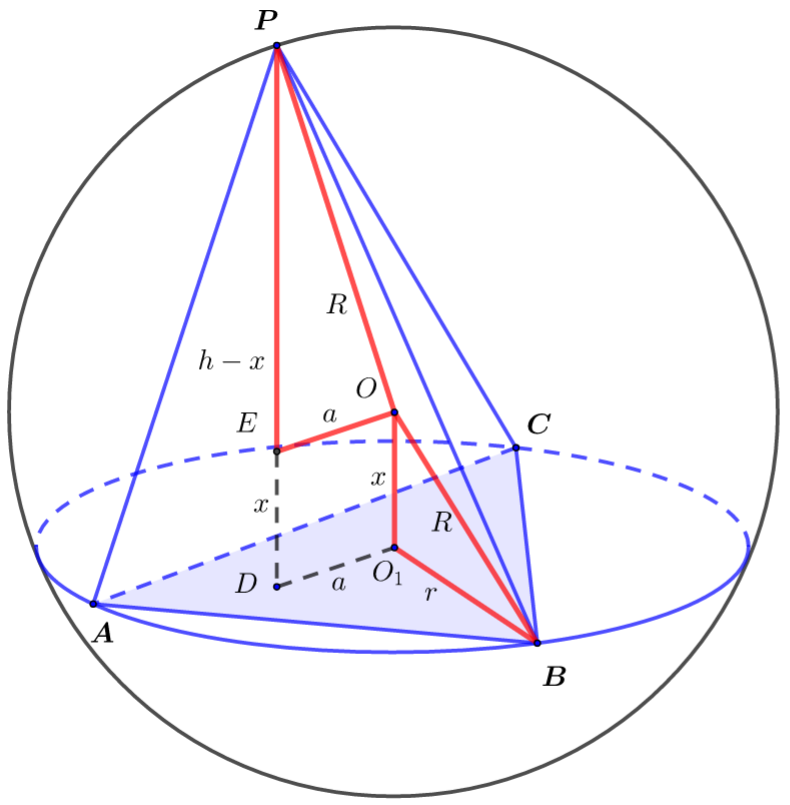
模型条件:三棱锥\(P-ABC\)中\(P\)的射影不是\(△ABC\)的外心\(O_1\).
解题步骤
① 由\(\dfrac{a}{\sin A}=2 r\)算出小圆\(O_1\)的半径\(BO_1=r\),由题意求出三棱锥的高\(PD=h\),\(DO_1=a\);
(一般求\(a\)有难度,需要确定点\(D\)的位置)
② 确定球心\(O\)的位置:球心\(O\)在过\(O_1\)且垂直平面\(ABC\)的直线上,设\(OO_1=x\);
(一般\(x\)求不出来,因为球心\(O\)很难确定,若可以题目就比较简单了!)
③ 求外接球半径\(R\):在\(Rt∆BOO_1\)和\(Rt∆PEO\)中可得
\(\left\{\begin{array}{c}
R^{2}=O B^{2}=O O_{1}^{2}+B O_{1}^{2}=x^{2}+r^{2} \\
R^{2}=O P^{2}=P E^{2}+O E^{2}=(h-x)^{2}+a^{2}
\end{array} \Rightarrow x^{2}+r^{2}=(h-x)^{2}+a^{2}\right.\)
求出\(x\),从而求出外接球半径\(R\).
(多数情况当\(P\)的射影不是\(△ABC\)的外心\(O_1\),需要在两个直角三角形中求出\(R\).)
经典例题
【典题1】正四棱锥\(S-ABCD\)的底面边长和各侧棱长都为\(\sqrt{2}\),各顶点都在同一个球面上,则此球的体积为\(\underline{\quad \quad}\).
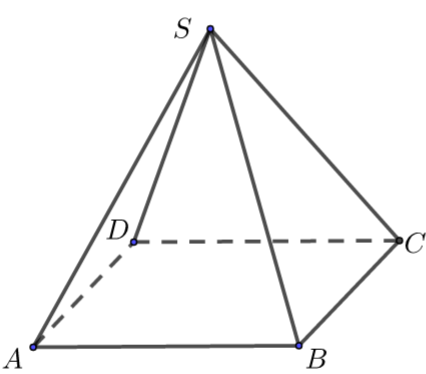
【解析】\({\color{Red}{ 方法一 }}\) 正方形\(ABCD\)的中心\(O_1\),易得外接圆半径\(r=AO_1=1\),\(SO_1=1\),
找球心\(O:\) \(∵SO_1⊥\)平面\(ABCD\),显然球心\(O\)在\(SO_1\)上,
求外接球半径\(R\):
在\(Rt∆OAO_1\)中,\(AO^2=AO_1^2+OO_1^2⇒R^2=1+(1-R)^2⇒R=1\)(即\(O\)、\(O_1\)重合)
\(\therefore V=\dfrac{4 \pi}{3}\).
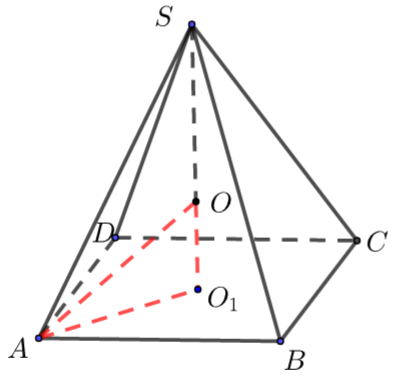
\({\color{Red}{方法二 }}\) 正方形\(ABCD\)的中心\(O\),易得\(AO=BO=CO=DO=1\),而\(SO=1\),
则外接球的球心就是\(O\),且半径\(R=1\),\(\therefore V=\dfrac{4 \pi}{3}\).
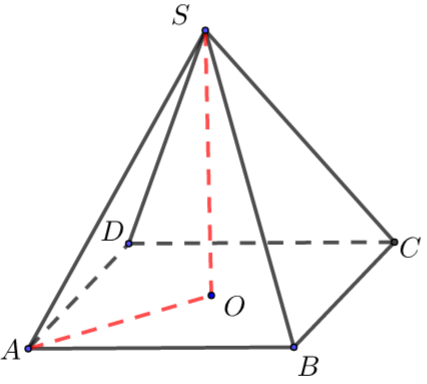
\({\color{Red}{ 方法三}}\) 大圆是轴截面所的外接圆,即大圆是\(△SAC\)的外接圆,此处特殊,\(Rt△SAC\)的斜边是球半径,\(2R=2\),\(R=1\),\(\therefore V=\dfrac{4 \pi}{3}\).
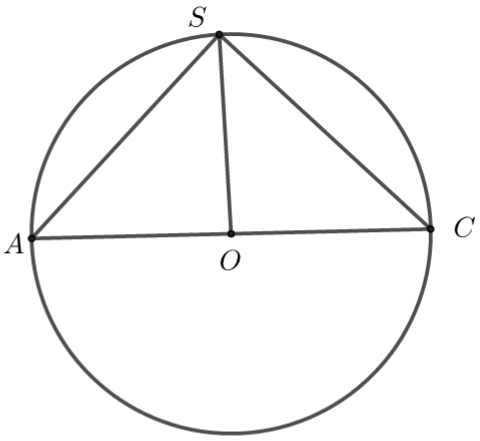
【点拨】
① 正四棱锥的外接球问题是显然属于“垂面模型”的(存在其高\(SO_1⊥\)底面\(ABCD\)),方法一就是按照模型的套路进行求解的;
② 本题具有特殊性,正四棱锥的侧棱与底面边长相等,方法一根据外接球的定义,直接确定了球心的位置并求出半径;方法二利用了大圆是轴截面所的外接圆与直角三角形的特性求出了半径;
③ 做题不能太“模型化”,要发散多思考几种方法,避免思维定势开拓自己的思维提高分析能力.
【典题2】已知三棱锥\(P-ABC\)四个顶点都在球\(O\)上,\(P A=P B=P C=2 \sqrt{3}\),\(BC=3\),\(∠BAC=60°\).则球\(O\)的表面积为( )
A. \(36 \pi\) \(\qquad \qquad \qquad \qquad\)B. \(16 \pi\) \(\qquad \qquad \qquad \qquad\)C. \(12 \pi\) \(\qquad \qquad \qquad \qquad\)D. \(\dfrac{16}{3} \pi\)
【解析】在\(△ABC\)中,\(BC=3\),\(∠BAC=60°\),
可得\(△ABC\)的外接圆半径 \(2 r=\dfrac{3}{\dfrac{\sqrt{3}}{2}}=2 \sqrt{3} \Rightarrow r=\sqrt{3}\),
如图所示,

设\(P\)点在平面\(ABC\)内的投影的为\(D\),则\(A D=r=\sqrt{3}\),
在\(Rt△PDA\)中,因为\(PD^2+AD^2=PA^2\),解得\(PD=3\),
设三棱锥 \(P-ABC\) 的外接球半径\(R\),
即\(OP=OA=R\),\(OD=3-R\),
在\(△ODA\)中,由勾股定理得
\(OD^2+DA^2=OA^2⇒(3-R)^2=(√3 )^2=R^2\),解得\(R=2\),
故三棱锥\(P-ABC\)的外接球半径为\(2\),
根据球体的表面积公式\(S=4πR^2\),
可得球\(O\)的表面积为 \(S=4π×2^2=16π\).
故选:\(B\).
【点拨】由\(PA=PB=PC\)可知,点\(P\)在平面\(ABC\)的投影是三角形\(ABC\)外心,本题属于垂面模型中的第二种情况,按照基本套路解题难度不大,在一个直角三角形\(△ODA\)利用勾股定理便得到关于\(R\)的方程进而求出\(R\).
【典题3】在四棱锥\(P-ABCD\)中,\(BC∥AD\),\(AD⊥AB\),\(A B=2 \sqrt{3}\),\(AD=6\),\(BC=4\),\(P A=P B=P D=4 \sqrt{3}\),则三棱锥\(P-BCD\)外接球的表面积为\(\underline{\quad \quad}\).
【解析】根据题意画出图形,如图所示;

取\(AD\)的两个三等分点\(O_1\),\(E\),
连接\(BD\),\(O_1 C\),\(CE\),\(BD∩O_1 C=H\),连接\(PH\),\(AH\);
由题意可得\(A H=B H=D H=\dfrac{1}{2} B D=\dfrac{1}{2} \times \sqrt{12+36}=2 \sqrt{3}\),
则\(O_1 B=O_1 C=O_1 D=4\),故\(O_1\)是\(△BCD\)的外接圆的圆心.
因为\(P A=P B=P D=4 \sqrt{3}\),\(H\)是\(Rt∆ABD\)的外接圆圆心,
所以\(PH⊥\)平面\(ABCD\),且\(P H=\sqrt{(4 \sqrt{3})^{2}-(2 \sqrt{3})^{2}}=6\).
在菱形\(AO_1 DC\)中,\(O_{1} H=\dfrac{1}{2} O C_{1}=2\),
设\(O\)为三棱锥\(P-BCD\)外接球的球心,
连接\(OO_1\),\(OP\),\(OD\),过\(O\)作\(OF⊥PH\),垂足为\(F\),
则四边形\(OO_1 HF\)是矩形,
设外接球的半径\(R\),\(OO_1=x\),
在\(Rt∆OO_1 D\)中有\(OD^2=OO_1^2+O_1 D^2⇒R^2=x^2+16\),
在\(Rt∆POF\)中有\(OP^2=OF^2+PF^2⇒R^2=4+(6-x)^2\)
则\(x^2+16=4+(6-x)^2\),解得\(x=2\),
从而\(R^2=20\),故三棱锥\(P-BCD\)外接球的表面积为\(4πR^2=80π\).
【点拨】
① 本题的模型对应的是垂面模型的情况三,点\(P\)到平面\(ABCD\)的投影不是底面\(BCD\)的外心;
② 本题难点一:确定三角形\(BCD\)外接圆圆心\(O_1\);思路:由于四边形\(ABCD\)是确定的,可解出三角形\(BCD\),进而利用\(\dfrac{a}{\sin A}=2 r\)求出其外接圆\(r\),由三角形外接圆圆心是三边中垂线的交点也就可知圆心\(O_1\)在\(AD\)的三等分点处;题目有多线段的数量和位置关系,多用平几的知识点求解出其他线段或者角度,这样更有助于找到解题思路;
③ 本题难点二:\(P\)到平面\(ABCD\)的投影\(H\)的位置;思路:\(∵PA=PB=PD\),\(∴\)点\(H\)是三角形\(ABD\)外心,又\(∵∆ABD\)是直角三角形,故点\(H\)在\(BD\)的中点处.
④ 遇到垂面模型的第三种情况,往往利用两个直角三角形(比如本题的\(Rt∆OO_1 D\)、\(Rt∆POF\))得到外接球半径R的方程.
巩固练习
1(★★★)在四面体\(S-ABC\)中,\(SA⊥\)平面\(ABC\),\(∠BAC=120^∘\) ,\(SA=AC=2\) ,\(AB=1\), 则该四面体的外接球的表面积为\(\underline{\quad \quad}\).
2(★★★)正四棱锥的顶点都在同一球面上,若该棱锥的高为\(1\),底面边长为\(2 \sqrt{3}\),则该球的表面积为\(\underline{\quad \quad}\).
3(★★★)已知正三棱锥\(S-ABC\)的四个顶点都在球\(O\)的球面上,且球心\(O\)在三棱锥的内部,若该三棱锥的侧面积为\(7 \sqrt{3}\),\(BC=2\),则球\(O\)的表面积为\(\underline{\quad \quad}\).
4(★★★)在三棱锥\(P-ABC\)中,\(AB=2\),\(AC⊥BC\),\(D\)为\(AB\)中点,\(PD=2\),若该三棱锥的体积的最大值为\(\dfrac{2}{3}\),则其外接球表面积为\(\underline{\quad \quad}\).
参考答案
- 【答案】\(49π\)
【解析】由正弦定理或找球心都可得\(2R=7\),\(S=4πR^2=49π\). - 【答案】\(\dfrac{40 \pi}{3}\)
【解析】在\(△ABC\)中,\(B C^{2}=A C^{2}+A B^{2}-2 A B \cdot A C \cdot \cos 120^{\circ}=7 \Rightarrow B C=\sqrt{7}\),
\(△ABC\)的外接球直径为\(2 r=\dfrac{B C}{\sin \angle B A C}=\dfrac{2 \sqrt{7}}{\sqrt{3}}\),
\(\therefore(2 R)^{2}=(2 r)^{2}+S A^{2}=\left(\dfrac{2 \sqrt{7}}{\sqrt{3}}\right)^{2}+4=\dfrac{40}{3} \Rightarrow S=4 \pi R^{2}=\dfrac{40 \pi}{3} .\) - 【答案】\(\dfrac{169 \pi}{9}\)
【解析】作 \(SM⊥\)平面\(ABC\),连结\(AM\) 并延长交 \(BC\)于点\(D\),连结\(SD\),
正三棱雉外接球的球心\(O\)在高\(SM\)上,连结 \(OA\),

\(\because S=\dfrac{1}{2} \times 2 \times S D \times 3=7 \sqrt{3}\),解得\(S D=\dfrac{7 \sqrt{3}}{3}\),
正三角形\(ABC\)中,\(D M=\dfrac{\sqrt{3}}{6} B C=\dfrac{\sqrt{3}}{3}\),\(A M=\dfrac{2 \sqrt{3}}{3}\),
\(\therefore S M=\sqrt{S D^{2}-D M^{2}}=4\),
设\(SO=AO=R\),\(△OAM\)中,
\(R^{2}=(4-R)^{2}+\left(\dfrac{2 \sqrt{3}}{3}\right)^{2}\),解得\(R=\dfrac{13}{6}\),
则球\(O\) 的表面积\(S=4 \pi R^{2}=\dfrac{169 \pi}{9}\). - 【答案】\(D\)
【解析】由题意可得
\(V_{\text {锥}}=\dfrac{1}{3} S_{\triangle A B C} \cdot h \leq \dfrac{1}{3} \cdot \dfrac{1}{2} A C \cdot B C \cdot P D\)\(\leq \dfrac{1}{3} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2}\left(A C^{2}+B C^{2}\right) \cdot P D\)\(=\dfrac{1}{12} \cdot A B^{2} \cdot 2=\dfrac{1}{12} \cdot 4 \cdot 2=\dfrac{2}{3}\),
当且仅当\(AC=BC\),\(PD⊥\)面\(ABC\)时,该三棱锥的体积的最大值为\(\dfrac{2}{3}\),
设外接球的半径为\(R\),球心为\(O\),
则由题意可得\(O\)在\(PD\)上,底面外接圆的半径\(r=\dfrac{A B}{2}=1\),
可得\((2-R)^{2}+r^{2}=R^{2}\),即\((2-R)^{2}+1=R^{2}\),解得\(R=\dfrac{5}{4}\),
所以外接球的表面积\(S=4 \pi R^{2}=\dfrac{25}{4} \pi\),故选:\(D\).

题型四 一般模型
知识剖析
以上几种模型,都有具体的条件要求,它们对应有简便的求解方法,那现在提出一个一般情况的问题:如何求解任一锥体的外接球的半径?(这个问题解决了面积、体积等各种问题也不成问题).
预备知识
球体的截面都是圆,设两个不平行的截面小圆的圆心为\(O_1\) ,\(O_2\),分别过\(O_1\) ,\(O_2\)作两个截面的垂线,则球心\(O\)是两条垂线的交点.
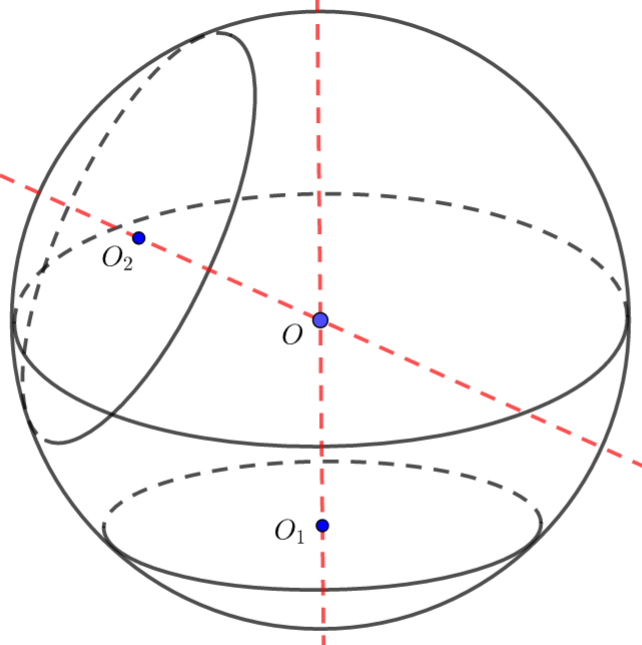
不失一般性,如下图进行分析:已知三棱锥\(A-BCD\)每条棱长度,求其外接球的半径.
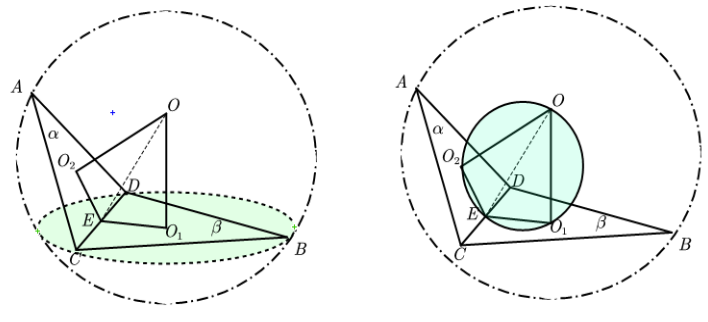
解题步骤
① 确定球心\(O\)的位置:找出\(∆BCD\)和\(∆ACD\)的外心\(O_1\)和\(O_2\),过\(O_1\)和\(O_2\)分别作平面\(BCD\)和平面\(ACD\)的垂线,两垂线的交点即为球心\(O\),此时点\(O\)、\(O_1\)、\(O_2\) 、\(E\)肯定共面;
② 求半径\(R\):这里提供二个思路
(1) 在\(Rt∆OO_1 C\)中有\(R^{2}=C O^{2}=O_{1} C^{2}+O O_{1}^{2}\),其中\(O_1 C\)用正弦定理\(\dfrac{a}{\sin A}=2 r\)可求,而\(OO_1\)的求法各异,要根据二面角\(∠O_2 EO_1\)确定;
(2) 在\(Rt∆OEC\)中有\(R^{2}=C O^{2}=E C^{2}+E O^{2}=\left(\dfrac{C D}{2}\right)^{2}+E O^{2}\),其中\(CD\)是已知的,而\(EO\)可在四边形\(O_2 EO_1 O\)求解出,其中\(∵OO_1⊥O_1 E\),\(OO_2⊥O_2 E\),所以\(O_2\)、\(E\)、\(O_1\)、\(O\)四点共圆,\(OE\)是圆的直径则\(O E=\dfrac{O_{1} O_{2}}{\sin \angle O_{2} E O_{1}}\),接着根据题意再用平几的方法求解便可.
经典例题
【典题1】已知三棱锥\(A-BCD\)中,\(∆BAC\)和\(∆BDC\)是全等的等边三角形,边长为\(2\),当三棱锥体积最大时,三棱锥的外接球表面积为\(\underline{\quad \quad}\).
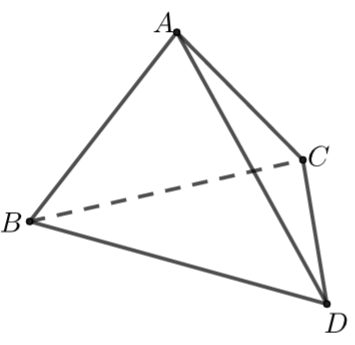
【解析】如图,当平面\(BAC⊥\)平面\(BDC\)时,三棱锥体积最大,

取\(BC\)中点\(E\),连接\(AE\)、\(DE\),则\(AE⊥BC\),\(DE⊥BC\),
因为平面\(BAC⊥\)平面\(BDC\),
所以可证得\(AE⊥\)平面\(BCD\),\(DE⊥\)平面\(ABC\),
取三角形\(BCD\)的外心\(F\),作\(FM∥AE\),则\(F、M、E、A\)四点共面,
取三角形\(ABC\)的外心\(H\),过点\(H\)作\(EF\)的平行线交\(FM\)于点\(O\),
因为\(EF\)垂直平面\(ABC\),则\(HO\)垂直平面\(ABC\),
于是点\(O\)到\(A、B、C、D\)四点的距离相等,
所以点\(O\)为三棱锥\(A-BCD\)外接球的球心.
连接\(OC\),可求得\(O F=H E=\dfrac{\sqrt{3}}{3}\),\(C F=\dfrac{2 \sqrt{3}}{3}\),
所以\(R^{2}=O C^{2}=O F^{2}+C F^{2}=\dfrac{1}{3}+\dfrac{4}{3}=\dfrac{5}{3}\),
所以外接球表面积为\(S=4 \pi R^{2}=\dfrac{20 \pi}{3}\).
【点拨】\(BAC⊥\)本题中平面平面\(BDC\),是两平面垂直(即二面角为\(90^°\))的情况,球心还是比较好确定的,即过三角形\(BAC\)、\(BDC\)的外心作的垂线交点,此时四边形\(HOFE\)是矩形,很多量都好求.
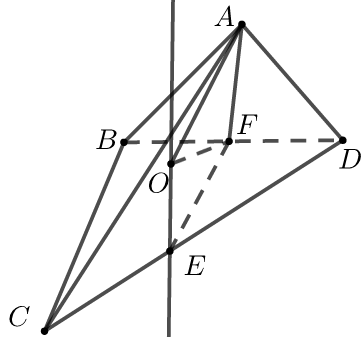
【典题2】如图所示,三棱锥\(P-ABC\)中,\(\angle A P B=\dfrac{2 \pi}{3}\),\(P A=P B=\sqrt{3}\),\(AC=5\),\(BC=4\),且平面\(PAB⊥\)平面\(ABC\),则该三棱锥的外接球的表面积为( )
A.\(16π\) \(\qquad \qquad \qquad \qquad\)B.\(32π\) \(\qquad \qquad \qquad \qquad\) C.\(24π\)\(\qquad \qquad \qquad \qquad\)D.\(28π\)
【解析】\(∆PAB\)中,\(\angle A P B=\dfrac{2 \pi}{3}\),\(P A=P B=\sqrt{3}\),
\(\therefore \angle P A B=\dfrac{\pi}{6}\)
设\(∆PAB\)的外心为\(H\),外接圆半径为\(r\),
则\(2 r=\dfrac{P B}{\sin \angle P A B}=\dfrac{\sqrt{3}}{\dfrac{1}{2}}=2 \sqrt{3} \Rightarrow P H=r=\sqrt{3}\),
取\(AB\)的中点\(D\),连接\(PD\),则\(PD\)是线段\(AB\)的中垂线,
根据三角形外心的定义,可知点\(H\)在直线\(PD\)上,
\(\because P D=P B \cdot \cos \dfrac{\pi}{3}=\sqrt{3} \cdot \dfrac{1}{2}=\dfrac{\sqrt{3}}{2}<P H\),
\(∴\)点\(H\)在\(∆ABC\)外,
在\(∆ABC\)中可得\(AC=5\),\(BC=4\),\(AB=3\),
所以可得\(AB^2+BC^2=AC^2\),即\(\angle A B C=\dfrac{\pi}{2}\),
取\(AC\)的中点\(O_1\),
则可得\(O_1\)为\(△ABC\)的外接圆的圆心,\(D O_{1}=\dfrac{1}{2} B C=\dfrac{1}{2} \times 4=2\),
过\(H\)、\(O_1\)分别作平面\(PAB\)、\(ABC\)的垂线\(l_1\) ,\(l_2\),
\(∴l_1\) ,\(l_2\)垂直且相交,设交点为\(O\),即为球心,
在\(Rt∆PHO\)中,\(R^{2}=O P^{2}=P H^{2}+O H^{2}=(\sqrt{3})^{2}+2^{2}=7\),
所以外接球的表面积\(S=4πR^2=4π×7=28π\),
故选:\(D\).
【点拨】
① 本题平面\(PAB⊥\)平面\(ABC\),属于两平面垂直(即二面角为\(90^°\))的情况,球心不难找,但是要细心些点\(H\)在三角形\(ABP\)内还是外;
② 思考 垂线\(l_1\) ,\(l_2\)会不会是异面直线,那它们就不交于点\(O\)?
分析 不会的,\(∵\)平面\(PAB⊥\)平面\(ABC\),平面\(PAB∩\)平面\(ABC=AB\),\(∴PD⊥\)面ABC,\(∴PD//l_2\),
同理\(DO_1⊥l_1\),
故点\(D、H、O、O_1\)四点共面,其实题目求三棱锥\(ABCP\)的外接球,则两条垂直\(l_1\) ,\(l_2\)的交点一定是球心\(O\).
【典题3】如图,四面体\(ABCD\)中,面\(ABD\)和面\(BCD\)都是等腰\(Rt∆\),\(A B=\sqrt{2}\),\(\angle B A D=\angle C B D=\dfrac{\pi}{2}\),且二面角\(A-BD-C\)的大小为\(\dfrac{5 \pi}{6}\),若四面体\(ABCD\)的顶点都在球\(O\)上,则球\(O\)的表面积为( )

A. \(12 \pi\) \(\qquad \qquad \qquad \qquad\)B. \(20 \pi\) \(\qquad \qquad \qquad \qquad\)C. \(24 \pi\) \(\qquad \qquad \qquad \qquad\)D. \(36 \pi\)
【解析】取\(CD\)中点\(E\),\(BD\)中点\(F\),连结\(BE、AF、EF\),
\(∵\)四面体\(ABCD\)中,面\(ABD\)和面\(BCD\)都是等腰\(Rt∆\),
\(A B=\sqrt{2}\),\(\angle B A D=\angle C B D=\dfrac{\pi}{2}\),且二面角\(A-BD-C\)的大小为\(\dfrac{5 \pi}{6}\),
\(∴AF⊥BD\),\(EF⊥BD\),
\(∴∠AFE\)是二面角\(A-BD-C\)的平面角,\(\angle A F E=\dfrac{5 \pi}{6}\),
\(B D=B C=\sqrt{2+2}=2\),\(C D=\sqrt{4+4}=2 \sqrt{2}\),\(C E=D E=\sqrt{2}\),
\(AF=BF=DF=EF=1\),\(E F=\dfrac{1}{2} B C=1\),
则点\(E\)为\(∆BCD\)外接圆的圆心,点\(F\)为\(∆ABD\)外接圆的圆心,
过点\(E\)作平面\(BCD\)的垂线\(EO\),过点\(F\)作平面\(ABD\)的垂线\(FO\),
且直线\(EO\)与直线\(FO\)交于点\(O\),
则点\(O\)为四面体\(ABCD\)外接球的球心,\(OA\)为半径,
如下图所示,
易知\(\angle A F O=\angle O E F=\dfrac{\pi}{2}\),\(\angle O F E=\angle A F E-\dfrac{\pi}{2}=\dfrac{\pi}{3}\),
所以\(O F=\dfrac{E F}{\cos \angle O F E}=2\),
所以\(O A=\sqrt{A F^{2}+O F^{2}}=\sqrt{5}\),
则四面体\(ABCD\)的外接球半径为\(\sqrt{5}\),
因此球\(O\)的表面积为\(4 \pi \cdot(\sqrt{5})^{2}=20 \pi\),
故选:\(B\).
【点拨】
① 要注意常见三角形(等腰三角形、直角三角形、等边三角形等)外接圆圆心的位置;
② 这是典型的“折叠模型”,二面角不是\(90^°\),在找球心的时候,要确定两个“折面”的圆心,因为球心是过两个圆心的垂线交点.
③ 在求外接球半径时,把含两垂线\(OE\)、\(OF\)和半径\(OA\)的平面四边形\(OAFE\)拿出来分析求出半径,要注意二面角的使用.
巩固练习
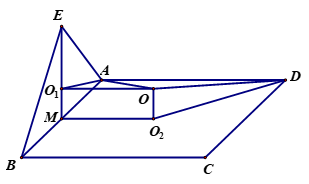
1(★★★)已知\(△EAB\)所在的平面与矩形\(ABCD\)所在的平面互相垂直,\(EA=EB=3\) ,\(AD=2\),\(∠AEB=60^°\),则多面体\(E-ABCD\)的外接球的表面积为\(\underline{\quad \quad}\).
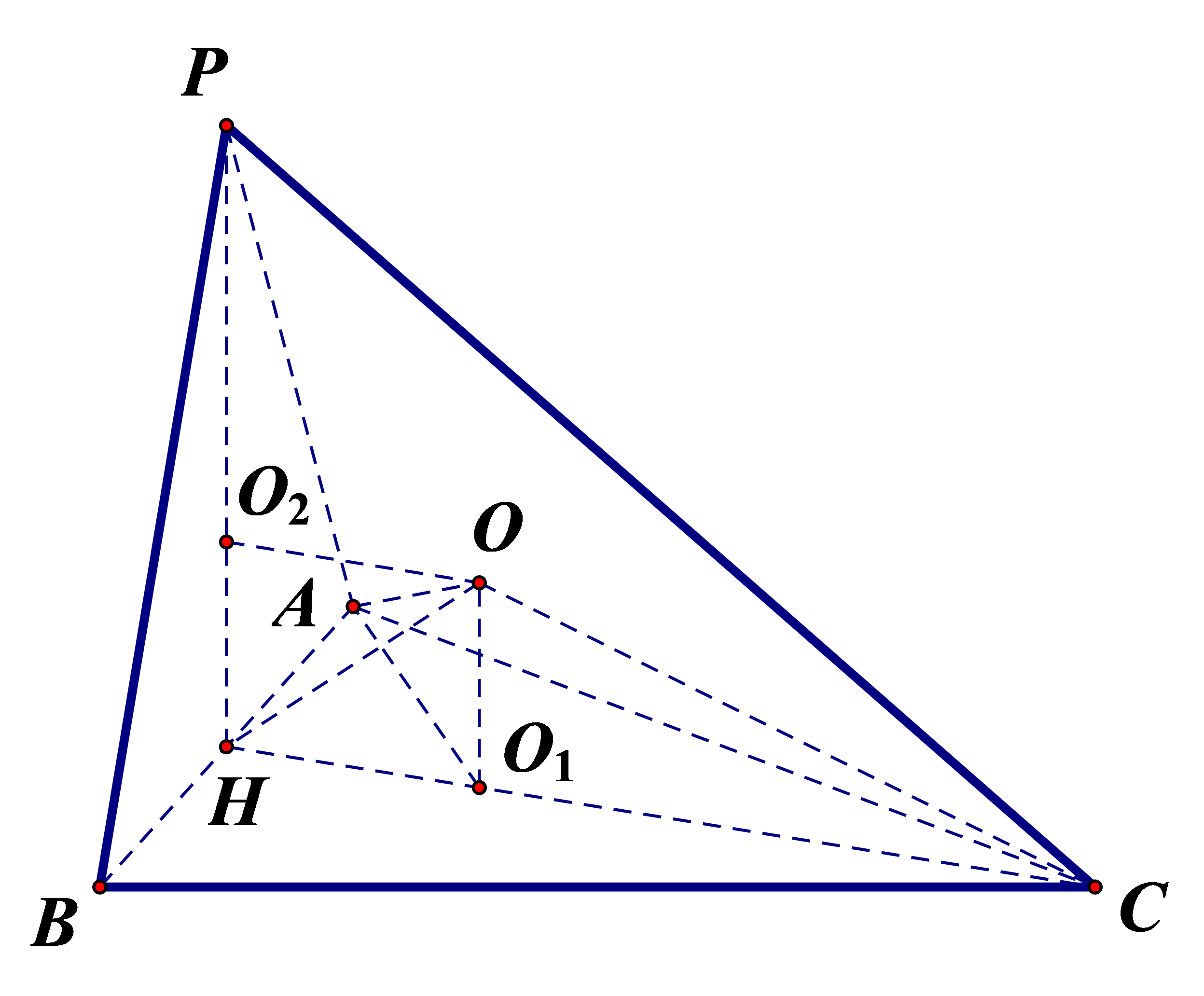
2(★★★)三棱锥\(P-ABC\)中,平面\(PAC⊥\)平面\(ABC\),\(△PAC\)和\(△ABC\)均为边长为\(2\)的正三角形,则三棱锥\(P-ABC\)外接球的半径为\(\underline{\quad \quad}\).
3(★★★)如图,在菱形\(ABCD\)中,\(∠BAD=60°\),\(A B=2 \sqrt{3}\),\(E\)为对角线\(BD\)的中点,将\(△ABD\)沿\(BD\)折起到\(△PBD\)的位置,若\(∠PEC=120°\),则三棱锥\(P-BCD\)的外接球的表面积为\(\underline{\quad \quad}\) .

4(★★★)已知四边形\(ABCD\)是边长为\(5\)的菱形,对角线\(BD=8\)(如图\(1\)),现以\(AC\)为折痕将菱形折起,使点\(B\)达到点\(P\)的位置.棱\(AC\),\(PD\)的中点分别为\(E\),\(F\),且四面体\(PACD\)的外接球球心落在四面体内部(如图\(2\)),则线段\(EF\)长度的取值范围为\(\underline{\quad \quad}\).

参考答案
-
【答案】\(16π\)
【解析】折叠型,法一:\(△EAB\)的外接圆半径为\(r_{1}=\sqrt{3}\),\(OO_1=1\),\(R=2\)
法二:\(O_{1} M=\dfrac{\sqrt{3}}{2}\),\(r_{2}=O_{2} D=\dfrac{\sqrt{13}}{2}\),\(R^{2}=\dfrac{3}{4}+\dfrac{13}{4}=4\),\(R=2\),\(S=16π\).
-
【答案】\(\dfrac{\sqrt{15}}{3}\)
【解析】\(2 r_{1}=2 r_{2}=\dfrac{2}{\sin 60^{\circ}}=\dfrac{4}{\sqrt{3}}\),\(r_{1}=r_{2}=\dfrac{2}{\sqrt{3}}\),\(O_{2} H=\dfrac{1}{\sqrt{3}}\),
\(R^{2}=O_{2} H^{2}+r_{1}^{2}=\dfrac{1}{3}+\dfrac{4}{3}=\dfrac{5}{3}\),\(R=\dfrac{\sqrt{15}}{3}\);
法二 \(O_{2} H=\dfrac{1}{\sqrt{3}}\),\(O_{1} H=\dfrac{1}{\sqrt{3}} A H=1\),\(R^{2}=A O^{2}=A H^{2}+O_{1} H^{2}=\dfrac{5}{3}\),\(R=\dfrac{\sqrt{15}}{3}\).
-
【答案】\(28π\)
【解析】过球心\(O\)作\(OO′⊥\)平面\(BCD\),则\(O′\)为等边三角形\(BCD\)的中心,
\(∵\)四边形\(ABCD\)是菱形,\(A=60°\),
\(\therefore \triangle B C D\)是等边三角形,
\(∵∠PEC=120°\),连接\(OP\),\(OP=OC\),\(OE=OE\),\(PE=CE\),
\(∴△OPE≌△OCE\),\(∴∠OEC=∠OEP=60°\);
\(\because A B=2 \sqrt{3}\),\(∴CE=3\),
\(∴EO′=1\),\(CO′=2\),\(\therefore O O^{\prime}=\sqrt{3}\),
\(∴\)球的半径\(O C=\sqrt{3+4}=\sqrt{7}\).
\(∴\)三棱锥\(P-BCD\)的外接球的表面积为\(4 \pi \cdot 7=28 \pi\),

-
【答案】\((\dfrac{\sqrt{14}}{2},4)\)
【解析】如图,由题意可知\(△APC\)的外心\(O_{1}\)在中线\(PE\)上,
设过点\(O_{1}\)的直线\(l_1⊥\)平面\(APC\),可知\(l_{1} \subset\)平面\(PED\),
同理\(△ADC\)的外心\(O _{2}\)在中线\(DE\)上,设过点\(O _{2}\)的直线\(l_2⊥\)平面\(ADC\),
则\(l_{2} \subset\)平面\(PED\),由对称性知直线\(l_{1}, l_{2}\)的交点\(O\)在直线\(EF\)上.
根据外接球的性质,点\(O\)为四面体\(APCD\)的外接球的球心.
由题意得\(EA=3\),\(PE=4\),
而\(O_{1} A^{2}=O_{1} E^{2}+E A^{2}\),\(O_{1} A+O_{1} E=P E=4\),
\(\therefore O_{1} E=\dfrac{7}{8}\).
令\(∠PEF=θ\),显然\(0<\theta<\dfrac{\pi}{2}\),\(\therefore E F=P E \cos \theta=4 \cos \theta<4\).
\(\because \cos \theta=\dfrac{E F}{P E}=\dfrac{O_{1} E}{O E}\),\(\therefore O E \cdot E F=O_{1} E \cdot P E=\dfrac{7}{2}\),
又\(OE<EF\),\(\therefore E F^{2}>\dfrac{7}{2}\),即\(E F>\dfrac{\sqrt{14}}{2}\).
综上所述,\(\dfrac{\sqrt{14}}{2}<E F<4\).
\(∴\)线段\(EF\)长度的取值范围为\((\dfrac{\sqrt{14}}{2},4)\).

题型五 内切球问题
知识剖析
1 内切球的概念
如果一个球与简单多面体的各面或其延展部分都相切,且此球在多面体的内部,则称这个球为此多面体的内切球.
例:与圆柱两底面以及每条母线都相切的球称为这个圆柱的内切球.
2 三棱锥\(P-ABC\)是任意三棱锥,求其的内切球半径\(r\) .
等体积法
即内切球球心与四个面构成的四个三棱锥的体积之和与三棱锥\(P-ABC\)体积相等.
\(\begin{aligned}
\therefore V_{P-A B C} &=V_{O-A B C}+V_{O-P A B}+V_{O-P A C}+V_{O-P B C} \\
&=\dfrac{1}{3} S_{\triangle A B C} \cdot r+\dfrac{1}{3} S_{\triangle P A B} \cdot r+\dfrac{1}{3} S_{\triangle P A C} \cdot r+\dfrac{1}{3} S_{\triangle P B C} \cdot r \\
&=\dfrac{1}{3}\left(S_{\triangle A B C}+S_{\triangle P A B}+S_{\triangle P A C}+S_{\triangle P B C}\right) r
\end{aligned}\)
\(\therefore r=\dfrac{3 V_{P-A B C}}{S_{\triangle A B C}+S_{\triangle P A B}+S_{\triangle P A C}+S_{\triangle P B C}}\)
(可与三角形\(ABC\)内切圆的半径\(r=\dfrac{2 S_{\triangle A B C}}{C_{\triangle A B C}}\)类比,均可由等积法求得.)
经典例题
【典题1】如图,在圆锥\(PO\)的轴截面\(PAB\)中,\(∠APB=60°\),有一小球\(O_1\)内切于圆锥(球面与圆锥的侧面、底面都相切),设小球\(O_1\)的体积为\(V_1\),圆锥\(PO\)的体积为\(V\),则\(V_1:V\)的值为( )

A. \(\dfrac{1}{3}\) \(\qquad \qquad \qquad \qquad\)B. \(\dfrac{4}{9}\)\(\qquad \qquad \qquad \qquad\)C. \(\dfrac{5}{9}\) \(\qquad \qquad \qquad \qquad\)D. \(\dfrac{2}{3}\)
【解析】如图所示,作出轴截面,

\(∵∆PAB\)是正三角形,设\(PB=4\),则\(OB=2\),\(P O=2 \sqrt{3}\).
\(∵Rt∆PEO_1∽Rt∆POB\),\(\therefore \dfrac{O_{1} E}{P O_{1}}=\dfrac{O B}{P B}\).
设\(O_1 E=R\),则\(P O_{1}=2 \sqrt{3}-R\),
\(\therefore \dfrac{R}{2 \sqrt{3}-R}=\dfrac{1}{2}\),即\(R=\dfrac{2 \sqrt{3}}{3}\).
\(∴\)内切球的体积为\(V=\dfrac{1}{3} \pi \cdot O B^{2} \cdot P O=\dfrac{8 \sqrt{3}}{3} \pi\),
圆锥的体积为\(V=\dfrac{1}{3} \pi \cdot O B^{2} \cdot P O=\dfrac{8 \sqrt{3}}{3} \pi\),
\(\therefore V_{1}: V=\dfrac{\dfrac{32 \sqrt{3}}{27} \pi}{\dfrac{8 \sqrt{3}}{3} \pi}=\dfrac{4}{9}\).
故选:\(B\).
【点拨】
① 作出横截面,较好的观察到内切球半径、母线、底圆半径等量之间的关系,同时也把立体几何问题转化为平几问题;
② 题中求体积之比,没有明确任一线段的长度,设一线段长度具体值\(PB=4\),有利于求出其他线段长度,计算简便些.
【典题2】棱长为\(a\)的正四面体的内切球的表面积为\(\underline{\quad \quad}\).
【解析】
\({\color{Red}{方法一 }}\) 运用正四面体的二心合一性质,作出截面图,通过点、线、面关系解之.
如图,设\(O\)是内切球的球心,由对称性可知,点\(O\)也是外接球的球心,
设内切球的半径为\(r\),外接球的半径为\(R\),
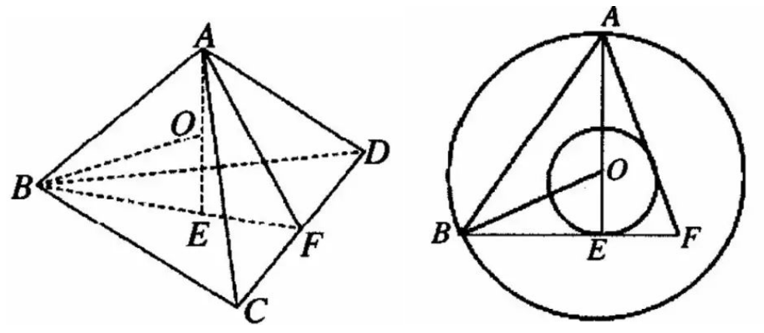
将正四面体放置正方体中,轻松求出\(R=\dfrac{\sqrt{6}}{4} a\),即\(O B=\dfrac{\sqrt{6}}{4} a\),
在等边\(∆BCD\)中,\(B E=\dfrac{a}{2 \cdot \sin 60^{\circ}}=\dfrac{\sqrt{3}}{3} a\)(\(E\)是\(∆BCD\)的外接圆圆心),
在\(Rt∆OEB\)中,\(r=O E=\sqrt{O B^{2}-B E^{2}}=\dfrac{\sqrt{6}}{12} a \Rightarrow S=4 \pi r^{2}=\dfrac{\pi a^{2}}{6}\).
\({\color{Red}{方法二 }}\) 连接\(OA\)、\(OB\)、\(OC\)、\(OD\),将四棱锥分成四个小棱锥,正四面体的四个面面积相等,
易知小棱锥的高是内切球的半径\(r\),
由\(V_{A-B C D}=V_{O-A B C}+V_{O-A B D}+V_{O-A C D}+V_{O-B C D}=4 V_{O-A B C}\)
得\(\dfrac{1}{3} \times A E \times S_{\triangle B C D}=4 \times \dfrac{1}{3} \times r \times S_{\triangle A B C}\)\(\Rightarrow 4 r=A E=\dfrac{\sqrt{6}}{3} a \Rightarrow r=\dfrac{\sqrt{6}}{12} a \Rightarrow S=4 \pi r^{2}=\dfrac{\pi a^{2}}{6}\).
【点拨】
① 方法一中很好的利用了几何体的对称性,巧妙知道正四面体的外接球与内切球的球心重合;横截面很好包含了球心、外接球半径、内切球半径等内容;
② 方法二中可知等积法求内切球半径是个很好的方法,同时可知正四面体的高\(h=4r\)(\(r\)为内切球半径),这个结论在很多题目常用.
③ 棱长为a的正四面体的高\(h=\dfrac{\sqrt{3}}{3} a\).
巩固练习
1(★★)将一个棱长为\(3cm\)的正方体铁块磨成一个球体零件,则可能制作的最大零件的体积为\(\underline{\quad \quad}\).
2(★★)若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为\(1\),当该圆锥体积取最小值时,该圆锥体积与其内切球体积比为\(\underline{\quad \quad}\).
3(★★)已知正三棱柱\(ABC-A_1 B_1 C_1\)的六个顶点在球\(O_1\)上,又球\(O_2\)与此三棱柱的\(5\)个面都相切,求球\(O_1\)与球\(O_2\)的体积比与表面积之比.
参考答案
- 【答案】\(\dfrac{9}{2} \pi c m^{3}\)
【解析】正方体的棱长为\(3\),要使制作成球体零件的体积最大,
则球内切于正方体,则球的直径为\(3cm\),半径为\(\dfrac{3}{2} cm\).
\(∴\)可能制作的最大零件的体积为\(\dfrac{4}{3} \pi \times\left(\dfrac{3}{2}\right)^{3}=\dfrac{9}{2} \pi \mathrm{cm}^{3}\). - 【答案】\(2:1\)
【解析】设圆锥的高为\(h\),底面半径为\(r\),
则当圆锥体积最小时,如图,
由\(△AOE~△ACF\)可得:\(\dfrac{1}{r}=\dfrac{\sqrt{(h-1)^{2}-1^{2}}}{h}\),即\(r=\dfrac{h}{\sqrt{h^{2}-2 h}}\),
\(∴\)圆锥的体积\(V=\dfrac{1}{3} \pi r^{2} h=\dfrac{\pi h^{2}}{3(h-2)}=\dfrac{\pi}{3}\left[(h-2)+\dfrac{4}{h-2}+4\right] \geq \dfrac{8 \pi}{3}\).
当且仅当\(h-2=2\),即\(h=4\)时取等号.
\(∴\)该圆锥体积的最小值为\(\dfrac{8 \pi}{3}\).内切球体积为\(\dfrac{4 \pi}{3}\).
该圆锥体积与其内切球体积比\(2:1\). - 【答案】\(5 \sqrt{5}: 1\)
【解析】欲求两球体积之比与表面积之比,关键是求两个球的半径之比.
先画出过球心的截面图,再来探求半径之间的关系.
如图:
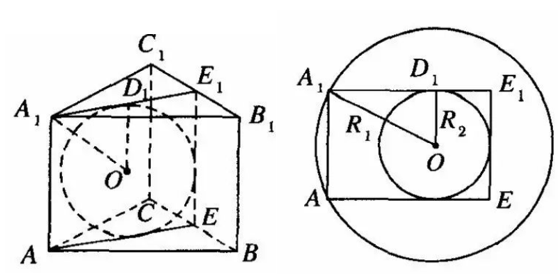
由题意可得两球\(O_1、O_2\)是重合的,过正三棱柱的一条侧棱\(AA_1\)和它们的球心作截面,
设正三棱柱底面边长为\(a\),
则\(R_{2}=D_{1} E_{1}=\dfrac{\sqrt{3}}{6} a\),正三棱柱的高\(h=2 R_{2}=\dfrac{\sqrt{3}}{3} a\),
在\(Rt∆A_1 D_1 O\)中有\(R_{1}^{2}=\left(\dfrac{\sqrt{3}}{3} a\right)^{2}+R_{2}^{2}=\left(\dfrac{\sqrt{3}}{3} a\right)^{2}+\left(\dfrac{\sqrt{3}}{6} a\right)^{2}=\dfrac{5}{12} a \Rightarrow R_{1}=\sqrt{\dfrac{5}{12}} a\)
\(\therefore S_{1}: S_{2}=R_{1}^{2}: R_{2}^{2}=5: 1\),\(V_{1}: V_{2}=R_{1}^{3}: R_{2}^{3}=5 \sqrt{5}: 1\).
题型六 多球与多面体的相切问题
经典例题
【典题1】\(4\)个半径为\(1\)的中球上层\(1\)个、下层\(3\)个两两相切叠放在一起.
(1) 有\(1\)个空心大球能把\(4\)个中球装在里面,求大球的半径至少是多少?
(2) 在它们围成的空隙内有\(1\)个小球与这\(4\)个中球都外切,求小球的半径?
【解析】(1) 连接\(4\)个中球的球心得到棱长为\(2\)的正四面体,它的外接球的半径长\(\dfrac{\sqrt{6}}{2}\),因此大球的半径至少为\(1+\dfrac{\sqrt{6}}{2}\);
(2)可知该小球和(1)问中的最小的大球是同心球,
则小球的半径是最小的大球的半径减去一个中球的直径,即\(\dfrac{\sqrt{6}}{2}-1\).
【点拨】大小一样的球体叠在一起,会出现正四面体.
【典题2】将半径都为\(1\)的四个钢球完全装入形状为正四面体的容器里,这个四面体的高的最小值为 \(\underline{\quad \quad}\).
【解析】\({\color{Red}{方法一(利用点线关系) }}\)
由题意得,四个半径为\(1\)的小球的球心\(O_1\) ,\(O_2\) ,\(O_3\) ,\(O_4\)恰好构成一个棱长为\(2\)的正四面体,并且各面与正四面体的容器\(P-ABC\)的各对应面的距离都为1(如图),
设点\(O\)、\(H\)分别是\(∆ABC\)、\(∆O_2 O_3 O_4\)的外心,显然\(HO=1\),
设\(N\)、\(F\)分别为\(AB\)、\(O_2 O_3\)的中点,
在棱长为\(2\)的正四面体\(O_1-O_2 O_3 O_4\)中,\(O_{1} F=\sqrt{3}\),\(O_{1} H=\dfrac{2 \sqrt{6}}{3}\),且\(\sin \angle F O_{1} H=\dfrac{1}{3}\),
作\(O_1 M⊥PN\),则\(O_1 M=1\),
由于\(∠O_1 PH=∠FO_1 H\),
\(\therefore P O_{1}=\dfrac{o_{1} M}{\sin \angle O_{1} P H}=\dfrac{O_{1} M}{\sin \angle F O_{1} H}=3\),
所以\(P O=P O_{1}+O_{1} H+H O=3+\dfrac{2 \sqrt{6}}{3}+1=\dfrac{2 \sqrt{6}+12}{3}\).

\({\color{Red}{ 方法二(利用相似关系) }}\)
由题意得,四个半径为\(1\)的小球的球心\(O_1\) ,\(O_2\) ,\(O_3\),\(O_4\)恰好构成一个棱长为\(2\)的正四面体,并且各面与正四面体的容器\(P-ABC\)的各对应面的距离都为\(1\)(如图),正四面体\(O_1-O_2 O_3 O_4\)与正四面体的容器\(P-ABC\)由共同的外接球球心\(O\)(同时也是内切球的球心)的相似正四面体,设它们相似比为\(k\),
从内切球的角度看,\(k=\dfrac{O H}{O Q}=\dfrac{O H}{O H+H Q}=\dfrac{O H}{O H+1}=\dfrac{\dfrac{\sqrt{6}}{6}}{\dfrac{\sqrt{6}}{6}+1}=\dfrac{\sqrt{6}-1}{5}\),
\({\color{Red}{(由等积法可知正四面体O_1-O_2 O_3 O_4内切球半径r=O H=\dfrac{\sqrt{6}}{6}, O O_{1}=O_{1} H-O H=\dfrac{\sqrt{6}}{2}) }}\)
从外接球的角度看,有\(k=\dfrac{O O_{1}}{O P} \Rightarrow O P=\dfrac{O O_{1}}{k}=\dfrac{\sqrt{6}}{2} \div \dfrac{\sqrt{6}-1}{5}=\dfrac{\sqrt{6}+6}{2}\),
所以\(P Q=O P+O Q=\dfrac{\sqrt{6}+6}{2}+\dfrac{\sqrt{6}}{6}+1=\dfrac{2 \sqrt{6}+12}{3}\).

\({\color{Red}{方法三(利用等体积法) }}\)
如图,从\(O_1\)点出发将三棱锥\(P-ABC\)分为四个小三棱锥\(O_1-PAB\) ,\(O_1-PBC\) ,\(O_1-PAC\) , \(O_1-ABC\) ,
于是有\(V_{P-A B C}=V_{O_{1}-P A B}+V_{O_{1}-P B C}+V_{O_{1}-P A C}+V_{O_{1}-A B C}\)
设正四面体的高是\(h\),
四个球的球心连线组成的正四面体\(O_1-O_2 O_3 O_4\)的高\(O_{1} H=\dfrac{2 \sqrt{6}}{3}\),则\(O_{1} Q=\dfrac{2 \sqrt{6}}{3}+1\)
从而\(\dfrac{1}{3} \times S_{\triangle A B C} \times h=\)\(\dfrac{1}{3} \times S_{\triangle P A B} \times 1+\dfrac{1}{3} \times S_{\triangle P B C} \times 1+\dfrac{1}{3} \times S_{\triangle P A C} \times 1+\dfrac{1}{3} \times S_{\triangle A B C} \times\left(\dfrac{2 \sqrt{6}}{3}+1\right)\)
所以\(h=\dfrac{2 \sqrt{6}+12}{3}\)

【点拨】解决多球相切问题,基本方法为三种:
① 抓住多球的堆垒放置规律;
② 抓住各球心位置,转化为多面体问题;
③ 适当选择截面,转化为平面几何问题.
巩固练习
1(★★★)在棱长为\(1\)的正方体内有两个球外切且有分别与正方体内切.
(1) 球两球的半径之和;
(2) 球的半径分别为多少时,两球体积之和最小.
2(★★★)将\(3\)个半径为\(1\)的球和\(1\)个半径为√2-1的球叠为两层放在桌面上,上层只放\(1\)个较小的球,\(4\)个球两两相切,求上层小球的最高点到桌面的距离.

参考答案
- 【答案】\((1) \dfrac{3-\sqrt{3}}{2} \qquad
(2) \dfrac{3-\sqrt{3}}{4}, \dfrac{3-\sqrt{3}}{4}\)
【解析】(1)如图,画出轴截面(对角面),球心\(O_1\)、\(O_2\)在\(AC\)上,过\(O_1\)、\(O_2\)分别作\(AD\)、\(BC\)的垂线交于\(E\)、\(F\),设两个球\(O_1\)、\(O_2\)的半径分别为\(r\)、\(R\),
则由\(AB=1\),\(A C=\sqrt{3}\)得\(A O_{1}=\sqrt{3} r\),\(C O_{2}=\sqrt{3} R\)
所以\(r+R+\sqrt{3}(r+R)=\sqrt{3}\),则\(r+R=\dfrac{3-\sqrt{3}}{2}\);
(2)设两球球体之和为\(V\),则
\(V=\dfrac{4}{3} \pi\left(r^{3}+R^{3}\right)=\dfrac{4}{3} \pi(r+R)\left(r^{2}-r R+R^{2}\right)\)\(=\dfrac{4}{3} \pi \times \dfrac{3-\sqrt{3}}{2}\left[3 R^{2}-\dfrac{3(3-\sqrt{3})}{2} R+\left(\dfrac{3-\sqrt{3}}{2}\right)^{2}\right]\)
于是当\(R=\dfrac{3-\sqrt{3}}{4}\)时,\(V\)有最小值,
故当\(r=R=\dfrac{3-\sqrt{3}}{4}\)时,体积之和最小

- 【答案】\(\dfrac{\sqrt{6}}{3}+\sqrt{2}\)
【解析】将球心\(O_{1}, O_{2}, O_{3}, O_{4}\)连接起来构成侧棱为\(\sqrt{2}\),底面边长为\(2\)的正三棱锥\(O_4-O_1 O_2 O_3\),
设底面三角形的中心为\(O\),则\(O O_{1}=\dfrac{2 \sqrt{3}}{3}\),
故正三棱锥\(O_{4}-O_{1} O_{2} O_{3}\)的高\(h=\sqrt{O_{1} O_{4}^{2}-O O_{1}^{2}}=\sqrt{(\sqrt{2})^{2}-\left(\dfrac{2 \sqrt{3}}{3}\right)^{2}}=\dfrac{\sqrt{6}}{3}\),
显然平面\(O_1 O_2 O_3\)到桌面的距离为\(1\),
所以上层小球的最高点\(A\)到桌面的距离为\(1+\dfrac{\sqrt{6}}{3}+(\sqrt{2}-1)=\dfrac{\sqrt{6}}{3}+\sqrt{2}\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号