专题 概率常见解答题
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第三册同步提高,难度4颗星!
模块导图
经典例题
【题型一】比赛型
【典题1】 下围棋既锻炼思维又愉悦身心,有益培养人的耐心和细心,舒缓大脑并让其得到充分休息.现某学校围棋社团为丰富学生的课余生活,举行围棋大赛要求每班选派一名围棋爱好者参赛.现某班有\(12\)位围棋爱好者,经商议决定采取单循环方式进行比赛,(规则采用“中国数目法”,没有和棋.)即每人进行\(11\)轮比赛,最后靠积分选出第一名去参加校级比赛.积分规则如下(每轮比赛采取\(5\)局\(3\)胜制,比赛结束时,取胜者可能会出现\(3:0\),\(3:1\),\(3:2\)三种赛式).
\(\begin{array}{|c|c|c|}
\hline & 3: 0 \text { 或3: } 1 & 3: 2 \\
\hline \text { 胜者积分 } & \text { 3分 } & \text { 2分 } \\
\hline \text { 负者积分 } & \text { 0分 } & \text { 1分 } \\
\hline
\end{array}\)
\(9\)轮过后,积分榜上的前两名分别为甲和乙,甲累计积分\(26\)分,乙累计积分\(22\)分.第\(10\)轮甲和丙比赛,设每局比赛甲取胜的概率均为\(\dfrac{2}{3}\),丙获胜的概率为\(\dfrac{1}{3}\),各局比赛结果相互独立.
(1)(i)在第\(10\)轮比赛中,甲所得积分为\(X\),求\(X\)的分布列;
(ii)求第\(10\)轮结束后,甲的累计积分\(Y\)的期望;
(2)已知第\(10\)轮乙得\(3\)分,判断甲能否提前一轮获得累计积分第一,结束比赛.(“提前一轮”即比赛进行\(10\)轮就结束,最后一轮即第\(11\)轮无论乙得分结果如何,甲累计积分最多)?若能,求出相应的概率;若不能,请说明理由.
【解析】 \((1)(i)\)\(X\)的可能取值为\(3 ,2 ,1 ,0\),
\(P(X=3)=\left(\dfrac{2}{3}\right)^{3}+C_{3}^{2}\left(\dfrac{2}{3}\right)^{2}\left(1-\dfrac{2}{3}\right) \times \dfrac{2}{3}=\dfrac{16}{27}\),
\(P(X=2)=C_{4}^{2}\left(\dfrac{2}{3}\right)^{2}\left(1-\dfrac{2}{3}\right)^{2} \times \dfrac{2}{3}=\dfrac{16}{81}\),
\(P(X=1)=C_{4}^{2}\left(\dfrac{2}{3}\right)^{2}\left(1-\dfrac{2}{3}\right)^{3}=\dfrac{8}{81}\),
\(P(X=0)=\left(1-\dfrac{2}{3}\right)^{3}+C_{3}^{1} \times \dfrac{2}{3} \times\left(1-\dfrac{2}{3}\right)^{3}=\dfrac{1}{9}\),
所以\(X\)的分布列为
\(\begin{array}{|c|c|c|c|c|}
\hline X & 3 & 2 & 1 & 0 \\
\hline P & \dfrac{16}{27} & \dfrac{16}{81} & \dfrac{8}{81} & \dfrac{1}{9} \\
\hline
\end{array}\)
\((ii)\)\(Y\)的可能取值为\(29 ,28 ,27 ,26\),
则\(E(Y)=\dfrac{16}{27} \times 29+\dfrac{16}{81} \times 28+\dfrac{8}{81} \times 27+\dfrac{1}{9} \times 26=\dfrac{2290}{81}\).
\((2)\)若\(X=3\),则甲\(10\)轮后的总积分为\(29\)分,
乙即便第\(10\)轮和第\(11\)轮都得\(3\)分,则\(11\)轮过后的总积分是\(28\)分,
所以甲如果第\(10\)轮积\(3\)分,则可提前一轮结束比赛,其概率为\(P(X=3)=\dfrac{16}{27}\).
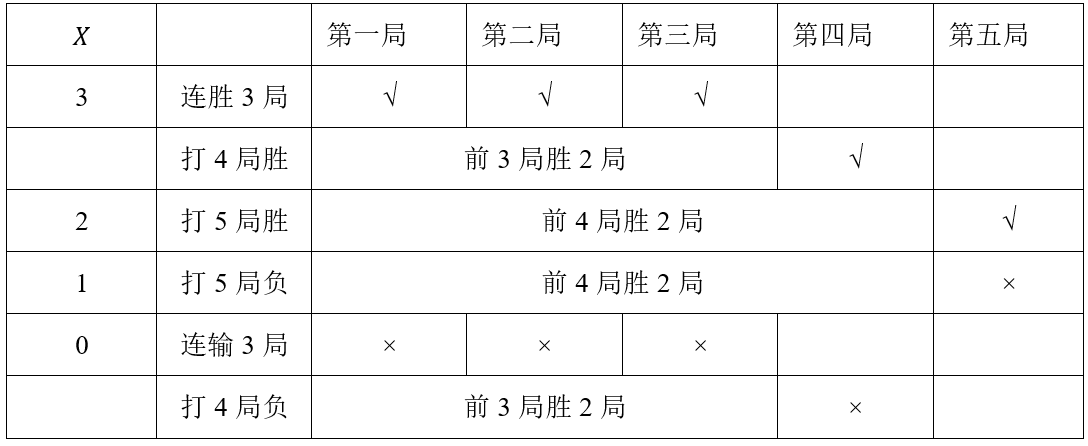
【点拨】
该题属于“比赛类”,要特别注意随机变量每个取值的“胜利情况”,可用列表的形式清晰思考,比如第一问
【题型二】方案型
【典题1】 党中央、国务院高度重视新冠病毒核酸检测工作,中央应对新型冠状病毒感染肺炎疫情工作领导小组会议作出部署,要求尽力扩大核酸检测范围,着力提升检测能力.根据统计发现,疑似病例核酸检测呈阳性的概率为\(p(0<p<1)\).现有\(4\)例疑似病例,分别对其取样、检测,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有病毒,则化验结果呈阳性.若混合样本呈阳性,则需将该组中备用的样本再逐个化验;若混合样本呈阴性,则判定该组各个样本均为阴性,无需再化验现有以下三种方案:
方案一:\(4\)个样本逐个化验;
方案二:\(4\)个样本混合在一起化验;
方案三:\(4\)个样本均分为两组,分别混合在一起化验.
在新冠肺炎爆发初期,由于检测能力不足,化验次数的期望值越小,则方案越“优”.
(1)若\(p=\dfrac{1}{3}\),按方案一,求\(4\)例疑似病例中恰有\(2\)例呈阳性的概率;
(2)若\(p=\dfrac{1}{10}\),现将该\(4\)例疑似病例样本进行化验,试比较以上三个方案中哪个最“优”,并说明理由.
【解析】 \(\text { (1) } p=\dfrac{1}{3}\),
按方案一,\(4\)例疑似病例中恰有2例呈阳性的概率:\(P=C_{4}^{2}\left(\dfrac{1}{3}\right)^{2}\left(\dfrac{2}{3}\right)^{2}=\dfrac{8}{27}\).
(2)方案一:逐个检测,检验次数为:\(4×1=4\),
方案二:检测次数为\(X\),\(X\)的可能取值为\(1 ,5\),
\(P(X=1)=\left(1-\dfrac{1}{10}\right)^{4}=\dfrac{6561}{10000}\),\(P(X=5)=1-\dfrac{6561}{10000}=\dfrac{3439}{10000}\),
\(∴X\)的分布列如下:
\(\begin{array}{|c|c|c|}
\hline X & 1 & 5 \\
\hline P & \dfrac{6561}{10000} & \dfrac{3439}{10000} \\
\hline
\end{array}\)
方案二的数学期望为:
\(E X=1 \times \dfrac{6561}{10000}+5 \times \dfrac{3439}{10000}=2.3756\).
方案三,由(1)知,每组两个样本检测时,
若呈阴性,则检测次数为\(1\),概率为\(\dfrac{81}{100}\),
若呈阳性则检测次数为\(3\),概率为\(1-\dfrac{81}{100}=\dfrac{19}{100}\),
故方案三的检测次数记为\(Y\),\(Y\)的可能取值为\(2,4,6\),
\(P(Y=2)=\dfrac{6561}{10000}\),\(P(Y=4)=2 \times \dfrac{81}{100} \times \dfrac{19}{100}=\dfrac{3078}{10000}\),\(P=(Y=6)=\left(\dfrac{19}{100}\right)^{2}=\dfrac{361}{10000}\),
\(∴Y\)的分布列为
\(\begin{array}{|c|c|c|c|}
\hline Y & 2 & 4 & 6 \\
\hline P & \dfrac{6561}{10000} & \dfrac{3078}{10000} & \dfrac{361}{10000} \\
\hline
\end{array}\)
方案三的期望为\(E(Y)=2 \times \dfrac{6561}{10000}+4 \times \dfrac{3078}{10000}+6 \times \dfrac{361}{10000}=2.76\),
\(∵E(X)<E(Y)<4\),
\(∴\)方案一、二,三中方案二最“优”.
【题型三】数列型
【典题1】 武汉又称江城,是湖北省省会城市,被誉为中部地区中心城市,它不仅有着深厚的历史积淀与丰富的民俗文化,更有着众多名胜古迹与旅游景点,每年来武汉参观旅游的人数不胜数,其中黄鹤楼与东湖被称为两张名片为合理配置旅游资源,现对已游览黄鹤楼景点的游客进行随机问卷调查,若不游玩东湖记\(1\)分,若继续游玩东湖记\(2\)分,每位游客选择是否游览东湖景点的概率均为\(\dfrac{1}{2}\),游客之间选择意愿相互独立.
(1)从游客中随机抽取\(3\)人,记总得分为随机变量\(X\),求\(X\)的分布列与数学期望;
(2)若从游客中随机抽取\(m\)人,记总分恰为\(m\)分的概率为\(A_m\),求数列\(\{A_m\}\)的前\(10\)项和;
(3)若每位游客选择游览景点概率为\(\dfrac{2}{3}\),在对所有游客进行随机问卷调查过程中,记已调查过的累计得分恰为\(n\)分的概率为\(B_n\),探讨\(B_n\)与\(B_{n-1}\)之间的关系,并求数列\(\left\{B_{n}\right\}\)的通项公式.
【解析】 (1) \({\color{Red}{(设选择游览东湖景点的人数为y,则y \sim B\left(3, \dfrac{1}{2}\right),求X的分布列不难) }}\)
\(X\)可能取值为\(3,4,5,6\).
\(P(X=3)=\left(\dfrac{1}{2}\right)^{3}=\dfrac{1}{8}\),\(P(X=4)=C_{3}^{1}\left(\dfrac{1}{2}\right)^{3}=\dfrac{3}{8}\)
\(P(X=5)=C_{3}^{2}\left(\dfrac{1}{2}\right)^{3}=\dfrac{3}{8}\),\(P(X=6)=C_{3}^{3}\left(\dfrac{1}{2}\right)^{3}=\dfrac{1}{8}\).
所以\(X\)的分布列为
\(\begin{array}{|c|c|c|c|c|}
\hline X & 3 & 4 & 5 & 6 \\
\hline P & \dfrac{1}{8} & \dfrac{3}{8} & \dfrac{3}{8} & \dfrac{1}{8} \\
\hline
\end{array}\)
所以\(E(X)=3 \times \dfrac{1}{8}+4 \times \dfrac{1}{8}+5 \times \dfrac{3}{8}+6 \times \dfrac{3}{8}=4.5\).
(2) \({\color{Red}{(抽取m人总分为m,即全部人均不去景点) }}\)
总分恰为\(m\)分的概率为\(A_{m}=\left(\dfrac{1}{2}\right)^{m}\),
\({\color{Red}{(把概率A_m看成数列的通项公式;若a_n=kn+b,则\{a_n\}是等差数列; a_n=A\cdot B^n,则\left\{a_{n}\right\}是等比数列) }}\)
所以数列\(\left\{A_{m}\right\}\)是首项为\(\dfrac{1}{2}\),公比为\(\dfrac{1}{2}\)的等比数列,
前\(10\)项和\(S_{10}=\dfrac{\dfrac{1}{2}\left(1-\dfrac{1}{2^{10}}\right)}{1-\dfrac{1}{2}}=\dfrac{1023}{1024}\).
(3) \({\color{Red}{方法一 }}\)
要得到\(n\)分,有两种可能:① 得到\(n-1\)分后再得\(1\)分,② 得到\(n-2\)分后再得\(2\)分,
即\(B_{n}=\dfrac{1}{3} B_{n-1}+\dfrac{2}{3} B_{n-2}(n \geq 3)\)
则可得\(B_{n}+\dfrac{2}{3} B_{n-1}=B_{n-1}+\dfrac{2}{3} B_{n-2}\),
即数列\(\left\{B_{n}+\dfrac{2}{3} B_{n-1}\right\}\)是常数列,
而\(B_{1}=\dfrac{1}{3}, B_{2}=\dfrac{1}{3} \times \dfrac{1}{3}+\dfrac{2}{3}=\dfrac{7}{9}\),则\(B_{2}+\dfrac{2}{3} B_{1}=1\)
即\(B_{n}+\dfrac{2}{3} B_{n-1}=1 \Rightarrow B_{n}=-\dfrac{2}{3} B_{n-1}+1\)
可得\(B_{n}-\dfrac{3}{5}=-\dfrac{2}{3}\left(B_{n-1}-\dfrac{3}{5}\right)\),
而\(B_{1}=\dfrac{1}{3}\),则\(B_{1}-\dfrac{3}{5}=-\dfrac{4}{15}\),
所以\(B_{n}-\dfrac{3}{5}=-\dfrac{4}{15} \cdot\left(-\dfrac{2}{3}\right)^{n-1}=\dfrac{2}{5} \cdot\left(-\dfrac{2}{3}\right)^{n}\),
所以\(B_{n}=\dfrac{3}{5}+\dfrac{2}{5} \cdot\left(-\dfrac{2}{3}\right)^{n}\).
\({\color{Red}{方法二 }}\)
已调查过的累计得分恰为\(n\)分的概率为\(B_n\),
得不到\(n\)分的情况只有先得\(n-1\)分,再得\(2\)分,概率为\(\dfrac{2}{3} B_{n-1}\),
故\(1-B_{n}=\dfrac{2}{3} B_{n-1}\),即\(B_{n}=-\dfrac{2}{3} B_{n-1}+1\),
则以下如方法一可得\(B_{n}=\dfrac{3}{5}+\dfrac{2}{5} \cdot\left(-\dfrac{2}{3}\right)^{n}\).
【点拨】
① 如何由数列的递推公式求得通项公式?
遇到\(a_{n+1}=k a_{n}+b(k \neq 0)\)或\(a_{n+1}=k a_{n}+b a_{n-1}(k, b \neq 0)\)可用待定系数法求解.
比如
(1) 由\(B_{n}=-\dfrac{2}{3} B_{n-1}+1\),设\(B_{n}+m=-\dfrac{2}{3}\left(B_{n-1}+m\right)\),
易得\(m=-\dfrac{3}{5}\),则构造了等比数列\(\left\{B_{n}-\dfrac{3}{5}\right\}\)
(2) 由\(B_{n}=\dfrac{1}{3} B_{n-1}+\dfrac{2}{3} B_{n-2}\),设\(B_{n}+m B_{n-1}=k\left(B_{n-1}+m B_{n-2}\right)\)
则\(k-m=\dfrac{1}{3}\),\(k m=\dfrac{2}{3}\),解得\(\left\{\begin{array}{l}
k=-\dfrac{2}{3} \\
m=-1
\end{array}\right.\)或\(\left\{\begin{array}{l}
k=1 \\
m=\dfrac{2}{3}
\end{array}\right.\),
本题就用了\(\left\{\begin{array}{l}
k=1 \\
m=\dfrac{2}{3}
\end{array}\right.\)得到\(B_{n}+\dfrac{2}{3} B_{n-1}=B_{n-1}+\dfrac{2}{3} B_{n-2}\),构造出常数列\(\left\{B_{n}+\dfrac{2}{3} B_{n-1}\right\}\);
若利用\(\left\{\begin{array}{l}
k=-\dfrac{2}{3} \\
m=-1
\end{array}\right.\)则得到\(B_{n}-B_{n-1}=-\dfrac{2}{3}\left(B_{n-1}-B_{n-2}\right)\),构造出等比数列\(\left\{B_{n}-B_{n-1}\right\}\),
后面的计算量就比较大了!
② 方法二则更巧妙些,利用得到\(n\)分与得不到\(n\)分的概率之和为\(1\),提前得到了\(B_{n}+\dfrac{2}{3} B_{n-1}=1\),即方法一中\(\left\{B_{n}+\dfrac{2}{3} B_{n-1}\right\}\)是常数列.
【典题2】 某校数学兴趣小组由水平相当的\(n\)位同学组成他们的学号依次为\(1,2,3,…,n\).辅导老师安排一个挑战数学填空题的活动,活动中有两个固定的题,同学们对这两个题轮流作答,每位同学在四分钟内答对第一题及四分钟内答对第二题的概率都为\(\dfrac{1}{2}\),每个同学的答题过程都是相互独立的挑战的具体规则如下:
①挑战的同学先做第一题,第一题做对才有机会做第二题;
②挑战按学号由小到大的顺序依次进行,第\(1\)号同学开始第\(1\)轮挑战;
③若第\(i(i=1,2,3,…,n-1)\)号同学在四分钟内未答对第一题,则认为第\(i\)轮挑战失败,由第\(i+1\)号同学继续挑战;
④若第\(i(i=1,2,3,…,n-1)\)号同学在四分钟内答对了第一题,满四分钟后,辅导老师安排该生答第二题,若该生在四分钟内又答对第二题,则认为挑战成功挑战在第\(i\)轮结束;若该生在四分钟内未答对第二题,则也认为第\(i\)轮挑战失败,由第\(i+1\)号同学继续挑战;
⑤若挑战进行到了第\(n\)轮,则不管第\(n\)号同学答对多少题,下轮不再安排同学挑战.
令随机变量\(X_n\)表示\(n\)名挑战者在第\(X_n (X_n=1,2,3,…,n)\)轮结束.
\((1)\)求随机变量\(X_4\)的分布列;
\((2)\)若把挑战规则①去掉,换成规则⑥:挑战的同学先做第一题,若有同学在四分钟内答对了第一题,以后挑战的同学不做第一题,直接从第二题开始作答.
令随机变量\(Y_n\)表示\(n\)名挑战者在第\(Y_n (Y_n=1,2,3,…,n)\)轮结束.
\((i)\)求随机变量\(Y_n (n∈N^*,n≥2)\)的分布列;
\((ii)\)证明:\(E\left(Y_{2}\right)<E\left(Y_{3}\right)<E\left(Y_{4}\right)<E\left(Y_{5}\right)<\cdots<E\left(Y_{n}\right)<\cdots<3\).
【解析】 \((1) P\left(X_{1}=k\right)=\left(1-\dfrac{1}{2} \times \dfrac{1}{2}\right)^{k-1} \times \dfrac{1}{4} \quad (k=1,2,3)\),
\(P\left(X_{4}=4\right)=\left(\dfrac{3}{4}\right)^{3}\)
因此\(X_4\)的分布列为
\(\begin{array}{|c|c|c|c|c|}
\hline X_{4} & 1 & 2 & 3 & 4 \\
\hline P & \dfrac{1}{4} & \dfrac{3}{16} & \dfrac{9}{64} & \dfrac{27}{64} \\
\hline
\end{array}\)
\(\text { (2)(i) } Y_{n}=k\left(1 \leq k \leq n-1, k \in N^{*}\right)\)时,第\(k\)人必答对第二题,
若前面\(k-1\)人都没有一人答对第一题,其概率为\(p_{k}^{\prime}=\left(\dfrac{1}{2}\right)^{k+1}\),
若前面\(k-1\)人有一人答对第一题,其概率为\(p_{k}^{\prime \prime}=(k-1)\left(\dfrac{1}{2}\right)^{k+1}\),
故\(P\left(Y_{n}=k\right)=p_{k}^{\prime}+p_{k}^{\prime \prime}=k\left(\dfrac{1}{2}\right)^{k+1}\).
当\(Y_n=n\)时,
若前面\(n-1\)人都没有一人答对第一题,其概率为\(p_{n}^{\prime}=\left(\dfrac{1}{2}\right)^{n-1}\),
若前面\(n-1\)人有一人答对第一题,其概率为\(p_{n}^{\prime \prime}=(n-1)\left(\dfrac{1}{2}\right)^{n}\),
故\(P\left(Y_{n}=n\right)=p_{n}^{\prime}+p_{n}^{\prime \prime}=(n+1)\left(\dfrac{1}{2}\right)^{n}\).
\(Y_{n}\)的分布列为
\(\begin{array}{|c|c|c|c|c|c|c|}
\hline Y_{n} & 1 & 2 & 3 & \cdots & n-1 & n \\
\hline P & \left(\dfrac{1}{2}\right)^{2} & 2 \times\left(\dfrac{1}{2}\right)^{3} & 3 \times\left(\dfrac{1}{2}\right)^{4} & \cdots & (n-1)\left(\dfrac{1}{2}\right)^{n} & (n+1)\left(\dfrac{1}{2}\right)^{n} \\
\hline
\end{array}\)
\(\text { (ii) } E\left(Y_{n}\right)=\sum_{k=1}^{n-1} k^{2}\left(\dfrac{1}{2}\right)^{k+1}+n(n+1)\left(\dfrac{1}{2}\right)^{n}\left(n \in N^{*}, n \geq 2\right)\).
\({\color{Red}{法1:}}\)
\(E\left(Y_{n+1}\right)-E\left(Y_{n}\right)=n^{2}\left(\dfrac{1}{2}\right)^{n+1}+(n+1)(n+2)\left(\dfrac{1}{2}\right)^{n+1}-n(n+1)\left(\dfrac{1}{2}\right)^{n}\)\(=(n+2)\left(\dfrac{1}{2}\right)^{n+1}>0\),
故\(E\left(Y_{2}\right)<E\left(Y_{3}\right)<E\left(Y_{4}\right)<E\left(Y_{5}\right)<\cdots<E\left(Y_{n}\right)<\cdots\),
求得\(E\left(Y_{2}\right)=\dfrac{7}{4}\),
故\(E\left(Y_{n}\right)=E\left(Y_{2}\right)+\left[E\left(Y_{3}\right)-E\left(Y_{2}\right)\right]+\left[E\left(Y_{4}\right)-E\left(Y_{3}\right)\right]+\cdots+\left[E\left(Y_{n}\right)-E\left(Y_{n-1}\right)\right]\)
\(\therefore E\left(Y_{n}\right)=\dfrac{7}{4}+4 \times\left(\dfrac{1}{2}\right)^{3}+5 \times\left(\dfrac{1}{2}\right)^{4}+\cdots+n\left(\dfrac{1}{2}\right)^{n-1}+(n+1)\left(\dfrac{1}{2}\right)^{n}\),①
\(2 E\left(Y_{n}\right)=\dfrac{7}{2}+4 \times\left(\dfrac{1}{2}\right)^{2}+5 \times\left(\dfrac{1}{2}\right)^{3}+6 \times\left(\dfrac{1}{2}\right)^{4}+\cdots+(n+1)\left(\dfrac{1}{2}\right)^{n-1}\),②
②-① 得,
\(E\left(Y_{n}\right)<\dfrac{7}{4}+1+\left(\dfrac{1}{2}\right)^{3}+\left(\dfrac{1}{2}\right)^{4}+\cdots+\left(\dfrac{1}{2}\right)^{n-1}<\dfrac{7}{4}+1+\dfrac{\dfrac{1}{8}}{1-\dfrac{1}{2}}=3\).
故\(E\left(Y_{2}\right)<E\left(Y_{3}\right)<E\left(Y_{4}\right)<E\left(Y_{5}\right)<\cdots<E\left(Y_{n}\right)<\cdots<3\).
\({\color{Red}{法2: }}\)令\(k^{2}\left(\dfrac{1}{2}\right)^{k+1}=\left(a k^{2}+b k+c\right)\left(\dfrac{1}{2}\right)^{k}-\left[a(k+1)^{2}+b(k+1)+c\right]\left(\dfrac{1}{2}\right)^{k+1}\),
则\(k^{2}=2\left(a k^{2}+b k+c\right)-\left[a k^{2}+(2 a+b) k+(a+b+c)\right]\)
\(=a k^{2}+(b-2 a) k+(c-a-b)\)
因此:\(E\left(Y_{n}\right)=\sum_{k=1}^{n-1} k^{2}\left(\dfrac{1}{2}\right)^{k+1}+n(n+1)\left(\dfrac{1}{2}\right)^{n}\).
又\(E\left(Y_{n+1}\right)-E\left(Y_{n}\right)=(n+3)\left(\dfrac{1}{2}\right)^{n}-(n+4)\left(\dfrac{1}{2}\right)^{n+1}=(n+2)\left(\dfrac{1}{2}\right)^{n+1}>0\),
故\(E\left(Y_{2}\right)<E\left(Y_{3}\right)<E\left(Y_{4}\right)<E\left(Y_{5}\right)<\cdots<E\left(Y_{n}\right)<\cdots<3\).
【题型四】最值型
【典题1】 某校高三男生体育课上做投篮球游戏,两人一组,每轮游戏中,每小组两人每人投篮两次,投篮投进的次数和不少于\(3\)次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为\(P_1\) ,\(P_2\).
(1)若\(P_{1}=\dfrac{2}{3}\),\(P_{2}=\dfrac{1}{2}\),则在第一轮游戏他们获“优秀小组”的概率;
(2)若\(P_{1}+P_{2}=\dfrac{4}{3}\),且游戏中小明小亮小组要想获得“优秀小组”次数为\(16\)次,则理论上至少要进行多少轮游戏才行?并求此时\(P_1\) ,\(P_2\)的值.
【解析】 \(\text { (1) } P_{1}=\dfrac{2}{3}, \quad P_{2}=\dfrac{1}{2}\),
则在第一轮游戏他们获“优秀小组”的概率:
\(P=\left(C_{2}^{1} \dfrac{2}{3} \cdot \dfrac{1}{3}\right)\left(C_{2}^{2} \dfrac{1}{2} \cdot \dfrac{1}{2}\right)+\left(C_{2}^{2} \dfrac{2}{3} \cdot \dfrac{2}{3}\right)\left(C_{2}^{1} \dfrac{1}{2} \cdot \dfrac{1}{2}\right)\)\(+\left(C_{2}^{2} \dfrac{2}{3} \cdot \dfrac{2}{3}\right)\left(C_{2}^{2} \dfrac{1}{2} \cdot \dfrac{1}{2}\right)=\dfrac{4}{9}\).
(2)他们在一轮游戏中获“优秀小组”的概率为:
\(P=C_{2}^{1} P_{1}\left(1-P_{1}\right) C_{2}^{2} P_{2}^{2}+C_{2}^{2} P_{1}^{2} C_{2}^{1} P_{2}\left(1-P_{2}\right)+C_{2}^{2} P_{1}^{2} C_{2}^{2} P_{2}^{2}\),
\(=2 P_{1} P_{2}\left(P_{1}+P_{2}\right)-3 P_{1}^{2} P_{2}^{2}\)
因为\(P_{1}+P_{2}=\dfrac{4}{3}\),所以\(P=\dfrac{8}{3} P_{1} P_{2}-3 P_{1}^{2} p_{2}^{2}\),
因\(0≤P_1≤1\),\(0≤P_2≤1\),
所以\(\dfrac{1}{3} \leq P_{1} \leq 1\),\(\dfrac{1}{3} \leq P_{2} \leq 1\),又\(P_{1} P_{2} \leq\left(\dfrac{P_{1}+P_{2}}{2}\right)^{2}=\dfrac{4}{9}\)
所以\(\dfrac{1}{9}<p_{1} p_{2} \leq \dfrac{4}{9}\),
令\(t=p_1 p_2\),以\(\dfrac{1}{9}<t \leq \dfrac{4}{9}\),则\(P=h(t)=-3 t^{2}+\dfrac{8}{3} t\),
当\(t=\dfrac{4}{9}\)时\(P_{\max }=\dfrac{16}{27}\),他们小组在\(n\)轮游戏中获“优秀小组”次数\(ξ\)满足\(\xi \sim B(n, p)\),
由\(n p_{\max }=16\),则\(n=27\),
所以理论上至少要进行\(27\)轮游戏.
此时\(P_{1}+P_{2}=\dfrac{4}{3}\),\(p_{1} p_{2}=\dfrac{4}{9}\),\(P_{1}=P_{2}=\dfrac{2}{3}\).
【典题2】 某高校的大一学生在军训结束前,需要进行各项过关测试,其中射击过关测试规定:每位测试的大学生最多有两次射击机会,第一次射击击中靶标,立即停止射击,射击测试过关,得\(5\)分;第一次未击中靶标,继续进行第二次射击,若击中靶标,立即停止射击,射击测试过关,得\(4\)分;若未击中靶标,射击测试未能过关,得\(2\)分.现有一个班组的\(12\)位大学生进行射击过关测试,假设每位大学生两次射击击中靶标的概率分别为\(m\),\(0.5\),每位大学生射击测试过关的概率为\(p\).
(1)求\(p\)(用\(m\)表示);
(2)设该班组中恰有\(9\)人通过射击过关测试的概率为\(f(p)\),求\(f(p)\)取最大值时\(p\)和\(m\)的值;
(3)在(2)的结果下,求该班组通过射击过关测试所得总分的平均数.
【解析】 (1)每位大学生射击测试过关的概率:\(P=1-(1-m)(1-0.5)=0.5+0.5m\).
\(\text { (2) } f(p)=C_{12}^{9} p^{9}(1-p)^{3}, \quad(0<p<1)\),
\(\therefore f^{\prime}(p)=C_{12}^{9}\left[9 p^{8}(1-p)^{3}-3 p^{9}(1-p)^{2}\right]\),
\(=3 C_{12}^{3} p^{8}(1-p)^{2}(3-4 p), \quad 0<p<1\)
由\(f'(p)>0\),得\(0<p<0.75\),
由\(f'(p)<0\),得\(0.75<p<1\),
\(∴f(p)\)在\((0 ,0.75)\)上是增函数,在\((0.75 ,1)\)上是减函数,
\(∴p=0.75\)是\(f(p)\)的极大值点,也是\(f(p)\)的最大值点,
此时,由\(0.5+0.5m=0.75\),解得\(m=0.5\).
\(∴f(p)\)取得最大值时,\(p ,m\)的值分别为\(0.75\),\(0.5\).
(3)设一位大学生射击过关测试所得分数为随机变量\(X\),
则\(X\)的可能取值分别为\(5,4,2\),
则\(P(X=5)=0.5\),\(P(X=4)=(1-0.5)×0.5=0.25\),
\(P(X=2)=(1-0.5)(1-0.5)=0.25\),
\(∴\)一位大学生射击过关测试所得分数的平均数:
\(E(X)=5×0.5+4×0.25+2×0.25=4\),
\(∴\)该班组通过射击过关测试所得总分的平均数为:\(12×4=48\).
【典题3】 垃圾分类,是指按一定规定或标准将垃圾分类储存、分类投放和分类搬运,从而转变成公共资源的一系列活动的总称.分类的目的是提高垃圾的资源价值和经济价值,力争物尽其用.垃圾分类后,大部分运往垃圾处理厂进行处理.为了监测垃圾处理过程中对环境造成的影响,某大型垃圾处理厂为此建立了\(5\)套环境监测系统,并制定如下方案:每年工厂的环境监测费用预算定为\(80\)万元,日常全天候开启3套环境监测系统,若至少有\(2\)套系统监测出排放超标,则立即检查污染处理系统;若有且只有\(1\)套系统监测出排放超标,则立即同时启动另外\(2\)套系统进行\(1\)小时的监测,且后启动的这\(2\)套监测系统中只要有\(1\)套系统监测出排放超标,也立即检查污染处理系统.设每个时间段(以\(1\)小时为计量单位)被每套系统监测出排放超标的概率均为\(p(0<p<1)\),且各个时间段每套系统监测出排放超标情况相互独立.
(Ⅰ)当\(p=\dfrac{1}{2}\)时,求某个时间段需要检查污染处理系统的概率;
(Ⅱ)若每套环境监测系统运行成本为\(20\)元/小时(不启动则不产生运行费用),除运行费用外,所有的环境监测系统每年的维修和保养费用需要\(6\)万元.现以此方案实施,问该工厂的环境监测费用是否会超过预算(全年按\(9000\)小时计算)?并说明理由.
【解析】 (Ⅰ)设某个时间段在需要开启\(3\)套系统就被确定需要检查污染源处理系统的事件为\(A\),
\(P(A)=C_{3}^{2} p^{2}(1-p)+C_{3}^{3} p^{3}=C_{3}^{2}\left(\dfrac{1}{2}\right)^{2} \times \dfrac{1}{2}+C_{3}^{3}\left(\dfrac{1}{2}\right)^{3}\),
\(=C_{3}^{2}\left(\dfrac{1}{2}\right)^{3}+C_{3}^{3}\left(\dfrac{1}{2}\right)^{3}=\dfrac{1}{2}\)
设某个时间段在需要开启另外\(2\)套系统才能确定需要检查污染源处理系统的事件为\(B\),
\(P(B)=C_{3}^{1} p(1-p)^{2}\left[1-(1-p)^{2}\right]=C_{3}^{1}\left(\dfrac{1}{2}\right)^{3}\left[1-\left(\dfrac{1}{2}\right)^{2}\right]=\dfrac{9}{32}\),
\(∴\)某个时间段需要检查污染源处理系统的概率为\(\dfrac{1}{2}+\dfrac{9}{32}=\dfrac{25}{32}\).
(Ⅱ)设某个时间段环境监测系统的运行费用为\(X\)元,则\(X\)的可能取值为\(60\),\(100\).
\(P(X=100)=C_{3}^{1} p(1-p)^{2}\),\(P(X=60)=1-C_{3}^{1} p(1-p)^{2}\)
\(E(X)=60\left[1-C_{3}^{1} p(1-p)^{2}\right]+100 \times C_{3}^{1} p(1-p)^{2}=60+120 p(1-p)^{2}\),
令\(g(p)=p(1-p)^2\) ,\(p∈(0 ,1)\),
则\(g'(p)=(1-p)^2-2p(1-p)=(3p-1)(p-1)\).
当\(p \in\left(0, \dfrac{1}{3}\right)\)时,\(g'(p)>0\),\(g(p)\)在\(\left(0, \dfrac{1}{3}\right)\)上单调递增,
当\(p \in\left(\dfrac{1}{3}, 1\right)\)时,\(g'(p)<0\) ,\(g(p)\)在\(\left(\dfrac{1}{3}, 1\right)\)上单调递减,
\(∴g(p)\)的最大值为\(g\left(\dfrac{1}{3}\right)=\dfrac{4}{27}\),
\(∴\)实施此方案,最高费用为\(6+9000\left(60+120 \times \dfrac{4}{27}\right) \times 10^{-4}=76\)(万元),
\(∵76<80\),故不会超过预算.
巩固练习
1(★★)\(1\)选手甲分别与乙、丙两选手进行象棋比赛,如果甲、乙比赛,那么每局比赛甲获胜的概率为\(\dfrac{3}{5}\),乙获胜的概率为\(\dfrac{2}{5}\),如果甲、丙比赛,那么每局比赛甲、丙获胜的概率均为\(\dfrac{1}{2}\).
(1)若采用\(3\)局\(2\)胜制,两场比赛甲获胜的概率分别是多少?
(2)若采用\(5\)局\(3\)胜制,两场比赛甲获胜的概率分别是多少?你能否据此说明赛制与选手实力对比赛结果的影响?
2(★★★) 某学校高三甲、乙两班同学进行拔河比赛,各局比赛相互之间没有影响.
(1)若单局比赛甲班胜乙班的概率为\(\dfrac{1}{2}\),比赛采用“\(3\)局\(2\)胜”制,即先胜两局的班获胜,那么甲、乙两班获胜的概率是否相等?并说明理由;
(2)设单局比赛甲班胜乙班的概率为\(p(0<p≤1)\),若比赛\(6\)局,甲班恰好获胜\(3\)局,当甲班恰好获胜\(3\)局的概率最大时,求\(p\)的值;
(3)若单局比赛甲班胜乙班的概率为(2)中的甲班恰好获胜\(3\)局的概率取最大值时\(p\)的值,比赛采用“\(5\)局\(3\)胜”制,设\(X\)为本场比赛的局数,求\(X\)的数学期望.
3(★★★)翡翠市场流行一种赌石“游戏规则”:翡翠在开采出来时有一层风化皮包裹着,无法知道其内的好坏,须切割后方能知道翡翠的价值,参加者先缴纳一定金额后可得到一块翡翠石并现场开石验证其具有的收藏价值.某举办商在赌石游戏中设置了甲、乙两种赌石规则,规则甲的赌中率为\(\dfrac{2}{3}\),赌中后可获得\(20\)万元;规则乙的赌中率为\(P_0 (0<P_0<1)\),赌中后可得\(30\)万元;未赌中则没有收获.每人有且只有一次赌石机会,每次赌中与否互不影响,赌石结束后当场得到兑现金额.
(1)收藏者张先生选择规则甲赌石,收藏者李先生选择规则乙赌石,记他们的累计获得金额数为\(X\)(单位:万元),若\(X≤30\)的概率为\(\dfrac{7}{9}\),求\(P_{0}\)的大小;
(2)若收藏者张先生、李先生都选择赌石规则甲或选择赌石规则乙进行赌石,问:他们选择何种规则赌石,累计得到金额的数学期望最大?
4(★★★)高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型,在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内.如图1所示的高尔顿板有\(7\)层小木块,小球从通道口落下,第一次与第\(2\)层中间的小木块碰撞,以\(\dfrac{1}{2}\)的概率向左或向右滚下,依次经过\(6\)次与小木块碰撞,最后掉入编号为\(1,2,…,7\)的球槽内.例如小球要掉入\(3\)号球槽,则在\(6\)次碰撞中有\(2\)次向右\(4\)次向左滚下.

(Ⅰ)如图\(1\),进行一次高尔顿板试验,求小球落入\(5\)号球槽的概率;
(Ⅱ)小红、小明同学在研究了高尔顿板后,利用高尔顿板来到社团文化节上进行盈利性“抽奖”活动.小红使用图\(1\)所示的高尔顿板,付费\(6\)元可以玩一次游戏,小球掉入\(m\)号球槽得到的奖金为\(ξ\)元,其中\(ξ=|16-4m|\).小明改进了高尔顿板(如图\(2\)),首先将小木块减少成\(5\)层,然后使小球在下落的过程中与小木块碰撞时,有\(\dfrac{1}{3}\)的概率向左,\(\dfrac{2}{3}\)的概率向右滚下,最后掉入编号为\(1,2,…,5\)的球槽内,改进高尔顿板后只需付费\(4\)元就可以玩一次游戏,小球掉入\(n\)号球槽得到的奖金为\(η\)元,其中\(η=(n-4)^2\).两位同学的高尔顿板游戏火爆进行,很多同学参加了游戏,你觉得小红和小明同学谁的盈利多?请说明理由.
5(★★★)一种游戏的规则为抛掷一枚硬币,每次正面向上得\(2\)分,反面向上得\(1\)分.
(1)设抛掷\(4\)次的得分为\(X\),求变量\(X\)的分布列和数学期望.
(2)当游戏得分为\(n(x∈N^*)\)时,游戏停止,记得\(n\)分的概率和为\(Q_n\),\(Q_{1}=\dfrac{1}{2}\).
①求\(Q_2\);
②当\(n∈N^*\)时,记\(A_{n}=Q_{n+1}+\dfrac{1}{2} Q_{n}\),\(B_{n}=Q_{n+1}-Q_{n}\)证明:数列\(\left\{A_{n}\right\}\)为常数列,数列\(\left\{B_{n}\right\}\)为等比数列.
6 (★★★★)甲口袋中装有\(2\)个黑球和\(1\)个白球,乙口袋中装有\(3\)个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复\(n\)次这样的操作,记甲口袋中黑球个数为\(X_n\),恰有\(2\)个黑球的概率为\(p_n\),恰有1个黑球的概率为\(q_n\).
(1)求\(p_1\),\(q_1\)和\(p_2\),\(q_2\);
(2)求\(2p_n+q_n\)与\(2 p_{n-1}+q_{n-1}\)的递推关系式和\(X_n\)的数学期望\(E\left(X_{n}\right)\)(用\(n\)表示).
7 (★★★★)射击是使用某种特定型号的枪支对各种预先设置的目标进行射击,以命中精确度计算成绩的一项体育运动.射击运动不仅能锻炼身体,而且可以培养细致、沉着、坚毅等优良品质,有益于身心健康.为了度过愉快的假期,感受体育运动的美好,法外狂徒张三来到私人靶场体验射击运动.
(1)已知用于射击打靶的某型号步枪的弹夹中一共有\(k(k∈N^*)\)发子弹,假设张三每次打靶的命中率均为\(p(0<p<1)\),靶场主规定:一旦出现子弹脱靶或者子弹打光耗尽的现象便立刻停止射击.记标靶上的子弹数量为随机变量\(X\),求\(X\)的分布列和数学期望.
(2)张三在休息之余用手机逛B站刷到了著名电视剧《津门飞鹰》中的经典桥段:中国队长燕双鹰和三合会何五姑玩起了俄罗斯轮盘.这让张三不由得想起了半人半鬼,神枪第一的那句家喻户晓的神话”我赌你的枪里没有子弹”.由此,在接下来的射击体验中,张三利用自己的人脉关系想办法找人更换了一把型号为M1917,弹容为\(6\)发的左轮手枪,弹巢中有\(m\)发实弹,其余均为空包弹.现规定:每次射击后,都需要在下一次射击之前填充一发空包弹.假设每次射击相互独立且均随机.在进行\(n(n∈N)\)次射击后,记弹巢中空包弹的发数\(X_n\).
\((i)\)当\(n∈N^*\)时,探究数学期望\(E(X_n)\)和\(E(X_{n-1})\)之间的关系;
\((ii)\)若无论m取何值,当射击次数达到一定程度后都可近似认为枪中没有实弹(以弹巢中实弹的发数的数学期望为决策依据,当弹巢中实弹的发数的数学期望\(<1\)时可近似认为枪中没有实弹),求该种情况下最小的射击次数\(n_0\).(参考数据:\(lg2≈0.301\)、\(lg3≈0.477\))
8 (★★★★) 公元1651年,法国一位著名的统计学家德梅赫(Demere)向另一位著名的数学家帕斯卡(B.Pascal)提请了一个问题,帕斯卡和费马(Fermat)讨论了这个问题,后来惠更斯(C.Huygens)也加入了讨论,这三位当时全欧洲乃至全世界最优秀的科学家都给出了正确的解答.该问题如下:
设两名赌徒约定谁先赢\(k(k>1 ,k∈N^*)\)局,谁便赢得全部赌注\(a\)元.每局甲赢的概率为\(p(0<p<1)\),乙赢的概率为\(1-p\),且每局赌博相互独立.在甲赢了\(m(m<k)\)局,乙赢了\(n(n<k)\)局时,赌博意外终止.赌注该怎么分才合理?这三位数学家给出的答案是:如果出现无人先赢\(k\)局则赌博意外终止的情况,甲、乙便按照赌博再继续进行下去各自赢得全部赌注的概率之比\(P_{\text {甲 }}: P_{乙}\)分配赌注.
(1)规定如果出现无人先赢\(k\)局则赌博意外终止的情况,甲、乙便按照赌博再继续进行下去各自赢得全部赌注的概率之比\(P_{\text {甲 }}: P_{乙}\)分配赌注.若\(a=243\) ,\(k=4\) ,\(m=2\) ,\(n=1\) ,\(p=\dfrac{2}{3}\),则甲应分得多少赌注?
(2)记事件\(A\)为“赌博继续进行下去乙赢得全部赌注”,试求当\(k=4\),\(m=2\) ,\(n=1\)时赌博继续进行下去甲赢得全部赌注的概率\(f(p)\),并判断当\(p \geq \dfrac{3}{4}\)时,事件A是否为小概率事件,并说明理由.
规定:若随机事件发生的概率小于\(0.05\),则称该随机事件为小概率事件.
9 (★★★★) 2019年12月以来,湖北武汉市发现多起病毒性肺炎病例,并迅速在全国范围内开始传播,专家组认为,本次病毒性肺炎病例的病原体初步判定为新型冠状病毒,该病毒存在人与人之间的传染,可以通过与患者的密切接触进行传染.我们把与患者有过密切接触的人群称为密切接触者,每位密切接触者被感染后即被称为患者.已知每位密切接触者在接触一个患者后被感染的概率为\(P(0<p<1)\),某位患者在隔离之前,每天有\(a\)位密切接触者,其中被感染的人数为\(X(0≤X≤a)\),假设每位密切接触者不再接触其他患者.
(1)求一天内被感染人数为\(X\)的概率\(P(X)\)与\(a\)、\(p\)的关系式和\(X\)的数学期望;
(2)该病毒在进入人体后有\(14\)天的潜伏期,在这\(14\)天的潜伏期内患者无任何症状,为病毒传播的最佳时间,设每位患者在被感染后的第二天又有\(a\)位密切接触者,从某一名患者被感染,按第\(1\)天算起,第\(n\)天新增患者的数学期望记为\(E_n (n≥2)\).
\((i)\)求数列\(\{E_n\}\)的通项公式,并证明数列\(\{E_n\}\)为等比数列;
\((ii)\)若戴口罩能降低每位密切接触者患病概率,降低后的患病概率\(p^{\prime}=\ln (1+p)-\dfrac{2}{3} p\).当\(p'\)取最大值时,计算此时\(p'\)所对应的\(E_6'\)值和此时\(p\)对应的\(E_6\)值,根据计算结果说明戴口罩的必要性.(取\(a=10\))
(结果保留整数,参考数据:\(ln5≈1.6\),\(ln3≈1.1\),\(ln2≈0.7\))
参考答案
-
【答案】 (1) 甲乙比赛甲获胜的概率\(p=\dfrac{81}{125}\), 甲丙比赛甲获胜的概率\(\dfrac{1}{2}\)
(2) 甲乙比赛,采用\(5\)局\(3\)胜制还是\(3\)局\(2\)胜制,甲获胜的概率都一样,这说明比赛局数越多对实力较强者有利.
【解析】 (1)采用\(3\)局\(2\)胜制,甲获胜的可能分\(2:0\),\(2:1\),
因为每局的比赛结果相互独立,
所以甲乙比赛甲获胜的概率\(P_{1}=\dfrac{3}{5} \times \dfrac{3}{5}+C_{2}^{1} \times\left(\dfrac{3}{5}\right)^{2} \times \dfrac{2}{5}=\dfrac{81}{125}\),
甲丙比赛甲获胜的概率\(P_{2}=\dfrac{1}{2} \times \dfrac{1}{2}+C_{2}^{1} \times\left(\dfrac{1}{2}\right)^{2} \times \dfrac{1}{2}=\dfrac{1}{2}\),
(2)采用\(5\)局\(3\)胜制,甲获胜的情况有\(3:0\),\(3:1\)或\(3:2\),
甲乙比赛,甲获胜的概率
\(P_{3}=\left(\dfrac{3}{5}\right)^{3}+C_{3}^{2} \times\left(\dfrac{3}{5}\right)^{3} \times \dfrac{2}{5}+C_{4}^{2} \times\left(\dfrac{3}{5}\right)^{3} \times\left(\dfrac{2}{5}\right)^{2}=\dfrac{27}{125} \times \dfrac{79}{25}=0.68256\),
甲丙比赛,甲获胜的概率\(P_{4}=\left(\dfrac{1}{2}\right)^{3}+C_{3}^{2} \times\left(\dfrac{1}{2}\right)^{3} \times \dfrac{1}{2}+C_{4}^{2} \times\left(\dfrac{1}{2}\right)^{3} \times\left(\dfrac{1}{2}\right)^{2}=0.5\),
因为\(P_1<P_3\),所以甲乙比赛,采用\(5\)局\(3\)胜制对甲有利,
\(P_2=P_4\),所以甲乙比赛,采用\(5\)局\(3\)胜制还是3局2胜制,甲获胜的概率都一样,这说明比赛局数越多对实力较强者有利. -
【答案】 (1) 甲、乙两班获胜的概率相等 \((2) \dfrac{1}{2} \quad (3) \dfrac{33}{8}\)
【解析】 (1)记“比赛两局,甲班全胜”为事件\(A\),“比赛三局,甲班前两局中一胜一负,第三局胜”为事件\(B\),
\(∵\)事件\(A\),\(B\)为互斥事件,\(∴P(A+B)=P(A)+P(B)=\left(\dfrac{1}{2}\right)^{2}+C_{2}^{1}\left(\dfrac{1}{2}\right)^{2}\left(1-\dfrac{1}{2}\right)=\dfrac{1}{2}\),
\(∴\)甲班获胜的概率是\(\dfrac{1}{2}\),从而乙班获胜的概率也是\(\dfrac{1}{2}\),
\(∴\)甲、乙两班获胜的概率相等.
(2)设比赛\(6\)局,甲班恰好获胜\(3\)局的概率为\(f(p)\),
则\(f(p)=C_6^3 p^3 (1-p)^3\),
\(f(p)=C_{6}^{3} p^{3}(1-p)^{3} \leq C_{6}^{3}\left[\left(\dfrac{p+(1-p)}{2}\right)^{2}\right]^{3}=\dfrac{5}{16}\),
\(∴\)当\(p=1-p\),即\(p=\dfrac{1}{2}\)时,甲班恰好获胜\(3\)局的概率最大.
(3)比赛\(3\)局有两种情况,即甲班胜\(3\)局,或乙班胜\(3\)局,
则\(P(X=3)=\left(\dfrac{1}{2}\right)^{3}+\left(\dfrac{1}{2}\right)^{3}=\dfrac{1}{4}\),
比赛\(4\)局结束有两种情况,即前\(3\)局甲班胜\(2\)局,第\(4\)局甲班胜,或前\(3\)局中乙班胜\(2\)局,第\(4\)局乙班胜,
则\(P(X=4)=C_{3}^{2}\left(\dfrac{1}{2}\right)^{2} \times \dfrac{1}{2} \times \dfrac{1}{2}+C_{3}^{2}\left(\dfrac{1}{2}\right)^{2} \times \dfrac{1}{2} \times \dfrac{1}{2}=\dfrac{3}{8}\),
比赛\(5\)局结束有两种情况,即前\(4\)局中甲班胜2局,第\(5\)局甲班胜或前\(4\)局乙班胜\(2\)局,第\(5\)局乙班胜,
则\(P(X=5)=C_{4}^{2}\left(\dfrac{1}{2}\right)^{2} \times\left(\dfrac{1}{2}\right)^{2} \times 1=\dfrac{3}{8}\),\(E(X)=3 \times \dfrac{1}{4}+4 \times \dfrac{3}{8}+5 \times \dfrac{3}{8}=\dfrac{33}{8}\). -
【答案】 \(\text { (1) } \dfrac{1}{3}\)
(2) 当\(0<P_{0}<\dfrac{4}{9}\)时,他们都选择规则甲进行赌石时,累计得到金额的数学期望最大;
当\(\dfrac{4}{9}<P_{0}<1\)时,他们都选择规则乙进行赌石时,累计得到金额的数学期望最大;
当\(P_{0}=\dfrac{4}{9}\)时,他们都选择规则甲或规则乙进行赌石时,累计得到金额的数学期望相等
【解析】 (1)由已知得收藏者张先生赌中的概率为\(\dfrac{2}{3}\),收藏者李先生赌中的概率为\(P_{0}\),且两人赌中与否互不影响.记“这\(2\)人的累计获得金额数为\(X\)(单位:万元)”的事件为\(A\),则事件\(A\)的对立事件为“\(X=50\)”.
因为\(P(X=50)=\dfrac{2}{3} P_{0}\),
所以\(P(A)=1-P(X=50)=1-\dfrac{2}{3} P_{0}=\dfrac{7}{9}\),求得\(P_{0}=\dfrac{1}{3}\).
(2)设收藏者张先生、李先生都选择规则甲赌中的次数为\(X_1\),都选择规则乙赌中的次数为\(X_2\),则这两人选择规则甲累计获奖得金额的数学期望为\(E(20X_1)\),选择规则乙累计获奖得金额的数学期望为\(E(30X_2)\).
由已知可得,\(X_{1} \sim B\left(2, \dfrac{2}{3}\right)\),\(X_{2} \sim B\left(2, P_{0}\right)\),
所以\(E\left(X_{1}\right)=\dfrac{4}{3}\),\(E\left(X_{2}\right)=2 P_{0}\),
从而\(E\left(20 X_{1}\right)=20 E\left(X_{1}\right)=20 \times \dfrac{4}{3}=\dfrac{80}{3}\),\(E(30X_2)=30E(X_2)=60P_0\).
若\(E\left(20 X_{1}\right)>E\left(30 X_{2}\right)\),则\(\dfrac{80}{3}>60 P_{0}\),解得\(0<P_{0}<\dfrac{4}{9}\);
若\(E\left(20 X_{1}\right)<E\left(30 X_{2}\right)\),则\(\dfrac{80}{3}<60 P_{0}\),解得\(\dfrac{4}{9}<P_{0}<1\);
若\(E\left(20 X_{1}\right)=E\left(30 X_{2}\right)\),则\(\dfrac{80}{3}=60 P_{0}\),解得\(P_{0}=\dfrac{4}{9}\).
综上所述,
当\(0<P_{0}<\dfrac{4}{9}\)时,他们都选择规则甲进行赌石时,累计得到金额的数学期望最大;
当\(\dfrac{4}{9}<P_{0}<1\)时,他们都选择规则乙进行赌石时,累计得到金额的数学期望最大;
当\(P_{0}=\dfrac{4}{9}\)时,他们都选择规则甲或规则乙进行赌石时,累计得到金额的数学期望相等. -
【答案】 \(\text { (1) } \dfrac{15}{64}\) (2) 小明的盈利多
【解析】 (Ⅰ)设这个小球掉入\(5\)号球槽为事件\(A\).掉入\(5\)号球槽,需要向右\(4\)次向左\(2\)次,
所以\(P(A)=C_{6}^{2}\left(\dfrac{1}{2}\right)^{2}\left(\dfrac{1}{2}\right)^{4}=\dfrac{15}{64}\).
所以这个小球掉入\(5\)号球槽的概率为\(\dfrac{15}{64}\).
(Ⅱ)小红的收益计算如下:每一次游戏中,\(ξ\)的可能取值为\(0,4,8,12\).
\(P(\xi=0)=P(m=4)=C_{6}^{3}\left(\dfrac{1}{2}\right)^{3}\left(\dfrac{1}{2}\right)^{3}=\dfrac{5}{16}\),
\(P(\xi=4)=P(m=3)+P(m=5)=C_{6}^{2}\left(\dfrac{1}{2}\right)^{2}\left(\dfrac{1}{2}\right)^{4}+C_{6}^{4}\left(\dfrac{1}{2}\right)^{4}\left(\dfrac{1}{2}\right)^{2}=\dfrac{15}{32}\),
\(P(\xi=8)=P(m=2)+P(m=6)=C_{6}^{1}\left(\dfrac{1}{2}\right)\left(\dfrac{1}{2}\right)^{5}+C_{6}^{5}\left(\dfrac{1}{2}\right)^{5}\left(\dfrac{1}{2}\right)=\dfrac{3}{16}\),
\(P(\xi=12)=P(m=1)+P(m=7)=C_{6}^{0}\left(\dfrac{1}{2}\right)^{6}+C_{6}^{6}\left(\dfrac{1}{2}\right)^{6}=\dfrac{1}{32}\)
\(ξ\)的分布列
\(\begin{array}{|c|c|c|c|c|} \hline \xi & 0 & 4 & 8 & 12 \\ \hline P & \dfrac{5}{16} & \dfrac{15}{32} & \dfrac{3}{16} & \dfrac{1}{32} \\ \hline \end{array}\)
一次游戏付出的奖金\(E \xi=0 \times \dfrac{5}{16}+4 \times \dfrac{15}{32}+8 \times \dfrac{3}{16}+12 \times \dfrac{1}{32}=\dfrac{15}{4}\),
则小红的收益为\(6-\dfrac{15}{4}=\dfrac{9}{4}\).
小明的收益计算如下:每一次游戏中,\(η\)的可能取值为\(0,1,4,9\).
\(P(\eta=0)=P(n=4)=C_{4}^{3}\left(\dfrac{1}{3}\right)\left(\dfrac{2}{3}\right)^{3}=\dfrac{32}{81}\),
\(P(\eta=1)=P(n=3)+P(n=5)=C_{4}^{2}\left(\dfrac{1}{3}\right)^{2}\left(\dfrac{2}{3}\right)^{2}+C_{4}^{4}\left(\dfrac{2}{3}\right)^{4}=\dfrac{40}{81}\),
\(P(\eta=4)=P(n=2)=C_{4}^{1}\left(\dfrac{1}{3}\right)^{3}\left(\dfrac{2}{3}\right)=\dfrac{8}{81}\),
\(P(\eta=9)=P(n=1)=\left(\dfrac{1}{3}\right)^{4}=\dfrac{1}{81}\).
\(∴η\)的分布列为
\(\begin{array}{|c|c|c|c|c|} \hline \eta & 0 & 1 & 4 & 9 \\ \hline P & \dfrac{32}{81} & \dfrac{40}{81} & \dfrac{8}{81} & \dfrac{1}{81} \\ \hline \end{array}\)
一次游戏付出的奖金\(E \eta=0 \times \dfrac{32}{81}+1 \times \dfrac{40}{81}+4 \times \dfrac{8}{81}+9 \times \dfrac{1}{81}=1\),
则小明的收益为\(4-1=3\).
\(\because 3>\dfrac{9}{4}\),\(∴\)小明的盈利多. -
【答案】 (1)\(X\)的分布列为
\(\begin{array}{|c|c|c|c|c|c|} \hline P & 4 & 5 & 6 & 7 & 8 \\ \hline X & \dfrac{1}{16} & \dfrac{1}{4} & \dfrac{3}{8} & \dfrac{1}{4} & \dfrac{1}{16} \\ \hline \end{array}\)
\(E(X)=6\).
\((2) ① \quad \dfrac{3}{4}\)
② 证明略
【解析】 (1)解:变量\(X\)的所有可能取值为\(4,5,6,7,8\),
\(∵\)每次抛掷一次硬币,正面向上的概率为\(\dfrac{1}{2}\),反面向上的概率为\(\dfrac{1}{2}\),
\(\therefore P(X=4)=\left(\dfrac{1}{2}\right)^{4}=\dfrac{1}{16}\),\(P(X=5)=C_{4}^{1}\left(\dfrac{1}{2}\right)^{4}=\dfrac{1}{4}\)
\(P(X=6)=C_{4}^{2}\left(\dfrac{1}{2}\right)^{4}=\dfrac{3}{8}\),\(P(X=7)=C_{4}^{3}\left(\dfrac{1}{2}\right)^{4}=\dfrac{1}{4}\)
\(P(X=8)=C_{4}^{4}\left(\dfrac{1}{2}\right)^{4}=\dfrac{1}{16}\),
\(∴X\)的分布列为
\(\begin{array}{|c|c|c|c|c|c|} \hline P & 4 & 5 & 6 & 7 & 8 \\ \hline X & \dfrac{1}{16} & \dfrac{1}{4} & \dfrac{3}{8} & \dfrac{1}{4} & \dfrac{1}{16} \\ \hline \end{array}\)
\(E(X)=4 \times \dfrac{1}{16}+5 \times \dfrac{1}{4}+6 \times \dfrac{3}{8}+7 \times \dfrac{1}{4}+8 \times \dfrac{1}{16}=6\).
(2)①解:得\(2\)分只需要抛掷一次正面向上或两次反面向上,
概率的和为:\(Q_{2}=\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^{2}=\dfrac{3}{4}\),
②证明:得\(n\)分分两种情况,第一种为得\(n-2\)分后抛掷一次正面向上,
第二种为得\(n-1\)分后,抛掷一次反面向上,
\(∴\)当\(n≥3\),且\(n∈N^*\)时,\(Q_{n}=\dfrac{1}{2} Q_{n-1}+\dfrac{1}{2} Q_{n-2}\),
\(A_{n+1}=Q_{n}+2+\dfrac{1}{2} Q_{n+1}=\dfrac{1}{2} Q_{n+1}+\dfrac{1}{2} Q_{n}+\dfrac{1}{2} Q_{n+1}\)\(=Q_{n+1}+\dfrac{1}{2} Q_{n}=A_{n}\)
\(∴\)数列\(\left\{A_{n}\right\}\)为常数列,
\(\because B_{n+1}=Q_{n+2}-Q_{n+1}=\dfrac{1}{2} Q_{n+1}+\dfrac{1}{2} Q_{n}-Q_{n+1}=-\dfrac{1}{2} Q_{n+1}+\dfrac{1}{2} Q_{n}\)
\(=-\dfrac{1}{2}\left(Q_{n+1}-Q n\right)=-\dfrac{1}{2} B_{n}\),
\(\because B_{1}=P_{2}-P_{1}=\dfrac{3}{4}-\dfrac{1}{2}=\dfrac{1}{4}\),
\(∴\)数列\(\left\{B_{n}\right\}\)为等比数列. -
【答案】 \(\text { (1) } p_{1}=\dfrac{1}{3}, q_{1}=\dfrac{2}{3}, p_{2}=\dfrac{7}{27}, q_{2}=\dfrac{16}{27}\)
\(\text { (2) } 2 p_{n}+q_{n}=\left(\dfrac{1}{3}\right)^{n}+1\),\(E\left(X_{n}\right)=\left(\dfrac{1}{3}\right)^{n}+1\)
【解析】 (1)由题意可知\(p_{1}=\dfrac{1}{3}\),\(q_{1}=\dfrac{2}{3}\),
则p\(p_{2}=\dfrac{1}{3} p_{1}+\dfrac{2}{3} \times \dfrac{1}{3} q_{1}=\dfrac{7}{27}\);
\(q_{2}=\dfrac{2}{3} p_{1}+\left(\dfrac{2}{3} \times \dfrac{2}{3}+\dfrac{1}{3} \times \dfrac{1}{3}\right) q_{1}=\dfrac{16}{27}\).
(2)由题意可知\(p_{n+1}=\dfrac{1}{3} p_{n}+\dfrac{2}{3} \times \dfrac{1}{3} q_{n}=\dfrac{1}{3} p_{n}+\dfrac{2}{9} q_{n}\),
\(q_{n+1}=\dfrac{2}{3} p_{n}+\left(\dfrac{2}{3} \times \dfrac{2}{3}+\dfrac{1}{3} \times \dfrac{1}{3}\right) q_{n}+\dfrac{2}{3}\left(1-p_{n}-q_{n}\right)=-\dfrac{1}{9} q_{n}+\dfrac{2}{3}\),
两式相加可得\(2 p_{n+1}+q_{n+1}=\dfrac{2}{3} p_{n}+\dfrac{1}{3} q_{n}+\dfrac{2}{3}=\dfrac{1}{3}\left(2 p_{n}+q_{n}\right)+\dfrac{2}{3}\),
则\(2 p_{n}+q_{n}=\dfrac{1}{3}\left(2 p_{n-1}+q_{n-1}\right)+\dfrac{2}{3}\),
所以\(2 p_{n}+q_{n}-1=\dfrac{1}{3}\left(2 p_{n-1}+q_{n-1}-1\right)\),
因为\(2 p_{1}+q_{1}-1=\dfrac{1}{3}\),数列\(\left\{2 p_{n}+q_{n}-1\right\}\)是首项为\(\dfrac{1}{3}\),公比为\(\dfrac{1}{3}\)的等比数列,
所以\(2 p_{n}+q_{n}-1=\left(\dfrac{1}{3}\right)^{n}\),
即\(2 p_{n}+q_{n}=\left(\dfrac{1}{3}\right)^{n}+1\),
所以\(E\left(X_{n}\right)=2 p_{n}+q_{n}+0 \times\left(1-p_{n}-q_{n}\right)=\left(\dfrac{1}{3}\right)^{n}+1\). -
【答案】 \((1) X\)的分布列为
\(\begin{array}{|c|c|c|c|c|c|c|} \hline X & 0 & 1 & 2 & \ldots & k-1 & k \\ \hline P & 1-p & p(1-p) & p^{2}(1-p) & \ldots & p^{k-1}(1-p) & p^{k} \\ \hline \end{array}\)
\(E(X)=\dfrac{p-p^{k+1}}{1-p}\)
\((2) (i) E\left(X_{n}\right)=\dfrac{5}{6} E\left(X_{n-1}\right)+1 \quad (ii) n_{0}=10\)
【解析】 (1)由题意,\(X\)的所有可能取值为:\(0,1,2,…,k-1,k\),
因为张三每次打靶的命中率均为\(p(0<p<1)\),
则\(P(X=m)=p^{m}(1-p)(m=0,1,2, \ldots, k-1)\),\(P(X=k)=p^{k}\)
所以\(X\)的分布列为
\(\begin{array}{|c|c|c|c|c|c|c|} \hline X & 0 & 1 & 2 & \ldots & k-1 & k \\ \hline P & 1-p & p(1-p) & p^{2}(1-p) & \ldots & p^{k-1}(1-p) & p^{k} \\ \hline \end{array}\)
所以\(X\)的数学期望为
\(E(X)=p(1-p)+2 p^{2}(1-p)+3 p^{3}(1-p)+\cdots+(k-1) p^{k-1}(1-p)+k p^{k}\),
令\(M=p+2 p^{2}+3 p^{3}+\cdots+(k-1) p^{k-1}\) ①,
则\(p M=p^{2}+2 p^{3}+3 p^{4}+\cdots+(k-1) p^{k}\) ②,
所以①-②可得,
\((1-p) M=p+p^{2}+p^{3}+\cdots+p^{k-1}-(k-1) p^{k}=\dfrac{p\left(1-p^{k-1}\right)}{1-p}-(k-1) p^{k}\)
则\(E(X)=M(1-p)+k p^{k}=\dfrac{p-p^{k}}{1-p}-(k-1) p^{k}+k p^{k}=\dfrac{p-p^{k+1}}{1-p}\);
\((2)(i)\)第\(n\)次射击后,可能包含两种情况:第\(n\)次射出空包弹或第\(n\)次射出实弹;
因为第\(n\)次射击前,剩余空包弹的期望为\(E\left(X_{n-1}\right)\),
若第\(n\)次射出空包弹,则此时对应的概率为\(\dfrac{E\left(X_{n-1}\right)}{6}\),
因为射击后要填充一发空包弹,
所以此时空包弹的数量为\(E\left(X_{n-1}\right)-1+1=E\left(X_{n-1}\right)\);
若第\(n\)次射出实弹,则此时对应的概率为\(1-\dfrac{E\left(X_{n-1}\right)}{6}\),
所以此时空包弹的数量为\(E\left(X_{n-1}\right)+1\);
综上,\(E\left(X_{n}\right)=\dfrac{E\left(X_{n-1}\right)}{6} \cdot E\left(X_{n-1}\right)+\left[1-\dfrac{E\left(X_{n-1}\right)}{6}\right]\left[E\left(X_{n-1}\right)+1\right]\)\(=\dfrac{5}{6} E\left(X_{n-1}\right)+1\);
\((ii)\)因为当\(n=0\)时,弹夹中有\(6-m\)发空包弹,则\(E(X_0)=6-m\);
由(i)可知:\(E\left(X_{n}\right)=\dfrac{5}{6} E\left(X_{n-1}\right)+1\left(n \in \boldsymbol{N}^{*}\right)\),
则\(E\left(X_{n+1}\right)-6=\dfrac{5}{6}\left[E\left(X_{n}\right)-6\right](n \in N)\),
所以\(\left\{E\left(X_{n}\right)-6\right\}(n \in \boldsymbol{N})\)是首项为\(-m\),公比为\(\dfrac{5}{6}\)的等比数列,
则\(E\left(X_{n}\right)-6=-m\left(\dfrac{5}{6}\right)^{n}\),即\(E\left(X_{n}\right)=6-m\left(\dfrac{5}{6}\right)^{n}(n \in \boldsymbol{N})\),
因此弹巢中实弹的发数的期望为\(6-E\left(X_{n}\right)=m\left(\dfrac{5}{6}\right)^{n}\),
为使弹巢中实弹的发数的数学期望小于\(1\),只需\(m\left(\dfrac{5}{6}\right)^{n}<1\),
则\(m<\left(\dfrac{6}{5}\right)^{n}\),所以\(\log _{\frac{6}{5}} m<n\)
为使\(\log _{\frac{6}{5}} m<n\)恒成立,只需\(\left(\log _{\frac{6}{5}} m\right)_{\max }<n\),
而\(\left(\log _{\frac{6}{5}} m\right)_{\max }=\log _{\frac{6}{5}} 6=\dfrac{\lg 6}{\lg \frac{6}{5}}=\dfrac{\lg 6}{\lg 6-\lg 5}\),
\(=\dfrac{\lg 2+\lg 3}{\lg 2+\lg 3-\ln +\lg 2}=\dfrac{\lg 2+\lg 3}{2 \lg 2+\lg 3-l}\)
\(=\dfrac{0.301+0.477}{0.602+0.477-1} \approx 9.848\)
又\(n∈N\),所以最小的射击次数\(n_0=10\). -
【答案】 \((1) 216\) \((2) f(p)=1-(1+3p) (1-p)^3\),事件\(A\)不是小概率事件
【解析】 (1)设赌博再继续进行X局甲赢得全部赌注,则最后一局必然甲赢.
由题意知,最多再进行\(4\)局,甲乙必然有人赢得全部赌注.
当\(X=2\)时,甲以\(4:1\)赢,所以\(P(X=2)=\left(\dfrac{2}{3}\right)^{2}=\dfrac{4}{9}\),
当\(X=3\)时,甲以\(4:2\)赢,所以\(P(X=3)=C_{2}^{1}\left(\dfrac{2}{3}\right)\left(1-\dfrac{2}{3}\right)\left(\dfrac{2}{3}\right)=\dfrac{8}{27}\),
当\(X=4\)时,甲以\(4:3\)赢,所以\(P(X=4)=C_{3}^{1}\left(\dfrac{2}{3}\right)\left(1-\dfrac{2}{3}\right)^{2}\left(\dfrac{2}{3}\right)=\dfrac{4}{27}\).
所以,甲赢的概率为\(\dfrac{4}{9}+\dfrac{8}{27}+\dfrac{4}{27}=\dfrac{8}{9}\).
所以,甲应分得的赌注为\(243 \times \dfrac{8}{9}=216\)元.
(2)设赌博继续进行\(X\)局乙赢得全部赌注,则最后一局必然乙赢.
当\(X=3\)时,乙以\(4:2\)赢,\(P(X=3)=(1-p)^3\),
当\(X=4\)时,乙以\(4:3\)赢,\(P(X=4)=C_{3}^{1} p(1-p)^{3}=3 p(1-p)^{3}\),
所以,乙赢得全部赌注的概率为\(P(A)=(1-p)^{3}+3 p(1-p)^{3}=(1+3 p)(1-p)^{3}\).
\(∴\)甲赢得全部赌注的概率\(f(p)=1-(1+3 p)(1-p)^{3}\).
求导\(f^{\prime}(p)=-3(1-p)^{3}-(1+3 p) \cdot 3(1-p)^{2} \cdot(-1)=12 p(1-p)^{2}\).
\(\because \dfrac{3}{4} \leq p<1\),\(\therefore f^{\prime}(p)>0\),\(∴f(p)\)在\(\left[\dfrac{3}{4}, 1\right)\)上单调递增,
于是\(f(p)_{\min }=f\left(\dfrac{3}{4}\right)=\dfrac{243}{256}\),
故乙赢的概率为\(1-\dfrac{243}{256}=\dfrac{13}{256} \approx 0.0508>0.05\),
故事件\(A\)不是小概率事件. -
【答案】 \(\text { (1) } P(X)=C_{a}^{x} p^{x}(1-p)^{a-x}\),\(EX=ap\)
\(\text { (2) (i) } E n=a p(1+a p)^{n-2} \quad (ii) E_{6 \prime}=16, E_{6}=6480\),戴口罩很有必要.
【解析】 (Ⅰ)由题意\(X~B(a,p)\),
则\(P(X)=C_{a}^{x} p^{x}(1-p)^{a-x}\),\(EX=ap\)
(Ⅱ)(i)第\(n\)天被感染人数为\((1+a p)^{n-1}\),第\(n-1\)天被感染人数为\((1+a p)^{n-2}\)
由题目中均值定义得:
\(E n=(1+a p)^{n-1}-(1+a p)^{n-2}=a p(1+a p)^{n-2}\).
\(\therefore \dfrac{E_{n}}{E_{n-1}}=1+a p\),且\(E_1=ap\),
\(\therefore\left\{E_{n}\right\}\)是以\(ap\)为首项,\(1+ap\)为公比的等比数列.
\((ii)\)令\(f(p)=\ln (1+p)-\dfrac{2}{3} p\),则\(f^{\prime}(p)=\dfrac{1}{p+1}-\dfrac{2}{3}=\dfrac{-2 p+1}{3(p+1)}\),
\(∴f(p)\)在\(\left(0, \dfrac{1}{2}\right)\)上单调递增,在\(\left(\dfrac{1}{2}, 1\right)\)上单调递减,
\(f(p)_{\max }=f\left(\dfrac{1}{2}\right)=\ln \dfrac{2}{3}-\dfrac{1}{3}\)\(=\ln 3-\ln 2-\dfrac{1}{3} \approx 1.1-0.7-0.3=0.1\).
则当\(a=10\),\(E_{n}=10 p(1+10 p)^{n-2}\),
\(E_{6}^{\prime}=10 \times 0.1(1+10 \times 0.1)^{4}=16\),
\(E_6=10×0.5(1+10×0.5)^4=6480\),
\(∵E_6>E_6'\),
\(∴\)戴口罩很有必要.

