欢迎到学科网下载资料学习【高分突破系列】 高一数学下学期同步知识点剖析精品讲义!
跟贵哥学数学,soeasy!
必修第二册同步拔高,难度 3 颗星!
模块导图
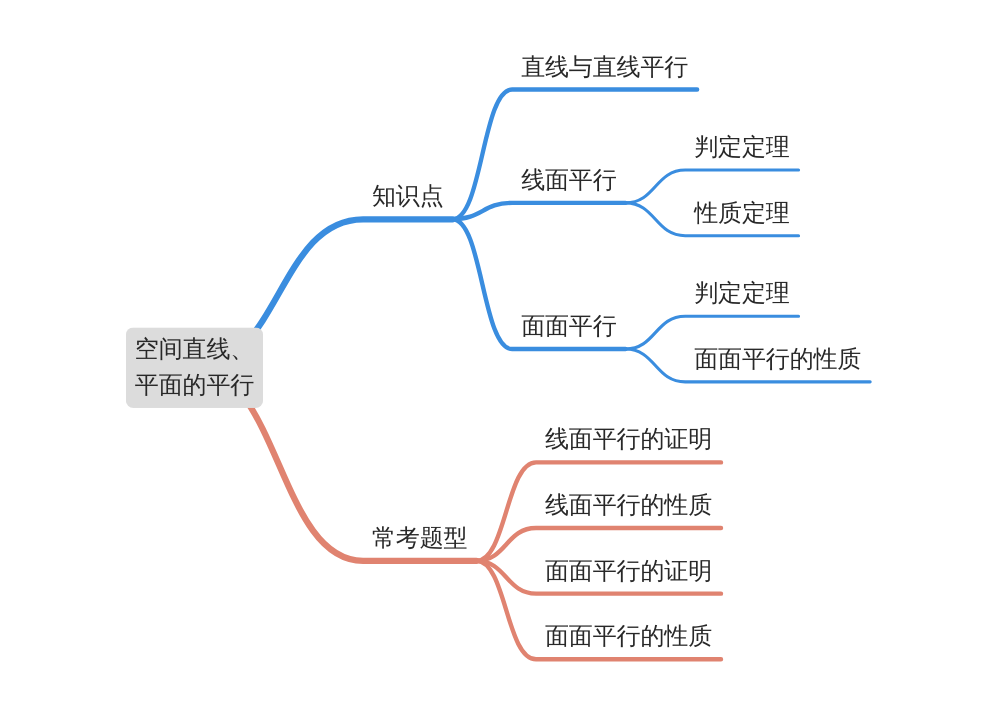
知识剖析
线线平行
1 基本事实 4
平行于同一条直线的两条直线平行 (平行线的传递公理)
符号表述:a//b,b//c⇒a//c
2 等角定理
如果空间中两个角度两条边分别对应平行,那么这两个角相等或互补.
线面平行
1 定义
直线与平面无交点.
2 判定定理
如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.
(俗说:若 a⊄α,要证明 a//α,则在平面 α 内找一条直线与直线 a 平行)
符号表述
a//ba⊄αb⊂α⎫⎪⎬⎪⎭⇒a//α (线线平行⇒线面平行)
3 性质定理
一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.
符号表述
a//αa⊂βα∩β=b⎫⎪⎬⎪⎭⇒a//b (线面平行⇒线线平行)
4 证明线面平行的方法
方法 1 定义法 (反证) l∩α=∅⇒l//α(用于判断)
方法 2 判定定理:a//ba⊄αb⊂α⎫⎪⎬⎪⎭⇒a//α (线线平行⟹线面平行)
方法 3 α//βa⊂α}⇒a//β(面面平行⇒线面平行)
方法 4 b⊥ab⊥αa⊄α⎫⎪⎬⎪⎭⇒a//α
面面平行
1 定义
α∩β=∅⟹α//β;
判断
(1) α 内有无穷多条直线都与 β 平行 (×);
(2) α 内的任何一条直线都与 β 平行 (√);
2 判定定理
如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行;
符号表述:a,b⊂α,a∩b=0,a//β,b//β⇒α//β
【如图】

推论:一个平面内的两条相交直线分别平行于另一个平面的两条直线,那么这两个平面互相平行.
符号表述:a,b⊂α ,a∩b=O ,a′,b′⊂β ,a//a′ ,b//b′⇒α//β
【如图】

3 面面平行的性质
性质 1 a⊂αα//β}⇒a//β (面面平行⇒线面平行)
性质 2 α//βα∩γ=aβ∩γ=b⎫⎪⎬⎪⎭⇒a//b (面面平行⇒线线平行)
性质 3 夹在两个平行平面间的平行线段相等.
4 证明面面平行的方法
方法 1 定义法;
方法 2 判定定理及推论 (常用)
经典例题
【题型一】线面平行的证明
【典题 1】 如图所示,在棱长为 a 的正方体 ABCD−A1B1C1D1 中,E,F ,P ,Q 分别是 BC, C1D1,AD1,BD 的中点.
(1) 求证:PQ// 平面 DCC1D1;
(2) 求 PQ 的长;
(3) 求证:EF// 平面 BB1D1D.

【解析】 (1) 如图所示,连接 AC,CD1
∵P,Q 分别为 AD1、AC 的中点,
∴PQ//CD1,
∵CD1⊂ 平面 DCC1D1,PQ⊄ 平面 DCC1D1,
∴PQ// 平面 DCC1D1.

(2) 由题意,可得 PQ=12D1C=√22a
(3) 连接 QE、D1Q,

∵E、Q 分别是 BC,BD 的中点,
∴QE//CD 且 QE=12CD,
又 D1F//CD 且 QE=12CD,∴D1F=QE,D1F//QE,
∴ 四边形 D1FEQ 是平行四边形
∴D1Q//EF
又 ∵D1Q⊂ 平面 D1FEQ,EF⊄ 平面 D1FEQ,
∴EF// 平面 BB1D1D.
【点拨】
① 在立体几何中,遇到中点我们往往会想到中位线;
② 证明线面平行的过程中,经常利用三角形的中位线 (如第一问) 和构造平行四边形的方法 (如第三问);
③ 证明线面平行可转化为证明线线平行或面面平行,本题第三问还有多种方法.
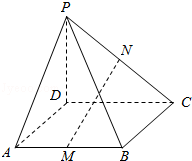
【典题 2】 如图所示,正四棱锥 P—ABCD 的各棱长均为 13,M ,N 分别为 PA ,BD 上的点,且 PM∶MA=BN∶ND=5∶8.
(1) 求证:直线 MN∥ 平面 PBC; (2) 求线段 MN 的长.

【解析】 (1) 证明 连接 AN 并延长交 BC 于 Q,连接 PQ,如图所示.

∵AD∥BQ,∴△QNB∽△AND,
∴NQAN=BNND=BQAD=58,
又 ∵PMMA=BNND=58,
∴MPAM=NQAN=58,∴MN//PQ,
又 ∵PQ⊂ 平面 PBC,MN⊄ 平面 PBC,
∴MN∥ 平面 PBC.
(2) 解 在等边 △PBC 中,∠PBC=60°,
在 △PBQ 中由余弦定理知
PQ2=PB2+BQ2−2PB⋅BQcos∠PBQ,
=132+(658)2−2×13×658×12=828164
∴PQ=918,
∵MN∥PQ,MN∶PQ=8∶13,
∴MN=918×813=7.
【点拨】
① 证明线面平行可转化为线线平行,而本题是利用线段成比例证明线线平行;
② 由于线段 PA 与 BD 是异面直线,则条件 PM∶MA=BN∶ND 不太好处理,一般要利用第三个 “比例” 把 PM∶MA 和 BN∶ND 联系起来,本题 NQ:AN 充当了这个角色;
③ 处理线段成比例中,要常注意以下几个模型,往往跟相似三角形有关:
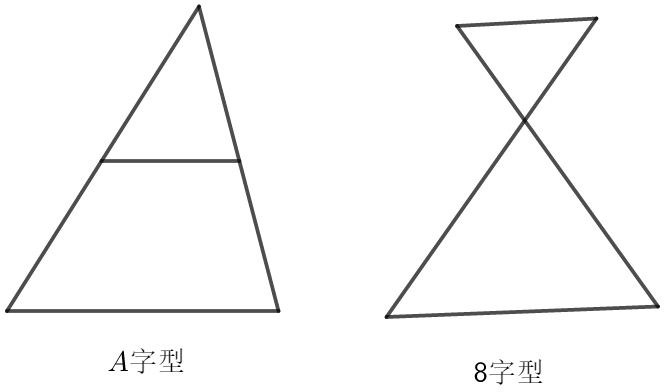
比如本题中的 △QNB∽△AND 就是属于 “8 字型”.
【题型二】线面平行的性质
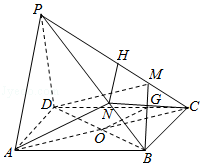
【典题 1】 如图,四棱锥 P-ABCD 的底面 ABCD 是平行四边形,M、N 分别为线段 PC、PB 上一点,若 PM∶MC=3∶1,且 AN∥ 平面 BDM,则 PN∶NB= ( )

A.4∶1 B.3∶1 C.3∶2 D.2∶1
【解析】 如图,连接 AC 交 BD 于点 O,连接 CN 交 BM 于点 G,
由 AN∥ 平面 BDM,可得 AN∥OG,(此处是根据线面平行的性质)
∵OA=OC,∴CG=NG,∴G 为 CN 的中点,
作 HN∥BM,∴CM=HM,
∵PM∶MC=3:1,∴PH=HC,
∴PN∶NB=PH∶HM=2:1,
故选:D.
【点拨】
① 题目中出现线面平行 AN∥ 平面 BDM,理当想到线面平行的性质;
② 线面平行的性质可由线面平行得到线线平行;
③ 在处理很多比例时,利用 “份” 的概念,可快速清楚各线段之间比例
比如
(1)  中 PM∶MC=3∶1,MC∶HM=2:1,则设最短线 HM=1(即 HM 为 “1 份”),则 MC=2 ,PM=7,则可得 PM∶MC=7:2;
中 PM∶MC=3∶1,MC∶HM=2:1,则设最短线 HM=1(即 HM 为 “1 份”),则 MC=2 ,PM=7,则可得 PM∶MC=7:2;
(2)  中 EF//BC,若 AE∶AB=3∶7,设 AE=3(即线段 AB 共 “7 份”,AE 占了 “3 份”),则 AB=7,BE=4,由于线段成比例,易得类似 FC:AC=4:7 等比例关系.
中 EF//BC,若 AE∶AB=3∶7,设 AE=3(即线段 AB 共 “7 份”,AE 占了 “3 份”),则 AB=7,BE=4,由于线段成比例,易得类似 FC:AC=4:7 等比例关系.
巩固练习
1 (★) 如图在正方体 ABCD-A1B1C1D1 中,棱长为 a,M、N 分别为 A1B、AC 的中点,则 MN 与平面 BB1C1C 的位置关系是 ( )

A. 相交 B. 平行 C. 垂直 D. 不能确定
2 (★) 如图所示,P 为 ▱ABCD 所在平面外一点,E 为 AD 的中点,F 为 PC 上一点,当 PA∥ 平面 EBF 时,PFFC=–––––.
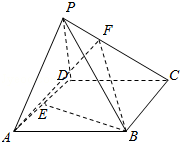
3 (★★) 如图,在四面体 ABCD 中,AB=CD=2,AD=BD=3,AC=BC=4,点 E,F,G,H 分别在棱 AD,BD,BC,AC 上,若直线 AB,CD 都平行于平面 EFGH,则四边形 EFGH 面积的最大值是 –––––.

4 (★★) 如图。在四棱锥 P-ABCD 中。底面 ABCD 是平行四边形,点 M 为棱 AB 上一点 AM=2MB. 点 N 为棱 PC 上一点,
(1) 若 PN=2NC,求证:MN∥ 平面 PAD;
(2) 若 MN∥ 平面 PAD,求证:PN=2NC.
5 (★★★) 如图所示,四边形 EFGH 为空间四边形 ABCD 的一个截面,若截面为平行四边形.
(1) 求证:AB∥ 平面 EFGH,CD∥ 平面 EFGH.
(2) 若 AB=4 ,CD=6,求四边形 EFGH 周长的取值范围.
参考答案
-
【答案】B
【解析】 连结 A1C、BC,取 A1C 的中点 Q,A1B 的中点 P,
连结 NQ、PQ、MN,
∵ 在正方体 ABCD−A1B1C1D1 中,棱长为 a,M、N 分别为 A1B、AC 的中点,
∴NQ∥CC1,PQ∥BC,
∵PQ∩NQ=Q,CC1∩BC=C,PQ,NQ⊂ 平面 PMN,CC1,BC⊂ 平面 A1BC1,
∴ 平面 PNQ∥ 平面 A1BC1,
∵MN⊂ 平面 PNQ,∴MN∥ 平面 BB1C1C.
故选:B.

-
【答案】12
【解析】 连接 AC 交 BE 于点 M,连接 FM.
∵PA∥ 平面 EBF,PA⊂ 平面 PAC,平面 PAC∩ 平面 EBF=EM,
∴PA∥EM,∴PFFC=AMMC=AEBC=12,故答案为:12.
-
【答案】1
【解析】 ∵ 直线 AB 平行于平面 EFGH,且平面 ABC 交平面 EFGH 于 HG,∴HG∥AB;
同理 EF∥AB,FG∥CD,EH∥CD,所以 FG∥EH,EF∥HG.
故:四边形 EFGH 为平行四边形.
又 ∵AD=BD,AC=BC 的对称性,可知 AB⊥CD.
所以四边形 EFGH 为矩形.
设 BF∶BD=BG∶BC=FG∶CD=x,(0≤x≤1),FG=2x,HG=2(1-x)
SEFGH=FG×HG=4x(1−x)=−4(x−12)2+1
根据二次函数的性质可知:SEFGH 面积的最大值 1.
-
【证明】 (1) 过 N 作 NE∥CD 交 PD 于 E,连接 AE.
则 ENCD=PNPC=23,∴EN=23CD,
又 AM=2MB,∴AM=23AB.
又 AB=CD,AB//CD
∴AM=EN,AM//EN
∴ 四边形 AMNE 是平行四边形,
∴MN∥AE,又 MN⊄ 平面 PAD,AE⊂ 平面 PAD,
∴MN∥ 平面 PAD.
(2) 过 N 作 NE∥CD 交 PD 于 E,
∵NE∥CD∥AB,∴NE∥AB,
∴A,M,N,E 四点共面,
∵MN∥ 平面 PAD,MN⊂ 平面 AMNE,平面 AMNE∩ 平面 PAD=AE,∴MN∥AE,
∴ 四边形 AMNE 是平行四边形,∴NE=AM=23AB=23CD.
∴PNPC=NECD=23,∴PN=2NC.
-
【答案】(1) 见解析 (2)(8,12)
【解析】 (1) 证明 ∵ 四边形 EFGH 为平行四边形,∴EF∥HG.
∵HG⊂ 平面 ABD,∴EF∥ 平面 ABD.
∵EF⊂ 平面 ABC,平面 ABD∩ 平面 ABC=AB,
∴EF∥AB. (线面平行的性质)
∴AB∥ 平面 EFGH.
同理可证,CD∥ 平面 EFGH.
(2) 解 设 EF=x(0<x<4),由于四边形 EFGH 为平行四边形,
∴CFCB=x4 . 则 FG6=BFBC=BC−CFBC=1−x4. 从而 FG=6−32x.
∴ 四边形 EFGH 的周长 l=2(x+6−32x)=12−x.
又 0<x<4,则有 8<l<12,
∴ 四边形 EFGH 周长的取值范围是 (8,12).
【题型三】面面平行的证明
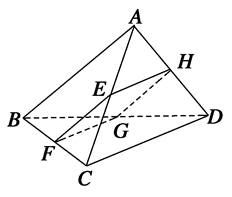
【典题 1】 如图,ABCD 与 ADEF 均为平行四边形,M,N,G 分别是 AB,AD,EF 的中点.
(1) 求证:BE∥ 平面 DMF;
(2) 求证:平面 BDE∥ 平面 MNG.

【解析】 (1) 方法1 连接 AE 交 DF 于 H,连接 HN,如图示

∵ADEF 均为平行四边形,∴H 是 AE 中点,
又 ∵M 是 AB 的中点,∴HN//EN
又 ∵HN⊂ 平面 DMF,BE⊄ 平面 DMF
∴BE∥ 平面 DMF.
方法2 作 DC 的中点 P,连接 PE、PB,
ABCD 与 ADEF 均为平行四边形,
M,N,G 分别是 AB,AD,EF 的中点.
∴PB∥DM,FM∥PE,且 FM,MD 交于 M 点,PB,PE 交于 P 点,
故平面 DFM∥ 平面 BPE,
∴BE∥ 平面 DMF;
(2)∵MN∥BD,GN∥DE,且 MN、GN 交于 N 点,DE、DB 交于 D 点,
∴ 平面 BDE∥ 平面 MNG.
【点拨】
① 遇到中点,可想到三角形的中位线;
② 利用三角形中位线和平行四边形证明线线平行是常见的方法;
③ 第一问中,证明线面平行可转化为线线平行或面面平行,方法 1 就是在平面 DMF 内找一直线平行 EB,充分利用了三角形的中位线;方法 2 是利用面面平行的性质,需要找到过直线 BE 且平行平面 DEF 的平面 EPB.
④ 第二问,面面平行的证明转化为线线平行:平面 BDE∥ 平面 MNG⇔MN∥BD,GN∥DE.
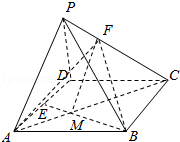
【典题 2】 如图,在四棱锥 P-ABCD 中,∠ABC=∠ACD=90∘,∠BAC=∠CAD=60∘,PA⊥ 平面 ABCD,PA=2,AB=1.设 M,N 分别为 PD,AD 的中点.
(1) 求证:平面 CMN∥ 平面 PAB;(2) 求三棱锥 P-ABM 的体积.

【解析】 (1) 证明 ∵M,N 分别为 PD,AD 的中点,
∴MN∥PA.
又 ∵MN⊄ 平面 PAB,PA⊂ 平面 PAB,
∴MN∥ 平面 PAB.
在 Rt△ACD 中,N 分别为 AD 的中点,∴CN=AN,
∴∠ACN=∠CAD=60∘.
又 ∵∠BAC=60∘,∴CN∥AB.
∵CN⊄ 平面 PAB,AB⊂ 平面 PAB,
∴CN∥ 平面 PAB.
又 ∵CN∩MN=N,∴ 平面 CMN∥ 平面 PAB.
(2) 由 (1) 知,平面 CMN∥ 平面 PAB,
∴ 点 M 到平面 PAB 的距离等于点 C 到平面 PAB 的距离.
由已知 AB=1,∠ABC=90∘,∠BAC=60∘,∴BC=√3,
∴ 三棱锥 P-ABM 的体积
VP−ABM=VM−PAB=VC−PAB=VP−ABC=13×PA×SABC=13×12×1×√3×2=√33.

【点拨】
① 面面平行可转化为线面平行:a,b⊂α ,a∩b=O ,a//β ,b//β⇒α//β; 要证明在平面 CMN∥ 平面 PAB,只需要在平面 CMN 找到两条相交线均平行平面 PAB 便行;
② 夹在两个平行平面间的平行线段相等,则点 M 到平面 PAB 的距离等于点 C 到平面 PAB 的距离;
③ 求三棱锥的体积常用等积法。三棱锥 P-ABM 的体积表示为 VP−ABM 即以点 P 到平面 ABM 的距离为高 h1、以平面 ABM 为底面,而表示为 VM−PAB 是以平面 PAB 为底面、点 M 到面 PAB 的距离为高 h2,而 h1 较难求,故想到 VP−ABM=VM−PAB. 等式 VP−ABM=VM−PAB=VC−PAB=VP−ABC(相当连续用了两次等积法).
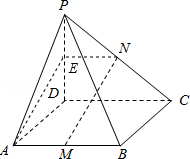
【典题 3】 如图,在棱长为 2 的正方体 ABCD−A1B1C1D1 中,M 是 A1B1 的中点,点 P 是侧面 CDD1C1 上的动点,且 MP// 截面 AB1C,则线段 MP 长度的取值范围是 ( )
A. [√2,√6] B. [√6,2√2]C. [√6,2√3] D.[√6,3]

【解析】

取 CD 的中点 N,CC1 的中点 R,B1C1 的中点 H,
则 MN//B1C//HR ,MH//AC,
故平面 MNRH// 平面 AB1C,
MP⊂ 平面 MNRH,线段 MP 扫过的图形是 △MNR,
由 AB=2,则 MN=2√2 ,NR=√2 ,MR=√6,
∴MN2=NR2+MR2 ,
∴∠MRN 是直角,
∴ 线段 MP 长度的取值范围是:(MR,MN),即 (√6,2√2).
故选:B.
【点拨】
① 本题的关键是找到满足条件的点 P 的轨迹,由已知 { 点 P 是侧面 CDD1C1 上的动点 MP// 截面 AB1C 可知点 P 的轨迹是过点 M 且平行面 AB1C 的平面与侧面 CDD1C1 的交线;怎么找到呢?以下提供另一思路:想象将面 AB1C 沿着 B1M 方向平移过点 M,较易得到面 MNQ(如下图 1),而面 MNQ 与侧面 CDD1C1 的交线就是所求交线了,那把面 MNQ 拓展成面 MQNJ,易得交线为 NR(如下图 2);
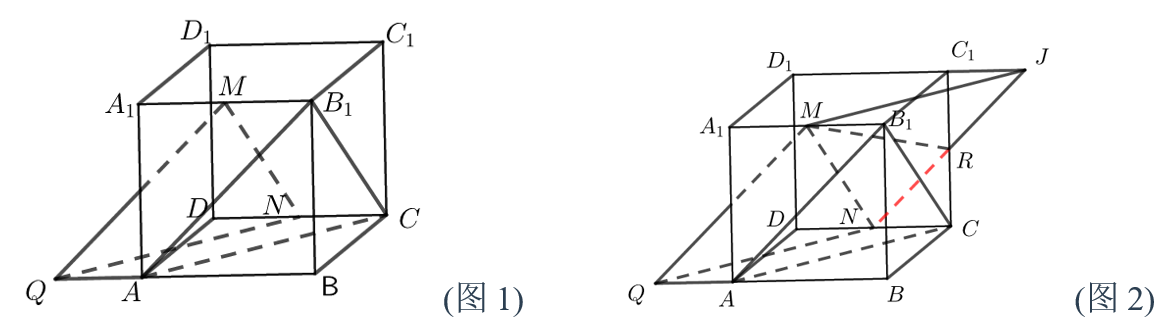
② 线段 MP 扫过的图形是 △MNR,则需要求出 △MNR 三边长度,确定 MP 的长度范围.
【题型四】面面平行的性质
【典题 1】 已知两条直线 a,b,两个平面 α,β,则下列结论中正确的是 ( )
A.若 a⊂β,且 α∥β,则 a∥α
B.若 b⊂α,a∥b,则 a∥α
C.若 a∥β,α∥β,则 a∥α
D.若 b∥α,a∥b,则 a∥α
【解析】 A∵α∥β,又 a⊂β,∴a∥α,故 A 正确;
B∵b⊂α,a∥b,若 a⊂α,则 a 不可能与 α 平行,故 B 错误;
C∵a∥β,α∥β,若 a⊂α,则结论不成立,故 C 错误;
D∵b∥α,a∥b,若 a⊂α,则结论不成立,故 D 错误;
故 A 正确;
【点拨】
① 线面的位置关系有三种:a∥α、a⊂α、a∩α=A;
② 证明某些选项是错只需要举个反例,比如选项 C 是怎么会想到 “a⊂α” 这个反例的呢?
运用 “运动的思想”,先由 α∥β 固定两个平面 α、β,再由 a∥β 把线段 a 由上至下 “运动” 下来,则 a、α 的关系有两种情况 a⊂α、a∥α. 选项 B、D 也可类似.
【典题 2】 已知平面 α∥ 面 β,AB、CD 为异面线段,AB⊂α,CD⊂β,且 AB=a,CD=b,AB 与 CD 所成的角为 θ,平面 γ∥ 面 α,且平面 γ 与 AC、BC、BD、AD 分别相交于点 M、N、P、Q.
(1) 若 a=b,求截面四边形 MNPQ 的周长;
(2) 求截面四边形 MNPQ 面积的最大值.
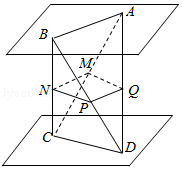
【解析】 (1)∵ 平面 α∥ 面 β,平面 ABC∩α=AB,平面 ABC∩β=MN,
∴AB∥MN,
同理 PQ∥AB,有 PQ∥MN,同理 NP∥MQ,
∴ 四边形 MNPQ 是一个平行四边形,
∴NPCD=BPBD,PQAB=DPBD,
∴NPCD+PQAB=BP+DPBD=1,
∵AB=CD=a,
∴NP+PQ=a,即四边形的周长是 2a.
(2) 设 AC=c,CM=x,
由 MN∥AB,得 MN=xca,同理 MQ=c−xcb,
又 AB 与 CD 所成的角为 θ,∴sin∠NMQ=sinθ
∴ 四边形的面积是 S=2×12⋅xc⋅a⋅c−xc⋅b⋅sinθ=abc2[−(x−c2)2+c24]sinθ
∴ 当 x=c2 时,S 的最大值是 ab4sinθ,
此时 M 为 AC 的中点.
【点拨】
① 面面平行的性质:α//βα∩γ=aβ∩γ=b⎫⎪⎬⎪⎭⇒a//b,由面面平行可得到线线平行;
② 在处理线线平行中线段的问题,注意 “A 字型”、“8 字型” 的模型;
③ 由三角形面积公式 S=12absinC,可得平行四边形 ABCD 的面积
S=2S△ABC=2×12AB×BC×sin∠ABC=AB×BC×sin∠ABC
④ 线线平行、线面平行、面面平行之间的转化关系

巩固练习
1 (★) 已知直线 a⊂α,给出以下三个命题:
①若平面 α∥ 平面 β,则直线 a∥ 平面 β;
②若直线 a∥ 平面 β,则平面 α∥ 平面 β;
③若直线 a 不平行于平面 β,则平面 α 不平行于平面 β.
其中正确的命题是 ( )
A. (2) B. (3) C. (1)(2) D. (1)(3)
2 (★★) 在正方体 ABCD-A1B1C1D1 中,E,F,G 分别是 A1B1,B1C1,BB1 的中点,给出下列四个推断:
①FG∥ 平面 AA1D1D; ②EF∥ 平面 BC1D1;
③FG∥ 平面 BC1D1; ④平面 EFG∥ 平面 BC1D1
其中推断正确的序号是 ( )
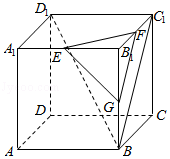
A. (1)(3) B. (1)(4) C. (2)(3) D. (2)(4)
3 (★★) 已知平面 α∥ 平面 β,P 是 α,β 外一点,过点 P 的直线 m 与 α,β 分别交于点 A,C,过点 P 的直线 n 与 α,β 分别交于点 B,D,且 PA=6,AC=9,PD=8,则 BD 的长为 ( )
A. 245 B. 125 C.245 或 24 D. 125 或 12
4 (★★) 已知两平行平面 α 与 β 之间的距离为 4,直线 a⊂β,点 A∈a,则平面 α 内到点 A 的距离为 5,且到直线 a 的距离为 2√5 的点的轨迹是 ( )
A.一组平行线 B.一条抛物线 C.两段圆弧 D.四个点
5 (★★) 如图,已知平面 α,β,γ,且 α∥β∥γ,直线 a,b 分别与平面 α,β,γ 交于点 A,B,C 和 D,E,F,若 AB=1,BC=2,DF=9,则 EF=–––––.

6 (★★) 如图所示,ABCD−A1B1C1D1 是棱长为 a 的正方体,M、N 分别是下底面的棱 A1B1,B1C1 的中点,P 是上底面的棱 AD 上的一点,AP=a3,过 P、M、N 的平面交上底面于 PQ,Q 在 CD 上,则 PQ=–––––.

7 (★★) 在长方体 ABCD−A1B1C1D1 中,DA=DC=1 ,DD1=2,分别在对角线 A1D,CD1 上取点 M,N,使得直线 MN// 平面 A1ACC1,则线段 MN 长的最小值为 –––––.
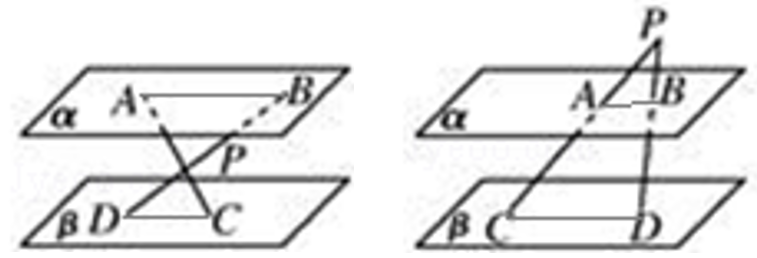
8 (★★) 已知:如图,平面 α、β 满足 α∥β,A、C∈α,B、D∈β,E∈AB,F∈CD,AC 与 BD 异面,且 AEEB=CFFD.求证:EF∥β.
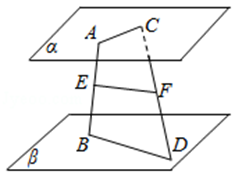
9 (★★★) 在正方体 ABCD−A1B1C1D1 中,M、N、P 分别是 AD1、BD 和 B1C 的中点,
求证:(1)MN∥CD1
(2)MN∥ 平面 CC1D1D.
(3) 平面 MNP∥ 平面 CC1D1D.

参考答案
- 【答案】D
【解析】 ①若平面 α∥ 平面 β,则直线 a∥ 平面 β;
因为直线 a⊂α,平面 α∥ 平面 β,则 α 内的每一条直线都平行平面 β.显然正确.
②若直线 a∥ 平面 β,则平面 α∥ 平面 β;因为当平面 α 与平面 β 相加时候,仍然可以存在直线 a⊂α 使直线 a∥ 平面 β.故错误.
③若直线 a 不平行于平面 β,则平面 α 不平行于平面 β,平面内有一条直线不平行与令一个平面,两平面就不会平行.故显然正确.
故选 D.
- 【答案】A
【解析】 ∵ 在正方体 ABCD−A1B1C1D1 中,E,F,G 分别是 A1B1,B1C1,BB1 的中点,
∴FG//BC1,∵BC1//AD1,∴FG//AD1,
∵FG⊄ 平面 AA1D1D,AD1⊂ 平面 AA1D1D,
∴FG∥ 平面 AA1D1D,故①正确;
∵EF//A1C1,A1C1 与平面 BC1D1 相交,
∴EF 与平面 BC1D1 相交,故②错误;
∵E,F,G 分别是 A1B1,B1C1,BB1 的中点,
∴FG//BC1,∵FG⊄ 平面 BC1D1,BC1⊂ 平面 BC1D1,
∴FG∥ 平面 BC1D1,故③正确;
∵EF 与平面 BC1D1 相交,
∴ 平面 EFG 与平面 BC1D1 相交,故④错误.
故选:A.
- 【答案】C
【解析】 连接 AB、CD;
①当点 P 在 CA 的延长线上,即 P 在平面 α 与平面 β 的同侧时,如图 1;
∵α∥β,平面 PCD∩α=AB,平面 PCD∩β=CD,
∴AB∥CD,∴PAAC=PBBD;
∵PA=6,AC=9,PD=8,
∴69=8−BDBD,解得 BD=245;
②当点 P 在线段 CA 上,即 P 在平面 α 与平面 β 之间时,如图 2;
类似①的方法,可得 PAPC=PBPD,
∵PA=6,PC=AC-PA=9-6=3,PD=8,
∴63=PB8,解得 PB=16;
∴BD=PB+PD=24;
综上,BD 的长为 245 或 24.
故选:C.
- 【答案】D
【解析】 设满足条件的点为 D,
过点 P 做平面 A 的垂线 PE,则 PE=4.
平面 α 内一点 D 到点 P 的距离为 PD=5,PD2=PE2+ED2,
∴ED2=36,即 D 为平面 α 上以垂足 E 为圆心,半径 R=ED=6 的圆上,
过垂足 E 做直线 L1 平行于直线 L,
则直线间距离 d1=PE=4,
在平面 α 内做直线 L2 使得 L2 到 L 的距离 d2=2√5,
设平面 α 内直线 L1、L2 距离为 M,
则有 d22=d21+M2,解得 M2=17,
即平面 α 内直线 L1、L2 距离为 √17<R=6,
所以同时满足到点 P 的距离为 5 且到直线 l 的距离为 2√5 的点的轨迹为:L2 与圆的四个交点.
故选:D.
- 【答案】6
【解析】 ∵AB=1,BC=2,DF=9,
若 A,B,C,D,E,F 六点共面
由面面平行的性质定理可得 AB∥CD∥EF
根据平行线分线段成比例定理可得:BCAC=EFDF=23=EF9
∴EF=6
若 A,B,C,D,E,F 六点不共面
连接 AF,交 β 于 M,连接 BM、EM、BE.
∵β∥γ,平面 ACF 分别交 β、γ 于 BM、CF,
∴BM∥CF.∴BCAC=MFAF
同理 MFAF=EFDF.
∴BCAC=EFDF=23=EF9 ∴EF=6
综上所述:EF=6
- 【答案】2√23a
【解析】 ∵ 平面 ABCD∥ 平面 A1B1C1D1,MN⊂ 平面 A1B1C1D1
∴MN∥ 平面 ABCD,又 PQ= 面 PMN∩ 平面 ABCD,
∴MN∥PQ.
∵M、N 分别是 A1B1、B1C1 的中点,
∴MN//A1C1//AC,
∴PQ∥AC,又 AP=a3,ABCD−A1B1C1D1 是棱长为 a 的正方体,∴CQ=a3,从而 DP=DQ=2a3,
∴PQ=√DQ2+DP2=√(2a3)2+(2a3)2=2√23a.
故答案为:2√23a
- 【答案】23
【解析】 作 MM1⊥AD 于点 M1,作 NN1⊥CD 于点 N1,

∵ 线段 MN 平行于对角面 ACC1A1,∴M1N1//AC.
(面面平行的判定和性质)
设 DM1=DN1=x,则 MM1=2x,NN1=2−2x,
(线段成比例)
在直角梯形 MNN1M1 中,
MN2=(√2x)2+(2−4x)2=18(x−49)2+49
∴ 当 x=49 时,MN 的最小值为 23.
- 【证明】 (Ⅰ) 证明:连接 AD,作 EG∥BD 交 AD 于点 G,连接 FG
∵EG∥BD,
∴AEEB=AGGD.
又 ∵AEEB=CFFD,∴AGGD=CFFD
∴FG∥AC,
∴FG∥α,又 α∥β,
∴FG∥β;
又因为 EG∩FG=G.
∴ 平面 EFG∥β,
而 EF⊂ 平面 EFG;
∴EF∥β.

- 【证明】 (1)∵ 正方体 ABCD−A1B1C1D1 中,M、N、P 分别是 AD1、BD 和 B1C 的中点,
∴ 连结 AC、BD,交于点 N,
∴ 由三角形中位线定理得:MN//CD1.
(2)∵MN//CD1,
MN⊂ 平面 CC1D1D,CD1⊄ 平面 CC1D1D,
∴MN∥ 平面 CC1D1D.
(3) 连结 B1C,BC1,交于点 P,则 P 是 BC1 的中点,
∴MP∥CD,
∵MP⊄ 平面 CC1D1D,CD⊂ 平面 CC1D1D,
∴MP∥ 平面 CC1D1D.
∵MN∥ 平面 CC1D1D,且 MP∩MN=M,MP、MN⊂ 平面 MNP,
∴ 平面 MNP∥ 平面 CC1D1D.











 中 ,,则设最短线 (即 为 “ 份”),则 ,,则可得 ;
中 ,,则设最短线 (即 为 “ 份”),则 ,,则可得 ; 中 ,若 ,设 (即线段 共 “ 份”, 占了 “ 份”),则 ,,由于线段成比例,易得类似 等比例关系.
中 ,若 ,设 (即线段 共 “ 份”, 占了 “ 份”),则 ,,由于线段成比例,易得类似 等比例关系.




























【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】