6.2.4 平面向量的数量积
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)
【高分突破系列】 高一数学下学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)
必修二同步拔高，难度3颗星！
模块导图
知识剖析
概念
如果两个非零向量\(\vec{a}\) ，\(\vec{b}\)，它们的夹角为\(\theta\)，我们把数量\(|\vec{a}||\vec{b}| \cosθ\)叫做与的数量积(或内积)，记作:\(\vec{a} \cdot \vec{b}\)，即\(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta\).规定：零向量与任一向量的数量积是\(0\).
\({\color{Red}{ PS }}\)数量积是一个实数，不再是一个向量.
投影
向量\(\vec{b}\)在向量\(\vec{a}\)上的投影：\(|\vec{b}| \cos \theta\)，它是一个实数，但不一定大于\(0\).
运算法则
对于向量\(\vec{a}\) ，\(\vec{b}\)，\(\vec{c}\)，和实数，有
(1) \(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}\)
(2) \((\lambda \vec{a}) \cdot \vec{b}=\lambda(\vec{a} \cdot \vec{b})=\vec{a} \cdot(\lambda \vec{b})\)
(3) \((\vec{a}+\vec{b}) \cdot \vec{c}=\vec{a} \cdot \vec{c}+\vec{b} \cdot \vec{c}\)
但是\((\vec{a} \cdot \vec{b}) \vec{c}=\vec{a}(\vec{b} \cdot \vec{c})\)不一定成立.
(当向量\(\vec{a}, \vec{c}\)不共线时，向量\(\vec{a}(\vec{b} \cdot \vec{c})\)与向量\((\vec{a} \cdot \vec{b}) \vec{c}\)肯定不共线，那怎么可能相等呢)
即向量的数量积满足交换律，分配率，但不满足结合律.
经典例题
【题型一】求数量积
【典题1】已知向量\(\vec{a}\) ，\(\vec{b}\)满足\(|\vec{a}+\vec{b}|=|\vec{b}|\)，且\(|\vec{a}|=2\)，则\(\vec{a} \cdot \vec{b}=\)\(\underline{\quad \quad}\)．
【解析】因为\(|\vec{a}+\vec{b}|=|\vec{b}|\)，即有\(|\vec{a}+\vec{b}|^{2}=|\vec{b}|^{2}\)，
所以\(\vec{a}^{2}+2 \vec{a} \cdot \vec{b}+\vec{b}^{2}=\vec{b}^{2}\)，则\(2 \vec{a} \cdot \vec{b}=-\vec{a}^{2}=-4\)，
所以\(\vec{a} \cdot \vec{b}=-2\)．
【点拨】①由数量积的定义可知\(|\vec{a}|^{2}=\vec{a}^{2}\)；
②题目中遇到类似\(|\vec{a}+\vec{b}|\)可尝试利用性质\(|\vec{a}|^{2}=\vec{a}^{2}\)达到去掉绝对值的目的.
【典题2】在三角形\(ABC\)中，若\(|\overrightarrow{A B}+\overrightarrow{B C}|=|\overrightarrow{A B}-\overrightarrow{B C}|\)，\(AC=6\)，\(AB=3\)，\(E，F\)为边\(BC\)的三等分点，则\(\overrightarrow{A E} \cdot \overrightarrow{A F}=\)\(\underline{\quad \quad}\)．
【解析】若\(|\overrightarrow{A B}+\overrightarrow{B C}|=|\overrightarrow{A B}-\overrightarrow{B C}|\)，
则\(\overrightarrow{A B}^{2}+\overrightarrow{B C}^{2}+2 \overrightarrow{A B} \cdot \overrightarrow{B C}=\overrightarrow{A B}^{2}+\overrightarrow{B C}^{2}-2 \overrightarrow{A B} \cdot \overrightarrow{B C}\)，
即有\(\overrightarrow{A B} \cdot \overrightarrow{B C}=0\)，
\(∵AC=6 ,AB=3\)，\(∴BC^2=6^2-3^2=27\)
\(∵E ,F\)为边\(BC\)的三等分点，
则\(\overrightarrow{A E} \cdot \overrightarrow{A F}=(\overrightarrow{A B}+\overrightarrow{B E})(\overrightarrow{A B}+\overrightarrow{B F})=\left(\overrightarrow{A B}+\dfrac{1}{3} \overrightarrow{B C}\right)\left(\overrightarrow{A B}+\dfrac{2}{3} \overrightarrow{B C}\right)\)
\({\color{Red}{(利用首尾相接法把向量向\overrightarrow{A B}、\overrightarrow{B C}靠拢 }})\)
\(=\dfrac{2}{9} \overrightarrow{B C}^{2}+\overrightarrow{A B}^{2}+\overrightarrow{A B} \cdot \overrightarrow{B C}=\dfrac{2}{9} \times 27+3^{2}+0=15\)．
【点拨】
①已知条件\(|\overrightarrow{A B}+\overrightarrow{B C}|=|\overrightarrow{A B}-\overrightarrow{B C}|\)利用性质\(|\vec{a}|^{2}=\vec{a}^{2}\)可得到\(\overrightarrow{A B} \cdot \overrightarrow{B C}=0\)，其实也可以通过平行四边形法则和三角形法则得到的；
②求数量积\(\overrightarrow{A E} \cdot \overrightarrow{A F}\)，第一个想法用数量积公式\(\overrightarrow{A E} \cdot \overrightarrow{A F}=|\overrightarrow{A E}| \cdot|\overrightarrow{A F}| \cos \angle E A F\)，但是发现题目已知条件中很难求解\(|\overrightarrow{A E}|\)、\(|\overrightarrow{A F}|\)、\(\cos \angle E A F\).又因为\(\overrightarrow{A B} \cdot \overrightarrow{B C}=0\)，又知道\(AB、BC\)的长度，故想到\(\overrightarrow{A E} \cdot \overrightarrow{A F}\)把转化为用\(\overrightarrow{A B}\)、\(\overrightarrow{B C}\)表示.
③在求数量积的时候，直接用公式很难求解，都尽量向“信息量大”的向量靠拢.
【题型二】求向量夹角
【典题1】已知向量\(\vec{a}\) ，\(\vec{b}\)满足\(|\vec{a}|=1\)，\(|\vec{b}|=2\)，\(|\vec{a}+2 \vec{b}|=\sqrt{21}\)，那么向量\(\vec{a}\)与\(\vec{b}\)的夹角为\(\underline{\quad \quad}\)．
【解析】\(\because|\vec{a}|=1\)，\(|\vec{b}|=2\)，\(|\vec{a}+2 \vec{b}|=\sqrt{21}\)
\(\therefore(\vec{a}+2 \vec{b})^{2}=\vec{a}^{2}+4 \vec{b}^{2}+4 \vec{a} \cdot \vec{b}=1+16+4 \vec{a} \cdot \vec{b}=21\)，
\(\therefore \vec{a} \cdot \vec{b}=1\)
\(\therefore \cos <\vec{a}, \vec{b}>=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{1}{2}\)，且\(0 \leq<\vec{a}, \vec{b}>\leq \pi\)，
\(\therefore \vec{a}\)与\(\vec{b}\)的夹角为\(\dfrac{\pi}{3}\)．
【典题2】已知向量\(\vec{a}\) ，\(\vec{b}\)满足\(|\vec{a}|=1\)，\((\vec{a}-\vec{b}) \perp(3 \vec{a}-\vec{b})\)，则向量\(\vec{a}\)与\(\vec{b}\)的夹角的最大值为\(\underline{\quad \quad}\)．
【解析】\(\because|\vec{a}|=1\)，\((\vec{a}-\vec{b}) \perp(3 \vec{a}-\vec{b})\)
\(\therefore(\vec{a}-\vec{b}) \cdot(3 \vec{a}-\vec{b})=3 \vec{a}^{2}+\vec{b}^{2}-4 \vec{a} \cdot \vec{b}=3+\vec{b}^{2}-4 \vec{a} \cdot \vec{b}=0\)，
\(\therefore \vec{a} \cdot \vec{b}=\dfrac{|\vec{b}|^{2}+3}{4}\)，
\(\therefore \cos <\vec{a}, \vec{b}>=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{|\vec{b}|^{2}+3}{4|\vec{b}|}=\dfrac{|\vec{b}|+\dfrac{3}{|\vec{b}|}}{4} \geq \dfrac{\sqrt{3}}{2}\)，且\(0^{\circ} \leq<\vec{a}, \vec{b}>\leq 180^{\circ}\)，
\(\therefore \cos <\vec{a}, \vec{b}>=\dfrac{\sqrt{3}}{2}\)时，\(\vec{a}\) ，\(\vec{b}\)的夹角最大为\(30^{\circ}\)．
【题型三】求数量积最值
【典题1】如图，已知等腰梯形\(ABCD\)中，\(AB=2DC=4\)，\(A D=B C=\sqrt{3}\)，\(E\)是\(DC\)的中点，\(F\)是线段\(BC\)上的动点，则\(\overrightarrow{E F} \cdot \overrightarrow{B F}\)的最小值是\(\underline{\quad \quad}\).
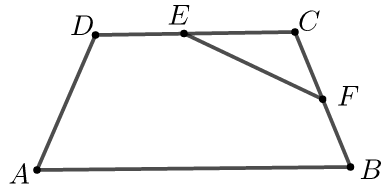
【解析】由等腰梯形的知识可知\(\cos B=\dfrac{\sqrt{3}}{3}\)，
设\(BF=x\)，则\(C F=\sqrt{3}-x\)，
\(\therefore \overrightarrow{E F} \cdot \overrightarrow{B F}=(\overrightarrow{E C}+\overrightarrow{C F}) \overrightarrow{B F}=\overrightarrow{E C} \cdot \overrightarrow{B F}+\overrightarrow{C F} \cdot \overrightarrow{B F}\)
\(=1 \cdot x\left(-\dfrac{\sqrt{3}}{3}\right)+(\sqrt{3}-x) \cdot x \cdot(-1)=x^{2}-\dfrac{4}{3} \sqrt{3} x\)，
\(\because 0 \leq x \leq \sqrt{3}\)，
\(∴\)当\(x=\dfrac{2}{3} \sqrt{3}\)时，\(\overrightarrow{E F} \cdot \overrightarrow{B F}\)取得最小值，最小值为\(\left(\dfrac{2}{3} \sqrt{3}\right)^{2}-\dfrac{2}{3} \sqrt{3} \times \dfrac{4}{3} \sqrt{3}=-\dfrac{4}{3}\)．
【典题2】如图，已知矩形\(ABCD\)的边长\(AB=2\)，\(AD=1\)．点\(P ,Q\)分别在边\(BC ,CD\)上，且\(\angle P A Q=45^{\circ}\)，则\(\overrightarrow{A P} \cdot \overrightarrow{A Q}\)的最小值为\(\underline{\quad \quad}\)．
【解析】设\(\angle P A B=\theta\)，则\(\angle D A Q=45^{\circ}-\theta\)，
\(\overrightarrow{A P} \cdot \overrightarrow{A Q}=|\overrightarrow{A P}||\overrightarrow{A Q}| \cos 45^{\circ}=\dfrac{2}{\cos \theta} \cdot \dfrac{1}{\cos \left(45^{\circ}-\theta\right)} \cdot \dfrac{\sqrt{2}}{2}\)\(=\dfrac{2}{\cos \theta \cdot\left(\dfrac{\sqrt{2}}{2} \cos \theta+\dfrac{\sqrt{2}}{2} \sin \theta\right)}\)\(=\dfrac{2}{\cos ^{2} \theta+\cos \theta \sin \theta}=\dfrac{2}{\dfrac{1+\cos 2 \theta}{2}+\dfrac{\sin 2 \theta}{2}}\)，
\(=\dfrac{2}{\dfrac{\sqrt{2}}{2} \sin \left(2 \theta+45^{\circ}\right)+\dfrac{1}{2}} \geq \dfrac{2}{\dfrac{\sqrt{2}}{2}+\dfrac{1}{2}}=4 \sqrt{2}-4\)，
当且仅当\(2 \theta+45^{\circ}=90^{\circ}\)，
\(\therefore \theta=22.5^{\circ}\)时取\(“=”\)，当\(\theta=22.5^{\circ}\)时，点\(P\)恰在边\(BC\)上，\(Q\)恰边\(CD\)上，满足条件，
综上所述，\(\overrightarrow{A P} \cdot \overrightarrow{A Q}\)的最小值为\(4 \sqrt{2}-4\)，
故答案为：\(4 \sqrt{2}-4\)．
【典题3】已知向量\(\vec{a}\) ，\(\vec{b}\)，\(\vec{c}\)满足\(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\)，\(|\vec{c}|=2 \sqrt{3}\)，\(\vec{c}\)与\(\vec{a}-\vec{b}\)所成的角为\(120°\)，则当\(t \in \boldsymbol{R}\)时，\(|t \vec{a}+(1-t) \vec{b}|\)的最小值是\(\underline{\quad \quad}\)．
【解析】
\(\because \vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\)，\(\therefore \vec{c}=-(\vec{a}+\vec{b})\)
又\(\vec{c}\)与\(\vec{a}-\vec{b}\)所成的角为\(120°\)，\(\therefore \angle O E A=120^{\circ}\)，
\({\color{Red}{ (此时由平行四边形法则和三角形法则构造出一个平行四边形)}}\)
\(\therefore \angle O E B=60^{\circ}\)，\(|\vec{c}|=2 \sqrt{3}\)
\(\therefore O D=2 \sqrt{3}\)，\(O E=\sqrt{3}\)，
\(|t \vec{a}+(1-t) \vec{b}|=|\vec{b}+t(\vec{a}-\vec{b})|=|\overrightarrow{O B}+t \overrightarrow{B A}|\)
\(\because \overrightarrow{B P}\)与\(\overrightarrow{B A}\)共线，\(\overrightarrow{B A} \neq \overrightarrow{0}\)，设\(\overrightarrow{B P}=t \overrightarrow{B A}\)，
则\(|t \vec{a}+(1-t) \vec{b}|=|\overrightarrow{O P}|\)(\(P\)是直线\(BA\)上的动点)，
\({\color{Red}{ (其实由性质“若\overrightarrow{O C}=x \overrightarrow{O A}+y \overrightarrow{O B}，x+y=1，则点C在直线AB上”很容易知道：直线BA上的存在}}\)
\({\color{Red}{ 一动点P使得\overrightarrow{O P}=t \vec{a}+(1-t) \vec{b}) }}\)
所以当\(OP\)垂直于\(AB\)时，\(|t \vec{a}+(1-t) \vec{b}|=|\overrightarrow{O P}|\)最小，为\(O E \times \sin 60^{\circ}=\sqrt{3} \times \dfrac{\sqrt{3}}{2}=\dfrac{3}{2}\).
【点拨】①题中遇到类似\(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\)的等式，很容易想到移项，再利用平行四边形法则进行构造图形求解；
②本题中求\(|t \vec{a}+(1-t) \vec{b}|\)的最小值，那我们根据平行四边形法则找到向量\(t \vec{a}+(1-t) \vec{b}\)，确定出\(|t \vec{a}+(1-t) \vec{b}|\)的几何意义从而求解成功.
巩固练习
1(★) 已知向量\(\vec{a}\) ，\(\vec{b}\)满足\(|\vec{a}+\vec{b}|=|\vec{b}|\)，且\(|\vec{a}|=2\)，则\(\vec{a} \cdot \vec{b}=\)\(\underline{\quad \quad}\) .
2(★★) 已知非零向量\(\vec{a}\) ，\(\vec{b}\)满足\(|\vec{a}|=\dfrac{3}{4}|\vec{b}|\)，\(\cos <\vec{a}, \vec{b}>=\dfrac{1}{3}\)，若\((m \vec{a}+4 \vec{b}) \perp \vec{b}\)，则实数\(m\)的值为\(\underline{\quad \quad}\).
3(★★) 已知向量\(\vec{a}\) ，\(\vec{b}\)满足\(|\vec{a}|=1\)，\((\vec{a}-\vec{b}) \perp(3 \vec{a}-\vec{b})\)，则\(\vec{a}\)与\(\vec{b}\)的夹角的最大值为\(\underline{\quad \quad}\) .
4(★★) 如图，在梯形\(ABCD\)中，\(AB∥CD\)，\(AB=4\)，\(AD=3\)，\(CD=2\)，\(\overrightarrow{A M}=2 \overrightarrow{M D}\)，\(\overrightarrow{A C} \cdot \overrightarrow{B M}=-3\)，则\(\overrightarrow{A B} \cdot \overrightarrow{A D}=\)\(\underline{\quad \quad}\) .
5(★★) 已知\(△ABC\)中，点\(M\)在线段\(AB\)上，\(\angle A C B=2 \angle B C M=60^{\circ}\)，且\(\overrightarrow{C M}-\lambda \overrightarrow{C B}=\dfrac{2}{3} \overrightarrow{C A}\)．若\(|\overrightarrow{C M}|=6\)，则 \(\overrightarrow{C M} \cdot \overrightarrow{A B}=\)\(\underline{\quad \quad}\).
6(★★★) 设\(H\)是\(△ABC\)的垂心，且\(3 \overrightarrow{H A}+4 \overrightarrow{H B}+5 \overrightarrow{H C}=\overrightarrow{0}\)，则\(\cos \angle B H C\)的值为\(\underline{\quad \quad}\).
7(★★★) 已知\(P\)为\(△ABC\)所在平面内的一点，\(\overrightarrow{B P}=2 \overrightarrow{P C}\)，\(|\overrightarrow{A P}|=4\)，若点\(Q\)在线段\(AP\)上运动，则\(\overrightarrow{Q A} \cdot(\overrightarrow{Q B}+2 \overrightarrow{Q C})\)的最小值为\(\underline{\quad \quad}\) .
8(★★★) 已知非零向量\(\vec{a}\) ，\(\vec{b}\)，\(\vec{c}\)满足：\((\vec{a}-2 \vec{c})(\vec{b}-2 \vec{c})=0\)且不等式\(|\vec{a}+\vec{b}|+|\vec{a}-\vec{b}| \geq \lambda|\vec{c}|\)恒立，则实数\(\lambda\)的最大值为\(\underline{\quad \quad}\) .
9(★★★) 已知平面向量\(\vec{a}\) ，\(\vec{b}\)，\(\vec{c}\)，对任意实数\(x ,y\)都有\(|\vec{a}-x \vec{b}| \geq|\vec{a}-\vec{b}|\)，\(|\vec{a}-y \vec{c}| \geq|\vec{a}-\vec{c}|\)成立．若\(|\vec{a}|=2\)，则\(\vec{b}(\vec{c}-\vec{a})\)的最大值是\(\underline{\quad \quad}\) .
10(★★★) 设为两个非零向量\(\vec{a}\) ，\(\vec{b}\)的夹角，已知对任意实数\(t\)，\(|\vec{b}-t \vec{a}|\)的最小值为\(1\)，则( )
A．若\(\theta\)确定，则\(|\vec{a}|\)唯一确定
B．若\(\theta\)确定，则\(|\vec{b}|\)唯一确定
C．若\(|\vec{a}|\)确定，则\(\theta\)唯一确定
D．若\(|\vec{b}|\)确定，则\(\theta\)唯一确定
参考答案
- 【答案】\(-2\)
【解析】因为\(|\vec{a}+\vec{b}|=|\vec{b}|\)，即有\(|\vec{a}+\vec{b}|^{2}=|\vec{b}|^{2}\)，
所以\(\vec{a}^{2}+2 \vec{a} \cdot \vec{b}+\vec{b}^{2}=\vec{b}^{2}\)，则\(2 \vec{a} \cdot \vec{b}=-\vec{a}^{2}=-4\)，
所以\(\vec{a} \cdot \vec{b}=-2\). - 【答案】\(－16\)
【解析】∵已知非零向量\(\vec{a}\) ，\(\vec{b}\)，满足\(|\vec{a}|=\dfrac{3}{4}|\vec{b}|\)，\(\cos <\vec{a}, \vec{b}>=\dfrac{1}{3}\)，
若\((m \vec{a}+4 \vec{b}) \perp \vec{b}\)，
\(\therefore(m \vec{a}+4 \vec{b}) \cdot \vec{b}=m \vec{a} \cdot \vec{b}+4 \vec{b}^{2}=m \cdot \dfrac{3}{4}|\vec{b}| \cdot|\vec{b}| \cdot \dfrac{1}{3}+4|\vec{b}|^{2}=0\)，
求得\(m=－16\). - 【答案】\(30°\)
【解析】\(\because |\vec{a}|=1\)，\((\vec{a}-\vec{b}) \perp(3 \vec{a}-\vec{b})\)
\(\therefore(\vec{a}-\vec{b}) \cdot(3 \vec{a}-\vec{b})=3 \vec{a}^{2}+\vec{b}^{2}-4 \vec{a} \cdot \vec{b}=3+\vec{b}^{2}-4 \vec{a} \cdot \vec{b}=0\)，
\(\therefore \vec{a} \cdot \vec{b}=\dfrac{|\vec{b}|^{2}+3}{4}\)，
\(\therefore \cos <\vec{a}, \quad \vec{b}>=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{|\vec{b}|^{2}+3}{4|\vec{b}|}=\dfrac{|\vec{b}|+\dfrac{3}{|\vec{b}|}}{4} \geq \dfrac{\sqrt{3}}{2}\)，且\(0^{\circ} \leq\langle\vec{a}, \vec{b}\rangle \leq 180^{\circ}\)，
\(\therefore \cos <\vec{a}, \quad \vec{b}>=\dfrac{\sqrt{3}}{2}\)时，\(\vec{a}\)与\(\vec{b}\)的夹角最大为\(30°\)． - 【答案】\(\dfrac{3}{2}\)
【解析】\(∵\)在梯形\(ABCD\)中，\(AB∥CD\)，\(AB=4\)，\(AD=3\)，\(CD=2\)，\(\overrightarrow{A M}=2 \overrightarrow{M D}\)，
\(\therefore \overrightarrow{A C} \cdot \overrightarrow{B M}=(\overrightarrow{A D}+\overrightarrow{D C}) \cdot(\overrightarrow{B A}+\overrightarrow{A M})=\left(\overrightarrow{A D}+\dfrac{1}{2} \overrightarrow{A B}\right) \cdot\left(-\overrightarrow{A B}+\dfrac{2}{3} \overrightarrow{A D}\right)\)\(=\dfrac{2}{3} \overrightarrow{A D}^{2}-\dfrac{1}{2} \overrightarrow{A B}^{2}-\dfrac{2}{3} \overrightarrow{A D} \cdot \overrightarrow{A B}=-3\)，
\(\therefore \dfrac{2}{3} \times 3^{2}-\dfrac{1}{2} \times 4^{2}-\dfrac{2}{3} \overrightarrow{A B} \cdot \overrightarrow{A D}=-3\)，
则\(\overrightarrow{A B} \cdot \overrightarrow{A D}=\dfrac{3}{2}\). - 【答案】\(27\)
【解析】以\(CM\)为对角线作平行四边形\(CPMQ\)，
\(∵CM\)平分\(∠ACB\)，\(∴\)四边形__\(XPMQ\)是菱形，
又\(CM=6\)，\(∠BCM=30°\)，
\(\therefore C P=C Q=2 \sqrt{3}\)，
\(\therefore \overrightarrow{C P} \cdot \overrightarrow{C Q}=2 \sqrt{3} \times 2 \sqrt{3} \times \cos 60^{\circ}=6\)，
\(\because \overrightarrow{C M}-\lambda \overrightarrow{C B}=\dfrac{2}{3} \overrightarrow{C A}\)，
即\(\overrightarrow{C M}=\dfrac{2}{3} \overrightarrow{C A}+\lambda \overrightarrow{C B}\)，且\(A，M，B\)三点共线，
\(\therefore \lambda=\dfrac{1}{3}\)，
又\(\overrightarrow{C M}=\overrightarrow{C P}+\overrightarrow{C Q}\)，
\(\therefore \overrightarrow{C A}=\dfrac{3}{2} \overrightarrow{C Q}\)，\(\overrightarrow{C B}=3 \overrightarrow{C P}\)
\(\therefore \overrightarrow{C M} \cdot \overrightarrow{A B}=(\overrightarrow{C P}+\overrightarrow{C Q}) \cdot\left(3 \overrightarrow{C P}-\dfrac{3}{2} \overrightarrow{C Q}\right)\)
\(=3 \overrightarrow{C P}^{2}-\dfrac{3}{2} \overrightarrow{C Q}^{2}+\dfrac{3}{2} \overrightarrow{C P} \cdot \overrightarrow{C Q}=3 \times 12-\dfrac{3}{2} \times 12+\dfrac{3}{2} \times 6=27\)． - 【答案】\(-\dfrac{\sqrt{70}}{14}\)
【解析】由三角形垂心性质可得，\(\overrightarrow{H A} \cdot \overrightarrow{H B}=\overrightarrow{H B} \cdot \overrightarrow{H C}=\overrightarrow{H C} \cdot \overrightarrow{H A}\)，
不妨设__\(\overrightarrow{H A} \cdot \overrightarrow{H B}=\overrightarrow{H B} \cdot \overrightarrow{H C}=\overrightarrow{H C} \cdot \overrightarrow{H A}=x\)，
\(\because 3 \overrightarrow{H A}+4 \overrightarrow{H B}+5 \overrightarrow{H C}=\overrightarrow{0}\)，
\(\therefore 3 \overrightarrow{H A} \cdot \overrightarrow{H B}+4 \overrightarrow{H B}^{2}+5 \overrightarrow{H C} \cdot \overrightarrow{H B}=0\)，
\(\therefore|\overrightarrow{H B}|=\sqrt{-2 x}\)，同理可求得\(|\overrightarrow{H C}|=\sqrt{-\dfrac{7 x}{5}}\)，
\(\therefore \cos \angle B H C=\dfrac{\overrightarrow{H B} \cdot \overrightarrow{H C}}{|\overrightarrow{H B}||\overrightarrow{H C}|}=-\dfrac{\sqrt{70}}{14}\)． - 【答案】\(－12\)
【解析】由题意，画图如下，
根据题意及图，可知\(\overrightarrow{B P}=\overrightarrow{Q P}-\overrightarrow{Q B}\)，\(\overrightarrow{P C}=\overrightarrow{Q C}-\overrightarrow{Q P}\)，
\(\because \overrightarrow{B P}=2 \overrightarrow{P C}\)，\(\therefore \overrightarrow{Q P}-\overrightarrow{Q B}=2(\overrightarrow{Q C}-\overrightarrow{Q P})\)，
整理，得\(\overrightarrow{Q B}+2 \overrightarrow{Q C}=3 \overrightarrow{Q P}\)，
则\(\overrightarrow{Q A} \cdot(\overrightarrow{Q B}+2 \overrightarrow{Q C})=\overrightarrow{Q A} \cdot 3 \overrightarrow{Q P}\)\(=-3|\overrightarrow{Q A}| \cdot|\overrightarrow{Q P}|=-3|\overrightarrow{Q A}| \cdot(4-|\overrightarrow{Q A}|)=3\left(|\overrightarrow{Q A}|^{2}-4|\overrightarrow{Q A}|\right)\)，
设\(|\overrightarrow{Q A}|=m\)，很明显\(m \in[0,4]\)，
故\(\overrightarrow{Q A} \cdot(\overrightarrow{Q B}+2 \overrightarrow{Q C})=3\left(|\overrightarrow{Q A}|^{2}-4|\overrightarrow{Q A}|\right)\)\(=3\left(m^{2}-4 m\right)=3(m-2)^{2}-12\)，
根据二次函数的性质，可知：
当\(m=2\)时，\(\overrightarrow{Q A} \cdot(\overrightarrow{Q B}+2 \overrightarrow{Q C})\)取得最小值为\(-12\)． - 【答案】\(4\)
【解析】\(\because(\vec{a}-2 \vec{c}) \cdot(\vec{b}-2 \vec{c})=\dfrac{1}{4}\left[(\vec{a}-2 \vec{c}+\vec{b}-2 \vec{c})^{2}-(\vec{a}-2 \vec{c}-\vec{b}+2 \vec{c})^{2}\right]\)
\(=\dfrac{1}{4}\left[(\vec{a}+\vec{b}-4 \vec{c})^{2}-(\vec{a}-\vec{b})^{2}\right]=0\)，
\(\therefore(\vec{a}+\vec{b}-4 \vec{c})^{2}=(\vec{a}-\vec{b})^{2}\)，
\(\therefore|\vec{a}+\vec{b}-4 \vec{c}|=|\vec{a}-\vec{b}|\)，
\(\therefore|\vec{a}+\vec{b}|+|\vec{a}-\vec{b}|=|\vec{a}+\vec{b}|+|\vec{a}+\vec{b}-4 \vec{c}| \geq|(\vec{a}+\vec{b})-(\vec{a}+\vec{b}-4 \vec{c})|=4|\vec{c}|\)，
又\(|\vec{a}+\vec{b}|+|\vec{a}-\vec{b}| \geq \lambda|\vec{c}|\)恒成立，
\(\therefore \lambda \leq 4\)，
\(\therefore \lambda\)的最大值为\(4\)． - 【答案】\(\dfrac{1}{2}\)
【解析】如图，
设\(\vec{a}=\overrightarrow{M A}\)，\(\vec{b}=\overrightarrow{M B}\)，\(\vec{c}=\overrightarrow{M C}\)，
若对任意实数\(x，y\)都有\(|\vec{a}-x \vec{b}| \geq|\vec{a}-\vec{b}|\)，\(|\vec{a}-y \vec{c}| \geq|\vec{a}-\vec{c}|\)成立，
则\(B\)，\(C\)在以\(MA\)为直径的圆上，过\(O\)作\(OD∥AC\)，交\(MC\)于\(E\)，交圆于\(D\)，\(\vec{b}=\overrightarrow{M B}\)在__\(OD\)上的射影最长为\(|E D|\)，
\(\vec{b} \cdot(\vec{c}-\vec{a})=\vec{b} \cdot \overrightarrow{A C}=|D E| \cdot|A C|\)．
设\(\angle A M C=\theta\)，则\(|A C|=2 \sin \theta\)，\(|O E|=\sin \theta\)，
\(|D E|=1-|O E|=1-\sin \theta\)，
\(\therefore \vec{b} \cdot(\vec{c}-\vec{a})=2 \sin \theta(1-\sin \theta)=-2 \sin ^{2} \theta+2 \sin \theta\)，
则当\(\sin \theta=\dfrac{1}{2}\)时，\(\vec{b} \cdot(\vec{c}-\vec{a})\)有最大值为\(\dfrac{1}{2}\)． - 【答案】\(A\)
【解析】令\(f(t)=|\vec{a}+t \vec{b}|^{2}=\vec{a}^{2}+2 t \cdot \vec{a} \cdot \vec{b}+t^{2} \cdot \vec{b}^{2}\)；
\(\therefore \Delta=4(\vec{a} \cdot \vec{b})^{2}-4 \vec{a}^{2} \cdot \vec{b}^{2}=4 \vec{a}^{2} \cdot \vec{b}^{2}(\cos \theta-1) \leq 0\)恒成立，
当且仅当\(\mathrm{t}=-\dfrac{2 \vec{a} \cdot \vec{b}}{2 \times \vec{b}^{2}}=-\dfrac{|\vec{a}|}{|\vec{b}|} \cos \theta\)时，\(f(t)\)取得最小值\(2\)，
\(\therefore\left(-\dfrac{|\vec{a}|}{|\vec{b}|} \cos \theta\right)^{2}+\vec{b}^{2}+2\left(-\dfrac{|\vec{a}|}{|\vec{b}|} \cos \theta\right) \cdot \vec{a} \cdot \vec{b}+\vec{a}^{2}=2,\)，
化简\(\vec{a}^{2} \sin ^{2} \theta=2\)．
\(\therefore \theta\)确定，则\(|\vec{a}|\)唯一确定，故选\(A\).
