8.1 成对数据的统计相关性
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第三册同步提高,难度3颗星!
模块导图
知识剖析
相关关系与确定关系
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
\({\color{Red}{ Eg }}\) 正方形面积与边长,高一定时圆锥的体积与底圆半径等均为确定关系;体重与身高,子女的身高与父亲的身高,空气污染指数与汽车保有量等均为相关关系.
正相关与负相关
如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,称这两个变量正相关;从散点图来看,点从左下角往右上角走.
如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现减少的趋势,称这两个变量负相关;从散点图来看,点从左上角往右下角走.
\({\color{Red}{ Eg }}\) 脂肪含量与年龄 , 子女的身高与父亲的身高正相关.
线性相关
一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关.
一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.
样本相关系数
对于变量\(x\)和变量\(y\),设经过随机抽样获得的成对样本数据为\(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{n}, y_{n}\right)\),其中\(x_{1}, x_{2}, \ldots, x_{n}\)和\(y_{1}, y_{2}, \ldots, y_{n}\)的均值分别为\(\bar{x}\)和\(\bar{y}\),则\(r=\dfrac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \sqrt{\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}}\)
我们称\(r\)为变量\(x\)和变量\(y\)的样本相关系数.
① 当\(r>0\)时,称成对数据正相关;当\(r<0\)时,称成对数据负相关.
② \(|r|\)越接近于\(1\),两个变量的线性相关性越强;
\(|r|\)接近于\(0\)时,两个变量之间几乎不存在线性相关关系.
③样本相关系数\(r\)也可以推导得到
\(r=\dfrac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \sqrt{\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}}=\dfrac{\sum_{i=1}^{n} x_{i} y_{i}-n \bar{x} \bar{y}}{\sqrt{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \sqrt{\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}}\)
经典例题
【题型一】相关关系与确定关系
【典题1】下面哪两个变量间是相关关系( )
A.出租车费与行驶的里程
B.房屋面积与房屋价格
C.身高与体重
D.铁块的大小与质量
【解析】根据题意,依次分析选项:
对于\(A\),出租车费与行驶的里程之间的关系是确定,是函数关系,不符合题意;
对于\(B\),房屋面积与房屋价格之间的关系是确定,是函数关系,不符合题意;
对于\(C\),身高与体重之间的关系是不确定,但在一定范围内,身高越高,体重越大,是相关关系,符合题意;
对于\(D\),铁块的大小与质量之间的关系是确定,是函数关系,不符合题意;
故选:\(C\).
【点拨】是确定关系还是相关关系,看两变量之间关系是否确定的.
【题型二】正相关与负相关
【典题1】有以下五组变量:
①某商品的销售价格与销售量;
②学生的学籍号与学生的数学成绩;
③坚持每天吃早餐的人数与患胃病的人数;
④气温与冷饮销售量;
⑤电瓶车的重量和行驶每千米的耗电量.
其中两个变量成正相关的是( )
A. \((1)(3)\) \(\qquad \qquad \qquad \qquad\) B. \((2)(4)\)\(\qquad \qquad \qquad \qquad\)C. \((2)(5)\) \(\qquad \qquad \qquad \qquad\) D. \((4)(5)\)
【解析】对于①,一般情况下,某商品的销售价格与销售量成负相关关系;
对于②,学生的学籍号与学生的数学成绩没有相关关系;
对于③,一般情况下,坚持每天吃早餐的人数与患胃病的人数成负相关关系;
对于④,一般情况下,气温与冷饮销售量成正相关关系;
对于⑤,一般情况下,电瓶车的重量和行驶每千米的耗电量成正相关关系.
综上所述,其中两个变量成正相关的序号是④⑤.
故选:\(D\).
【点拨】如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,称这两个变量正相关;如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现减少的趋势,称这两个变量负相关.
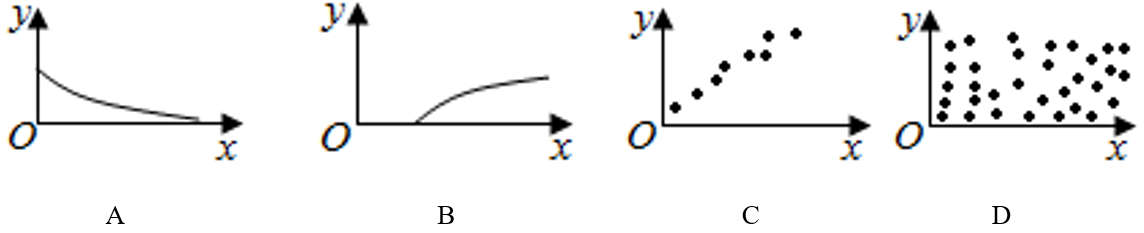
【典题2】在各散点图中,两个变量具有正相关关系的是( )

【解析】根据题意,依次分析选项为:
对于\(A\)、是相关关系,但不是正相关关系,不符合题意;
对于\(B\)、是相关关系,也是正相关关系,符合题意;
对于\(C\)、是相关关系,是负相关关系,不符合题意;
对于\(D\)、所示的散点图中,样本点不成带状分布,这两个变量不具有线性相关关系,不符合题意.
故选:\(B\).
【点拨】从散点图来看,点从左下角往右上角走是正相关;从散点图来看,点从左上角往右下角走是负相关.
【题型三】成对数据的统计相关系数
【典题1】对某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )

A. \(r_{4}<r_{2}<0<r_{1}<r_{3}\) \(\qquad \qquad \qquad \qquad\) B. \(r_{2}<r_{4}<0<r_{1}<r_{3}\)
C. \(r_{2}<r_{4}<0<r_{3}<r_{1}\) \(\qquad \qquad \qquad \qquad\) D. \(r_{4}<r_{2}<0<r_{3}<r_{1}\)
【解析】根据散点图的特征,数据大致呈增长趋势的是正相关,数据呈递减趋势的是负相关;由题中数据可知:(1)(3)为正相关,为负相关;
数据越集中在一条线附近,说明相关性越强,
故\(r_{1}>0, r_{3}>0\);\(r_{2}<0, r_{4}<0\);
又(1)与(2)中散点图更接近于一条直线,故\(r_1>r_3\),\(r_2<r_4\)
因此\(r_2<r_4<0<r_3<r_1\).
故选:\(C\).
【点拨】
①若散点图中数据集中所在的直线斜率为正,则正相关;斜率为负,则负相关.
②数据越集中在一条线附近,说明相关性越强;与该直线的斜率大小无关.
【典题2】如图所示,\(5\)个数据,去掉后,下列说法正确的是( )

A.相关系数\(r\)变大
B.残差平方和变大
C.相关指数\(R^2\)变小
D.解释变量\(x\)与预报变量\(y\)的相关性变强
【解析】由散点图知,去掉离群点\(D\)后,\(x\)与\(y\)的相关性变强,且为正相关,
所以相关系数\(r\)的值变大,相关指数\(R^2\)的值变大,残差平方和变小.
故选:\(AD\).
【点拨】
①相关系数\(r\)判断线性的相关性的强弱;而残差平方和与相关指数\(R^2\)判断的是模型的拟合效果,残差平方和越小,相关指数\(R^2\)越大,模型拟合效果越好;
②本题中点\(D\)属于“歧义点”,偏离回归直线较远,若剔除少数的“歧义点”,解释变量\(x\)与预报变量\(y\)的相关性变强.
巩固练习
1(★)下列两个量之间的关系是相关关系的为( )
A.正方体的体积与棱长的关系
B.学生的成绩和体重
C.路上酒后驾驶的人数和交通事故发生的多少
D.水的体积和重量
2(★)下列说法正确的是( )
A.圆的面积与半径之间的关系是相关关系
B.粮食产量与施肥量之间的关系是函数关系
C.一定范围内,学生的成绩与学习时间成正相关关系
D.人的体重与视力成负相关关系
3(★)变量有观测数据,得散点图(1);对变量,有观测数据,得散点图(2),由这两个散点图可以判断( )

A.变量\(x\)与\(y\)正相关,\(u\)与\(v\)正相关
B.变量\(x\)与\(y\)正相关,\(u\)与\(v\)负相关
C.变量\(x\)与\(y\)负相关,\(u\)与\(v\)正相关
D.变量\(x\)与\(y\)负相关,\(u\)与\(v\)负相关
4(★)判断如图所示的图形中具有相关关系的是( )
5(★)对两个变量的几组观测数据统计如表,则这两个相关变量的关系是( )
\(\begin{array}{|c|c|c|c|c|c|c|}
\hline x & 10 & 9 & 8 & 7 & 6 & 5 \\
\hline y & 2 & 3 & 3.5 & 4 & 4.8 & 5 \\
\hline
\end{array}\)
A.负相关 \(\qquad \qquad \qquad \qquad\) B.正相关 \(\qquad \qquad \qquad \qquad\) C.先正后负相关 \(\qquad \qquad \qquad \qquad\) D.先负后正相关
6(★)关于相关关系,下列说法不正确的是( )
A.相关关系是一种非确定关系
B.相关关系\(r\)越大,两个变量的相关性越强
C.当两个变量相关且相关系数时,表明两个变量正相关
D.相关系数\(r\)的绝对值越接近\(1\),表明两个变量的相关性越强
7(★)变量与相对应的一组数据为\((10,1)\),\((11.3,2)\),\((11.8,3)\),\((12.5,4)\),\((13,5)\),变量与相对应的一组数据为\((10,5)\),\((11.3,4)\),\((11.8,3)\),\((12.5,2)\),\((13,1)\).\(r_{1}\)表示变量\(Y\)与\(X\)之间的线性相关系数,表示变量\(V\)与\(U\)之间的线性相关系数,则( )
参考公式:线性相关系数\(r=\dfrac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \sqrt{\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}}\)
A. \(r_{2}<r_{1}<0\) \(\qquad \qquad \qquad \qquad\) B. \(0<r_{2}<r_{1}\) \(\qquad \qquad \qquad \qquad\) C. \(r_{2}<0<r_{1}\) \(\qquad \qquad \qquad \qquad\) D. \(r_{1}=r_{2}\)
8(★)【多选题】为了对变量与的线性相关性进行检验,由样本点\((x_1,y_1)\),\((x_2,y_2)\),...,\((x_{10},y_{10})\)求得两个变量的样本相关系数为\(r\),那么下面说法中错误的有( )
A.若所有样本点都在直线上\(y=-2x+1\),则\(r=1\)
B.若所有样本点都在直线上\(y=-2x+1\),则\(r=-2\)
C.若\(|r|\)越大,则变量\(x\)与\(y\)的线性相关性越强
D.若\(|r|\)越小,则变量\(x\)与\(y\)的线性相关性越强
9(★)对相关系数\(r\),下列说法正确的是( )
A.\(r\)越大,线性相关程度越大
B.\(r\)越小,线性相关程度越大
C.\(|r|\)越大,线性相关程度越小,\(|r|\)越接近\(0\),线性相关程度越大
D.\(|r|≤1\)且\(|r|\)越接近\(1\),线性相关程度越大,\(|r|\)越接近\(0\),线性相关程度越小
10(★)下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是( )

A. \((1)(3)\) \(\qquad \qquad \qquad \qquad\) B. \((1)(4)\) \(\qquad \qquad \qquad \qquad\) C. \((2)(3)\) \(\qquad \qquad \qquad \qquad\) D. \((1)(2)\)
11(★)已知甲、乙、丙、丁四组数据变量间对应的线性相关系数分别为\(0.46,0.79,-0.92,0.85\),则( )
A.甲组数据变量间的线性相关程度最强
B.乙组数据变量间的线性相关程度最弱
C.丙组数据变量间的线性相关程度最强
D.丁组数据变量间的线性相关程度最强
12(★)对两个变量\(x ,y\)进行线性相关检验,得线性相关系数\(r_1=0.7859\),对两个变量\(u ,v\)进行线性相关检验,得线性相关系数,则下列判断正确的是( )
A.变量\(x\)与\(y\)正相关,变量\(u\)与\(v\)负相关,变量\(x\)与\(y\)的线性相关性较强
B.变量\(x\)与\(y\)负相关,变量\(u\)与\(v\)正相关,变量\(x\)与\(y\)的线性相关性较强
C.变量\(x\)与\(y\)正相关,变量\(u\)与\(v\)负相关,变量\(u\)与\(v\)的线性相关性较强
D.变量\(x\)与\(y\)负相关,变量\(u\)与\(v\)正相关,变量\(u\)与\(v\)的线性相关性较强
参考答案
- 【答案】\(C\)
【解析】\(A\)、由正方体的棱长和体积的公式知,\(V=a^{3}(a>0)\),故\(A\)不对;
\(B\)、学生的成绩和体重,没有关系,故\(B\)不对;
\(C\)、路上酒后驾驶的人数会影响交通事故发生的多少,但不是唯一因素,它们之间有相关性,故\(C\)对;
\(D\)、水的体积_V_和重量_x_的关系为:\(V=k\cdot x\),是确定的函数关系,故\(D\)不对;
故选:\(C\). - 【答案】\(C\)
【解析】对于\(A\),圆的面积与半径之间的关系是确定的关系,是函数关系,所以\(A\)错误;
对于\(B\),粮食产量与施肥量之间的关系是不是函数关系,是相关关系,所以\(B\)错误;
对于\(C\),一定范围内,学生的成绩与学习时间是成正相关关系的,所以\(C\)正确;
对于\(D\),人的体重与视力是没有相关关系的,所以\(D\)错误.
故选:\(C\). - 【答案】\(C\)
【解析】由题图\(1\)可知,\(y\)随\(x\)的增大而减小,各点整体呈下降趋势,\(x\)与\(y\)负相关,由题图\(2\)可知,\(u\)随\(v\)的增大而增大,各点整体呈上升趋势,\(u\)与\(v\)正相关.
故选:\(C\). - (【答案】\(C\)
【解析】由题意,选项\(A\),\(B\)中的\(x\)与\(y\)的对应是确定的,
选项\(C\)、\(D\)是不确定的,
而在选项\(C\)、\(D\)中,\(C\)具有相关关系,
故选:\(C\). - 【答案】\(A\)
【解析】根据两个变量\(x\),\(y\)的几组观测数据统计表知,
\(y\)随\(x\)的增大而减小,所以这两个相关变量负相关.
故选:\(A\). - 【答案】\(B\)
【解析】对于\(A\),相关关系不同于函数关系,它是一种非确定的关系,\(A\)正确;
对于\(B\),相关关系\(|r|\)越大,两个变量的相关性越强,\(∴B\)错误;
对于\(C\),当两个变量相关且相关系数\(r>0\)时,说明两个变量正相关,\(∴C\)正确;
对于\(D\),相关系数\(r\)的绝对值越接近\(1\),表明两个变量的相关性越强,\(D\)正确.
故选:\(B\). - 【答案】\(C\)
【解析】由已知中的数据可知:第一组数据正相关,则相关系数大于零,
第二组数据负相关,则相关系数小于零,故选:\(C\). - (【答案】\(ABD\)
【解析】当所有样本点都在直线\(y=-2x+1\)上时,样本点数据完全负相关,其相关系数\(r=-1\),所以\(A\)、\(B\)都错误;
相关系数\(|r|\)值越大,则变量\(x\)与\(y\)的线性相关性越强,\(C\)正确;
相关系数\(|r|\)值越小,则变量\(x\)与\(y\)的线性相关性越弱,\(D\)错误.
综上知,以上错误的说法是\(ABD\).
故选:\(ABD\). - (【答案】D
【解析】两个变量之间的相关系数,\(r\)的绝对值越接近于\(1\),
表面两个变量的线性相关性越强,
\(r\)的绝对值越接近于\(0\),表示两个变量之间几乎不存在线性相关,
故选:\(D\). - 【答案】\(B\)
【解析】∵两个变量的散点图,
若样本点成带状分布,则两个变量具有线性相关关系,
\(∴\)两个变量具有线性相关关系的图是①和④.
故选:\(B\). - 【答案】\(C\)
【解析】因为线性相关系数的绝对值越大,线性相关性越强,甲、乙、丙、丁四组数据的线性相关系数分别为\(0.46,0.79,-0.92,0.85\),所以丙组数据的线性相关性最强.
故选:\(C\). - 【答案】\(C\)
【解析】由线性相关系数\(r_{1}=0.7859>0\)知\(x\)与\(y\)正相关,
由线性相关系数\(r_{2}=-0.9568<0\)知\(u,v\)负相关,
又\(\left|r_{1}\right|<\left|r_{2}\right|\),
\(∴\)变量\(u\)与\(v\)的线性相关性比\(x\)与\(y\)的线性相关性强.
故选:\(C\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号