7.5 正态分布
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第三册同步提高,难度3颗星!
模块导图
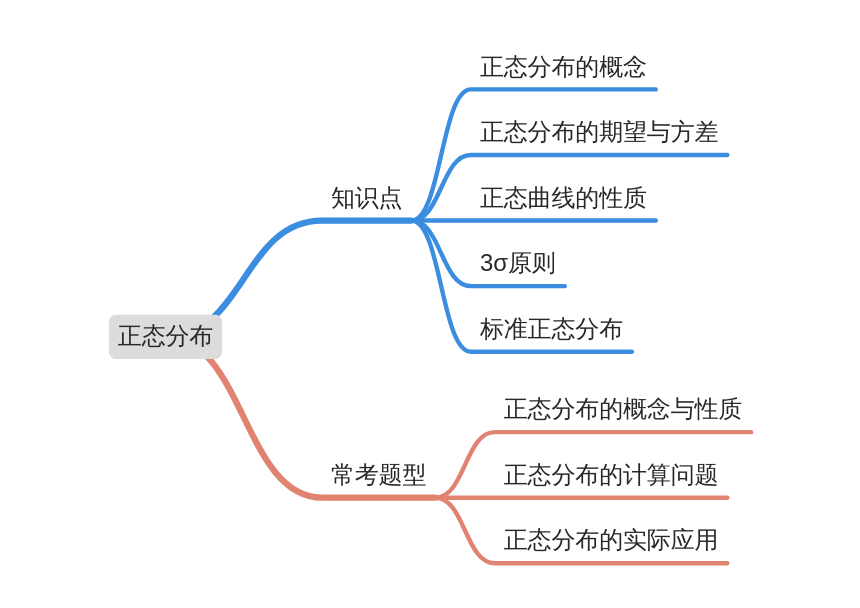
知识剖析
正态分布的概念
若连续型随机变量\(ξ\)的概率密度函数为\(f(x)=\dfrac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}, x \in(-\infty,+\infty)\),
其中\(σ\),\(μ\)为常数,且\(σ>0\),则称\(x\)服从正态分布,简记为\(x∼N(μ ,σ^2 )\).
\(f(x)\)的图象称为正态曲线.
正态分布的期望与方差
若\(ξ∼ N(μ ,σ^2)\),则 \(E(ξ)=μ\),\(D(ξ)=σ^2\);
正态曲线的性质
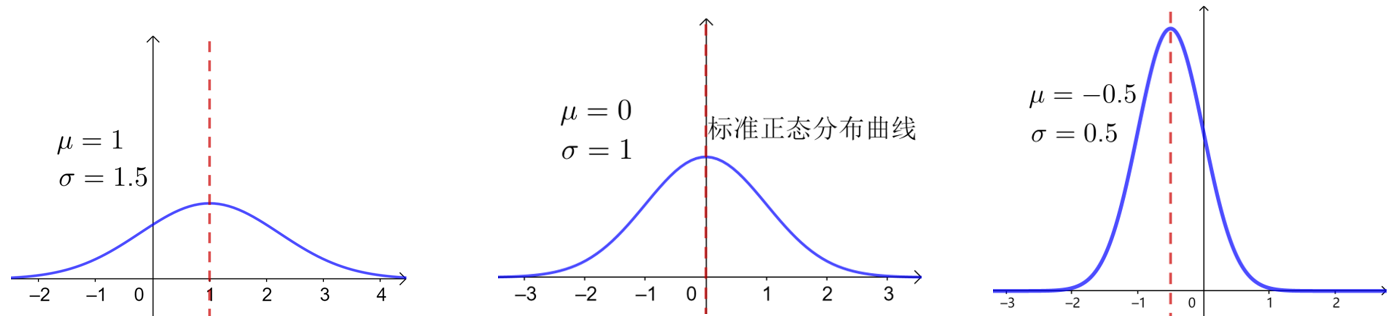
① 曲线在\(x\)轴的上方,与\(x\)轴不相交;
② 曲线关于直线\(x=μ\)对称;
③ 曲线在\(x=μ\)时达到峰值\(\dfrac{1}{\sigma \sqrt{2 \pi}}\);
④ 曲线与\(x\)轴之间的面积为\(1\);
⑤ 当\(x<μ\)时,曲线上升;当\(x>μ\)时,曲线下降.并且当曲线向左、右两边无限延伸时,以\(x\)轴为渐进线,向它无限靠近;
⑥ 曲线的形状由\(σ\)确定,
\(σ\)越大,峰值\(\dfrac{1}{\sigma \sqrt{2 \pi}}\)越小,曲线越“矮胖”,表示总体的分布越分散;
\(σ\)越小,峰值\(\dfrac{1}{\sigma \sqrt{2 \pi}}\)越大,曲线越“瘦高”,表示总体的分布越集中.
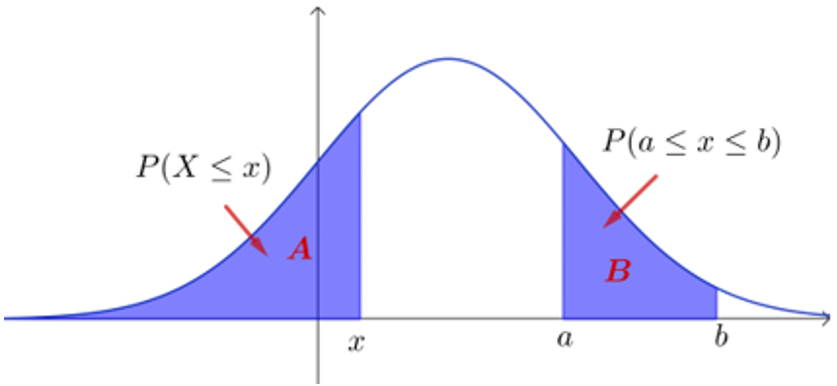
概率
若\(X \sim N\left(\mu, \sigma^{2}\right)\),\(X\)取值不超过\(x\)的概率\(P(X≤x)\)为区域\(A\)的面积,而\(P(a≤X≤b)\)为区域\(B\)的面积.
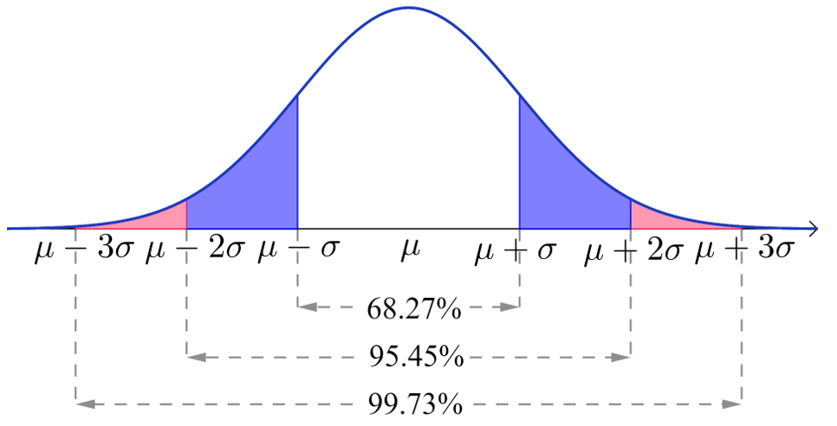
3σ原则
假设\(X~N(μ ,σ^2)\),对于给到的\(k∈N^*\),\(P(μ-kσ<x≤μ+kσ)\)是一个只与\(k\)有关的定值,特别地,
\(P(μ-σ<x≤μ+σ)=0.6827\)
\(P(μ-2 σ<x≤μ+2 σ)=0.9545\)
\(P(μ-3 σ<x≤μ+3 σ)=0.9973\)
标准正态分布
① 在标准正态分布表中相应于\(x_0\)的值\(Φ(x_0)\)是指总体取值小于\(x_0\)的概率,
即\(Φ(x_0)=P(x<x_0)\).
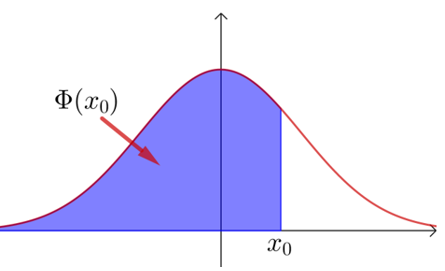
\(x_0≥ 0\)时,则\(Φ(x_0)\)的值可在标准正态分布表中查到;
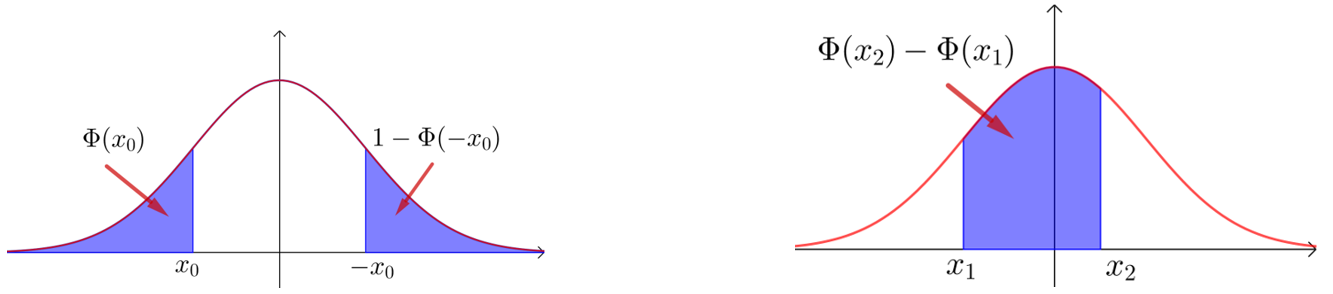
\(x_0<0\)时,可利用其图象的对称性获得\(Φ(x_0)=1-Φ(-x_0)\)来求出,
\(P(x_1<ξ<x_2)=P(ξ<x_2)-P(ξ<x_1)=Φ(x_2)-Φ(x_1)\)
②\(N(μ ,σ^2)\)与\(N(0 ,1)\)的关系:
\((i)\)若\(ξ∼N(μ ,σ^2)\),则\(\eta=\dfrac{\xi-\mu}{\sigma} \sim N(0,1)\),有\(P\left(\xi<x_{0}\right)=F\left(x_{0}\right)=\Phi\left(\dfrac{x_{0}-\mu}{\sigma}\right)\);
\((ii)\)若\(ξ∼ N(μ ,σ^2)\),则\(P\left(x_{1}<x<x_{2}\right)=\Phi\left(\dfrac{x_{2}-\mu}{\sigma}\right)-\Phi\left(\dfrac{x_{1}-\mu}{\sigma}\right)\).
经典例题
【题型一】正态分布的概念与性质
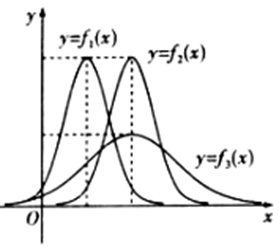
【典题1】已知三个正态分布密度函数\(P_{i}(x)=\dfrac{1}{\sqrt{2 \pi} \sigma_{i}} e^{-\frac{\left(x-\mu_{i}\right)^{2}}{2 \sigma_{i}^{2}}}\)\((x \in \boldsymbol{R}, i=1,2,3)\)的图象如图所示,则下列结论正确的是( )

A.\(σ_1=σ_2=σ_3\) \(\qquad \qquad\) B.\(σ_1=σ_2<σ_3\) \(\qquad \qquad\) C.\(μ_1=μ_2>μ_3\) \(\qquad \qquad\)D.\(μ_1<μ_2=μ_3\)
【解析】因为\(x=μ\)是对称轴,观察图象可知:\(μ_1<μ_2=μ_3\),
而\(y=φ_1 (x)\)与\(y=φ_2 (x)\)的图象可以相互平移得到,且\(y=φ_3 (x)\)的图象显得更“矮胖”,故\(σ_1=σ_2<σ_3\).
故选:\(BD\).
【点拨】在正态分布的密度函数曲线\(f(x)=\dfrac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}\),其中直线\(x=μ\)是其对称轴,\(σ\)确定曲线形状,\(σ\)越大曲线越“矮胖”,\(σ\)越小,曲线越“瘦高”.
【典题2】已知连续型随机变量\(X_i~N(u_i ,σ_i^2)(i=1 ,2 ,3)\),其正态曲线如图所示,则下列结论正确的是( )
A. \(P\left(X_{1} \leq \mu_{2}\right)<P\left(X_{2} \leq \mu_{1}\right)\)
B. \(P\left(X_{2} \geq \mu_{2}\right)>P\left(X_{3} \geq \mu_{3}\right)\)
C. \(P\left(X_{1} \leq \mu_{2}\right)<P\left(X_{2} \leq \mu_{3}\right)\)
D. \(P\left(\mu_{i}-2 \sigma_{i} \leq X_{i} \leq \mu_{i}+2 \sigma_{i}\right)=P\left(\mu_{i+1}-2 \sigma_{i+1} \leq X_{i+1} \leq \mu_{i+1}+2 \sigma_{i+1}\right)(i=1,2)\)
【解析】对于\(A\):\(P(X_1≤μ_2)\)是正态分布密度函数\(y=f_1 (x)\)在第二条虚线左侧与\(x\)轴围成的部分,显然大于\(0.5\),\(P(X_2≤μ_1)\)是正态分布密度函数\(y=f_2 (x)\)在第一条虚线左侧与\(x\)轴围成的部分,显然小于\(0.5\),故\(P(X_1≤μ_2)>P(X_2≤μ_1)\),故\(A\)错误;
对于\(B: P\left(X_{2} \geq \mu_{2}\right)=\dfrac{1}{2}\),\(P\left(X_{3} \geq \mu_{3}\right)=\dfrac{1}{2}\),则\(P(X_2≥μ_2)=P(X_3≥μ_3)\),故\(B\)错误;
对于\(C:P(X_1≤μ_2 )>0.5=P(X_2≤μ_3)\),故\(C\)错误;
对于\(D: P\left(\mu_{i}-2 \sigma_{i} \leq X_{i} \leq \mu_{i}+2 \sigma_{i}\right)\)\(=P\left(\mu_{i+1}-2 \sigma_{i+1} \leq X_{i+1} \leq \mu_{i+1}+2 \sigma_{i+1}\right)(i=1,2)\)成立,故\(D\)正确.
故选:\(D\).
【点拨】
① 在正态分布中,概率\(P(X<x)\)相当于看对应的“面积”;
② 若\(X~N(μ ,σ^2)\),对于给到的\(k∈N^*\),\(P(μ-kσ<x≤μ+kσ)\)是一个只与\(k\)有关的定值,与正态分布密度函数无关,故\(D\)正确.
巩固练习
1(★)【多选题】已知\(X~N(μ ,σ^2)\),\(f(x)=\dfrac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}\),\(x∈R\),则( )
A.曲线\(y=f(x)\)与\(x\)轴围成的几何图形的面积小于\(1\)
B.函数\(f(x)\)图象关于直线\(x=μ\)对称
C.\(P(X>μ-σ)=2P(μ<X<μ+σ)+P(X≥μ+σ)\)
D.函数\(F(x)=P(X>x)\)在\(R\)上单调递增
2(★)【多选题】已知三个正态分布密度函数\(\varphi_{i}(x)=\dfrac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{\left(x-\mu_{i}\right)^{2}}{2 \sigma_{i}^{2}}}\)\((x \in \boldsymbol{R}, I=1,2,3)\)的图象如图所示,则下列结论正确的是( )

A. \(\sigma_{1}=\sigma_{2}\) \(\qquad \qquad \qquad \qquad\) B. \(\mu_{1}>\mu_{3}\) \(\qquad \qquad \qquad \qquad\) C. \(\mu_{1}=\mu_{2}\) \(\qquad \qquad \qquad \qquad\) D. \(\sigma_{2}<\sigma_{3}\)
3(★)设随机变量\(X~N(μ ,7)\),若\(P(X<2)=P(X>4)\),则( )
A. \(\mu=3\), \(D X=7\) \(\qquad \qquad\) B. \(\mu=6\), \(D X=\sqrt{7}\) \(\qquad \qquad\) C.\(\mu=3\), \(D X=\sqrt{7}\) \(\qquad \qquad\) D. \(\mu=6\), \(D X=7\)
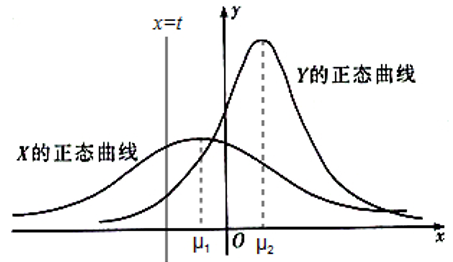
4(★★)设\(X~N(μ_1 ,σ_1^2)\) ,\(Y~N(μ_2 ,σ_2^2)\),这两个正态曲线如图所示,下列说法正确的是( )

A.\(P(Y≤μ_1)≥P(Y≤μ_2)\)
B.\(P(X≥σ_1)≥P(X≥σ_2)\)
C.若\(t<0\),则\(P(X≤t)≤P(Y≤t)\)
D.若\(t<0\),则\(P(X≥t)≤P(Y≥t)\)
参考答案
- 【答案】\(BC\)
【解析】\(A\).曲线\(y=f(x)\)与\(x\)轴围成的几何图形的面积等于\(1\),因此\(A\)不正确;
\(B\).函数\(f(x)\)图象关于直线\(x=μ\)对称,可得\(B\)正确;
\(C\).\(∵P(μ>X>μ-σ)=P(μ<X<μ+σ)\),\(∴P(X>μ-σ)=2P(μ<X<μ+σ)+P(X≥μ+σ)\),因此\(C\)正确;
\(D\).函数\(F(x)=P(X>x)\)在\(R\)上单调递减,可得\(D\)不正确.
故选:\(BC\). - 【答案】\(AD\)
【解析】根据正态曲线关于\(x=μ\)对称,且\(μ\)越大图象越靠近右边,
所以\(μ_1<μ_2=μ_3\),\(BC\)错误;
又\(σ\)越小数据越集中,图象越瘦长,
所以\(σ_1=σ_2<σ_3\),\(AD\)正确.
故选:\(AD\). - 【答案】\(A\)
【解析】\(∵\)随机变量\(X~N(μ,7)\),若\(P(X<2)=P(X>4)\),
则\(μ=3\),\(DX=7\),
故选:\(A\).
4【答案】\(D\)
【解析】\(∵\)正态分布密度曲线图象关于\(x=μ\)对称,
\(∴μ_1<μ_2\),
由图象形状可得\(\sigma_{1}>\sigma_{2}\),
由正态分布曲线的对称性可得:若\(t<0\),则\(P(X≥t)≤P(Y≥t)\).
故选:\(D\).
【题型二】 正态分布的计算问题
【典题1】已知随机变量\(ξ\)服从正态分布\(N(1 ,σ^2)\),若\(P(ξ≥2)=a\),\(P(0<ξ≤1)=1-3a\),则\(P(ξ≤0)=\)( )
A. \(\dfrac{1}{4}\) \(\qquad \qquad \qquad \qquad\) B. \(\dfrac{1}{3}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{3}{4}\)
【解析】随机变量\(ξ\)服从正态分布\(N(1 ,σ^2)\),\(P(ξ≥2)=a\),\(P(0<ξ≤1)=1-3a\),
\(∴P(ξ≤0)=P(ξ≥2)=a\),\(\therefore a+1-3 a=\dfrac{1}{2}\),解得\(a=\dfrac{1}{4}\),
则\(P(\xi \leq 0)=\dfrac{1}{4}\).
故选:\(A\).
【点拨】① 在求解正态分布的概率时,要注意其曲线对称轴\(x=μ\),利用对称性进行求解,若对题目中数值不是很敏感,建议画图进行思考,其关系容易获得;
② 正态曲线与\(x\)轴之间的面积,即概率总和为\(1\),则概率\(P(x \leq \mu)=P(x \geq \mu)=\dfrac{1}{2}\).
【典题2】随机变量\(X\)服从正态分布\(X~N(10 ,σ^2)\),\(P(X>12)=m\),\(P(8≤X≤10)=n\),则\(\dfrac{2}{m}+\dfrac{1}{n}\)的最小值为\(\underline{\quad \quad}\).
【解析】\(∵\)随机变量\(X\)服从正态分布\(X~N(10 ,σ^2)\),\(\therefore P(X \geq 10)=\dfrac{1}{2}\),
由\(P(8≤X≤10)=n\),得\(P(10≤X≤12)=n\),
\({\color{Red}{(留意到8, 12 的平均数就是μ=10 ) }}\)
又\(P(X>12)=m\),
\(\therefore m+n=\dfrac{1}{2}\),且\(m>0\),\(n>0\),
则\(\dfrac{2}{m}+\dfrac{1}{n}=\left(\dfrac{2}{m}+\dfrac{1}{n}\right)(2 m+2 n)\)\(=6+\sqrt{\dfrac{4 n}{m} \cdot \dfrac{2 m}{n}} \geq 6+2=6+4 \sqrt{2}\).
当且仅当\(\dfrac{4 n}{m}=\dfrac{2 m}{n}\),即\(m=\dfrac{2-\sqrt{2}}{2}, n=\dfrac{\sqrt{2}-1}{2}\)时等号成立.
\(\therefore \dfrac{2}{m}+\dfrac{1}{n}\)的最小值为\(6+4 \sqrt{2}\).
故答案为:\(6+4 \sqrt{2}\).
【点拨】
① 本题为正态分布与基本不等式的结合题,要对题中的数值\(8\),\(10\),\(12\)有所注意;
② 利用基本不等式“若\(a>0\),\(b>0\),则\(a+b \geq 2 \sqrt{a b}\)”时要注意是否满足“正、定、等”三字.
巩固练习
1(★★)若随机变量\(X\)服从分布\(X~N(2 ,σ^2)\),且\(2P(X≥3)=P(1≤X≤2)\),则\(P(X<3)=\)( )
A. \(\dfrac{1}{3}\) \(\qquad \qquad \qquad \qquad\) B. \(\dfrac{5}{6}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{1}{6}\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{2}{3}\)
2(★★)若随机变量\(X~B(3 ,p)\) ,\(Y~N(2 ,σ^2)\),若\(P(X≥1)=0.657\),\(P(0<Y<2)=p\),则\(P(Y>4)=\)( )
A.\(0.2\) \(\qquad \qquad \qquad \qquad\)B.\(0.3\) \(\qquad \qquad \qquad \qquad\) C.\(0.7\) \(\qquad \qquad \qquad \qquad\)D.\(0.8\)
3(★★)2012年国家开始实行法定节假日高速公路免费通行政策,某收费站在统计了2019年清明节前后车辆通行数量,发现该站近几天每天通行车辆的数量\(ξ\)服从正态分布\(ξ~N(1000 ,σ^2)\),若\(P(ξ>1200)=a\) ,\(P(800<ξ<1200)=b\),则\(\dfrac{1}{a}+\dfrac{2}{b}\)的最小值为\(\underline{\quad \quad}\).
参考答案
- 【答案】\(B\)
【解析】设\(P(X≥3)=x\),则\(P(1≤X≤2)=2x\),
根据对称性,\(P(2≤X≤3)=2x\),
则\(P(X \geq 2)=3 x=\dfrac{1}{2}\),\(\therefore P(X \geq 3)=x=\dfrac{1}{6}\).
即\(P(X \geq 3)=\dfrac{1}{6}\),\(\therefore P(X<3)=\dfrac{5}{6}\),
故选:\(B\). - 【答案】\(A\)
【解析】\(∵P(X≥1)=0.657\),\(\therefore 1-(1-p)^{3}=0.657\),即\((1-p)^{3}=0.343\),解得\(p=0.3\).
\(∴P(0<Y<2)=p=0.3\),
则\(P(Y>4)=\dfrac{1-2 P(0<Y<2)}{2}=\dfrac{1-2 \times 0.3}{2}=0.2\),
故选:\(A\). - 【答案】\(8\)
【解析】由\(\xi \sim N\left(1000, \sigma^{2}\right)\),且\(P(ξ>1200)=a\),所以\(P(ξ<800)=P(ξ>1200)=a\),
所以\(P(800<ξ<1200)=1-2a=b\),所以\(2a+b=1\),\(a>0\),\(b>0\),
所以\(\dfrac{1}{a}+\dfrac{2}{b}=\left(\dfrac{1}{a}+\dfrac{2}{b}\right)(2 a+b)=4+\dfrac{b}{a}+\dfrac{4 a}{b} \geq 4+2 \sqrt{\dfrac{b}{a} \cdot \dfrac{4 a}{b}}=8\),\(b=2a\)时取“=”,
\(\dfrac{1}{a}+\dfrac{2}{b}\)的最小值为\(8\).
故答案为:\(8\).
【题型三】 正态分布的实际应用
【典题1】为了研究新冠疫情期间学生上网课的学习效果,学生返校复课后,某市对高三年级组织了一次调研考试,考试后统计的数学成绩服从正态分布,其密度曲线函数为\(f(x)=\dfrac{1}{9 \sqrt{2} \pi} e^{-\frac{(x-85)^{2}}{162}}\),\(x∈(-∞ ,+∞)\),则下列说法正确的是( )
A.本次调研考试的平均分为\(85\)
B.本次调研考试的方差为\(81\)
C.随机抽查一名学生,其成绩在\(125\)分以上的概率比成绩在\(45\)分以下的概率大
D.本次调研考试,其成绩在\((75,85)\)和在\((85,95)\)的人数大致一样多
【解析】由正态分布密度曲线函数为\(f(x)=\dfrac{1}{9 \sqrt{2} \pi} e^{-\frac{(x-85)^{2}}{162}}\),\(x∈(-∞ ,+∞)\),
所以平均数\(μ=85\),方差\(σ^2=81\),所以选项\(A\)、\(B\)正确;
又\(P(x>125)=P(x<45)\),所以成绩在\(125\)分以上的概率等于成绩在\(45\)分以下的概率,选项\(C\)错误;
根据正态分布的对称性知,成绩在\((75,85)\)和在\((85,95)\)的人数大致一样多,选项\(D\)正确.
故选:\(ABD\).
【点拨】
① 对正态分布的密度函数解析式\(f(x)=\dfrac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}\)有些了解,才确定\(2σ^2=162\);其中期望为\(μ\),可理解为数据中的平均数,而\(σ\)是标准差,\(σ^2\)才是方差,看数据的稳定性就看它了;
② 比较两个区间成绩的概率或人数,看在正态分布中对应的概率便可.
【典题2】甲、乙两类水果的质量(单位:kg)分别服从正态分布\(N(μ_1 ,δ_1^2)\),\(N(μ_2 ,δ_2^2)\),其正态分布的密度曲线如图所示,则下列说法错误的是( )

A.甲类水果的平均质量\(μ_1=0.4kg\)
B.甲类水果的质量比乙类水果的质量更集中于平均值左右
C.甲类水果的平均质量比乙类水果的平均质量小
D.乙类水果的质量服从的正态分布的参数\(δ_2=1.99\)
【解析】由图象可知甲图象关于直线\(x=0.4\)对称,乙图象关于直线\(x=0.8\)对称,
\(∴μ_1=0.4\),\(μ_2=0.8\),\({\color{Red}{ (水果的平均质量就看期望μ) }}\)
故\(A\)正确,\(C\)正确,
\(∵\)甲图象比乙图象更“高瘦”,
\(∴\)甲类水果的质量比乙类水果的质量更集中于平均值左右,故\(B\)正确;
\({\color{Red}{ (质量集中于平均值,指的是在平均值附近概率要大些,形状更“高瘦”,即标准差δ_i 更小) }}\)
\(∵\)乙图象的最大值为\(1.99\),即\(\dfrac{1}{\sqrt{2 \pi} \delta_{2}}=1.99\),
\(∴δ_2≠1.99\),故\(D\)错误.
\({\color{Red}{ (要了解正态分布密度函数解析式确定最大值是\dfrac{1}{\sqrt{2 \pi} \delta_{2}},而δ_2 是标准差)}}\)
故选:\(D\).
【点拨】
在正态分布的应用中,对每个数据对应的实际意义有所理解;数据的平均值看期望\(μ\),数据稳定性看标准差\(σ\),数据的集中程度看标准差\(σ\).
【典题3】2020年某市教育主管部门为了解近期举行的数学竞赛的情况,随机抽取\(500\)名参赛考生的数学竞赛成绩进行分析,并制成如下的频率分布直方图:

(1)求这\(500\)名考生的本次数学竞赛的平均成绩\(\bar{x}\)(精确到整数);
(2)由频率分布直方图可认为:这次竞赛成绩\(X\)服从正态分布\(N(μ ,σ^2)\),其中\(μ\)近似等于样本的平均数\(\bar{x}\),\(σ\)近似等于样本的标准差\(s\),并已求得\(s≈18\).用该样本的频率估计总体的概率,现从该市所有考生中随机抽取\(10\)名学生,记这次数学竞赛成绩在\((86,140]\)之外的人数为\(Y\),求\(P(Y=2)\)的值(精确到\(0.001\)).
附:(1)当\(X~N(μ ,σ^2)\)时,\(P(μ-σ<X≤μ+σ)=0.6827\),\(P(μ-2σ<X≤μ+2σ)=0.9545\);(2)\(0.8186^{8} \times 0.1814^{2} \approx 0.0066\).
【解析】(1)\(\bar{x}=10(65 \times 0.0028+75 \times 0.01+85 \times 0.01+95 \times 0.018+105 \times 0.02+115 \times 0.018\)\(+125 \times 0.012+135 \times 0.008+145 \times 0.0012)=10 \times 10.416=104.16 \approx 104\);
(2)由题意知\(X~N(μ ,σ^2)\),且\(μ=104\),\(σ=18\),
\(∴86=104-18=μ-σ\),\(140=104+18×2=μ+2σ\),
\(\therefore P(86<X \leq 140)=P(\mu-\sigma<X \leq \mu+2 \sigma)=\dfrac{0.6827+0.9545}{2}=0.8186\),
则\(P(X≤μ-σ或X>μ+2σ)=1-0.8186=0.1814\),
可得\(Y~B(10 ,0.1814)\),
\(∴P(Y=2)=C_{10}^2×0.1814^2×0.8186^8≈45×0.00663≈0.298\).
【点拨】
① 在直方图中,若第\(i\)组的组中值为\(x_i\),概率为\(p_i\),则平均值\(\bar{x}=\sum_{i=1}^{n} x_{i} p_{i}\);
② 确定正态分布的\(μ=104\),\(σ=18\)后,要留心区间\((86,140]\)中\(86\)、\(140\)与\(μ\)、\(σ\)的数值关系\((86=μ-σ,140=μ+2σ)\),从而求出区间\((86,140]\)内的概率.
【典题4】“公平正义”是社会主义和谐社会的重要特征,是社会主义法治理念的价值追求.“考试”作为一种公平公正选拔人才的有效途径,正被广泛采用.每次考试过后,考生最关心的问题是:自己的考试名次是多少?自己能否被录取?能获得什么样的职位?某单位准备通过考试(按照高分优先录取的原则)录用\(300\)名,其中\(275\)个高薪职位和\(25\)个普薪职位.实际报名人数为\(2000\)名,考试满分为\(400\)分.(一般地,对于一次成功的考试来说,考试成绩应服从正态分布)考试后考试成绩的部分统计结果如下:
考试平均成绩是\(180\)分,\(360\)分及其以上的高分考生\(30\)名.
(1)最低录取分数是多少?(结果保留为整数)
(2)考生甲的成绩为\(286\)分,若甲被录取,能否获得高薪职位?若不能被录取,请说明理由.
参考资料:(1)当\(X~N(μ ,σ^2)\)时,令\(Y=\dfrac{X-\mu}{\sigma}\),则\(Y~N(0 ,1)\).
(2)当\(Y~N(0 ,1)\)时,\(P(Y≤2.17)≈0.985\),\(P(Y≤1.28)≈0.900\),
\(P(Y≤1.09)≈0.863\),\(P(Y≤1.04)≈0.85\).
(3) \(P\left(X>x_{1}\right)=P\left(Y>\dfrac{x_{1}-u}{\sigma}\right)\)
【解析】(1)设考生的成绩为\(X\),
则由题意可得\(X\)应服从正态分布,即\(X~N(180 ,σ^2)\),
令\(Y=\dfrac{X-180}{\sigma}\),则\(Y~N(0 ,1)\).
\({\color{Red}{ (本题只给出标准正态分布中的概率,需要把原正态分布转化为标准正态分布) }}\)
由\(360\)分及以上高分考生\(30\)名可得\(P(X \geq 360)=\dfrac{30}{2000}\),即\(P(X<360)=1-\dfrac{30}{2000}=0.985\),
即有\(P\left(Y<\dfrac{360-180}{\sigma}\right)=0.985\),则\(\dfrac{360-180}{\sigma} \approx 2.17\),可得\(σ≈83\),
可得\(X~N(180 ,83^2)\),
\({\color{Red}{(由X~N(μ ,σ^2 )与Y~N(0 ,1)的关系P\left(X>x_{1}\right)=P\left(Y>\dfrac{x_{1}-u}{\sigma}\right)确定原正态分布) }}\)
设最低录取分数线为\(x_0\),则\(\mid P\left(X \geq x_{0}\right)=P\left(Y \geq \dfrac{x_{0}-180}{83}\right)=\dfrac{300}{2000}\),
即有\(P\left(Y<\dfrac{x_{0}-180}{83}\right)=1-\dfrac{300}{2000}=0.85\),即有\(\dfrac{x_{0}-180}{83}=1.04\),
可得\(x_0=266.32\),即最低录取分数线为\(266\);
(2) \({\color{Red}{ 方法一}}\) 考生甲的成绩\(286>267\),所以能被录取,
\(P(X<286)=P\left(Y<\dfrac{286-180}{83}\right)=P(Y<1.28) \approx 0.90\),表明不低于考生甲的成绩的人数大约为总人数的\(1-0.90=0.10\),\(2000×0.10=200\),
即考生甲大约排在第\(200\)名,排在前\(275\)名之前,所以能被录取为高薪职位.
\({\color{Red}{ (求出甲的排名,再与275 比较) }}\)
\({\color{Red}{方法二 }}\) 设前\(275\)名最低录取分数为\(x_1\),则\(P\left(X<x_{1}\right)=1-\dfrac{275}{2000}=0.8615\),
而\(P(Y≤1.09)≈0.863⇒P(x≤270)≈0.863\)
\(∴P(X<x_1 )<P(x≤270)⇒270>x_1\)
而\(286>270\),所以能被录取为高薪职位.
\({\color{Red}{ (设前275名最低录取分数为x_1,甲录取什么职位就看他的成绩对应的概率P(X>286)与P(X>x_1)的关系) }}\)
【点拨】
① 本题要先理解非标准正态分布与标准正态分布之间的转化方法;
② 要找到给出的数据之间的关系,大胆求值(比如本题中把涉及到\(Y\)的概率都转化为\(X\)的概率,分数\(360\),\(286\)对应的概率等),遇到值相等或近似时,可意识到它们存在某些关系,再结合正态分布的图象进行思考,确定它们的关系!
【典题5】2019年4月,河北、辽宁、江苏、福建、湖北、湖南、广东、重庆等8省市发布高考综合改革实施方案,决定从2018年秋季入学的高中一年级学生开始实施“3+1+2”高考模式.所谓“3+1+2”,即“3”是指考生必选语文、数学、外语这三科;“1”是指考生在物理、历史两科中任选一科;“2”是指考生在生物、化学、思想政治、地理四科中任选两科.
(1)若某考生按照“3+1+2”模式随机选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.
(2)新冠疫情期间,为积极应对“3+1+2”新高考改革,某地高一年级积极开展线上教学活动.教育部门为了解线上教学效果,从当地不同层次的学校中抽取高一学生\(2500\)名参加语数外的网络测试,并给前\(400\)名颁发荣誉证书,假设该次网络测试成绩服从正态分布,且满分为\(450\)分.
①考生甲得知他的成绩为\(270\)分,考试后不久了解到如下情况:“此次测试平均成绩为\(171\)分,\(351\)分以上共有\(57\)人”,请用你所学的统计知识估计甲能否获得荣誉证书,并说明理由;
②考生丙得知他的实际成绩为\(430\)分,而考生乙告诉考生丙:“这次测试平均成绩为\(201\)分,\(351\)分以上共有\(57\)人”,请结合统计学知识帮助丙同学辨别乙同学信息的真伪,并说明理由.
附:\(P(μ-σ≤X≤μ+σ)=0.6828\);\(P(μ-2σ≤X≤μ+2σ)=0.9544\);
\(P(μ-3σ≤X≤μ+3σ)=0.9974\).
【解析】(1)设事件\(A\):选出的六科中含有“语文,数学,外语,物理,化学”,则\(P(A)=\dfrac{C_{3}^{1}}{C_{2}^{1} \cdot C_{4}^{2}}=\dfrac{1}{4}\);
(2)设此次网络测试的成绩记为\(X\),则\(X~N(μ ,σ^2)\).
①平均成绩为\(171\),即\(μ=171\),\({\color{Red}{ (由平均成绩确定期望μ)}}\)
\(∵351\)分以上共有\(57\)人,\(\therefore P(x \geq 351)=\dfrac{57}{2500}=0.0228\),
而\(P(x \geq \mu+2 \sigma)=\dfrac{1-P(\mu-2 \sigma \leq X \leq \mu+2 \sigma)}{2}=\dfrac{1-0.9544}{2}=0.0228\),
\(\therefore \mu+2 \sigma=351 \Rightarrow \sigma=\dfrac{351-\mu}{2}=\dfrac{351-171}{2}=90\),
\({\color{Red}{(由3σ原则求出标准差σ从而确定正态分布.此时要注意得到P(x≥351)=0.0228后,它与3σ原则中哪个范围的概率相等) }}\)
设获得荣誉证书最低分为\(x_0\),则\(P\left(X \geq x_{0}\right)=\dfrac{400}{2500}=0.16\),
而\(P(X \geq \mu+\sigma)=\dfrac{1-P(\mu-\sigma \leq X \leq \mu+\sigma)}{2}\)\(=\dfrac{1-0.6828}{2}=0.1587<0.16=P\left(X \geq x_{0}\right)\).
\(∴\)获得荣誉证书的最低分\(x_0<μ+σ=261\).
而\(270>261\),\(∴\)甲同学能获得荣誉证书;
\({\color{Red}{(若要获得证书,则P(X≥270)< P(X≥x_0 )) }}\).
而由\(3σ\)原则给出的概率确定\(P(X≥261)<P(X≥x_0 )\),显然能获得证书.
②假设乙所说的为真,则\(μ=201\),
\(P(X \geq \mu+2 \sigma)=\dfrac{1-P(\mu-2 \sigma \leq X \leq \mu+2 \sigma)}{2}=\dfrac{1-0.9544}{2}=0.0228\),
\(∵351\)分以上共有\(57\)人,\(\therefore P(x \geq 351)=\dfrac{57}{2500}=0.0228\),
\(\therefore \mu+2 \sigma=351 \Rightarrow \sigma=\dfrac{351-201}{2}=75\),
\({\color{Red}{ (求出符合乙同学信息的正态分布X \sim N\left(201,75^{2}\right)) }}\)
从而\(μ+3σ=201+3×75=426<430\),
而\(P(X \geq \mu+3 \sigma)=\dfrac{1-P(\mu-3 \sigma \leq X \leq \mu+3 \sigma)}{2}=\dfrac{1-0.9974}{2}=0.0013\).
\({\color{Red}{ (判定乙同学信息的真伪,用“假设法”,是先假设乙同学说的为真)}}\)
第一种结论:可以认为乙同学信息为假,理由如下:
事件“\(X≥μ+3σ\)”为小概率事件,即“丙同学的成绩为\(430\)分”是小概率事件,可认为其不可能发生,但却又发生了,所以可认为乙同学信息为假;
第二种结论:无法辨别乙同学信息真假,理由如下:
事件“\(X≥μ+3σ\)”即“丙同学的成绩为\(430\)分”发生的概率虽然很小,一般不容易发生,但是还是有可能发生的,所以无法辨别乙同学信息真假.
【点拨】
① 落在\((μ-3σ ,μ+3σ)\)以外的概率小于千分之三,在实际问题中常认为相应的事件不会发生;
② 判断信息真假,可用“假设法”,先确定信息是真的,再看在此基础上得到哪些结论,它们是否符合常理或说存在谬论;分析结论时,有时候答应也不一定是唯一的,只要能够“自圆其说”就行,现在题目会越来越灵活.
巩固练习
1(★)【多选题】甲、乙两名高中同学历次数学测试成绩(百分制)分别服从正态分布\(N(μ_1 ,σ_1^2)\) ,\(N(μ_2 ,σ_2^2)\),其正态分布的密度曲线如图所示,则下列说法中正确的是( )
附:若随机变量\(X\)服从正态分布\(N(μ ,σ^2)\),则\(P(μ-σ<X<μ+σ)≈0.6826\)

A.乙同学的平均成绩优于甲同学的平均成绩
B.甲同学的平均成绩优于乙同学的平均成绩
C.甲同学的成绩比乙同学成绩更集中于平均值附近
D.若\(σ_1=5\),则甲同学成绩高于\(80\)分的概率约为\(0.1587\)
2(★)为了研究不同性别在处理多任务时的表现差异,召集了男女志愿者各\(300\)名,让他们同时完成多个任务.以下\(4\)个结论中,对志愿者完成任务所需时间分布图表理解正确的是( )
①总体看女性处理多任务平均用时更短;
②所有女性处理多任务的能力都要优于男性;
③男性的时间分布更接近正态分布;
④女性处理多任务的用时为正数,男性处理多任务的用时为负数,且男性处理多任务的用时绝对值大.

A. \((1)(4)\) \(\qquad \qquad \qquad \qquad\) B. \((2)(3)\) \(\qquad \qquad \qquad \qquad\) C. \((1)(3)\) \(\qquad \qquad \qquad \qquad\) D. \((2)(4)\)
3(★★)某批零件的尺寸\(X\)服从正态分布\(N(10 ,σ^2)\),且满足\(P(X<9)=\dfrac{1}{8}\),零件的尺寸与\(10\)的误差不超过\(1\)即合格,从这批产品中抽取\(n\)件,若要保证抽取的合格零件不少于\(2\)件的概率不低于\(0.9\),则\(n\)的最小值为( )
A.\(7\) \(\qquad \qquad \qquad \qquad\) B.\(6\) \(\qquad \qquad \qquad \qquad\) C.\(5\) \(\qquad \qquad \qquad \qquad\) D.\(4\)
4(★★)近几年,中国进入一个鲜花消费的增长期,某农户利用精准扶贫政策,贷款承包了一个新型温室鲜花大棚,种植和销售红玫瑰和白玫瑰.该农户从去年的销售数据中随机抽取了红玫瑰\(10\)天的销量数据如下(单位:枝):
\(615,575,625,590,600,600,570,615,580,630\).
(Ⅰ)求这\(10\)天红玫瑰销量的平均数\(\bar{x}\)和方差\(s^2\);
(Ⅱ)若这个大棚红玫瑰的日销量\(X\)服从正态分布\(N(μ ,σ^2)\),其中\(μ\) ,\(σ^2\)可分别用(Ⅰ)中的\(\bar{x}\)和\(s^2\)代替,白玫瑰的日销量\(Y\)服从正态分布\(N(280 ,40^2)\),又已知红玫瑰的售价为\(2\)元/枝,白玫瑰的售价为\(4\)元/枝,预计今年哪种玫瑰的日销售额超过\(1280\)元的天数更多.
5(★★★)2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了\(200\)名学生每周阅读时间\(X\)(单位:小时)并绘制如图所示的频率分布直方图.
(1)求这\(200\)名学生每周阅读时间的样本平均数\(\bar{x}\)和样本方差\(s^2\)(同一组中的数据用该组区间的中间值代表);
(2)由直方图可以认为,目前该校学生每周的阅读时间\(X\)服从正态分布\(N(μ ,σ^2)\),其中\(μ\)近似为样本平均数\(\bar{x}\),\(σ^2\)近似为样本方差\(s^2\).
(i)一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若\(X~N(μ ,σ^2)\),令\(Y=\dfrac{X-\mu}{\sigma}\),则\(Y~N(0 ,1)\),且\(P(X \leq a)=P\left(Y \leq \dfrac{a-\mu}{\sigma}\right)\).
利用直方图得到的正态分布,求\(P(X≤10)\).
(ii)从该高校的学生中随机抽取\(20\)名,记Z表示这\(20\)名学生中每周阅读时间超过\(10\)小时的人数,求\(P(Z≥2)\)(结果精确到\(0.0001\))以及Z的数学期望.
参考数据:\(\sqrt{178} \approx \dfrac{40}{3}\) ,\(0.7734^{19} \approx 0.0076\).若\(Y~N(0 ,1)\),则\(P(Y≤0.75)=0.7734\).

6(★★★)新型冠状病毒最近在全国蔓延,具有很强的人与人之间的传染性,该病毒在进入人体后一般有14天的潜伏期,在这14天的潜伏期内患者无任何症状,为病毒传播的最佳时间.假设每位病毒携带者在潜伏期内每天有\(n\)位密切接触者,接触病毒携带者后被感染的概率为\(p\),每位密切接触者不用再接触其他病毒携带者.
(1)求一位病毒携带者一天内感染的人数\(X\)的均值;
(2)若\(n=3\),\(p=\dfrac{1}{3}\)时,从被感染的第一天算起,试计算某一位病毒携带者在14天潜伏期内,被他平均累计感染的人数(用数字作答);
(3)3月16日20时18分,由我国军事科学院军事科学研究院陈薇院士领衔的科学团队,研制重组新型冠状病毒疫苗获批进入临床状态,新疫苗的使用,可以极大减少感染新型冠状病毒的人数,为保证安全性和有效性,某科研团队抽取\(500\)支新冠疫苗,观测其中某项质量指标值,得到如图频率分布直方图:

①求这\(500\)支该项质量指标值得样本平均值\(\bar{x}\)(同一组的数据用该组区代表间的中点值);
②由直方图可以认为,新冠疫苗的该项质量指标值Z服从正态分布\(N(μ ,σ^2)\),其中\(μ\)近似为样本平均数\(\bar{x}\),\(σ^2\)近似为样本方差\(s^2\),经计算可得这\(500\)支新冠疫苗该项指标值的样本方差\(s^2=150\).现有\(5\)名志愿者参与临床试验,观测得出该项指标值分别为:\(206,178,195,160,229\)试问新冠疫苗的该项指标值是否正常,为什么?
参考数据:\(\sqrt{150}=12.2\),若\(Z~N(μ ,σ^2)\),则\(P(μ-σ<Z<μ+σ)=0.6827\),\(P(μ-2σ<Z<μ+2σ)=0.9545\),\(P(μ-3σ<Z<μ+3σ)=0.9973\).
7(★★★★)2019年7月1日至3日,世界新能源汽车大会在海南博鳖召开,以“新时代、新变革、新产业”为主题,突出电动化、智能化、共享化融合发展特色.某汽车公司顺应时代潮流,新研发了一款新能源汽车,并在出厂前对100辆汽车进行了单次最大续航里程(理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程)的测试.现对测试数据进行分析,得到如图所示的频率分布直方图.
(1)估计这\(100\)辆汽车的单次最大续航里程的平均值\(x\)(同一组中的数据用该组区间的中点值代表);
(2)根据大量的汽车测试数据,可以认为这款汽车的单次最大续航里程\(X\)近似地服从正态分布\(N(μ ,σ^2)\),用样本平均数\(x\)作为\(μ\)的近似值,用样本标准差\(s\)作为\(σ\)的估计值,经计算样本标准差\(s\)的近似值为\(50\),现任取一辆汽车,求它的单次最大续航里程恰在\(250\)千米到\(400\)千米之间的概率.
参考数据:若随机变量\(ξ\)服从正态分布\(N(μ ,σ^2)\),则\(P(μ-σ<ξ≤μ+σ)≈0.6827\),
\(P(μ-2σ<ξ≤μ+2σ)≈0.9545\),\(P(μ-3σ<ξ≤μ+3σ)≈0.9973\).
(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在方格图上行进,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.已知硬币出现正反面的概率都是\(\dfrac{1}{2}\),方格图上标有第0格、第1格、第2格、…、第50格.遥控车开始在第0格,客户每掷一次硬币,遥控车向前移动一次,若掷出正面,遥控车向前移动一格(从\(k\)到\(k+1\)),若掷出反面,遥控车向前移动两格(从\(k\)到\(k+2\)),直到遥控车移到第\(49\)格(胜利大本营)或第\(50\)格(失败大本营)时,游戏结束.设遥控车移到第\(n\)格的概率为\(P_n\),试说明\(\left\{P_{n}-P_{n-1}\right\}\)是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车.

参考答案
- 【答案】\(ACD\)
【解析】由图象可知甲图象关于直线\(x=75\)对称,乙图象关于直线\(x=85\)对称,
\(\therefore \mu_{1}=75, \mu_{2}=85\),
故\(A\)正确,\(B\)错误,
\(∵\)甲图象比乙图象更“高瘦”,
\(∴\)甲的成绩比乙的成绩更集中于平均值左右,故\(C\)正确;
若\(\sigma_{1}=5\),则甲同学成绩高于\(80\)分的概率约为:\(\dfrac{1-0.6826}{2}=0.1587\),故\(D\)正确.
故选:\(ACD\). - 【答案】\(C\)
【解析】①女性处理多任务平均用时集中在\(2-3\)分钟,男性的集中在\(3-4.5\)分钟,即①正确;
②从图中可以看到男性与女性处理任务所需的时间有交叉,所以并不是“所有女性都优于男性”,即②错误;
③根据正态分布的性质可知③正确;
④女性和男性处理多任务的用时均为正数,即④错误.
故选:\(C\). - 【答案】\(D\)
【解析】\(∵X\)服从正态分布\(N\left(10, \sigma^{2}\right)\),且\(P(X<9)=\dfrac{1}{8}\),
\(\therefore P(9<X<11)=\dfrac{3}{4} \text {, }\),即每个零件合格的概率为\(\dfrac{3}{4}\).
合格零件不少于\(2\)件的对立事件是合格零件个数为零个或一个.
合格零件个数为零个或一个的概率为\(C_{n}^{0} \cdot\left(\dfrac{1}{4}\right)^{n}+C_{n}^{1} \cdot \dfrac{3}{4} \cdot\left(\dfrac{1}{4}\right)^{n-1}\),
由\(C_{n}^{0} \cdot\left(\dfrac{1}{4}\right)^{n}+C_{n}^{1} \cdot \dfrac{3}{4} \cdot\left(\dfrac{1}{4}\right)^{n-1}<0.1\),
得\((3 n+1) \cdot\left(\dfrac{1}{4}\right)^{n}<0.1\),
令\(f(n)=(3 n+1) \cdot\left(\dfrac{1}{4}\right)^{n}\left(n \in \mathbf{N}^{*}\right)\),
\(\because \dfrac{f(n+1)}{f(n)}=\dfrac{3 n+4}{12 n+4}<1\),\(∴f(n)\)单调递减,
又\(f(4)<0.1\),\(f(3)>0.1\),
\(∴\)不等式\((3 n+1) \cdot\left(\dfrac{1}{4}\right)^{n}<0.1\)的解集为\(\{n \mid n \geq 4\}\).
\(∴n\)的最小值为\(4\).
故选:\(D\). - 【答案】\((1)400\) \((2)\)预计今年白玫瑰的日销售额超过\(1280\)元的天数更多
【解析】(Ⅰ)由条件可知,
\(\bar{x}=\dfrac{1}{10}(615+575+625+590+600+600+570+615+580+630)=600\),
\(s^{2}=\dfrac{1}{10}\left(15^{2}+25^{2}+25^{2}+10^{2}+0+0+30^{2}+15^{2}+20^{2}+30^{2}\right)=400\);
(Ⅱ)由(Ⅰ)可知\(X \sim N\left(600,20^{2}\right)\).
若红玫瑰的日销售额超过\(1280\)元,则需\(X>640=600+2×20\).
若白玫瑰的日销售额超过\(1280\)元,则需\(Y>320=280+1×40\).
根据正态分布的特征可知\(P(X>640)<P(Y>320)\),
即白玫瑰的日销售额超过\(1280\)元的概率更大,故预计今年白玫瑰的日销售额超过\(1280\)元的天数更多. - 【答案】\((1)1.78 \quad (2)(i)0.7734 \quad (ii)4.532\)
【解析】(1)\(\bar{x}=6 \times 0.03+7 \times 0.1+8 \times 0.2+9 \times 0.35\)\(+10 \times 0.19+11 \times 0.09+12 \times 0.04=9\),
\(s^{2}=(6-9)^{2} \times 0.03+(7-9)^{2} \times 0.1+(8-9)^{2} \times 0.2+(9-9)^{2} \times 0.35+\)\((10-9)^{2} \times 0.19+(11-9)^{2} \times 0.09+(12-9)^{2} \times 0.04=1.78\);
(2)(i)由题知\(μ=9\),\(\sigma^{2}=1.78\),\(∴X~N(9,1.78)\),\(\sigma=\sqrt{1.78}=\dfrac{\sqrt{178}}{10} \approx \dfrac{4}{3}\).
\(\therefore P(X \leq 10)=P\left(Y \leq \dfrac{10-9}{\frac{4}{3}}\right)=P(Y \leq 0.75)=0.7734\);
(ⅱ)由(i)知\(P(X>10)=1-P(X≤10)=0.2266\),
可得\(Z \sim B(20,0.2266)\),
\(P(Z≥2)=1-P(Z=0)-P(Z=1)\)
\(=1-0.7734^{20}-C_{20}^{1} \times 0.2266 \times 0.7734^{19}\)
\(=1-(0.7734+20 \times 0.2266) \times 0.0076\)
\(≈0.9597\).
\(∴Z\)的数学期望\(E(Z)=20×0.2266=4.532\). - 【答案】\((1)np\) \(\text { (2) } 8192\) \((3)\)① \(200\) ② 新冠肺炎的该项指标值不正常
【解析】(1)依题意可知\(X~B(n,p)\),则\(E(X)=np\),
故一天内被感染人数\(X\)的均值为\(np\);
(2)不妨记前\(m\)天平均累计感染的人数为\(am\),
则\(a_{1}=1, a_{2}=1+n p, a_{3}=(1+n p)^{2}, \ldots, a_{m}=(1+n p)^{m-1}\).
当\(n=3\),\(p=\dfrac{1}{3}\)时,一位病毒携带者在14天潜伏期内,被他平均累计感染的人数为:\(a_{14}=\left(1+3 \times \dfrac{1}{3}\right)^{13}=2^{13}=8192\);
(3)①由频率分布直方图得,这\(500\)支该项指标值的样本平均值为:\(\bar{x}=170 \times 0.02+180 \times 0.09+190 \times 0.22+\)\(200 \times 0.33+210 \times 0.24+220 \times 0.08+230 \times 0.02=200\);
②新冠肺炎该项指标值不正常,理由如下:
由题意知\(Z~N(200,150)\),\(P(μ-3σ<Z<μ+3σ)=P(163.4<Z<236.6)=0.9973\),
即该项指标落在\((163.4,236.6)\)之外的概率为\(0.0027\),是小概率事件.
而\(160∉(163.4,236.6)\),根据\(3σ\)原则,新冠肺炎的该项指标值不正常. - 【答案】\((1)300\) \((2)0.8186\) \((3)\)见解析
【解析】(1)\(\bar{x}=0.002 \times 50 \times 205+0.004 \times 50 \times 255+0.009 \times 50 \times 305\)\(+0.004 \times 50 \times 355+0.001 \times 50 \times 405=300\)(千米).
(2)由\(X~N(300,50^2)\).
\(\therefore P(250<X \leq 400)=0.9545-\dfrac{0.9545-0.6827}{2}=0.8186\).
(3)遥控车开始在第\(0\)格为必然事件,\(P_0=1\).第一次掷硬币出现正面,遥控车移到第一格,其概率为\(\dfrac{1}{2}\),即\(P_{1}=\dfrac{1}{2}\).
遥控车移到第\(n(2≤n≤49)\)格的情况是下面两种,而且只有两种:
①遥控车先到第\(n-2\)格,又掷出反面,其概率为\(\dfrac{1}{2} P_{n-2}\).
②遥控车先到第\(n-1\)格,又掷出正面,其概率为\(\dfrac{1}{2} P_{n-1}\).
\(\therefore P_{n}=\dfrac{1}{2} P_{n-2}+\dfrac{1}{2} P_{n-1}\).
\(\therefore P_{n}-P_{n-1}=-\dfrac{1}{2}\left(P_{n-1}-P_{n-2}\right)\).
\(∴1≤n≤49\)时,数列\(\left\{P_{n}-P_{n-1}\right\}\)是等比数列,首项为\(P_{1}-P_{0}=-\dfrac{1}{2}\),公比为\(-\dfrac{1}{2}\)的等比数列.
\(\therefore P_{1}-1=-\dfrac{1}{2}, P_{2}-P_{1}=\left(-\dfrac{1}{2}\right)^{2}, P_{3}-P_{2}=\left(-\dfrac{1}{2}\right)^{3}, \ldots \ldots, P_{n}-P_{n-1}=\left(-\dfrac{1}{2}\right)^{n}\).
\(\therefore P_{n}=\left(P_{n}-P_{n-1}\right)+\left(P_{n-1}-P_{n-2}\right)+\cdots \ldots+\left(P_{1}-P_{0}\right)+P_{0}\)
\(=\left(-\dfrac{1}{2}\right)^{n}+\left(-\dfrac{1}{2}\right)^{n-1}+\cdots \cdots-\dfrac{1}{2}+1\)
\(=\dfrac{1-\left(-\dfrac{1}{2}\right)^{n+1}}{1-\left(-\dfrac{1}{2}\right)}=\dfrac{2}{3}\left[1-\left(-\dfrac{1}{2}\right)^{n+1}\right]\),\((n=0,1,……,49)\).
\(∴\)遥控车停在“胜利大本营”的概率\(P_{49}=\dfrac{2}{3}\left[1-\left(-\dfrac{1}{2}\right)^{50}\right]\),
遥控车停在“失败大本营”的概率\(P_{50}=\dfrac{1}{2} P_{48}=\dfrac{1}{2} \times \dfrac{2}{3}\left[1-\left(-\dfrac{1}{2}\right)^{49}\right]=\dfrac{1}{3}\left[1+\left(\dfrac{1}{2}\right)^{49}\right]\).
\(\therefore P_{49}-P_{50}=\dfrac{2}{3}\left[1-\left(-\dfrac{1}{2}\right)^{50}\right]-\dfrac{1}{3}\left[1+\left(\dfrac{1}{2}\right)^{49}\right]=\dfrac{1}{3}\left[1-\left(\dfrac{1}{2}\right)^{48}\right]>0\).
\(∴\)遥控车停在“胜利大本营”的概率大.
\(∴\)此方案能成功吸引顾客购买该款新能源汽车.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号