7.1 条件概率与全概率公式
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第三册同步提高,难度3颗星!
模块导图
知识剖析
条件概率
①定义
一般地,设\(A ,B\)为两个事件,且\(P(A)>0\) ,称\(P(B \mid A)=\dfrac{P(A B)}{P(A)}\)为在事件\(A\)发生的条件下,事件\(B\)发生的条件概率.
\({\color{Red}{解释}}\)
(1) 求“事件\(A\)已发生,事件\(B\)发生的概率”,可理解:如图,事件\(A\)已发生,则\(A\)为样本空间,此时事件\(B\)发生的概率是\(AB\)包含的样本点数与\(A\)包含的样本点数的比值,即
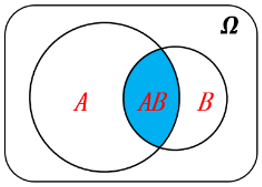
(通俗些理解,条件概率只是缩小了样本空间,\(P(B \mid A)\)就是以\(A\)为样本空间计算\(AB\)的概率)
\({\color{Red}{ Eg }}\) 某地\(7\)月份吹南风(事件\(A\))的概率是\(\dfrac{1}{3}\),下雨(事件\(B\))的概率是\(\dfrac{1}{4}\),即吹南风又下雨的概率是\(\dfrac{1}{5}\),那在吹南风的条件下下雨的概率是\(P(B \mid A)=\dfrac{P(A B)}{P(A)}=\dfrac{\frac{1}{5}}{\frac{1}{4}}=\dfrac{4}{5}\), 在下雨的条件下吹南风的的概率是\(P(A \mid B)=\dfrac{P(A B)}{P(B)}\).
(2) 当\(P(A)>0\)时,当且仅当事件\(A\)与\(B\)相互独立时,有\(P(B \mid A)=P(B)\);
②概率的乘法公式
对任意两个事件\(A\)与\(B\),若\(P(A)>0\),则\(P(A B)=P(A) P(B \mid A)\)
设\(P(A)>0\),则
(1) \(P(\Omega \mid A)=1\);
(2) 如果\(B\)和\(C\)互斥,那么\(P[(B \cup C) \mid A]=P(B \mid A)+P(C \mid A)\);
(3) 设\(\bar{B}\)和\(B\)互为对立事件,则\(P(\bar{B} \mid A)=1-P(B \mid A)\).
全概率公式
一般地,设\(A_{1}, A_{2}, \ldots, A_{n}\)是一组两两互斥的事件,\(A_{1} \cup A_{2} \cup \ldots \cup A_{n}=\Omega\),且\(P\left(A_{i}\right)>0\),\(i=1 ,2 ,… ,n\),则对任意的事件\(B \subseteq \Omega\),有
我们称它为全概率公式.
贝叶斯公式
设\(A_{1}, A_{2}, \ldots, A_{n}\)是一组两两互斥的事件,\(A_{1} \cup A_{2} \cup \ldots \cup A_{n}=\Omega\),且\(P\left(A_{i}\right)>0\),\(i=1 ,2 ,… ,n\),则对任意的事件\(B \subseteq \Omega\),\(P(B)>0\),有
经典例题
【题型一】求条件概率
【典题1】某校从学生文艺部\(6\)名成员(\(4\)男\(2\)女)中,挑选\(2\)人参加学校举办的文艺汇演活动.
(1)求男生甲被选中的概率;
(2)在已知男生甲被选中的条件下,女生乙被选中的概率;
(3)在要求被选中的两人中必须一男一女的条件下,求女生乙被选中的概率.
【解析】(1)从\(6\)名成员中挑选\(2\)名成员,共有\(C_{6}^{2}=15\)种情况,
记“男生甲被选中”为事件,事件所包含的基本事件数为\(5\)种,故\(P(A)=\dfrac{1}{3}\).
(2)记“男生甲被选中”为事件\(A\),“女生乙被选中”为事件\(B\),
则\(P(A B)=\dfrac{1}{15}\),
由(1)知\(P(A)=\dfrac{1}{3}\),故\(P(B \mid A)=\dfrac{P(A B)}{P(A)}=\dfrac{1}{5}\).
(3)记“挑选的\(2\)人一男一女”为事件\(C\),则\(P(C)=\dfrac{C_{4}^{1} C_{2}^{1}}{C_{6}^{2}}=\dfrac{8}{15}\),
“女生乙被选中”为事件\(B\),\(P(B C)=\dfrac{C_{4}^{1}}{C_{6}^{2}}=\dfrac{4}{15}\),故\(P(B \mid C)=\dfrac{P(B C)}{P(C)}=\dfrac{1}{2}\).
【点拨】 ①第一问是古典概型;②第二问是条件概率\(P(B \mid A)=\dfrac{P(A B)}{P(A)}\).
【典题2】已知箱中共有\(6\)个球,其中红球、黄球、蓝球各\(2\)个.每次从该箱中取\(1\)个球 (有放回,每球取到的机会均等),共取三次.设事件\(A\):“第一次取到的球和第二次取到的球颜色相同”,事件\(B\):“三次取到的球颜色都相同”,则\(P(B \mid A)=\)( )
A. \(\dfrac{1}{6}\) \(\qquad \qquad \qquad \qquad\)B. \(\dfrac{1}{3}\) \(\qquad \qquad \qquad \qquad\)C. \(\dfrac{2}{3}\) \(\qquad \qquad \qquad \qquad\)D. \(1\)
【解析】\({\color{Red}{方法一 }}\)
由题意\(P(A B)=\dfrac{3 C_{2}^{1} \cdot C_{2}^{1} \cdot C_{2}^{1}}{C_{6}^{1} \cdot C_{6}^{1} \cdot C_{6}^{1}}=\dfrac{1}{9}\),\(P(A)=\dfrac{3\left(C_{2}^{1} \cdot C_{2}^{1} \cdot C_{4}^{1}+C_{2}^{1} \cdot C_{2}^{1} \cdot C_{2}^{1}\right)}{C_{6}^{1} \cdot C_{6}^{1} \cdot C_{6}^{1}}=\dfrac{1}{3}\),
则\(P(B \mid A)=\dfrac{P(A B)}{P(A)}=\dfrac{1}{3}\),故选\(B\).
\({\color{Red}{方法二 }}\)
\(P(B \mid A)=\dfrac{n(A B)}{n(A)}=\dfrac{3 C_{2}^{1} C_{2}^{1} C_{2}^{1}}{3\left(C_{2}^{1} C_{2}^{1} C_{2}^{1}+C_{2}^{1} C_{2}^{1} C_{4}^{1}\right)}=\dfrac{1}{3}\)
\({\color{Red}{ (事件分为①第一,二次摸球同色,与第三次球不同色,②三次颜色一样) }}\)
【点拨】求条件概率,可以使用\(\left.P(B \mid A)=\dfrac{n(A B)}{n(A)}\right)\)或\(P(B \mid A)=\dfrac{P(A B)}{P(A)}\),一般情况下用\(P(B \mid A)=\dfrac{n(A B)}{n(A)}\)更简单.
巩固练习
1(★) [多选题]下列说法有可能成立的是( )
A. \(P(B \mid A)<P(A B)\) \(\qquad \qquad \qquad \qquad\) B. \(P(B)=P(A) P(B \mid A)\)
C. \(P(A B)=P(A) \cdot P(B)\) \(\qquad \qquad \qquad \qquad\)D. \(P(A \mid B)=P(B \mid A)\)
2(★) 某种疾病的患病率为\(0.5 \%\),已知在患该种疾病的条件下血检呈阳性的概率为\(99 \%\),则患该种疾病且血检呈阳性的概率为( )
A. \(0.495 \%\) \(\qquad \qquad \qquad \qquad\) B. \(0.9405 \%\) \(\qquad \qquad \qquad \qquad\) C. \(0.9995 \%\) \(\qquad \qquad \qquad \qquad\) D. \(0.99 \%\)
3(★)将四颗骰子各掷一次,记事件\(A=\)“四个点数互不相同”,\(B=\)“至少出现一个\(5\)点”,则概率\(P(B \mid A)\)等于( )
A. \(\dfrac{2}{3}\) \(\qquad \qquad \qquad \qquad\) B. \(\dfrac{1}{6}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{60}{671}\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{240}{671}\)
4(★★) 袋中有\(10\)个大小、材质都相同的小球,其中红球\(3\)个,白球\(7\)个.每次从袋中随机摸出\(1\)个球,摸出的球不再放回.求:
(1)第一次摸到红球的概率;
(2)在第一次摸到红球的条件下,第二次也摸到红球的概率;
(3)第二次摸到红球的概率.
参考答案
-
【答案】\(BCD\)
【解析】根据题意,依次分析选项:
对于__\(A\),\(P(B \mid A)=\dfrac{P(A B)}{P(A)}\),变形可得\(P(A B)=P(B \mid A) P(A)\),
而\(P(A)≤1\),则\(P(B|A)≥P(AB)\),\(A\)错误,
对于\(B\),\(P(B \mid A)=\dfrac{P(A B)}{P(A)}\),变形可得\(P(AB)=P(B|A)P(A)\),
当\(P(A)=1\)时,有\(P(B)=P(A)P(B|A)\),\(B\)正确,
对于\(C\),当\(A、B\)是相互独立事件时,\(P(AB)=P(A)\cdot P(B)\),\(C\)正确,
对于\(D\),当\(A、B\)是互斥事件时,\(P(A|B)=P(B|A)=0\),\(D\)正确,
故选:\(BCD\). -
【答案】\(A\)
【解析】设事件\(A\)表示“患某种疾病”,设事件\(B\)表示“血检呈阳性”,
则\(P(A)=0.5 \%\),\(P(B \mid A)=99 \%\),
\(∴\)患该种疾病且血检呈阳性的概率为:\(P(A B)=0.5 \% \times 99 \%=0.495 \%\).
故选:\(A\). -
【答案】\(A\)
【解析】根据题意,记事件\(A=\)“四个点数互不相同”,\(B=\)“至少出现一个\(5\)点”,
则\(P(A B)=\dfrac{4 \cdot A_{5}^{3}}{6 \times 6 \times 6 \times 6}\),\(P(A)=\dfrac{A_{6}^{4}}{6 \times 6 \times 6 \times 6}\),
则\(P(B \mid A)=\dfrac{P(A B)}{P(A)}=\dfrac{4 \times A_{5}^{3}}{A_{6}^{4}}=\dfrac{2}{3}\),
故选:\(A\). -
【答案】\((1) \dfrac{3}{10} \qquad (2) \dfrac{2}{9}\qquad (3) \dfrac{3}{10}\)
【解析】根据题意,设事件\(A\):第一次摸到红球;事件\(B\):第二次摸到红球,
则事件\(\bar{A}\):第一次摸到白球.
(Ⅰ)袋中有\(10\)个球,第一次从\(10\)个球中摸一个共\(10\)种不同的结果,其中是红球的结果共\(3\)种,所以\(P(A)=\dfrac{3}{10}\),
(Ⅱ)由(Ⅰ)的结论,\(P(A)=\dfrac{3}{10}\),前两次都摸到红球的概率\(P(A B)=\dfrac{3}{10} \times \dfrac{2}{9}=\dfrac{1}{15}\),
则\(P(B \mid A)=\dfrac{P(A B)}{p(A)}=\dfrac{2}{9}\);
(Ⅲ) \(P(A)=\dfrac{3}{10}\),则\(P(\bar{A})=1-P(A)=\dfrac{7}{10}\),\(P(\bar{A} B)=\dfrac{7}{10} \times \dfrac{3}{9}=\dfrac{7}{30}\),
则\(P(B)=P(A B)+P(\bar{A} B)=\dfrac{1}{15}+\dfrac{7}{30}=\dfrac{3}{10}\);
所以第二次摸到红球的概率\(P(B)=\dfrac{3}{10}\).
【题型二】全概率公式、贝叶斯公式的运用
【典题1】(1) 在\(12\)件产品中有\(4\)件次品,在先取\(1\)件的情况下,求任取\(2\)件产品皆为正品的概率.
(2) 在\(12\)件产品中有\(4\)件次品,在先取\(1\)件的情况下,任取\(2\)件产品皆为正品,求先取\(1\)件为次品的概率.
【解析】令\(A=\{\)先取的\(1\)件是次品\(\}\),\(P(A)=\dfrac{1}{3}\),\(P(\bar{A})=\dfrac{2}{3}\)
令\(B=\{\)后取的\(2\)件皆为正品\(\}\),则\(P(B \mid A)=\dfrac{C_{8}^{2}}{C_{11}^{2}}=\dfrac{28}{55}\),\(P(B \mid \bar{A})=\dfrac{C_{7}^{2}}{C_{11}^{2}}=\dfrac{21}{55}\)
(1) 由全概率公式得\(P(B)=P(A) P(B \mid A)+P(\bar{A}) P(B \mid \bar{A})=\dfrac{1}{3} \times \dfrac{28}{55}+\dfrac{2}{3} \times \dfrac{21}{55}=\dfrac{14}{33}\)
(2) 由贝叶斯公式得\(P(A \mid B)=\dfrac{P(A B)}{P(B)}=\dfrac{P(A) P(B \mid A)}{P(A) P(B \mid A)+P(\bar{A}) P(B \mid \bar{A})}=\dfrac{\dfrac{1}{3} \times \dfrac{28}{55}}{\dfrac{1}{3} \times \dfrac{28}{55}+\dfrac{2}{3} \times \dfrac{21}{55}}=\dfrac{2}{5}\)
【点拨】
①若随机试验可以看成分两个阶段进行,且第一阶段的各试验结果具体结果未知,那么:
(1) 如果要求的是第二阶段某一个结果发生的概率,则用全概率公式;
(2) 如果第二个阶段的某一个结果是已知的,要求的是此结果为第一阶段某一个结果所引起的概率,一般用贝叶斯公式,类似于求条件概率.
熟记这个特征,在遇到相关的题目时,可以准确地选择方法进行计算,保证解题的正确高效.
②本试验视为分成两个阶段,第一阶段是“先取\(1\)件”,结果未知;第二阶段是“在剩下的\(11\)件中再取\(2\)件”,结果已知:都是正品.
求“任取\(2\)件产品皆为正品的概率”,用全概率公式;
求第一阶段中“先取\(1\)件为次品的概率”,用贝叶斯公式.
【典题2】用一门大炮对某目标进行三次独立射击, 第一、二、三次的命中率分别为\(0.4\)、\(0.5\)、\(0.7\), 若命中此目标一、二、三弹, 该目标被摧毁的概率分别为\(0.2\)、\(0.6\)和\(0.8\), 试求此目标被摧毁的概率.
【解析】设事件\(A_{i}=\{\)第\(i\)次命中目标\(\}\),事件\(B_{i}=\{\)目标被命中\(i\)弹\(\}(i=1,2,3)\),事件\(C=\{\)目标被摧毁\(\}\),
依题意得\(P\left(A_{1}\right)=0.4\),\(P\left(A_{2}\right)=0.5\),\(P\left(A_{2}\right)=0.7\)
由于三次射击时相互独立的,所以
\(P\left(B_{0}\right)=P\left(\overline{A_{1}} \overline{A_{2}} \overline{A_{3}}\right)=P\left(\overline{A_{1}}\right) P\left(\overline{A_{2}}\right) P\left(\overline{A_{3}}\right)=0.09\),
\(P\left(B_{1}\right)=P\left(\overline{A_{1}} \overline{A_{2}} A_{3}+\overline{A_{1}} A_{2} \overline{A_{3}}+A_{1} \overline{A_{2}} \overline{A_{3}}\right)=\)\(P\left(\overline{A_{1}} \overline{A_{2}} A_{3}\right)+P\left(\overline{A_{1}} A_{2} \overline{A_{3}}\right)+P\left(A_{1} \overline{A_{2}} \overline{A_{3}}\right)=0.36\),
\(P\left(B_{2}\right)=P\left(\overline{A_{1}} A_{2} A_{3}+A_{1} \overline{A_{2}} A_{3}+A_{1} A_{2} \overline{A_{3}}\right)=\)\(P\left(\overline{A_{1}} A_{2} A_{3}\right)+P\left(A_{1} \overline{A_{2}} A_{3}\right)+P\left(A_{1} A_{2} \overline{A_{3}}\right)=0.41\),
\(P\left(B_{3}\right)=P\left(A_{1} A_{2} A_{3}\right)=P\left(A_{1}\right) P\left(A_{2}\right) P\left(A_{2}\right)=0.14\)
由全概率公式可得
\(P(C)=P\left(B_{0}\right) P\left(C \mid B_{0}\right)+P\left(B_{1}\right) P\left(C \mid B_{1}\right)+P\left(B_{2}\right) P\left(C \mid B_{2}\right)+P\left(B_{3}\right) P\left(C \mid B_{3}\right)=0.43\)
【典题3】近年来,我国外卖业发展迅猛,外卖小哥穿梭在城市的大街小巷成为一道道亮丽的风景线.他们根据外卖平台提供的信息到外卖店取单.某外卖小哥每天来往于\(r\)个外卖店(外卖店的编号分别为\(1,2, \ldots \ldots, r\),其中\(r \geq 3\),约定:每天他首先从\(1\)号外卖店取单,叫做第\(1\)次取单,之后,他等可能的前往其余\(r-1\)个外卖店中的任何一个店取单叫做第\(2\)次取单,依此类推.假设从第\(2\)次取单开始,他每次都是从上次取单的店之外的\(r-1\)个外卖店取单.设事件\(A_{k}=\{\)第次取单恰好是从\(1\)号店取单\(\}\),\(P\left(A_{k}\right)\)是事件\(A_{k}\)发生的概率,显然\(P\left(A_{1}\right)=1\),\(P\left(A_{2}\right)=0\),则\(P\left(A_{3}\right)=\),\(P\left(A_{k+1}\right)\)与\(P\left(A_{k}\right)\)的关系式为\(\underline{\quad \quad}\) .
【解析】由于约定外卖小哥“首先从\(1\)号外卖店取单”,所以肯定有\(P\left(A_{1}\right)=1\),
根据“游戏规则”,第二次取单肯定不会\(1\)号店了,故\(P\left(A_{2}\right)=0\);
第二次是\(1\)号外的一家店取单,那第三次在剩下\(r-1\)的家店中随机得到\(1\)号店取单的概率当然是\(\dfrac{1}{r-1}\),即\(P\left(A_{3}\right)=\dfrac{1}{r-1}\);
第\(k+1\)次是否“从\(1\)号店取单”,取决于第\(k\)次的情况,
\(\begin{aligned}
P\left(A_{k+1}\right) &=P\left(\bar{A}_{k}\right) P\left(A_{k+1} \mid \bar{A}_{k}\right)+P\left(A_{k}\right) P\left(A_{k+1} \mid A_{k}\right) \\
&=\left[1-P\left(A_{k}\right)\right] \dfrac{1}{r-1}+P\left(A_{k}\right) \cdot 0 \\
&=\left[1-P\left(A_{k}\right)\right] \dfrac{1}{r-1}
\end{aligned}\)
\({\color{Red}{(P\left(A_{k+1} \mid \bar{A}_{k}\right)=\dfrac{1}{r-1}--在第k次不是从1号店取单条件下第k+1次从1号店取单的概率为\dfrac{1}{r-1},}}\)
\({\color{Red}{ P\left(A_{k+1} \mid A_{k}\right)=0--第k次从1号店取单下第k+1次从1号店取单的概率当然为0) }}\)
故答案为:\(\dfrac{1}{r-1}\);\(P\left(A_{k+1}\right)=\left[1-P\left(A_{k}\right)\right] \dfrac{1}{r-1}\).
巩固练习
1(★★)从\(1 , 2 , 3 ,… , 15\)中,甲、乙两人各任取一数(不重复),已知甲取到的数是\(5\)的倍数,求甲数大于乙数的概率\(\underline{\quad \quad}\).
2(★★)从数字\(1 ,2 ,3 ,4\)中任取一个数,记为\(x\),再从\(1 ,… ,x\)中任取一个数,记为\(y\),则 \(P(y=2)=\) \(\underline{\quad \quad}\) .
3(★★)盒中有\(a\)个红球,\(b\)个黑球,今随机地从中取出一个,观察其颜色后放回,并加上同色球\(c\)个,再从盒中第二次抽取一球,第二次抽出的是黑球的概率为\(\underline{\quad \quad}\) .
4(★★)设某公路上经过的货车与客车的数量之比为\(2:1\),货车中途停车修理的概率为\(0.02\),客车为\(0.01\),今有一辆汽车中途停车修理,该汽车是货车的概率为\(\underline{\quad \quad}\) .
5(★★)有三个同样的箱子,甲箱中有\(2\)只红球,\(6\)只白球,乙箱中有\(6\)只红球,\(4\)只白球,丙箱中有\(3\)只红球,\(5\)只白球.
(1)随机从甲、乙、丙三个箱子中各取一球,求三球都为红球的概率;
(2)从甲,乙、丙中随机取一箱,再从该箱中任取一球,求该球为红球的概率.
6(★★★)袋中装有\(8\)只红球 , \(2\)只黑球,每次从中任取一球, 不放回地连续取两次, 求下列事件的概率.
(1)取出的两只球都是红球;
(2)取出的两只球都是黑球;
(3)取出的两只球一只是红球,一只是黑球;
(4)第二次取出的是红球.
参考答案
-
【答案】\(\dfrac{9}{14}\)
【解析】设事件\(A=\{\)甲取到的数比乙的大\(\}\),\(B=\{\)甲取到的数是\(5\)的倍数\(\}\),
则显然所要求的概率为\(P(A \mid B)\)
\(P(B)=\dfrac{3}{15}=\dfrac{1}{5}\),\(P(A B)=\dfrac{C_{4}^{1}+C_{9}^{1}+C_{14}^{1}}{C_{14}^{1} C_{15}^{1}}=\dfrac{9}{70}\),
\(\therefore P(A \mid B)=\dfrac{P(A B)}{P(B)}=\dfrac{9}{14}\). -
【答案】\(\dfrac{13}{48}\)
【解析】由离散型随机变量的概率分布有
\(P(x=1)=P(x=2)=P(x=3)=P(x=4)=\dfrac{1}{4}\)
由题意得\(P(y=2 \mid x=1)=0\),\(P(y=2 \mid x=2)=\dfrac{1}{2}\),\(P(y=2 \mid x=3)=\dfrac{1}{3}\),\(P(y=2 \mid x=4)=\dfrac{1}{4}\),
则根据全概率公式得到
\(P(y=2)=P(x=1) P(y=2 \mid x=1)+P(x=2) P(y=2 \mid x=2)+P(x=3) P(y=2 \mid x=3)+\)\(P(x=4) P(y=2 \mid x=4)=\dfrac{1}{4}\left(0+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}\right)=\dfrac{13}{48}\). -
【答案】\(\dfrac{b}{a+b}\)
【解析】设\(A=\{\)第一次抽出的是黑球\(\}\),\(B=\{\)第二次抽出的是黑球\(\}\),
由题意得\(P(A)=\dfrac{b}{a+b}, P(B \mid A)=\dfrac{b+c}{a+b+c}\),\(P(\bar{A})=\dfrac{a}{a+b}, P(B \mid \bar{A})=\dfrac{b}{a+b+c}\),
有分解\(B=A B \cup \bar{A} B\),
由全概率公式得 \(P(B)=P(A) P(B \mid A)+P(\bar{A}) P(B \mid \bar{A})\)\(=\dfrac{b(b+c)}{(a+b)(a+b+c)}+\dfrac{a b}{(a+b)(a+b+c)}=\dfrac{b}{a+b}\). -
【答案】\(0.8\)
【解析】设\(B=\{\)中途停车修理\(\}\),\(A_{1}=\{\)经过的是货车\(\}\),经过的是客车,则\(B=A_{1} B \cup A_{2} B\),由贝叶斯公式有\(P\left(A_{1} \mid B\right)=\dfrac{P\left(A_{1} B\right)}{P(B)}=\dfrac{P\left(A_{1}\right) P\left(B \mid A_{1}\right)}{P\left(A_{1}\right) P\left(B \mid A_{1}\right)+P\left(A_{2}\right) P\left(B \mid A_{2}\right)}\)\(=\dfrac{\dfrac{2}{3} \times 0.02}{\dfrac{2}{3} \times 0.02+\dfrac{1}{3} \times 0.01}=0.8\) -
【答案】\((1) \dfrac{9}{160} \qquad (2) \dfrac{49}{120}\)
【解析】(1)根据题意,记事件\(A_1\):从甲箱中取一球为红球,事件\(A_2\):从乙箱中取一球为红球,事件\(A_3\):从丙箱中取一球为红球,
记事件\(B\):取得的三球都为红球,且事件\(A_1\),\(A_2\),\(A_3\)相互独立,
所以\(P(B)=P\left(A_{1}\right) \cdot P\left(A_{2}\right) \cdot P\left(A_{3}\right)=\dfrac{1}{4} \times \dfrac{3}{5} \times \dfrac{3}{8}=\dfrac{9}{160}\),
所以三球都为红球的概率为\(\dfrac{9}{160}\).
(2)记事件\(C\):该球为红球,事件\(D_1\):取甲箱,事件\(D_2\):取乙箱,事件\(D_3\):取丙箱
因为\(P\left(C \mid D_{1}\right)=\dfrac{1}{4}, P\left(C \mid D_{2}\right)=\dfrac{3}{5}, P\left(C \mid D_{3}\right)=\dfrac{3}{8}\),
所以\(P(C)=P\left(D_{1}\right) \cdot P\left(C \mid D_{1}\right)+P\left(D_{2}\right) \cdot P\left(C \mid D_{2}\right)+P\left(D_{3}\right) \cdot P\left(C \mid D_{3}\right)\)\(=\dfrac{1}{3} \times \dfrac{1}{4}+\dfrac{1}{3} \times \dfrac{3}{5}+\dfrac{1}{3} \times \dfrac{3}{8}=\dfrac{49}{120}\),
所以该球为红球的概率为\(\dfrac{49}{120}\). -
【答案】\((1) \dfrac{28}{45} \quad (2) \dfrac{1}{45} \quad (3) \dfrac{16}{45} \quad (4) \dfrac{4}{5}\)
【解析】设事件\(A_{1}=\{\)第一次取到的红球\(\}\),事件\(A_{2}=\{\)第二次取到的红球\(\}\)
(1) 要求的是\(P\left(A_{1} A_{2}\right)\),根据题意\(P\left(A_{1}\right)=\dfrac{4}{5}\),\(P\left(\overline{A_{1}}\right)=\dfrac{1}{5}\),\(P\left(A_{2} \mid A_{1}\right)=\dfrac{7}{9}\),
\(\therefore P\left(A_{1} A_{2}\right)=P\left(A_{1}\right) P\left(A_{2} \mid A_{1}\right)=\dfrac{4}{5} \times \dfrac{7}{9}=\dfrac{28}{45}\).
(2) 要求的是\(P\left(\overline{A_{1} A_{2}}\right)\),根据题意\(P\left(\overline{A_{1}}\right)=\dfrac{1}{5}\),\(P\left(\overline{A_{2}} \mid \overline{A_{1}}\right)=\dfrac{1}{9}\),
\(\therefore P\left(\overline{A_{1} A_{2}}\right)=P\left(\overline{A_{1}}\right) P\left(\overline{A_{2}} \mid \overline{A_{1}}\right)=\dfrac{1}{45}\).
(3)要求的是取出一只红球一只黑球,它包括两种情况,即求\(P\left(A_{1} \overline{A_{2}}+\overline{A_{1}} A_{2}\right)\),
\(P\left(\overline{A_{2}} \mid A_{1}\right)=\dfrac{2}{9}\),\(P\left(A_{2} \mid \overline{A_{1}}\right)=\dfrac{8}{9}\),
\(\therefore P\left(A_{1} \overline{A_{2}}\right)=P\left(A_{1}\right) P\left(\overline{A_{2}} \mid A_{1}\right)=\dfrac{8}{45}\),\(P\left(\overline{A_{1}} A_{2}\right)=P\left(\overline{A_{1}}\right) P\left(A_{2} \mid \overline{A_{1}}\right)=\dfrac{8}{45}\),
\(\therefore P\left(A_{1} \overline{A_{2}}+\overline{A_{1}} A_{2}\right)=P\left(A_{1} \overline{A_{2}}\right)+P\left(\overline{A_{1}} A_{2}\right)=\dfrac{16}{45}\);
(4)要求第二次取出红球,即求\(P\left(A_{2}\right)\),
\(P\left(A_{2}\right)=P\left(A_{1}\right) P\left(A_{2} \mid A_{1}\right)+P\left(\overline{A_{1}}\right) P\left(A_{2} \mid \overline{A_{1}}\right)=\dfrac{4}{5}\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号