专题 分类讨论含参函数的单调性
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第二册同步提高,难度4颗星!
模块导图
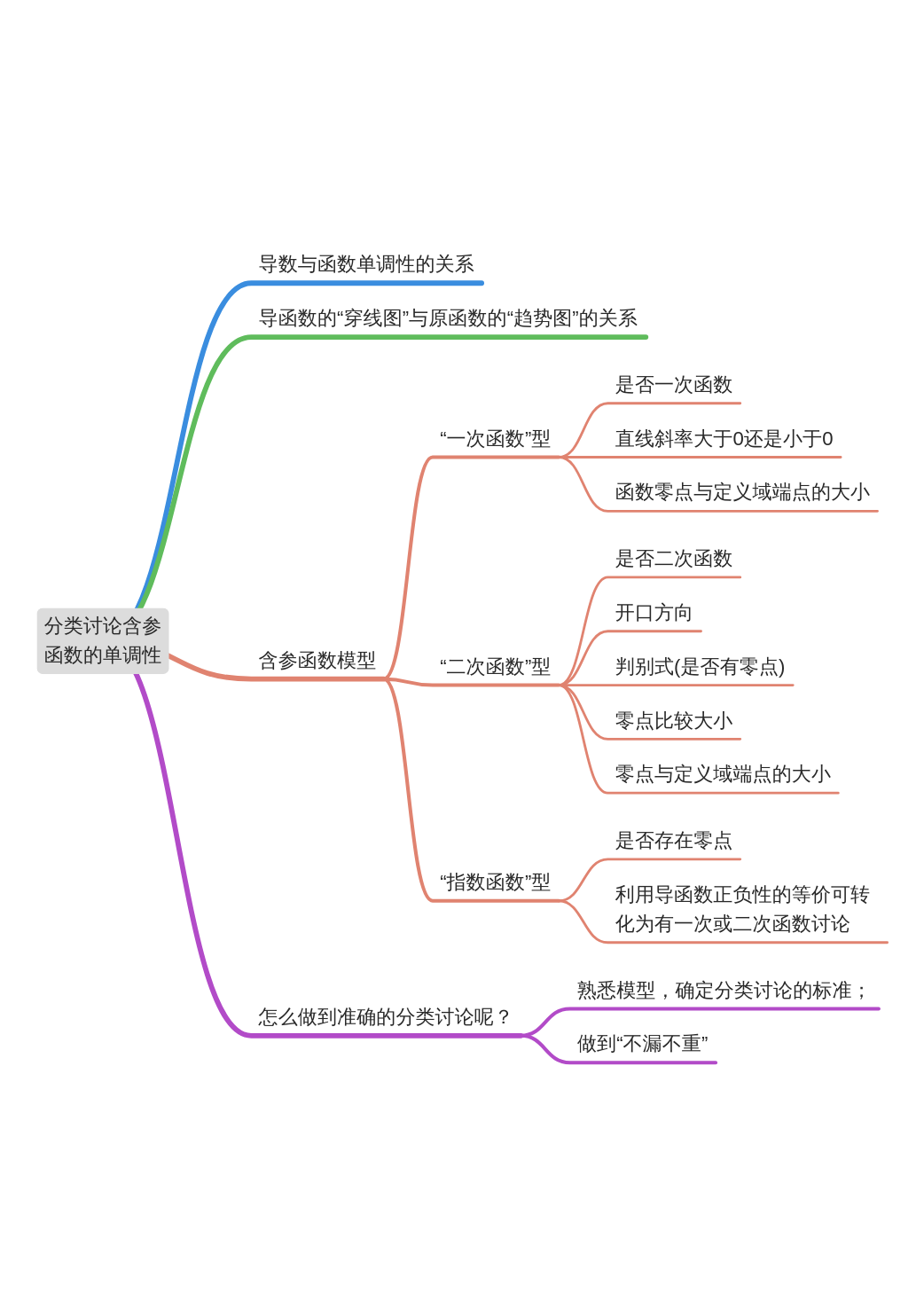
知识剖析
导数与函数单调性的关系
在某个区间\((a ,b)\)内,若\(f'(x)>0\),则函数\(y=f(x)\)在这个区间内单调递增;
若\(f'(x)<0\),则函数\(y=f(x)\)在这个区间内单调递减.
对含参函数单调性的分析思路
\((1)\) 如何分析原函数的单调性?
答:分析原函数的单调性等价于分析导函数的正负性.
\((2)\)那如何分析导函数的正负性呢?
答:数形结合,若能得到导函数的“穿线图”(即解导数不等式,与其零点有莫大关系),看图“说话”便可,进而得出原函数的“趋势图”(即原函数的大致趋势)也不难了(看下图).

\({\color{Red}{ (导函数看“零点”,原函数看单调性) }}\)
\((3)\)那要得到导函数的“穿线图”,要注意什么呢?
答:掌握“一次函数”型、“二次函数”型、“指数函数”型常见模型,画“穿线图”思考以下问题:
① 导函数是否存在零点;
② 若存在,有几个零点呢?若有两个以上,哪个零点大?
③ 零点是否在定义域内?
\((4)\)怎么做到准确的分类讨论呢?
答:① 熟悉模型,确定分类讨论的标准;
② 做到分类讨论“不漏不重”,把每项分类看成一个集合,每个集合的交集为空集则“不重”,所有集合的并集为参数的全集则为“不漏”.
各模型分类讨论的标准
分类讨论要确定每步分类的标准,做到有根有据.
\((1)\)“一次函数”型:是否一次函数,直线斜率大于\(0\)还是小于\(0\),函数零点与定义域端点的大小;
\((2)\)“二次函数”型:确定是否二次函数,开口方向,判别式(是否有零点),零点比较大小,零点与定义域端点的大小;
\((3)\)“指数函数”型:是否存在零点;利用导函数正负性的等价可转化为二次函数讨论.
经典例题
【题型一】原函数图象与导函数图象间的转化
【典题1】设\(f^{\prime}(x)\)是函数\(f(x)\)的导函数,\(y=f^{\prime}(x)\)的图象如图所示,则\(y=f(x)\)的图象可能是( )
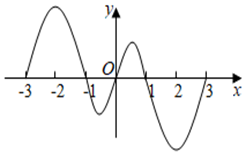
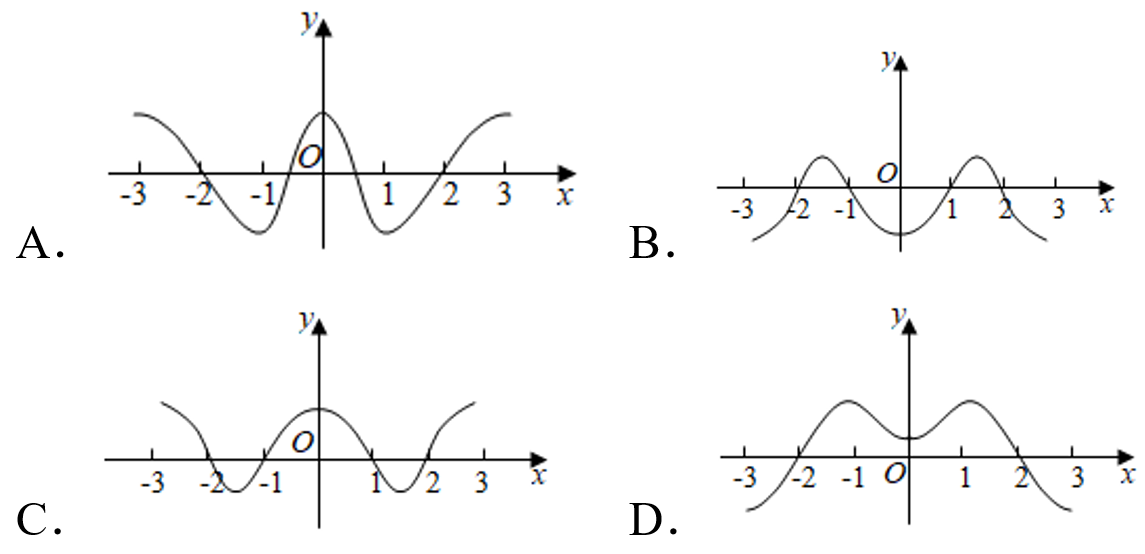
【解析】 由\(y=f'(x)\)的图象可知,函数\(f(x)\)的增区间为\((-3 ,-1)\),\((0 ,1)\);减区间为\((-1 ,0)\),\((1 ,3)\);观察选项可知,只有\(D\)选项符合题意;故选:\(D\).
【点拨】 导函数的零点\(x=-3\),\(-1\),\(0\) ,\(1\) ,\(3\)才影响到导函数的正负性,从而影响到原函数单调性,而\(-2 ,2\)没影响!充分理解导函数的穿线图与原函数的趋势图之间的关系.
巩固练习
1 (★) 函数\(y=f(x)\)的图象如图所示,则导函数\(y=f^{\prime} (x)\)的图象可能是 ( )
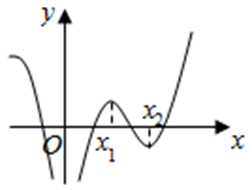

2 (★) 已知函数\(y=(x-1)f^{\prime}(x)\)的图象如图所示(其中\(f^{\prime}(x)\)是函数\(f(x)\)的导函数),则\(y=f(x)\)的图象可能是( )


答案
- \(D\)
- \(B\)
【题型二】 “一次函数”型
【典题1】求函数\(f(x)=ln(x-1)-k(x-1)+1\)的单调区间.
【解析】 \(f(x)\)的定义域是\((1 ,+∞)\),
\({\color{Red}{(优先讨论函数定义域) }}\)
\(f^{\prime}(x)=\dfrac{1}{x-1}-k=\dfrac{-k x+k+1}{x-1}\),
\({\color{Red}{ (通分, x>1⇒ x-1>0,则y=f^{\prime}(x)的正负性等价于y=-kx+k+1(x>1)的正负性) }}\)
\({\color{Red}{ (判断y=-kx+k+1的函数类型,分k=0和k≠0) }}\)
(1)当\(k=0\)时,\(f^{\prime}(x)=\dfrac{1}{x-1}>0\),\(f(x)\)在\((1 ,+∞)\)上递增;
(2)当\(k≠0\)时,令\(f^{\prime}(x)=0\),解得\(x=\dfrac{1}{k}+1\),
\({\color{Red}{ (一次函数y=-kx+k+1的斜率-k正数还是负数会影响导函数的正负性,分k<0和k>0讨论;}}\)
\({\color{Red}{ 同时注意零点x=\dfrac{1}{k}+1与定义域端点1的比较,结合图像就容易理解)}}\)
①当\(k<0\)时,\(x=\dfrac{1}{k}+1<1\),在\((1 ,+∞)\)上,\(f^{\prime}(x)>0\),\(f(x)\)递增;

②当\(k>0\)时,\(x=\dfrac{1}{k}+1>1\),

在\((1 ,\dfrac{1}{k}+1)\)上,\(f^{\prime}(x)>0\),\(f(x)\)递增;在\((\dfrac{1}{k}+1 ,+∞)\)上,\(f^{\prime}(x)<0\),\(f(x)\)递减;
综上所述,
当\(k≤0\)时,\(f(x)\)在\((1 ,+∞)\)上递增;
当\(k>0\)时,\(f(x)\)在\((1 ,\dfrac{1}{k}+1)\)上递增,\(f(x)\)在\((\dfrac{1}{k}+1 ,+∞)\)上递减.
【点拨】
① 本题分类讨论的思考:
 ;
;
② “一次函数”型要注意的是:是否一次函数,直线斜率大于\(0\)还是小于\(0\),函数零点与定义域端点的大小!
③ 本题对于导函数\(f^{\prime}(x)=\dfrac{1}{x-1}-k\)的分类讨论\(k=0\),\(k<0\) ,\(k>0\),您还可以有两个角度:
(1)从代数角度,\(x>1⇒\dfrac{1}{x-1}>0\),则\(k≤0\)时\(f^{\prime}(x)>0\),而\(k>0\)时\(f^{\prime}(x)\)有零点;
(2) \(f^{\prime}(x)=\dfrac{1}{x-1}-k\)看成分式函数\(y=\dfrac{1}{x-1}\)上下平移得到,则\(k≤0\)时图象与\(x\)轴相离且\(f^{\prime}(x)>0\),而\(k>0\)时与\(x\)轴相交,即\(f^{\prime} (x)\)有零点.
故分类的角度可以多样的,要灵活处理.
巩固练习
1 (★★) 求函数\(f(x)=xe^{kx}\)的单调区间.
2 (★★) 已知\(a\)是实数,求函数\(f(x)=\sqrt{x}(x-a)\)的单调区间.
3 (★★) 求函数\(f(x)=lnx-ax\)的单调区间.
参考答案
- 若\(k=0\),\(f(x)\)在\(R\)上递增;若\(k>0\),则\(f(x)\)在\(\left(-\infty,-\dfrac{1}{k}\right)\)上递减,在\((-\dfrac{1}{k},+∞)\)上增函数;
若\(k<0\),则\(f(x)\)在\((-∞ ,-\dfrac{1}{k})\)上递增,在\((-\dfrac{1}{k},+∞)\)上递减. - 当\(a≤0\)时,\(f(x)\)在\([0 ,+∞)\)递增;当\(a>0\)时,\(f(x)\)在\([0 ,\dfrac{a}{3}]\)递减,在\([\dfrac{a}{3},+∞)\)递增.
- 若\(a≤0\)时,\(f(x)\)在\((0 ,+∞)\)递增;若\(a>0\)时,\(f(x)\)在\((0,\dfrac{1}{a})\)递增,\(f(x\))在\((\dfrac{1}{a},+∞)\)递减.
【题型三】 “二次函数”型
【情况1】讨论开口方向
已知函数\(f(x)=plnx+(p-1) x^2+1\), 当\(p>0\)时,讨论函数\(f(x)\)的单调性.
【解析】 \(f(x)\)的定义域为\((0 ,+∞)\),
\(f^{\prime}(x)=\dfrac{p}{x}+2(p-1) x=\dfrac{2(p-1) x^{2}+p}{x}\),
\({\color{Red}{ (因为x>0,所以y=f^{\prime}(x)的正负性等价于2(p-1) x^2+p的正负性;先确定函数类型,分p=1和p≠1) }}\)
(1)若\(p=1\)时,\(f^{\prime}(x)=\dfrac{1}{x}>0\),故\(f(x)\)在\((0 ,+∞)\)单调递增;
(2)若\(p≠1\)时,
\({\color{Red}{(抛物线的开口方向会影响导函数的正负性,分p>1和0<p<1) }}\)
①若\(p>1\)时,
\(f^{\prime} (x)>0\),故\(f(x)\)在\((0 ,+∞)\)单调递增;

②若\(0<p<1\)时,
令\(f^{\prime}(x)=0\),解得\(x=\sqrt{\dfrac{p}{2(1-p)}}\),

则当\(0<x<\sqrt{\dfrac{p}{2(1-p)}}\)时,\(f^{\prime} (x)>0\),\(f(x)\)递增;
当\(x>\sqrt{\dfrac{p}{2(1-p)}}\)时,\(f^{\prime}(x)<0\),\(f(x)\)递减.
综上所述
当\(p≥1\)时,\(f(x)\)在\((0 ,+∞)\)单调递增;
当\(0<p <1\)时,\(f(x)\)在\((0 ,\sqrt{\dfrac{p}{2(1-p)}} )\)单调递增,在\((\sqrt{\dfrac{p}{2(1-p)}} ,+∞)\)单调递减.
【点拨】
① 本题分析函数\(y=2(p-1) x^2+p\)的正负性,先确定是否二次函数,再确定二次函数开口方向.
② 从代数的角度,也可知当\(p≥1\)时\(f^{\prime}(x)=\dfrac{2(p-1) x^{2}+p}{x}>0\),\(p<1\)时有零点,分\(p≥1\)和\(p<1\)两种情况讨论便可.
【情况2】 讨论判别式
求函数\(f(x)=\dfrac{1}{3} x^{3}+\dfrac{a}{2} x^{2}-2 a x+1\)的单调性.
【解析】 \(f^{\prime}(x)=x^2+ax-2a\),其判别式为\(∆=4a^2+8a\),
\({\color{Red}{ (x^2+ax-2a不一定能在实数内因式分解,故思考导函数是否存在零点,由判别式决定,分∆≤0和∆>0讨论) }}\)
(1)若\(∆≤0\),即\(-2≤a≤0\)时,\(f^{\prime}(x)≥0\),\(f(x)\)在\(R\)上递增;

(2)若\(∆>0\),即\(a<-2\)或\(a>0\)时,
令\(f^{\prime}(x)=0\),解得\(x_{1}=\dfrac{-a-\sqrt{4 a^{2}+8 a}}{2}\)或\(x_{2}=\dfrac{-a+\sqrt{4 a^{2}+8 a}}{2}\),其中\(x_2>x_1\),

当\(x_1<x<x_2\)时,\(f^{\prime}(x)<0\),\(f(x)\)递减;
当\(x>x_2\)或\(x<x_1\)时,\(f^{\prime}(x)>0\),\(f(x)\)递增.
综上所述,当\(-2≤a≤0\)时, \(f(x)\)在\(R\)上递增;
当 \(a<-2\)或\(a>0\)时,\(f(x)\)在\(\left(\dfrac{-a-\sqrt{4 a^{2}+8 a}}{2}, \dfrac{-a+\sqrt{4 a^{2}+8 a}}{2}\right)\)上递减,
在\(\left(-\infty, \dfrac{-a-\sqrt{4 a^{2}+8 a}}{2}\right)\),\(\left(\dfrac{-a+\sqrt{4 a^{2}+8 a}}{2},+\infty\right)\)递增.
【点拨】 对于“二次函数”型,求导后要思考下能否可以因式分解,若不能,则对判别式进行讨论,确定导函数零点存在情况!
【情况3】 讨论零点大小
求函数\(f(x)=x-\dfrac{2 a}{x}-(a+2) \ln x\)的单调区间.
【解析】 \(f(x)\)的定义域为\((0 ,+∞)\)
\(f^{\prime}(x)=1+\dfrac{2 a}{x^{2}}-\dfrac{a+2}{x}\)\(=\dfrac{x^{2}-(a+2) x+2 a}{x^{2}}=\dfrac{(x-2)(x-a)}{x^{2}}\)
\({\color{Red}{ (求导后通分、因式分解,确保有零点存在) }}\)
令\(f^{\prime}(x)=0\),得\(x_1=2 ,x_2=a\),
\({\color{Red}{(对导函数零点2、a与定义域端点0三者比较大小,先比较a与0的大小,分 a>0和a≤0) }}\)
(1)若\(a≤0\)时,

当\(0<x<2\)时,\(f^{\prime}(x)<0\),\(f(x)\)递减;
当\(x>2\)时,\(f^{\prime}(x)>0\),\(f(x)\)递增;
(2)若\(a>0\)时,
\({\color{Red}{ (判断导函数零点2、a的大小,分a=2、a>2、a<2三种情况)}}\)
①若\(a=2\)时,

\(f^{\prime}(x)=(x-2)^2≥0\),\(f(x)\)递增;
\({\color{Red}{ (不要遗忘零点相等的情况)}}\)
②若\(a>2\)时,

当\(0<x<2\)或\(x>a\)时,\(f^{\prime}(x)>0\),\(f(x)\)递增;
当\(2<x<a\)时,\(f^{\prime} (x)<0\),\(f(x)\)递减;
③若\(0<a<2\)时,

当\(0<x<a\)或\(x>2\)时,\(f^{\prime}(x)>0\),\(f(x)\)递增;
当\(a<x<2\)时,\(f^{\prime} (x)<0\),\(f(x)\)递减.
综上所述
当\(a<0\)时,\(f(x)\)递减区间为\((0 ,2)\),\(f(x)\)递增区间为\((2 ,+∞)\);
当\(a=2\)时,\(f(x)\)递增区间为\((0 ,+∞)\);
当\(a>2\)时,\(f(x)\)递增区间为\((0 ,2)\)或\((a ,+∞)\),\(f(x)\)递减区间为\((2 ,a)\);
当\(0<a<2\)时,\(f(x)\)递增区间为\((0 ,a)\)或\((2 ,+∞)\),\(f(x)\)递减区间\((a ,2)\).
【点拨】
① 求导后能够因式分解,说明导函数存在零点;
② 若函数存在零点,需要注意零点的大小比较,并且零点是否在定义域范围内,结合图象会更容易得到分类讨论的标准!
【综合题型】
讨论\(f(x)=-\ln x+a x+\dfrac{a-1}{x}+1\)的单调性.
【解析】 \(y=f(x)\)的定义域为\((0 ,+∞)\),
\({\color{Red}{(注意函数的定义域) }}\)
\(f^{\prime}(x)=-\dfrac{1}{x}+a-\dfrac{a-1}{x^{2}}\)\(=\dfrac{a x^{2}-x+1-a}{x^{2}}=\dfrac{(x-1)(a x+a-1)}{x^{2}}\),
\({\color{Red}{(通分,因式分解) }}\)
令\(g(x)=(x-1)(ax+a-1),x>0\),
此时\(g(x)\)与\(f^{\prime}(x)\)符号相同.
\({\color{Red}{(第一步:讨论函数类型) }}\)
(1)当\(a=0\)时,\(g(x)=-x+1\)
当\(x∈(0 ,1)\)时,\(g(x)>0\),即\(f^{\prime} (x)>0\),函数\(f(x)\)单调递增;
当\(x∈(1 ,+∞)\)时,\(g(x)<0\),即\(f^{\prime}(x)<0\),函数\(f(x)\)单调递减;
(2)当\(a≠0\)时,由\(g(x)=0\),解\(x_{1}=1, x_{2}=\dfrac{1}{a}-1\);
\({\color{Red}{(第二步:讨论开口方向) }}\)
①当\(a<0\)时,
抛物线\(g(x)=(x-1)(ax+a-1)\)开口向下,
由于\(\dfrac{1}{a}-1<0\)
\({\color{Red}{ (留意导函数零点和定义域的大小) }}\)

\(x∈(0 ,1)\)时,\(g(x)>0\),即\(f^{\prime}(x)>0\),函数\(f(x)\)单调递增;
\(x∈(1 ,+∞)\)时,\(g(x)<0\),即\(f^{\prime}(x)<0\),函数\(f(x)\)单调递减.
②当\(a>0\)时,抛物线\(g(x)=(x-1)(ax+a-1)\)开口向上,
\({\color{Red}{(第三步:比较导函数零点大小) }}\)
ⅰ当\(a=\dfrac{1}{2}\)时,\(x_1=x_2\),\(g(x)>0\)恒成立,即\(f^{\prime} (x)≥0\),函数\(f(x)\)在\((0 ,+∞)\)上单调递增;

ⅱ当\(0<a<\dfrac{1}{2}\)时,\(\dfrac{1}{a}-1>1>0\),\(x_2>x_1>0\),

\(x∈(0 ,1)\)或\(x \in\left(\dfrac{1}{a}-1,+\infty\right)\)时,\(g(x)>0\),即\(f^{\prime} (x)>0\),函数\(f(x)\)单调递增;
\(x \in\left(0, \dfrac{1}{a}-1\right)\)时,\(g(x)<0\),即\(f^{\prime} (x)<0\),函数\(f(x)\)单调递减;
ⅲ当\(\dfrac{1}{2}<a<1\)时,\(1>\dfrac{1}{a}-1>0\),\(x_1>x_2>0\)

\(x \in\left(0, \dfrac{1}{a}-1\right)\)或\(x∈(1 ,+∞)\)时,\(g(x)>0\) ,
即\(f^{\prime}(x)<0\),函数\(f(x)\)单调递增;
\(x \in\left(\dfrac{1}{a}-1,1\right)\)时,\(g(x)<0\),即\(f^{\prime}(x)<0\),函数\(f(x)\)单调递减;
ⅳ当\(a≥1\)时,\(\dfrac{1}{a}-1 \leq 0\),

\(x∈(0 ,1)\)时,\(g(x)<0\),即\(f^{\prime}(x)<0\),函数\(f(x)\)单调递减;
\(x∈(1 ,+∞)\)时,\(g(x)>0\),即\(f^{\prime} (x)>0\),函数\(f(x)\)单调递增;
综上所述:
当\(a≤0\)时,函数\(f(x)\)在\((0 ,1)\)上单调递增;函数\(f(x)\)在\((1 ,+∞)\)上单调递减;
当\(a=\dfrac{1}{2}\)时,函数\(f(x)\)在\((0 ,+∞)\)上单调递增;
当\(0<a<\dfrac{1}{2}\)时,函数\(f(x)\)在\((0 ,1)\)上单调递增;函数\(f(x)\)在\(\left(1, \dfrac{1}{a}-1\right)\)单调递减, 在\(\left(\dfrac{1}{a}-1,+\infty\right)\)上单调递增,
当\(\dfrac{1}{2}<a<1\)时,函数\(f(x)\)在\((0 ,\dfrac{1}{a}-1)\) ,\((1 ,+∞)\)单调递减,在\((\dfrac{1}{a}-1 ,1)\)单调递增;
当\(a≥1\)时,函数\(f(x)\)在\((0 ,1)\)单调递减;在\((1 ,+∞)\)单调递增.
【点拨】
①求导后,通分,因式分解是个好习惯,能因式分解说明不需要讨论\(∆\).
\(f^{\prime}(x)=-\dfrac{1}{x}+a-\dfrac{a-1}{x^{2}}\)\(=\dfrac{a x^{2}-x+1-a}{x^{2}}=\dfrac{(x-1)(a x+a-1)}{x^{2}}\)
② 分类讨论思路

③“二次函数”型,经常分类讨论的标准有:确定是否二次函数,开口方向,判别式(是否有零点),零点比较大小,零点与定义域端点的大小;
④分类讨论的次序不是固定的,本题中也可以先讨论零点大小,再讨论零点与定义域端点的大小;
⑤在讨论繁琐时,建议以思维导图形式,画“导函数穿线图和原函数趋势图”梳理思路.
巩固练习
1 (★★) 讨论函数\(f(x)=(a+1)\ln x+ax^2+1\)的单调性.
2 (★★★) 若函数\(f(x)=a x+\dfrac{2}{x}+\ln x\),求函数的单调区间.
3 (★★★★) \(f(x)=2lnx-2x-3\) ,\(g(x)=(p-2) x+\dfrac{p+2}{x}-3\),若对任意的\(x∈[1 ,2]\),\(f(x)≥g(x)\)恒成立,求实数\(p\)的取值范围.
参考答案
- 当\(a≥0\)时,\(f(x)\)在\((0 ,+∞)\)上递增;当\(a≤-1\)时,\(f(x)\)在\((0 ,+∞)\)上递减;
当\(-1<a<0\)时,\(f(x)\)在\(\left(0, \sqrt{-\dfrac{a+1}{2 a}}\right)\)上递增,在\((\sqrt{-\dfrac{a+1}{2 a}},+∞)\)上递减. - \(a<0\)时,\(f(x)\)的递减区间为\(\left(0, \dfrac{-1+\sqrt{1+8 a}}{2 a}\right)\),\(\left(\dfrac{-1-\sqrt{1+8 a}}{2 a},+\infty\right)\),递增区间为:\(\left(\dfrac{-1+\sqrt{1+8 a}}{2 a}, \dfrac{-1-\sqrt{1+8 a}}{2 a}\right)\);
\(a=0\)时,\(f(x)\)递减区间为\((0 ,2)\),递增区间为\((2 ,+∞)\);
\(a>0\)时,\(f(x)\)的减区间为\(\left(0, \dfrac{-1+\sqrt{1+8 a}}{2 a}\right)\),增区间为\(\left(\dfrac{-1+\sqrt{1+8 a}}{2 a},+\infty\right)\). - \((-∞ ,-1]\).
【题型四】 “指数函数”型
【典题1】举一个与导函数\(f^{\prime}(x)=(e^x-e)(-e^x+e^2)\)的正负性一致的导函数: \(\underline{\quad \quad}\) .
【解析】 导函数\(f^{\prime}(x)=(e^x-e)(-e^x+e^2)\)由\(y=e^x-e\)和\(y=-e^x+e^2\)相乘,而\(y=e^x-e\),\(y=-e^x+e^2\)的正负性分别与\(y=x-1\),\(y=-x+2\)的正负性一致,则导函数\(g^{\prime} (x)=(x-1)(-x+2)\)的正负性与\(f^{\prime} (x)=(ex-e)(-ex+e^2)\)的正负性一致,在\((-∞ ,1)\) ,\((2 ,+∞)\)为负,在\((1 ,2)\)为正.
【点拨】 若能把“指数函数”型转化为“二次函数”型,那在画“导函数穿线图”上会显得更简单.
【典题2】已知函数\(f(x)=e^x-ax\)求函数的单调区间.
【解析】 \(f^{\prime} (x)=e^x-a\),
若\(a≤0\)时,\(f^{\prime} (x)>0\), \(f(x)\)在\(R\)上递增;

若\(a>0\)时,令\(f^{\prime} (x)=0\),解得\(x=lna\),

当\(x>lna\)时,\(f^{\prime}(x)>0\),\(f(x)\)递增;
当\(x<lna\) 时,\(f^{\prime}(x)<0\),\(f(x)\)递减.
综上所述:
若\(a≤0\)时,\(f(x)\)在\(R\)上递增;
若\(a>0\)时,\(f(x)\)在\((lna ,+∞)\)递增,\(f(x)\)在\((-∞ ,lna)\)递减.
【点拨】
①导函数\(f^{\prime} (x)=e^x-a\)的图象可以看成是由\(y=e^x\)下平移而来,当\(a<0\)时,图象向上平移,不产生零点;当\(a>0\)时,图象向下平移,存在一个零点\(x=lna\).
②不要一开始就令\(f^{\prime}(x)=e^x-a\)\(⇒x=lna\),误认为导函数一直存在零点,其实看下\(lna\),也可知当\(a>0\)时,\(lna\)才有意义!
【典题3】求函数\(f(x)=(x-2) e^{x}+\dfrac{1}{2} a(x-1)^{2}+e\)(其中\(a∈R\))的单调性.
【解析】 由题意得\(f'(x)=(x-1) e^x+a(x-1)=(x-1)(e^x+a)\),
\({\color{Red}{ (求导因式分解,知道存在零点x=1,那要分析y=e^x+a的正负性) }}\)
(1)若\(a≥0\)时,
当\(x<1\)时,\(f^{\prime}(x)<0\),\(f(x)\)递减;
当\(x>1\)时,\(f'(x)>0\),\(f(x)\)递增;
(2)若\(a<0\)时,令\(f'(x)=0\)\(⇒x_1=1\)或\(x_2=ln(-a)\);
\({\color{Red}{(比较两个零点的大小,此时f'(x)=(x-1)(e^x+a)正负性等价于y=(x-1)(x-ln(-a))的正负性) }}\)
①当\(a=-e\)时,\(x_2=ln(-a)=1=x_1\),\(f'(x)>0\),\(f(x)\)在\(R\)上递增;

②若\(-e<a<0\)时,\(x_2=ln(-a)<1=x_1\),

当\(ln(-a)<x<1\)时,\(f^{\prime} (x)<0\),\(f(x)\)递减;
当\(x>1\)或\(x<ln(-a)\)时,\(f^{\prime}(x)>0\),\(f(x)\)递增.
③若\(a<-e\)时,\(x_2=ln(-a)>1=x_1\),

当\(1<x<ln(-a)\)时,\(f^{\prime}(x)<0\),\(f(x)\)递减;
当\(x>ln(-a)\)或\(x<1\)时,\(f'(x)>0\),\(f(x)\)递增.
综上所述
当\(a≥0\)时,\(f(x)\)在\((-∞ ,1)\)递减,在\((1 ,+∞)\)递增;
当\(a=-e\)时,\(f(x)\)在\(R\)上递增;
当\(-e<a<0\)时,,\(f(x)\)在\((ln(-a) ,1)\)递减, 在\((-∞ ,ln(-a))\),\((1 ,+∞)\)递增;
当\(a<-e\)时,\(f(x)\)在\((1 ,ln(-a))\)递减, 在\((-∞ ,1)\),\((ln(-a) ,+∞)\)递增.
【点拨】
① 求导后的因式分解很重要,从而确定零点个数;
② 当\(a<0\)时,导函数\(f'(x)=(x-1)(e^x+a)\)正负性转化为二次函数\(y=(x-1)(x-ln(-a))\)的正负性,转为熟悉模型,更容易分析!
巩固练习
1 (★) 以下哪个导函数的正负性与导函数\(f^{\prime}(x)=x-1\)的正负性一致 ( )
A.\(g^{\prime} (x)=e^x-1\) \(\qquad \qquad\) B.\(u^{\prime} (x)=lnx\) \(\qquad \qquad\)C.\(s^{\prime}(x)=1-\dfrac{1}{x}\) \(\qquad \qquad\) D.\(t^{\prime} (x)=e^x-e\)
2 (★★) 求函数\(f(x)=e^x-2ax+3a^2 e^{-x}\)的单调性.
3 (★★★) 求函数\(f(x)=(x-3) e^{x}-\dfrac{a}{2}(x-2)^{2}\)的单调性.
4 (★★★★) 讨论函数\(f(x)=a(x-1)^{2}-\dfrac{x}{e^{x}}\) 的单调性.
参考答案
- \(D\)
- 当\(a=0\)时,\(f(x)\)在\(R\)上单调递增;
当\(a>0\)时,\(x∈(-∞ ,ln(3a))\)时\(f(x)\)单调递减,\(x∈(ln(3a) ,+∞)\)时\(f(x)\)单调递增;
当\(a<0\)时,\(x∈(-∞ ,ln(-a))\)时\(f(x)\)单调递减,\(x∈(ln(-a) ,+∞)\)时\(f(x)\)单调递增. - 当\(a≤0\)时,\(f(x)\)在\((-∞ ,2)\)递减;在\((2 ,+∞)\)递增;
当\(a=e^2\)时,\(f(x)\)在\(R\)上递增;
当\(0<a<e^2\)时,\(f(x)\)在\((-∞ ,lna)\),\((2 ,+∞)\)递增,在\((lna ,2)\)递减;
当\(a>e^2\)时,\(f(x)\)在\((-∞ ,2)\),\((lna ,+∞)\)递增;在\((2 ,lna)\)递减. - 当\(a≥0\)时,\(f(x)\)在\((-∞ ,1)\)递减,在\((1 ,+∞)\)递增;
当\(a=-\dfrac{1}{2 e}\)时,\(f(x)\)在\(R\)上递减;
当\(a<-\dfrac{1}{2 e}\)时,\(f(x)\)在\((\ln \left(-\dfrac{1}{2 a}\right), 1)\)递增, 在\((-∞ ,\ln \left(-\dfrac{1}{2 a}\right))\),\((1 ,+∞)\)递减;
当\(-\dfrac{1}{2 e}<a<0\)时,\(f(x)\)在\((1 ,\ln \left(-\dfrac{1}{2 a}\right))\)递增, 在\((-∞ ,1)\),\((\ln \left(-\dfrac{1}{2 a}\right),+∞)\)递减.
【题型五】 “二次求导”型
【典题】 求\(g(x)=e^x+\cos x-ax-2(x≥0)\)的单调性.
【解析】 \(g'(x)=e^x-\sin x-a\),
令\(p(x)=g'(x) =e^x-\sin x-a\),故\(p^{\prime} (x)=e^x-\cos x\)
当\(x≥0\)时,\(p'(x)≥0\),故\(p(x)\)在\([0 ,+∞)\)上单调递增,
\({\color{Red}{(要注意三角函数有界性) }}\)
\({\color{Red}{ (此时p(x)_{min}=p(0)=1-a,分析导函数是否有零点,分1-a≤0和1-a>0讨论.)}}\)
①当\(a≤1\)时,\(p(x)≥p(0)=1-a≥0\),即\(g^{\prime} (x)≥0\),
故\(g(x)\)在\([0 ,+∞)\)上单调递增;

②当\(a>1\)时,\(p(0)=1-a<0\),且\(p(\ln (a+1))=1-\sin (\ln a(a+1))≥0\),
故存在\(x_0∈(0 ,\ln (a+1)]\),使得\(p(x_0)=g'(x_0)=0\),
当\(0<x<x_0\)时,\(g'(x)<0\),\(g(x)\)单调递减;
当\(x>x_0\)时,\(g^{\prime}(x)>0\),\(g(x)\)单调递增.
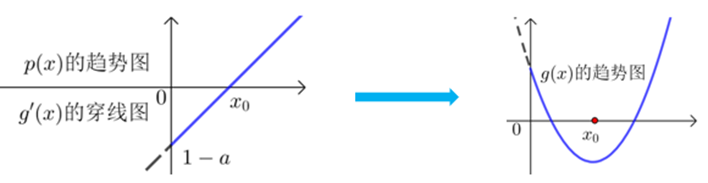
综上所述,当\(a≤1\)时,\(g(x)\)在\([0 ,+∞)\)上单调递增;
当\(a>1\)时,\(g(x)\)在\([0 ,+∞)\)上先减后增.
【点拨】
① 当一次求导后的导函数\(g'(x) =e^x-\sin x-a\)不属于前面三种情况,形式比较复杂,若能分析出\(y=g'(x)\)的图象,分析其正负性时就容易些,那函数可以“二次求导”分析\(y=g'(x)\)的单调性、最值从而得到函数图象.
② 解题思考图如下

③ 解题的整体思想还是数形结合,有些复杂题型可能还要三次求导.
巩固练习
1 (★★) 求函数\(f(x)=x \cos x-a x+a, x \in\left[0, \dfrac{\pi}{2}\right]\),\((a≥1)\)的单调区间.
2 (★★★) 求函数\(f(x)=(x+a)lnx (a>0)\)的单调性.
参考答案
1.\(f(x)\)的单调递减区间是\(\left[0, \dfrac{\pi}{2}\right]\),没有单调递增区间.
- 当\(a≥e^{-2}\)时,\(f(x)\)在\((0 ,+∞)\)递增;
当\(a<e^{-2}\)时\(f(x)\)在\((0 ,+∞)\)上先增后减再增.

