专题 导数中的二次求导

\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学下学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)

选择性必修第二册同步拔高，难度4颗星！

模块导图

知识剖析

二阶导数的概念

如果函数\(y=f(x)\)的导数\(f'(x)\)在\(x\)处可导，则称\(y'\)的导数为函数\(y=f(x)\)在\(x\)处的二阶导数，记为\(f''(x)\).
\({\color{Red}{ Eg: }}\)若函数\(f(x)=x^3\)，则\(f^{\prime}(x)=3x^2\)，\(f^{\prime \prime}(x)=\left[f^{\prime}(x)\right]^{\prime}=\left[3 x^{2}\right]^{\prime}=6 x\).
 

二阶导数的意义

二阶导数是一阶导数的导数.从原理上看，它表示一阶导数的变化率；从图形上看，它反映的是函数图像的凹凸性.
若在\((a,b)\)内\(f^{\prime \prime} (x)>0\)，则\(f(x)\)在\((a,b)\)内为凹函数；若在\((a,b)\)内\(f^{\prime \prime} (x)<0\)，则\(f(x)\)在\((a,b)\)内为凸函数；
\({\color{Red}{ Eg：}}\) \(f(x)=e^x\)，其二次导数为\(f^{\prime \prime}(x)=e^x>0\)，凹函数；
\(f(x)=lnx\)，其二次导数\(f^{\prime \prime}(x)=-\dfrac{1}{x^{2}}<0\)，为凸函数；

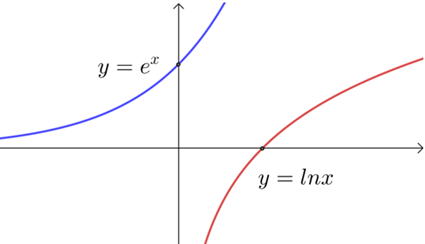
了解函数凹凸性，对于部分题型有助于更快地找到解题思路，特别是在切线放缩.
 

二次求导的运用

\({\color{Red}{ ①}}\) 二阶导数在高中教材中没有介绍，我们不好直接使用二阶导数性质，甚至它的符号\(f''(x)\).
\({\color{Red}{② }}\) 二次求导除了可以判断函数凹凸性，还有一个重要运用，
\({\color{Red}{ (i) }}\)使用场景：某些函数一次求导\(f^{\prime}(x)\)后，解\(f^{\prime}(x)>0\)和\(f^{\prime}(x)<0\)难度较大或甚至解不出(即很难得到\(f^{\prime}(x)\)的正负性)，则需要进行”二次求导”.
\({\color{Red}{ (ii) }}\)思考：若能知道\(y=f^{\prime}(x)\)的图像(或草图)，其正负性是否更好分析呢？那图如何而来?求导便可画图拉，分析其单调性、极值、最值等，这样一想便有了以下解题步骤；
\({\color{Red}{ (iii) }}\)解题步骤：设\(g(x)=f^{\prime}(x)\)，对\(g(x)\)求导\(g^{\prime} (x)\)，求出\(g^{\prime}(x)>0\)和\(g^{\prime}(x)<0\)的解，便可得到\(g(x)\)的单调性，进而求其最值，不难得到\(g(x)=f^{\prime}(x)\)的正负性，由图可知原函数\(f(x)\)的单调性.
若\(g^{\prime}(x)>0\)也很难求解呢？那就要三次求导.

 

经典例题

【题型一】判断函数的凹凸性

【典题1】判断以下几个超越函数的凹凸性
\((1) f(x)=x\cdot e^x\) \(\qquad \qquad\) \((2)f(x)=\dfrac{e^x}{x}\) \(\qquad \qquad\) \((3) f(x)=x\cdot \ln x\)
【解析】 \((1)f^{\prime}(x)=(x+1) e^{x}\)， \(f^{\prime \prime}(x)=(x+2) e^{x}\)，
故\(f(x)\)在\((-∞,-2)\)上凸，在\((-2,+∞)\)上凹；

\((2)f^{\prime}(x)=\dfrac{(x-1) e^{x}}{x^{2}}\)，\(f^{\prime \prime}(x)=\dfrac{\left(x^{2}-2 x+2\right) e^{x}}{x^{3}}\),
故\(f(x)\)在\((-∞,0)\)上凸，在\((0,+∞)\)上凹；

\((3)f^{\prime}(x)=\ln x+1\)，\(f^{\prime \prime}(x)=\dfrac{1}{x}\)，
故\(f(x)\)在\((0,+∞)\)上凹；

【点拨】对于常见的超越函数，需要了解下它们的图象，特别是凹凸性，日后会经常见到它们的踪影，比如二次求导、求最值.、不等式证明、切线放缩等.
 

巩固练习

1 (★) 判断以下几个超越函数的凹凸性
\((1) f(x)=\dfrac{\ln x}{x}\) \(\qquad \qquad\) \((2)f(x)=\dfrac{ x}{\ln x}\) \(\qquad \qquad\) \((3)f(x)=\dfrac{x}{e^x}\)
 
 

参考答案

1. \((1) f(x)\)在\((0,e^{\frac{3}{2}})\)上凸，在\(\left(e^{\frac{3}{2}},+\infty\right)\)上凹；
   \((2) f(x)\)在\((0,1)\)上凸，在\((1,+∞)\)上凹；
   \((3) f(x)\)在\((-∞,2)\)上凸，在\((2,+∞)\)上凹.
    

【题型二】 二次求导与函数的单调性

【典题1】若函数\(f(x)=\dfrac{\sin x}{x}\)，\(0<x_{1}<x_{2}<\pi\)，设\(a=f(x_1 ),b=f(x_2)\)，试比较\(a ,b\)的大小.

【解析】
\({\color{Red}{ (要比较a, b的大小，显然想到y=f(x)单调性)}}\)
\(f^{\prime}(x)=\dfrac{x \cos x-\sin x}{x^{2}}\) ，
设\(g(x)=x\cos x-\sin x\)，
\({\color{Red}{(要知道原函数y=f(x)的单调性，则分析y=x\cos x-\sin x的正负性，}}\)
\({\color{Red}{而它不太好分析，可构造函数y=g(x)二次求导，分析其单调性最值得到其函数图像便利于分析其正负性) }}\)
则\(g^{\prime}(x)=-x\sin x+\cos x-\cos x=-x\sin x\)
当\(0<x<π\)时，\(g^{\prime}(x)<0\)，即\(g(x)\)在\((0 ,π)\)上递减，
\(∴g(x)<g(0)=0\)，
\({\color{Red}{ (此时得到函数y=g(x)的草图，正负性便确定)}}\)
\(∴f^{\prime}(x)<0\)，\(∴f(x)在(0 ,π)\)上递减，
\(∴\)当\(0<x_1<x_2<π\)，\(f(x_1 )>f(x_2)\)，即\(a>b\).

【点拨】
① 要研究函数的单调性，则需要分析导函数的正负性；
② 当一次求导后，发现导函数不太“友善”(不能转化为常见的“一次型导数\(y=kx+b\)”， “二次型导数\(y=ax^2+bx+c\)"，“指数型导数\(y=ke^x+b\)”或其混合型等)，则可考虑构造新函数进行二次求导.
 

【典题2】求函数\(f(x)=\ln ^{2}(x+1)-\dfrac{x^{2}}{1+x}\)的单调性.

【解析】\(f(x)\)的定义域是\((-1 ,+∞)\)，
\(f^{\prime}(x)=\dfrac{2 \ln (x+1)}{x+1}-\dfrac{x^{2}+2 x}{(x+1)^{2}}\)\(=\dfrac{2(x+1) \ln (x+1)-x^{2}-2 x}{(x+1)^{2}}\)，
设\(g(x)=2(x+1) ln⁡(x+1)-x^2-2x\)，
\({\color{Red}{(导函数y=f^{\prime} (x)的正负性与y=g(x)一致， y=g(x)不能因式分解，函数较为复杂，}}\)
\({\color{Red}{要判断它的正负性，若能知道它的图象就好了，便想到二次求导) }}\)
则\(g^{\prime}(x)=2 ln(x+1)-2x=2[ln(x+1)-x]\)，
\({\color{Red}{(此时要分析y=g^{\prime} (x)的正负性，也不容易，则可再次求导分析单调性、最值得到它的图象从而分析正负性) }}\)
令\(t(x)=g^{\prime}(x)=ln(x+1)-x\)，
则\(t^{\prime}(x)=-\dfrac{x}{1+x}\)，
当\(-1<x<0\)时，\(t^{\prime} (x)>0\)，\(g^{\prime} (x)\)在\((-1 ,0)\)上单调递增；
当\(x>0\)时，\(t^{\prime} (x)<0\)，\(g^{\prime} (x)\)在\((-1 ,0)\)上单调递减；
\(∴g^{\prime} (x)\)在\(x=0\)处有最大值，而\(g^{\prime} (0)=0\)，
\({\color{Red}{ (注意到g^{\prime} (0)=0， g^{\prime} (x)的零点)}}\)

\(∴g^{\prime} (x)≤0\),函数\(g(x)\)在\((-1 ,+∞)\)上是单调递减，
当\(-1<x<0\)时，\(g(x)>g(0)=0\)，\(f^{\prime} (x)>0\)， \(f(x)\)递增；
当\(x>0\)时，\(g(x)<g(0)=0\)， \(f^{\prime} (x)<0\)，\(f(x)\)递减；
\({\color{Red}{ (注意到g(0)=0，事情就这么巧，分析出y=f^{\prime} (x)正负性了)}}\)

\(∴f(x)\)的单调增区间是\((-1 ,0)\) ,递减区间是\((0 ,+∞)\).

【点拨】
① 本题的思路是

② 本题中作了“\(3\)次求导”；当导函数形式较为复杂，利用导数画出导函数的趋势图，数形结合便较容易得到它的正负性了，此时也要注意一些特殊点，比如\(g^{\prime}(0)=0\) ,\(g(0)=0\).
 

【典题3】求\(g(x)=e^x+\cos x-ax-2(x≥0)\)的单调性.
【解析】\(g^{\prime}(x)=e^x-\sin x-a\)， 令\(p(x)=g^{\prime}(x)=e^x-\sin x-a\)，
\({\color{Red}{(构造函数二次求导) }}\)
故\(p^{\prime}(x)=e^x-\cos x\)，
当\(x≥0\)时，\(p^{\prime}(x)≥1-\cos x≥0\)，
故\(p(x)\)在\([0 ,+∞)\)上单调递增，
\({\color{Red}{(注意三角函数的有界性) }}\)
\({\color{Red}{(此时p(x)_{min}=p(0)=1-a，分析正负性要确定导函数是否有零点，分1－a<0和1－a≥0讨论.) }}\)
①当\(a≤1\)时，\(p(x)≥p(0)=1-a≥0\)，即\(g^{\prime} (x)≥0\)，
故\(g(x)\)在\([0 ,+∞)\)上单调递增；

②当\(a>1\)时，\(p(0)=1-a<0\)，且\(p(ln(a+1))=1-\sin (\ln a(a+1))≥0\)，
故存在\(x_0∈(0 ,\ln (a+1)]\)，使得\(p(x_0)=g'(x_0)=0\)，
\({\color{Red}{ (\ln (a+1)这取点较难，而当x→+∞，p(x)→+∞，也可知y=p(x)零点x_0的存在)}}\)
当\(0<x<x_0\)时，\(g'(x)<0\)，\(g(x)\)单调递减；
当\(x>x_0\)时，\(g^{\prime} (x)>0\)，\(g(x)\)单调递增.

综上所述，当\(a≤1\)时，\(g(x)\)在\([0 ,+∞)\)上单调递增；
当\(a>1\)时，\(g(x)\)在\([0 ,+∞)\)上先减后增.

【点拨】本题是二次求导在处理含参函数单调性中的运用，在分析导函数正负性，要确定是否存在零点，有时要分类讨论.
 

巩固练习

1 (★★) 求函数\(f(x)=\dfrac{(x+1)\ln x}{x-1}\)的单调性.
 
 

2 (★★) 求函数\(f(x)=\sin x\cdot \ln x\)在区间\((1 ,π)\)的单调性.
 
 

3 (★★★) 求函数\(f(x)=(x+a)\ln x-x+1\)在\((1 ,+∞)\)的单调性.
 
 

参考答案

1. \(f(x)\)在\((0,1)\)上递减，在\((1 ,+∞)\)递增

2. \(f(x)\)在\((1 ,π)\)内先增后减.

3. 当\(a≥0\)时，\(f(x)\)在\((1 ,+∞)\)递增；
   当\(a<0\)时\(f(x)\)在\((1 ,+∞)\)上先减后增.
    

【题型三】二次求导与不等式证明

【典题1】已知函数\(f(x)=(x+1)lnx-x+1\)，
(1) 若\(xf^{\prime} (x)≤x^2+ax+1\)，求\(a\)的取值范围；
(2) 证明\((x-1)f(x)≥0.\)
【解析】(1)\(f^{\prime}(x)=\dfrac{x+1}{x}+\ln x-1=\ln x+\dfrac{1}{x}\)，
\(x f'(x)=xlnx+1\)，
题设\(xf^{\prime}(x)≤x^2+ax+1\)等价于\(lnx-x≤a\)\({\color{Red}{(分离参数法) }}\)
令\(g(x)=\ln x-x\)，则\(g'(x)=\dfrac{1}{x}-1\)
当\(0<x<1\)，\(g'(x)>0\)；
当\(x≥1\)时，\(g'(x)≤0\)，
\(x=1\)是\(g(x)\)的最大值点，\(g(x)≤g(1)=-1\)，
综上，\(a\)的取值范围是\([-1 ,+∞)\)．
(2) \({\color{Red}{方法1 }}\)
要证\((x-1)f(x)≥0\)，
只须证明\(0<x≤1\)时，\(f(x)<0\)；
当\(x>1\)时，\(f(x)>0\)即可 \((*)\).
\({\color{Red}{ (即需要了解函数f(x)的图像)}}\)
由(1)可知\(f^{\prime}(x)= \ln x+\dfrac{1}{x}\)，
\({\color{Red}{ (该函数正负性有些难判断，想到可二次求导)}}\)
令\(g(x)=f^{\prime}(x)= \ln x+\dfrac{1}{x}\)，
则\(g^{\prime}(x)=\dfrac{1}{x}-\dfrac{1}{x^{2}}=\dfrac{x-1}{x^{2}}\)，
显然当\(0<x≤1\)时，\(g^{\prime}(x)≤0\)；
当\(x>1\)时，\(g^{\prime}(x)>0\)，
即\(f^{\prime}(x)= \ln x+\dfrac{1}{x}\)在\((0 ,1)\)上为减函数，在\((1 ,+∞)\)上为增函数，
\(∴f^{\prime}(x)≥f(1)=1>0\)，
即\(f(x)\)在\((0 ,+∞)\)为增函数，
由于\(f(1)=0\)
\({\color{Red}{(这点关键，解题中多注意“特殊点”，由于要“了解函数f(x)的图像”和“证明(*)”的思路也不难想到) }}\)
则\(0<x≤1\)时，\(f(x)<0\)；当\(x>1\)时，\(f(x)>0\)
\(∴(x-1)f(x)≥0\).
方法2 由(1)知，\(g(x)≤g(1)=-1\)，即\(lnx-x+1≤0\)．
当\(0<x≤1\)时，\(f(x)=(x+1)lnx-x+1\)\(=xlnx+(lnx-x+1)≤0\)；
当\(x>1\)时，\(f(x)=\ln x+(x\ln x-x+1)\)\(=\ln x+x(\ln x+\dfrac{1}{x}-1)\)，
\({\color{Red}{ (这步提出x有些“巧妙”) }}\)
令\(h(x)=lnx+\dfrac{1}{x}-1(x>1)\)，\(h'(x)=\dfrac{x-1}{x^2} (x>1)\)，
所以当\(x>1\)时，\(h'(x)>0\) 恒成立，
所以当\(x>1\) 时，\(h(x)>h(1)=0\)，
即 \(x>1\)时，\(f(x)=\ln x+(x \ln x-x+1)\)\(=\ln x+x\left(\ln x+\dfrac{1}{x}-1\right)>0,\)，
所以当\(x>1\)时，\((x-1)f(x)>0\)，
综上，\((x-1)f(x)≥0\)．
【点拨】比较第二问两种方法，还是方法一的“二次求导”的思路来得自然些，当一次求导后感觉到“解\(f^{\prime}(x)>0\)和\(f^{\prime}(x)<0\)难度较大或甚至解不出(即很难得到\(f^{\prime} (x)\)的正负性)”，则可尝试下“二次求导”.在整个过程中，数形结合的思想“如影随形”，不管是原函数\(f(x)\)还是导函数\(f^{\prime}(x)\)的图像.
 

【典题2】设函数\(f(x)=ax-lnx-2(a∈R)\)，
(1) 求\(f(x)\)的单调区间
(2) 若\(g(x)=ax-e^x\)，求证：在\(x>0\)时，\(f(x)>g(x)\)．
【解析】(1)\(f^{\prime}(x)=a-\dfrac{1}{x}=\dfrac{a x-1}{x}(x>0)\)
①当\(a≤0\)时，\(f'(x)<0\)在\((0 ,+∞)\)上恒成立，
\(∴f(x)\)在\((0 ,+∞)\)上是单调减函数，
②当\(a>0\)时，令\(f'(x)=0\)，解得\(x=\dfrac{1}{a}\)，
当\(x∈(0 ,\dfrac{1}{a})\)时，\(f'(x)<0\)，\(f(x)\)单调减，
当\(x∈(\dfrac{1}{a},+∞)\)时，\(f'(x)>0\)，\(f(x)\)单调增，
综上所述：当\(a≤0\)时，\(f(x)\)的单调减区间为\((0 ,+∞)\)；
当\(a>0\)时，\(f(x)\)的单调减区间为\((0 ,1/a)\)，单调增区间为\((\dfrac{1}{a},+∞)\)．
(2)证明：当\(x>0\)时，要证\(f(x)-ax+e^x>0\)，
即证\(e^x-lnx-2>0\)，
令\(h(x)=e^x-lnx-2(x>0)\)，只需证\(h(x)>0\)，
\(∵h'(x)=e^x-\dfrac{1}{x}\)
\({\color{Red}{(求解e^x-\dfrac{1}{x}>0很难，得不到h'(x)的正负性，故想到二次求导) }}\)
令\(s(x)=e^x-\dfrac{1}{x}(x>0)\)，
则\(s^{\prime}(x)=e^{x}+\dfrac{1}{x^{2}}>0\)，函数\(s(x)\)在\((0 ,+∞)\)单调递增，
又\(∵s(1)=e-1>0\)，\(s(\dfrac{1}{3})=e^{\dfrac{1}{3}}-3<0\)
\(∴s(x)\)在\((\dfrac{1}{3},1)\)内存在唯一的零点，
\({\color{Red}{ (这是“隐零点问题”，得到零点的取值范围较为关键) }}\)
即\(h'(x)\)在\((0,+∞)\)上有唯一零点，
设\(h'(x)\)的零点为\(t \quad (\dfrac{1}{3}<t<1)\)，
则\(h^{\prime}(t)=e^{t}-\dfrac{1}{t}=0\)，即\(e^{t}=\dfrac{1}{t}\)，
\(∴\)当\(x∈(0 ,t)\)时，\(h'(x)<h'(t)=0\)，\(h(x)\)为减函数，
当\(x∈(t ,+∞)\)时，\(h'(x)>h'(t)=0\)，\(h(x)\)为增函数，
\(∴\)当\(x>0\)时，\(h(x)≥h(t)=e^t-lnt-2=\dfrac{1}{t}+t-2\)，
又\(\dfrac{1}{3}<t<1\)，\(∴\dfrac{1}{t}+t>2\)，
\({\color{Red}{ (对勾函数y=\dfrac{1}{t}+t可知) }}\)
\(∴h(x)>0=\dfrac{1}{t}+t-2≥2-2=0\)．
即在\(x>0\)时，\(f(x)>g(x)\).
 

巩固练习

1 (★★★) 证明当\(x>0\)时，\(x-\dfrac{x^{3}}{6}<\sin x<x\).
 
 
2 (★★★) 已知函数\(f(x)=e^x\)，\(g(x)=\dfrac{a}{x}\)，\(a\)为实常数，
(1)设\(F（x）=f(x)-g(x)\)，当\(a>0\)时，求函数\(F(x)\)的单调区间；
(2)当\(a=-e\)时，直线\(x=m\) ,\(x=n(m>0 ,n>0)\)与函数\(f(x)\) ,\(g(x)\)的图像共有四个不同的交点，且以此四点为顶点的四边形恰为平行四边形，求证：\((m-1)(n-1)<0\).
 
 

3 (★★★★) 已知函数\(f(x)=ax^2-ax-xlnx\)，且\(f(x)≥0\)，
(1)求\(a\)；
(2)证明：\(f(x)\)存在唯一的极大值点\(x_0\)，且\(e^{-2}<f(x)<2^{-2}\).
 
 

参考答案

1. 提示：构造函数，二次求导

2. (1) \(F(x)\)的单调递增区间为\((－∞ ,0)\) ,\((0 ,+∞)\)，无单调递减区间；
   (2) 证明略，提示：二次求导

3. (1) \(a=1\)

   (2)证明略，提示：二次求导