5.3 导数与函数的单调性

\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学下学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)

选择性必修第二册同步拔高，难度3颗星！

模块导图

知识剖析

1 函数单调性与导数
在某个区间\((a ,b)\)内，若\(f'(x)>0\)，则函数\(y=f(x)\)在这个区间内单调递增；
若\(f'(x)<0\)，则函数\(y=f(x)\)在这个区间内单调递减．
 

2 若函数\(y=f(x)\)在某个区间\((a ,b)\)内单调递增，则\(∀x∈(a，b)\) ,\(f^{\prime}(x)≥0\)\({\color{Red}{ (含等号) }}\)恒成立，但不存在一区间\((c ,d)⊆(a ,b)\)内使得\(f^{\prime}(x)=0\)；
\({\color{Red}{ 解释}}\)
假如存在一区间\((c ,d)⊆(a ,b)\)内使得\(f^{\prime}(x)=0\)，那原函数\(y=f(x)\)在区间\((c ,d)\)内恒等于一个常数，即\(f(x)=m\)(\(m\)是个常数)，则原函数不可能在\((a ,b)\)内单调递增.

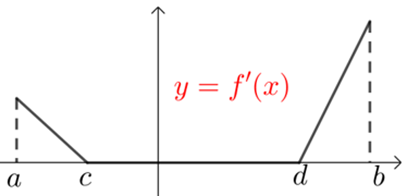$ \qquad$

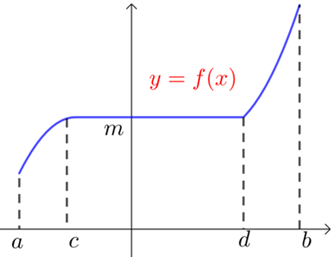
函数\(y=f(x)\)在某个区间\((a ,b)\)内单调递减有类似结论！
 

经典例题

【题型一】 不含参函数的单调性

【典题1】 函数\(f(x)\)的定义域为\(R\)，且图象如图所示，则不等式\(xf'(x)<0\)的解集为\(\underline{\quad \quad}\) .

【解析】由图可知，\(f(x)\)在\((-∞ ,-\dfrac{1}{2})\)和\((\dfrac{1}{2} ,1)\)上单调递增，在\((-\dfrac{1}{2} ,\dfrac{1}{2})\)上单调递减，
\(∴\)当\(x∈(-∞ ,-\dfrac{1}{2})∪(\dfrac{1}{2},1)\)时，\(f'(x)>0\)；
当\(x∈(-\dfrac{1}{2} ,\dfrac{1}{2})\)时，\(f'(x)<0\)．
\(∵\)不等式\(xf'(x)<0\)可等价于\(\left\{\begin{array}{l} x>0 \\ f^{\prime}(x)<0 \end{array}\right.\)或\(\left\{\begin{array}{l} x<0 \\ f^{\prime}(x)>0 \end{array}\right.\)，
\(∴\)当\(x>0\)时，有\(x∈(-\dfrac{1}{2} ,\dfrac{1}{2})\)，即\(x∈(0 ,\dfrac{1}{2})\)；
当\(x<0\)时，有\(x∈(-∞ ,-\dfrac{1}{2})∪(\dfrac{1}{2} ,1)\)，即\(x∈(-∞ ,-\dfrac{1}{2})\)，
综上所述，不等式的解集为\((-∞ ,-\dfrac{1}{2})∪(0 ,\dfrac{1}{2})\)．
【点拨】由原函数\(y=f(x)\)图像判断出原函数的单调性，继而得到导函数\(f'(x)\)的正负性(导函数的穿线图)，再看图易得不等式解集.注意原函数的趋势图与导函数的穿线图之间的转化.

 

【典题2】 若函数\(f(x)=-x^3+ax^2+4x\)在区间\((0 ,2)\)上单调递增，则实数\(a\)的取值范围为\(\underline{\quad \quad}\) .
【解析】\(f(x)=-x^3+ax^2+4x\)，
则\(f^{\prime}(x)=-3x^2+2ax+4\)，
若\(f(x)\)在区间\((0 ,2)\)上单调递增，
则\(-3x^2+2ax+4≥0\)在\((0 ,2)\)恒成立\((*)\)，
\({\color{Red}{方法一 \quad 分离参数法 }}\)
要\((*)\)成立等价于\(a \geq \dfrac{3 x}{2}-\dfrac{2}{x}\)在\((0 ,2)\)恒成立，
令\(g(x)=\dfrac{3 x}{2}-\dfrac{2}{x}\)，\(x∈(0 ,2)\)，
则\(g^{\prime}(x)=\dfrac{3}{2}+\dfrac{2}{x^{2}}>0\)，\(g(x)\)在\((0 ,2)\)递增，
故\(g(x)<g(2)=2\)，
故\(a≥2\)，
\({\color{Red}{ 方法二 \quad 数形结合法}}\)
令\(t(x)=-3x^2+2ax+4\)，它是开口向下，过定点\((0 ,4)\)，
结合图像可知若要\((*)\)成立，只需要\(t(2)≥0\)\(⇒-12+4a+4≥0⇒a≥2\).
【点拨】
① 若函数\(y=f(x)\)在某个区间\((a ,b)\)内单调递增，则\(∀x∈(a ,b)\) ,\(f^{\prime}(x)≥0\)\({\color{Red}{(含等号) }}\)恒成立，但不存在一区间\((c ,d)⊆(a ,b)\)内使得\(f^{\prime}(x)=0\)；
② 处理恒成立问题，方法多样，比如直接转化为最值问题，利用分离参数法转化为最值问题，数形结合等.
 

【典题3】 已知函数\(f(x)\)是定义在\(R\)上的奇函数，其导函数为\(f'(x)\)，且对任意实数\(x\)都有\(f(x)+f'(x)>1\)，则不等式\(e^x f(x)>e^x-1\)的解集为\(\underline{\quad \quad}\).
【解析】设\(g(x)=e^x [f(x)-1]\)，
则\(g^{\prime}(x)=e^x [f(x)-1]+e^x f^{\prime} (x)\)\(=e^x [f(x)+f^{\prime}(x)-1]>0\)．
故\(g(x)\)在\(R\)上单调递增，
因为\(f(x)\)是定义在\(R\)上的奇函数，所以\(f(0)=0\)，
所以\(g(0)=-1\)，
而不等式\(e^x f(x)>e^x-1⇒e^x [f(x)-1]>-1\)，
即\(g(x)>g(0)\)，
又\(∵g(x)\)在\(R\)上单调递增，\(∴x>0\)．
【点拨】
本题属于构造函数题型，如何构造呢？角度有二
（1） 从已知条件\(f(x)+f^{\prime}(x)>1⇒f(x)+f^{\prime} (x)-1>0\)入手，
思考\([某函数g(x)]^{\prime}=f(x)+f^{\prime}(x)-1\)，
这需要熟悉求导法则的逆运用，下表举例供参考(其中c是常数)：
①\(f^{\prime} (x)+h'(x)\)形式，构造函数\(g(x)=f(x)+h(x)+c\)；
②\(xf'(x)+f(x)\)形式，构造函数 \(g(x)=xf(x)+c\)；
③\(xf'(x)+nf(x)\)形式，构造函数\(g(x)=x^n f(x)+c\)；
④\(xf'(x)－f(x)\)形式，构造函数\(g(x)=\dfrac{f(x)}{x}+c\)；
⑤\(f^{\prime} (x)+f(x)\)形式，构造函数\(g(x)=e^x f(x)+c\)；
⑥\(f^{\prime} (x)-f(x)\)形式，构造函数\(g(x)=\dfrac{f(x)}{e^x} +c\)；
形式多样，不需要死记，要灵活运用，本题可利用第(5)个例子.
（2）从求证入手，要求不等式\(e^x f(x)>e^x-1\)，变形得\(e^x [f(x)-1]+1>0\)，想到构造函数\(g(x)=e^x [f(x)-1]+1\)也不难.
 

【典题4】 求函数\(f(x)=\dfrac{x^2-1}{2}-xlnx\)的单调区间.
【解析】函数\(f(x)\)的定义域是\((0 ,+∞)\)，
\({\color{Red}{(注意定义域) }}\)
由\(f(x)=\dfrac{x^2-1}{2}-xlnx\)，得\(f'(x)=x-lnx-1\)，
令\(g(x)=x-lnx-1\)，则\(g'(x)=1-\dfrac{1}{x}\)，
令\(g'(x)>0\)，解得\(x>1\)，
令\(g'(x)<0\)，解得\(0<x<1\)，
故\(g(x)\)在\((0 ,1)\)递减，在\((1,+∞)\)递增，
故\(f'(x)≥f'(1)=0\)，
故\(f(x)\)在\((0 ,+∞)\)递增，无递减区间.
【点拨】
① 本题其实是对原函数进行了“二次求导”，思路可以如下
求原函数\(f(x)=\dfrac{x^2-1}{2}-xlnx\)的单调区间
\(⇔\)分析导函数\(f'(x)=x-lnx-1\)的正负性(即\(y=f'(x)\)的零点问题)
\(⇔\)若能画出导函数\(y=f'(x)\)的图像一切就清楚，那就再分析\(y=x-lnx-1\)的单调性和最值，故二次求导了.
② 原函数的单调性与导函数的正负性相关，分析导函数的正负性利用注重导函数的零点问题；
③\(lnx≤x-1\)是个重要的不等式.
 

巩固练习

1(★) 已知定义在区间\((-2 ,2)\)上的函数\(y=f(x)\)的图象如图所示，若函数\(f'(x)\)是\(f(x)\)的导函数，则不等式\(\dfrac{f^{\prime}(x)}{x+1}>0\)的解集为\(\underline{\quad \quad}\) .

 

2(★★) 已知\(x>0\)，\(a=x\)，\(b=x-\dfrac{x^2}{2}\)，\(c=ln(1+x)\)，则(　　)
A．\(c<b<a\) \(\qquad \qquad\) B．\(b<a<c\) \(\qquad \qquad\) C．\(c<a<b\) \(\qquad \qquad\) D．\(b<c<a\)
 

3(★★) 已知定义在\(R\)上的函数\(f(x\))满足\(f(1)=3\)，对\(∀x∈R\)恒有\(f'(x)<2\)，则\(f(x)≥2x+1\)的解集为(　　)
A.\([1 ,+∞)\) \(\qquad \qquad \qquad \qquad\)B.\((－∞ ,1]\) \(\qquad \qquad \qquad \qquad\) C. \((1 ,+∞)\) \(\qquad \qquad \qquad \qquad\) D.\((－∞ ,1)\)
 

4(★★) 已知函数\(f(x)=x^2-x\sin x\)，若\(a=f(log_{0.2}⁡3)\)，\(b=f(log_3⁡0.2)\)，\(c=f(0.2^3)\)则(　　)
A.\(a>b>c\) \(\qquad \qquad\)B.\(b>a>c\) \(\qquad \qquad\)C.\(c>b>a\) \(\qquad \qquad\) D.\(b>c>a\)
 

5(★★) 若函数\(f(x)=\sin2x-4x-m\sin x\)在\([0 ,2π]\)上单调递减，则实数\(m\)的取值范围为(　　)
A.\((-2，2)\) \(\qquad \qquad \qquad \qquad\) B.\([-2，2]\) \(\qquad \qquad \qquad \qquad\) C.\((-1，1)\) \(\qquad \qquad \qquad \qquad\) D.\([-1，1]\)
 

6(★★★) 定义在\((0 ,+∞)\)上的函数\(f(x)\)满足\(f(x)>0\)，\(f'(x)\)为\(f(x)\)的导函数，且\(2f(x)<xf'(x)<3f(x)\)对\(x∈(0 ,+∞)\)恒成立，则\(\dfrac{f(2)}{f(3)}\)的取值范围是(　　)
A.\(\left(\dfrac{8}{27}, \dfrac{4}{9}\right)\) \(\qquad \qquad\)B.\(\left(-∞ ,\dfrac{8}{27}\right)\) \(\qquad \qquad\) C.\(\left(\dfrac{4}{9},1\right)\) \(\qquad \qquad\) D.\(\left(\dfrac{4}{9},+∞\right)\)
 

7(★★★) 求函数\(f(x)=e^{x-1}-x \ln x\)的单调性.
 
 

答案

1. \((-2 ,-1)∪(-1 ,1)\)
2. \(D\)
3. \(B\)
4. \(B\)
5. \(B\)
6. \(A\)
7. 函数\(f(x)\)的单调递增区间为\((0 ,+∞)\)，无单调递减区间.

 

【题型二】 含参函数的单调性

【典题1】 讨论\(f(x)=-\ln x+a x+\dfrac{a-1}{x}-1\)的单调性.
【解析】\(y=f(x)\)的定义域为\((0 ,+∞)\)，
\({\color{Red}{(注意定义域) }}\)
\(f^{\prime}(x)=-\dfrac{1}{x}+a-\dfrac{a-1}{x^{2}}\)\(=\dfrac{a x^{2}-x+1-a}{x^{2}}\)\(=\dfrac{(x-1)(a x+a-1)}{x^{2}}\)，
\({\color{Red}{(通分，因式分解是常规操作) }}\)
令\(g(x)=(x-1)(ax+a-1)\) ,\(x∈(0 ,+∞)\)；
\({\color{Red} {(g(x) 与f^{\prime}(x)的符号相同)}}\)
\({\color{Red}{(第一步：讨论函数类型) }}\)
(1)当\(a=0\)时，\(g(x)=-x+1\)
当\(x∈(0 ,1)\)时，\(g(x)>0\)，即\(f^{\prime} (x)>0\)，函数\(f(x)\)单调递增；
当\(x∈(1 ,+∞)\)时，\(g(x)<0\)，即\(f^{\prime} (x)<0\)，函数\(f(x)\)单调递减；
(2)当\(a≠0\)时，令\(g(x)=0\)，解得\(x_1=1\) ,\(x_2=\dfrac{1}{a}-1\)；
\({\color{Red}{(第二步：讨论二次函数开口方向) }}\)
①当\(a<0\)时，抛物线\(g(x)=(x-1)(ax+a-1)\)开口向下，
由于\(\dfrac{1}{a}-1<0\)
\({\color{Red}{ (留意导函数零点和定义域端点0的大小)}}\)
\(x∈(0 ,1)\)时，\(g(x)>0\)，即\(f^{\prime} (x)>0\)，函数\(f(x)\)单调递增；
\(x∈(1 ,+∞)\)时，\(g(x)<0\)，即\(f^{\prime} (x)<0\)，函数\(f(x)\)单调递减.

②当\(a>0\)时，抛物线\(g(x)=(x-1)(ax+a-1)\)开口向上，
\({\color{Red}{(第三步：比较导函数零点大小) }}\)

(i)当\(a=\dfrac{1}{2}\)时，\(x_1=x_2\)，\(g(x)>0\)恒成立，
\({\color{Red}{(不要忘了两根相等的情况) }}\)
此时\(f^{\prime} (x)≥0\)，函数\(f(x)\)在\((0 ,+∞)\)上单调递增；

(ii)当\(0<a<\dfrac{1}{2}\)时，\(0<1<\dfrac{1}{a}-1\)，\(0<x_1< x_2\) ,
\(x∈(0 ,1)\)时，\(g(x)>0\)，即\(f^{\prime}(x)>0\)，函数\(f(x)\)单调递增；
\(x∈(1 ,\dfrac{1}{a}-1)\)时，\(g(x)<0\)，即\(f^{\prime}(x)<0\)，函数\(f(x)\)单调递减；
\(x∈(\dfrac{1}{a}-1 ,+∞)\)时，\(g(x)>0\),即\(f^{\prime}(x)>0\)，函数\(f(x)\)单调递增；

(ⅲ)当\(\dfrac{1}{2}<a<1\)时，\(0<\dfrac{1}{a}-1<1\) ,\(0<x_2< x_1\)
\(x∈(0 ,\dfrac{1}{a}-1)\)时，\(g(x)>0\) ,即\(f^{\prime}(x)>0\)，函数\(f(x)\)单调递增；
\(x∈(\dfrac{1}{a}-1,1)\)时，\(g(x)<0\)，即\(f^{\prime}(x)<0\)，函数\(f(x)\)单调递减；
\(x∈(1 ,+∞)\)时，\(g(x)>0\)，即\(f^{\prime}(x)>0\)，函数\(f(x)\)单调递增；

(ⅳ)当\(a≥1\)时，\(\dfrac{1}{a}-1≤0\)，\(x_2<0<x_1\)
\({\color{Red}{ (留意导函数零点和定义域端点0的大小) }}\)
\(x∈(0 ,1)\)时，\(g(x)<0\),即\(f^{\prime} (x)<0\)，函数\(f(x)\)单调递减；
\(x∈(1 ,+∞)\)时，\(g(x)>0\)，即\(f^{\prime}(x)>0\)，函数\(f(x)\)单调递增；
综上所述
当\(a≤0\)时，函数\(f(x)\)在\((0 ,1)\)上单调递增 , 在\((1 ,+∞)\)上单调递减；
当\(a=\dfrac{1}{2}\)时，函数\(f(x)\)在\((0 ,+∞)\)上单调递增；
当\(0<a<\dfrac{1}{2}\)时，函数\(f(x)\)在\((0 ,1)\) ,\((\dfrac{1}{a}-1 ,+∞)\)上单调递增 , 在\((1 ,\dfrac{1}{a}-1)\)上单调递减；
当\(\dfrac{1}{2}<a<1\)时，函数\(f(x)\)在\((0 ,\dfrac{1}{a}-1)\) ,\((1 ,+∞)\)单调递增，在\((\dfrac{1}{a}-1 ,1)\)单调递减；
当\(a≥1\)时，函数\(f(x)\)在\((0 ,1)\)单调递减 , 在\((1 ,+∞)\)单调递增.
【点拨】
①原函数的单调性等价于导函数的正负性，我们注重导函数是否存在零点，零点的个数，零点的大小等；
②求导后，通分、因式分解是个好习惯，
\(f^{\prime}(x)=-\dfrac{1}{x}+a-\dfrac{a-1}{x^{2}}\)\(=\dfrac{a x^{2}-x+1-a}{x^{2}}\)\(=\dfrac{(x-1)(a x+a-1)}{x^{2}}\) ；能因式分解说明导函数存在零点，本题就不需要考虑讨论判别式\(∆\).
③ 本题分类讨论思路

④ 在第二，第三步讨论中，要注意导函数零点和定义域端点\(0\)的大小.
⑤ 在讨论繁琐时，建议以思维导图形式，画“导函数图像”梳理思路，并画上对应每个分类讨论步骤中导函数与原函数的草图.
 

【典题2】 已知函数\(f(x)=e^x-2ae^{-x}-(2+a)x\)的单调性.
【解析】\(f^{\prime}(x)=e^{x}+2 a e^{-x}-(2+a)\)\(=\dfrac{\left(e^{x}-2\right)\left(e^{x}-a\right)}{e^{x}}\)，
(1)若\(a≤0\)时，\(e^x-a>0\)，
由\(e^x－2=0\)，解得\(x=ln2\)，
当\(x<ln2\)时，\(f^{\prime}(x)<0\)；当\(x>ln2\)，\(f^{\prime} (x)>0\)，
故\(f(x)\)在\((-∞ ,ln2)\)递减，在\((ln2 ,+∞)\)递增；
(2)若\(a>0\)时，
由\(f^{\prime}(x)=0\)，解得\(x_1=ln2\)或\(x_2=lna\)，
①当\(0<a<2\)时，\(x_2< x_1\)，
当\(lna<x<ln2\)时，\(f^{\prime} (x)<0\)；
当\(x>ln2\)或\(x<lna\)时，\(f^{\prime} (x)>0\)，
故\(f(x)\)在\((lna ,ln2)\)递减，在\((-∞ ,lna)\)，\((ln2 ,+∞)\)递增，
②当\(a=2\)时，\(x_2= x_1\)，\(f^{\prime} (x)≥0\)在\(R\)上恒成立，
故\(f(x)\)在\(R\)上单调递增，
③当\(a>2\)时，\(x_1< x_2\)，
当\(ln2<x<lna\)时，\(f^{\prime}(x)<0\)；
当\(x>lna\)或\(x<ln2\)时，\(f^{\prime} (x)>0\)，
故\(f(x)\)在\((ln2 ,lna)\)递减，在\((-∞ ,ln2)\),\((lna ,+∞)\)上单调递增；

综上：当\(a≤0\)，\(f(x)\)在\((-∞ ,ln2)\)递减，在\((ln2 ,+∞)\)递增，
当\(0<a<2\)时，\(f(x)\)在\((lna ,ln2)\)递减，在\((-∞ ,lna)\) ,\((ln2 ,+∞)\)递增，
当\(a=2\)时，\(f(x)\)在\(R\)上单调递增，
当\(a>2\)时，\(f(x)\)在\((ln2 ,lna)\)递减，在\((-∞ ,ln2)\) ,\((lna ,+∞)\)上单调递增．

【点拨】
① 令\(g(x)=(e^x-2)(e^x-a)\)，\(∵e^x>0\)，
\(∴ y=f^{\prime}(x)\)与\(y=g(x)\)的正负性一致，若令\(g(x)=0\)，解得\(x=ln2\)或\(x=lna\)是错的，因为当\(a>0\)时\(lna\)才有意义，故要按照\(a>0\)和\(a≤0\)分类讨论；
② 若\(a>0\)时，零点有两个\(x_1=ln2\)或\(x_2=lna\)，讨论\(g(x)=(e^x-2)(e^x-a)\)的正负性，
由于\(y=e^x-2\)与\(y=x-ln2\)的正负性一样，
所以\(g(x)=(e^x-2)(e^x-a)\)与\(y=(x-ln2)(x-lna)\)的正负性一样.
③ 分类讨论思维导图如下

\({\color{Red}{ 分类讨论有两点较难的地方}}\)
(1) 分类的“不漏不重”:把每段分类看成一个集合，每两个集合间交集为空集即为“不重”，所有集合的并集是全集即为“不漏”；
(2) 分类的标准:在利用导数求含参函数的单调性，归纳成以下方法，仅供参考理解，

• 导函数是否存在零点；
• 若有零点，有几个？有两个以上，再比较零点大小；
• 零点与定义域端点的大小比较.

整个分类讨论的思考过程，结合导函数与原函数的图像进行分析能让思路更清晰.
 

【典题3】 设函数\(f(x)=e^x-\dfrac{1}{2} x^2-ax\)的单调性.
【解析】\(f^{\prime}(x)=e^x-x-a\)，
令函数\(g(x)=f^{\prime}(x)\)，则\(g^{\prime}(x)=e^x-1\)，
令\(g^{\prime}(x)>0\)，解得：\(x>0\)，
令\(g^{\prime} (x)<0\)，解得：\(x<0\)，
故\(g(x)\)在\((-∞ ,0)\)递减，在\((0 ,+∞)\)递增，
故\(g(x)_{min}=g(0)=1-a\)，
当\(a≤1\)时，\(g(x)_{min}=1-a≥0\)，则\(f(x)\)在\(R\)是单调递增，
当\(a>1\)时，\(g(x)_{min}=1-a<0\)，
易知当\(x→-∞\)时，\(g(x)→+∞\)，当\(x→+∞\)时，\(g(x)→+∞\)，
由零点存在性定理知：存在\(x_1 ,x_2\)，使得\(g(x_1)=g(x_2)=0\)，
不妨设\(x_1<x_2\)，
当\(x∈(-∞ ,x_1)\)时，\(g(x)>0\)，即\(f^{\prime}(x)>0\)，
当\(x∈(x_1 ,x_2)\)时，\(g(x)<0\)，即\(f^{\prime}(x)<0\)，
当\(x∈(x_2 ,+∞)\)时，\(g(x)>0\)，即\(f^{\prime}(x)>0\)，
故函数\(f(x)\)在\((-∞ ,x_1)\)递增，在\((x_1 ,x_2)\)递减，在\((x_2 ,+∞)\)递增.
综上，当\(a≤1\)时，\(f(x)\)在R是单调递增；当\(a>1\)时，\(f(x)\)先递增再递减再递增.
 

巩固练习

1(★★) 求函数\(f(x)=alnx-ax-3\)的单调区间.
 

2(★★) 求函数\(f(x)=ax^2+(2-a)lnx+2\)的单调性.
 

3(★★★) 求函数\(f(x)=-\dfrac{1}{2} a(x-1)^2+(x-2) e^x (a>0)\)的单调性.

 

答案

1. 若\(a=0\)，原函数不具有单调性；
   若\(a>0\)，函数\(f(x)\)在\((0 ,1)\)递增，在\([1 ,+∞)\)递减；
   若\(a<0\)，函数\(f(x)\)在\((0 ,1)\)递减，在\([1 ,+∞)\) 递增.
2. \(a<0\)时，函数\(f(x)\)在\(\left(0, \sqrt{\dfrac{a-2}{2 a}}\right)\)上单调递增，在\(( \sqrt{\dfrac{a-2}{2 a}}，+∞)\)单调递减．
   \(0≤a≤2\)时，函数\(f(x)\)在\((0 ,+∞)\)上单调递增，
   \(a>2\)时，函数\(f(x)\)在\((0，\sqrt{\dfrac{a-2}{2 a}})\)上单调递减，在\((\sqrt{\dfrac{a-2}{2 a}}，+∞)\)单调递增．
3. (i)当\(0<a<e\)时，\(f(x)\)在\((1 ,+∞)\),\((-∞ ,lna)\)上递增，\(f(x)\)在\((lna ,1)\)上递减；
   (ii)当\(a=e\)时， \(f(x)\)在\(R\)上单调递增；
   (iii)当\(a>e\)时，\(f(x)\)在\((lna ,+∞)\) ,\((-∞ ,1)\)上递增，\(f(x)\)在\((1 ,lna)\)上递减.
    

【题型三】函数单调性的应用

【典题1】 已知\(a<5\)且\(ae^5=5e^a\)，\(b<4\)且\(be^4=4e^b\)，\(c<3\)且\(ce^3=3e^c\)，则(　　)
A．\(c<b<a\) \(\qquad \qquad \qquad \qquad\) B． \(b<c<a\) \(\qquad \qquad \qquad \qquad\) C．\(a<c<b\) \(\qquad \qquad \qquad \qquad\) D． \(a<b<c\)
【解析】根据题意，设\(f(x)=\dfrac{e^{x}}{x}\)， (同构)
\(a<5\)且\(ae^5=5e^a\)，变形可得\(\dfrac{e^{a}}{a}=\dfrac{e^{5}}{5}\)，即\(f(a)=f(5)\)，
\(b<4\)且\(be^4=4e^b\)，变形可得\(\dfrac{e^{b}}{b}=\dfrac{e^{4}}{4}\)，即\(f(b)=f(4)\)，
\(c<3\)且\(ce^3=3e^c\)，变形可得\(\dfrac{e^{c}}{c}=\dfrac{e^{3}}{3}\)，即\(f(c)=f(3)\)，
\(f(x)=\dfrac{e^{x}}{x}\)，其导数\(f^{\prime}(x)=\dfrac{e^{x}(x-1)}{x^{2}}\)，
在区间\((0 ,1)\)上，\(f'(x)<0\)，则\(f(x)\)为减函数，
在区间\((1 ,+∞)\)上，\(f'(x)>0\)，则\(f(x)\)为增函数，
其草图如图，则有\(0<a<b<c<1\)，

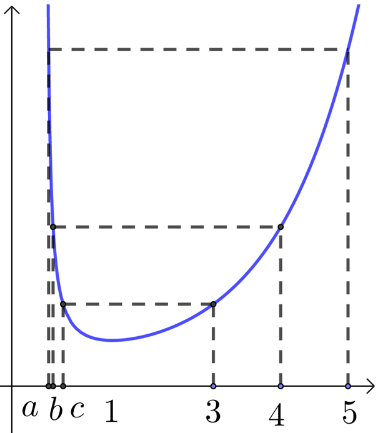
故选：\(D\)．
【点拨】
① 本题通过构造函数再利用单调性判断大小. 如何构造函数呢？
通过变形寻找“相似结构”为关键，\(ae^5=5e^a\)通过移项变形为\(\dfrac{e^{a}}{a}=\dfrac{e^{5}}{5}\)，此时等式两边式子的结构想到函数\(f(x)=\dfrac{e^{x}}{x}\).
下面再举些例子：
(1) \(x-e^y>y-e^x\)移项易得函数\(f(x)=x+e^x\)；
(2)\(\ln \dfrac{x_{1}}{x_{2}}<e^{x_{1}}-e^{x_{2}}\)变形可得函数\(f(x)=e^x-lnx\)；
(3)\(m^{n}>n^{m}\)两边取对数得\(n\cdot \ln m>m\cdot \ln n\)易得函数\(f(x)=\dfrac{lnx}{x}\).
(4)\(\dfrac{x_{1}}{x_{2}}<\sqrt{e^{x_{1}-x_{2}}}\)两边取对数得\(\ln \dfrac{x_{1}}{x_{2}}<\dfrac{1}{2}\left(x_{1}-x_{2}\right)\)可得函数\(f(x)=lnx-\dfrac{1}{2} x\)，或者两边平方得\(\dfrac{x_{1}^{2}}{x_{2}^{2}}<\dfrac{e^{x_{1}}}{e^{x_{2}}}\)可得函数\(f(x)=x^2 e^x\).
(5)\(alna>be^b\)通过变形\(lna\cdot e^{lna}>be^b\)可得函数 \(f(x)=xe^x\), 则有\(f(lna)>f(b)\).
② \(f(x)=\dfrac{e^x}{x}\)是常见的超越函数，其图象如下图.

 

【典题2】 已知\(0<α<β<\dfrac{π}{2}\)，则下列不等式中恒成立的是(　　)
A．\(α^α<β^β\) \(\qquad \qquad \qquad \qquad\) B．\(α^α≤β^β\) \(\qquad \qquad \qquad \qquad\) C．\(α^β>β^α\) \(\qquad \qquad \qquad \qquad\) D．\(α^β<β^α\)
【解析】构造函数\(f(x)=\dfrac{lnx}{x}\)，则\(f'(x)=\dfrac{1-lnx}{x}\)，
令\(f'(x)>0\)，解得\(0<x<e\)，令\(f'(x)<0\)，解得\(x>e\)，
\(∴\)函数\(f(x)\)在\((0，e)\)上单调递增，在\((e，+∞)\)上单调递减，
\(∴\)函数\(f(x)\)在\((0 ,\dfrac{π}{2})\)上单调递增，
\(∴f(α)<f(β)\)，即\(\dfrac{\ln \alpha}{\alpha}<\dfrac{\ln \beta}{\beta}\)，
\(∴βlnα<αlnβ\)，即\(lnα^β<lnβ^α⇒α^β<β^α\)，
故选：\(D\)．
【点拨】
① 遇到“指数型函数”可两边取对数找到需要构造的函数.
② 对于选项\(α^α<β^β\)左右式子“结构相似”可构造函数\(g(x)=x^x\) , 但这函数复杂故放弃，两边取对数可得\(αlnα<βlnβ\), 则可构造函数\(f(x)=xlnx\), 它在\((0 ,\dfrac{1}{e})\)上递减，\((\dfrac{1}{e} ,+∞)\)上递增 , 故判断不了\(α、β\)大小.
③\(f(x)=\dfrac{lnx}{x}\)是常见的超越函数，其图象如下图.

 

巩固练习

1(★★) 若\(a=\dfrac{\ln 4}{4}\) ,\(, b=\dfrac{\ln 5.3}{5.3}\)，\(c=\dfrac{\ln 6}{6}\)，则\(a、b、c\)的大小是(　　)
A．\(a<b<c\) \(\qquad \qquad \qquad \qquad\) B．\(c<b<a\) \(\qquad \qquad \qquad \qquad\) C．\(c<a<b\) \(\qquad \qquad \qquad \qquad\) D．\(b<a<c\)
 

2(★★) 若\(α ,β∈[-\dfrac{π}{2},\dfrac{π}{2}]\)，且\(α\sinα-β\sinβ>\cosα-\cosβ\)，则下列结论中必定成立的是(　　)
A．\(α>β\) \(\qquad \qquad \qquad \qquad\) B．\(α>－β\) \(\qquad \qquad \qquad \qquad\) C．\(α<β\) \(\qquad \qquad \qquad \qquad\) D．\(|α|>|β|\)
 

3(★★) 若\(\ln x-\ln y<\dfrac{1}{\ln x}-\dfrac{1}{\ln y}(x>1, y>1)\)，则(　　)
A．\(e^{y-x}>1\) \(\qquad \qquad \qquad \qquad\) B．\(e^{y-x}<1\) \(\qquad \qquad \qquad \qquad\) C．\(e^{y-x-1}>1\) \(\qquad \qquad \qquad \qquad\) D．\(e^{y-x-1}<1\)
 

4(★★★) 已知\(α ,β∈(0 ,π)\)，\(α≠β\)，若\(e^α-e^β=\cosα-2\cosβ\)，则下列结论一定成立的是(　　)
A．\(\sinα<\sinβ\) \(\qquad \qquad \qquad \qquad\)B．\(\cosα<\cosβ\) \(\qquad \qquad \qquad \qquad\) C．\(\sinα>\sinβ\) \(\qquad \qquad \qquad \qquad\) D．\(\cosα>\cosβ\)
 

参考答案

1. \(B\)
2. \(D\)
3. \(A\)
4. \(A\)