5.2 导数的几何意义
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第二册同步拔高,难度3颗星!
模块导图
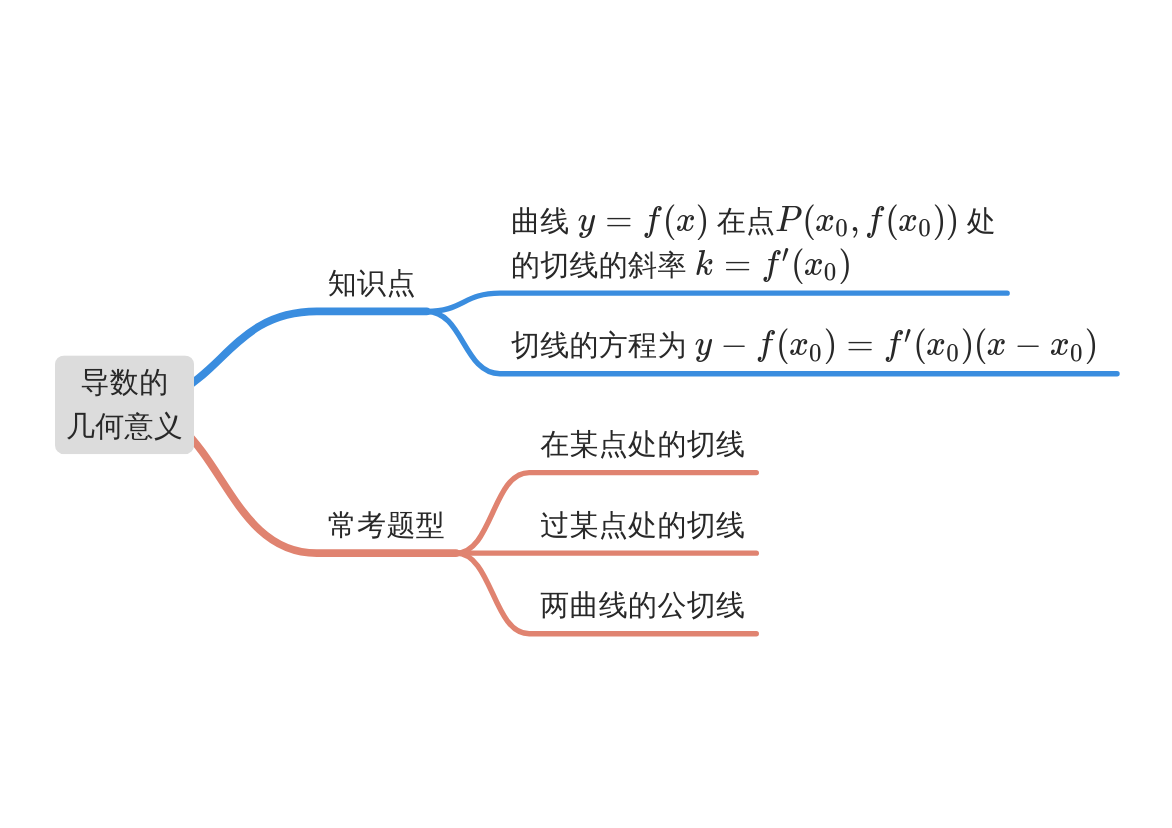
知识剖析
导数的几何意义
函数\(y=f(x)\)在点\(x=x_0\)处的导数的几何意义是曲线\(y=f(x)\)在点\(P(x_0 ,f(x_0))\)处的切线的斜率,即:曲线\(y=f(x)\)在点\(P(x_0 ,f(x_0))\)处的切线\(l\)的斜率\(k=f'(x_0)\),
切线\(l\)的方程为\(y-f(x_0)=f'(x_0)(x-x_0)\).
"过点\(x=x_0\)”与"在点\(x=x_0\)处"的区别
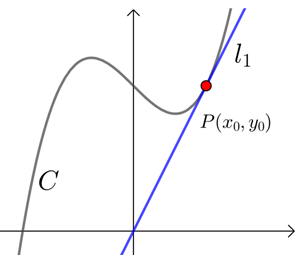
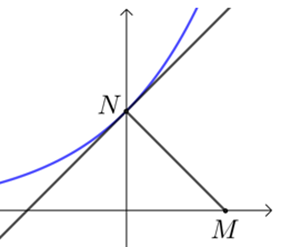
曲线\(C:y=f(x)\)在点\(P(x_0 ,y_0)\)处的切线指的是\(P\)为切点的切线,如图一;
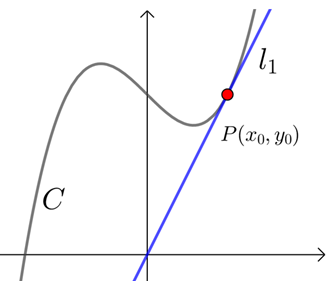
过点\(P(x_0 ,y_0)\)的切线是指切线过点\(P\),点\(P\)是否切点均可,切线可多条,如图二.
 $\qquad \qquad$
$\qquad \qquad$
经典例题
【题型一】在某点处的切线
【典题1】 函数\(y=f(x)\)的图象如图所示,\(f'(x)\)是函数\(f(x)\)的导函数,下列数值排序正确的是( )

A.\(f^ {\prime}(2)<f^{\prime} (6)<f(6)-f(2)<0\) \(\qquad \qquad\) B.\(f^{\prime}(6)<f^{\prime}(2)<f(6)-f(2)<0\)
C.\(f(6)-f(2)<f^{\prime} (6)<f^{\prime}(2)<0\) \(\qquad \qquad\) D.\(f^{\prime} (2)<f(6)-f(2)<f^{\prime}(6)<0\)
【解析】根据题意,设\(M(2 ,f(2))\)、\(N(6,f(6))\)为函数的上的点,
则\(f'(2)\)为函数\(f(x)\)在\(x=2\)处切线的斜率\(k_1\),
\(f^{\prime}(6)\)为函数\(f(x)\)在\(x=6\)处切线的斜率\(k_2\),
\(f(6)-f(2)=\dfrac{f(6)-f(2)}{3-2}\)为直线\(MN\)的斜率\(k_3\),
结合图象分析可得\(k_1<k_3<k_2<0\),
即\(f^{\prime} (2)<f(6)-f(2)<f^{\prime}(6)<0\);
故选:\(D\).
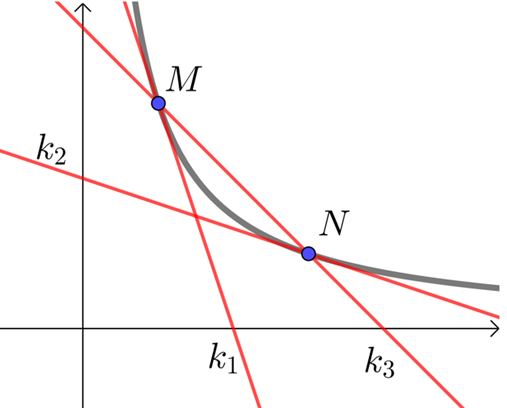
【点拨】\(k=tanα\),直线越靠近\(y\)轴,斜率\(|k|\)越大.
【典题2】 若直线\(y=x\)是曲线\(f(x)=x^3-3x^2+ax\)的切线,则\(a=\)\(\underline{\quad \quad}\).
【解析】依题意得\(f^{\prime}(x)=3x^2-6x+a\)
设切点\(P(x_0 ,y_0)\)
则由导数的几何意义可得 \(f^{\prime}(x_0 )=1⇒3x_0^2-6x_0+a=1\) ①
\(∵\)点\(P\)在切线\(y=x\)上 \(∴y_0=x_0\) ②
\(∵\)点\(P\)在曲线上 \(∴y_0=x_0^3-3x_0^2+ax_0\) ③
由①,②, ③联立得\(\left\{\begin{array}{l}
3 x_{0}^{2}-6 x_{0}+a=1 \\
y_{0}=x_{0} \\
y_{0}=x_{0}^{3}-3 x_{0}^{2}+a x_{0}
\end{array}\right.\),
解得\(a=1\)或\(\dfrac{13}{4}\)
\(∴a\)的值为\(1\)或\(\dfrac{13}{4}\).
【点拨】由于本题不知道切点,由待定系数法的想法,设切点\(P(x_0 ,y_0)\),它即在切线上又在曲线上,又由导数的几何意义得到了关于\(x_0 ,y_0 ,a\)的方程组!
【典题3】 已知\(M(1 ,0)\),\(N\)是曲线\(y=e^x\)上一点,则\(|MN|\)的最小值为\(\underline{\quad \quad}\) .
【解析】\(y=e^x\)的导数为\(y'=e^x\).
设\(N(m ,e^m)\),可得过\(N\)的切线的斜率为\(e^m\),
当\(MN\)垂直于切线时,\(|MN|\)取得最小值,
可得\(\dfrac{e^{m}}{m-1} \cdot e^{m}=-1\),即\(e^{2m}+m-1=0\),
因为\(f(x)=e^{2x}+x-1\)单调递增,且\(f(0)=0\),
所以\(m=0\),即\(N(0 ,1)\),
所以\(|MN|\)的最小值为\(\sqrt2\).
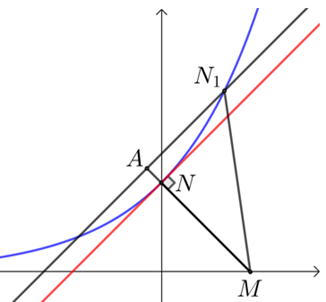
【点拨】当\(MN\)垂直切线时,\(|MN|\)取得最小值;如图,\(MN≤MA≤MN_1\).
巩固练习
1(★)已知函数\(f(x)\)在\(R\)上可导,其部分图象如图所示,设\(k=\dfrac{f\left(x_{1}\right)-f\left(x_{2}\right)}{x_{1}-x_{2}}\),则下列不等式正确的是( )

A.\(k<f'(x_1)<f'(x_2)\) \(\qquad \qquad \qquad \qquad\)B.\(f'(x_1)<k<f'(x_2)\) \(\qquad \qquad\)
C.\(f'(x_2)<f'(x_1)<k\) \(\qquad \qquad \qquad \qquad\)D.\(f'(x_1)<f'(x_2)<k\)
2(★)曲线\(y=x^3+lnx+1\)在点\((1 ,2)\)处的切线方程为\(\underline{\quad \quad}\).
3(★★)曲线\(y=lnx-\dfrac{1}{x}\)在\(x=1\)处的切线的倾斜角为\(α\),则\(sin2α=\)\(\underline{\quad \quad}\).
4(★★★)已知函数\(y=e^x\)的图象在点\((a_k ,e^{a_k})\)处的切线与\(x\)轴的交点的横坐标为\(a_{k+1}\),其中\(k∈N^*\),\(a_1=0\),则\(a_1+a_3+a_5=\)\(\underline{\quad \quad}\).
5(★★★)若函数\(f(x)=ax+\sinx\)的图象上存在互相垂直的切线,则实数\(a\)的值为\(\underline{\quad \quad}\).
参考答案
- \(B\)
- \(4x-y-2=0\)
- \(\dfrac{4}{5}\)
- \(-6\)
- \(0\)
【题型二】过某点处的切线
【典题1】 已知曲线\(f(x)=2x^3+4\),曲线过点\(P(-1 ,2)\)的切线方程.
【解析】\(∵f(x)=2x^3+4\) \(∴f^{\prime}(x)=6x^2\)
设切点为\((x_0 ,2x_0^3+4)\),则切线斜率\(k=f^{\prime}(x_0 )=6x_0^2\),
切线方程为\(y-(2x_0^3+4)=6x_0^2 (x-x_0 )\)\(⟹y=6x_0^2 x-4x_0^3+4\)
\(∵\)切线过点\(P(-1 ,2)\)
\(∴-6x_0^2-4x_0^3+4=2\)\(⇒2x_0^3+3x_0^2-1=0\)
解得\(x_0=-1\)或\(\dfrac{1}{2}\),
则切线方程为\(y=6x+8\)或\(y=\dfrac{3}{2}x+\dfrac{7}{2}\).
【点拨】
① 本题点\(P(-1 ,2)\)不一定是切点,故可先设切点\((x_0 ,2x_0^3+4)\),利用“在某点处的切线”方法求出含参数\(x_0\)的切线方程,再把点\(P\)代入求出\(x_0\),进而容易得到切线方程;
② 如何求解方程\(2x_0^3+3x_0^2-1=0\)?
\({\color{Red}{ 方法一 \quad 拆项分组因式分解}}\)
\(2x_0^3+3x_0^2-1=0\)
\(⇒3x_0^3+3x_0^2-(1+x_0^3 )=0\)\(⇒3x_0^2 (x_0+1)-(x_0+1)(x_0^2-x_0+1)=0\)\(⇒ (x_0+1)(2x_0^2-x_0-1)=0\)
\(⇒ (x_0+1)^2 (2x_0-1)=0\)
\(⇒x_0=-1\)或\(x_0=\dfrac{1}{2}\)
\({\color{Red}{ 方法二 \quad 待定系数法}}\)
先由方程特点猜出有一个解是\(x_0=-1\),则可知\(x_0+1\)是\(2x_0^3+3x_0^2-1\)的因式,
设\(2x_0^3+3x_0^2-1=(x_0+1)(2x_0+mx_0-1)\),把右式展开易得\(m=-1\),
则\(2x_0^3+3x_0^2-1=(x_0+1)(2x_0^2-x_0-1)\)\(=(x_0+1)^2 (2x_0-1)\)
\(∴x_0=-1\)或\(x_0=\dfrac{1}{2}\)
【典题2】 若过点\(P(-1 ,m)\)可以作三条直线与曲线\(C:y=xe^x\)相切,则\(m\)的取值范围是\(\underline{\quad \quad}\).
【解析】\(y^{\prime}=(x+1) e^x\)
设切点为\((x_0 ,x_0 e^{x_0})\),
过点\(P\)的切线方程为\(y=\left(x_{0}+1\right) e^{x_{0}}\left(x-x_{0}\right)+x_{0} e^{x_{0}}\),
代入点\(P\)坐标化简为\(m=\left(-x_{0}^{2}-x_{0}-1\right) e^{x_{0}}\),
即这个方程有三个不等根即可,
令\(f(x)=(-x^2-x-1) e^x\),
求导得到\(f^{\prime}(x)=(-x-1)(x+2) e^x\),
函数在\((-∞ ,-2)\)上单调递减,在\((-2 ,-1)\)上单调递增,在\((-1 ,+∞)\)上单调递减,
故得到\(f(-2)<m<f(-1)\)\(\Rightarrow-\dfrac{3}{e^{2}}<m<-\dfrac{1}{e}\)
答案为\((-\dfrac{3}{e^{2}},-\dfrac{1}{e})\).
【点拨】过某点作曲线的切线可以有多条,先求在曲线上一点处的切线方程,把问题转化为方程解的个数.
巩固练习
1(★★)已知曲线\(y=lnx\)的切线过原点,则此切线的斜率为\(\underline{\quad \quad}\).
2(★★)过点\(A(2 ,1)\)做曲线\(f(x)=x^3-3x\)的切线,最多有\(\underline{\quad \quad}\)条.
3(★★)已知曲线\(f(x)=4x^2\)的一条切线经过点\((0 ,-1)\),求该切线方程.
4(★★)已知函数\(f(x)=x^3-4x^2+5x-4\),求经过点\(A(2 ,-2)\)的曲线\(f(x)\)的切线方程.
参考答案
- \(\dfrac{1}{e}\)
- \(3\)
- \(y=2x-1\)或\(y=-2x-1\)
- \(y+2=0\)或\(x-y-4=0\)
【题型三】两曲线的公切线
【典题1】 若直线\(y=kx+b\)是曲线\(y=e^{x-2}\)的切线,也是曲线\(y=e^x-1\)的切线,则\(b=\)\(\underline{\quad \quad}\).
【解析】设直线\(y=kx+b\)与\(y=e^{x-2}\)和\(y=e^x-1\)的切点分别为\((x_1 ,e^{x_1-2})\)和\((x_2 ,e^{x_2}-1)\),
则切线分别为\(y-e^{x_1-2}=e^{x_1-2} (x-x_1)\),\(y-e^{x_2}+1=e^{x_2} (x-x_2)\)
化简得:\(y=e^{x_1-2} x+e^{x_1-2}-x_1 e^{x_1-2}\),\(y=e^{x_2} x+e^{x_2}-1-x_2 e^{x_2}\)
依题意有:\(\left\{\begin{array}{l}
e^{x_{1}-2}=e^{x_{2}} & (1)\\
e^{x_{1}-2}-x_{1} e^{x_{1}-2}=e^{x_{2}}-1-x_{2} e^{x_{2}} & (2)
\end{array}\right.\),
由方程①得\(x_1=2+x_2\),代入方程②解得\(x_2=-ln2\),
则\(b=e^{x_{2}}-1-x_{2} e^{x_{2}}=\dfrac{1}{2} \ln 2-\dfrac{1}{2}\).
故答案为:\(\dfrac{1}{2} \ln 2-\dfrac{1}{2}\).
【点拨】先分别求出两条切线,由于是公切线,所以它们是同一直线,两切线的斜率和\(y\)轴上的截距相等.
【典题2】 若曲线 \(C_1:y=x^2\)与曲线\(C_2:y=ae^x (a≠0)\)存在公共切线,则\(a\)的取值范围为\(\underline{\quad \quad}\).
【解析】\(y=x^2\)在点\((m ,m^2)\)的切线斜率为\(2m\),
切线方程为\(y=2m(x-m)+m^2=2mx-m^2\);
\(y=ae^x\)在点\((n ,ae^n)\)的切线斜率为\(ae^n\),
切线方程为\(y=ae^n x+a(1-n)e^n\);
如果两个曲线存在公共切线,那么两切线相同,
则有\(\left\{\begin{array}{l}
2 m=a e^{n} & (1) \\
-m^{2}=a(1-n) e^{n}&(2)
\end{array}\right.\),
\(∵a≠0\),\(∴m≠0\),
由②÷①得\(-m=2(1-n)\),即\(m=2n-2\),
代入\(2m=ae^n\)得\(4n-4=ae^n (*)\),
存在公共切线,等价于方程\((*)\)有解,
由\(y=4x-4\) ,\(y=ae^x\)的图象有交点即可.
设它们相切,切点为\(P(s ,t)\),
则\(ae^s=4\),且\(t=4s-4=ae^s\),
解得\(s=2,t=4\),\(a=\dfrac{4}{e^2}\) ,
由图易得要满足题意\(a≤\dfrac{4}{e^2}\),
又\(a≠0\),
故答案为\((-∞ ,0)∪(0 ,\dfrac{4}{e^2}]\).
【点拨】得到”\(4n-4=ae^n\)有解",可用分离参数法转化为\(a=\dfrac{4 n-4}{e^{n}}\)有解,
即\(y=a\)与\(f(x)=\dfrac{4 x-4}{e^{x}}\)有交点,从而转化为求函数的\(f(x)=\dfrac{4 x-4}{e^{x}}\)的值域;
\(\because f^{\prime}(x)=\dfrac{8 x-4}{e^{x}}\)
\(∴f(x)\)在\((-∞ ,2)\)递增,在\((2 ,+∞)\)递减,\(∴f(x)≤f(2)=\dfrac{4}{e^2}\)
\(∴a≤\dfrac{4}{e^2}\) 且\(a≠0\).
巩固练习
1(★★)已知曲线\(f(x)=xlnx\)在点\((e ,f(e))\)处的切线与曲线\(y=x^2+a\)相切,则\(a=\)\(\underline{\quad \quad}\).
2(★★)若存在过点\((1 ,0)\)的直线与曲线\(y=x^3\)和\(y=ax^2+\dfrac{15}{4} x-9\)都相切,则实数\(a=\)\(\underline{\quad \quad}\).
3(★★★)若二次函数\(f(x)=x^2+1\)的图象与曲线\(C:g(x)=ae^x+1(a>0)\)存在公共切线,则实数\(a\)的取值范围为\(\underline{\quad \quad}\).
4(★★★)若曲线\(y=x^2\)与\(y=a\ln x(a≠0)\)存在公共切线,则实数\(a\)的取值范围是\(\underline{\quad \quad}\).
参考答案
- \(1-e\)
- \(a=-\dfrac{25}{64}\)或\(-1\)
- \((0 ,\dfrac{4}{e^2} ]\)
- \((-∞ ,0)∪(0 ,2e]\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号